2  ดอกเบี้ย (Interest)

Importantหมายเหตุ

ก่อนเริ่มการคำนวณเชิงสัญลักษณ์ด้วยซิมไพ ขอให้ผู้อ่านทำการเรียกใช้คำสั่งดังต่อไปนี้ก่อน

from sympy import symbols, Eq, solve

เพื่อจะได้ไม่ต้องเรียกใช้งานทุกครั้ง

2.1 ดอกเบี้ยคืออะไร (What is Interest?)

ดอกเบี้ย คือ “ค่าตอบแทนของการใช้เงินในช่วงเวลาหนึ่ง” ผู้ให้ยืมเงินจะได้รับดอกเบี้ยเป็นการตอบแทนจากผู้ยืมเงินที่นำเงินนั้นไปใช้

มุมมองที่สำคัญ

• ถ้าเราให้คนอื่นยืมเงิน ดอกเบี้ยคือ รายได้ของเรา

• ถ้าเรายืมเงิน ดอกเบี้ยคือ ต้นทุนที่เราต้องจ่าย

โดยดอกเบี้ยที่ได้จะขึ้นอยู่กับตัวแปรหรือปัจจัย 3 ตัวเป็นหลัก

• $P$ = เงินต้น (Principal)

• $i$ = อัตราดอกเบี้ยต่อช่วงเวลา (interest rate per period)

• $t$ = จำนวนช่วงเวลา (number of periods)

2.2 คุณสมบัติทั่วไปของฟังก์ชันดอกเบี้ย (General Properties of Interest Functions)

ฟังก์ชันดอกเบี้ย (Interest Function) คือฟังก์ชันที่แสดงมูลค่าเงินสะสมเมื่อเวลาผ่านไป โดยมีคุณสมัติดังต่อไปนี้:

1. Initial Value $$a(0)=1$$ ฟังก์ชันสะสมต้องมีค่าเริ่มต้นเป็น 1 เสมอ หมายถึง 1 หน่วยของเงินในวันนี้มีค่าเป็น 1 หน่วยเสมอ

2. Monotonic Increasing $$a(t_2)>a(t_1)\text{for}{t}_2>t_1$$ ฟังก์ชันดอกเบี้ยเป็นฟังก์ชัน เพิ่มเสมอ เมื่อ $i>0$ นั่นคือเงินจะมีค่ามากขึ้นเมื่อเวลาผ่านไป

3. Multiplicative Property (Semigroup) $$a(s+t)=a(s)\cdot a(t)$$ โดยเฉพาะในดอกเบี้ยทบต้น สมบัตินี้สำคัญมากในแคลคูลัสของการเงิน เช่น การใช้ force of interest

4. Continuity and Differentiability (กรณีต่อเนื่อง): ในกรณีที่ $a(t)$ เป็นฟังก์ชันต่อเนื่อง เช่น $a(t)=e^{rt}$, เราสามารถหากำลังของดอกเบี้ย (force of interest) ได้ $$\delta (t)=\frac{a^{\prime }(t)}{a(t)}$$ ซึ่งบ่งบอกถึง อัตราดอกเบี้ยในช่วงเวลาเล็กมาก (instantaneous rate)

2.3 ตัวอย่างฟังก์ชันดอกเบี้ยมาตราฐาน

ฟังก์ชันดอกเบี้ยเป็นเครื่องมือพื้นฐานในคณิตศาสตร์การเงิน ใช้เพื่อวิเคราะห์มูลค่าเงินตามเวลา (time value of money) โดยแสดงความสัมพันธ์ระหว่างเงินต้น อัตราดอกเบี้ย และเวลา ซึ่งสามารถแบ่งได้เป็น 2 ประเภทหลัก คือ ดอกเบี้ยอย่างง่าย (Simple Interest) และ ดอกเบี้ยทบต้น (Compound Interest)

2.3.1 ดอกเบี้ยอย่างง่าย (Simple Interest)

Noteนิยาม

ดอกเบี้ยคำนวณจากเงินต้นเพียงอย่างเดียว ไม่สะสมดอกเบี้ยที่เกิดขึ้นในรอบต่อไป

$$\text{Interest}=P\cdot i\cdot t$$ ฟังก์ชันสะสม (Accumulation Function)

$$a(t)=1+it$$

คุณสมบัติ

• เป็น ฟังก์ชันเชิงเส้น (Linear)

• เงินสะสมเติบโตแบบ เส้นตรง

• ไม่มีการทบต้น

• ใช้งานง่าย เหมาะกับเงินกู้หรือการลงทุนระยะสั้น

• ดอกเบี้ยที่ได้รับในแต่ละงวดเท่ากันเสมอ

2.3.2 ดอกเบี้ยทบต้น (Compound Interest)

Noteนิยาม

ดอกเบี้ยคำนวณจาก เงินต้นรวมกับดอกเบี้ยที่เกิดขึ้นก่อนหน้า (ทบต้นทุกงวด) $$\text{Accumulated Value}=P\cdot (1+i{)}^t$$ ฟังก์ชันดอกเบี้ย $$a(t)=(1+i{)}^t$$ คุณสมบัติ

• เป็น ฟังก์ชันเอ็กซ์โปเนนเชียล (Exponential)

• เงินสะสมเติบโตแบบ เร่ง (ยิ่งเวลานาน ยิ่งเพิ่มเร็ว)

• ใช้ในการลงทุนระยะยาว เช่น หุ้น พันธบัตร

• มีคุณสมบัติของ semi-group $$a(s+t)=a(s)\cdot a(t)$$

• ถ้าใช้การทบต้นแบบต่อเนื่อง $$a(t)=e^{rt},\delta (t)=\frac{a^{\prime }(t)}{a(t)}=r$$ โดย $\delta (t)$ คือ force of interest

ตารางเปรียบเทียบ

คุณสมบัติ	ดอกเบี้ยอย่างง่าย	ดอกเบี้ยทบต้น
ฟังก์ชันสะสม $a(t)$	$1+it$	$(1+i{)}^t$
ประเภทฟังก์ชัน	เชิงเส้น (Linear)	เอ็กซ์โปเนนเชียล (Exponential)
ลักษณะการเติบโต	คงที่	เร่งขึ้นตามเวลา
มีการทบต้นหรือไม่	ไม่มี	มี
เหมาะกับ	เงินกู้/ลงทุนระยะสั้น	การลงทุนระยะยาว
Semi-group $a(s+t)=a(s)\cdot a(t)$	ไม่ใช่	ใช่

2.3.3 ตัวอย่างฟังก์ชันดอกเบี้ยแบบอื่น (Non-standard or Generalized Interest Functions)

1. Variable (Time-dependent) Interest Rate อัตราดอกเบี้ยไม่คงที่ ขึ้นกับเวลา $$a(t)=\exp ({\int }_0^t\delta (s)ds)$$

   • โดย $\delta (s)$ คือ force of interest ที่เปลี่ยนไปตามเวลา

   • ใช้ในกรณีที่อัตราดอกเบี้ยผันผวน เช่น ในตลาดตราสารหนี้

ตัวอย่าง $$\delta (t)=0.05+0.01t\Rightarrow a(t)=\exp (0.05t+0.005t^2)$$

2. Piecewise Interest Function อัตราดอกเบี้ยเปลี่ยนเป็นช่วง ๆ $$a(t)=\{\begin{array}{ll}(1+i_1{)}^t& \text{if }t\le T\\ (1+i_1{)}^T\cdot (1+i_2{)}^{t-T}& \text{if }t>T\end{array}$$

   • ใช้ในสัญญาที่กำหนดดอกเบี้ยคงที่ช่วงแรก แล้วเปลี่ยนในภายหลัง

ตัวอย่าง

• ปีที่ 1–5 อัตราดอกเบี้ย 5%

• หลังจากนั้น อัตราดอกเบี้ย 3%

3. Stochastic Interest Function อัตราดอกเบี้ยเป็น ตัวแปรสุ่ม ใช้ใน financial economics $$a(t)=\mathbb{E}[\exp \left({\int }_0^t{r}_{s}ds\right)]$$

   • $r_s$ stochastic interest rate process (เช่น Vasicek, CIR)

   • ใช้ในการวิเคราะห์ราคาอนุพันธ์ เช่นพันธบัตร หรือ swap

4. Stepwise (Discrete Change) อัตราดอกเบี้ยเพิ่มขึ้นแบบขั้นบันได เช่น โปรแกรมเงินฝากระยะยาว $$a(t)=\prod _{k=1}^t(1+i_k)$$

   • โดย $i_k$ คืออัตราดอกเบี้ยปีที่ $k$

   • ไม่ใช่ฟังก์ชันต่อเนื่องเหมือน compound ปกติ

ตัวอย่าง

• $i_1=0.03$, $i_2=0.04$, $i_3=0.05$

• $a(3)=(1+0.03)(1+0.04)(1+0.05)$

5. Hyperbolic Discount Function (Behavioral economics) ใช้ในพฤติกรรมของผู้บริโภคที่ลดค่าของอนาคตแบบ ไม่เป็นเลขชี้กำลัง (exponential) $$a(t)=\frac{1}{1+kt}$$

   • ไม่ใช่ดอกเบี้ยอย่างง่ายเพราะไม่เป็นเชิงเส้น

   • ไม่ใช่ดอกเบี้ยทบต้นเพราะไม่เป็นเลขชี้กำลัง

   • ใช้ใน behavioral finance เช่น วิเคราะห์การเลือกของมนุษย์

สรุป

แบบ	ฟังก์ชัน	ใช้เมื่อ
Time-dependent	$\exp ({\int }_0^t\delta (s)ds)$	อัตราดอกเบี้ยแปรผัน
Piecewise	เปลี่ยนดอกเบี้ยเป็นช่วง	สัญญาดอกเบี้ยเปลี่ยนระยะ
Stochastic	$\mathbb{E}[\cdots ]$	วิเคราะห์ตราสารอนุพันธ์
Stepwise	$\prod (1+i_k)$	เงินฝาก/พันธบัตรแบบขั้นบันได
Hyperbolic	$\frac{1}{1+kt}$	การเงินพฤติกรรม

ในหนังสือเล่มนี้พิจารณาดอกเบี้ยอย่างง่ายและดอกเบี้ยทบต้นเท่านั้น

จำนวนดอกเบี้ยที่ได้รับคือผลตอบแทนที่ได้จากการลงทุน นั่นคือเงินสะสมลบด้วยเงินลงทุนนั่นเอง

1. ดอกเบี้ยอย่างง่าย (Simple Interest) $$\text{Interest}=P\cdot i\cdot t$$

2. ดอกเบี้ยทบต้น (Compound Interest) $$\text{Future Value}=P\cdot (1+i{)}^t-P$$ ตัวอย่างการสร้างฟังก์ชันเบี้ยและการคำนวณด้วยซิมไพ

3. ดอกเบี้ยอย่างง่าย (Simple Interest) สูตร $$A=P(1+it)$$ โดยที่

• $A$ มูลค่ารวมเมื่อครบกำหนด

• $P$ เงินต้น

• $i$ อัตราดอกเบี้ยต่อปี

• $t$ ระยะเวลา (ปี)

# กำหนดตัวแปร
P, i, t = symbols('P i t', positive=True)
# สมการดอกเบี้ยอย่างง่าย
simple_int =  P * (1 + i * t)
# แสดงสมการ
simple_int

${\displaystyle P(it+1)}$

ถ้าต้องการแทนค่าลงไป เช่น $P=1000$, $i=0.05$, $t=3$ ปี

simple_int.subs({P: 1000, i: 0.05, t: 3})

${\displaystyle 1150.0}$

ถ้าต้องการทศนิยม 2 ตำแหน่งให้เมท๊อด (method) .evalf() ช่วย

simple_int.subs({P: 1000, i: 0.05, t: 3}).evalf(6)

${\displaystyle 1150.0}$

2. ดอกเบี้ยทบต้น (Compound Interest) สูตร $$A=P(1+i{)}^t$$

# สมการดอกเบี้ยทบต้น
compound_int = P * (1 + i)**t
# แสดงสมการ
compound_int

${\displaystyle P{(i+1)}^t}$

ถ้าต้องการแทนค่าลงไป เช่น $P=1000$, $i=0.05$, $t=3$

compound_int.subs({P: 1000, i: 0.05, t: 3}).evalf(6)

${\displaystyle 1157.63}$

หมายเหตุ เราสามารถใช้ Lambda เพื่อสร้างฟังก์ชันทั่วไปได้ด้วย เช่น

from sympy import Lambda, lambdify
# ฟังก์ชันดอกเบี้ยอย่างง่าย
# P = เงินต้น, i = อัตราดอกเบี้ย, t =เวลา (ปี)
SI = Lambda((P, i, t), P * (1 + i*t))
SI(1000, 0.05, 3)

${\displaystyle 1150.0}$

ต้องการทศนิยม 2 ตำแหน่งอย่าลืมใช้เมท๊อด .evalf()

SI(1000, 0.05, 3).evalf(7)

${\displaystyle 1150.0}$

# ฟังก์ชันดอกเบี้ยทบต้น
# P = เงินต้น, i = อัตราดอกเบี้ย, t =เวลา (ปี)
CI = Lambda((P, i, t), P * (1 + i)**t)
CI(1000, 0.05, 3).evalf(6) 

${\displaystyle 1157.63}$

ทำไมดอกเบี้ยอย่างง่ายถึงเหมาะกับการลงทุนระยะสั้นและดอกเบี้ยทบต้นเหมาะกับการลงทุนระยะยาว เพราะว่าระยะเวลาการลงทุนน้อยกว่า 1 ปีดอกเบี้ยอย่างง่ายจะให้ผลตอบแทนมากกว่าเพราะว่า

• ดอกเบี้ยอย่างง่าย (Simple Interest) ดอกเบี้ยจะคำนวณเฉพาะจาก “เงินต้น” เท่านั้น ไม่ว่าระยะเวลาจะยาวนานแค่ไหน ดอกเบี้ยในแต่ละรอบจะเท่าเดิม

• ดอกเบี้ยทบต้น (Compound Interest) ดอกเบี้ยที่ได้จะถูกนำกลับไปทบกับเงินต้นทุกงวด ดังนั้นยิ่งเวลาผ่านไปนาน ผลของดอกเบี้ยทบต้น (interest on interest) จะยิ่งเด่นชัด และผลตอบแทนจะเติบโตแบบเอ็กซ์โพเนนเชียล

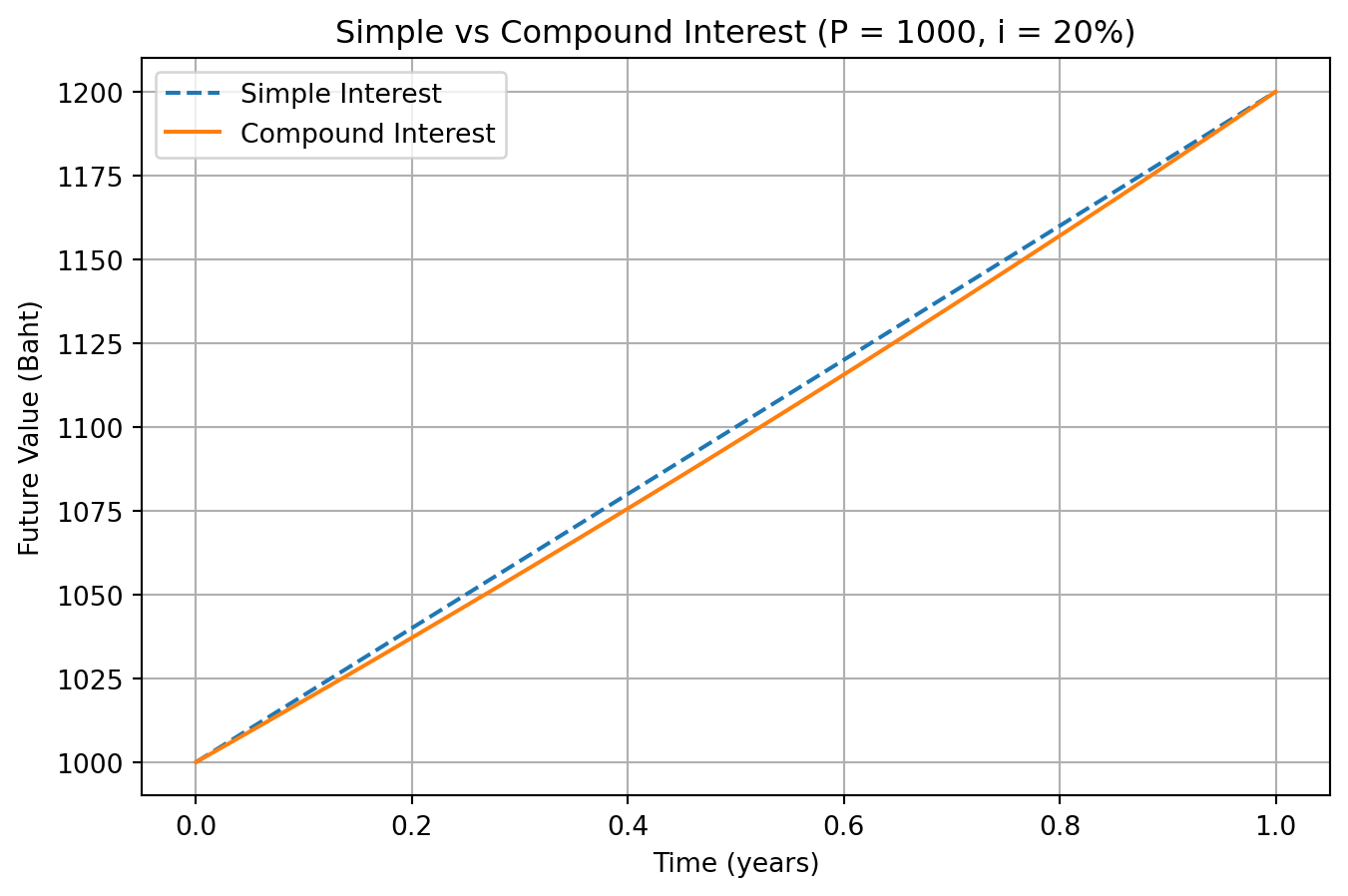
สามารถเปรียบผลตอบแทนภายในระยะเวลา 1 ปีระหว่างดอกเบี้ยอย่างง่ายกับดอกเบี้ยทบต้นได้ดังนี้ถ้ากำหนดเงินลง $P=1,000$ และดอกเบี้ยเท่ากับ $20\mathrm{\%}$

ผลตอบแทนระหว่างอัตราดอกเบี้ยอย่างง่ายกับดอกเบี้ยทบต้นในระยะเวลาไม่เกิน 1 ปี

2.4 อัตราดอกเบี้ยพึงระบุและอัตราดอกเบี้ยแท้จริง (Nominal and Effective Interest Rates)

ความหมายของอัตราดอกเบี้ย

• Nominal Interest Rate (อัตราดอกเบี้ยพึงระบุ) คืออัตราดอกเบี้ยต่อปีที่ประกาศไว้โดยไม่คำนึงถึงความถี่ของการทบต้น ตัวอย่างเช่น 12% ต่อปี ทบต้นรายเดือน หรือรายไตรมาส นิยมใช้เพื่อการสื่อสารในตลาดการเงิน เช่น ประกาศในสัญญาสินเชื่อ หรือโบรชัวร์ธนาคาร

• Effective Interest Rate (อัตราดอกเบี้ยแท้จริง) คืออัตราดอกเบี้ยต่อปีที่แท้จริงซึ่งคำนึงถึงความถี่ในการทบต้นเรียบร้อยแล้ว เป็นอัตราที่สะท้อนผลตอบแทนหรือภาระต้นทุนจริงในรอบปี เหมาะสำหรับใช้ในการวิเคราะห์เปรียบเทียบทางการเงิน

ความสัมพันธ์ระหว่างอัตราดอกเบี้ยพึงระบุ และ อัตราดอกเบี้ยแท้จริงกำหนดให้

• $r^{(m)}$ อัตราดอกเบี้ยพึงระบุ ต่อปี ที่ทบต้น $m$ ครั้งต่อปี

• $i$ อัตราดอกเบี้ยแท้จริง (Effective Annual Rate หรือ EAR)

• $m$ จำนวนครั้งที่ทบต้นใน 1 ปี

ความสัมพันธ์ระหว่างทั้งสองคือ $$i={(1+\frac{r^{(m)}}{m})}^m-1$$ หรือเขียนกลับเพื่อหาค่าอัตราดอกเบี้ยที่แท้จริง $$r^{(m)}=m((1+i{)}^{1/m}-1)$$ ตัวอย่างที่ 1 คำนวณ Effective จาก Nominal

หากอัตราดอกเบี้ยพึงระบุ $r^{(12)}=12\mathrm{\%}$ และทบต้นรายเดือน ($m=12$) จะได้

# นิยามตัวแปร
i, r, m = symbols('i i^{(m)} m', positive=True)
r # Nominal interest

${\displaystyle i^{(m)}}$

# สร้างนิพจน์ของอัตราดอกเบี้ยแท้จริง
i = (1 + r/m)**m - 1
i

${\displaystyle {(\frac{i^{(m)}}{m}+1)}^m-1}$

# แทนค่าจริง
i_numeric = i.subs({r: 0.12, m: 12})
i_numeric.evalf(4)

${\displaystyle 0.1268}$

แสดงว่าแม้ธนาคารจะประกาศดอกเบี้ย 12% ต่อปี แต่เมื่อคิดผลของการทบต้นรายเดือนแล้ว จะให้ผลตอบแทนจริงประมาณ 12.68%

ตัวอย่างที่ 3 ถ้าทราบค่า Effective Annual Rate(i) และต้องการหา Nominal Interest Rate ที่ทบต้น $m$ ครั้งต่อปี หรือก็คือ $i^{(m)}$ ด้วยซิมไพ เราสามารถแก้สมการด้วยซิมไพได้ดังนี้

จากความสัมพันธ์: $$i={(1+\frac{i^{(m)}}{m})}^m-1$$

เราต้องการ แก้สมการหา $i^{(m)}$ ซึ่งเรียกว่า Nominal Annual Rate compounded m times per year หรือ $i^{(m)}$ ขั้นตอนในซิมไพคือ

# กำหนด symbol
i, r, m = symbols('i i^{(m)} m', positive=True)
# สมการจาก EAR
eq = Eq((1 + r/m)**m-1, i)
eq

${\displaystyle {(\frac{i^{(m)}}{m}+1)}^m-1=i}$

แก้สมการด้วยคำสั่ง solve()

sol = solve(eq, r)
sol[0]

${\displaystyle -m+{\left(m^m(i+1)\right)}^{\frac{1}{m}}}$

ตัวอย่างที่ 3 เปรียบเทียบ Nominal ต่างกัน

สมมุติว่ามี 2 ตัวเลือก

• กองทุน A เสนอผลตอบแทน 12% ต่อปี ทบต้นรายปี (ปีละครั้ง)

• กองทุน B เสนอ 11.8% ต่อปี ทบต้นรายเดือน

ให้เปรียบเทียบว่ากองทุนใดให้ผลตอบแทนแท้จริงสูงกว่า

กองทุน A ให้อัรตาดอกเบี้ย $i_A=0.12$ ต้องเปลี่ยนอัตราดอกเบี้ย $i^{(12)}=0.118$ ให้เป็น $i$ กองทุน B:จากตัวอย่างที่ 1 ที่ผ่านมาจะได้

# สร้างนิพจน์ของอัตราดอกเบี้ยแท้จริง
i = (1 + r/m)**m - 1
i_numeric = i.subs({r: 0.118, m: 12})
i_numeric

${\displaystyle 0.124595717465678}$

ถ้าต้องการทศนิยม 4ตำแหน่งสามารถใช้ .evalf() ช่วยได้ คือ

i_numeric.evalf(4) # ตัวเลขในวงเล็บ คือจำนวนหลักของตัวเลขที่ปรากฏ

${\displaystyle 0.1246}$

แม้กองทุน B จะมี Nominal ต่ำกว่า แต่ด้วยการทบต้นรายเดือน ผลตอบแทนจริงกลับสูงกว่ากองทุน A

หรือจะเปลี่ยน $i_A$ เป็น $i_A^{(12)}$ ก็ได้ เนื่องจาก คำสั่ง solve(eq, r) คืนค่าเป็น ลิสต์ (list) ของคำตอบ และ sol เป็นลิสต์ ที่มี 1 ตัว ดังนั้น ต้องใช้ sol[0] เพื่อดึงนิพจน์ทางคณิตศาสตร์ออกมา

# กำหนด symbol
i, r, m = symbols('i r m', positive=True)
# สมการจาก EAR
eq = Eq((1 + r/m)**m - 1, i)
sol = solve(eq, r)
sol[0].subs({i: .12, m: 12}).evalf(4)

${\displaystyle 0.1139}$

จะเห็นว่า $i_A^{(12)}=.1139$ น้อยกว่า $i_B^{(12)}=.118$

Noteข้อสังเกตุ

• ยิ่งจำนวนครั้งในการทบต้น $m$ มากขึ้น (เช่น รายเดือน รายวัน รายชั่วโมง) ผลของดอกเบี้ยทบต้นจะยิ่งมากขึ้น

• เมื่อ $m\to \mathrm{\infty }$ (ทบต้นต่อเนื่อง) จะได้ $$i=e^r-1$$

• Nominal ที่ไม่มีการทบต้น (หรือทบต้นแค่ปีละครั้ง) จะเท่ากับ Effective

แน่นอนครับ! ด้านล่างคือการพิสูจน์ว่า

$$\underset{m\to \mathrm{\infty }}{lim}{(1+\frac{r}{m})}^m=e^r$$

ซึ่งเป็นพื้นฐานของการเปลี่ยนจาก อัตราดอกเบี้ยแบบทบต้นจำนวนครั้งไม่จำกัด (continuous compounding) สู่รูปแบบ $e^r$

เราสามารถใช้ซิมไพหาค่าลิมิตได้ โดยใช้คำสั่ง limit() เพื่อแสดงว่าได้ผลลัพธ์เป็น $e^r$ จริง

from sympy import limit, oo 
# สร้าง symbol
r, m = symbols('r m', positive=True, real=True)
# นิพจน์ด้านซ้ายของลิมิต
expr = (1 + r/m)**m
# คำนวณลิมิตเมื่อ m เข้าใกล้ oo
lim_expr = limit(expr, m, oo)
lim_expr

${\displaystyle e^r}$

ความหมายทางการเงิน

• เมื่อจำนวนรอบการทบต้นในปีเพิ่มขึ้นเรื่อย ๆ (เช่น รายเดือน $\to$ รายวัน $\to$ รายชั่วโมง $\to$ รายวินาที)

• มูลค่าสะสมของเงินต้นที่ลงทุนด้วยอัตรา $r$ ต่อปีจะเข้าใกล้ $A=P{e}^{rt}$ ซึ่งเป็น สูตรทบต้นต่อเนื่อง (continuous compounding)

2.5 ความสัมพันธ์ระหว่างดอกเบี้ยแบบต่างๆ

สัญลักษณ์	ความหมาย
$i$	อัตราดอกเบี้ยแบบ effective ต่อปี
$v$	มูลค่าปัจจุบันของ 1 บาทใน 1 ปี = $\frac{1}{1+i}$
$j={\displaystyle \frac{i^{(m)}}{m}}$	อัตราดอกเบี้ยแบบ nominal ต่อปี (ทบปีละ $m$ ครั้ง)
$i^{(m)}$	อัตราดอกเบี้ย effective ต่อปี จากการทบปีละ $m$ ครั้ง
$r$	อัตราดอกเบี้ยแบบต่อเนื่อง (force of interest)
$e^r$	การทบต้นแบบต่อเนื่อง

สูตรความสัมพันธ์ทั้งหมด

ระหว่าง $i$ และ $v$
$$v=\frac{1}{1+i}\text{และ}i=\frac{1-v}{v}$$ ระหว่าง $i$ และ $i^{(m)}$ หรือ Nominal rate $$i^{(m)}={(1+\frac{j}{m})}^m-1$$

$$j=m((1+i{)}^{1/m}-1)$$

เมื่อ $j$ คือ nominal annual rate ทบต้นปีละ $m$ ครั้ง

ระหว่าง $i$ และ $r$ (ต่อเนื่อง) $$1+i=e^r\text{หรือ}r=\ln (1+i)$$

$$i=e^r-1$$ ระหว่าง $v$ และ $r$
$$v=e^{-r}\text{และ}r=-\ln (v)$$

สรุปความสัมพันธ์

ความสัมพันธ์	สูตร
$v\leftrightarrow i$	$v=\frac{1}{1+i}$, $i=\frac{1-v}{v}$
$i^{(m)}\leftrightarrow j$	$i^{(m)}={(1+\frac{j}{m})}^m-1$, $j=m[(1+i{)}^{1/m}-1]$
$i\leftrightarrow r$	$1+i=e^r$, $r=\ln (1+i)$, $i=e^r-1$
$v\leftrightarrow r$	$v=e^{-r}$, $r=-\ln (v)$

2.6 อัตราตราส่วนลด (Discount Rate)

ผู้อ่านคงเคยพบการยืมเงินในรูปแบบนี้ ต้องการยืมเงิน 1000 คิดดอกเบี้ย 10% ต่อปี แต่ผู้กู้ได้รับเงินเพียง 900 บาทและเมื่อครบปีต้องชำระหนี้ด้วยเงิน 1,000 บาท นั้นก็คืออัตราส่วนลด

ในคณิตศาสตร์การเงิน “อัตราส่วนลด” ใช้ในการหามูลค่าปัจจุบัน (Present Value, $PV$) จากมูลค่าในอนาคต (Future Value, $FV$) โดยคิดว่าเงินจะถูก “ลดลง” แทนที่จะ “งอกขึ้น” (เหมือนดอกเบี้ย) และสัญลักษณ์ที่คือ $d$

2.7 อัตราส่วนลดอย่างง่าย (Simple Discount Rate)

แนวคิด ใช้อัตราส่วนลดแบบเส้นตรง โดยหักเงินจาก $F$ ลงมาตรงๆ ตามจำนวนปี $$PV=FV\cdot (1-d\cdot t)$$ โดยที่

• $PV$ = มูลค่าปัจจุบัน

• $FV$ = มูลค่าในอนาคต

• $d$ = อัตราส่วนลดแบบ simple ต่อปี

• $t$ = จำนวนปี

2.7.1 อัตราส่วนลดทบต้น (Compound Discount Rate)

แนวคิด คล้ายกับ compound interest แต่กลับด้าน เป็นการลดลงแบบทบต้น $$PV=FV\cdot (1-d{)}^t\text{หรือ}v=1-d$$ ### ความสัมพันธ์ระหว่าง $d$ $i$ และ $v$ $$d=1-v=\frac{i}{1+i}$$ ดังนั้น $$i=\frac{d}{1-d}$$ และ $$v=1-d$$

Importantหมายเหตุ

ในหนังสือเล่มจะไม่สนใจอัตราส่วนลด จะพิจารณาเฉพาะอัตราดอกเบี้ย $i$ เป็นหลักเท่านั้น

2.8 แบบฝึกหัด

Cautionหัวข้อ Interest, Accumulation, and Amount Functions

1. อธิบายความแตกต่างระหว่างฟังก์ชันอัตราดอกเบี้ย (interest function) กับฟังก์ชันการสะสม (accumulation function) และยกตัวอย่างสถานการณ์ทางการเงินที่เหมาะสมกับแต่ละฟังก์ชัน

2. หากมีฟังก์ชันการสะสม $a(t)$ เป็น $a(t)=(1+0.05{)}^t$ จงอธิบายว่าอัตราดอกเบี้ยแบบใดที่ใช้ และใช้ฟังก์ชันนี้อย่างไรในการคำนวณมูลค่าอนาคตของเงินลงทุน

3. สมมติให้ฟังก์ชัน $a(t)=1+0.08t$ เป็นฟังก์ชันการสะสม จงอธิบายว่าฟังก์ชันนี้บ่งชี้ถึงลักษณะของการคิดดอกเบี้ยแบบใด พร้อมทั้งเปรียบเทียบกับฟังก์ชัน $a(t)=e^{0.08t}$

Cautionหัวข้อ Simple Interest

4. นายก้องต้องการกู้เงิน 50,000 บาท โดยตกลงว่าจะชำระคืนแบบดอกเบี้ยอย่างง่ายเป็นเวลา 3 ปี ธนาคารเสนออัตราดอกเบี้ย 6% ต่อปี จงเขียนแผนผังกระแสเงินสด และอธิบายว่ามูลค่าเงินจะเปลี่ยนแปลงอย่างไรในแต่ละปี

5. ถ้ามีสองทางเลือกการลงทุน: (ก) ดอกเบี้ย 5% แบบอย่างง่าย และ (ข) ดอกเบี้ย 4.5% แบบทบต้น คุณจะใช้เกณฑ์อะไรในการเลือกการลงทุน? ให้เหตุผลโดยใช้แนวคิดของอัตราดอกเบี้ยแท้จริง

6. มีเงินลงทุน 100,000 บาทในโครงการที่เสนอผลตอบแทนแบบ simple interest 7% ต่อปี ผู้ลงทุนรายหนึ่งเข้าใจผิดว่าดอกเบี้ยนี้จะทบต้น อธิบายผลที่เกิดขึ้นหากเขาประเมินรายได้ผิด

Cautionหัวข้อ Compound Interest

7. บริษัทแห่งหนึ่งวางแผนลงทุนเงินก้อนเพื่อใช้จ่ายในอีก 10 ปีข้างหน้า หากต้องการให้เงินเติบโตเป็น 2 เท่าด้วยดอกเบี้ยทบต้น คุณจะใช้อัตราดอกเบี้ยขั้นต่ำเท่าใด?

8. อธิบายผลของการเพิ่มความถี่ในการทบต้น (เช่น รายปี $\to$ รายเดือน $\to$ รายวัน) โดยใช้ตัวอย่างเงินลงทุน 10,000 บาท และแสดงแนวโน้มของการเติบโตของเงิน

9. นักลงทุนรายหนึ่งกำลังพิจารณาฝากเงินในบัญชีที่มีการทบต้นรายเดือน อธิบายว่าจะสามารถคำนวณมูลค่าของเงินได้อย่างไร โดยใช้อัตราดอกเบี้ยและระยะเวลา

10. ให้เปรียบเทียบผลตอบแทนจากการลงทุนในบัญชีที่ทบต้นแบบรายปีและแบบทบต้นรายเดือน โดยใช้หลักการของ compound interest และอธิบายผลต่างที่เกิดขึ้นจากการทบต้นถี่ขึ้น

Cautionหัวข้อ Nominal vs Effective Interest Rates

11. ธนาคาร A เสนออัตราดอกเบี้ย 6% ต่อปีทบต้นรายปี ขณะที่ธนาคาร B เสนอ 5.8% ต่อปีแต่ทบต้นรายเดือน ถ้าคุณต้องเลือกฝากเงินกับธนาคารใด ควรพิจารณาจากปัจจัยใด และควรคำนวณอย่างไร

12. จงอธิบายว่าทำไมการเปรียบเทียบอัตราดอกเบี้ยระหว่างแหล่งเงินทุนต่าง ๆ ควรใช้อัตรา Effective Rate แทน Nominal Rate

13. นักลงทุนบางคนเข้าใจผิดว่าอัตราดอกเบี้ยพึงระบุ (Nominal) คืออัตราที่ได้รับจริงเสมอ คุณจะอธิบายความแตกต่างนี้อย่างไร โดยยกตัวอย่างให้เข้าใจง่าย

14. นายประทีปเลือกลงทุนในพันธบัตรที่จ่ายดอกเบี้ยแบบ nominal 10% ต่อปี ทบต้นรายไตรมาส เขาต้องการทราบว่าอัตราดอกเบี้ยแท้จริงที่เขาได้รับคือเท่าใด และมีผลต่อการวางแผนการเงินของเขาอย่างไร

15. นักลงทุน 2 คนเลือกลงทุนในกองทุนต่างกัน คนแรกได้อัตรา effective 6.2% ต่อปี ส่วนอีกคนได้ nominal 6.5% ต่อปี ทบต้นปีละ 2 ครั้ง จงอธิบายว่าใครได้รับผลตอบแทนมากกว่า

[1]

จลีพร โกลากุล และ จุฬาลงกรณ์มหาวิทยาลัย. คณะพาณิชยศาสตร์และการบัญชี, คณิตศาสตร์การเงิน, พิมพ์ครั้งที่ 2. กรุงเทพฯ: คณะพาณิชยศาสตร์และการบัญชี จุฬาลงกรณ์มหาวิทยาลัย, 1984.

[2]

ประสิทธิ์ พยัคฆพงษ์, คณิตศาสตร์การเงินและการลงทุน, พิมพ์ครั้งที่ 1. กรุงเทพฯ: สำนักพิมพ์มหาวิทยาลัยเกษตรศาสตร์, 2004.

[3]

S. G. Kellison, The Theory of interest. ใน Irwin series in insurance and economic security. Homewood, Ill: R. D. Irwin, 1970.

[4]

มานพ วราภักดิ์, ทฤษฎีดอกเบี้ย = Theory of interest. กรุงเทพฯ: สำนักพิมพ์แห่งจุฬาลงกรณ์มหาวิทยาลัย, 2006.

[5]

A. Meurer และคณะ, “SymPy: symbolic computing in Python”, PeerJ Computer Science, ปี 3, น. e103, ม.ค. 2017, doi: 10.7717/peerj-cs.103.

[6]

J. D. Hunter, “Matplotlib: A 2D graphics environment”, Computing in Science & Engineering, ปี 9, ฉบับที่ 3, น. 90–95, 2007, doi: 10.1109/MCSE.2007.55.