6 เงินงวดถาวร (Perpetuities) – Financial Mathematics: A Practical Approach with SymPy

6.1 แนวคิดของเงินงวดถาวร (Concept of Perpetual Annuities)

ในความหมายงง่ายๆ ก็คือถ้าอัตราดอกเบี้ยไม่มีการเปลี่ยนแปลง เราสามารถถอนเฉพาะดอกเบี้ยที่ได้รับออกมาเท่านั้น ซึ่งส่งผลให้เงินต้นไม่ลดและจะได้ได้รับดอกเบี้ยเท่าเดิมตลอดไป จนกว่าอัตราดอกเบี้ยจะมีการเปลี่ยนแปลงนั่นเอง

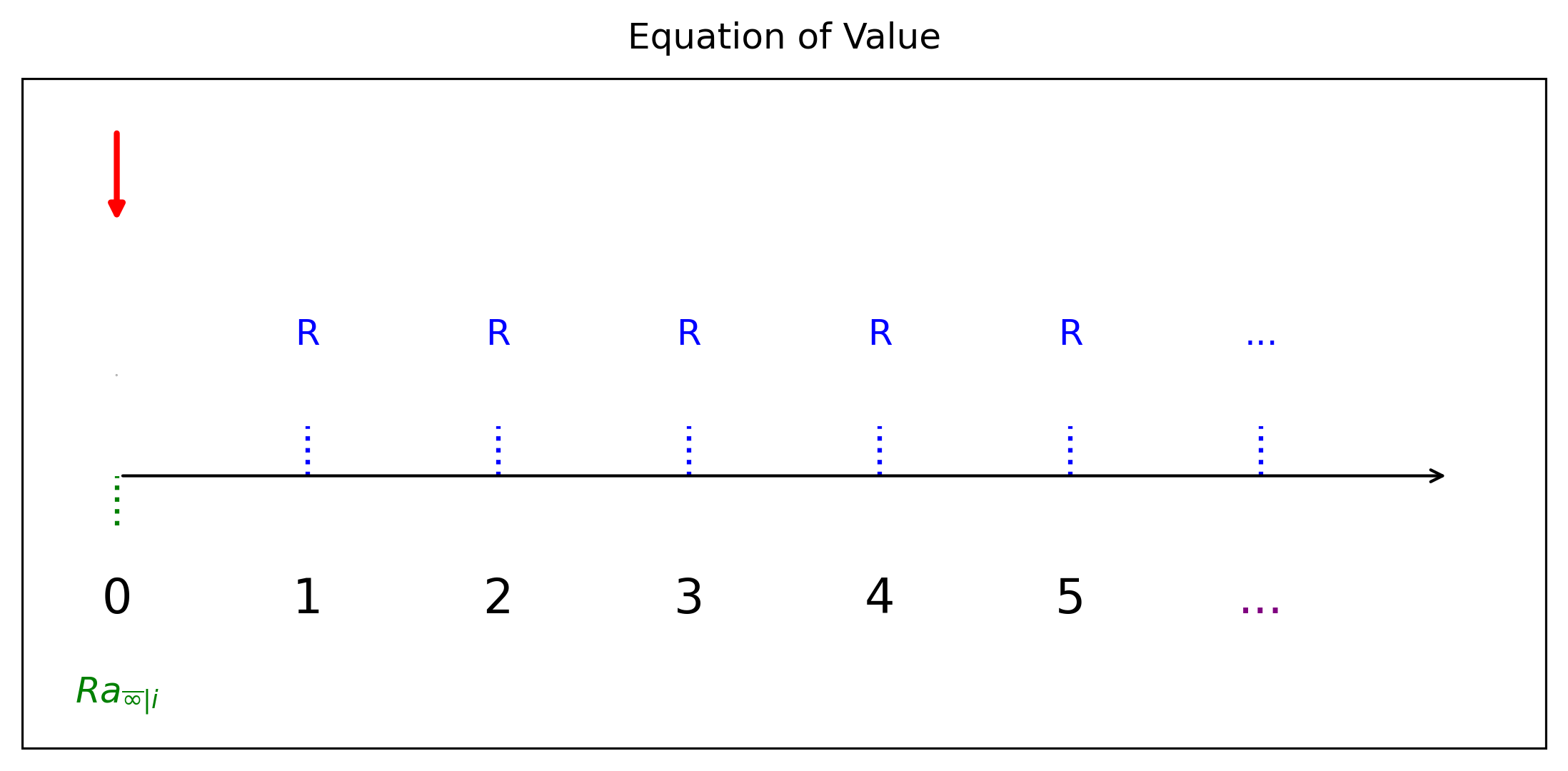
เงินงวดถาวร (Perpetuity) หมายถึง ชุดของเงินงวดที่จ่ายตลอดไปโดยไม่มีวันสิ้นสุด โดยมีค่างวดเท่ากันในทุกช่วงเวลา เช่น ถ้าต้องการได้รับเงิน $R$ หน่วยทุกสิ้นงวดด้วยอัตราดอกเบี้ย $i$ จะฝากเงินเป็นจำนวนเท่าใดในวันนี้ $P V = R v + R v^{2} + R v^{3} + \dots = \sum_{k = 1}^{\infty} R v^{k} = R \cdot a_{\overset{―}{\infty} | i} = R \cdot (lim_{n \to \infty} \frac{1 - v^{n}}{i}) = R \frac{1}{i}$

ซึ่งเป็นอนุกรมเรขาคณิตที่ลดลง โดยที่:

$R$ ค่างวดที่ได้รับ
$v = \frac{1}{1 + i}$ ตัวลดค่า
$i$ อัตราดอกเบี้ยต่อช่วง

สามารถใช้ซิมไพหาคำตอบได้ ดังนี้

from sympy import Sum, oo, simplify
i, k, a_n = symbols('i k a_n', positive = True)
v = 1/(1+i)
a_n = Sum(v**k, (k, 1, oo))
a_n.doit()

$\frac{1}{(1 - \frac{1}{i + 1}) (i + 1)}$

สามารถจัดให้อยู่อย่างง่ายด้วยคำสั่ง simplify()

simplify(a_n.doit())

$\frac{1}{i}$

จะได้ผลลัพธ์ตรงตามทฤษฏี

คำสั่ง simplify() และ oo

simlpify() เป็นคำสั่ง หลัก ที่ใช้ในการทำสมการให้อยู่ในรูปที่ “ง่ายที่สุด” เท่าที่เป็นไปได้ โดยอัตโนมัติ โดยจะใช้หลายเทคนิคพร้อมกัน เช่น

รวมพจน์
หารตัวร่วม
แยกตัวประกอบ
ตัดเศษส่วน
ใช้กฎฟังก์ชันตรีโกณ ฯลฯ

oo หมายถึง infinity ( $\infty$ ) หรือ “อนันต์”

oo ย่อมาจาก “order of infinity”
ใช้แทนค่า $\infty$ (บวกอนันต์) ในการคำนวณเชิงสัญลักษณ์
เป็นอ็อบเจ็กต์ชนิดหนึ่งของซิมไพซึ่งไม่ใช่ float หรือ int

6.2 เงินงวดถาวรที่เริ่มล่าช้า (Deferred Perpetuities)

ให้ผู้อ่านนึกถึง การฝากเงินในวันนี้เป็นเวลา $n$ ปีโดยไม่มีการถอนเงินออกมาเลย หลังจากนั้นจะเริ่มถอนเฉพาะดอกเบี้ยที่ได้รับออกไปทุกปี โดยเริ่มถอนครั้งแรก เมื่อฝากเงินครบ $n + 1$ ปี เป็นต้นไปทุกปี

นั่นคือหากเงินงวดถาวรไม่ได้เริ่มจ่ายทันที แต่เริ่มหลังผ่านไป $n$ งวด เช่น เริ่มจ่ายตั้งแต่งวดที่ $n + 1$ เป็นต้นไป มูลค่าปัจจุบันของเงินงวดดังกล่าวคือ $P V = R \cdot a_{\overset{―}{\infty} | i} \cdot v^{n} = \frac{R}{i (1 + i)^{n}}$

ซึ่งแสดงให้เห็นว่าการเลื่อนการจ่ายเงินจะลดมูลค่าปัจจุบันลงตามตัวลดค่า $v^{n}$

6.3 การประยุกต์ (Applications)

การประเมินมูลค่าหุ้นที่จ่ายปันผลคงที่ตลอดไป $P_{0} = \frac{D}{i} หรือ P_{0} = D \cdot a_{\overset{―}{\infty} | i}$

กองทุนที่ให้ผลตอบแทนรายปีแบบไม่จำกัด
เงินบริจาคถาวรที่จ่ายผลตอบแทนให้หน่วยงานหรือบุคคลตลอดชีวิต

6.4 แบบฝึกหัดท้ายบท

อธิบายความหมายของเงินงวดถาวร (Perpetuity) พร้อมยกตัวอย่างการใช้งานจริง เช่น หุ้นกู้ที่จ่ายดอกเบี้ยตลอดไป
ใช้ซิมไพเพื่อคำนวณมูลค่าปัจจุบันของเงินงวดถาวรที่จ่าย 1,000 บาทต่อปี เมื่ออัตราดอกเบี้ยเท่ากับ 5% ต่อปี
หามูลค่าปัจจุบันของเงินงวดถาวรที่เริ่มจ่ายหลังจาก 5 ปี ด้วยเงินงวด 1,000 บาท และ i = 6%
เงินงวดเพิ่มขึ้นแบบเลขคณิต (Arithmetic Increasing Perpetuity) จงคำนวณมูลค่าปัจจุบันของเงินงวดถาวรที่เพิ่มขึ้นปีละ 100 บาท เริ่มจาก 100 บาท โดยใช้ซิมไพ
เงินงวดเพิ่มขึ้นแบบเรขาคณิต (Geometric Increasing Perpetuity) ถ้าเงินงวดเพิ่มขึ้นเรื่อย ๆ ตามอัตรา 3% ต่อปี และเริ่มจาก 1,000 บาท ให้นิยามสูตรและคำนวณด้วยซิมไพ
สร้างฟังก์ชันโดยใช้ซิมไพ สำหรับมูลค่าปัจจุบันของเงินงวดถาวรทั่วไปที่รับ R และ i แล้วคืนค่ามูลค่าปัจจุบันของเงินงวดถาวร
เปรียบเทียบมูลค่าปัจจุบันของเงินงวดถาวรเมื่ออัตราดอกเบี้ยเปลี่ยน

โดยคำนวณและเปรียบเทียบว่า PV ต่างกันอย่างไรเมื่อ i = 3%, 5%, และ 8%

วิเคราะห์ความไวต่อดอกเบี้ย (Sensitivity Analysis)

นิยามฟังก์ชัน $P V (i) = \frac{R}{i}$ แล้วหาค่าอนุพันธ์ด้วย diff() เพื่อดูว่า PV เปลี่ยนแปลงเร็วเพียงใดเมื่อ i เปลี่ยน

การประยุกต์ใช้งานจริง

ให้นักเรียนค้นหาตัวอย่างจากข่าวสารหรือการเงินจริง เช่น perpetual bonds หรือ preferred stocks แล้ววิเคราะห์ PV ของสินทรัพย์นั้นด้วยสูตรจากบทนี้

แสดงว่าเมื่อ $n \to \infty$ , $a_{\overset{―}{n} | i} = \frac{1 - v^{n}}{i} \to \frac{1}{i}$ โดยใช้ limit() จากชิมไพ