3  สมการเปรียบเทียบมูลค่าเงินในเวลาต่างกัน (Equations of Value)

Importantหมายเหตุ

ก่อนเริ่มการคำนวณเชิงสัญลักษณ์ด้วยซิมไพ ขอให้ผู้อ่านทำการเรียกใช้คำสั่งดังต่อไปนี้ก่อน

from sympy import symbols, Eq, solve

เพื่อจะได้ไม่ต้องเรียกใช้งานทุกครั้ง

3.1 การเปรียบเทียบมูลค่าต่างเวลา (Comparison of Values at Different Times)

แนวคิดหลัก

ในการเงิน มูลค่าของเงินเปลี่ยนแปลงตามเวลาเนื่องจากดอกเบี้ย ดังนั้นจึง ไม่สามารถเปรียบเทียบมูลค่าเงินที่เกิดขึ้นต่างเวลากันได้โดยตรง จำเป็นต้อง “แปลง” เงินทุกจำนวนให้มาอยู่ในช่วงเวลาเดียวกันก่อน

การเปรียบเทียบมูลค่าเงินจึงต้องอาศัย

• การหามูลค่าในอนาคต (Future Value)

• การหามูลค่าในปัจจุบัน (Present Value)

3.2 การเปรียบเทียบมูลค่าต่างเวลา โดยใช้ $v=\frac{1}{1+i}$

ความหมายของ $v$ ในคณิตศาสตร์การเงิน เรานิยมเขียน $$v=\frac{1}{1+i}$$ ซึ่งหมายถึง

• ค่าปัจจุบันของเงิน 1 หน่วยที่จะได้รับในอีก 1 งวดข้างหน้า

• หรือเรียกว่า discount factor

การแปลงมูลค่าเงินโดยใช้ $v$ หากต้องการเปรียบเทียบมูลค่าเงินในเวลาต่างกัน ให้ใช้ $v^t$ สำหรับลดมูลค่าเงินจากอนาคตกลับมาสู่ปัจจุบัน $$\text{Present Value of }A\text{ at time }t=A\cdot v^t=\frac{A}{(1+i{)}^t}$$ ตัวอย่างสมการของมูลค่า สมมุติว่ามีเงินสดจำนวนหลายก้อนในเวลาต่างกัน และต้องการเปรียบเทียบกับเงินก้อนเดียวที่จุดเวลาอื่น $$A_1{v}^{t_1}+A_2{v}^{t_2}+\cdots +A_n{v}^{t_n}=X{v}^t$$

ตัวอย่าง นายสมชายมีภาระหนี้ 5,000 บาทในปีที่ 1 และ 7,000 บาทในปีที่ 3 เขาเสนอว่าจะชำระหนี้ทั้งหมดด้วยก้อนเดียวในปีที่ 2 ถ้าอัตราดอกเบี้ยคือ 6% ต่อปี ควรชำระเท่าใด? เราต้องใช้สมการของมูลค่าที่ $t=2$
$$5,000\cdot v^{1-2}+7,000\cdot v^{3-2}=X$$ $$5,000\cdot v^{-1}+7,000\cdot v=X$$ แทน $v=\frac{1}{1.06}$ แล้วคำนวณหาคำตอบ เพื่อความง่ายในการคำนวณจะใช้หลักการนี้

ผลรวมของมูลค่าปัจจุบันทั้งหมดของเงินรับเข้า(money inflow) เท่ากับ ผลรวมทั้งหมดของมูลค่าปัจจุบันของเงินไหลออก (money outflow)

3.2.1 การใช้ซิมไพช่วยแก้สมการ

v, X = symbols('v X', positive=True)
eq = Eq(5000 * v**-1 + 7000 * v, X)
result = eq.subs(v, 1/1.06)
solve(result, X)[0].evalf(7)

${\displaystyle 11903.77}$

ตัวอย่างการนำไปใช้ นายธนาได้ทำการฝากเงินเข้าบัญชีที่อัตราดอกเบี้ยทบต้น 6% ต่อปี โดยเขาฝากเงิน 3,000 บาทในปีที่ 1 และอีก 2,000 บาทในปีที่ 2 ต่อมาในปีที่ 5 นายธนาได้รับเงินคืนเป็นก้อนเดียวจำนวน 8,000 บาท

หากใช้อัตราดอกเบี้ยที่กำหนดนี้ ให้ตั้งสมการของมูลค่าโดยอ้างอิงที่เวลา $t=0$ และตรวจสอบว่าอัตราดอกเบี้ย 6% ต่อปีนั้นทำให้สมการสมดุลหรือไม่

วาดกราฟ

แผนภาพสมการแห่งมูลค่า

เนื่องจากพิจารณาที่จุด $t=0$ สมการของมูลค่า $$3000v+2000v^2=8000v^5$$ หรือ เช็คสมการทางซ้ายมือ

v, i = symbols('v i', positive = True)
eq = Eq(3000*v+2000*v**2, 8000*v**5)
# แก้สมการหา v
solutions = solve(eq, v)
# เนื่องจากมีสมการ polynomialดีกรี 5  จะมีทั้งหมด 5 คำตอบ
for sol in solutions:
    print(sol.evalf(4))

-0.102 - 0.7894*I
-0.102 + 0.7894*I
0.8781
-0.6741

คำตอบที่ต้องการคือ ลำดับที่ 3

# python เริ่่มตั้นจาก 0
solutions[2].evalf(4)

${\displaystyle 0.8781}$

แก้สมการหาค่า $i$ จะได้

# จาก v =1/(1+i) 
eq2 =Eq(v,1/(1+i))
sol = solve(eq2, i)
sol

[(1 - v)/v]

ดังนั้น

sol[0].subs({v: solutions[2].evalf()}).evalf(4)

${\displaystyle 0.1388}$

อัตราดอกเบี้ยที่ได้ไม่ใช่ 6% ต่อปีแต่เป็นประมาณ 13.88% ต่อปี

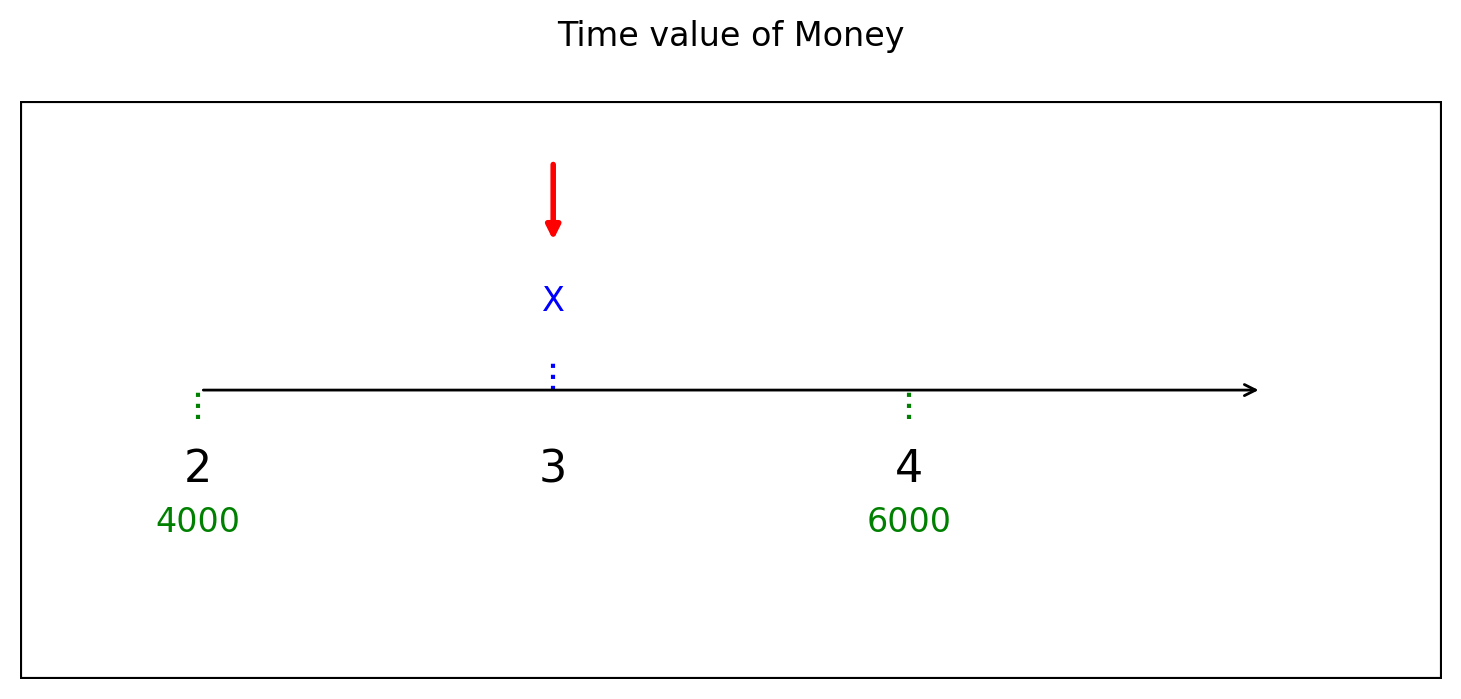
ตัวอย่างที่ 2 นายศราวุธวางแผนการชำระหนี้โดยจะจ่ายเงิน 4,000 บาทในปีที่ 2 และอีก 6,000 บาทในปีที่ 4 เขาต้องการจ่ายแทนด้วยเงินก้อนเดียวในปีที่ 3 ถ้าใช้อัตราดอกเบี้ย 5% ต่อปี จงหาเงินที่ควรจ่ายในปีที่ 3

วาดรูปจากคำสั่งที่สร้างไว้ โดยเลือกจุดพิจารณาคือ $t=3$

แผนภาพสมการแห่งมูลค่า

• $v=\frac{1}{1.05}$

• สมการของมูลค่า ณ เวลา $t=3$: $$4000\cdot v^{-1}+6000\cdot v^1=X$$

$$4000\cdot v^{-1}+6000\cdot v=X$$ ใช้ซิมไพหาคำตอบ

i, v = symbols('i v', positive=True)
v = 1/(1+i)
X = 4000*v**-1+6000*v**1
X

${\displaystyle 4000i+4000+\frac{6000}{i+1}}$

X.subs({i: 0.05}).evalf(6)

${\displaystyle 9914.29}$

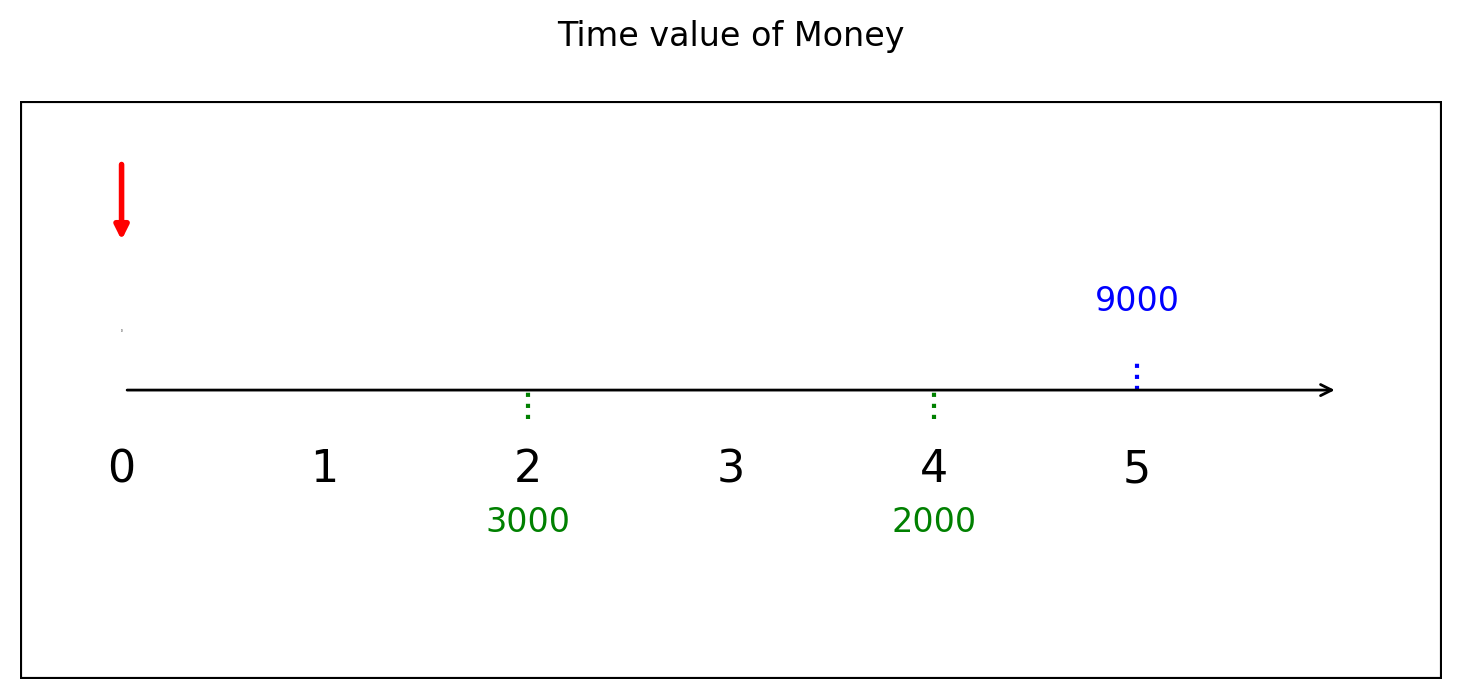
ตัวอย่างที่ 3 คุณนิตยาได้รับเงิน 2 ก้อน: 3,000 บาทในปีที่ 1 และ 2,000 บาทในปีที่ 2 ต่อมาเธอจ่ายคืน 9,000 บาทในปีที่ 5 จงหาอัตราดอกเบี้ยที่ทำให้การรับและการจ่ายมีมูลค่าเท่ากันเมื่ออ้างอิงที่เวลา 0

แผนภาพสมการแห่งมูลค่า

ตั้งสมการ $$3000\cdot v^1+2000\cdot v^2=9000\cdot v^5$$ จากนั้นใช้ซิมไพ แก้หา $v$ แล้วคำนวณ $i$ จาก:

i, v = symbols('i v', positive=True)
eq = Eq(3000*v + 2000*v**2, 9000*v**5)
solutions = solve(eq, v)

# เนื่องจากมีสมการ polynomialดีกรี 5  จะมีทั้งหมด 5 คำตอบ
for sol in solutions:
    print(sol.evalf(4))

-0.09618 - 0.7661*I
-0.09618 + 0.7661*I
0.8501
-0.6577

คำตอบที่ต้่องการคือ ลำดับที่ 3

# python เริ่มต้นจาก 0
solutions[2].evalf(4)

${\displaystyle 0.8501}$

แก้สมการหาค่า $i$ จะได้

# จาก v =1/(1+i) 
eq2 =Eq(v,1/(1+i))
sol = solve(eq2, i)
sol

[(1 - v)/v]

ดังนั้น

sol[0].subs({v: solutions[2]}).evalf(4)

${\displaystyle 0.1763}$

หรือจะแก้สมการหาค่าโดยตรงเลยก็สามารถทำได้

i, v = symbols('i v', positive=True)
eq = Eq(3000*v + 2000*v**2, 9000*v**5)
v = 1/(1+i)
solutions = solve(eq, i)

# เนื่องจากมีสมการ polynomialดีกรี 5  จะมีทั้งหมด 5 คำตอบ
for sol in solutions:
    print(sol.evalf(4))

คำตอบที่เป็นเลขจำนวนจริงบวก $i=0.1763$

ในบ้างครั้งปัญหาของการลงทุน คือเราไม่ทราบระยะเวลาที่แน่นอน เช่น

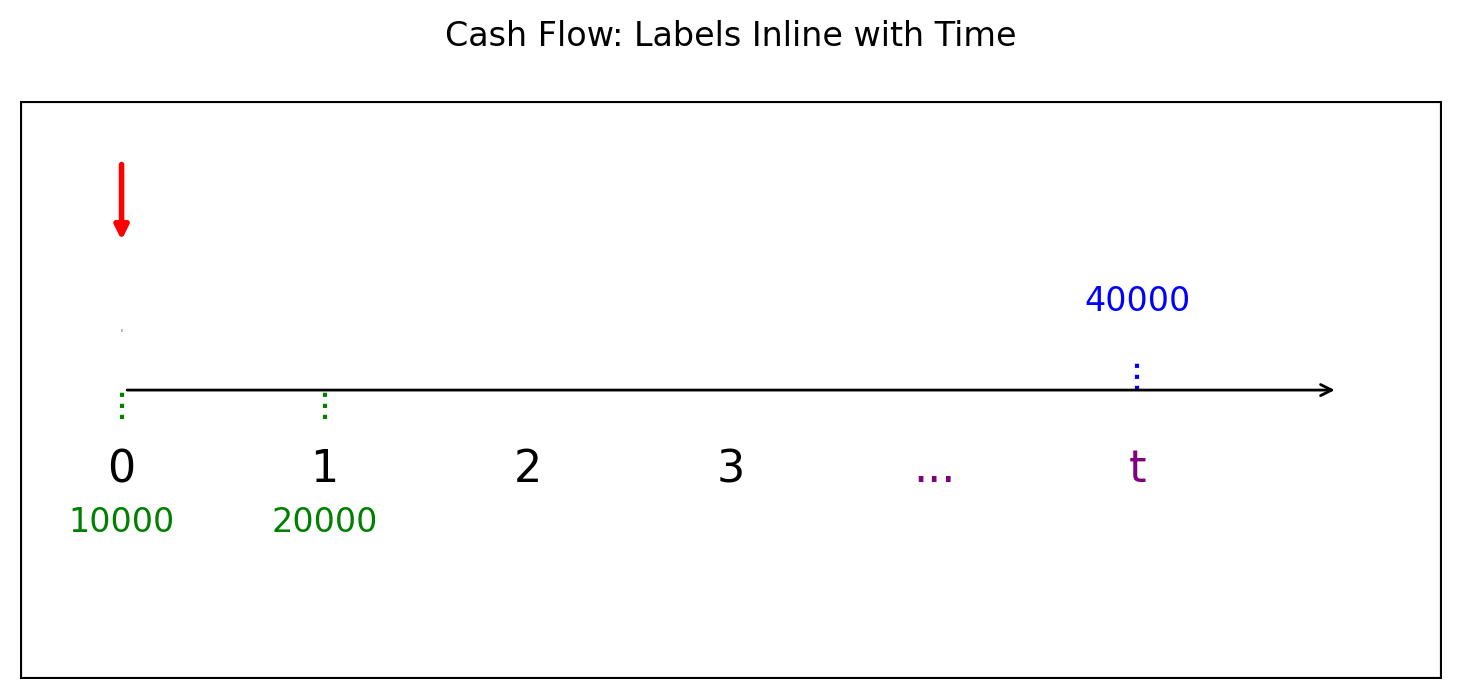
ตัวอย่างที่ 4 ฝากเงินวันนี้ เป็นจำนวน 10,000 บาท และเมื่อครบ 1 ปีฝากเพิ่มอีก 20,000 บาท ถ้าสถาบันการเงินให้ดอกเบี้ย 15% ต่อปี จะใช้เวลาเท่าไหร่ถึงจะมีเงินสะสมเท่ากับ 40,000 บาท

แผนภาพสมการแห่งมูลค่า

จากภาพเป็นการประมาณการเท่านั้นว่า $t$ อาจจะอยู่ระหว่าง

สมการค่าเงินคือ $$10000+20000v=40000v^t$$ สามารถใช้ซิมไพ แก้สมการหาเวลา $t$ ได้ดังนี้

t = symbols('t', positive = True)
i =0.15
v = 1/(1+i)
eq =Eq(10000+20000*v, 40000*v**t)
Sol = solve(eq,t)
Sol[0].evalf(3)

${\displaystyle 2.71}$

ใช้เวลาประมาณ 2.71 ปีจะได้เงินสะสมเท่ากับ 40,000 บาท

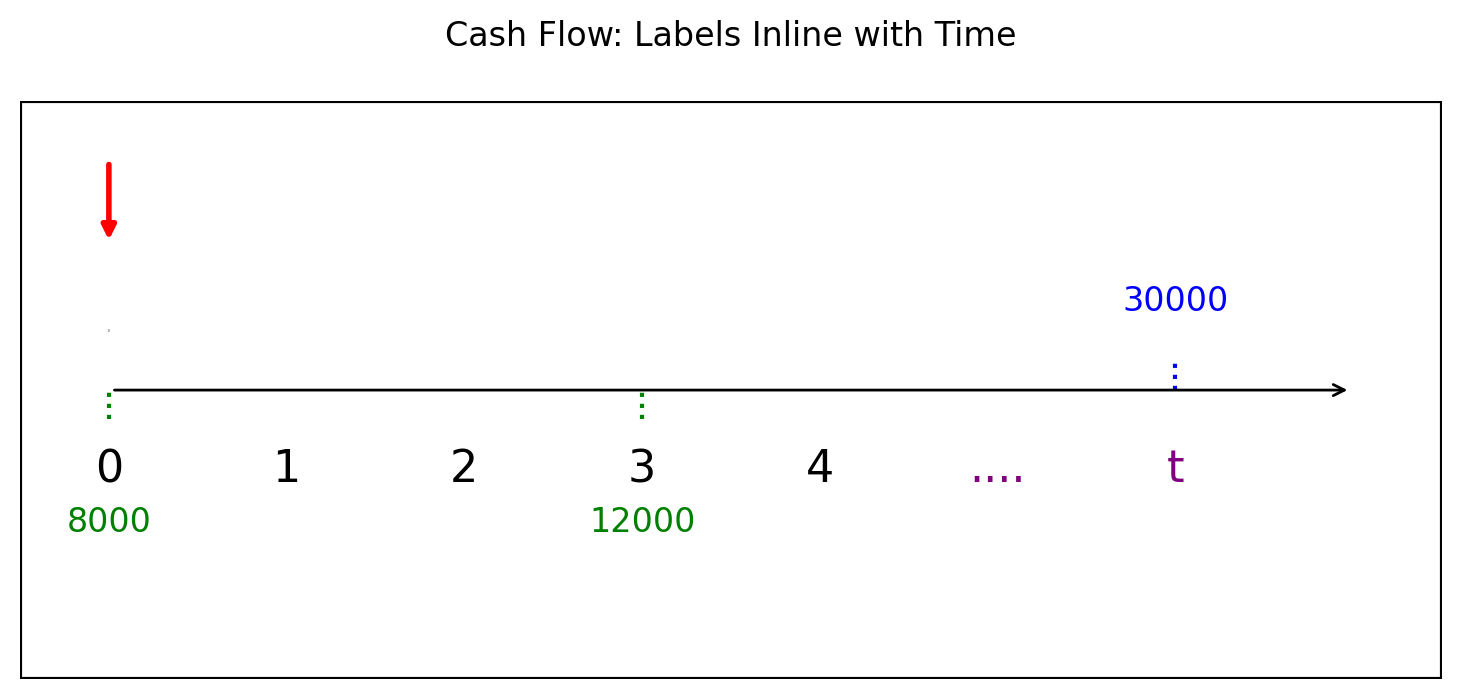
ตัวอย่างที่ 5 นาย B วางแผนเก็บเงินเพื่อซื้อรถในอนาคต โดยในวันนี้เขาฝากเงินจำนวน 8,000 บาท และอีก 3 ปีถัดไปจะฝากเพิ่มอีก 12,000 บาท หากธนาคารให้ดอกเบี้ย 10% ต่อปีแบบทบต้น และนาย B ต้องการมีเงินสะสมรวม 30,000 บาท จะต้องใช้เวลากี่ปี นับจากวันนี้จึงจะถึงเป้าหมาย?

แผนภาพสมการแห่งมูลค่า

สมการแห่งมูลค่าคือ $$8000+12000v^3=30000v^t$$ สามารถใช้ซิมไพ แก้สมการหาเวลา $t$ ได้ดังนี้

t = symbols('t', positive = True)
i =0.10
v = 1/(1+i)
eq =Eq(8000+12000*v**3, 30000*v**t)
Sol = solve(eq,t)
Sol[0].evalf(3)

${\displaystyle 5.95}$

ใช้เวลาประมาณ 5.95 ปีจะได้เงินสะสมเท่ากับ 30,000 บาท

3.3 ตัวอย่างโจทย์: Equation of Value (Nominal Rate)

ตัวอย่างที่ 6 คุณฝากเงิน 50,000 บาทไว้ในธนาคาร และได้รับเงิน 56,136.25 บาทในอีก 2 ปี หากดอกเบี้ยถูกทบทุกครึ่งปี (2 ครั้งต่อปี) จงหาว่าอัตราดอกเบี้ยแบบ nominal ต่อปีคือเท่าใด

วาดรูป

แผนภาพสมการแห่งมูลค่า

สมการมูลค่า คือ $$50000=56136.25v^2,v={\left({\displaystyle \frac{1}{1+{\displaystyle \frac{i^{(2)}}{2}}}}\right)}^2$$ สามารถใช้ซิมไพ หาคำตอบได้ดังนี้

# ให้ i^(2) คือ i2
i2, v = symbols('i^{(2)} v', positive = True)
v= (1/(1+i2/2))**2
v

${\displaystyle \frac{1}{{(\frac{i^{(2)}}{2}+1)}^2}}$

eq = Eq(50000, 56136.25*v**2)
Sol = solve(eq,i2)
Sol[0].evalf(4)

${\displaystyle 0.05872}$

ดังนั้น $i^{(2)}=0.0587=5.87$ ต่อปี ทบต้นทุก 6 เดือน

ตัวอย่างที่ 7 คุณต้องการมีเงิน 100,000 บาทในอีก 3 ปีหากธนาคารให้ดอกเบี้ยแบบ nominal ร้อยละ 8 ต่อปี ทบปีละ 4 ครั้ง (quarterly) คุณควรลงทุนเป็นจำนวนเท่าใดในวันนี้?

วาดรูป

แผนภาพสมการแห่งมูลค่า

สมการมูลค่า คือ $$X=100000v^3,v={\left({\displaystyle \frac{1}{1+{\displaystyle \frac{i^{(4)}}{4}}}}\right)}^4$$ สามารถใช้ซิมไพ หาคำตอบได้ดังนี้

v, X = symbols('v X', positive = True)
v = (1/(1+.08/4))**4
v

0.9238454260265141

จากสมการ

eq = Eq(X, 1e5*v**3)
Sol = solve(eq,X)
Sol[0].evalf(7)

${\displaystyle 78849.32}$

ดังนั้นต้องฝากเงิน 78,749.32 บาท

ตัวอย่างที่ 8 ลงทุน 75,000 บาทในวันนี้ โดยได้อัตราดอกเบี้ยแบบ nominal ร้อยละ 6 ต่อปี ทบเดือนละ 1 ครั้ง (monthly) เมื่อครบ 4 ปี จะมีเงินสะสมเท่าใด?

วาดรูป

แผนภาพสมการแห่งมูลค่า

สมการมูลค่า คือ $$75000=X\cdot v^4,v={\left({\displaystyle \frac{1}{1+{\displaystyle \frac{i^{(12)}}{12}}}}\right)}^{12}$$ สามารถใช้ซิมไพ หาคำตอบได้ดังนี้

v, X= symbols('v X', positive = True)
v= (1/(1+0.06/12))**12
v

0.9419053396659195

แก้สมการ

eq = Eq(7.5e4, X*v**4)
Sol = solve(eq,X)
Sol[0].evalf(7)

${\displaystyle 95286.69}$

ดังนั้น เมื่อครบ 4 ปีจะเงินสะสมเท่ากับ $95,286.69$ บาท

ตัวอย่างที่ 9 คุณมีเงินในวันนี้ 20,000 บาท และต้องการให้กลายเป็น 30,000 บาท ถ้าดอกเบี้ยแบบ nominal ร้อยละ 10 ต่อปี ทบปีละ 2 ครั้ง (semiannually) ต้องใช้เวลากี่ปี?

วาดรูป

แผนภาพสมการแห่งมูลค่า

สมการมูลค่า คือ $$20000=30000\cdot v^t,v={\left({\displaystyle \frac{1}{1+{\displaystyle \frac{i^{(2)}}{2}}}}\right)}^2$$ สามารถใช้ซิมไพ หาคำตอบได้ดังนี้

# ให้ i^(2) คือ i2
t, v = symbols('t v', positive = True)
v= (1/(1+.10/2))**2
v

0.9070294784580498

eq = Eq(20000, 30000*v**t)
Sol = solve(eq,t)
Sol[0].evalf(3)

${\displaystyle 4.16}$

จะใช้เวลา 4.16 ปี เงินสะสมจะมีมูลค่า $30,0000$ บาท

3.4 กฎ 72 (Rule of 72)

ในทางการเงินมีกฎที่เรียกว่า “กฎ 72” (Rule of 72) ซึ่งเป็น กฎประมาณการ ที่นิยมใช้กันมากในการคำนวณว่า “จะใช้เวลากี่ปีในการทำให้เงินลงทุนเติบโตเป็น 2 เท่า” ด้วย ดอกเบี้ยทบต้น (compound interest)

สูตร $$\text{จำนวนปี}\approx \frac{72}{i}$$ โดยที่

• $i$ คือ อัตราดอกเบี้ยต่อปี (เป็นเปอร์เซ็นต์ เช่น 6, 8, 12)

• ผลลัพธ์คือ จำนวนปีโดยประมาณ ที่เงินจะเพิ่มขึ้นเป็น 2 เท่า

ตัวอย่าง ถ้าลงทุนที่อัตราดอกเบี้ย $i=6\mathrm{\%}$ $$\text{จำนวนปี}\approx \frac{72}{6}=12\text{ ปี}$$ เงินลงทุนจะ เพิ่มขึ้นเป็น 2 เท่าในประมาณ 12 ปี

Noteทำไมถึงใช้ 72?

เพราะจากสมการดอกเบี้ยทบต้น $$2=(1+i{)}^t\Rightarrow t=\frac{\ln (2)}{\ln (1+i)}$$ สำหรับ $i$ ขนาดเล็ก (5%–10%) เราสามารถประมาณ $\ln (1+i)\approx i$ (เมื่อ i แปลงเป็นเลขทศนิยม เช่น 0.06) ดังนั้นโดยประมาณ: $$t\approx \frac{0.693}{i}\Rightarrow t\approx \frac{69.3}{i}$$ ค่าจริงคือ 69.3 แต่ในทางปฏิบัติใช้ 72 เพราะ

• หารง่ายกว่า (72 หารด้วยหลายตัวเลขลงตัว เช่น 6, 8, 9, 12)

• ความแม่นยำยังอยู่ในช่วงยอมรับได้

Note

ในอดีตจนถึงปัจจุบัน ถ้าไม่ได้ใช้ซิมไพหรือโปรแกรมอื่นๆ เช่น R หรือ Excel ที่มีคำสั่งสำหรับการคำนวณทางการเงิน จะได้ต้องใช้เครื่องคิดเลขทางวิทยาศาสตร์หรือเครื่องคิดเลขทางการเงินช่วย และผู้อ่านจะต้องมีความรู้ในเครื่องการวิเคราะห์เชิงตัวเลขช่วยแก้ปัญหา เช่น วิธีแบ่งครึ่ง (bisection method) หรือ วิธีนิวตัน-ราฟสัน (Newton-Raphson method) ถ้าผู้อ่านเปิดหนังสือคณิตศาสตร์การเงินหรือทฤษฏีการเงินเล่มอื่นๆ ก็จะพบตารางอัตราดอกเบี้ยพร้อมสัญลักษณ์อื่นๆ สำหรับช่วยคำนวนที่เวลาต่างๆ

3.5 แบบฝึกหัดท้ายบท ให้วาดรูปและใช้ซิมไพในการหาคำตอบ

1. บริษัทแห่งหนึ่งมีแผนจะขยายโรงงานในอีก 4 ปีข้างหน้า และจะต้องใช้เงินลงทุนจำนวน 2,000,000 บาท ถ้าต้องการเริ่มสะสมเงินตั้งแต่วันนี้โดยฝากเงินครั้งเดียว อัตราดอกเบี้ยร้อยละ 6 ต่อปี ต้องฝากเงินวันนี้เป็นจำนวนเท่าใด?

2. นักศึกษาคนหนึ่งได้รับทุนการศึกษา 10,000 บาทในวันนี้ และนำเงินไปฝากธนาคารโดยไม่ถอนออก หากธนาคารให้ดอกเบี้ยแบบ nominal ร้อยละ 5 ต่อปี ทบปีละ 2 ครั้ง เมื่อครบ 5 ปี นักศึกษาจะมีเงินสะสมเท่าใด?

3.คุณยายของวิทย์ตั้งใจจะให้หลาน 50,000 บาทในวันเกิดปีที่ 18 ซึ่งเหลือเวลาอีก 6 ปี ถ้าคุณยายฝากเงินวันนี้ และได้ดอกเบี้ยแบบ nominal ร้อยละ 4 ต่อปี ทบปีละ 2 ครั้ง จะต้องฝากเงินเท่าใด?

4. คุณสมชายต้องการมีเงิน 1,000,000 บาทไว้ใช้หลังเกษียณในอีก 10 ปี โดยจะฝากเงินปีละ 70,000 บาท เริ่มจากสิ้นปีนี้ไปจนถึงครบ 10 ปี จงหาว่าเขาต้องได้รับดอกเบี้ยต่อปีเท่าใด?

5. ร้านค้าแห่งหนึ่งต้องการซื้อเครื่องจักรราคา 300,000 บาทในอีก 3 ปี หากมีเงินในวันนี้ 240,000 บาท จงคำนวณว่าอัตราดอกเบี้ยแบบ nominal ที่จำเป็นต้องได้รับคือเท่าใด (ทบปีละ 2 ครั้ง)

6. คุณศิริวางแผนเก็บเงินสำหรับค่าเรียนบุตรจำนวน 500,000 บาทในอีก 8 ปี โดยจะฝากปีละ 50,000 บาท เริ่มตั้งแต่สิ้นปีนี้ อัตราดอกเบี้ยควรเป็นเท่าใด?

7. คุณต้องการมีเงิน 200,000 บาทในอีก 5 ปี หากธนาคารให้ดอกเบี้ยร้อยละ 7 ต่อปีแบบทบต้น ต้องฝากเงินวันนี้เป็นจำนวนเท่าใด?

8. คุณมีเงินในวันนี้ 50,000 บาท และต้องการให้เติบโตเป็น 100,000 บาท ถ้าอัตราดอกเบี้ยแบบ nominal ร้อยละ 10 ต่อปี ทบปีละ 2 ครั้ง ต้องใช้เวลากี่ปี?

9. คุณปัทมาฝากเงิน 10,000 บาททุกสิ้นปีเป็นเวลา 5 ปี หากธนาคารให้ดอกเบี้ยร้อยละ 8 ต่อปี เมื่อครบ 5 ปีจะมีเงินสะสมทั้งหมดเท่าใด?

10. คุณลงทุน 30,000 บาทในวันนี้ และอีก 30,000 บาทในอีก 2 ปี ต้องการให้มีมูลค่ารวม 80,000 บาทในปีที่ 5 ถ้าอัตราดอกเบี้ยแบบ nominal ร้อยละ 6 ต่อปี ทบปีละ 2 ครั้ง การลงทุนเพียงพอหรือไม่?

11. คุณธนาได้รับเงิน 15,000 บาททุกปีเป็นเวลา 4 ปี หากอัตราดอกเบี้ยแบบ nominal ร้อยละ 5 ต่อปี ทบปีละ 2 ครั้ง จงหามูลค่าปัจจุบันของเงินทั้งหมด

12. คุณต้องการซื้อรถในอีก 2 ปีข้างหน้า และต้องการเงิน 500,000 บาท ถ้าธนาคารเสนออัตราดอกเบี้ยร้อยละ 3 ต่อปีแบบทบต้น ต้องมีเงินวันนี้เท่าใด?

13. คุณวุฒิฝากเงิน 25,000 บาทในวันนี้ และจะได้รับดอกเบี้ยร้อยละ 4 ต่อปี เมื่อครบ 6 ปีจะมีเงินสะสมเท่าใด?

14. นักลงทุนคนหนึ่งต้องการให้ผลตอบแทนรวมเป็น 200,000 บาทใน 5 ปี โดยลงทุนเริ่มต้น 120,000 บาทในวันนี้ อัตราดอกเบี้ยเฉลี่ยต่อปีที่ต้องได้รับคือเท่าใด?

15. คุณอารีย์จะฝากเงิน 5,000 บาททุกปีเป็นเวลา 10 ปี เริ่มจากปีหน้า หากอัตราดอกเบี้ยแบบ nominal ร้อยละ 6 ต่อปี ทบปีละ 2 ครั้ง
    เมื่อครบ 10 ปี จะมีเงินสะสมเท่าใด?

16. คุณลงทุนในพันธบัตรที่จะให้เงิน 10,000 บาทต่อปี เป็นเวลา 3 ปี ต้องการรู้มูลค่าปัจจุบันของกระแสเงินสดนี้ที่อัตราดอกเบี้ยร้อยละ 7 ต่อปี

17. นายเอกจะฝากเงินปีละ 60,000 บาทเป็นเวลา 20 ปี เพื่อเก็บไว้ใช้ยามเกษียณ
    ถ้าอัตราดอกเบี้ยร้อยละ 5 ต่อปี เมื่อครบ 20 ปี เขาจะมีเงินเท่าใด?

18. บริษัท ABC ต้องการให้เงินลงทุน 500,000 บาท เติบโตเป็น 1,000,000 บาทภายใน 7 ปี ถ้าลงทุนแบบดอกเบี้ยทบต้น อัตราผลตอบแทนต่อปีควรเป็นเท่าใด?

19. คุณสุกัญญาต้องการมีเงิน 250,000 บาทในอีก 5 ปี แต่สามารถฝากเงินต้นได้เพียง 180,000 บาท ถ้าอัตราดอกเบี้ยแบบ nominal ร้อยละ 6 ต่อปี ทบปีละ 2 ครั้ง
    เงินออมนี้เพียงพอหรือไม่?

20. คุณถอนเงินปีละ 20,000 บาทจากบัญชีเงินออมเป็นเวลา 4 ปี หากบัญชีให้ดอกเบี้ยแบบ nominal ร้อยละ 5 ต่อปี ทบปีละ 2 ครั้ง จงหามูลค่าปัจจุบันของการถอนทั้งหมด

[1]

จลีพร โกลากุล และ จุฬาลงกรณ์มหาวิทยาลัย. คณะพาณิชยศาสตร์และการบัญชี, คณิตศาสตร์การเงิน, พิมพ์ครั้งที่ 2. กรุงเทพฯ: คณะพาณิชยศาสตร์และการบัญชี จุฬาลงกรณ์มหาวิทยาลัย, 1984.

[2]

ประสิทธิ์ พยัคฆพงษ์, คณิตศาสตร์การเงินและการลงทุน, พิมพ์ครั้งที่ 1. กรุงเทพฯ: สำนักพิมพ์มหาวิทยาลัยเกษตรศาสตร์, 2004.

[3]

S. G. Kellison, The Theory of interest. ใน Irwin series in insurance and economic security. Homewood, Ill: R. D. Irwin, 1970.

[4]

มานพ วราภักดิ์, ทฤษฎีดอกเบี้ย = Theory of interest. กรุงเทพฯ: สำนักพิมพ์แห่งจุฬาลงกรณ์มหาวิทยาลัย, 2006.

[5]

A. Meurer และคณะ, “SymPy: symbolic computing in Python”, PeerJ Computer Science, ปี 3, น. e103, ม.ค. 2017, doi: 10.7717/peerj-cs.103.

[6]

J. D. Hunter, “Matplotlib: A 2D graphics environment”, Computing in Science & Engineering, ปี 9, ฉบับที่ 3, น. 90–95, 2007, doi: 10.1109/MCSE.2007.55.