5  เงินงวดแบบเปลี่ยนแปลง (Varying Annuities)

Importantหมายเหตุ

ก่อนเริ่มการคำนวณเชิงสัญลักษณ์ด้วยซิมไพ ขอให้ผู้อ่านทำการเรียกใช้คำสั่งดังต่อไปนี้ก่อน

from sympy import symbols, Eq, solve

เงินงวดแบบเปลี่ยนแปลงคือกรณีที่เงินชำระในแต่ละงวด ไม่เท่ากัน ซึ่งพบได้บ่อยในโลกจริง เช่น เงินสมทบที่เพิ่มขึ้นทุกปี หรือภาระผ่อนชำระที่ลดลงเมื่อเวลาเปลี่ยนไป หรืออาจจะมีค่าไม่เท่ากันแต่รูปแบบที่แน่นอน (pattern) ชัดเจน เช่น เพิ่มขึ้นหรือลดลง 10% ทุกงวดเป็นต้น

5.1 อนุกรมเงินทั่วไป (General Annuity)

แผนภาพสมการแห่งมูลค่า

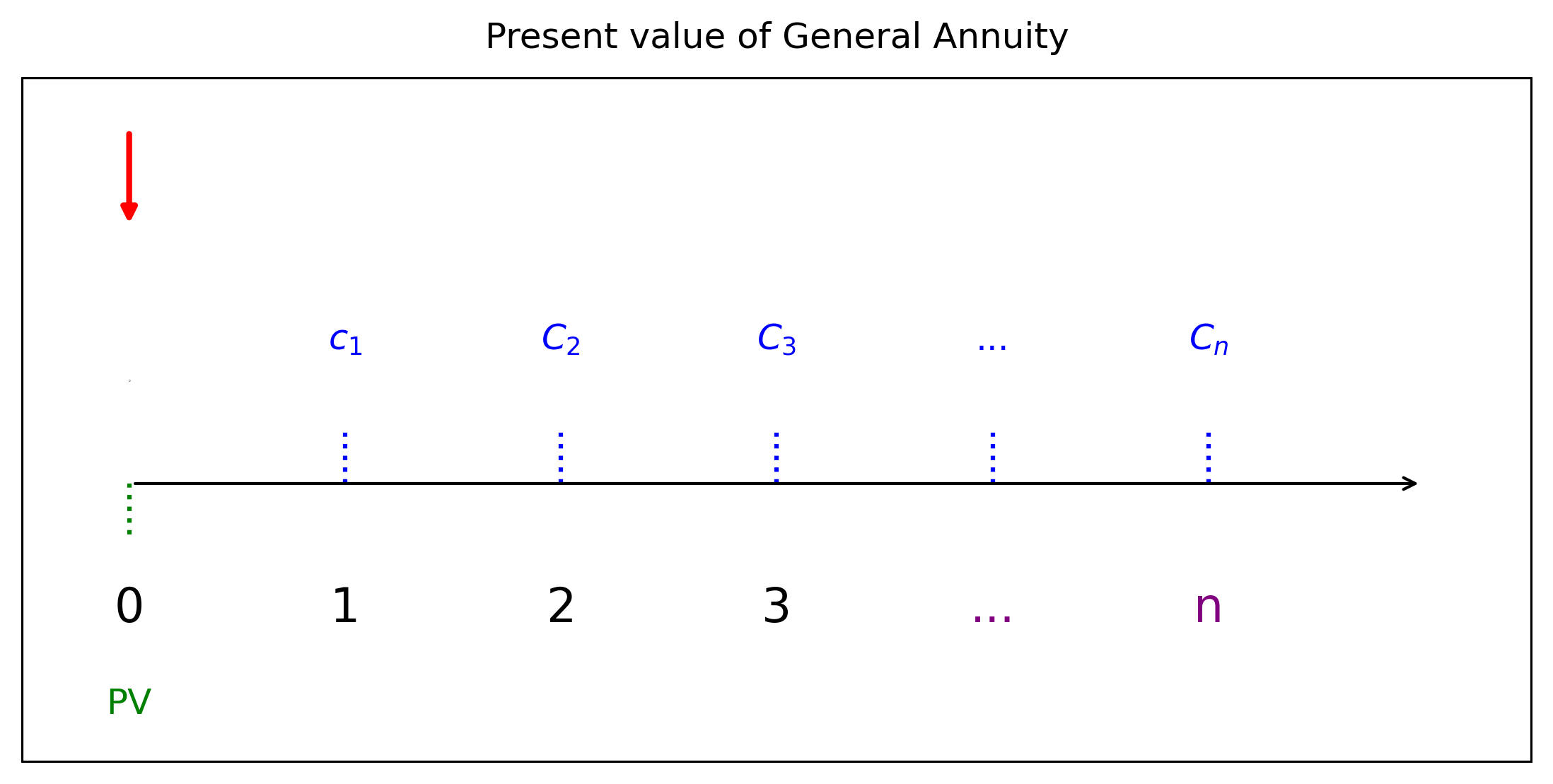
อนุกรมเงินทั่วไป คืออนุกรมเงินที่ชำระไม่จำเป็นต้องเป็นงวดเท่ากันทุกระยะเวลา หรือไม่มีรูปแบบเหมือนบทที่ผ่านมา หรือหัวข้อด้านบน

• $C_1$ ที่เวลา $t_1$

• $C_2$ ที่เวลา $t_2$

• $\cdots$

• $C_n$ ที่เวลา $t_n$

เราต้องการคำนวณมูลค่าปัจจุบันด้วย $$PV=\sum _{k=1}^n{C}_k\cdot v^k,\text{โดยที่ }v=\frac{1}{1+i}$$

ซึ่งสามารถเขียนเป็นผลคูณภายใน (inner product) ระหว่าง

• เวกเตอร์กระแสเงินสด $\mathbf{C}=[C_1,C_2,\dots ,C_n]$

• กับเวกเตอร์ส่วนลด $\mathbf{v}=[v^1,v^2,\dots ,v^{t_n}]$ จะได้ $$PV=⟨\mathbf{C},\mathbf{v}⟩=\sum _{k=1}^n{C}_k\cdot v^k$$

ถ้า $C_i=1,\mathrm{\forall }i=1,2,\cdots ,n$ ก็คือเนื้อหาบทที่ผ่านมานั่นเอง

ก่อนที่จะการคำนวณด้วยซิมไพโดยใช้ผลคูณภายใน ต้องรู้ถึงการสร้างลำดับ (sequence) ด้วยซิมไพก่อน

ตัวอย่าง เช่นลำดับตัวเลข 1 ถึง 10 จะสร้างเป็นเมตริกซืขนาด $1\times 10$

from sympy import Matrix
seq = Matrix(range(1, 11)).T # สร้างลำดับตั้งแต่เลข 1 แต่ไม่เกิน 11
seq

${\displaystyle \left[\begin{array}{cccccccccc}1& 2& 3& 4& 5& 6& 7& 8& 9& 10\end{array}\right]}$

Importantหมายเหตุ

ผู้เขียนเลือกที่จะสร้างเมตริกซ์ชนาด $1\times n$ เพื่อที่จะประหยัดกระดาษเท่านั้น ผู้อ่านสามารถใช้คำสั่ง

seq = Matrix(range(1, 11))

ได้เลยโดยไม่ต้องตามด้วยเมท็อด .T (.T คือการเปลี่ยนเป็นเมตริกซ์ผกผัน) และเมื่อทำการหาผลคูณภายในต้องจะเป็นเมติกซ์ทั้งสองตัวต้องมีขนาดเดียวกัน

5.1.1 การเข้าถึงค่าหรือเปลี่ยนแปลงค่าในลำดับ

ตำแหน่งในไพธอนเริ่มต้นจาก 0 ถ้าต้องการเห็นหรือใช้่ค่าใน seq ตัวแรก สามารถทำได้โดย

seq[0]

${\displaystyle 1}$

ถ้าต้องการเปลี่ยนค่า seq[0] เท่ากับ 100 ทำได้โดย

seq[0] = 100
seq[0]

${\displaystyle 100}$

from sympy import symbols, Matrix, Rational
import numpy as np
# สร้างสัญลักษณ์ v และมูลค่าปัจจุบัน PV
v, PV = symbols('v PV', positive=True) 
# เวลาของแต่ละงวด
t = np.arange(1, 11, 1)  # สร้าง t= [1,2,3,...,10]
# กระแสเงินสด (สมมุติว่าเท่ากัน 1000)
C = Matrix([1000]*len(t)) # C= [1000, 1000,..., 1000] (10 ตัว)
# เวกเตอร์ของ v^t
v_vector = Matrix([v**ti for ti in t])
# หาผลคูณภาพในด้วยเมท๊อด .dot()
eq =Eq(PV, C.dot(v_vector))
eq # แสดงสมการ

${\displaystyle PV=1000v^{10}+1000v^9+1000v^8+1000v^7+1000v^6+1000v^5+1000v^4+1000v^3+1000v^2+1000v}$

สมมุติใช้อัตราดอกเบี้ย 5% แทนค่าลงไป

eq.subs({v:1/(1.05)}).evalf(7)

${\displaystyle PV=7721.735}$

ถ้าการจ่ายรายงวดแบบทั่วไปที่ไม่ได้มีขนาดยาวมาก เช่นไม่เกิน 10 งวด สามารถสร้างเมตริกซได้เองดังนี้

C = Matrix([1, 2, 4, 6, 100, 10, 100]).T
C

${\displaystyle \left[\begin{array}{ccccccc}1& 2& 4& 6& 100& 10& 100\end{array}\right]}$

5.2 เงินงวดเพิ่มขึ้นทุกงวด (Increasing Annuities)

เป็นกรณีที่เงินงวดเพิ่มขึ้นตามลำดับ เช่น $R,2R,3R,\dots ,nR$ จะมี มูลค่าปัจจุบัน (Present Value) $$PV=\sum _{k=1}^{n}k\cdot R\cdot v^k$$ ใช้ชิมไพหาคำตอบได้ดังนี้

from sympy import symbols, diff, Sum, sympify
k, n, v, R, A, PV =symbols('k n v R A PV')
A = Sum(k*R*v**k,(k, 1, n))
A

${\displaystyle \sum _{k=1}^{n}Rk{v}^k}$

ผลรวมจากการคำนวณด้วยซิมไพ

A.doit()

${\displaystyle R\left(\{\begin{array}{ll}\frac{n^2}{2}+\frac{n}{2}& \text{for}v=1\\ \frac{v(nv{v}^n-n{v}^n-v^n+1)}{{(v-1)}^2}& \text{otherwise}\end{array}\right)}$

ถ้าต้องการพิสูจน์สูตรน้ีด้วยซิมไพ สามารถทำได้ดังนี้โดยเริ่ม สิ่งที่รู้จากบทที่ผ่านมาคือ

$$a_{\bar{n}|i}=\sum _{k=1}^n{v}^k=v{\displaystyle \frac{1-v^n}{1-v}}$$ หาอนุพันธ์ $${\displaystyle \frac{d{a}_{\bar{n}|i}}{dv}}=\sum _{k=1}^{n}k\cdot v^{k-1}$$ ใช้ซิมไพ

dA=diff(Sum(v**k, (k, 1, n)), v )
dA.doit()

${\displaystyle \frac{\{\begin{array}{ll}\frac{n^2}{2}+\frac{n}{2}& \text{for}v=1\\ \frac{v(nv{v}^n-n{v}^n-v^n+1)}{{(v-1)}^2}& \text{otherwise}\end{array}}{v}}$

เมื่อคูณ $v$ เข้าไปจะได้ $$v{\displaystyle \frac{d{a}_{\bar{n}|i}}{dv}}=\sum _{k=1}^{n}k\cdot v^k$$ ดังนั้นจะได้

sympify(v*dA.doit())

${\displaystyle \{\begin{array}{ll}\frac{n^2}{2}+\frac{n}{2}& \text{for}v=1\\ \frac{v(nv{v}^n-n{v}^n-v^n+1)}{{(v-1)}^2}& \text{otherwise}\end{array}}$

คูณ $v$ เข้าไปในสมการทั้งสองข้างจะได้ $$v\cdot {\displaystyle \frac{d{a}_{\bar{n}|i}}{dv}}=\sum _{k=1}^{n}k\cdot v^k$$ นั่นคือสูตรการจ่ายรายงวดที่ได้

A = Sum(v**k,(k, 1, n)).doit()
dA = diff(Sum(v**k,(k, 1, n)).doit(),v)

# ดึงเฉพาะกรณีที่เงื่อนไขเป็น True จาก v ไม่เท่ากับ 1
for e, cond in dA.args:
    if cond == True:
        result = e

dA = result
dA

${\displaystyle \frac{1-\frac{v^{n+1}(n+1)}{v}}{1-v}+\frac{v-v^{n+1}}{{(1-v)}^2}}$

คูณ $dA$ ด้วย v จะได้

vdA = v*dA
vdA

${\displaystyle v(\frac{1-\frac{v^{n+1}(n+1)}{v}}{1-v}+\frac{v-v^{n+1}}{{(1-v)}^2})}$

ทดสอบการคำนวณด้วยการแทนค่าโดยใช้ผลคูณภายในและผลการคำนวณโดยใช้สูตรที่ได้จากซิมไพ

แผนภาพสมการแห่งมูลค่า

กำหนดอัตราดอกเบี้ยเท่ากับ 5% จะได้

v, PV = symbols('v PV', positive=True) 
# เวลาของแต่ละงวด
t = np.arange(1, 11, 1)  # สร้าง t= [1,2,3,...,10]
# กระแสเงินสด (สมมุติว่าเท่ากัน 1000)
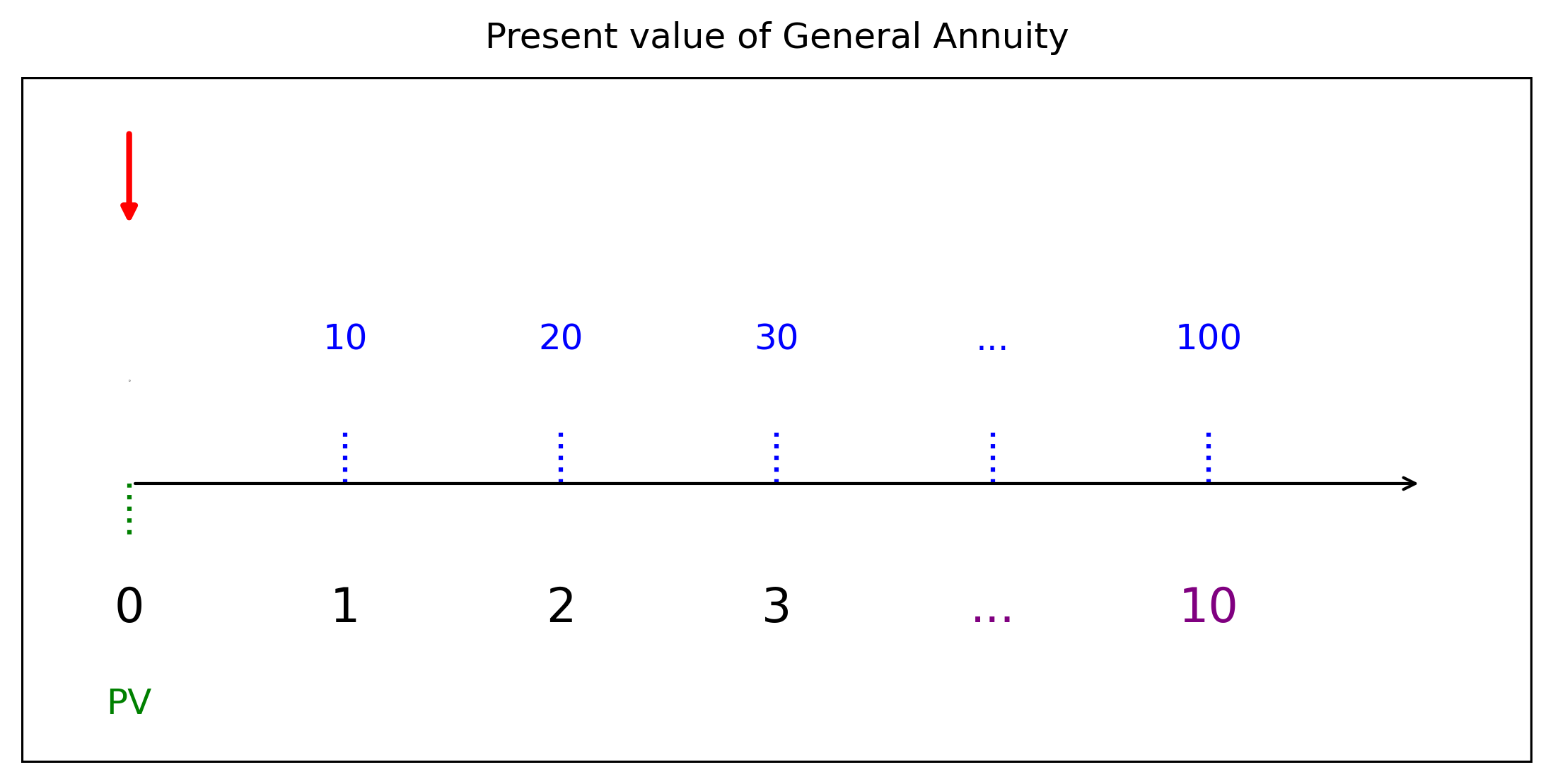
C = Matrix([10]*t).T # C= [10 20,..., 100] (10 ตัว)
# เวกเตอร์ของ v^t
v_t = Matrix([v**ti for ti in t])
PV =C.dot(v_t)
PV

${\displaystyle 100v^{10}+90v^9+80v^8+70v^7+60v^6+50v^5+40v^4+30v^3+20v^2+10v}$

แทนค่า $v=1/1.05$

PV.subs({v:1/1.05}).evalf(5)

${\displaystyle 393.74}$

แทนค่าสูตรที่คำนวณได้จากตัวอย่างที่ผ่านมา

vdA

${\displaystyle v(\frac{1-\frac{v^{n+1}(n+1)}{v}}{1-v}+\frac{v-v^{n+1}}{{(1-v)}^2})}$

PV = 10*vdA.subs({n:10, v:1/1.05}).doit().evalf(5)
PV

${\displaystyle 10v(\frac{1.0-11.0v^{10}}{1.0-v}+\frac{-v^{11}+v}{{(1.0-v)}^2})}$

ทั้งสองวิธีมีค่าเท่ากัน ผู้อ่านต้องเลือกใช้งานให้เหมาะสมตามความถนัดของตนเอง ในทางคณิตศาสตร์การเงินเราใช้สัญลักษณ์สำหรับรายงวดที่ลักษณ์เพิ่มขึ้นงวดละ 1 หน่วย มีมูลค่าปัจจุบันเท่ากับ $$PV={\left(Ia\right)}_{\bar{n}|i}={\displaystyle \frac{{\ddot{a}}_{\bar{n}|i}-n\cdot v^n}{i}}$$ และมูลค่าในอนาคต ณ ปีที่ $n$ คือ $$FV={\left(Is\right)}_{\bar{n}|i}=(1+i{)}^n\cdot {\left(Ia\right)}_{\bar{n}|i}={\displaystyle \frac{{\ddot{s}}_{\bar{n}|i}-n}{i}}$$

5.3 เงินงวดลดลงทุกงวด (Decreasing Annuities)

เงินงวดลดลงทีละงวด เช่น $nR,(n-1)R,\dots ,R$

มูลค่าปัจจุบัน (Present Value) สำหรับรายงวด $n,n-1,\cdots ,1$ คือ $$PV=\sum _{k=1}^n(n-k+1)R\cdot v^k={\left(Da\right)}_{\bar{n}|i}={\displaystyle \frac{n-a_{\bar{n}|i}}{i}}$$ และมูลค่าอนาคต ณ สิ้นปีที่ $n$ $$FV={\left(Ds\right)}_{\bar{n}|i}=(1+i{)}^n\cdot {\left(Da\right)}_{\bar{n}|i}={\displaystyle \frac{n\cdot (1+i{)}^n-s_{\bar{n}|i}}{i}}$$

ผู้อ่านสามารถใช้ได้ทั้งแบบการคำนวณแบบใช้ผลคูณภายใน หรือใช้การหาผลรวมโดยตรง หรือจะใช้สูตรที่ใช้ก็สามารถใช้ซิมไพทำได้ทั้งหมด

5.4 เงินงวดแบบขั้นบันได (Step Annuities)

เงินงวดที่เปลี่ยนค่าทีละช่วง เช่น $R,R,R,2R,2R,2R,3R,3R,3R,\dots$

สามารถกำหนดแบบเป็นช่วงด้วย Piecewise() ในซิมไพ

5.5 สูตรทั่วไปโดยใช้อัตราการเติบโต (General Formulas with Symbolic Series)

กำหนดให้อัตราการเติบโตของเงินงวดคือ $g$ (growth rate)

มูลค่าปัจจุบันแบบทั่วไป

$$PV=\sum _{k=1}^n\frac{R(1+g{)}^{k-1}}{(1+i{)}^k}$$

กรณีนี้รวมทั้งอนุกรมที่โตตาม $g$ และสามารถประยุกต์ได้กับการเติบโตแบบเรขาคณิต (Geometric growth annuities)

5.6 การทำให้ง่ายขึ้นด้วยคำสั่ง simplify() (Simplifying with simplify())

เมื่อใช้ .doit() เพื่อหาผลรวมของอนุกรม มักได้ผลลัพธ์ที่ซับซ้อน ลองใช้คำสั่ง simplify() เพื่อลดรูป

from sympy import simplify
simplified_pv = simplify(PV_expr.doit())

5.7 ตัวอย่างการคำนวณมูลค่าปัจจุบัน (Example: Computing Present Value)

กำหนด: $R=100,i=0.05,n=5$ ใช้ซิมไพคำนวณ

PV_num = PV_inc.subs({R: 100, i: 0.05, n: 5}).doit()
(PV_num)  # ได้ผลลัพธ์เชิงตัวเลข

5.8 สรุปเปรียบเทียบประเภทของเงินงวด (Summary of Varying Annuities)

ประเภท (Type)	เงินงวด (Payment)	การเขียนในซิมไพ(SymPy Expression)
เพิ่มขึ้น (Increasing)	$kR$	k * R / (1+i)**k
ลดลง (Decreasing)	$(n-k+1)R$	(n - k + 1) * R / (1+i)**k
ขั้นบันได (Step)	เปลี่ยนช่วง	Piecewise(...)
โตตาม g (Growth)	$R(1+g{)}^{k-1}$	R * (1 + g)**(k-1) / (1 + i)**k

5.9 กรณีที่ใช้สัญลักษณ์ทั้งหมด

# สร้างสัญลักษณ์ cashflow และเวลา
n = 3
C = symbols(f'C1:{n+1}')       # C1, C2, C3
T = symbols(f't1:{n+1}')       # t1, t2, t3

# เวกเตอร์
C_vec = Matrix(C)
v_vec = Matrix([v**T[k] for k in range(n)])

# มูลค่าปัจจุบันทั่วไป
PV = C_vec.dot(v_vec)
print(PV)

ได้ผลลัพธ์เป็น

$$PV=C_1{v}^{t_1}+C_2{v}^{t_2}+C_3{v}^{t_3}$$

5.10 สรุป

องค์ประกอบ	ความหมาย
$C_k$	กระแสเงินสดในงวดที่ $k$
$t_k$	เวลาที่จ่ายเงินสดในงวดที่ $k$
$v=\frac{1}{1+i}$	อัตราส่วนลด
$PV=\mathbf{C}\cdot {\mathbf{v}}^{\mathbf{t}}$	มูลค่าปัจจุบันของ general annuity

5.11 แบบฝึกหัดท้ายบท

1. ให้สร้างสูตรของมูลค่าปัจจุบันของเงินงวดที่เพิ่มขึ้นปีละ 1 หน่วยจนครบ $n$ งวด โดยใช้อัตราดอกเบี้ย $i$

2. คำนวณมูลค่าปัจจุบันของเงินงวดเพิ่มขึ้นปีละ 100 บาท เป็นเวลา 5 ปี ที่อัตราดอกเบี้ย 6%

3. สร้างสูตรของมูลค่าปัจจุบันสำหรับเงินงวดที่ลดลงปีละ 1 หน่วย เริ่มจาก $n$ หน่วย

4. เงินงวดเพิ่มขึ้นแบบเรขาคณิต จงสร้่างสูตรสำหรับเงินงวดที่เพิ่มขึ้นตามเรขาคณิตด้วยอัตรา $g$ โดยเริ่มจาก 1 หน่วย

5. หาค่าประมาณของเงินงวดเรขาคณิต คำนวณมูลค่าปัจจุบันของเงินงวดที่เพิ่มขึ้น 3% ต่อปี เป็นเวลา 10 ปี ด้วยดอกเบี้ย 5%

6. การใช้สูตรลัดสำหรับเงินงวดเลขคณิต

ใช้สูตรลัด $\ddot{I}{a}_{\bar{n}|i}=\frac{a_{\bar{n}|i}-n{v}^n}{i}$ เพื่อหามูลค่าปัจจุบันของเงินงวดที่เพิ่มขึ้น

7. ใช้ซิมไพแสดงผลรวมของลำดับเลขคณิต และตรวจสอบว่าสามารถเทียบเท่ากับสูตรทั่วไปได้

8. ให้ใช้ไลบรารี Matplotlib แสดงกระแสเงินสดที่เพิ่มขึ้นปีละ 1 หน่วย จากปี 1 ถึงปี 5

9. ความสัมพันธ์กับสูตรพื้นฐาน จงอธิบายว่าเงินงวดที่เพิ่มขึ้นสามารถสร้างจากการผสมระหว่างเงินงวดคงที่และอนุกรมเลขคณิตอย่างไร พร้อมใช้ ซิมไพแสดงให้เห็น

[1]

จลีพร โกลากุล และ จุฬาลงกรณ์มหาวิทยาลัย. คณะพาณิชยศาสตร์และการบัญชี, คณิตศาสตร์การเงิน, พิมพ์ครั้งที่ 2. กรุงเทพฯ: คณะพาณิชยศาสตร์และการบัญชี จุฬาลงกรณ์มหาวิทยาลัย, 1984.

[2]

ประสิทธิ์ พยัคฆพงษ์, คณิตศาสตร์การเงินและการลงทุน, พิมพ์ครั้งที่ 1. กรุงเทพฯ: สำนักพิมพ์มหาวิทยาลัยเกษตรศาสตร์, 2004.

[3]

S. G. Kellison, The Theory of interest. ใน Irwin series in insurance and economic security. Homewood, Ill: R. D. Irwin, 1970.

[4]

มานพ วราภักดิ์, ทฤษฎีดอกเบี้ย = Theory of interest. กรุงเทพฯ: สำนักพิมพ์แห่งจุฬาลงกรณ์มหาวิทยาลัย, 2006.

[5]

A. Meurer และคณะ, “SymPy: symbolic computing in Python”, PeerJ Computer Science, ปี 3, น. e103, ม.ค. 2017, doi: 10.7717/peerj-cs.103.

[6]

J. D. Hunter, “Matplotlib: A 2D graphics environment”, Computing in Science & Engineering, ปี 9, ฉบับที่ 3, น. 90–95, 2007, doi: 10.1109/MCSE.2007.55.