Chapter 6 Topic Distribtuion
Let \(\theta_{d,t}\) represent the topic proportions for individual \(d\) at time \(t\), and \(w_{d,t}\) represent the new disease diagnoses observed for that individual at time \(t\). Let \(\gamma_d\) represent the genetic stickiness parameter for individual \(d\), which influences the rate at which their topic proportions change over time.
Given the new observations \(w_{d,t}\), we update \(\theta_{d,t}\) as follows:
The probability of \(\theta_{d,t}\) given \(w_{d,t}\), \(\eta_{t}\), and \(\gamma_d\) is expressed as:
Given:
- \(\theta_{d,t-1}\): The topic proportions for individual \(d\) at time \(t-1\).
- \(w_{d,t}\): The new disease diagnoses observed for individual \(d\) at time \(t\).
- \(\beta_{k,v,t}\): The probability of disease \(v\) in topic \(k\) at time \(t\), derived from the
normalized_array. - \(\gamma_d\): The genetic stickiness parameter for individual \(d\).
The update rule for \(\theta_{d,t}\), the topic proportions at time \(t\), is given by:
Compute the likelihood of observing the new diagnoses given each topic:
\[ \text{likelihood}_k = \prod_{v \in w_{d,t}} \beta_{k,v,t} \]
Update the topic proportions by multiplying the prior topic proportions by the likelihood and the genetic stickiness factor, then normalize:
\[ \text{unnormalized_posterior}_k = \theta_{d,t-1,k} \cdot \gamma_d \cdot \text{likelihood}_k \]
\[ \theta_{d,t,k} = \frac{\text{unnormalized_posterior}_k}{\sum_{k=1}^{K} \text{unnormalized_posterior}_k} \]
Where: - \(\theta_{d,t,k}\) is the updated proportion of topic \(k\) for individual \(d\) at time \(t\). - The normalization step ensures that the updated topic proportions sum to 1.
First we need to simulate a theta that changes with time. We will make it a function of genetics so that individuals with greater genetic ‘pull’ move less
6.1 Population shifts
library(reshape2)
library(dplyr)
library(ggplot2)
linear_trend <- function(time,
slope = 0.1,
intercept = 0) {
return(slope * time + intercept)
}
logistic_growth <-
function(t, carrying_capacity, growth_rate, t_mid) {
carrying_capacity / (1 + exp(-growth_rate * (t - t_mid)))
}
exponential_decay <- function(t, initial_value, decay_rate) {
initial_value * exp(-decay_rate * t)
}
gaussian_peak <- function(t, mean, variance) {
exp(-(t - mean) ^ 2 / (2 * variance))
}
polynomial_trend <- function(t, coefficients) {
sum(sapply(1:length(coefficients), function(i)
coefficients[i] * t ^ (i - 1)))
}
sinusoidal_pattern <- function(t, amplitude, period, phase) {
amplitude * sin((2 * pi / period) * t + phase)
}
cov_function <- function(t1, t2, lengthscale, variance) {
return(variance * exp(-0.5 * (t1 - t2) ^ 2 / lengthscale ^ 2))
}
time_points <- 1:T
# Create a list to hold the mu vectors for each topic
mu_vectors <- list()
# Assign a mean function to each topic based on expected behavior
mu_vectors[[1]] <-
sapply(time_points,
linear_trend,
slope = 0.02,
intercept = 0.5)
mu_vectors[[2]] <-
sapply(
time_points,
logistic_growth,
carrying_capacity = 1,
growth_rate = 0.1,
t_mid = T / 2
)
mu_vectors[[3]] <-
sapply(time_points,
exponential_decay,
initial_value = 1,
decay_rate = 0.05)
genetic_predisposition <-
matrix(MCMCpack::rdirichlet(D, alpha = c(1, 1, 1)), nrow = D, byrow = T)
predisposition_adjustment <-
function(mu, predisposition_score, topic_effect_size) {
# Apply the effect size to the predisposition score to get the adjustment
adjustment <- predisposition_score * topic_effect_size
# Adjust the population mean mu with the individual's predisposition adjustment
adjusted_mu <- mu + adjustment
return(adjusted_mu)
}
mu_population = array(dim = c(K, T))
for (k in 1:K) {
mu_population[k,] = mu_vectors[[k]] # Each topic's population-level mean over time
}6.2 Step 2: Generate individual-specific topic distributions
alpha_individual = array(dim = c(D, K, T))
adjusted_mu_individual = array(dim = c(D, K, T))
alpha_pop = array(dim = c(K, T))
## generate population Thetas to show population level trajectories
variance <- runif(n = K, min = 1, max = 2)
lengthscale <-
runif(n = K, min = 95, max = 100) # Example lengthscale, could change more for some topics but it doesn't
effect_size_topic = runif(n = K)
cov_matrix_pops = list()
for (k in 1:K) {
# Adjust the mean based on individual genetic predisposition
mu_k <- mu_population[k, ]
# Define the effect size (you might have different effect sizes for different topics)
effect_size_k <- effect_size_topic[k]
topic_variance = variance[k]
topic_lengthscale = lengthscale[k]
# Generate the covariance matrix using the individual's genetic factor
cov_matrix_pop = matrix(0, nrow = T, ncol = T)
for (i in 1:T) {
for (j in 1:T) {
cov_matrix_pop[i, j] = cov_function(i, j, lengthscale = topic_lengthscale, variance = topic_variance)
}
}
cov_matrix_pops[[k]] = cov_matrix_pop
alpha_pop[k, ] = mvrnorm(1, mu = mu_k, Sigma = cov_matrix_pop)
for (d in 1:D) {
# Get this individual's predisposition score for this topic
predisposition_score_dk <- genetic_predisposition[d, k]
# Adjust the population-level mean mu_k for this individual's predisposition
adjusted_mu_k <-
predisposition_adjustment(mu_k, predisposition_score_dk, effect_size_k)
adjusted_mu_individual[d, k,] = adjusted_mu_k
# Sample from the GP for this individual and topic
alpha_individual[d, k, ] = mvrnorm(1, mu = adjusted_mu_k, Sigma = cov_matrix_pop)
}
}6.3 Step 3: Normalize the proportions for each individual across topics at each time point
Theta_individual = array(dim = c(D, K, T))
for (d in 1:D) {
for (t in 1:T) {
Theta_individual[d, , t] = softmax_normalize(alpha_individual[d, , t])
}
}
Theta_pop = array(dim = c(K, T))
for (t in 1:T) {
Theta_pop[, t] = softmax_normalize(alpha_pop[, t])
}6.3.1 now show for Population
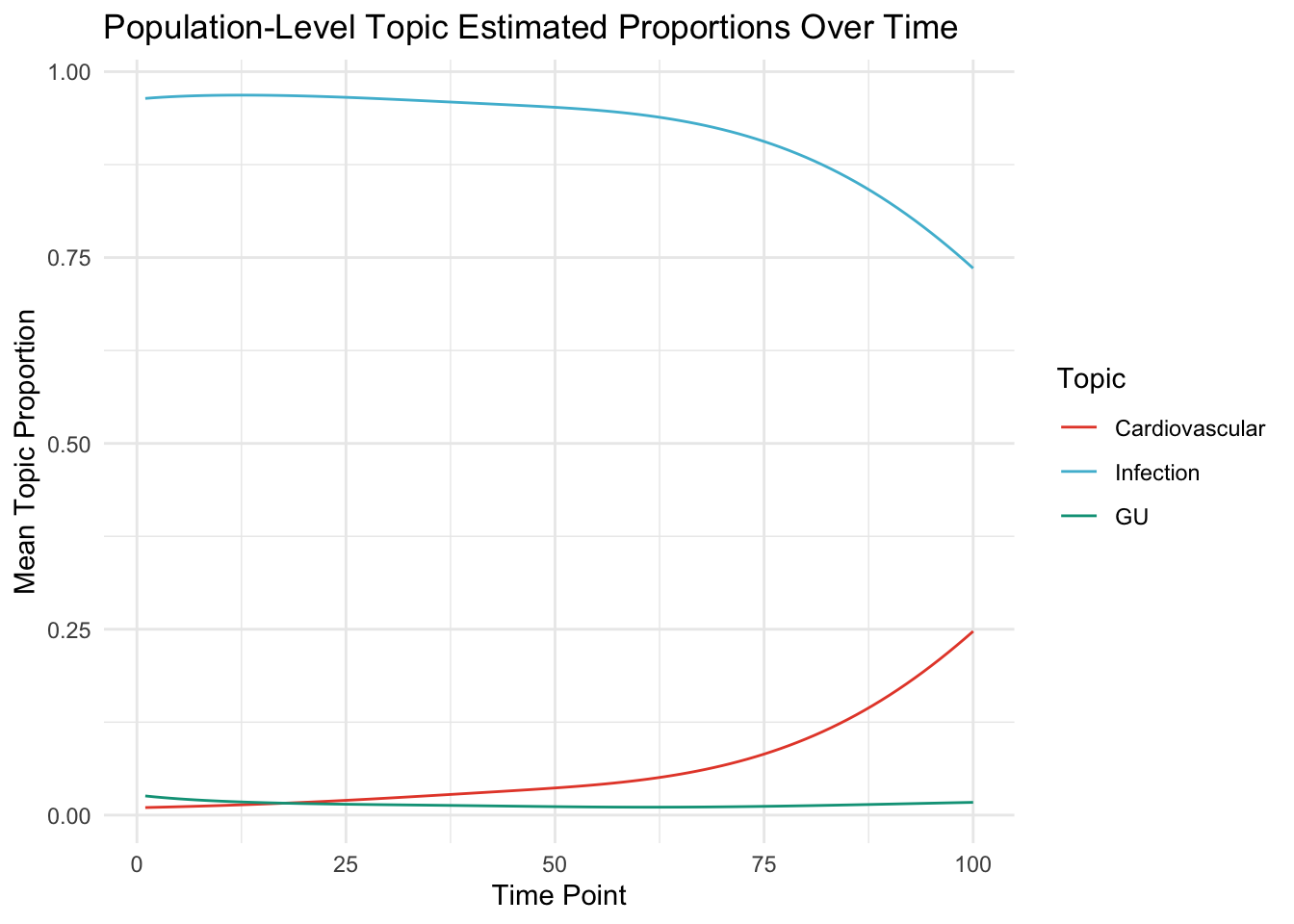
Here we look at the mean level of the topic weight for each time period across population.
proportions_df = melt(Theta_pop)
names(proportions_df) <- c("Topic", "Time", "Proportion")
proportions_df$Topic = factor(
proportions_df$Topic,
levels = c(1, 2, 3),
labels = c("Cardiovascular", "Infection", "GU")
)
tab = proportions_df %>% group_by(Time, Topic) %>% summarise(Proportion =
mean(Proportion))## `summarise()` has grouped output by 'Time'. You can override using the
## `.groups` argument.# Plot
ggplot(tab, aes(x = Time, y = Proportion, col = as.factor(Topic))) +
geom_line() +
theme_minimal() +scale_color_npg()+
labs(
title = "Population-Level Topic Estimated Proportions Over Time",
x = "Time Point",
y = "Mean Topic Proportion",
color = "Topic"
)
6.4 Population Mean function
Here we show how this matches population means
– this will be more or less true depending on how fine the lengthscale is – if the vairance is small and lengthscale large, then the pattern will roughly approximate the man
softmax_population <- apply(mu_population, 2, softmax_normalize)
# Convert softmaxed population means to a data frame for plotting
population_probs_df <- as.data.frame(t(softmax_population))
population_probs_df$Time <- 1:T
population_probs_df <- melt(population_probs_df, id.vars = "Time")
# Automating topic assignment
population_probs_df$Topic <-
as.numeric(gsub("V", "", population_probs_df$variable))
ggplot(population_probs_df,
aes(
x = Time,
y = value,
group = Topic,
color = as.factor(Topic)
)) +
geom_line() +
theme_minimal() +
labs(title = "Population-Level Topic Means (softmax) Over Time",
x = "Time Point",
y = "Probability") +
scale_color_npg()
6.5 Population to Individual
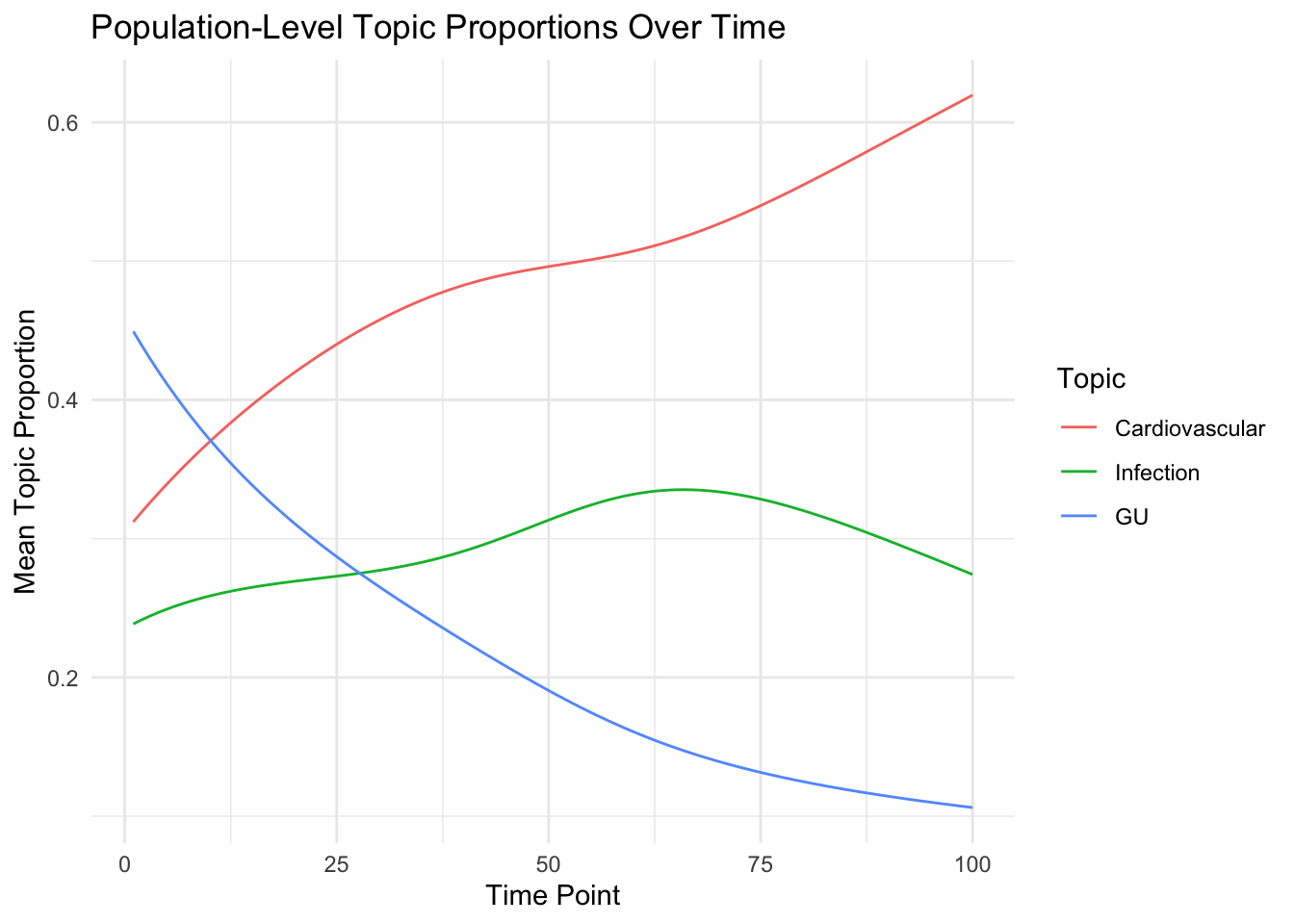
Now show individual mimics pouplation level patterns:
We melt across individuals (i.e., theta after adjustment for individual genetifsc)
library(reshape2)
proportions_df = melt(Theta_individual)
names(proportions_df) <-
c("Individual", "Topic", "Time", "Proportion")
proportions_df$Topic = factor(
proportions_df$Topic,
levels = c(1, 2, 3),
labels = c("Cardiovascular", "Infection", "GU")
)
tab = proportions_df %>% group_by(Time, Topic) %>% summarise(Proportion =
mean(Proportion))## `summarise()` has grouped output by 'Time'. You can override using the
## `.groups` argument.# Plot
ggplot(tab, aes(x = Time, y = Proportion, col = as.factor(Topic))) +
geom_line() +
theme_minimal() +
labs(
title = "Population-Level Topic Proportions Over Time",
x = "Time Point",
y = "Mean Topic Proportion",
color = "Topic"
)
6.6 Population versus Genetically Selected Individuals
Instead of considering the theta, we can look at individual genetic functions of the mean.
Plot the \(\mu\) for the population and compare with individuals
# Identify the individual with the highest genetic predisposition for each topic
high_rankers <-
data.frame(t(apply(genetic_predisposition, 1, function(x) {
top = which.max(x)
return(list = c(topic = top, ratio = x[top] / sum(x[-top])))
})))
top_individuals_per_topic = vector()
top_individuals_per_topic[1] = which(high_rankers[, 1] == 1 &
high_rankers[, 2] > 2)[1]
top_individuals_per_topic[2] = which(high_rankers[, 1] == 2 &
high_rankers[, 2] > 2)[1]
top_individuals_per_topic[3] = which(high_rankers[, 1] == 3 &
high_rankers[, 2] > 2)[1]
top_individuals_info <- data.frame(
Topic = factor(1:K),
Individual = as.character(top_individuals_per_topic),
GeneticPredispositionRatio = high_rankers[top_individuals_per_topic, "ratio"]
)
amt = array(NA, dim = c(D, K, T))
for (d in 1:D) {
amt[d, , ] = apply(adjusted_mu_individual[d, , ], 2, softmax)
}
### but folks with high topic 3 could also have high topic 1... need to relfect population means
population_probs_df$Topic = as.factor(population_probs_df$Topic)
# Assuming D, K, T are defined; and Theta_individual is your D x K x T array
D <- dim(Theta_individual)[1]
K <- dim(Theta_individual)[2]
T <- dim(Theta_individual)[3]
# Let's create a comparison plot for a specific individual, for example, Individual 3
individual_number = top_individuals_per_topic
individual_probs_df <-
melt(amt[individual_number, , , drop = FALSE], varnames = c("Individual", "Topic", "Time"))
individual_probs_df$Topic <- as.factor(individual_probs_df$Topic)
individual_probs_df$Individual <- as.factor(individual_number)
combined_df <- bind_rows(population_probs_df %>% mutate(Individual = "Population"),
individual_probs_df)
# Update the topic names in the dataframe
combined_df$Topic <-
recode_factor(combined_df$Topic,
`1` = "CVD",
`2` = "GI",
`3` = "Congenital")
# Update top_individuals_info to reflect the new topic names
top_individuals_info$Topic <- factor(
top_individuals_info$Topic,
levels = c(1, 2, 3),
labels = c("CVD", "GI", "Congenital")
)
#Round the genetic predisposition ratios for display
top_individuals_info$GeneticPredispositionRatio <-
round(top_individuals_info$GeneticPredispositionRatio, 2)
# Plot with annotations for genetic predisposition ratios
ggplot(combined_df,
aes(
x = Time,
y = value,
group = Individual,
color = Individual
)) +
geom_line(aes(linetype = Topic)) +
facet_wrap( ~ Topic, scales = "free_y", ncol = K) +
geom_text(
data = top_individuals_info,
aes(
x = Inf,
y = Inf,
label = paste(
"Highest Ranking Individua is:",
Individual,
"\nRatio:",
round(GeneticPredispositionRatio, 2)
)
),
position = position_nudge(y = -0.1),
# Nudging text down a bit
hjust = 1.1,
vjust = 1.1,
# Adjust text position
check_overlap = TRUE,
size = 3,
inherit.aes = FALSE
) +
theme_minimal() +
labs(
title = "Topic Probabilities for Individuals with Highest Genetic Predisposition vs Population",
x = "Time Point",
y = "Probability",
color = "Individual",
linetype = "Topic"
) +
scale_color_npg() +
theme(legend.position = "bottom", strip.text = element_text(size = 8)) +
theme(plot.margin = margin(1, 1, 1, 1, "cm")) # Adjust plot margins