Chapter 10 Estimating Beta
Now plot est_beta versus real:
# Assuming you have the beta array and diags list available
# Assuming you have the beta array (D x K x V x T) and individual diagnosis data (diags)
# Calculate average theta for each topic across all individuals
average_theta <- apply(Theta, 2, mean) # Assuming Theta is D x K x T
# Calculate weighted population beta trajectories
marginal_beta=array(dim=c(D,V,T))
for (v in 1:V) {
for (t in 1:T) {
for (d in 1:D) {
marginal_beta[d,v, t] <- t(Theta[d,,t])%*%beta[d, , v, t]
}
}}
## weight across individuals so we have the average for everage disease and time
weighted_population_beta=apply(marginal_beta,c(2,3),mean)
# Determine individual disease onset times, create a matrix of Disease * time
individual_onset_times =matrix(0,nrow=T,ncol=V)
for(d in 1:D){
for(v in 1:V){
# Find the first time point at which the disease v is diagnosed for individual d
onset_times <- sapply(diags[[d]], function(diag_time) v %in% diag_time)
if (any(onset_times)) {
individual_onset_times[which(onset_times),v]=individual_onset_times[which(onset_times),v]+1 # Return the first time point of diagnosis
} else {
individual_onset_times[which(onset_times),v]=individual_onset_times[which(onset_times),v] # No diagnosis for this disease
}}}
individual_onset_times=apply(individual_onset_times,1,function(x){x/sum(x)})
# Compare individual onset times to weighted population trajectories
# Determine individual disease onset times, create a matrix of Disease * time
individual_onset_times_first <- sapply(1:D, function(d) {
sapply(1:V, function(v) {
# Find the first time point at which the disease v is diagnosed for individual d
onset_times <- sapply(diags[[d]], function(diag_time) v %in% diag_time)
if (any(onset_times)) {
return(which(onset_times)[1]) # Return the first time point of diagnosis
} else {
return(NA) # No diagnosis for this disease
}
})
})
# Function to plot population trajectories
plot_population_trajectories <- function(population_beta) {
pop_beta_melt <- melt(t(population_beta))
colnames(pop_beta_melt) <- c("Time", "Disease", "Probability")
ggplot(pop_beta_melt, aes(x = Time, y = Probability, color = as.factor(Disease), group = Disease)) +
geom_line() +
theme_minimal() +
labs(title = "Marginal Disease Probability Over Time for Population",
x = "Time",
y = "Marginal Disease Probability",
color = "Disease")
}
library(ggplot2)
library(reshape2)
# Function to plot density of individual onset times along with population trajectories
plot_density_onset <- function(individual_onset_times, population_beta) {
pop_beta_melt <- melt(t(population_beta))
colnames(pop_beta_melt) <- c("Time","Disease","Probability")
onset_melt <- melt(individual_onset_times)
colnames(onset_melt) <- c("Disease","Time","Count")
onset_melt <- onset_melt[!is.na(onset_melt$Count),] # Remove NA values
# Plot population trajectories
p1 <- ggplot(pop_beta_melt, aes(x = Time, y = Probability, col = as.factor(Disease), group = Disease)) +
geom_line() +
theme_minimal() +
labs(title = "Marginal Disease Probability Over Time for Population with Onset Time Densities",
x = "Age",
y = "Marginal Disease Probability",
color = "Disease")
# Overlay density plots for individual onset times
p2 <- ggplot(data = onset_melt, aes(x = Time, y=Count,col = as.factor(Disease),group=Disease))+geom_smooth(fill=NA) +
scale_color_manual(values = scales::hue_pal()(length(unique(onset_melt$Disease)))) +
guides(color = guide_legend(override.aes = list(shape = 1)), fill = guide_legend(title = "Disease Density"))+labs(x="Age")
onset_melt <- melt(individual_onset_times_first)
colnames(onset_melt) <- c("Disease", "Individual", "Time")
onset_melt <- onset_melt[!is.na(onset_melt$Time),] # Remove NA values
p3 <- ggplot(data = onset_melt, aes(x = Time, fill = as.factor(Disease), alpha = 10, adjust = 1.5, position = "identity")) +geom_density()+
scale_fill_manual(values = scales::hue_pal()(length(unique(onset_melt$Disease)))) + labs(x="Age of First Onset")+
guides(color = guide_legend(override.aes = list(shape = 1)), fill = guide_legend(title = "Disease Onset (first) Density"))
ggpubr::ggarrange(p1,p2,p3,common.legend = TRUE,nrow=1)
}
library(ggpubr)
plot_density_onset(individual_onset_times = individual_onset_times, population_beta = weighted_population_beta)## `geom_smooth()` using method = 'loess' and formula = 'y ~ x'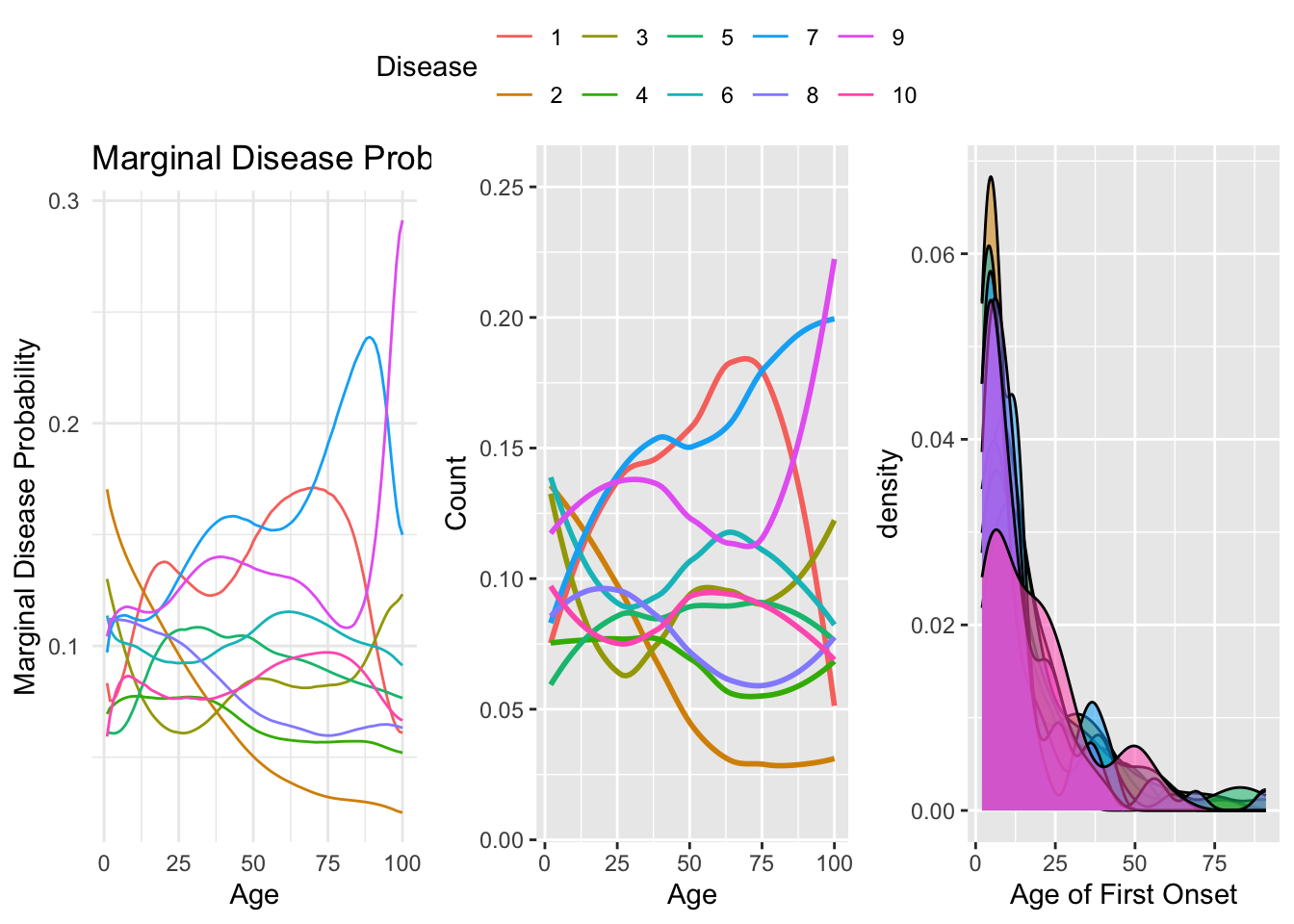
And here we try to estimate beta:
diagnosis_counts <- array(0, dim = c(D, K, V, T))
count_array <- array(0, dim = c(D, K, V, T)) # To keep track of the counts for averaging
for (d in 1:D) {
diagnoses_person <- diags[[d]]
for (k in 1:K) {
for (t in 1:T) {
og_mapped_times <- which(warped_t_array[d, k, ] == t) # Original times that map to current time t
for (og_time in og_mapped_times) {
diag_count <- unlist(diagnoses_person[t])
for (w in diag_count) {
diagnosis_counts[d, k, w, og_time] <- diagnosis_counts[d, k, w, og_time] + Theta[d, k, t]
count_array[d, k, w, og_time] <- count_array[d, k, w, og_time] + 1
}
}
}
}
}
## we want to make inference about popoulation beta
## plot eta with softmax and warping ....
normalize=function(x){x/sum(x)}
beta_est=apply(diagnosis_counts,c(2,3,4),sum)
for(k in 1:K){
for(t in 1:T){
beta_est[k,,t]=softmax_normalize(beta_est[k,,t])
}}
true_beta=array(0,dim = c(K,V,T))
bias_value=max(eta)
for (topic_idx in 1:K) {
# Retrieve the diseases and their risk periods for this topic
#specific_diseases_periods <- topic_disease_risk_periods[[topic_idx]]
bias_increase <- disease_topic_matrix[,topic_idx]*bias_value
for (time_idx in 1:T) {
disease_values <- eta[topic_idx, , time_idx]
dv <- disease_values+bias_increase
# Apply softmax normalization
normalized_disease <- softmax_normalize(dv)
true_beta[topic_idx, , time_idx] <- normalized_disease
}
}# Function to plot heatmaps
# Function to plot heatmaps
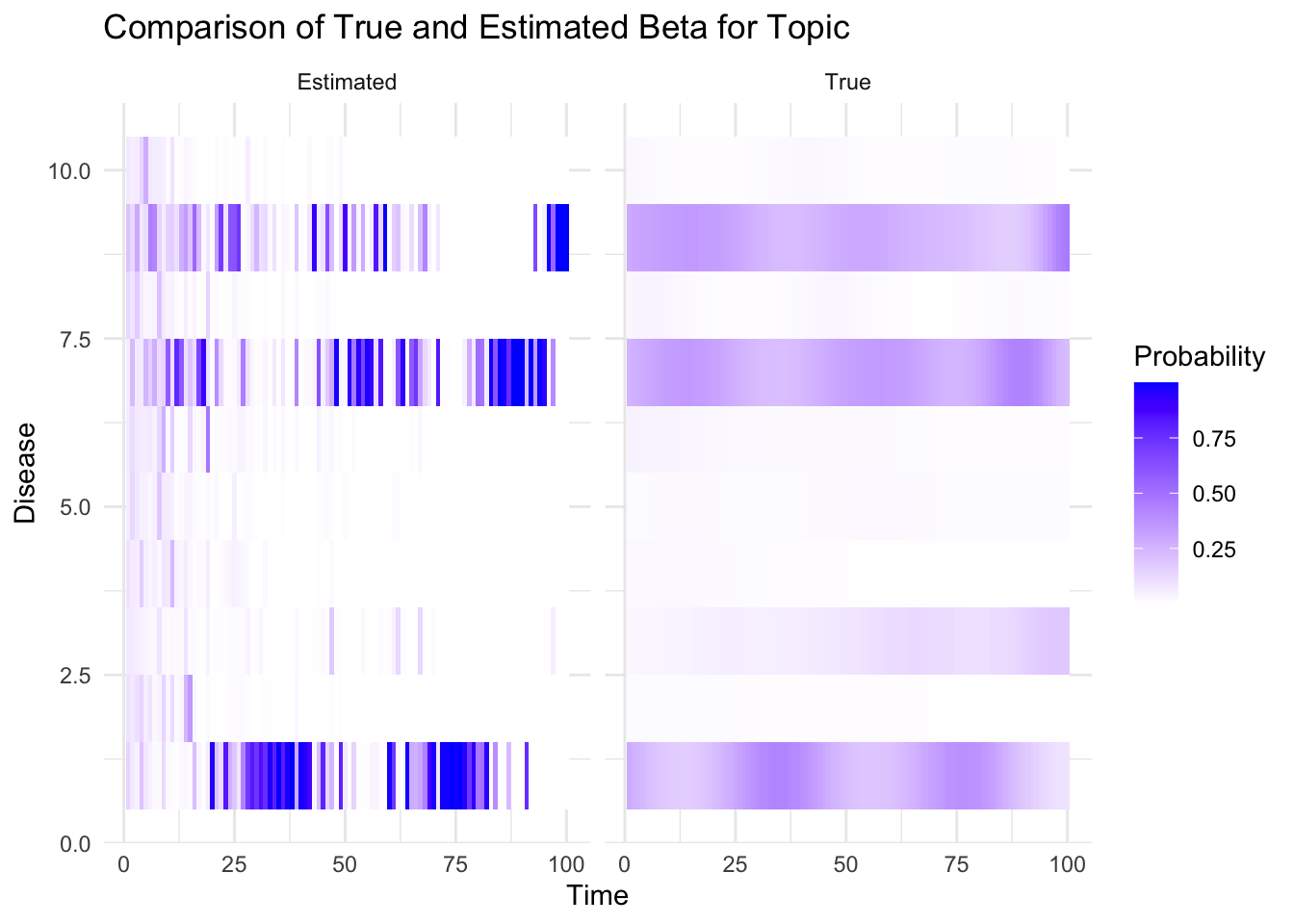
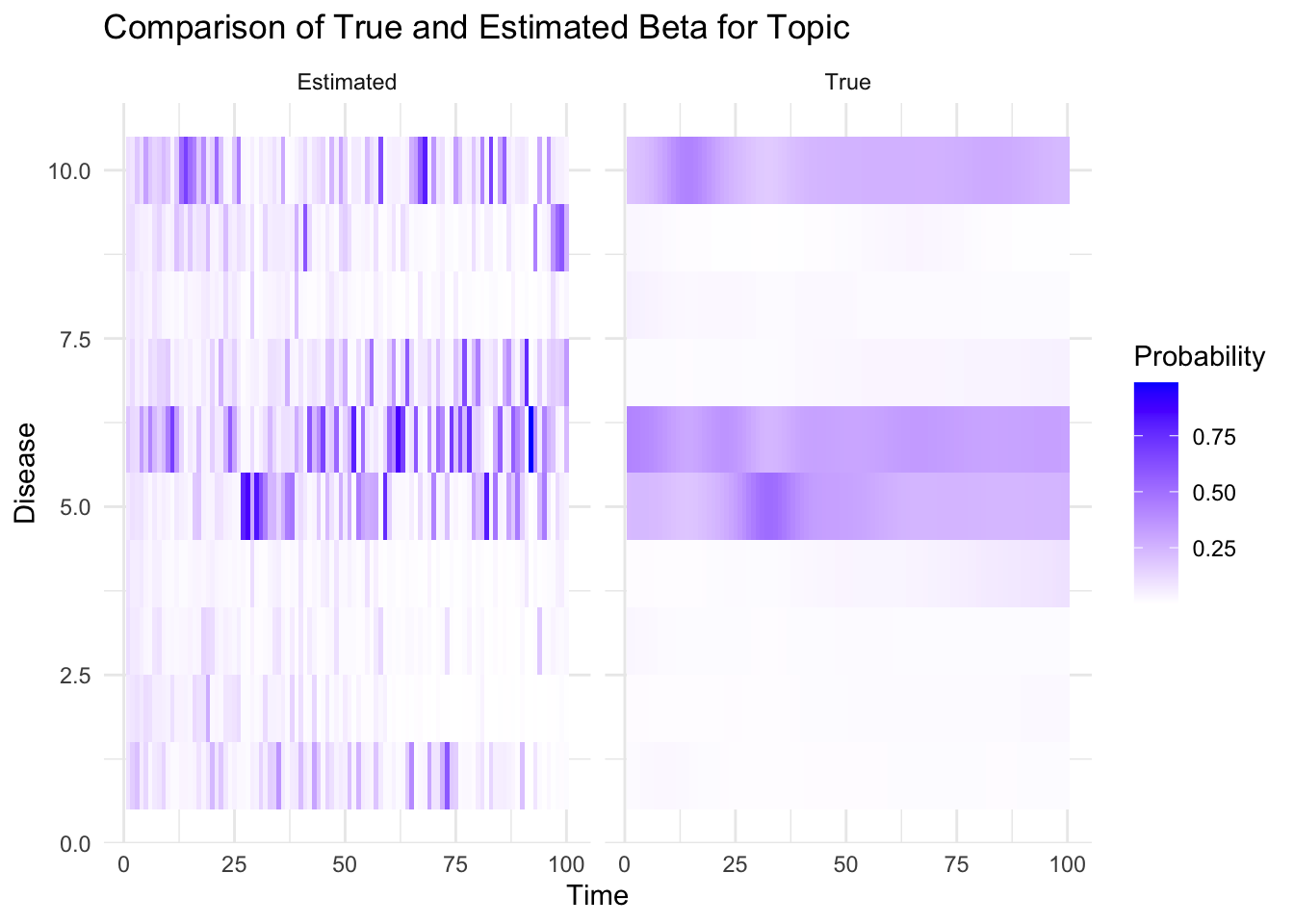
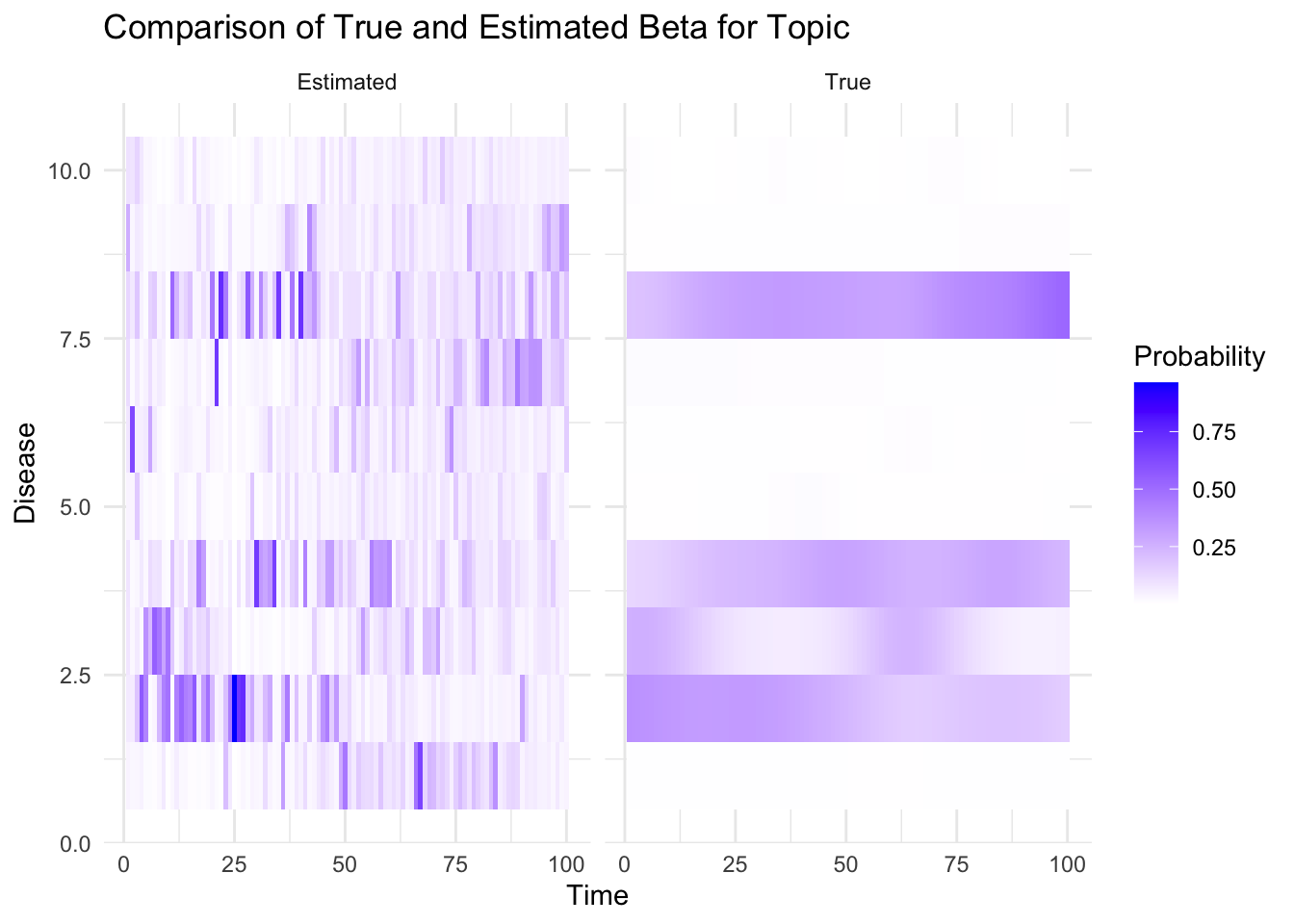
plot_heatmaps <- function(true_beta, est_beta,K, V, T, topic) {
true_beta_df <- melt(true_beta[topic, , ])
colnames(true_beta_df) <- c("Disease", "Time", "Probability")
true_beta_df$Type <- "True"
est_beta_df <- melt(est_beta[topic, , ])
colnames(est_beta_df) <- c("Disease", "Time", "Probability")
est_beta_df$Type <- "Estimated"
combined_df <- rbind(true_beta_df, est_beta_df)
p=ggplot(combined_df, aes(x = Time, y = Disease, fill = Probability)) +
geom_tile() +
facet_wrap(~ Type) +
scale_fill_gradient(low = "white", high = "blue") +
labs(title = "Comparison of True and Estimated Beta for Topic", topic, "and Individual",
x = "Time", y = "Disease") +
theme_minimal()
return(p)
}
# Plot heatmaps for a specific topic and individual (replace with your desired topic and individual)
plot_difference <- function(beta_est, beta_true, D, K, V, T) {
par(mfrow = c(1, 1))
# Plot difference between estimated and true beta
image(t(abs(beta_est[1, 1, , 1] - beta_true[1, 1, , 1])), main = "Difference between Estimated and True Beta", xlab = "Diseases", ylab = "Time")
}