Chapter 11 Prediction

generate_predicted_diagnoses <- function(Theta, beta_est, D, K, V, T) {
  predicted_diagnoses <- vector("list", D)
  for (d in 1:D) {
    predicted_diagnoses[[d]] <- vector("list", T)
    for (t in 1:T) {
      lambda_dt <- (t * 5) / T
      Nd <- max(1, rpois(1, lambda = lambda_dt))
      diagnoses_dt <- rep(NA, Nd)
      for (n in 1:Nd) {
        z <- sample(K, size = 1, prob = Theta[d, , t])
        beta_tk <- beta_est[d, z, , t]
        diagnoses_dt[n] <- sample(V, size = 1, prob = beta_tk)
      }
      predicted_diagnoses[[d]][[t]] <- diagnoses_dt
    }
  }
  return(predicted_diagnoses)
}

calculate_performance_metrics <- function(true_diagnoses, predicted_diagnoses, D, T) {
  true_positive <- 0
  false_positive <- 0
  false_negative <- 0
  total <- 0
  
  for (d in 1:D) {
    for (t in 1:T) {
      true_diagnoses_t <- true_diagnoses[[d]][[t]]
      predicted_diagnoses_t <- predicted_diagnoses[[d]][[t]]
      
      true_positive <- true_positive + sum(predicted_diagnoses_t %in% true_diagnoses_t)
      false_positive <- false_positive + sum(!(predicted_diagnoses_t %in% true_diagnoses_t))
      false_negative <- false_negative + sum(!(true_diagnoses_t %in% predicted_diagnoses_t))
      total <- total + length(true_diagnoses_t)
    }
  }
  
  accuracy <- true_positive / total
  precision <- true_positive / (true_positive + false_positive)
  recall <- true_positive / (true_positive + false_negative)
  f1_score <- 2 * (precision * recall) / (precision + recall)
  
  return(list(accuracy = accuracy, precision = precision, recall = recall, f1_score = f1_score))
}

# Generate predictions using time-dependent Theta
predicted_diagnoses_time_dependent <- generate_predicted_diagnoses(Theta, beta, D, K, V, T)

# Generate predictions using single Theta estimate
Theta_single <- apply(Theta, c(1, 2), mean)
Theta_single <- array(rep(Theta_single, T), dim = c(D, K, T))
predicted_diagnoses_single <- generate_predicted_diagnoses(Theta_single, beta, D, K, V, T)

# Calculate performance metrics
metrics_time_dependent <- calculate_performance_metrics(diags, predicted_diagnoses_time_dependent, D, T)
metrics_single <- calculate_performance_metrics(diags, predicted_diagnoses_single, D, T)

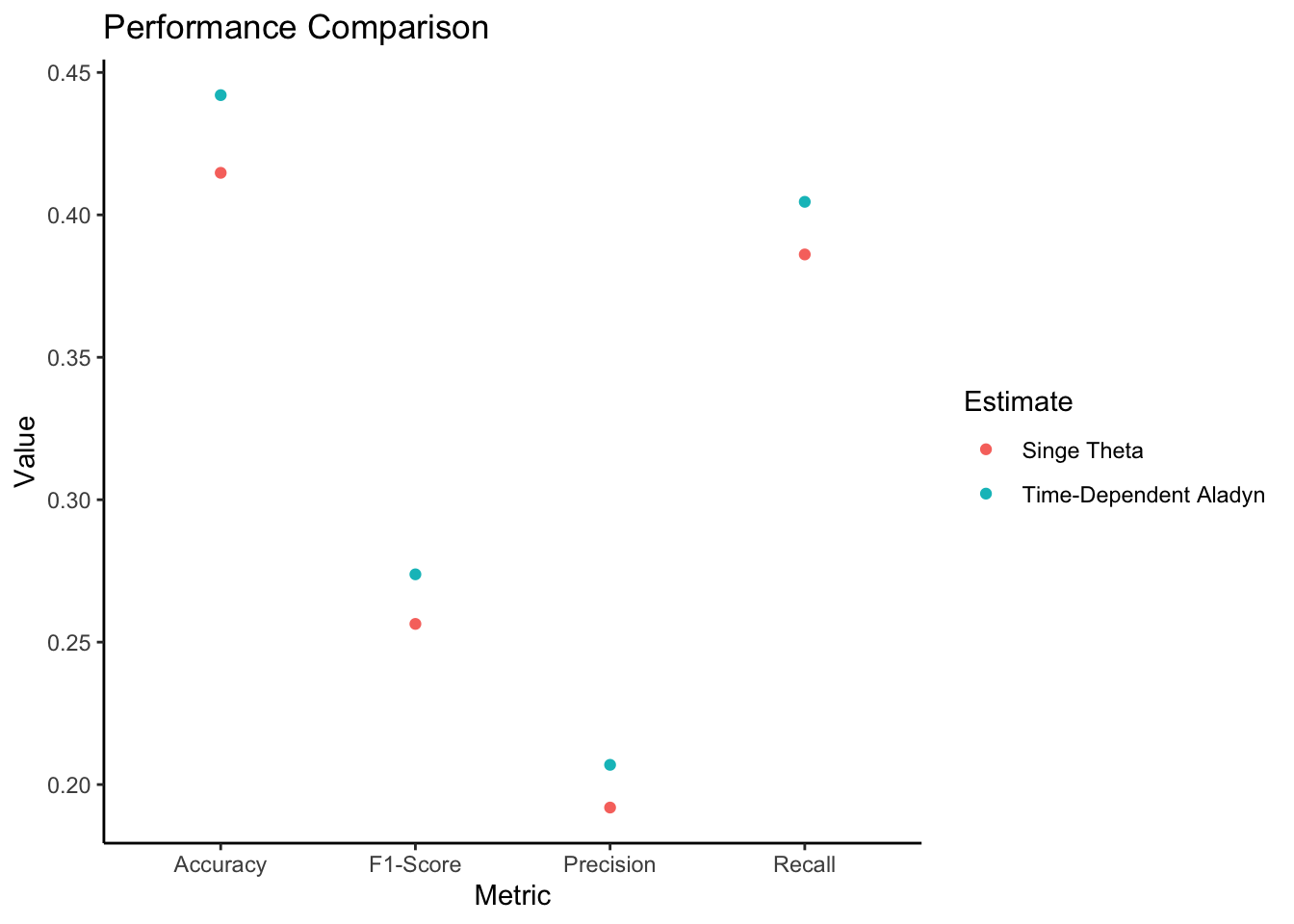
plot_performance_comparison <- function(metrics_time_dependent, metrics_single) {
  metrics_df <- data.frame(
    Metric = rep(c("Accuracy", "Precision", "Recall", "F1-Score"), 2),
    Value = c(metrics_time_dependent$accuracy, metrics_time_dependent$precision, metrics_time_dependent$recall, metrics_time_dependent$f1_score,
              metrics_single$accuracy, metrics_single$precision, metrics_single$recall, metrics_single$f1_score),
    Estimate = rep(c("Time-Dependent Aladyn", "Singe Theta"), each = 4)
  )
  
  ggplot(metrics_df, aes(x = Metric, y = Value, col = Estimate)) +
    geom_point() +
    labs(title = "Performance Comparison", x = "Metric", y = "Value") +
    theme_classic()
}

# Plot the performance comparison
plot_performance_comparison(metrics_time_dependent, metrics_single)

# Assuming you have the following variables defined:
# D, K, V, T: dimensions
# diags: observed diagnoses
# Theta: known topic distributions (time-dependent)
# beta_est: estimated beta values
# beta_true: true beta values for comparison

# Step 1: Generate predictions using time-dependent Theta
predicted_diagnoses_time_dependent <- generate_predicted_diagnoses(Theta, beta, D, K, V, T)

# Step 2: Generate predictions using single Theta estimate
Theta_single <- apply(Theta, c(1, 2), mean)
Theta_single <- array(rep(Theta_single, T), dim = c(D, K, T))
predicted_diagnoses_single <- generate_predicted_diagnoses(Theta_single, beta, D, K, V, T)

# Step 3: Calculate performance metrics
metrics_time_dependent <- calculate_performance_metrics(diags, predicted_diagnoses_time_dependent, D, T)
metrics_single <- calculate_performance_metrics(diags, predicted_diagnoses_single, D, T)

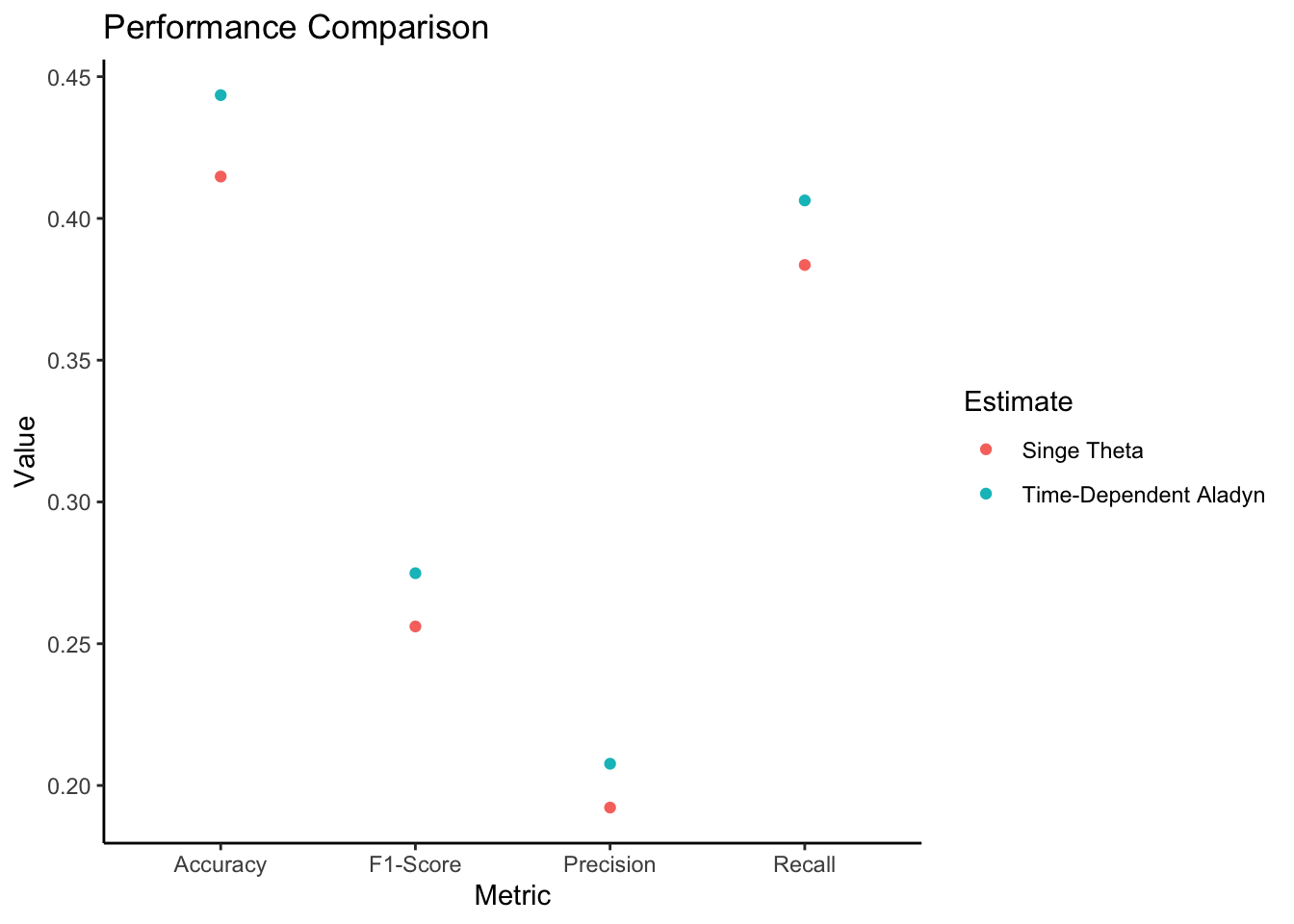
# Step 4: Plot the performance comparison
plot_performance_comparison(metrics_time_dependent, metrics_single)