Chapter 6 Using EMC2 for EAMs II - Race Models
In this example, we provide examples of race models – a class of EAMs where the model assumes a race between accumulators. Examples of race models include the linear ballistic accumulator (LBA; Brown and Heathcote (2008)) and the racing diffusion model (RDM; Tillman, Van Zandt, and Logan (2020)). Compared to the DDM example, we use the same model checks and data set, so these examples are slightly shorter than the previous chapter. By the end of this chapter, we should have three models (DDM, LBA, RDM) which all nicely fit the data, and in the following chapter, we’ll show you how you can compare these differing accounts.
6.1 LBA
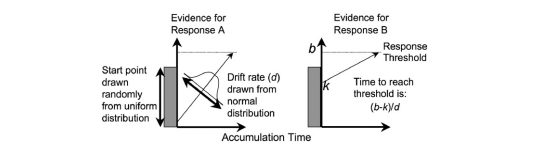
Figure 6.1: The linear ballistic accumulator model
The LBA is a “race” model of evidence accumulation, where evidence is assumed to accumulate balistically towards threshold for a number of accumulators (each representing a choice alternative). A graphical example of the model can be seen above. The LBA has similar parameters to the DDM, however, we use some slightly different names for these (consistent with the rtdists package). The parameters of the LBA are as follows;
v: Drift rate.The rate of evidence accumulation for each accumulator. For the models, we generally estimate intercept and difference terms, such that the difference is the difference in drift rate between competing accumulators. The intercept drift term is often seen as the urgency term.sv: Drift rate variance. This is the between trial variance parameter for the drift rate distribution. Typically,svis set as a constant to 1 (Donkin et al. 2011) (however we show options below for this).B: Response threshold or response caution. The arbitrary amount of evidence needed before the corresponding response is executed. Generally,b = B + Ato ensure that threshold is greater than start point.A: Start point interval or evidence in accumulator before beginning of decision process. Start point varies from trial to trial in the interval [0, A] (uniform distribution). Average amount of evidence before evidence accumulation across trials is A/2.t0: non-decision time or response time constant (in seconds). Lower bound for the duration of all non-decisional processes (encoding and response execution).
6.1.1 LBA models in EMC2 (and checks)
In this section, we show a variety of models that we try for the Forstmann (2008) data, where the main factor of interest is the emphasis manipulation. We show the design functions for each of these models, some custom contrasts and then some extra checks we propose. First, let’s load in the data as before.
rm(list=ls())
source("emc/emc.R")
source("models/RACE/LBA/lbaB.R")
print( load("Data/PNAS.RData"))
dat <- data[,c("s","E","S","R","RT")]
names(dat)[c(1,5)] <- c("subjects","rt")
levels(dat$R) <- levels(dat$S)
# NB: This data has been truncated at 0.25s and 1.5sNow, we’re going to fit a series of models to the Forstmann (2008) data. The first model will only vary threshold with emphasis. The second varies threshold, drift and non-decision time with emphasis (saturated). The next three models include the estimation of a variability parameter sv. In the first models we set sv=1 to establish a scale.
In the three later models, we fit a series of models where sv differs between matching and mismatching accumulators, with its intercept fixed at 1 to establish scaling. Typically allowing this difference greatly improves LBA fit and results in sv_TRUE (i.e., match) > sv_FALSE. All of these designs are effect coded, so it’s worth checking out the sampled_p_vector of each model to understand which parameters are being estimated and think about how these would be mapped.
# Average rate = intercept, and rate d = difference (match-mismatch) contrast
ADmat <- matrix(c(-1/2,1/2),ncol=1,dimnames=list(NULL,"d"))
Emat <- matrix(c(0,-1,0,0,0,-1),nrow=3)
dimnames(Emat) <- list(NULL,c("a-n","a-s"))
# Only B affected by E
design_B <- make_design(
Ffactors=list(subjects=levels(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,S=ADmat,E=Emat),
Flist=list(v~lM,sv~1,B~E,A~1,t0~1),
constants=c(sv=log(1)),
model=lbaB)
# samplers <- make_samplers(dat,design_B,type="standard",rt_resolution=.02)
# save(samplers,file="sPNAS_B.RData")
# B, v and t0 affected by E
design_Bvt0 <- make_design(
Ffactors=list(subjects=unique(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,S=ADmat,E=Emat),
Flist=list(v~E*lM,sv~1,B~lR*E,A~1,t0~E),
constants=c(sv=log(1)),
model=lbaB)
# samplers <- make_samplers(dat,design_Bvt0,type="standard",rt_resolution=.02)
# save(samplers,file="sPNAS_Bvt0.RData")
# First, allowing E to affect B and t0
design_Bt0_sv <- make_design(
Ffactors=list(subjects=unique(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,S=ADmat,E=Emat),
Flist=list(v~lM,sv~lM,B~lR*E,A~1,t0~E),
constants=c(sv=log(1)),
model=lbaB)
# samplers <- make_samplers(dat,design_Bt0_sv,type="standard",rt_resolution=.02)
# save(samplers,file="sPNAS_Bt0_sv.RData")
# Now E affects B and v
design_Bv_sv <- make_design(
Ffactors=list(subjects=unique(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,S=ADmat,E=Emat),
Flist=list(v~E*lM,sv~lM,B~lR*E,A~1,t0~1),
constants=c(sv=log(1)),
model=lbaB)
# samplers <- make_samplers(dat,design_Bv_sv,type="standard",rt_resolution=.02)
# save(samplers,file="sPNAS_Bv_sv.RData")
# Now all three
design_Bvt0_sv <- make_design(
Ffactors=list(subjects=unique(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,S=ADmat,E=Emat),
Flist=list(v~E*lM,sv~lM,B~lR*E,A~1,t0~E),
constants=c(sv=log(1)),
model=lbaB)
# samplers <- make_samplers(dat,design_Bvt0_sv,type="standard",rt_resolution=.02)
# save(samplers,file="sPNAS_Bvt0_sv.RData")We can run these five models and check the fit metrics as we did in the previous chapter. The last model fails to converge (or rather some parameter were so strongly autocorrelated it would have taken an impractically large run to produce anything useful). This might happen when doing complex modelling and can be the result of several issues, however, these issues generally relate to the amount of information available. For example, if we have a model with many parameters across varying conditions, it is likely that we have less information for each cell of the estimated design, and in these scenarios, the sampler may struggle to converge. Further, if we have a low number of subjects, this will also cause difficulty.
Here we talk about autocorrelation (using the integrated autocorrelation time stat) and effective sample sizes - these are good metrics to evaluate the quality of sampling. The basic idea behind autocorrelation is that the samples in chains are not independent, so we should estimate the effective number of independent samples. This is often because new samples are based on the previous sample in an MCMC chain. If we see high autocorrelation, this may be because we have not yet reached the posterior mode for sampling or the posterior distribution is multi-modal. We can run the sampler for a very long time, which would give us a huge number of samples, and then we could assess the effective sample size (i.e., the number of independent samples). Generally however, these problems can be solved by thinking about the model being estimated.
Looking at estimates, most issues were around the a_n contrast, which might not be surprising given this had a weak manifest effect. Here we fit this model again but dropping the a_n contrast for the emphasis effects on drift and non-decision time, instead estimating an intercept and the difference between the average of accuracy and neutral and speed, a 14 parameter model.
E_AVan_s_mat <- matrix(c(1/4,1/4,-1/2),nrow=3)
dimnames(E_AVan_s_mat) <- list(NULL,c("an-s"))
design_Bvt0_sv_NOa_n <- make_design(
Ffactors=list(subjects=unique(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(v=list(E=E_AVan_s_mat,lM=ADmat),sv=list(lM=ADmat),
B=list(E=Emat,lR=ADmat),t0=list(E=E_AVan_s_mat)),
Flist=list(v~E*lM,sv~lM,B~lR*E,A~1,t0~E),
constants=c(sv=log(1)),
model=lbaB)
# samplers <- make_samplers(dat,design_Bvt0_sv_NOa_n,type="standard",rt_resolution=.02)
# save(samplers,file="sPNAS_Bvt0_sv_NOa_n.RData")For the sv=1 models we used a similar script as for the DDM. For the other LBA models we use a slightly “smarter” script that only fits the next stage if the previous one worked, e.g., for the Bvsv model.
Given that we have already run these models, let’s look through some functions to check whether burn-in was completed, adaptation was completed and some other checks.
# Here we test if burn in had been done previously.
#
if (is.null(attr(samplers,"burnt")) || is.na(attr(samplers,"burnt"))) {
sPNAS_Bv_sv <- run_burn(samplers,cores_per_chain=4)
save(sPNAS_Bv_sv,file="sPNAS_Bv_sv.RData")
}
# Here we check if adaptation was already done
#
if (is.null(attr(sPNAS_Bv_sv,"adapted")) && !is.na(attr(sPNAS_Bv_sv,"burnt"))) {
sPNAS_Bv_sv <- run_adapt(sPNAS_Bv_sv,cores_per_chain=4)
save(sPNAS_Bv_sv,file="sPNAS_Bv_sv.RData")
}
# Here we only move on to sampling of adaptation was successful
#
if (!is.null(attr(sPNAS_Bv_sv,"adapted")) && attr(sPNAS_Bv_sv,"adapted")) {
sPNAS_Bv_sv <- run_sample(sPNAS_Bv_sv,iter=2000,cores_per_chain=4)
save(sPNAS_Bv_sv,file="sPNAS_Bv_sv.RData")
}As a side note, this code below was run later after choosing this as the best model and knowing that the first 2000 iterations of the sample run had to be discarded, giving 5000*3 = 15000 good samples to work with.
sPNAS_Bv_sv <- run_sample(sPNAS_Bv_sv,iter=4000,cores_per_chain=10)
save(sPNAS_Bv_sv,file="sPNAS_Bv_sv.RData")
ppPNAS_Bv_sv <- post_predict(sPNAS_Bv_sv,n_cores=19,subfilter=2000)
save(ppPNAS_Bv_sv,sPNAS_Bv_sv,file="sPNAS_Bv_sv.RData")6.1.2 Inference for the LBA
For inference, lets first load in all of the models we estimated.
#### Load model results ----
print(load("~/Desktop/emc2/models/RACE/LBA/examples/samples/sPNAS_B.RData")) ## [1] "sPNAS_B"print(load("~/Desktop/emc2/models/RACE/LBA/examples/samples/sPNAS_Bvt0.RData"))## [1] "sPNAS_Bvt0"print(load("~/Desktop/emc2/models/RACE/LBA/examples/samples/sPNAS_Bt0_sv.RData"))## [1] "sPNAS_Bt0_sv"print(load("~/Desktop/emc2/models/RACE/LBA/examples/samples/sPNAS_Bv_sv.RData"))## [1] "ppPNAS_Bv_sv" "sPNAS_Bv_sv"print(load("~/Desktop/emc2/models/RACE/LBA/examples/samples/sPNAS_Bvt0_sv.RData")) # Failed model, forced to adapt and sample ## [1] "sPNAS_Bvt0_sv"print(load("~/Desktop/emc2/models/RACE/LBA/examples/samples/sPNAS_Bvt0_sv_NOa_n.RData"))## [1] "sPNAS_Bvt0_sv_NOa_n"Note that this includes one of the failed models (Bvt0_sv). It’s worth taking a look at the chains and diagnostics for this model to help identify problems in your own modelling. Comparing these estimates to a “good” run will be immediately obvious, with stuck chains, parameters not showing stationarity, low GD statistics and low effective sample sizes.
6.1.3 Model Checks
We’re now going to again go through some basic checks to see how our models fared. We’ve left notes in the code so that you are able to check these yourself and see what we saw. For the simple B model, we can use this as a comparison for the other models.
It is important to note the difference between a good model and good estimation. For any model we estimate, we need to be able to estimate it well such that we can make clear inference on the posterior. It is this posterior that dictates whether this is an accurate model of the data, and it is on the posterior that we do model comparison. If the sampling has failed, this could indicate a poor model or just poor sampling, but regardless, it is problematic to make inference when we have not reached the posterior. On the other hand, if sampling has been completed, this does not indicate a good model, only that we have reached the posterior (which could be wrong).
Note Running the check_run function will prompt you to press ‘Enter’ to see each statistic. It will also save these plots as pdf files.
#### Check convergence ----
# Aim to get 1000 good samples as a basis for model comparison (but note this
# is not enough for inference on some parameters)
check_run(sPNAS_B)
# Slow to converge, but there by 4500
check_run(sPNAS_Bvt0,subfilter = 4500,layout=c(3,3))
# Low efficiency for t0_Ea-n, t0, and B_lRd:Ea-n
check_run(sPNAS_Bt0_sv,subfilter=2000,layout=c(3,5))
# B_lRd:Ea-n, B_Ea-n, v_Ea-n, v_Ea-n:lMd all inefficient. Some slow-wave
# oscillations, definitely need longer series if using the parameter estimates
# (even though likely stationary after 2000)
check_run(sPNAS_Bv_sv,subfilter=2000,layout=c(3,5))
# After extensive burn (although not achieving Rhat < 1.2), adaptation was quick
# but chains were very poor. Decided not to pursue further.
check_run(sPNAS_Bvt0_sv,subfilter=1000)
# Burned in quickly and converged well after 1000, B_lRd:Ea-n and especially
# t0_Ean-s quite inefficient
check_run(sPNAS_Bvt0_sv_NOa_n,subfilter=1000,layout=c(3,5)) 6.1.4 Model selection
We fit 5 different LBA models, and so in a standard modelling application, we would want to know which is the best model. More importantly, we would want to objectively know which model is best using some quantifiable measures. Here, we compare information criteria (IC) for 5 different models. The ICs we compare are deviance information criterion (DIC) and Bayesian predictive information criterion (BPIC). For both of these ICs, lower IC is indicative of better model fit.
IC methods are generally a “quick and dirty” method for model comparison, where model complexity is penalized “post-hoc” and the model fit is the key metric. For these metrics, we want the model to closely match the data, as this would indicate a good fit. However, ICs can potentially miss over fitting or issues related to model complexity (i.e., sometimes a simpler model does not fit quite as well, but is more flexible to potential future data, whereas a more complex model may only fit the observed data). We’ll discuss this further in the [Model Comparison with IS2] chapter.
Let’s first compare these using the compare_IC function;
compare_IC(list(B=sPNAS_B,Bvt0=sPNAS_Bvt0,Bt0sv=sPNAS_Bt0_sv,Bvsv=sPNAS_Bv_sv,
Bvt0sv=sPNAS_Bvt0_sv_NOa_n),subfilter=list(0,4500,2000,2001:3000,1000))## DIC wDIC BPIC wBPIC EffectiveN meanD Dmean minD
## B -15243 0 -15100 0.000 143 -15386 -15485 -15529
## Bvt0 -15946 0 -15711 0.000 236 -16182 -16336 -16418
## Bt0sv -16870 0 -16667 0.000 203 -17073 -17206 -17276
## Bvsv -17200 1 -16986 0.999 214 -17414 -17569 -17627
## Bvt0sv -17182 0 -16973 0.001 209 -17391 -17542 -17601ICs <- compare_ICs(list(B=sPNAS_B, Bvt0=sPNAS_Bvt0, Bt0sv=sPNAS_Bt0_sv,
Bvsv=sPNAS_Bv_sv, Bvt0sv=sPNAS_Bvt0_sv_NOa_n),subfilter=list(0,4500,2000,2001:3000,1000))## wDIC_B wDIC_Bvt0 wDIC_Bt0sv wDIC_Bvsv wDIC_Bvt0sv wBPIC_B wBPIC_Bvt0
## as1t 0 0.000 0.028 0.124 0.848 0 0.000
## bd6t 0 0.000 0.000 0.592 0.408 0 0.000
## bl1t 0 0.000 0.000 0.507 0.493 0 0.000
## hsft 0 0.000 0.000 0.548 0.452 0 0.000
## hsgt 0 0.000 0.001 0.636 0.363 0 0.000
## kd6t 0 0.000 0.254 0.454 0.292 0 0.000
## kd9t 0 0.000 0.003 0.511 0.485 0 0.000
## kh6t 0 0.000 0.150 0.496 0.354 0 0.000
## kmat 0 0.000 0.992 0.002 0.007 0 0.000
## ku4t 0 0.001 0.000 0.688 0.311 0 0.001
## na1t 0 0.000 0.044 0.595 0.360 0 0.000
## rmbt 0 0.000 0.000 0.926 0.073 0 0.000
## rt2t 0 0.000 0.000 0.918 0.082 0 0.000
## rt3t 0 0.000 0.005 0.119 0.877 0 0.000
## rt5t 0 0.001 0.228 0.319 0.452 0 0.001
## scat 0 0.000 0.330 0.255 0.416 0 0.000
## ta5t 0 0.000 0.000 0.945 0.055 0 0.000
## vf1t 0 0.000 0.000 0.867 0.133 0 0.000
## zk1t 0 0.000 0.020 0.869 0.111 0 0.000
## wBPIC_Bt0sv wBPIC_Bvsv wBPIC_Bvt0sv
## as1t 0.030 0.068 0.901
## bd6t 0.000 0.504 0.496
## bl1t 0.000 0.614 0.386
## hsft 0.000 0.587 0.413
## hsgt 0.002 0.673 0.324
## kd6t 0.368 0.394 0.237
## kd9t 0.008 0.366 0.626
## kh6t 0.118 0.498 0.384
## kmat 0.998 0.000 0.001
## ku4t 0.001 0.784 0.215
## na1t 0.119 0.523 0.358
## rmbt 0.001 0.740 0.259
## rt2t 0.000 0.961 0.039
## rt3t 0.001 0.070 0.929
## rt5t 0.311 0.326 0.362
## scat 0.332 0.217 0.452
## ta5t 0.000 0.959 0.041
## vf1t 0.000 0.858 0.142
## zk1t 0.003 0.790 0.207Comparing all 5 models, clearly we need sv (NB: use only 1000 from Bvsv after convergence, more added for parameter inference as this is the winning model). We noted this above, as the sv parameter often helps to capture some noise in the distributions. Let’s now try this across subjects. The latter function returns a list of matrices for each participant, so we can use that to count winners as follows.
table(unlist(lapply(ICs,function(x){row.names(x)[which.min(x$DIC)]})))##
## Bt0sv Bvsv Bvt0sv
## 1 14 4table(unlist(lapply(ICs,function(x){row.names(x)[which.min(x$BPIC)]})))##
## Bt0sv Bvsv Bvt0sv
## 1 13 5Again here we see mostly Bvsv winning, second Bvt0sv with no Ea_n, and one clear Bt0sv. We could try the simpler E contrast with the Bvsv model, but we are going to leave that as an extension exercise for you try. Now that we know the best LBA model, let’s compare this LBA model to the best fitting DDM. Let’s first load in the DDM
Comparing the best (by IC methods) DDM (16 parameters) to the best (15 parameter) LBA model, we see that the latter has a slight edge. This is born out in testing fit, as we see that both models fit well but the small overestimation of error RT in the speed condition evident in the DDM is no longer evident in the LBA.
source("models/DDM/DDM/ddmTZD.R")
load("~/Desktop/emc2/models/DDM/DDM/examples/samples/sPNAS_avt0_full.RData")Now we can compare the ICs of the two “best” models;
# For the remaining analysis add 4000 iterations to Bvsv model
compare_IC(list(avt0=sPNAS_avt0_full,Bvsv=sPNAS_Bv_sv),subfilter=list(500,2000))## DIC wDIC BPIC wBPIC EffectiveN meanD Dmean minD
## avt0 -17043 0 -16802 0 240 -17283 -17468 -17523
## Bvsv -17188 1 -16964 1 224 -17412 -17564 -17636From the table of ICs, we can see that the LBA has slightly lower criteria for both metrics. Let’s now plot the fit of the winning LBA model.
#### Fit of winning (Bvsv) model ----
# post predict did not use first 2000, so inference based on 5000*3 samples
plot_fit(dat,ppPNAS_Bv_sv,layout=c(2,3),factors=c("E","S"),lpos="right",xlim=c(.25,1.5))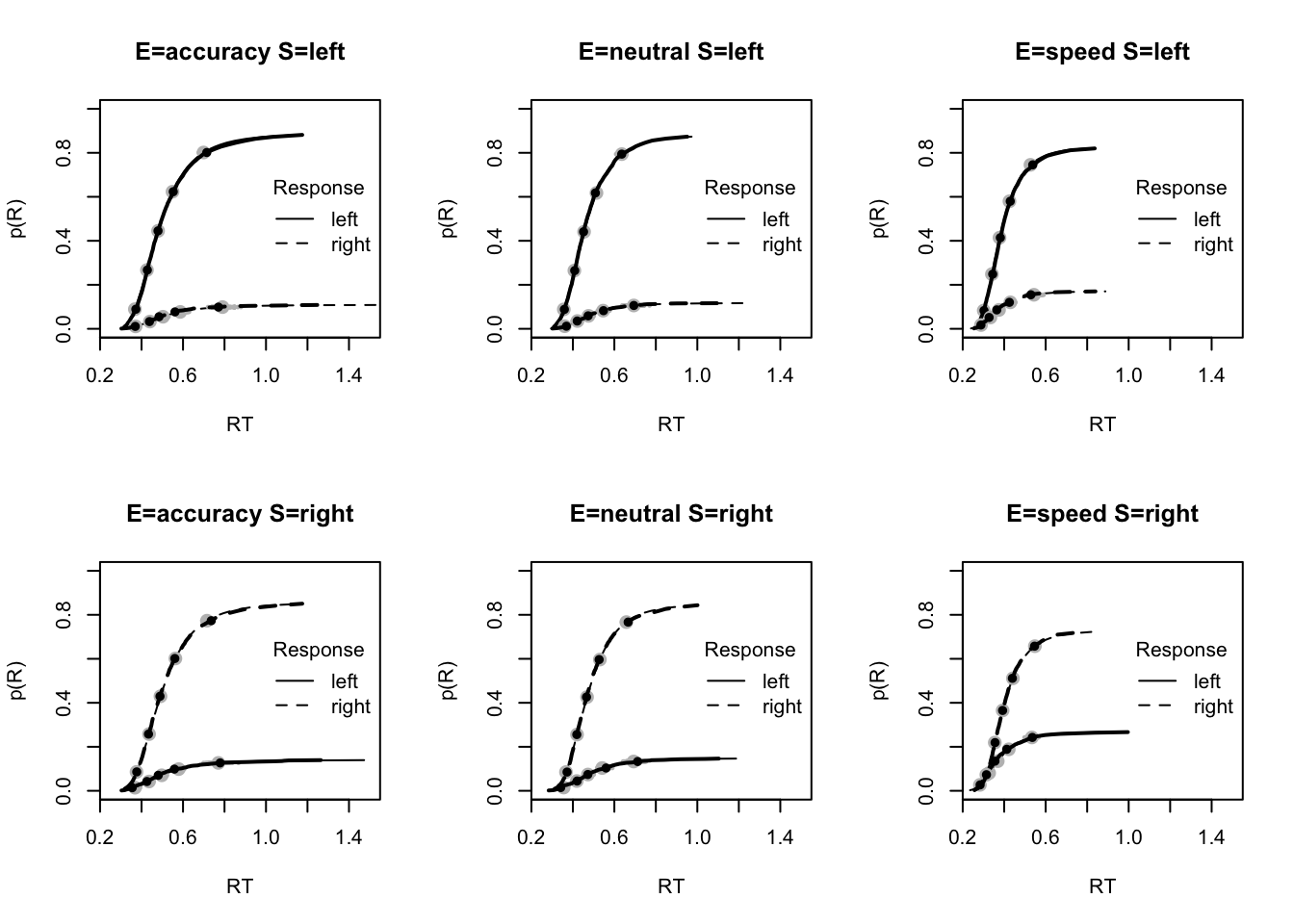
#plot_fits(dat,ppPNAS_Bv_sv,layout=c(2,3),lpos="right")You’ll see by running the code below that there is no great evidence of misfit. Again, for these plots, it is useful to assess a variety of metrics (as we show here). These include the mean RTs and accuracy, as well as upper and lower quantiles to see the fit across the spread of the data, the standard deviation, and the fit to different types of responses (i.e., correct and error), as often error response times can be difficult to fit.
# No evidence of any misfit
pc <- function(d) 100*mean(d$S==d$R)
plot_fit(dat,ppPNAS_Bv_sv,layout=c(2,3),factors=c("E","S"),
stat=pc,stat_name="Accuracy (%)",xlim=c(70,95))
tab <- plot_fit(dat,ppPNAS_Bv_sv,layout=c(2,3),factors=c("E","S"),
stat=function(d){mean(d$rt)},stat_name="Mean RT (s)",xlim=c(0.375,.625))
tab <- plot_fit(dat,ppPNAS_Bv_sv,layout=c(2,3),factors=c("E","S"),xlim=c(0.275,.4),
stat=function(d){quantile(d$rt,.1)},stat_name="10th Percentile (s)")
tab <- plot_fit(dat,ppPNAS_Bv_sv,layout=c(2,3),factors=c("E","S"),xlim=c(0.525,.975),
stat=function(d){quantile(d$rt,.9)},stat_name="90th Percentile (s)")
tab <- plot_fit(dat,ppPNAS_Bv_sv,layout=c(2,3),factors=c("E","S"),
stat=function(d){sd(d$rt)},stat_name="SD (s)",xlim=c(0.1,.355))
tab <- plot_fit(dat,ppPNAS_Bv_sv,layout=c(2,3),factors=c("E","S"),xlim=c(0.375,.725),
stat=function(d){mean(d$rt[d$R!=d$S])},stat_name="Mean Error RT (s)")6.1.5 Posterior parameter inference
Given we are now happy with the fit of the model (relative to other models and in an absolute sense), we can begin making inference on the parameter estimates. If there is some misfit present, it is important to always contextualize inference with the level of misfit of the model to the data.
6.1.5.1 Population level
For inference, let’s start at the population level, looking at mean parameters. First we see that the priors (red lines) are all well dominated except for some rate parameters.
### Population mean (mu) tests
ciPNAS_Bv_sv <- plot_density(sPNAS_Bv_sv,layout=c(3,6),selection="mu",subfilter=2000)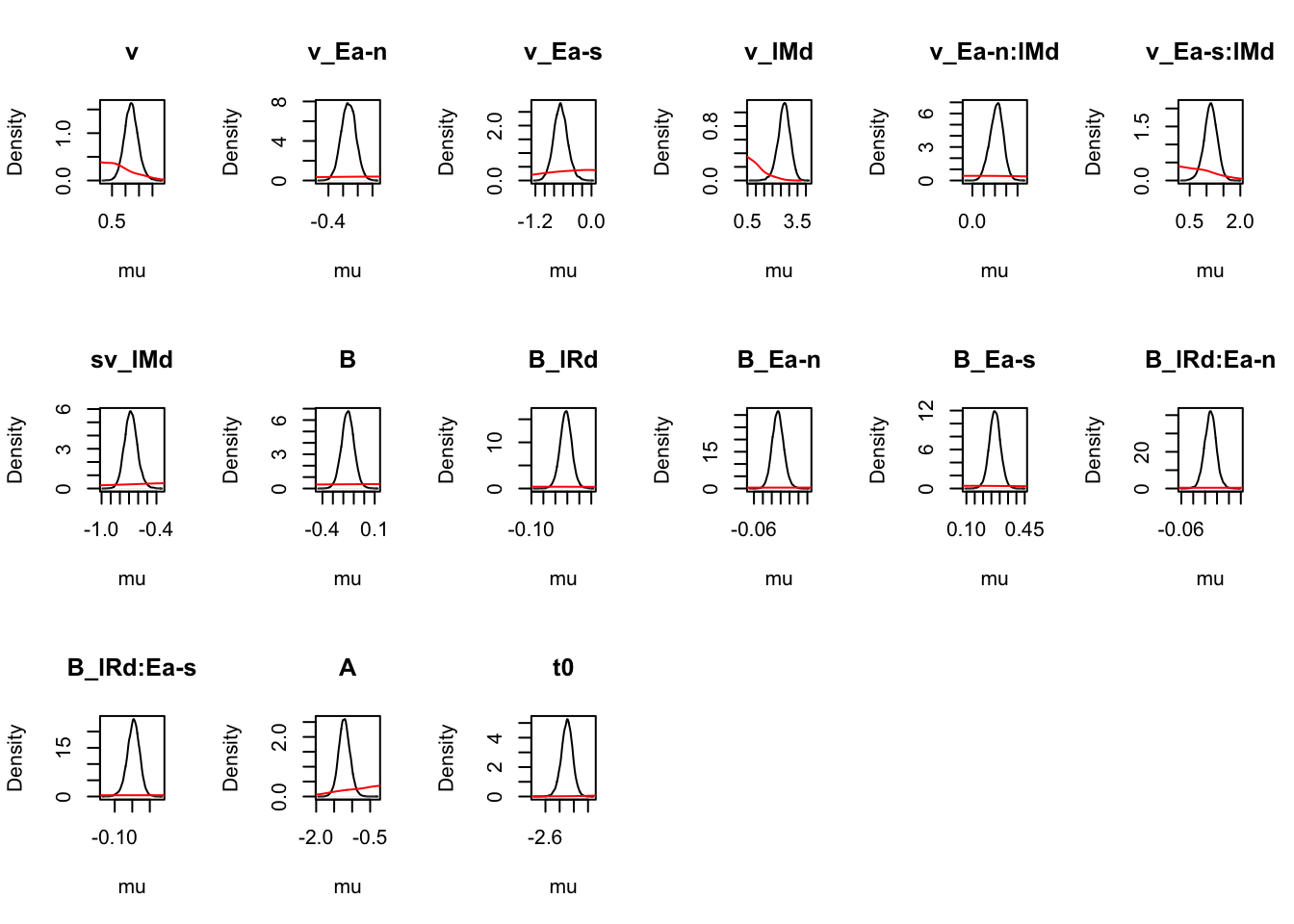
On the natural scale it is evident that this is because the mismatch (FALSE) rates are least well updated, due to the fairly low error rates (errors give the most information about FALSE rates). In many modelling exercises, we may be using data with low error rates. Literature has been somewhat varied on this, with ranges of 60% to 90% accuracy said to be in a “good” range for accuracy. However, with less information (in this case, less errors), parameters are less informed, which leads to estimation difficulties.
Let’s look at the density again where we use mapped=TRUE to alternate the figures to show correct and error (rather than left and right) responses.
ciPNAS_Bv_sv_mapped <- plot_density(sPNAS_Bv_sv,layout=c(3,6),
selection="mu",mapped=TRUE)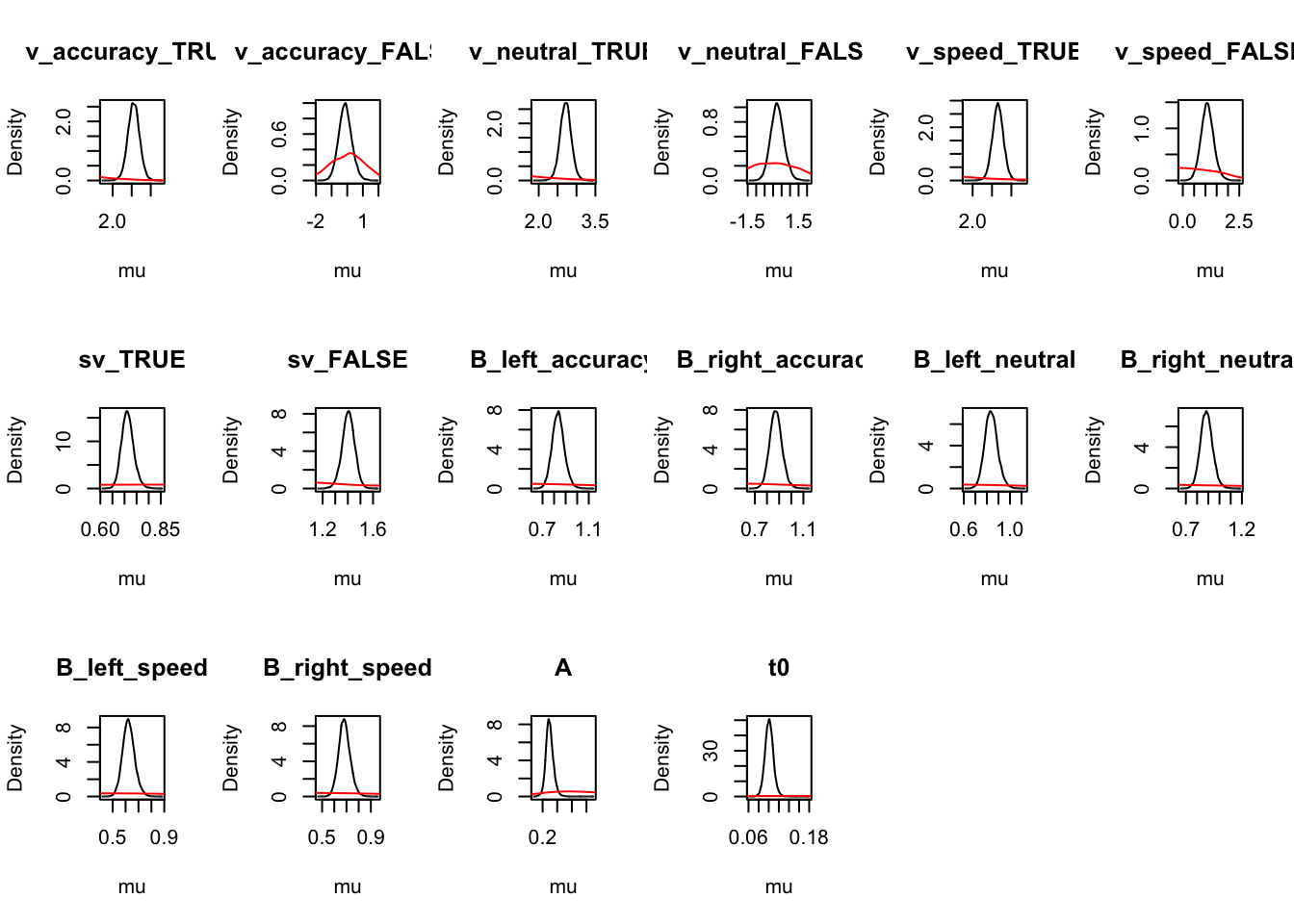
We can now compare the parameters both with and without mapping. We find this is often useful when considering the effects that may be estimated by the model, as only looking at one variation may cause us to miss effects in the other variation.
round(ciPNAS_Bv_sv,2)## v v_Ea-n v_Ea-s v_lMd v_Ea-n:lMd v_Ea-s:lMd sv_lMd B B_lRd B_Ea-n
## 2.5% 0.73 -0.36 -0.94 1.94 0.10 0.72 -0.81 -0.28 -0.01 -0.03
## 50% 1.21 -0.26 -0.66 2.70 0.22 1.12 -0.68 -0.16 0.04 -0.01
## 97.5% 1.74 -0.17 -0.35 3.38 0.32 1.49 -0.53 -0.04 0.09 0.02
## B_Ea-s B_lRd:Ea-n B_lRd:Ea-s A t0
## 2.5% 0.20 -0.03 -0.08 -1.52 -2.46
## 50% 0.27 -0.01 -0.05 -1.22 -2.30
## 97.5% 0.34 0.01 -0.01 -0.90 -2.15round(ciPNAS_Bv_sv_mapped,2)## v_accuracy_TRUE v_accuracy_FALSE v_neutral_TRUE v_neutral_FALSE v_speed_TRUE
## 2.5% 2.25 -0.92 2.42 -0.50 2.37
## 50% 2.55 -0.14 2.71 0.24 2.65
## 97.5% 2.86 0.73 3.01 1.06 2.94
## v_speed_FALSE sv_TRUE sv_FALSE B_left_accuracy B_right_accuracy B_left_neutral
## 2.5% 0.54 0.67 1.3 0.74 0.78 0.73
## 50% 1.08 0.71 1.4 0.83 0.87 0.84
## 97.5% 1.66 0.77 1.5 0.95 0.98 0.96
## B_right_neutral B_left_speed B_right_speed A t0
## 2.5% 0.78 0.54 0.59 0.20 0.09
## 50% 0.88 0.62 0.68 0.29 0.10
## 97.5% 1.00 0.72 0.78 0.41 0.12For simpler estimates, we see that;
Ais usually found with the LBAsv_true>sv_falset0is quite small (100ms)- In this case start point noise (.29) is small relative to
B(which has interceptexp(-.16) = 0.85, so about 1/4 ofb).
6.1.5.2 Threshold effects
Let’s now look at the all important threshold effects. Remember for this task we were looking at an instructions manipulated speed-accuracy tradeoff effect (i.e., be fast or be accurate), where the hypothesis was that thresholds would vary with emphasis.
First we check the mapping to recall the parameterisation.
# Recall the map used with
get_map(sPNAS_Bv_sv)$B## lR E B B_lRd B_Ea-n B_Ea-s B_lRd:Ea-n B_lRd:Ea-s
## 1 left accuracy 1 -0.5 0 0 0.0 0.0
## 7 right accuracy 1 0.5 0 0 0.0 0.0
## 2 left neutral 1 -0.5 -1 0 0.5 0.0
## 8 right neutral 1 0.5 -1 0 -0.5 0.0
## 3 left speed 1 -0.5 0 -1 0.0 0.5
## 9 right speed 1 0.5 0 -1 0.0 -0.5Second we test right vs left response thresholds.
p_test(x=sPNAS_Bv_sv,x_name="B_lRd",subfilter=2000)## B_lRd mu
## 2.5% -0.01 NA
## 50% 0.04 0
## 97.5% 0.09 NA
## attr(,"less")
## [1] 0.037B_lRd tests threshold_right - threshold_left. Although not quite credible, it indicates slightly higher right thresholds (i.e., a bias to respond left).
Then we check the difference in thresholds between accuracy and neutral (B_Ea-n) and accuracy and speed (B_Ea-s).
p_test(x=sPNAS_Bv_sv,x_name="B_Ea-n",subfilter=2000)## B_Ea-n mu
## 2.5% -0.03 NA
## 50% -0.01 0
## 97.5% 0.02 NA
## attr(,"less")
## [1] 0.69p_test(x=sPNAS_Bv_sv,x_name="B_Ea-s",subfilter=2000)## B_Ea-s mu
## 2.5% 0.20 NA
## 50% 0.27 0
## 97.5% 0.34 NA
## attr(,"less")
## [1] 0B_Ea-n and B_Ea-s measure differences in response caution, accuracy - neutral and accuracy - speed respectively. These include thresholds averaged over left and right accumulators. Caution (threshold) for accuracy is clearly higher than speed, but not credibly greater than neutral (i.e., neutral ~= accuracy).
Next we construct a test showing the threshold advantage is greater for speed than neutral;
p_test(x=sPNAS_Bv_sv,mapped=TRUE,x_name="average B: neutral-speed",
x_fun=function(x){mean(x[c("B_left_neutral","B_right_neutral")]) -
mean(x[c("B_left_speed","B_right_speed")])})## average B: neutral-speed mu
## 2.5% 0.16 NA
## 50% 0.21 0
## 97.5% 0.26 NA
## attr(,"less")
## [1] 0However, we see no evidence of a difference between accuracy and neutral thresholds;
p_test(x=sPNAS_Bv_sv,x_name="B_Ea-n",subfilter=2000)## B_Ea-n mu
## 2.5% -0.03 NA
## 50% -0.01 0
## 97.5% 0.02 NA
## attr(,"less")
## [1] 0.69Looking at the accuracy vs speed difference though;
p_test(x=sPNAS_Bv_sv,x_name="B_Ea-s",subfilter=2000)## B_Ea-s mu
## 2.5% 0.20 NA
## 50% 0.27 0
## 97.5% 0.34 NA
## attr(,"less")
## [1] 0We see thresholds are clearly higher for speed (by about 0.2 on the natural scale).
The remaining terms test interactions with bias (i.e., lR), with evidence of a small but just credibly stronger bias to respond left (i.e., a lower threshold for the left accumulator) for speed than accuracy.
p_test(x=sPNAS_Bv_sv,x_name="B_lRd:Ea-s",subfilter=1500,digits=2)## B_lRd:Ea-s mu
## 2.5% -0.08 NA
## 50% -0.05 0
## 97.5% -0.01 NA
## attr(,"less")
## [1] 0.9966.1.5.3 Drift rate effects
Next, lets look at drift rate effects. For these, we’ll again look at the mapping first, and then look at the difference parameters between accuracy and neutral or speed conditions.
# Again recall the map used with
get_map(sPNAS_Bv_sv)$v## E lM v v_Ea-n v_Ea-s v_lMd v_Ea-n:lMd v_Ea-s:lMd
## 1 accuracy TRUE 1 0 0 0.5 0.0 0.0
## 7 accuracy FALSE 1 0 0 -0.5 0.0 0.0
## 2 neutral TRUE 1 -1 0 0.5 -0.5 0.0
## 8 neutral FALSE 1 -1 0 -0.5 0.5 0.0
## 3 speed TRUE 1 0 -1 0.5 0.0 -0.5
## 9 speed FALSE 1 0 -1 -0.5 0.0 0.5Here, v_Ea-n and v_Ea-s indicate that processing rate (the average of matching and mismatching rates) is least in accuracy, slightly greater in neutral and the highest in speed.
p_test(x=sPNAS_Bv_sv,x_name="v_Ea-n",subfilter=2000)## v_Ea-n mu
## 2.5% -0.36 NA
## 50% -0.26 0
## 97.5% -0.17 NA
## attr(,"less")
## [1] 1p_test(x=sPNAS_Bv_sv,x_name="v_Ea-s",subfilter=2000)## v_Ea-s mu
## 2.5% -0.94 NA
## 50% -0.66 0
## 97.5% -0.35 NA
## attr(,"less")
## [1] 1Let’s now check whether processing is faster in the speed condition, i.e., the instruction leads to some form of faciliation.
p_test(x=sPNAS_Bv_sv,mapped=TRUE,x_name="average v: speed-neutral",
x_fun=function(x){mean(x[c("v_speed_TRUE","v_speed_FALSE")]) -
mean(x[c("v_neutral_TRUE","v_neutral_FALSE")])})## average v: speed-neutral mu
## 2.5% 0.12 NA
## 50% 0.39 0
## 97.5% 0.64 NA
## attr(,"less")
## [1] 0.004Looking at the parameter v_lMd tests the quality of selective attention, i.e., rate for match minus rate for mismatch.
p_test(x=sPNAS_Bv_sv,x_name="v_lMd",subfilter=2000)## v_lMd mu
## 2.5% 1.94 NA
## 50% 2.70 0
## 97.5% 3.38 NA
## attr(,"less")
## [1] 0Next, v_Ea-n tests if quality neutral is different to quality accuracy.
p_test(x=sPNAS_Bv_sv,x_name="v_Ea-n:lMd",subfilter=2000)## v_Ea-n:lMd mu
## 2.5% 0.10 NA
## 50% 0.22 0
## 97.5% 0.32 NA
## attr(,"less")
## [1] 0The difference is ~5 times larger for accuracy - speed;
p_test(x=sPNAS_Bv_sv,x_name="v_Ea-s:lMd",subfilter=2000)## v_Ea-s:lMd mu
## 2.5% 0.72 NA
## 50% 1.12 0
## 97.5% 1.49 NA
## attr(,"less")
## [1] 0Finally, The neutral - speed difference is also highly credible, and can be tested in the mapped form;
p_test(x=sPNAS_Bv_sv,mapped=TRUE,x_name="quality: accuracy-neutral",
x_fun=function(x){diff(x[c("v_neutral_FALSE","v_neutral_TRUE")]) -
diff(x[c("v_speed_FALSE","v_speed_TRUE")])})## quality: accuracy-neutral mu
## 2.5% 0.52 NA
## 50% 0.90 0
## 97.5% 1.25 NA
## attr(,"less")
## [1] 0Or from the sampled parameters;
p_test(x=sPNAS_Bv_sv,x_name="v_Ea-s:lMd",y=sPNAS_Bv_sv,y_name="v_Ea-n:lMd",
subfilter=2000,digits=3)## v_Ea-s:lMd v_Ea-n:lMd v_Ea-s:lMd-v_Ea-n:lMd
## 2.5% 0.721 0.096 0.530
## 50% 1.123 0.216 0.908
## 97.5% 1.486 0.323 1.255
## attr(,"less")
## [1] 06.1.5.4 Visualising results
In this section, we’re going to show some extensions of visualizations, by first extracting the parameter estimates, and then plotting these using ggplot2. Let’s start by extracting the parameters and checking the means of the posterior.
library(tidyverse)
# Get parameter data frame
ps <- parameters_data_frame(sPNAS_Bv_sv, mapped = TRUE)
head(ps)## v_accuracy_TRUE v_accuracy_FALSE v_neutral_TRUE v_neutral_FALSE v_speed_TRUE
## 1 2.526213 -0.06444518 2.718539 0.42221219 2.624610
## 2 2.300613 -0.71180244 2.671168 -0.05991449 2.497907
## 3 2.323223 -0.65978316 2.604941 0.05056899 2.610084
## 4 2.518273 -1.12244957 2.694049 -0.43434192 2.630910
## 5 2.318271 -1.00748037 2.571730 -0.48496663 2.585076
## 6 2.469045 -0.91488990 2.640153 -0.41631866 2.575907
## v_speed_FALSE sv_TRUE sv_FALSE B_left_accuracy B_right_accuracy B_left_neutral
## 1 0.7279810 0.7438907 1.344284 0.8047483 0.8436372 0.8285359
## 2 0.8849442 0.6881459 1.453180 0.6733857 0.6792392 0.7070098
## 3 0.9512200 0.7026347 1.423215 0.7070980 0.7797117 0.7136950
## 4 0.2649155 0.6663098 1.500803 0.7374192 0.7577417 0.7872392
## 5 0.7612078 0.6742474 1.483135 0.7428754 0.7602723 0.7493119
## 6 0.4505837 0.6699235 1.492708 0.8672715 0.9165751 0.8490002
## B_right_neutral B_left_speed B_right_speed A t0
## 1 0.8568205 0.6007733 0.6544962 0.3326415 0.11728475
## 2 0.7152202 0.4372691 0.4839382 0.3086353 0.13019744
## 3 0.8233317 0.5219825 0.6400104 0.3057428 0.10378461
## 4 0.7791123 0.5582606 0.5846386 0.1722742 0.10862906
## 5 0.7820744 0.5250702 0.5770507 0.2128573 0.11958983
## 6 0.9113578 0.6808935 0.7485422 0.2276435 0.09364553# Calculate means
pmeans <- data.frame(lapply(ps, mean))
pmeans## v_accuracy_TRUE v_accuracy_FALSE v_neutral_TRUE v_neutral_FALSE v_speed_TRUE
## 1 2.553057 -0.1260086 2.712327 0.2487697 2.652366
## v_speed_FALSE sv_TRUE sv_FALSE B_left_accuracy B_right_accuracy B_left_neutral
## 1 1.087434 0.7131412 1.404017 0.836204 0.8730531 0.8374889
## B_right_neutral B_left_speed B_right_speed A t0
## 1 0.8846271 0.6237197 0.6834642 0.2959662 0.1008881Next, we calculate the quality (match-mismatch difference) and quantity (match-mismatch average) of accumulation rates
vmeans <- data.frame(
a_quality = mean(ps$v_accuracy_TRUE - ps$v_accuracy_FALSE),
n_quality = mean(ps$v_neutral_TRUE - ps$v_neutral_FALSE),
s_quality = mean(ps$v_speed_TRUE - ps$v_speed_FALSE),
a_quantity = mean(c(ps$v_accuracy_TRUE, ps$v_accuracy_FALSE)),
n_quantity = mean(c(ps$v_neutral_TRUE, ps$v_neutral_FALSE)),
s_quantity = mean(c(ps$v_speed_TRUE, ps$v_speed_FALSE))
)
vmeans## a_quality n_quality s_quality a_quantity n_quantity s_quantity
## 1 2.679066 2.463557 1.564932 1.213524 1.480548 1.8699Reshaping this to a long format;
QQ <- vmeans %>% transmute(Accuracy_Quality = a_quality,
Neutral_Quality = n_quality,
Speed_Quality = s_quality,
Accuracy_Quantity = a_quantity,
Neutral_Quantity = n_quantity,
Speed_Quantity = s_quantity) %>%
pivot_longer(cols = everything(),
names_to = c("Emphasis", "Measure"),
names_pattern = "(.*)_(.*)",
values_to = "v")
QQ## # A tibble: 6 x 3
## Emphasis Measure v
## <chr> <chr> <dbl>
## 1 Accuracy Quality 2.68
## 2 Neutral Quality 2.46
## 3 Speed Quality 1.56
## 4 Accuracy Quantity 1.21
## 5 Neutral Quantity 1.48
## 6 Speed Quantity 1.87Using the drift rate parameters, we can plot quality and quantity. As our parameter tests above showed, processing quality is poorer in the speed emphasis condition, but quantity is higher. This reflects additional effort or resources deployed in order to respond more quickly, without necessarily improving the quality of processing.
QQ_plot <- ggplot(data = QQ, aes(Emphasis, v, col = Measure)) +
geom_line(aes(group = Measure), lty = "dashed", lwd = 1) +
geom_point(size = 4, shape = 19) +
ylim(0.8, 3) +
theme_minimal() + theme(text = element_text(size = 15))
QQ_plot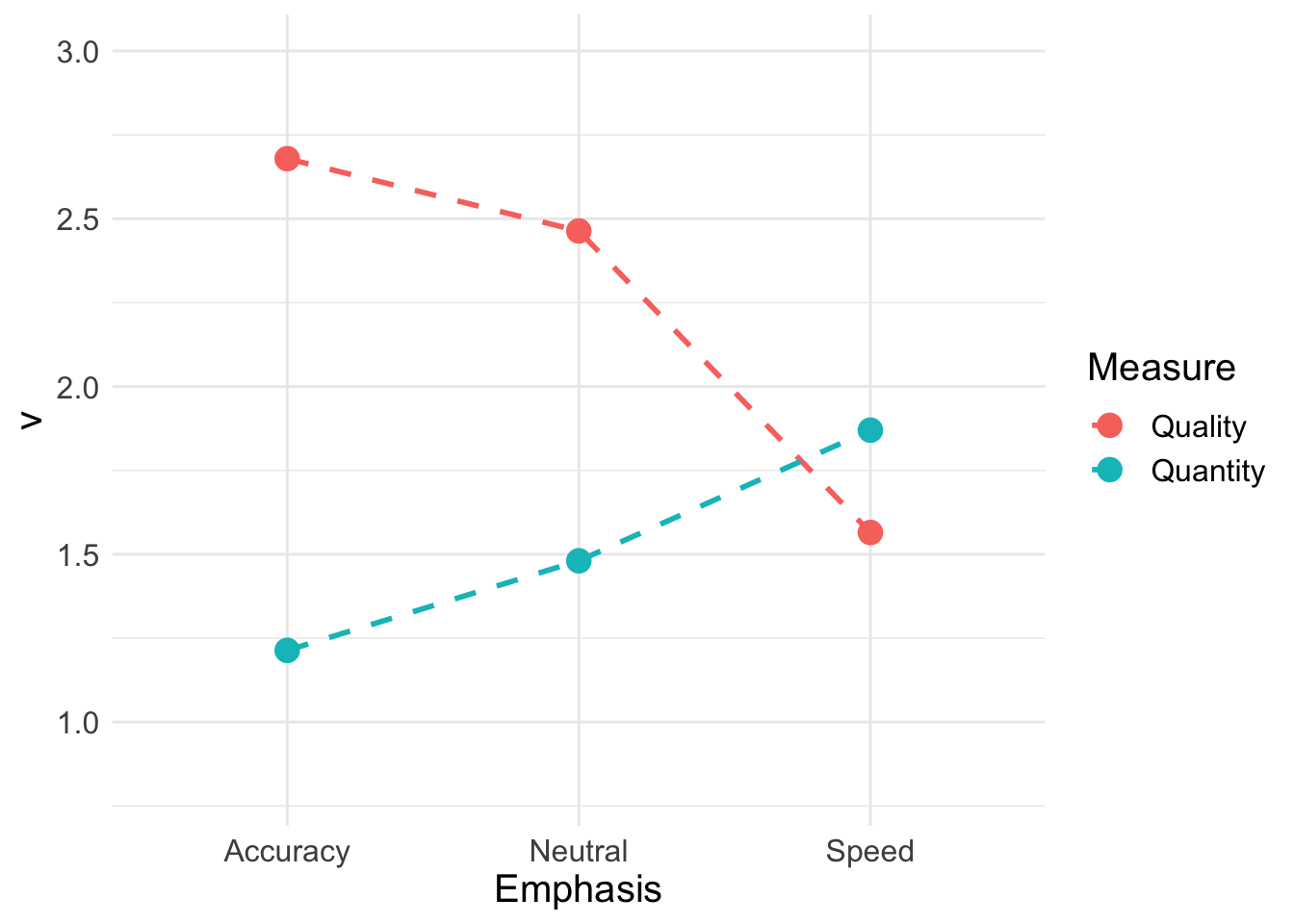
Now, let’s look at thresholds;
B <- pmeans %>% transmute(Accuracy_Left = B_left_accuracy,
Accuracy_Right = B_right_accuracy,
Neutral_Left = B_left_neutral,
Neutral_Right = B_right_neutral,
Speed_Left = B_left_speed,
Speed_Right = B_right_speed) %>%
pivot_longer(cols = everything(),
names_to = c("Emphasis", "Accumulator"),
names_pattern = "(.*)_(.*)",
values_to = "B")
B## # A tibble: 6 x 3
## Emphasis Accumulator B
## <chr> <chr> <dbl>
## 1 Accuracy Left 0.836
## 2 Accuracy Right 0.873
## 3 Neutral Left 0.837
## 4 Neutral Right 0.885
## 5 Speed Left 0.624
## 6 Speed Right 0.683Plotting separately for left and right accumulators shows the overall bias towards responding ‘left’.
B_plot <- ggplot(data = B, aes(Emphasis, B, col = Accumulator)) +
geom_line(aes(group = Accumulator), lty = "dashed", lwd = 1) +
geom_point(size = 4, shape = 19) +
ylim(0.5, 1) +
theme_minimal() + theme(text = element_text(size = 15))
B_plot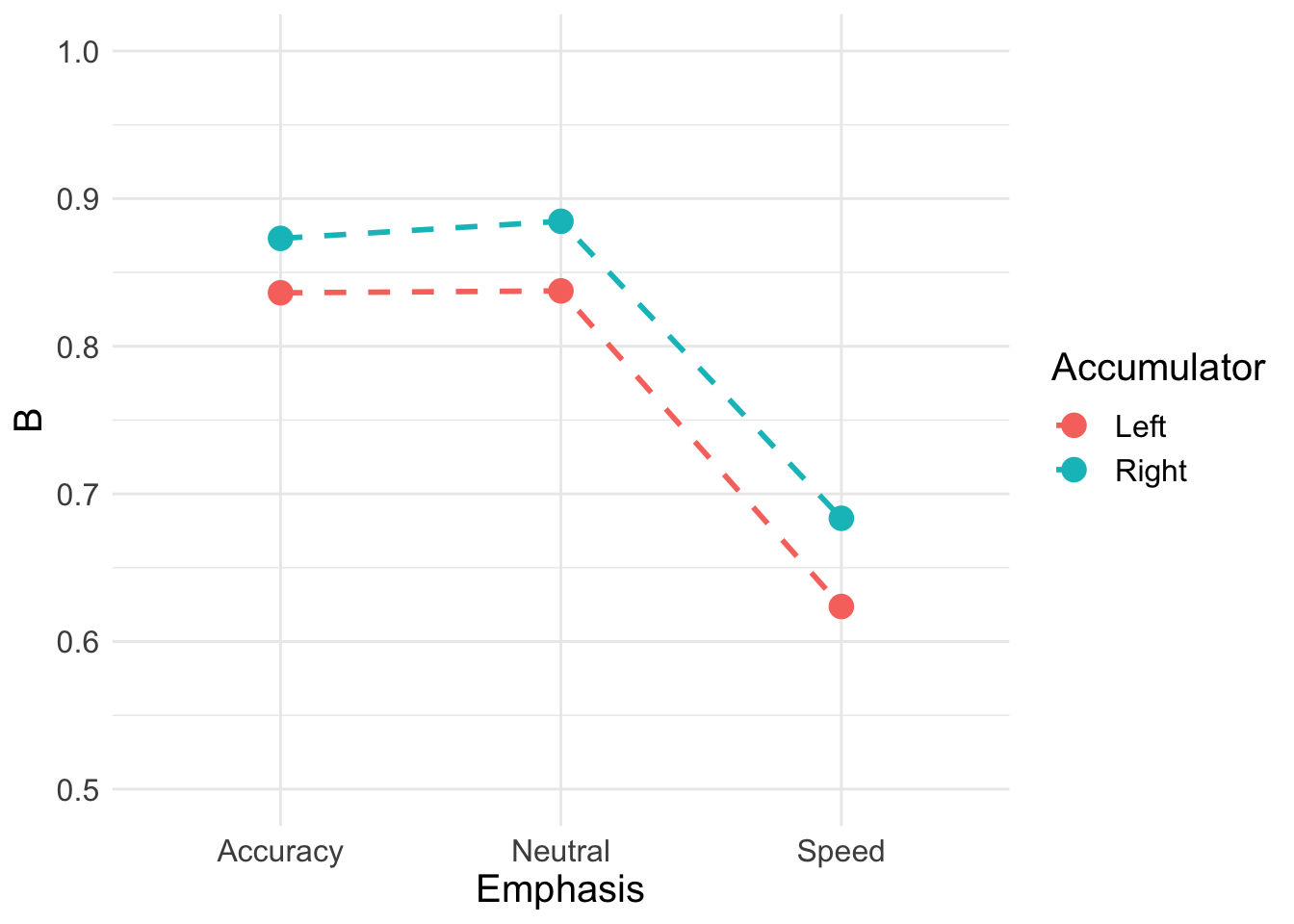
6.2 RDM
The Racing Diffusion Model (RDM) is a model which utilises both the race structure and diffusion model framework. Here, we use a diffusion process towards a single threshold for each accumulator of the model. A grpahical example can be seen below.
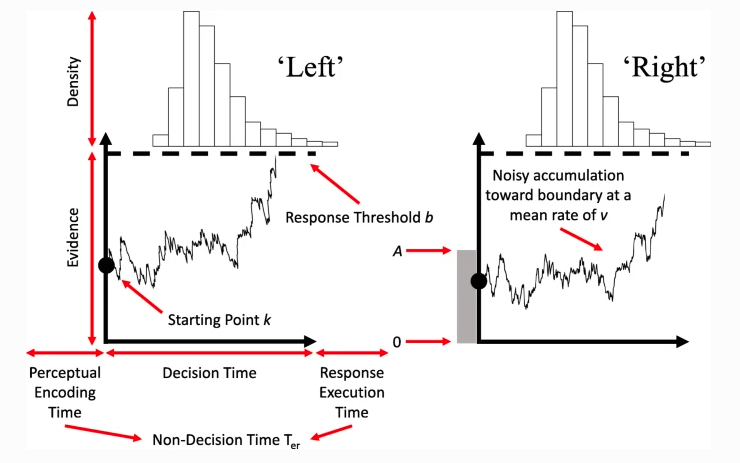
Figure 6.2: The racing diffusion model
6.2.1 RDM in EMC2
To use the RDM, we show the a similar structure as we did for the LBA and LNR. First, let’s prepare our environment.
rm(list=ls())
source("emc/emc.R")
source("models/RACE/RDM/rdmB.R")
print( load("Data/PNAS.RData"))
dat <- data[,c("s","E","S","R","RT")]
names(dat)[c(1,5)] <- c("subjects","rt")
levels(dat$R) <- levels(dat$S)6.2.2 RDM Model Design
Now we can look at the design for our model. The parameters we specify for the RDM are very similar to the LBA, with v the mean rate of evidence accumulation, B the threshold, A the start point and t0 the non-decision time. We can also include additional variability parameters as is shown below.
In this code, we again show several different types of model designs that vary different parameters. These include a thresholds only model; threshold, drift and t0 model; threshold and t0 model; and a threshold and drift model.
# Average and difference matrix
ADmat <- matrix(c(-1/2,1/2),ncol=1,dimnames=list(NULL,"d"))
Emat <- matrix(c(0,-1,0,0,0,-1),nrow=3)
dimnames(Emat) <- list(NULL,c("a-n","a-s"))
design_B <- make_design(
Ffactors=list(subjects=levels(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,S=ADmat,E=Emat),
Flist=list(v~lM,B~lR*E,A~1,t0~1),
model=rdmB)
design_Bvt0<- make_design(
Ffactors=list(subjects=levels(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,S=ADmat,E=Emat),
Flist=list(v~lM*E,B~lR*E,A~1,t0~E),
model=rdmB)
design_Bt0<- make_design(
Ffactors=list(subjects=levels(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,S=ADmat,E=Emat),
Flist=list(v~lM,B~lR*E,A~1,t0~E),
model=rdmB)
design_Bv<- make_design(
Ffactors=list(subjects=levels(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,S=ADmat,E=Emat),
Flist=list(v~lM*E,B~lR*E,A~1,t0~1),
model=rdmB)
# rdm_B <- make_samplers(dat,design_B,type="standard",rt_resolution=.02)
# rdm_Bvt0<- make_samplers(dat,design_Bvt0,type="standard",rt_resolution=.02)
# rdm_Bt0 <- make_samplers(dat,design_Bt0,type="standard",rt_resolution=.02)
# rdm_Bv <- make_samplers(dat,design_Bv,type="standard",rt_resolution=.02)
# All of these models are run in a single file, run_rdm.R using the run_emc function. This function is given the name of the file containing the samplers object and any arguments to its constituent functions (run_burn, run_adapt and run_sample). For example the first model was fit with 8 cores per chain and so 24 cores in total given the default of 3 chains.
run_emc(“rdmPNAS_B.RData”,cores_per_chain=8)
If any stage fails run_check stops, saving the progress so far. The only argument unique to this function is nsample, which determines the number of iterations performed if the sample stage is reached (by default 1000).
After the convergence checking reported below extra samples were obtained for some models that converged slowly, so all had 1000 converged samples. This was done by adding another run_emc call with nsamples set appropriately (run_emc recognizes that burn and adapt stages are complete and so just adds on the extra samples at the end).
Finally for the selected model, extra samples were added to obtain 5000 iterations, so posterior inference was reliable, and posterior predictives were obtained. (NB: if the file is run several times some lines must be commented out or unwanted sample stage iteration will be added). First, let’s load the pre-sampled models from the osf.
print(load("~/Desktop/emc2/models/RACE/RDM/examples/samples/rdmPNAS_B.RData"))## [1] "rdm_B"print(load("~/Desktop/emc2/models/RACE/RDM/examples/samples/rdmPNAS_Bt0.RData"))## [1] "rdm_Bt0"print(load("~/Desktop/emc2/models/RACE/RDM/examples/samples/rdmPNAS_Bv.RData"))## [1] "rdm_Bv"print(load("~/Desktop/emc2/models/RACE/RDM/examples/samples/rdmPNAS_Bvt0.RData"))## [1] "rdm_Bvt0" "pprdm_Bvt0"Next, we can again do check_run for each of these models. Remember, running the code below will ask you to press enter across a series of checks.
#### Check convergence ----
check_run(rdm_B)
check_run(rdm_Bt0,subfilter=500)
check_run(rdm_Bv,subfilter=1500)
check_run(rdm_Bvt0,subfilter=1500)6.2.3 Model selection
Next, we’ll again look at model comparisons using some quick IC measures. First, we’ll start with group level measures.
compare_IC(list(B=rdm_B,Bt0=rdm_Bt0,Bv=rdm_Bv,Bvt0=rdm_Bvt0),
subfilter=list(0,500,1500,1500))## DIC wDIC BPIC wBPIC EffectiveN meanD Dmean minD
## B -16514 0 -16333 0 180 -16694 -16844 -16874
## Bt0 -16511 0 -16309 0 202 -16714 -16863 -16916
## Bv -16628 0 -16420 1 208 -16836 -16999 -17044
## Bvt0 -16648 1 -16403 0 245 -16893 -17054 -17137We see here that Bvt0 wins, with Bt0 second across the different RDM models. This is similar to our LBA and DDM examples. Let’s also check this out at the subject level.
ICs <- compare_ICs(list(B=rdm_B,Bt0=rdm_Bt0,Bv=rdm_Bv,Bvt0=rdm_Bvt0),
subfilter=list(0,500,1500,1500:2500))## wDIC_B wDIC_Bt0 wDIC_Bv wDIC_Bvt0 wBPIC_B wBPIC_Bt0 wBPIC_Bv wBPIC_Bvt0
## as1t 0.123 0.249 0.394 0.234 0.259 0.344 0.297 0.099
## bd6t 0.000 0.000 0.007 0.993 0.000 0.000 0.013 0.987
## bl1t 0.000 0.000 0.000 1.000 0.000 0.000 0.000 1.000
## hsft 0.000 0.001 0.052 0.947 0.002 0.001 0.135 0.862
## hsgt 0.045 0.030 0.244 0.681 0.070 0.033 0.344 0.553
## kd6t 0.232 0.115 0.264 0.389 0.570 0.128 0.202 0.101
## kd9t 0.012 0.030 0.261 0.697 0.035 0.047 0.272 0.645
## kh6t 0.220 0.073 0.679 0.027 0.241 0.015 0.740 0.004
## kmat 0.553 0.396 0.019 0.032 0.647 0.334 0.008 0.011
## ku4t 0.088 0.094 0.445 0.373 0.113 0.110 0.507 0.270
## na1t 0.038 0.032 0.216 0.714 0.112 0.084 0.297 0.507
## rmbt 0.001 0.000 0.745 0.253 0.003 0.000 0.710 0.287
## rt2t 0.063 0.059 0.699 0.179 0.074 0.079 0.718 0.128
## rt3t 0.208 0.683 0.079 0.031 0.150 0.797 0.044 0.009
## rt5t 0.345 0.364 0.208 0.083 0.326 0.431 0.208 0.034
## scat 0.105 0.458 0.151 0.286 0.180 0.704 0.054 0.061
## ta5t 0.017 0.007 0.523 0.453 0.048 0.005 0.545 0.402
## vf1t 0.000 0.000 0.019 0.981 0.000 0.000 0.017 0.983
## zk1t 0.394 0.025 0.452 0.129 0.628 0.002 0.356 0.014table(unlist(lapply(ICs,function(x){row.names(x)[which.min(x$DIC)]})))##
## B Bt0 Bv Bvt0
## 1 3 7 8table(unlist(lapply(ICs,function(x){row.names(x)[which.min(x$BPIC)]})))##
## B Bt0 Bv Bvt0
## 3 4 5 7We see similar results here, but at the subject level the Bv model is second. Let’s now compare these with the best DDM and LBA models.
## DIC wDIC BPIC wBPIC EffectiveN meanD Dmean minD
## DDM_avt0 -17043 0 -16802 0 240 -17283 -17468 -17523
## LBA_Bvsv -17188 1 -16964 1 224 -17412 -17564 -17636
## RDM_Bvt0 -16648 0 -16403 0 245 -16893 -17054 -17137source("models/DDM/DDM/ddmTZD.R")
load("~/Desktop/emc2/models/DDM/DDM/examples/samples/sPNAS_avt0_full.RData")
source("models/RACE/LBA/lbaB.R")
load("~/Desktop/emc2/models/RACE/LBA/examples/samples/sPNAS_Bv_sv.RData")
compare_IC(list(DDM_avt0=sPNAS_avt0_full,LBA_Bvsv=sPNAS_Bv_sv,RDM_Bvt0=rdm_Bvt0),
subfilter=list(500,2000,1500))Comparing the “best” RDM with the “best” DDM (16 parameter) and LBA (15 parameter) models, we see that the RDM is the worst out of these three. Let’s look at the model fit and start analysing why this might be.
6.2.4 Model fit
Here we use the plot_fit on posterior predictive data from the Bvt0 model.
# post predict did not use first 1500, so inference based on 5000*3 samples
plot_fit(dat,pprdm_Bvt0,layout=c(2,3),factors=c("E","S"),lpos="right",xlim=c(.25,1.5))
#plot_fits(dat,pprdm_Bvt0,layout=c(2,3),lpos="right")The fits seem to be pretty decent. These plots below also show a pretty good fit, with a slight under-estimation of 10th percentile and over-estimation of error RT in speed. Here, we only show these plots where misfit is present.
pc <- function(d) 100*mean(d$S==d$R)
plot_fit(dat,pprdm_Bvt0,layout=c(2,3),factors=c("E","S"),
stat=pc,stat_name="Accuracy (%)",xlim=c(70,95))
tab <- plot_fit(dat,pprdm_Bvt0,layout=c(2,3),factors=c("E","S"),
stat=function(d){mean(d$rt)},stat_name="Mean RT (s)",xlim=c(0.375,.625))
tab <- plot_fit(dat,pprdm_Bvt0,layout=c(2,3),factors=c("E","S"),xlim=c(0.275,.4),
stat=function(d){quantile(d$rt,.1)},stat_name="10th Percentile (s)")
tab <- plot_fit(dat,pprdm_Bvt0,layout=c(2,3),factors=c("E","S"),xlim=c(0.525,.975),
stat=function(d){quantile(d$rt,.9)},stat_name="90th Percentile (s)")
tab <- plot_fit(dat,pprdm_Bvt0,layout=c(2,3),factors=c("E","S"),
stat=function(d){sd(d$rt)},stat_name="SD (s)",xlim=c(0.1,.355))
tab <- plot_fit(dat,pprdm_Bvt0,layout=c(2,3),factors=c("E","S"),xlim=c(0.375,.725),
stat=function(d){mean(d$rt[d$R!=d$S])},stat_name="Mean Error RT (s)")pc <- function(d) 100*mean(d$S==d$R)
tab <- plot_fit(dat,pprdm_Bvt0,layout=c(2,3),factors=c("E","S"),xlim=c(0.275,.4),
stat=function(d){quantile(d$rt,.1)},stat_name="10th Percentile (s)")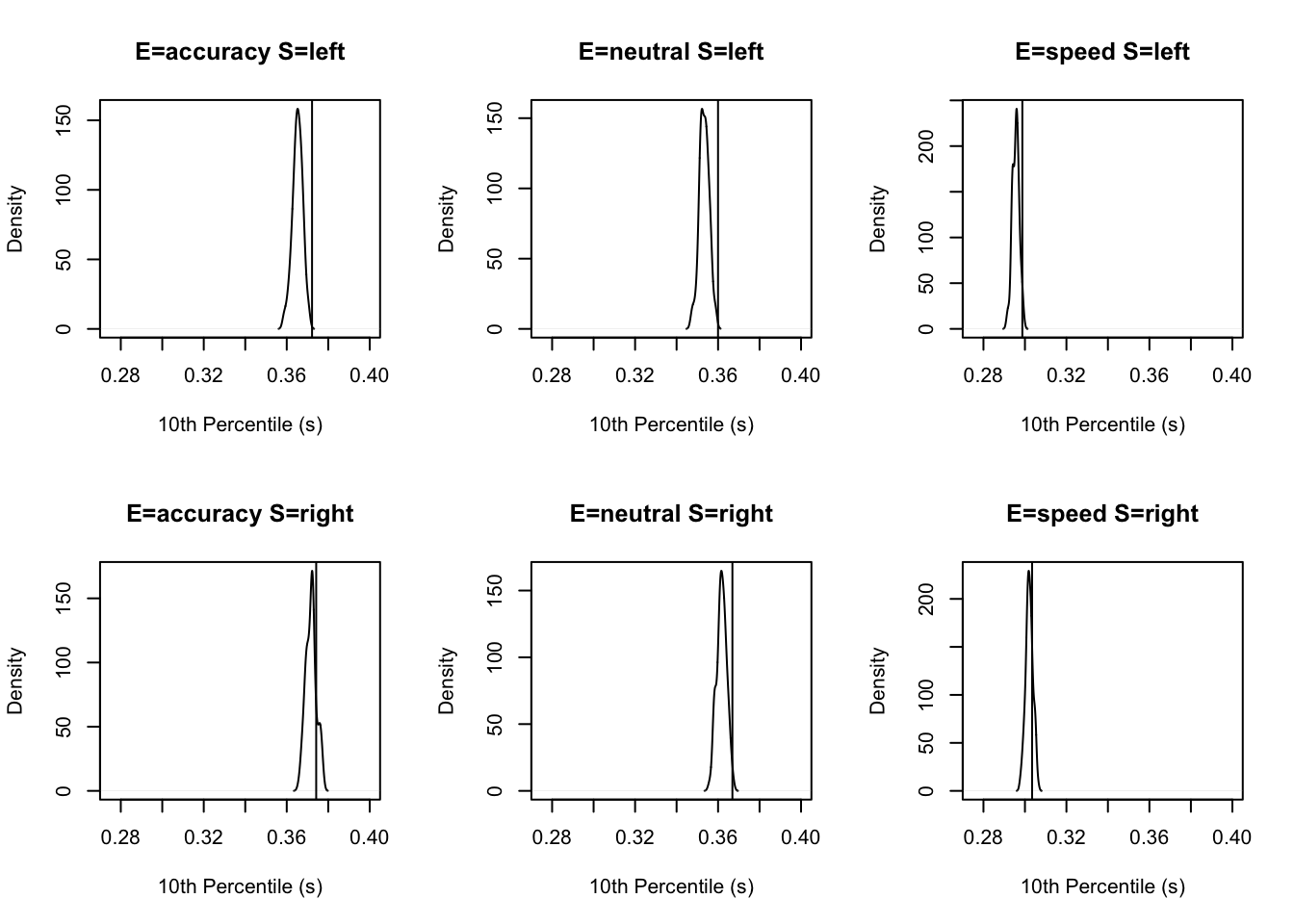
tab <- plot_fit(dat,pprdm_Bvt0,layout=c(2,3),factors=c("E","S"),xlim=c(0.375,.725),
stat=function(d){mean(d$rt[d$R!=d$S])},stat_name="Mean Error RT (s)")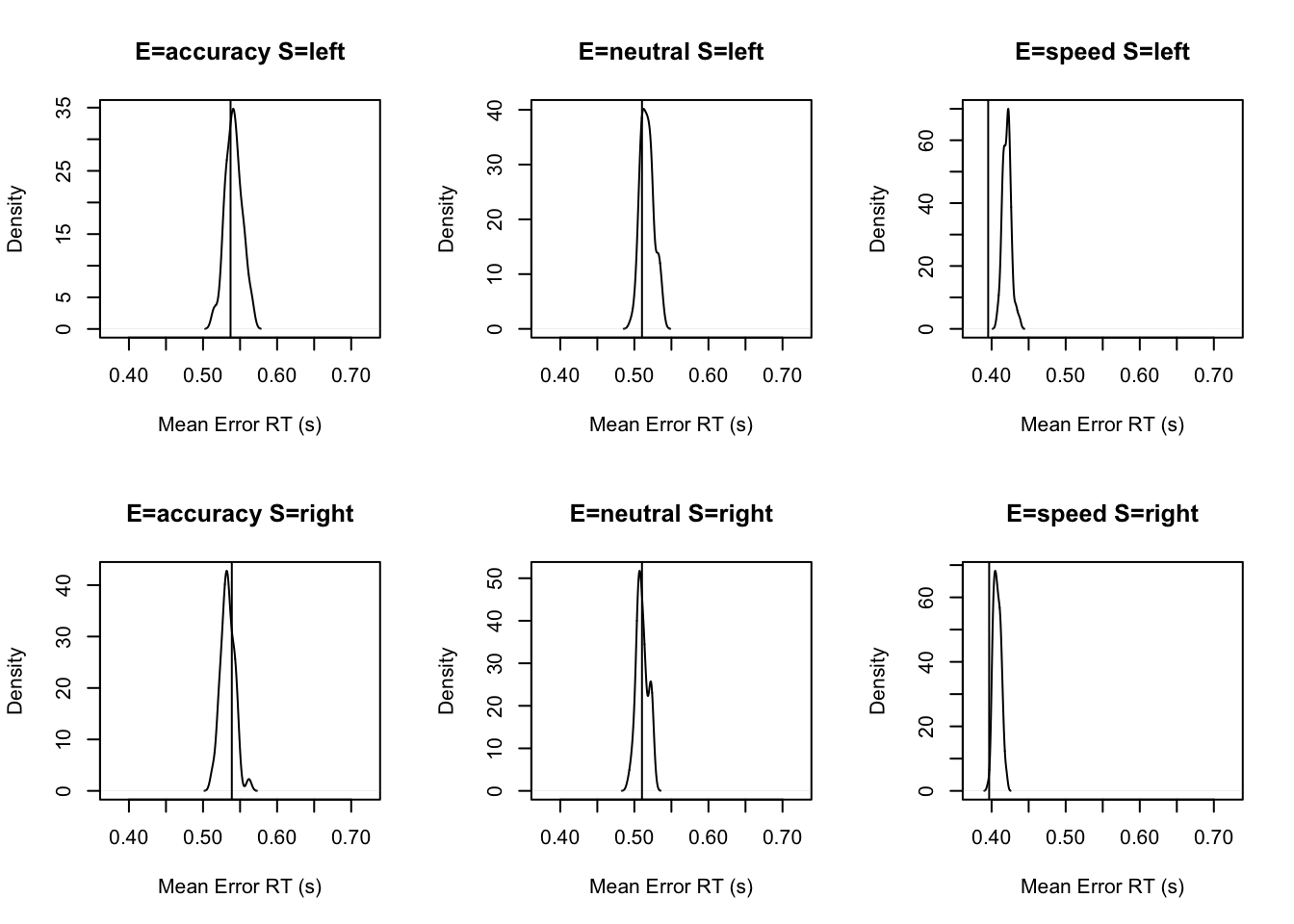
6.2.5 Posterior parameter inference
Now that we’ve analysed the fit, we can also look at some posterior inference to try and understand whether this model shows any differences to the LBA or DDM. We start by looking at the group level tests. Here we show parameter estimates both with and without mapping.
# Priors all well dominated except some rate parameters
cirdm_Bvt0 <- plot_density(rdm_Bvt0,layout=c(3,6),selection="mu",subfilter=1500)
# On the natural scale it is evident this is because the mismatch (FALSE) rates
# are least well updated, due to the fairly low error rates (errors give the
# most information about FALSE rates).
cirdm_Bvt0_mapped <- plot_density(rdm_Bvt0,layout=c(3,6),
selection="mu",mapped=TRUE)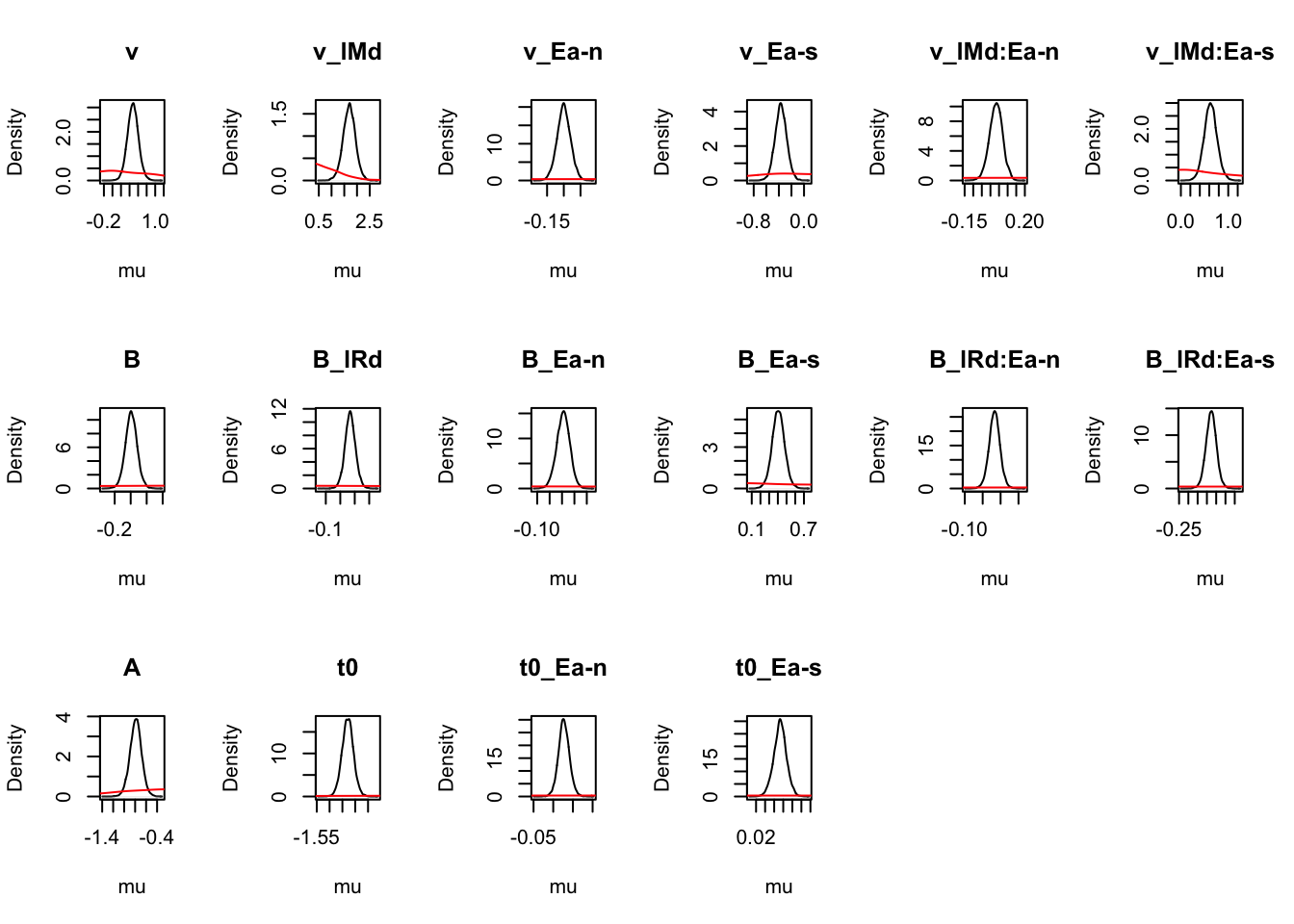
# Looking at parameters both with and without mapping
round(cirdm_Bvt0,2)## v v_lMd v_Ea-n v_Ea-s v_lMd:Ea-n v_lMd:Ea-s B B_lRd B_Ea-n B_Ea-s
## 2.5% 0.23 1.20 -0.14 -0.55 -0.05 0.36 -0.17 0.00 -0.05 0.26
## 50% 0.48 1.70 -0.10 -0.37 0.03 0.63 -0.10 0.07 0.01 0.41
## 97.5% 0.74 2.17 -0.06 -0.18 0.11 0.90 -0.02 0.14 0.06 0.55
## B_lRd:Ea-n B_lRd:Ea-s A t0 t0_Ea-n t0_Ea-s
## 2.5% -0.05 -0.13 -1.00 -1.47 0.00 0.04
## 50% -0.02 -0.08 -0.79 -1.43 0.03 0.07
## 97.5% 0.01 -0.02 -0.58 -1.38 0.06 0.10round(cirdm_Bvt0_mapped,2)## v_TRUE_accuracy v_FALSE_accuracy v_TRUE_neutral v_FALSE_neutral v_TRUE_speed
## 2.5% 3.11 0.43 3.37 0.46 3.23
## 50% 3.77 0.69 4.09 0.76 3.97
## 97.5% 4.54 1.10 4.92 1.25 4.82
## v_FALSE_speed B_left_accuracy B_right_accuracy B_left_neutral B_right_neutral
## 2.5% 0.93 0.81 0.87 0.78 0.86
## 50% 1.36 0.88 0.94 0.87 0.94
## 97.5% 1.93 0.96 1.02 0.95 1.03
## B_left_speed B_right_speed A t0_accuracy t0_neutral t0_speed
## 2.5% 0.47 0.56 0.36 0.23 0.22 0.21
## 50% 0.56 0.65 0.45 0.24 0.23 0.22
## 97.5% 0.66 0.76 0.56 0.25 0.25 0.23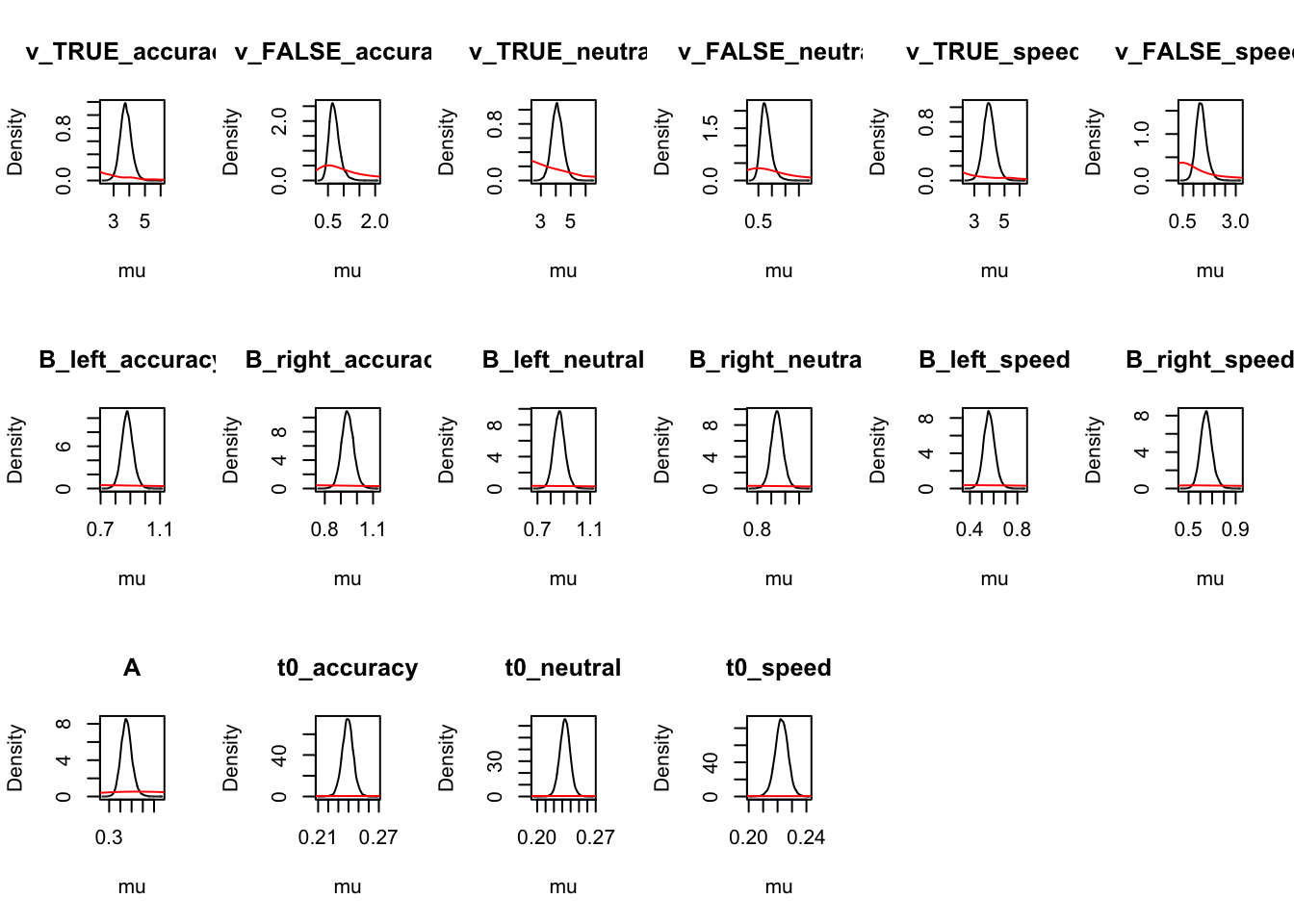
For simpler estimates: 1) t0 is longer than the LBA 2) Start point noise slightly larger relative to B than for the LBA.
6.2.5.1 B effects
Let’s now check our all important threshold effects. First, recall the mapping used for B
get_map(rdm_Bvt0)$B## lR E B B_lRd B_Ea-n B_Ea-s B_lRd:Ea-n B_lRd:Ea-s
## 1 left accuracy 1 -0.5 0 0 0.0 0.0
## 7 right accuracy 1 0.5 0 0 0.0 0.0
## 2 left neutral 1 -0.5 -1 0 0.5 0.0
## 8 right neutral 1 0.5 -1 0 -0.5 0.0
## 3 left speed 1 -0.5 0 -1 0.0 0.5
## 9 right speed 1 0.5 0 -1 0.0 -0.5Now let’s look at B_lRd which tests threshold right - threshold left, similar to in the LBA.
p_test(x=rdm_Bvt0,x_name="B_lRd",subfilter=1500,digits=3)## B_lRd mu
## 2.5% -0.004 NA
## 50% 0.068 0
## 97.5% 0.142 NA
## attr(,"less")
## [1] 0.031Although not quite credible, it indicates slightly higher right thresholds (i.e., a bias to respond left).
Similar to the LBA, B_Ea-n and B_Ea-s measure differences in response caution (i.e., thresholds averaged over left and right accumulators), accuracy - neutral and accuracy - speed respectively.
p_test(x=rdm_Bvt0,x_name="B_Ea-n",subfilter=1500)## B_Ea-n mu
## 2.5% -0.05 NA
## 50% 0.01 0
## 97.5% 0.06 NA
## attr(,"less")
## [1] 0.419p_test(x=rdm_Bvt0,x_name="B_Ea-s",subfilter=1500)## B_Ea-s mu
## 2.5% 0.26 NA
## 50% 0.41 0
## 97.5% 0.55 NA
## attr(,"less")
## [1] 0Caution for accuracy is clearly higher than speed, but not credibly greater than neutral.
Here we construct a test on the natural scale showing caution is greater for neutral than speed;
p_test(x=rdm_Bvt0,mapped=TRUE,x_name="average B: neutral-speed",
x_fun=function(x){mean(x[c("B_left_neutral","B_right_neutral")]) -
mean(x[c("B_left_speed","B_right_speed")])})## average B: neutral-speed mu
## 2.5% 0.21 NA
## 50% 0.30 0
## 97.5% 0.39 NA
## attr(,"less")
## [1] 0The remaining term (B_lRd:Ea-s) tests interactions with bias (i.e., lR), with evidence of a small but credibly stronger bias to respond left (i.e., a lower threshold for the left accumulator) for speed than accuracy.
p_test(x=rdm_Bvt0,x_name="B_lRd:Ea-s",subfilter=1500,digits=2)## B_lRd:Ea-s mu
## 2.5% -0.13 NA
## 50% -0.08 0
## 97.5% -0.02 NA
## attr(,"less")
## [1] 0.9946.2.6 v effects
Let’s now check for any drift rate effects. First, let’s look at the mapping used.
get_map(rdm_Bvt0)$v## lM E v v_lMd v_Ea-n v_Ea-s v_lMd:Ea-n v_lMd:Ea-s
## 1 TRUE accuracy 1 0.5 0 0 0.0 0.0
## 7 FALSE accuracy 1 -0.5 0 0 0.0 0.0
## 2 TRUE neutral 1 0.5 -1 0 -0.5 0.0
## 8 FALSE neutral 1 -0.5 -1 0 0.5 0.0
## 3 TRUE speed 1 0.5 0 -1 0.0 -0.5
## 9 FALSE speed 1 -0.5 0 -1 0.0 0.5Here, v_Ea-n and v_Ea-s indicate that processing rate (the average of matching and mismatching rates) is less in the accuracy condition than in neutral or speed.
p_test(x=rdm_Bvt0,x_name="v_Ea-n",subfilter=1500)## v_Ea-n mu
## 2.5% -0.14 NA
## 50% -0.10 0
## 97.5% -0.06 NA
## attr(,"less")
## [1] 1p_test(x=rdm_Bvt0,x_name="v_Ea-s",subfilter=1500)## v_Ea-s mu
## 2.5% -0.55 NA
## 50% -0.37 0
## 97.5% -0.18 NA
## attr(,"less")
## [1] 1However, neutral and speed do not credibly differ;
p_test(x=rdm_Bvt0,mapped=TRUE,x_name="average v: speed-neutral",
x_fun=function(x){mean(x[c("v_TRUE_speed","v_FALSE_speed")]) -
mean(x[c("v_TRUE_neutral","v_FALSE_neutral")])})## average v: speed-neutral mu
## 2.5% -0.06 NA
## 50% 0.23 0
## 97.5% 0.55 NA
## attr(,"less")
## [1] 0.059v_lMd tests the “quality” of selective attention, rate match - rate mismatch.
p_test(x=rdm_Bvt0,x_name="v_lMd",subfilter=1500)## v_lMd mu
## 2.5% 1.20 NA
## 50% 1.70 0
## 97.5% 2.17 NA
## attr(,"less")
## [1] 0v_Ea-n indicates quality does not differ credibly between accuracy and neutral.
p_test(x=rdm_Bvt0,x_name="v_lMd:Ea-n",subfilter=1500)## v_lMd:Ea-n mu
## 2.5% -0.05 NA
## 50% 0.03 0
## 97.5% 0.11 NA
## attr(,"less")
## [1] 0.196In contrast there is a strong difference for accuracy - speed;
p_test(x=rdm_Bvt0,x_name="v_lMd:Ea-s",subfilter=1500)## v_lMd:Ea-s mu
## 2.5% 0.36 NA
## 50% 0.63 0
## 97.5% 0.90 NA
## attr(,"less")
## [1] 0The neutral - speed difference is also highly credible, here is is tested in the mapped form.
p_test(x=rdm_Bvt0,mapped=TRUE,x_name="quality: accuracy-neutral",
x_fun=function(x){diff(x[c("v_FALSE_neutral","v_TRUE_neutral")]) -
diff(x[c("v_FALSE_speed","v_TRUE_speed")])})## quality: accuracy-neutral mu
## 2.5% 0.35 NA
## 50% 0.71 0
## 97.5% 1.08 NA
## attr(,"less")
## [1] 06.2.6.1 Visualising results
In this section, as we do for the LBA, we’re again going to show some extensions of visualizations, by first extracting the parameter estimates, and then plotting these using ggplot2. Let’s start by extracting the parameters and checking the means of the posterior.
# Here we visualize these threshold and rate effects
library(tidyverse)
# Get parameter data frame
ps <- parameters_data_frame(rdm_Bvt0, mapped = TRUE)
head(ps)## v_TRUE_accuracy v_FALSE_accuracy v_TRUE_neutral v_FALSE_neutral v_TRUE_speed
## 1 3.431639 0.3446701 4.239264 0.5468789 3.870593
## 2 3.947793 0.6922556 4.394294 0.9208254 4.211111
## 3 4.058286 0.5966165 4.342919 0.6887796 4.521430
## 4 3.993086 0.4738672 4.664679 0.5177178 4.635995
## 5 3.547141 1.2149620 4.090971 1.4267556 3.506973
## 6 3.148097 0.5603768 3.594237 0.5885173 3.423264
## v_FALSE_speed B_left_accuracy B_right_accuracy B_left_neutral B_right_neutral
## 1 0.7505228 0.7918152 0.8460093 0.8862445 0.9515371
## 2 1.3238674 0.7591425 0.8086740 0.8692756 0.9276422
## 3 1.4160110 0.8000483 0.9496064 0.8030501 0.9474515
## 4 1.2893575 0.8030587 0.8549157 0.7966596 0.8564589
## 5 1.4739013 0.8388881 0.8914065 0.8796424 0.9465314
## 6 1.1172589 0.7788311 0.9010827 0.8365712 0.9730959
## B_left_speed B_right_speed A t0_accuracy t0_neutral t0_speed
## 1 0.4498708 0.5225185 0.5251879 0.2418921 0.2213071 0.2214772
## 2 0.6561390 0.7430251 0.5257231 0.2570650 0.2345159 0.2237344
## 3 0.4949914 0.6179072 0.5172401 0.2495441 0.2367346 0.2313448
## 4 0.5303871 0.5965826 0.5233095 0.2471920 0.2425336 0.2226937
## 5 0.5499901 0.5886816 0.5283719 0.2239879 0.2119343 0.2105091
## 6 0.5314943 0.6575876 0.4881616 0.2417799 0.2354508 0.2254859# Get means
pmeans <- data.frame(lapply(ps, mean))
pmeans## v_TRUE_accuracy v_FALSE_accuracy v_TRUE_neutral v_FALSE_neutral v_TRUE_speed
## 1 3.7817 0.705524 4.108446 0.7857492 3.987888
## v_FALSE_speed B_left_accuracy B_right_accuracy B_left_neutral B_right_neutral
## 1 1.377339 0.8803732 0.9419822 0.8660072 0.9425966
## B_left_speed B_right_speed A t0_accuracy t0_neutral t0_speed
## 1 0.5634169 0.6511609 0.4547375 0.239195 0.2331849 0.222763Next, we look at thresholds by emphasis and accumulator;
B <- pmeans %>% transmute(Accuracy_Left = B_left_accuracy,
Accuracy_Right = B_right_accuracy,
Neutral_Left = B_left_neutral,
Neutral_Right = B_right_neutral,
Speed_Left = B_left_speed,
Speed_Right = B_right_speed) %>%
pivot_longer(cols = everything(),
names_to = c("Emphasis", "Accumulator"),
names_pattern = "(.*)_(.*)",
values_to = "B")
B## # A tibble: 6 x 3
## Emphasis Accumulator B
## <chr> <chr> <dbl>
## 1 Accuracy Left 0.880
## 2 Accuracy Right 0.942
## 3 Neutral Left 0.866
## 4 Neutral Right 0.943
## 5 Speed Left 0.563
## 6 Speed Right 0.651We can the plot thresholds
B_plot <- ggplot(data = B, aes(Emphasis, B, col = Accumulator)) +
geom_line(aes(group = Accumulator), lty = "dashed", lwd = 1) +
geom_point(size = 4, shape = 19) +
ylim(0.5, 1) +
theme_minimal() + theme(text = element_text(size = 15))
B_plot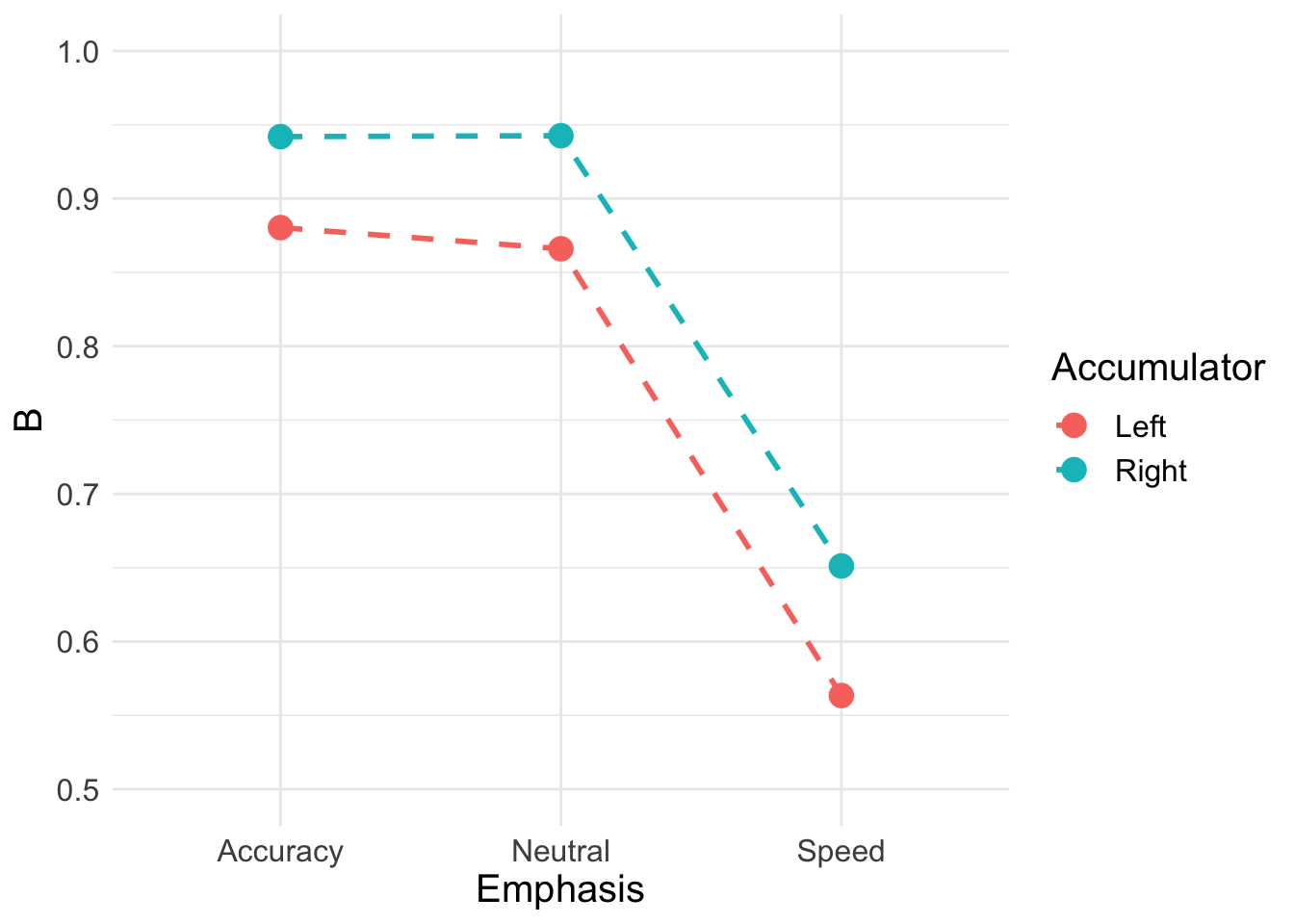
Here, instead we will calculate the difference between thresholds for left and right responses to better illustrate the change in bias across emphasis conditions
Bmeans <- data.frame(
a_bias = mean(ps$B_right_accuracy - ps$B_left_accuracy),
n_bias = mean(ps$B_right_neutral - ps$B_left_neutral),
s_bias = mean(ps$B_right_speed - ps$B_left_speed)
)
Bmeans## a_bias n_bias s_bias
## 1 0.06160906 0.07658941 0.08774396Now looking at the long format;
B_bias <- Bmeans %>% transmute(Accuracy = a_bias,
Neutral = n_bias,
Speed = s_bias) %>%
pivot_longer(cols = everything(),
names_to = c("Emphasis"),
names_pattern = "(.*)",
values_to = "Bias")
B_bias## # A tibble: 3 x 2
## Emphasis Bias
## <chr> <dbl>
## 1 Accuracy 0.0616
## 2 Neutral 0.0766
## 3 Speed 0.0877Plot threshold bias;
B_plot <- ggplot(data = B_bias, aes(Emphasis, Bias)) +
geom_line(aes(group = 1), lty = "dashed", lwd = 1) +
geom_point(size = 4, shape = 19) +
ylim(0, 0.12) +
theme_minimal() + theme(text = element_text(size = 15))
B_plot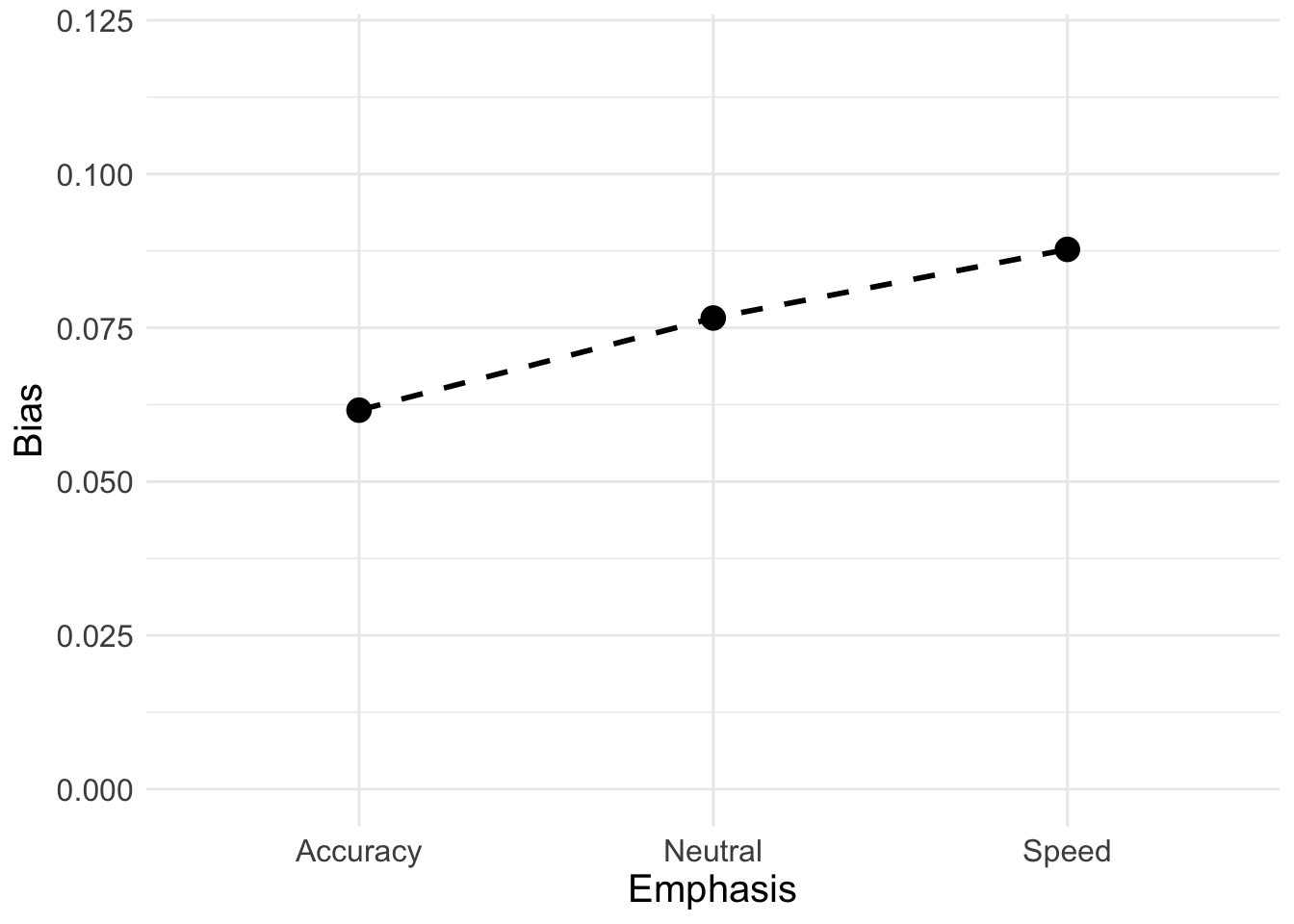
Now we will calculate the quality (match-mismatch difference) and quantity (match-mismatch average) of accumulation rates;
vmeans <- data.frame(
a_quality = mean(ps$v_TRUE_accuracy - ps$v_FALSE_accuracy),
n_quality = mean(ps$v_TRUE_neutral - ps$v_FALSE_neutral),
s_quality = mean(ps$v_TRUE_speed - ps$v_FALSE_speed),
a_quantity = mean(c(ps$v_TRUE_accuracy, ps$v_FALSE_accuracy)),
n_quantity = mean(c(ps$v_TRUE_neutral, ps$v_FALSE_neutral)),
s_quantity = mean(c(ps$v_TRUE_speed, ps$v_FALSE_speed))
)
vmeans## a_quality n_quality s_quality a_quantity n_quantity s_quantity
## 1 3.076175 3.322696 2.610549 2.243612 2.447097 2.682614Let’s now look at our quantile-quantile plots;
QQ <- vmeans %>% transmute(Accuracy_Quality = a_quality,
Neutral_Quality = n_quality,
Speed_Quality = s_quality,
Accuracy_Quantity = a_quantity,
Neutral_Quantity = n_quantity,
Speed_Quantity = s_quantity) %>%
pivot_longer(cols = everything(),
names_to = c("Emphasis", "Measure"),
names_pattern = "(.*)_(.*)",
values_to = "v")
QQ## # A tibble: 6 x 3
## Emphasis Measure v
## <chr> <chr> <dbl>
## 1 Accuracy Quality 3.08
## 2 Neutral Quality 3.32
## 3 Speed Quality 2.61
## 4 Accuracy Quantity 2.24
## 5 Neutral Quantity 2.45
## 6 Speed Quantity 2.68Again, we’ll do a QQ plot for quality and quantity. Similar to what we saw with the LBA, quality degrades under speed emphasis but participants deploy more overall resources (quantity) to meet the extra demands of faster responding.
QQ_plot <- ggplot(data = QQ, aes(Emphasis, v, col = Measure)) +
geom_line(aes(group = Measure), lty = "dashed", lwd = 1) +
geom_point(size = 4, shape = 19) +
ylim(1.8, 3.6) +
theme_minimal() + theme(text = element_text(size = 15))
QQ_plot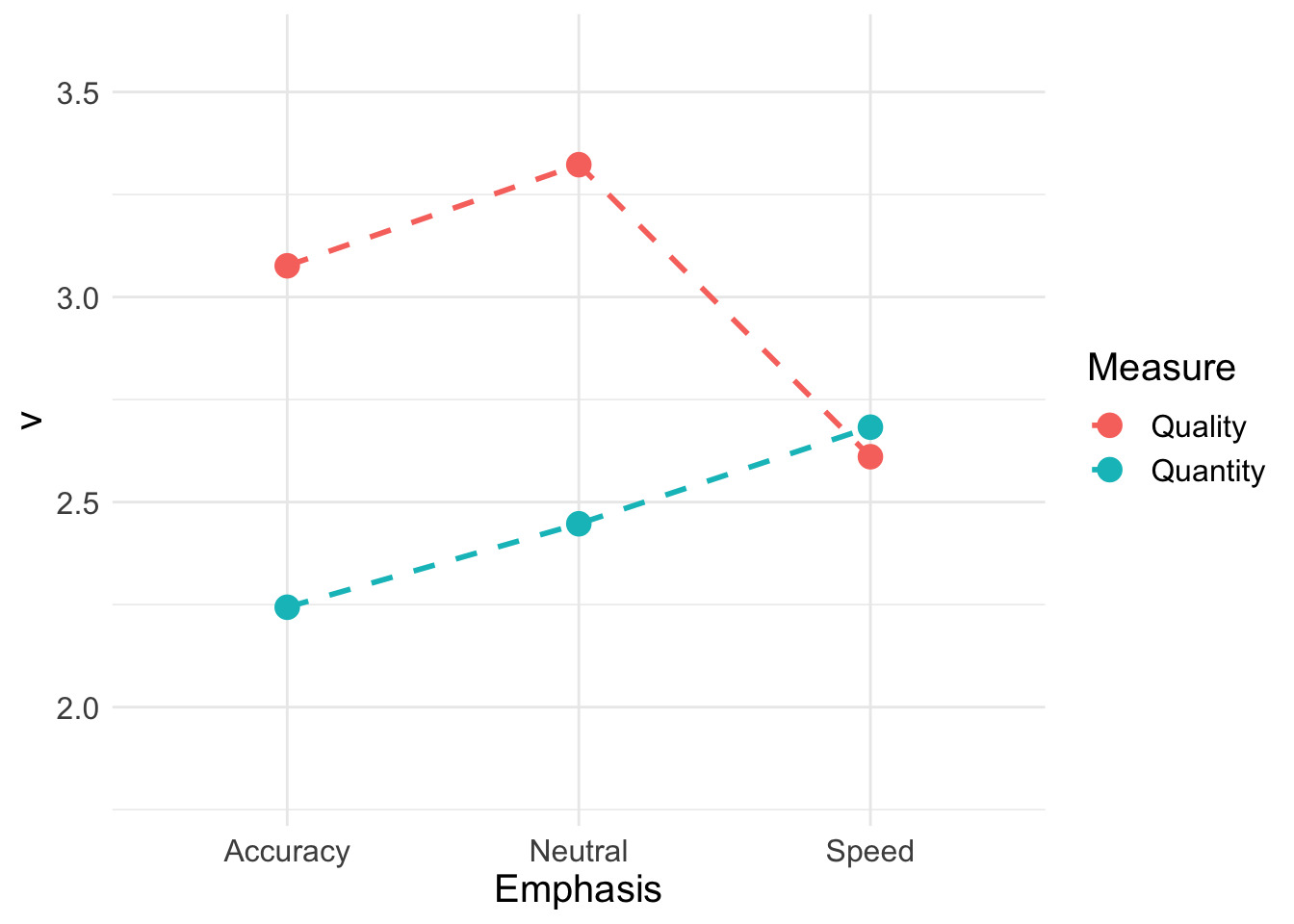
6.3 LNR
The Lognormal distribution: a distribution whose logarithm is normal.
The log-normal distribution has long history of being used to model RT distribution with the near universal positively skewed shape evident for RT. It is another type of central limit for the product of random variables, xi. The log-normal distribution is similar to a response time distribution, but the log-normal distribution starts at 0, whereas (as we discussed above), response time should begin a bit later than that (maybe around .2 seconds). To overcome this, we can add a shift the the log-normal. For this example we will use the shifted log-normal to model RT distribution:
\(RT ~ shift + Lognormal(meanlog,sdlog)\)
$meanlog/sdlog = mean and sd $ on the log scale
Figure 6.3: The diffusion decision model
This paper (Heathcote and Love 2012) discusses this history and how the log-normal distribution can arise from different psychological processes such as a “cascade” process where the random variable are the rates of each stage in the cascade. The paper also develops a model of choice, which we will briefly return to in subsequent chapters. The log-normal race model is the most tractable of EMC2’s race models. For now, we will use the shifted log-normal to model RT distribution. For more on the log-normal race model that addresses choice processing see (Rouder et al. 2015).
6.3.1 Theory and Model
First, let’s graphically look at the log-normal distribution;
Again, this looks similar to the response time distributions we saw above. When thinking about how the “model” works, we can take the log of the distribution, which stretches out our distribution to give us something that resembles a normal distribution (which is easy to estimate);
6.3.2 EMC2 for Lognormal Race
Let’s now look at how to specify the LNR using EMC2. A lot of this is similar to the previous race models, but the parameters are noticeably different.
rm(list=ls())
source("emc/emc.R")
source("models/RACE/LNR/lnrMS.R")
print( load("Data/PNAS.RData"))
dat <- data[,c("s","E","S","R","RT")]
names(dat)[c(1,5)] <- c("subjects","rt")
levels(dat$R) <- levels(dat$S)Let’s specify our contrasts;
# Average and difference matrix
ADmat <- matrix(c(-1/2,1/2),ncol=1,dimnames=list(NULL,"d"))
ADmat## d
## [1,] -0.5
## [2,] 0.5Emat <- matrix(c(0,-1,0,0,0,-1),nrow=3)
dimnames(Emat) <- list(NULL,c("a-n","a-s"))
Emat## a-n a-s
## [1,] 0 0
## [2,] -1 0
## [3,] 0 -16.3.3 LNR Designs
Here, we show five different designs, that sequentially build up the parameters. In the first, Mu (i.e., the mean of the distribution) varies by stimulus, emphasis, and latent match. Secondly, we let sigma also vary by latent match. In the third model, let t0 vary by speed-accuracy emphasis. In the fourth model, sigma varies with emphasis and latent match. And finally, for the fifth model, again let t0 vary by emphasis.
It’s important to remember that we do not just start with these designs, these designs were generated by incorporating our hypotheses and then exploring many different models that add in parameters to improve the fit. Evidently, the full model space is quite large, so building up the models this way is a good test - as long as we include alternate models to test against and do not rely just on intuition.
design_mu <- make_design(
Ffactors=list(subjects=levels(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,E=Emat,S=ADmat),
Flist=list(m~S*E*lM,s~1,t0~1),
model=lnrMS)## m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n
## 0 0 0 0 0 0
## m_Sd:Ea-s m_Sd:lMd m_Ea-n:lMd m_Ea-s:lMd m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd
## 0 0 0 0 0 0
## s t0
## 0 0
## attr(,"map")
## attr(,"map")$m
## m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n m_Sd:Ea-s m_Sd:lMd m_Ea-n:lMd m_Ea-s:lMd
## 1 1 -0.5 0 0 0.5 0.0 0.0 -0.25 0.0 0.0
## 229 1 -0.5 0 0 -0.5 0.0 0.0 0.25 0.0 0.0
## 39 1 -0.5 -1 0 0.5 0.5 0.0 -0.25 -0.5 0.0
## 267 1 -0.5 -1 0 -0.5 0.5 0.0 0.25 0.5 0.0
## 77 1 -0.5 0 -1 0.5 0.0 0.5 -0.25 0.0 -0.5
## 305 1 -0.5 0 -1 -0.5 0.0 0.5 0.25 0.0 0.5
## 20 1 0.5 0 0 -0.5 0.0 0.0 -0.25 0.0 0.0
## 248 1 0.5 0 0 0.5 0.0 0.0 0.25 0.0 0.0
## 58 1 0.5 -1 0 -0.5 -0.5 0.0 -0.25 0.5 0.0
## 286 1 0.5 -1 0 0.5 -0.5 0.0 0.25 -0.5 0.0
## 96 1 0.5 0 -1 -0.5 0.0 -0.5 -0.25 0.0 0.5
## 324 1 0.5 0 -1 0.5 0.0 -0.5 0.25 0.0 -0.5
## m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd
## 1 0.00 0.00
## 229 0.00 0.00
## 39 0.25 0.00
## 267 -0.25 0.00
## 77 0.00 0.25
## 305 0.00 -0.25
## 20 0.00 0.00
## 248 0.00 0.00
## 58 0.25 0.00
## 286 -0.25 0.00
## 96 0.00 0.25
## 324 0.00 -0.25
##
## attr(,"map")$s
## s
## 1 1
##
## attr(,"map")$t0
## t0
## 1 1# lnr_mu <- make_samplers(dat,design_mu,type="standard",rt_resolution=.02)
# save(lnr_mu,file="lnrPNAS_mu.RData")
design_mu_slM <- make_design(
Ffactors=list(subjects=levels(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,E=Emat,S=ADmat),
Flist=list(m~S*E*lM,s~lM,t0~1),
model=lnrMS)## m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n
## 0 0 0 0 0 0
## m_Sd:Ea-s m_Sd:lMd m_Ea-n:lMd m_Ea-s:lMd m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd
## 0 0 0 0 0 0
## s s_lMd t0
## 0 0 0
## attr(,"map")
## attr(,"map")$m
## m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n m_Sd:Ea-s m_Sd:lMd m_Ea-n:lMd m_Ea-s:lMd
## 1 1 -0.5 0 0 0.5 0.0 0.0 -0.25 0.0 0.0
## 229 1 -0.5 0 0 -0.5 0.0 0.0 0.25 0.0 0.0
## 39 1 -0.5 -1 0 0.5 0.5 0.0 -0.25 -0.5 0.0
## 267 1 -0.5 -1 0 -0.5 0.5 0.0 0.25 0.5 0.0
## 77 1 -0.5 0 -1 0.5 0.0 0.5 -0.25 0.0 -0.5
## 305 1 -0.5 0 -1 -0.5 0.0 0.5 0.25 0.0 0.5
## 20 1 0.5 0 0 -0.5 0.0 0.0 -0.25 0.0 0.0
## 248 1 0.5 0 0 0.5 0.0 0.0 0.25 0.0 0.0
## 58 1 0.5 -1 0 -0.5 -0.5 0.0 -0.25 0.5 0.0
## 286 1 0.5 -1 0 0.5 -0.5 0.0 0.25 -0.5 0.0
## 96 1 0.5 0 -1 -0.5 0.0 -0.5 -0.25 0.0 0.5
## 324 1 0.5 0 -1 0.5 0.0 -0.5 0.25 0.0 -0.5
## m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd
## 1 0.00 0.00
## 229 0.00 0.00
## 39 0.25 0.00
## 267 -0.25 0.00
## 77 0.00 0.25
## 305 0.00 -0.25
## 20 0.00 0.00
## 248 0.00 0.00
## 58 0.25 0.00
## 286 -0.25 0.00
## 96 0.00 0.25
## 324 0.00 -0.25
##
## attr(,"map")$s
## s s_lMd
## 1 1 0.5
## 229 1 -0.5
##
## attr(,"map")$t0
## t0
## 1 1# lnr_mu_slM <- make_samplers(dat,design_mu_slM,type="standard",rt_resolution=.02)
# save(lnr_mu_slM,file="lnrPNAS_mu_slM.RData")
design_mu_slM_t0 <- make_design(
Ffactors=list(subjects=levels(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,E=Emat,S=ADmat),
Flist=list(m~S*E*lM,s~lM,t0~E),
model=lnrMS)## m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n
## 0 0 0 0 0 0
## m_Sd:Ea-s m_Sd:lMd m_Ea-n:lMd m_Ea-s:lMd m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd
## 0 0 0 0 0 0
## s s_lMd t0 t0_Ea-n t0_Ea-s
## 0 0 0 0 0
## attr(,"map")
## attr(,"map")$m
## m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n m_Sd:Ea-s m_Sd:lMd m_Ea-n:lMd m_Ea-s:lMd
## 1 1 -0.5 0 0 0.5 0.0 0.0 -0.25 0.0 0.0
## 229 1 -0.5 0 0 -0.5 0.0 0.0 0.25 0.0 0.0
## 39 1 -0.5 -1 0 0.5 0.5 0.0 -0.25 -0.5 0.0
## 267 1 -0.5 -1 0 -0.5 0.5 0.0 0.25 0.5 0.0
## 77 1 -0.5 0 -1 0.5 0.0 0.5 -0.25 0.0 -0.5
## 305 1 -0.5 0 -1 -0.5 0.0 0.5 0.25 0.0 0.5
## 20 1 0.5 0 0 -0.5 0.0 0.0 -0.25 0.0 0.0
## 248 1 0.5 0 0 0.5 0.0 0.0 0.25 0.0 0.0
## 58 1 0.5 -1 0 -0.5 -0.5 0.0 -0.25 0.5 0.0
## 286 1 0.5 -1 0 0.5 -0.5 0.0 0.25 -0.5 0.0
## 96 1 0.5 0 -1 -0.5 0.0 -0.5 -0.25 0.0 0.5
## 324 1 0.5 0 -1 0.5 0.0 -0.5 0.25 0.0 -0.5
## m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd
## 1 0.00 0.00
## 229 0.00 0.00
## 39 0.25 0.00
## 267 -0.25 0.00
## 77 0.00 0.25
## 305 0.00 -0.25
## 20 0.00 0.00
## 248 0.00 0.00
## 58 0.25 0.00
## 286 -0.25 0.00
## 96 0.00 0.25
## 324 0.00 -0.25
##
## attr(,"map")$s
## s s_lMd
## 1 1 0.5
## 229 1 -0.5
##
## attr(,"map")$t0
## t0 t0_Ea-n t0_Ea-s
## 1 1 0 0
## 39 1 -1 0
## 77 1 0 -1# lnr_mu_slM_t0 <- make_samplers(dat,design_mu_slM_t0,type="standard",rt_resolution=.02)
# save(lnr_mu_slM_t0,file="lnrPNAS_mu_slM_t0.RData")
design_mu_sElM <- make_design(
Ffactors=list(subjects=levels(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,E=Emat,S=ADmat),
Flist=list(m~S*E*lM,s~E*lM,t0~1),
model=lnrMS)## m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n
## 0 0 0 0 0 0
## m_Sd:Ea-s m_Sd:lMd m_Ea-n:lMd m_Ea-s:lMd m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd
## 0 0 0 0 0 0
## s s_Ea-n s_Ea-s s_lMd s_Ea-n:lMd s_Ea-s:lMd
## 0 0 0 0 0 0
## t0
## 0
## attr(,"map")
## attr(,"map")$m
## m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n m_Sd:Ea-s m_Sd:lMd m_Ea-n:lMd m_Ea-s:lMd
## 1 1 -0.5 0 0 0.5 0.0 0.0 -0.25 0.0 0.0
## 229 1 -0.5 0 0 -0.5 0.0 0.0 0.25 0.0 0.0
## 39 1 -0.5 -1 0 0.5 0.5 0.0 -0.25 -0.5 0.0
## 267 1 -0.5 -1 0 -0.5 0.5 0.0 0.25 0.5 0.0
## 77 1 -0.5 0 -1 0.5 0.0 0.5 -0.25 0.0 -0.5
## 305 1 -0.5 0 -1 -0.5 0.0 0.5 0.25 0.0 0.5
## 20 1 0.5 0 0 -0.5 0.0 0.0 -0.25 0.0 0.0
## 248 1 0.5 0 0 0.5 0.0 0.0 0.25 0.0 0.0
## 58 1 0.5 -1 0 -0.5 -0.5 0.0 -0.25 0.5 0.0
## 286 1 0.5 -1 0 0.5 -0.5 0.0 0.25 -0.5 0.0
## 96 1 0.5 0 -1 -0.5 0.0 -0.5 -0.25 0.0 0.5
## 324 1 0.5 0 -1 0.5 0.0 -0.5 0.25 0.0 -0.5
## m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd
## 1 0.00 0.00
## 229 0.00 0.00
## 39 0.25 0.00
## 267 -0.25 0.00
## 77 0.00 0.25
## 305 0.00 -0.25
## 20 0.00 0.00
## 248 0.00 0.00
## 58 0.25 0.00
## 286 -0.25 0.00
## 96 0.00 0.25
## 324 0.00 -0.25
##
## attr(,"map")$s
## s s_Ea-n s_Ea-s s_lMd s_Ea-n:lMd s_Ea-s:lMd
## 1 1 0 0 0.5 0.0 0.0
## 229 1 0 0 -0.5 0.0 0.0
## 39 1 -1 0 0.5 -0.5 0.0
## 267 1 -1 0 -0.5 0.5 0.0
## 77 1 0 -1 0.5 0.0 -0.5
## 305 1 0 -1 -0.5 0.0 0.5
##
## attr(,"map")$t0
## t0
## 1 1# lnr_mu_sElM <- make_samplers(dat,design_mu_sElM,type="standard",rt_resolution=.02)
# save(lnr_mu_sElM,file="lnrPNAS_mu_sElM.RData")
design_mu_sElM_t0 <- make_design(
Ffactors=list(subjects=levels(dat$subjects),S=levels(dat$S),E=levels(dat$E)),
Rlevels=levels(dat$R),matchfun=function(d)d$S==d$lR,
Clist=list(lM=ADmat,lR=ADmat,E=Emat,S=ADmat),
Flist=list(m~S*E*lM,s~E*lM,t0~E),
model=lnrMS)## m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n
## 0 0 0 0 0 0
## m_Sd:Ea-s m_Sd:lMd m_Ea-n:lMd m_Ea-s:lMd m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd
## 0 0 0 0 0 0
## s s_Ea-n s_Ea-s s_lMd s_Ea-n:lMd s_Ea-s:lMd
## 0 0 0 0 0 0
## t0 t0_Ea-n t0_Ea-s
## 0 0 0
## attr(,"map")
## attr(,"map")$m
## m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n m_Sd:Ea-s m_Sd:lMd m_Ea-n:lMd m_Ea-s:lMd
## 1 1 -0.5 0 0 0.5 0.0 0.0 -0.25 0.0 0.0
## 229 1 -0.5 0 0 -0.5 0.0 0.0 0.25 0.0 0.0
## 39 1 -0.5 -1 0 0.5 0.5 0.0 -0.25 -0.5 0.0
## 267 1 -0.5 -1 0 -0.5 0.5 0.0 0.25 0.5 0.0
## 77 1 -0.5 0 -1 0.5 0.0 0.5 -0.25 0.0 -0.5
## 305 1 -0.5 0 -1 -0.5 0.0 0.5 0.25 0.0 0.5
## 20 1 0.5 0 0 -0.5 0.0 0.0 -0.25 0.0 0.0
## 248 1 0.5 0 0 0.5 0.0 0.0 0.25 0.0 0.0
## 58 1 0.5 -1 0 -0.5 -0.5 0.0 -0.25 0.5 0.0
## 286 1 0.5 -1 0 0.5 -0.5 0.0 0.25 -0.5 0.0
## 96 1 0.5 0 -1 -0.5 0.0 -0.5 -0.25 0.0 0.5
## 324 1 0.5 0 -1 0.5 0.0 -0.5 0.25 0.0 -0.5
## m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd
## 1 0.00 0.00
## 229 0.00 0.00
## 39 0.25 0.00
## 267 -0.25 0.00
## 77 0.00 0.25
## 305 0.00 -0.25
## 20 0.00 0.00
## 248 0.00 0.00
## 58 0.25 0.00
## 286 -0.25 0.00
## 96 0.00 0.25
## 324 0.00 -0.25
##
## attr(,"map")$s
## s s_Ea-n s_Ea-s s_lMd s_Ea-n:lMd s_Ea-s:lMd
## 1 1 0 0 0.5 0.0 0.0
## 229 1 0 0 -0.5 0.0 0.0
## 39 1 -1 0 0.5 -0.5 0.0
## 267 1 -1 0 -0.5 0.5 0.0
## 77 1 0 -1 0.5 0.0 -0.5
## 305 1 0 -1 -0.5 0.0 0.5
##
## attr(,"map")$t0
## t0 t0_Ea-n t0_Ea-s
## 1 1 0 0
## 39 1 -1 0
## 77 1 0 -1# lnr_mu_sElM_t0 <- make_samplers(dat,design_mu_sElM_t0,type="standard",rt_resolution=.02)
# save(lnr_mu_sElM_t0,file="lnrPNAS_mu_sElM_t0.RData")Let’s load in the presampled models.
# Load saved samples
print(load("~/Desktop/emc2/models/RACE/LNR/examples/samples/lnrPNAS_mu.RData"))## [1] "lnr_mu"print(load("~/Desktop/emc2/models/RACE/LNR/examples/samples/lnrPNAS_mu_slM.RData"))## [1] "lnr_mu_slM"print(load("~/Desktop/emc2/models/RACE/LNR/examples/samples/lnrPNAS_mu_slM_t0.RData"))## [1] "lnr_mu_slM_t0"print(load("~/Desktop/emc2/models/RACE/LNR/examples/samples/lnrPNAS_mu_sElM.RData"))## [1] "lnr_mu_sElM"print(load("~/Desktop/emc2/models/RACE/LNR/examples/samples/lnrPNAS_mu_sElM_t0.RData"))## [1] "lnr_mu_sElM_t0" "pplnr_musElMt0"Again we can conduct our sampling checks, pressing ‘Enter’ for each model check;
# Sampling checks
check_run(lnr_mu,layout=c(3,5),subfilter=500)
check_run(lnr_mu_slM,layout=c(3,5),subfilter=500)
check_run(lnr_mu_slM_t0,layout=c(3,5),subfilter=1000)
check_run(lnr_mu_sElM,layout=c(3,5),subfilter=1500)
check_run(lnr_mu_sElM_t0,layout=c(3,5),subfilter=2000:3000)6.3.3.0.1 Model selection
For the LNR, we can now compare the models using IC methods. Here we see that muElMt0 wins by DIC but mulMt0 wins by BPIC;
compare_IC(list(mu=lnr_mu,mulM=lnr_mu_slM,mulMt0=lnr_mu_slM_t0,
muElM=lnr_mu_sElM,muElMt0=lnr_mu_sElM_t0), subfilter=list(500,500,1000,1500,2000))## DIC wDIC BPIC wBPIC EffectiveN meanD Dmean minD
## mu -15080 0 -14869 0 211 -15290 -15451 -15501
## mulM -16840 0 -16633 0 207 -17047 -17217 -17254
## mulMt0 -17102 0 -16879 1 223 -17325 -17509 -17548
## muElM -17053 0 -16809 0 245 -17298 -17501 -17542
## muElMt0 -17129 1 -16846 0 283 -17411 -17609 -17694# On an individual basis muElMt0 also wins
ICs <- compare_ICs(list(mu=lnr_mu,mulM=lnr_mu_slM,mulMt0=lnr_mu_slM_t0,
muElM=lnr_mu_sElM,muElMt0=lnr_mu_sElM_t0), subfilter=list(0,0,0,500,1000))## wDIC_mu wDIC_mulM wDIC_mulMt0 wDIC_muElM wDIC_muElMt0 wBPIC_mu wBPIC_mulM
## as1t 0 0.003 0.657 0.102 0.239 0 0.003
## bd6t 0 0.020 0.165 0.002 0.814 0 0.121
## bl1t 0 0.000 0.210 0.000 0.789 0 0.000
## hsft 0 0.000 0.188 0.037 0.775 0 0.000
## hsgt 0 0.001 0.042 0.000 0.956 0 0.021
## kd6t 0 0.000 0.138 0.118 0.745 0 0.000
## kd9t 0 0.000 0.081 0.012 0.908 0 0.000
## kh6t 0 0.000 0.002 0.955 0.043 0 0.000
## kmat 0 0.001 0.005 0.807 0.187 0 0.002
## ku4t 0 0.027 0.299 0.662 0.012 0 0.061
## na1t 0 0.005 0.013 0.001 0.980 0 0.017
## rmbt 0 0.000 0.070 0.154 0.776 0 0.000
## rt2t 0 0.000 0.745 0.078 0.177 0 0.000
## rt3t 0 0.665 0.209 0.087 0.039 0 0.880
## rt5t 0 0.004 0.162 0.478 0.357 0 0.006
## scat 0 0.000 0.097 0.275 0.627 0 0.001
## ta5t 0 0.000 0.460 0.449 0.090 0 0.000
## vf1t 0 0.000 0.658 0.000 0.342 0 0.000
## zk1t 0 0.000 0.001 0.172 0.827 0 0.000
## wBPIC_mulMt0 wBPIC_muElM wBPIC_muElMt0
## as1t 0.766 0.066 0.165
## bd6t 0.544 0.001 0.333
## bl1t 0.687 0.000 0.312
## hsft 0.204 0.043 0.753
## hsgt 0.591 0.004 0.384
## kd6t 0.255 0.195 0.550
## kd9t 0.196 0.017 0.787
## kh6t 0.003 0.981 0.016
## kmat 0.002 0.908 0.088
## ku4t 0.410 0.528 0.001
## na1t 0.030 0.002 0.951
## rmbt 0.081 0.211 0.708
## rt2t 0.928 0.033 0.039
## rt3t 0.079 0.030 0.010
## rt5t 0.173 0.286 0.536
## scat 0.282 0.456 0.262
## ta5t 0.432 0.531 0.038
## vf1t 0.940 0.000 0.060
## zk1t 0.003 0.288 0.709sort(table(unlist(lapply(ICs,function(x){row.names(x)[which.min(x$DIC)]}))))##
## mulM muElM mulMt0 muElMt0
## 1 4 4 10sort(table(unlist(lapply(ICs,function(x){row.names(x)[which.min(x$BPIC)]}))))##
## mulM muElM mulMt0 muElMt0
## 1 5 6 7Let’s now compare the RDM with the best DDM (16 parameter) model, the best (15 parameter) LBA model and the best (16 parameter) RDM. The best LNR model included 21 parameters - muElMt0. For the comparison, we see that the LNR comes in second.
## [1] "ppPNAS_avt0_full" "sPNAS_avt0_full"## [1] "ppPNAS_Bv_sv" "sPNAS_Bv_sv"## [1] "rdm_Bvt0" "pprdm_Bvt0"## DIC wDIC BPIC wBPIC EffectiveN meanD Dmean minD
## DDM_avt0 -17043 0 -16802 0 240 -17283 -17468 -17523
## LBA_Bvsv -17188 1 -16964 1 224 -17412 -17564 -17636
## RDM_Bvt0 -16648 0 -16403 0 245 -16893 -17054 -17137
## LNRmulMt0 -17129 0 -16846 0 283 -17411 -17609 -17694source("models/DDM/DDM/ddmTZD.R")
source("models/RACE/LBA/lbaB.R")
source("models/RACE/RDM/rdmB.R")
print(load("~/Desktop/emc2/models/DDM/DDM/examples/samples/sPNAS_avt0_full.RData"))
print(load("~/Desktop/emc2/models/RACE/LBA/examples/samples/sPNAS_Bv_sv.RData"))
print(load("~/Desktop/emc2/models/RACE/RDM/examples/samples/rdmPNAS_Bvt0.RData"))
compare_IC(list(DDM_avt0=sPNAS_avt0_full,LBA_Bvsv=sPNAS_Bv_sv,RDM_Bvt0=rdm_Bvt0,
LNRmulMt0=lnr_mu_sElM_t0),subfilter=list(500,2000,1500,2000))Here we add in the version of the winning DDM model that did not use cell coding. We see that there is very little effect on the ICs;
print(load("~/Desktop/emc2/models/DDM/DDM/examples/samples/sPNAS_avt0_full_nocell.RData")) ## [1] "sPNAS_avt0_full_nocell"compare_IC(list(DDM_avt0=sPNAS_avt0_full_nocell,LBA_Bvsv=sPNAS_Bv_sv,RDM_Bvt0=rdm_Bvt0,
LNRmulMt0=lnr_mu_sElM_t0),subfilter=list(500,2000,1500,2000))## DIC wDIC BPIC wBPIC EffectiveN meanD Dmean minD
## DDM_avt0 -17039 0 -16806 0 233 -17271 -17449 -17504
## LBA_Bvsv -17188 1 -16964 1 224 -17412 -17564 -17636
## RDM_Bvt0 -16648 0 -16403 0 245 -16893 -17054 -17137
## LNRmulMt0 -17129 0 -16846 0 283 -17411 -17609 -17694Now let’s check the fit of the winning (E on mu, sigma and t0) LNR model.
# post predict did not use first 2000, so inference based on 5000*3 samples
plot_fit(dat,pplnr_musElMt0,layout=c(2,3),factors=c("E","S"),lpos="right",xlim=c(.25,1.5))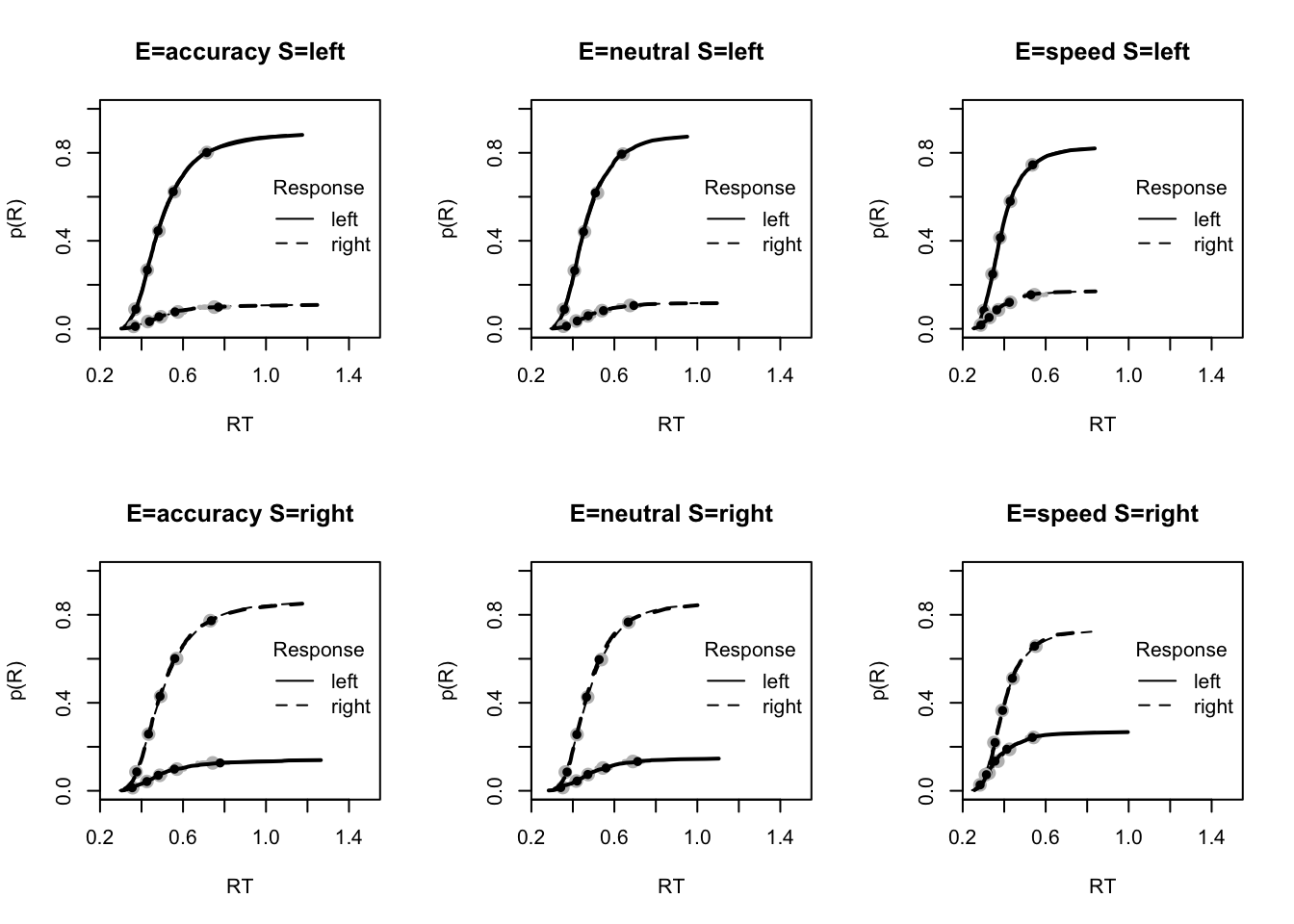
#plot_fits(dat,pplnr_musElMt0,layout=c(2,3),lpos="right")We see this is a very accurate fit! You can look at some more fit plots by using the code below.
pc <- function(d) 100*mean(d$S==d$R)
plot_fit(dat,pplnr_musElMt0,layout=c(2,3),factors=c("E","S"),
stat=pc,stat_name="Accuracy (%)",xlim=c(70,95))
tab <- plot_fit(dat,pplnr_musElMt0,layout=c(2,3),factors=c("E","S"),
stat=function(d){mean(d$rt)},stat_name="Mean RT (s)",xlim=c(0.375,.625))
tab <- plot_fit(dat,pplnr_musElMt0,layout=c(2,3),factors=c("E","S"),xlim=c(0.275,.4),
stat=function(d){quantile(d$rt,.1)},stat_name="10th Percentile (s)")
tab <- plot_fit(dat,pplnr_musElMt0,layout=c(2,3),factors=c("E","S"),xlim=c(0.525,.975),
stat=function(d){quantile(d$rt,.9)},stat_name="90th Percentile (s)")
tab <- plot_fit(dat,pplnr_musElMt0,layout=c(2,3),factors=c("E","S"),
stat=function(d){sd(d$rt)},stat_name="SD (s)",xlim=c(0.1,.355))
tab <- plot_fit(dat,pplnr_musElMt0,layout=c(2,3),factors=c("E","S"),xlim=c(0.375,.725),
stat=function(d){mean(d$rt[d$R!=d$S])},stat_name="Mean Error RT (s)")6.3.3.1 Posterior parameter inference
First, let’s look at the population mean (mu) tests, where we see that the priors all well dominated ;
cilnr_mu_sElM_t0 <- plot_density(lnr_mu_sElM_t0,layout=c(2,3),selection="mu",subfilter=2000)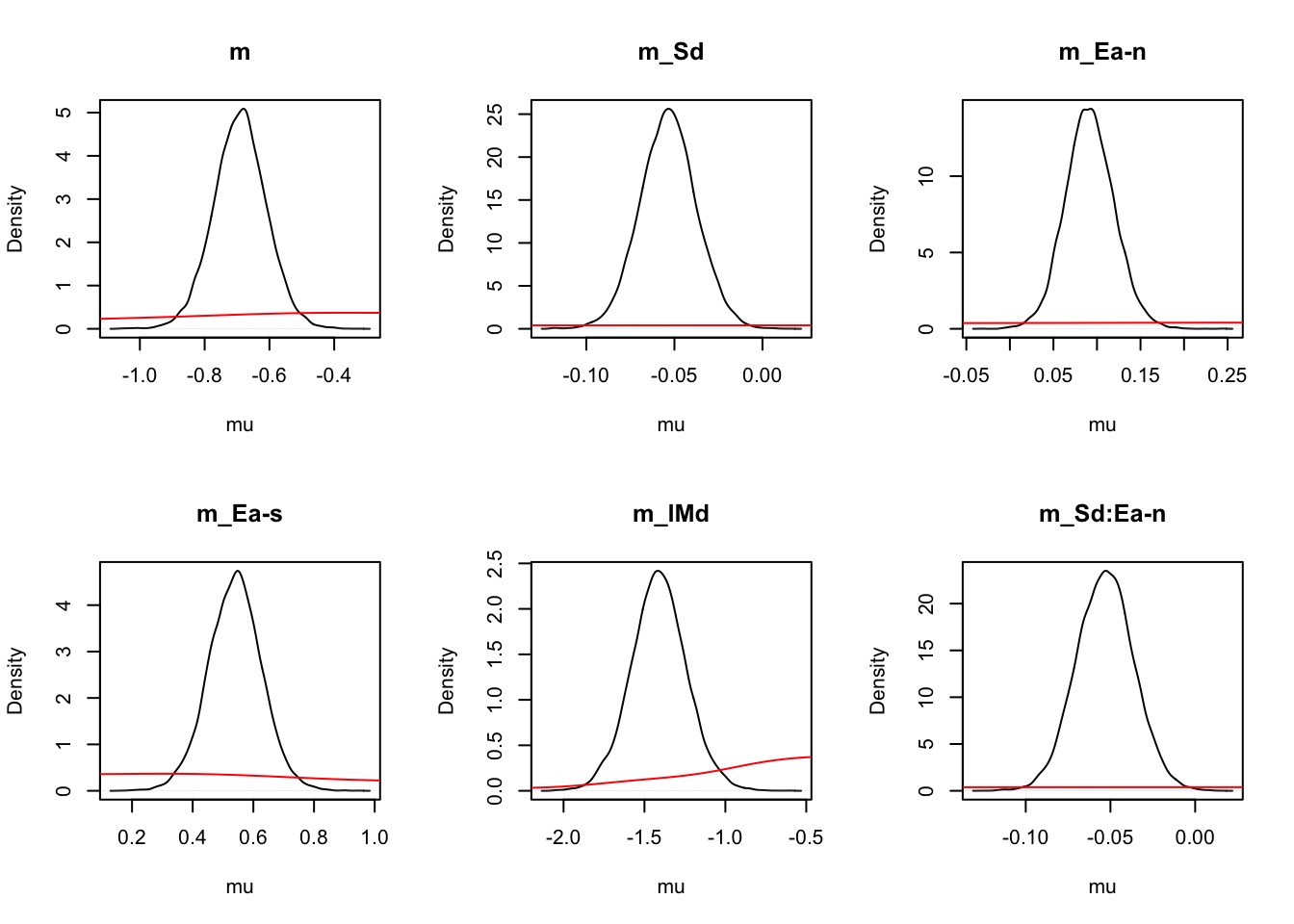
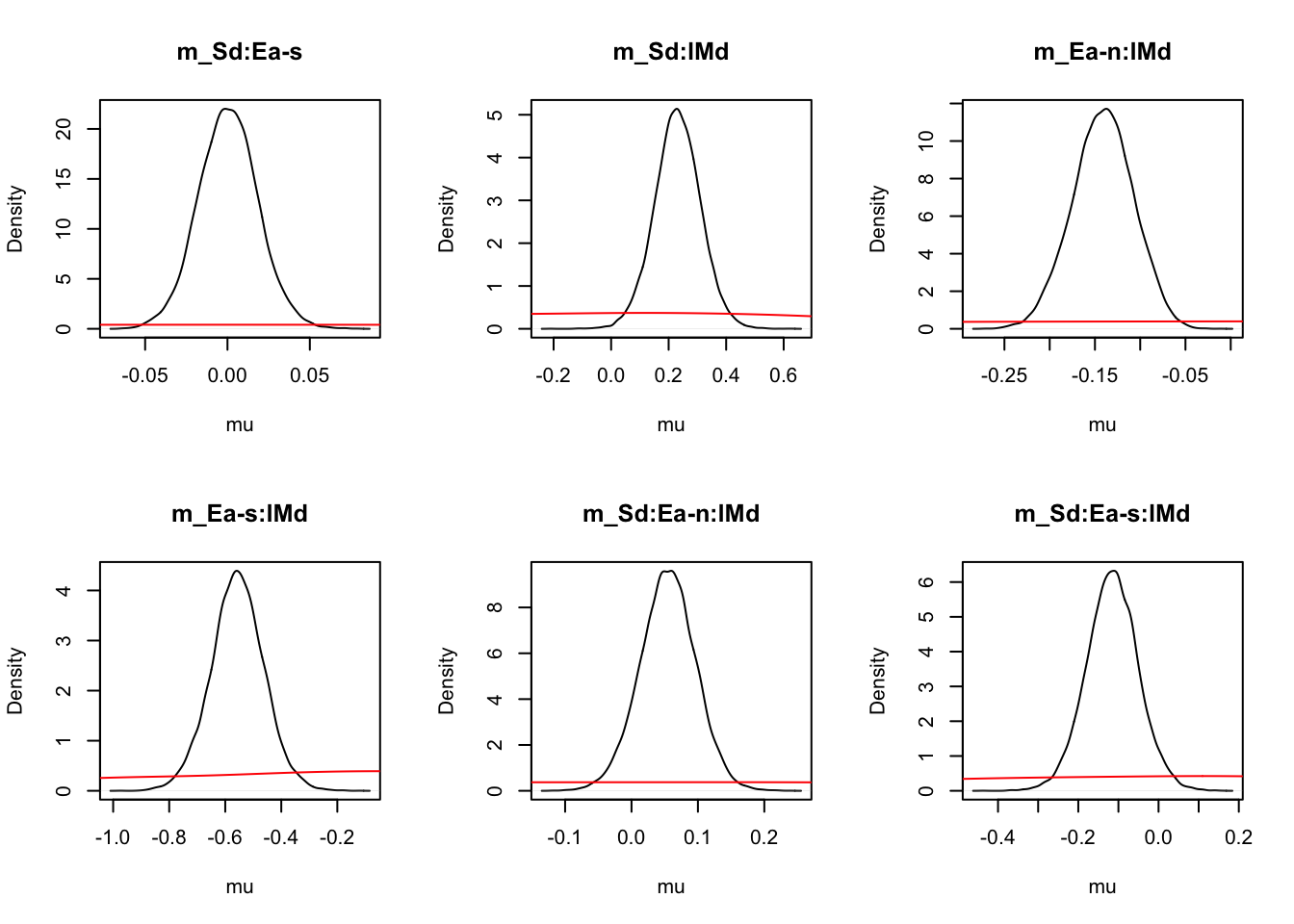
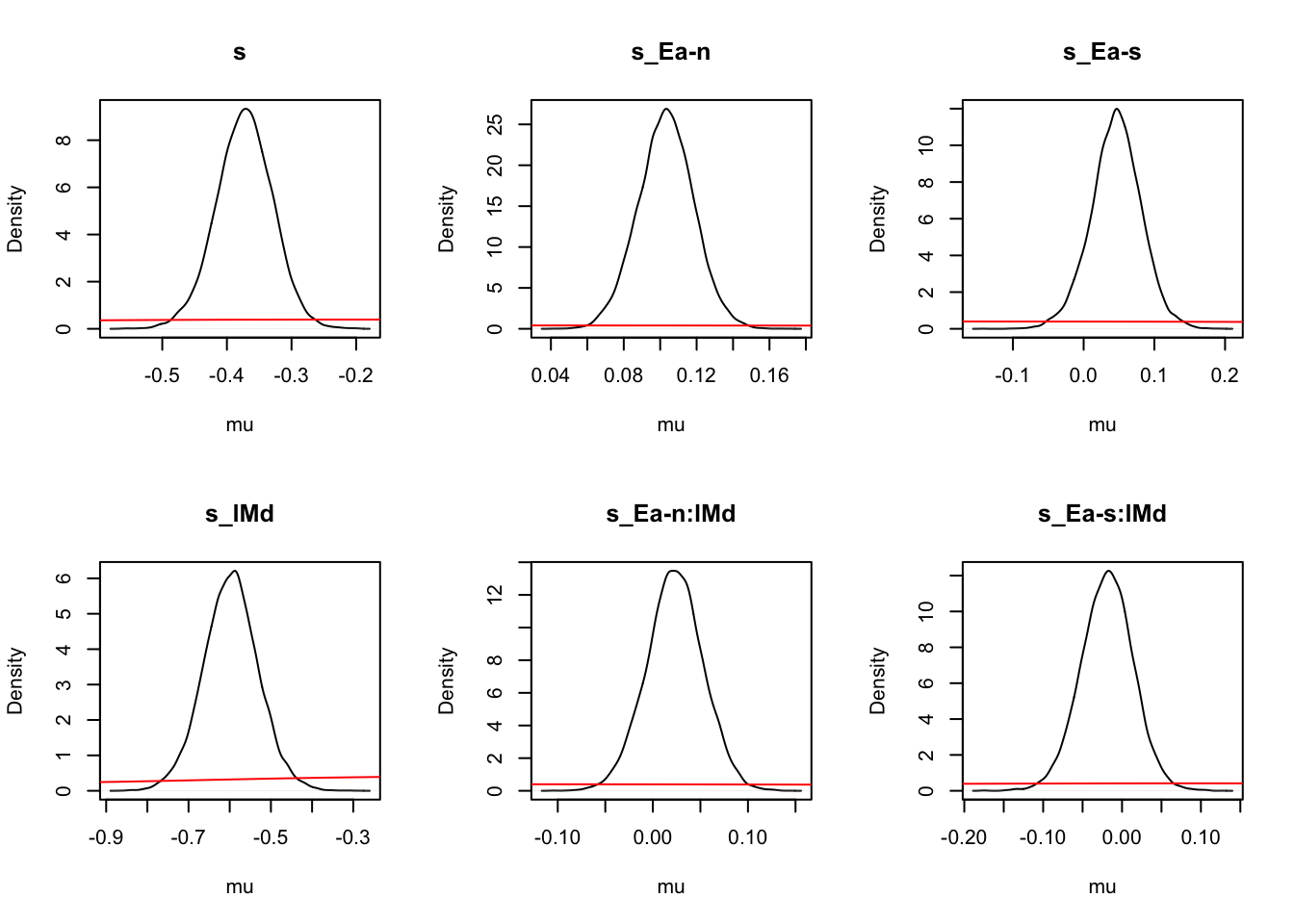
# On the natural scale it is evident this is because the mismatch (FALSE) rates
# are least well updated, due to the fairly low error rates (errors give the
# most information about FALSE rates).
cilnr_mu_sElM_t0_mapped <- plot_density(lnr_mu_sElM_t0,layout=c(2,3),subfilter=2000,
selection="mu",mapped=TRUE)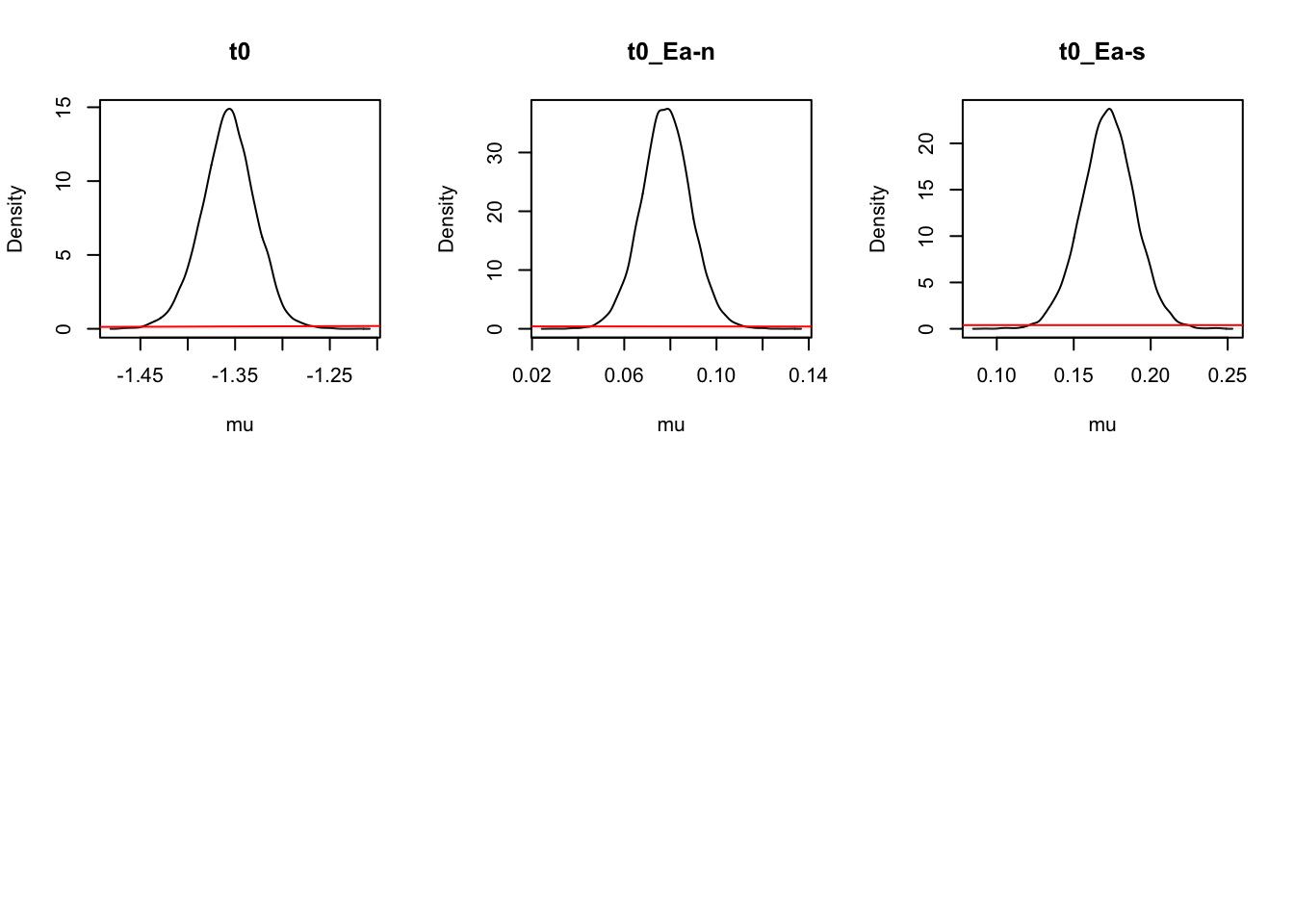
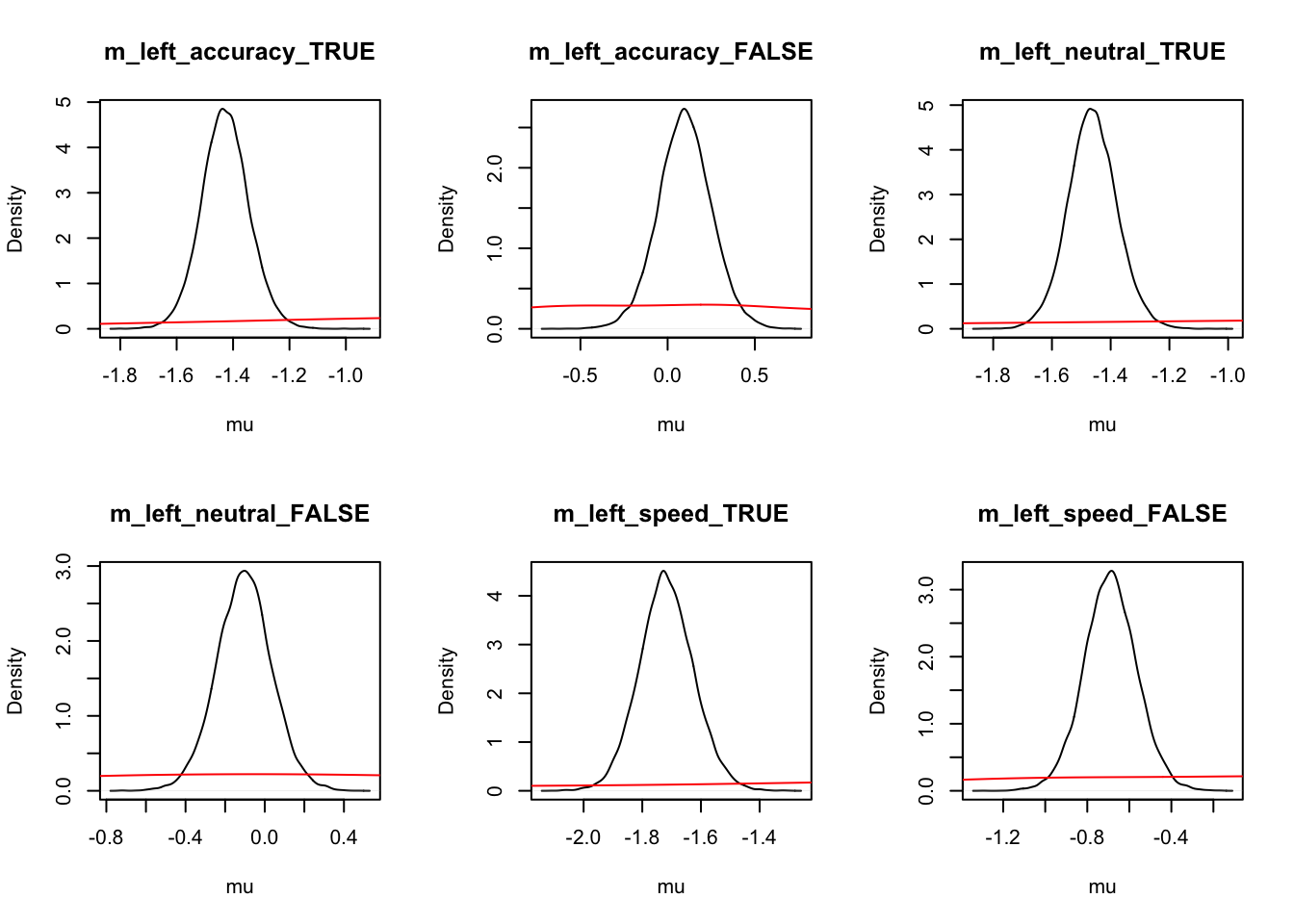
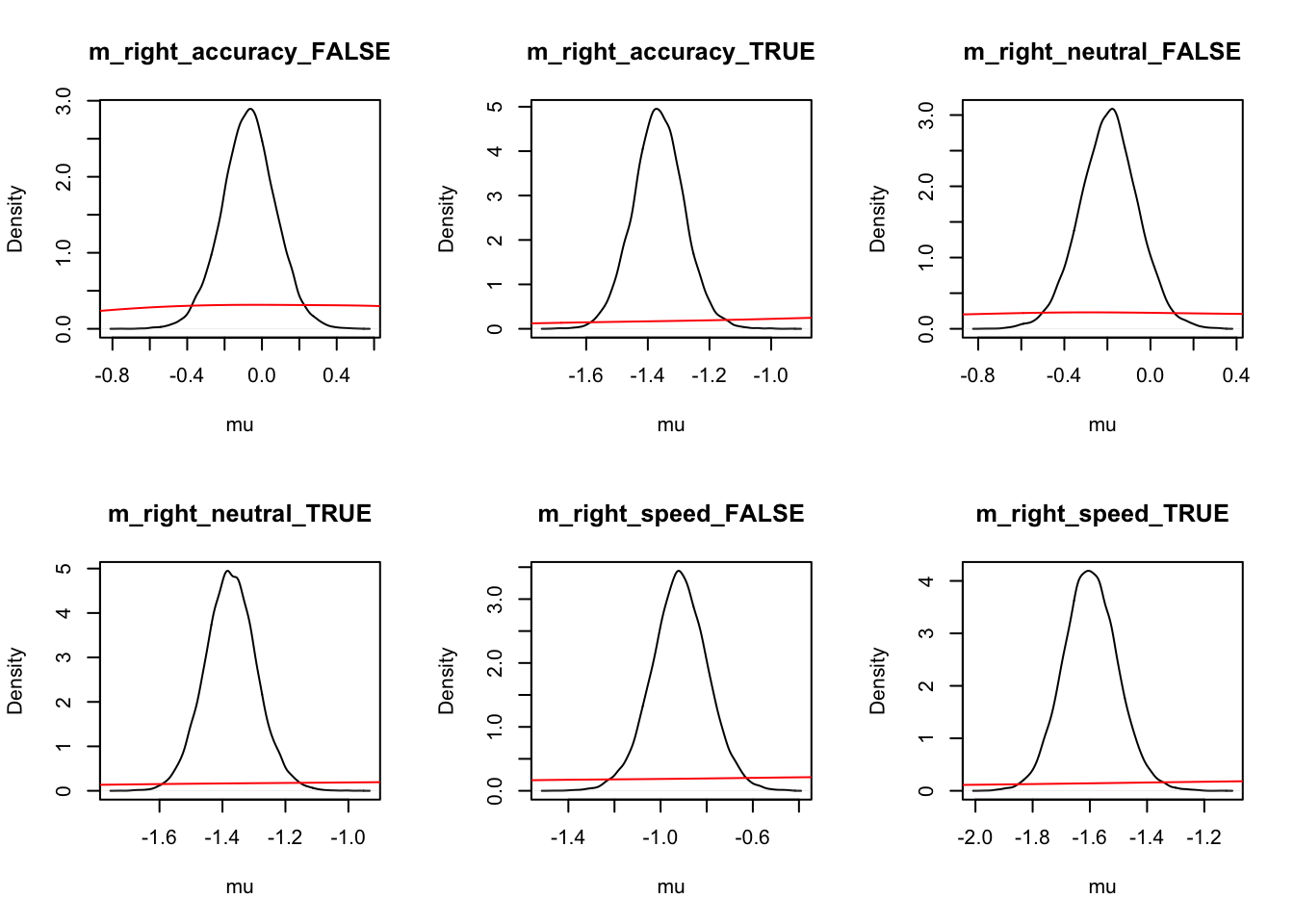
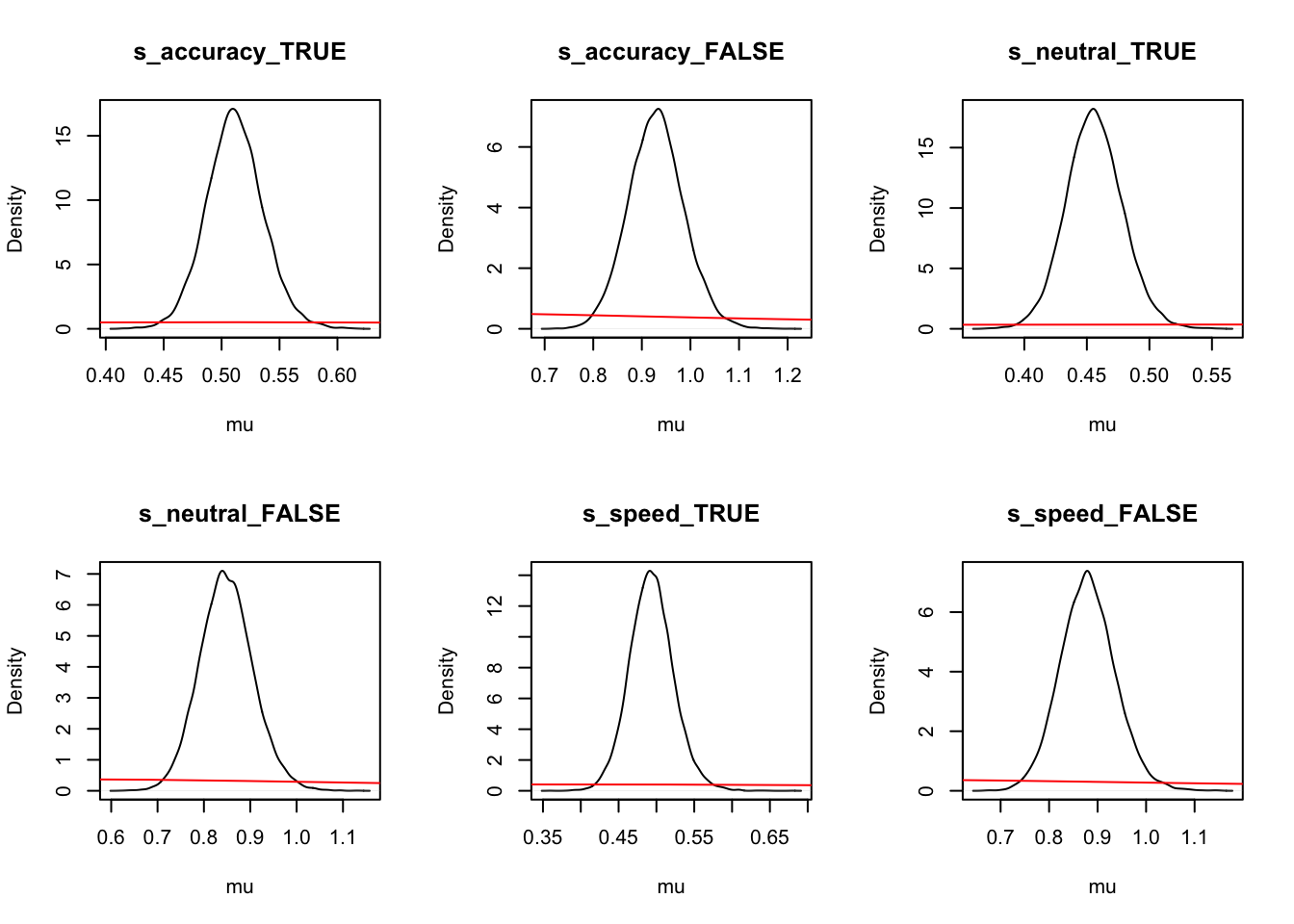
# Looking at parameters both with and without mapping
round(cilnr_mu_sElM_t0,2)## m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n m_Sd:Ea-s m_Sd:lMd m_Ea-n:lMd
## 2.5% -0.85 -0.08 0.04 0.36 -1.75 -0.09 -0.04 0.07 -0.21
## 50% -0.69 -0.05 0.09 0.54 -1.41 -0.05 0.00 0.23 -0.14
## 97.5% -0.53 -0.02 0.15 0.71 -1.06 -0.02 0.04 0.39 -0.08
## m_Ea-s:lMd m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd s s_Ea-n s_Ea-s s_lMd s_Ea-n:lMd
## 2.5% -0.75 -0.03 -0.24 -0.46 0.07 -0.03 -0.73 -0.04
## 50% -0.56 0.05 -0.12 -0.37 0.10 0.05 -0.60 0.02
## 97.5% -0.37 0.14 0.01 -0.29 0.13 0.11 -0.46 0.08
## s_Ea-s:lMd t0 t0_Ea-n t0_Ea-s
## 2.5% -0.09 -1.41 0.06 0.14
## 50% -0.02 -1.36 0.08 0.17
## 97.5% 0.05 -1.30 0.10 0.21round(cilnr_mu_sElM_t0_mapped,2)## m_left_accuracy_TRUE m_left_accuracy_FALSE m_left_neutral_TRUE
## 2.5% -1.59 -0.21 -1.63
## 50% -1.43 0.10 -1.46
## 97.5% -1.26 0.40 -1.29
## m_left_neutral_FALSE m_left_speed_TRUE m_left_speed_FALSE
## 2.5% -0.38 -1.90 -0.94
## 50% -0.10 -1.72 -0.69
## 97.5% 0.17 -1.53 -0.44
## m_right_accuracy_FALSE m_right_accuracy_TRUE m_right_neutral_FALSE
## 2.5% -0.36 -1.53 -0.46
## 50% -0.07 -1.37 -0.19
## 97.5% 0.21 -1.20 0.07
## m_right_neutral_TRUE m_right_speed_FALSE m_right_speed_TRUE s_accuracy_TRUE
## 2.5% -1.53 -1.16 -1.78 0.46
## 50% -1.37 -0.92 -1.60 0.51
## 97.5% -1.21 -0.68 -1.40 0.56
## s_accuracy_FALSE s_neutral_TRUE s_neutral_FALSE s_speed_TRUE s_speed_FALSE
## 2.5% 0.82 0.41 0.74 0.44 0.77
## 50% 0.93 0.46 0.85 0.49 0.88
## 97.5% 1.04 0.50 0.97 0.55 1.00
## t0_accuracy t0_neutral t0_speed
## 2.5% 0.24 0.22 0.20
## 50% 0.26 0.24 0.22
## 97.5% 0.27 0.25 0.23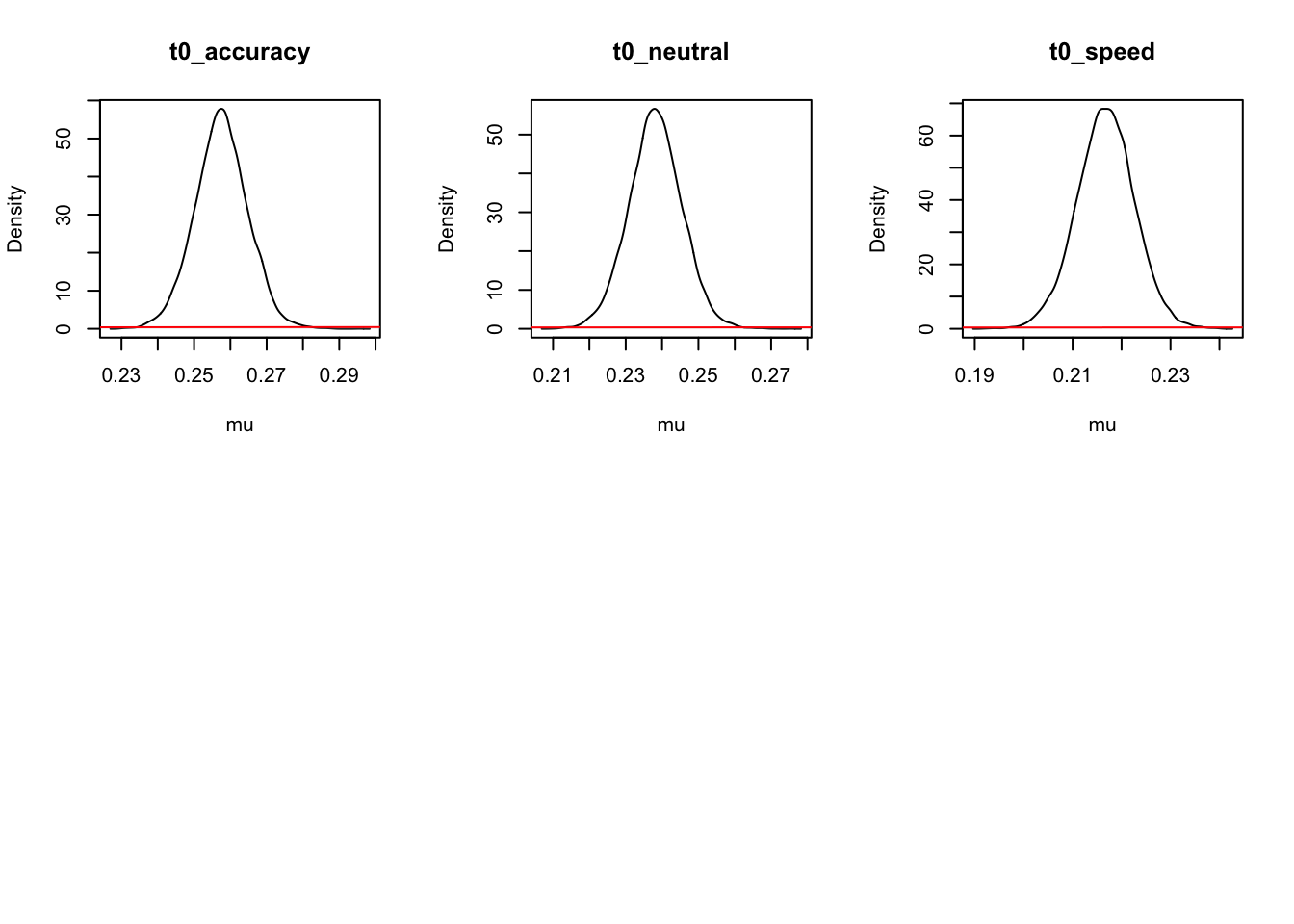
Let’s remember the mapping used;
get_map(lnr_mu_sElM_t0)$m## S E lM m m_Sd m_Ea-n m_Ea-s m_lMd m_Sd:Ea-n m_Sd:Ea-s m_Sd:lMd
## 1 left accuracy TRUE 1 -0.5 0 0 0.5 0.0 0.0 -0.25
## 7 left accuracy FALSE 1 -0.5 0 0 -0.5 0.0 0.0 0.25
## 2 left neutral TRUE 1 -0.5 -1 0 0.5 0.5 0.0 -0.25
## 8 left neutral FALSE 1 -0.5 -1 0 -0.5 0.5 0.0 0.25
## 3 left speed TRUE 1 -0.5 0 -1 0.5 0.0 0.5 -0.25
## 9 left speed FALSE 1 -0.5 0 -1 -0.5 0.0 0.5 0.25
## 4 right accuracy FALSE 1 0.5 0 0 -0.5 0.0 0.0 -0.25
## 10 right accuracy TRUE 1 0.5 0 0 0.5 0.0 0.0 0.25
## 5 right neutral FALSE 1 0.5 -1 0 -0.5 -0.5 0.0 -0.25
## 11 right neutral TRUE 1 0.5 -1 0 0.5 -0.5 0.0 0.25
## 6 right speed FALSE 1 0.5 0 -1 -0.5 0.0 -0.5 -0.25
## 12 right speed TRUE 1 0.5 0 -1 0.5 0.0 -0.5 0.25
## m_Ea-n:lMd m_Ea-s:lMd m_Sd:Ea-n:lMd m_Sd:Ea-s:lMd
## 1 0.0 0.0 0.00 0.00
## 7 0.0 0.0 0.00 0.00
## 2 -0.5 0.0 0.25 0.00
## 8 0.5 0.0 -0.25 0.00
## 3 0.0 -0.5 0.00 0.25
## 9 0.0 0.5 0.00 -0.25
## 4 0.0 0.0 0.00 0.00
## 10 0.0 0.0 0.00 0.00
## 5 0.5 0.0 0.25 0.00
## 11 -0.5 0.0 -0.25 0.00
## 6 0.0 0.5 0.00 0.25
## 12 0.0 -0.5 0.00 -0.25lMd tests match minus mismatch, which is strongly negative, as the match racer is much faster than the mismatch racer.
p_test(x=lnr_mu_sElM_t0,x_name="m_lMd",subfilter=2000)## m_lMd mu
## 2.5% -1.75 NA
## 50% -1.41 0
## 97.5% -1.06 NA
## attr(,"less")
## [1] 1m_Sd tests main effect of stimulus (the mean for (right - left), and indicates a smaller mean (faster processing) for right (-.92) than left (-0.88).
p_test(x=lnr_mu_sElM_t0,x_name="m_Sd",subfilter=2000)## m_Sd mu
## 2.5% -0.08 NA
## 50% -0.05 0
## 97.5% -0.02 NA
## attr(,"less")
## [1] 0.999m_Sd:lMd tests right(match-mismatch) - left(match-mismatch) which is positive, indicating better discrimination for right than left. Rearranging this is also (right_match+left_mismatch) - (left_match+right_mismatch) = right accumulator - left accumulator, so it is also a measure of response bias. The positive value indicates a bias to respond left (i.e., a lesser time for the left racer to finish). These two interpretations cannot be disambiguated from LNR parameter estimates.
p_test(x=lnr_mu_sElM_t0,x_name="m_Sd:lMd",subfilter=2000)## m_Sd:lMd mu
## 2.5% 0.07 NA
## 50% 0.23 0
## 97.5% 0.39 NA
## attr(,"less")
## [1] 0.003m_Ea-n and m_Ea-s measure differences the time overall race time between accuracy and neutral/speed. Both are positive indicating the race time is slowest for accuracy.
p_test(x=lnr_mu_sElM_t0,x_name="m_Ea-n",subfilter=2000)## m_Ea-n mu
## 2.5% 0.04 NA
## 50% 0.09 0
## 97.5% 0.15 NA
## attr(,"less")
## [1] 0.001p_test(x=lnr_mu_sElM_t0,x_name="m_Ea-s",subfilter=2000)## m_Ea-s mu
## 2.5% 0.36 NA
## 50% 0.54 0
## 97.5% 0.71 NA
## attr(,"less")
## [1] 0We can test neutral - speed as follows, showing speed is quicker than neutral;
p_test(x=lnr_mu_sElM_t0,x_name="m_Ea-s",y=lnr_mu_sElM_t0,y_name="m_Ea-n",subfilter=2000)## m_Ea-s m_Ea-n m_Ea-s-m_Ea-n
## 2.5% 0.36 0.04 0.30
## 50% 0.54 0.09 0.45
## 97.5% 0.71 0.15 0.59
## attr(,"less")
## [1] 0We will not look at the remaining interactions here sigma effects. Again recall the map used with;
get_map(lnr_mu_sElM_t0)$s## E lM s s_Ea-n s_Ea-s s_lMd s_Ea-n:lMd s_Ea-s:lMd
## 1 accuracy TRUE 1 0 0 0.5 0.0 0.0
## 7 accuracy FALSE 1 0 0 -0.5 0.0 0.0
## 2 neutral TRUE 1 -1 0 0.5 -0.5 0.0
## 8 neutral FALSE 1 -1 0 -0.5 0.5 0.0
## 3 speed TRUE 1 0 -1 0.5 0.0 -0.5
## 9 speed FALSE 1 0 -1 -0.5 0.0 0.5This gives the overall mean on the natural scale.
p_test(x=lnr_mu_sElM_t0,x_name="sigma",subfilter=2000,x_fun=function(x){exp(x["s"])})## sigma mu
## 2.5% 0.63 NA
## 50% 0.69 0
## 97.5% 0.75 NA
## attr(,"less")
## [1] 0s_Ea-n and s_Ea-s show sigma is credibly greater for accuracy than neutral, but not for speed.
p_test(x=lnr_mu_sElM_t0,x_name="s_Ea-n",subfilter=2000)## s_Ea-n mu
## 2.5% 0.07 NA
## 50% 0.10 0
## 97.5% 0.13 NA
## attr(,"less")
## [1] 0p_test(x=lnr_mu_sElM_t0,x_name="s_Ea-s",subfilter=2000)## s_Ea-s mu
## 2.5% -0.03 NA
## 50% 0.05 0
## 97.5% 0.11 NA
## attr(,"less")
## [1] 0.098Sigma is substantially less for match than mismatch;
p_test(x=lnr_mu_sElM_t0,x_name="s_lMd",subfilter=2000)## s_lMd mu
## 2.5% -0.73 NA
## 50% -0.60 0
## 97.5% -0.46 NA
## attr(,"less")
## [1] 1s_Ea-n:lMd and s_Ea-s:lMd (interactions) show no credible differences in the match vs. mismatch difference between accuracy and neutral or speed, suggesting an additive model would be better (E+lM).
p_test(x=lnr_mu_sElM_t0,x_name="s_Ea-n:lMd",subfilter=2000)## s_Ea-n:lMd mu
## 2.5% -0.04 NA
## 50% 0.02 0
## 97.5% 0.08 NA
## attr(,"less")
## [1] 0.213p_test(x=lnr_mu_sElM_t0,x_name="s_Ea-s:lMd",subfilter=2000)## s_Ea-s:lMd mu
## 2.5% -0.09 NA
## 50% -0.02 0
## 97.5% 0.05 NA
## attr(,"less")
## [1] 0.72Looking at t0 effects, first recall the map used with;
get_map(lnr_mu_sElM_t0)$t0## t0 t0_Ea-n t0_Ea-s
## 1 1 1 0 0
## 39 2 1 -1 0
## 77 3 1 0 -1From the tables we see that t0 for accuracy (0.26s) is credibly greater than for neutral and speed. The following test shows that neutral is credibly greater than speed.
p_test(mapped=TRUE,subfilter=2000,x=lnr_mu_sElM_t0,x_name="t0_neutral",
y=lnr_mu_sElM_t0,y_name="t0_speed")## t0_neutral t0_speed t0_neutral-t0_speed
## 2.5% 0.22 0.20 0.01
## 50% 0.24 0.22 0.02
## 97.5% 0.25 0.23 0.03
## attr(,"less")
## [1] 0p_test(mapped=TRUE,subfilter=2000,x=lnr_mu_sElM_t0,x_name="t0_accuracy",
y=lnr_mu_sElM_t0,y_name="t0_neutral")## t0_accuracy t0_neutral t0_accuracy-t0_neutral
## 2.5% 0.24 0.22 0.01
## 50% 0.26 0.24 0.02
## 97.5% 0.27 0.25 0.02
## attr(,"less")
## [1] 06.3.3.2 Visualising results
As we do above, we’re again going to show some extensions of visualizations, by first extracting the parameter estimates, and then plotting these using ggplot2. Let’s start by extracting the parameters and checking the means of the posterior.
# Make parameter plots
library(tidyverse)
# Get parameter data frame
ps <- parameters_data_frame(lnr_mu_sElM_t0, mapped = TRUE)
head(ps)## m_left_accuracy_TRUE m_left_accuracy_FALSE m_left_neutral_TRUE
## 1 -1.428823 -0.05764236 -1.439785
## 2 -1.364566 -0.15423333 -1.384132
## 3 -1.461074 -0.08887203 -1.524404
## 4 -1.279325 -0.02028169 -1.349081
## 5 -1.466642 -0.07482722 -1.446334
## 6 -1.440625 0.14385488 -1.504156
## m_left_neutral_FALSE m_left_speed_TRUE m_left_speed_FALSE m_right_accuracy_FALSE
## 1 -0.21603425 -1.869920 -0.6965596 -0.12567363
## 2 -0.28652571 -1.757259 -0.6123884 -0.24570387
## 3 -0.22219493 -1.867271 -0.5252956 -0.24281879
## 4 -0.26268193 -1.607256 -0.3120321 -0.05174350
## 5 -0.16574172 -1.767169 -0.6096806 -0.20729331
## 6 -0.09894226 -1.706098 -0.3641162 0.07800542
## m_right_accuracy_TRUE m_right_neutral_FALSE m_right_neutral_TRUE
## 1 -1.410301 -0.22218216 -1.444755
## 2 -1.333929 -0.37537926 -1.346274
## 3 -1.369590 -0.33527778 -1.351359
## 4 -1.317917 -0.15515511 -1.344875
## 5 -1.419014 -0.31421202 -1.399972
## 6 -1.422158 0.01006113 -1.463113
## m_right_speed_FALSE m_right_speed_TRUE s_accuracy_TRUE s_accuracy_FALSE
## 1 -0.9149364 -1.785443 0.5109779 0.9015137
## 2 -0.8849329 -1.670659 0.5510193 0.8764208
## 3 -0.8586790 -1.748387 0.4991804 0.8748535
## 4 -0.6085621 -1.615860 0.4725567 0.9646245
## 5 -0.8988785 -1.709416 0.4927625 0.9169674
## 6 -0.5240941 -1.727374 0.5216469 1.0098260
## s_neutral_TRUE s_neutral_FALSE s_speed_TRUE s_speed_FALSE t0_accuracy t0_neutral
## 1 0.4560181 0.7906519 0.5411936 1.005409 0.2685825 0.2471035
## 2 0.5027792 0.7692438 0.5936935 1.007716 0.2553711 0.2344799
## 3 0.4547302 0.7755225 0.5536948 1.030833 0.2537479 0.2340374
## 4 0.4295109 0.8040917 0.4680630 1.047541 0.2615501 0.2431886
## 5 0.4400312 0.8071623 0.5448357 1.044816 0.2540929 0.2331306
## 6 0.4912248 0.8554349 0.5640184 1.156585 0.2596239 0.2369449
## t0_speed
## 1 0.2451876
## 2 0.2357603
## 3 0.2354981
## 4 0.2349378
## 5 0.2337057
## 6 0.2341568# Calculate means
pmeans <- data.frame(lapply(ps, mean))
pmeans## m_left_accuracy_TRUE m_left_accuracy_FALSE m_left_neutral_TRUE
## 1 -1.426817 0.1132749 -1.457047
## m_left_neutral_FALSE m_left_speed_TRUE m_left_speed_FALSE m_right_accuracy_FALSE
## 1 -0.1163084 -1.718697 -0.6876808 -0.06514239
## m_right_accuracy_TRUE m_right_neutral_FALSE m_right_neutral_TRUE
## 1 -1.363143 -0.2031698 -1.371207
## m_right_speed_FALSE m_right_speed_TRUE s_accuracy_TRUE s_accuracy_FALSE
## 1 -0.9186984 -1.599274 0.5105725 0.9325671
## s_neutral_TRUE s_neutral_FALSE s_speed_TRUE s_speed_FALSE t0_accuracy t0_neutral
## 1 0.4553644 0.8401986 0.4952231 0.884088 0.2573007 0.2373127
## t0_speed
## 1 0.2172329Next, let’s plot the Mu’s
m <- pmeans %>% transmute(Accuracy_left_TRUE = m_left_accuracy_TRUE,
Accuracy_left_FALSE = m_left_accuracy_FALSE,
Accuracy_right_TRUE = m_right_accuracy_TRUE,
Accuracy_right_FALSE = m_right_accuracy_FALSE,
Neutral_left_TRUE = m_left_neutral_TRUE,
Neutral_left_FALSE = m_left_neutral_FALSE,
Neutral_right_TRUE = m_right_neutral_TRUE,
Neutral_right_FALSE = m_right_neutral_FALSE,
Speed_left_TRUE = m_left_speed_TRUE,
Speed_left_FALSE = m_left_speed_FALSE,
Speed_right_TRUE = m_right_speed_TRUE,
Speed_right_FALSE = m_right_speed_FALSE) %>%
pivot_longer(cols = everything(),
names_to = c("Emphasis", "Stimulus", "Match"),
names_pattern = "(.*)_(.*)_(.*)",
values_to = "m")
m## # A tibble: 12 x 4
## Emphasis Stimulus Match m
## <chr> <chr> <chr> <dbl>
## 1 Accuracy left TRUE -1.43
## 2 Accuracy left FALSE 0.113
## 3 Accuracy right TRUE -1.36
## 4 Accuracy right FALSE -0.0651
## 5 Neutral left TRUE -1.46
## 6 Neutral left FALSE -0.116
## 7 Neutral right TRUE -1.37
## 8 Neutral right FALSE -0.203
## 9 Speed left TRUE -1.72
## 10 Speed left FALSE -0.688
## 11 Speed right TRUE -1.60
## 12 Speed right FALSE -0.919m_plot <- ggplot(data = m, aes(Emphasis, m, col = Match)) +
geom_line(aes(group = Match), lty = "dashed", lwd = 1) +
geom_point(size = 4, shape = 19) +
facet_grid(Stimulus ~ .) +
ylim(-2, 1) +
theme_minimal() + theme(text = element_text(size = 15))
m_plot
Now, plotting sigma. We can really start to visualise the effects we found to be credible above.
s <- pmeans %>% transmute(Accuracy_TRUE = s_accuracy_TRUE,
Accuracy_FALSE = s_accuracy_FALSE,
Neutral_TRUE = s_neutral_TRUE,
Neutral_FALSE = s_neutral_FALSE,
Speed_TRUE = s_speed_TRUE,
Speed_FALSE = s_speed_FALSE) %>%
pivot_longer(cols = everything(),
names_to = c("Emphasis", "Match"),
names_pattern = "(.*)_(.*)",
values_to = "s")
s## # A tibble: 6 x 3
## Emphasis Match s
## <chr> <chr> <dbl>
## 1 Accuracy TRUE 0.511
## 2 Accuracy FALSE 0.933
## 3 Neutral TRUE 0.455
## 4 Neutral FALSE 0.840
## 5 Speed TRUE 0.495
## 6 Speed FALSE 0.884s_plot <- ggplot(data = s, aes(Emphasis, s, col = Match)) +
geom_line(aes(group = Match), lty = "dashed", lwd = 1) +
geom_point(size = 4, shape = 19) +
ylim(0.3, 1) +
theme_minimal() + theme(text = element_text(size = 15))
s_plot
Finally, plotting non-decision time;
t0 <- pmeans %>% transmute(Accuracy = t0_accuracy,
Neutral = t0_neutral,
Speed = t0_speed) %>%
pivot_longer(cols = everything(),
names_to = c("Emphasis"),
names_pattern = "(.*)",
values_to = "t0")
t0## # A tibble: 3 x 2
## Emphasis t0
## <chr> <dbl>
## 1 Accuracy 0.257
## 2 Neutral 0.237
## 3 Speed 0.217t0_plot <- ggplot(data = t0, aes(Emphasis, t0)) +
geom_line(aes(group = 1), lty = "dashed", lwd = 1) +
geom_point(size = 4, shape = 19) +
ylim(0.18, 0.3) +
theme_minimal() + theme(text = element_text(size = 15))
t0_plot
6.4 Conclusion (important)
Despite us running several different designs across a number of different models, we’re seeing clear patterns. In many applications, it may not be useful to try all these different model fits - instead we may focus on one model with many different competing designs.
In these examples, we want to make the point about inference. Making inference from models can be difficult, especially when different designs produce different explanations. For this, there are several methods for drawing stronger inference. First, we should do model selection to rule out other models – for example, if a v model won in these examples, then we would seriously need to reconsider our inference. Secondly, we want to look at the effects across the designs and models.
In the PNAS data from Forstmann et al., (2008), we hypothesized a threshold effect from emphasis. We then fit a variety of models, where the B only model was not the winner. Instead, we regularly found that B, v and t0 effects were preferenced to better explain the data. Across all of these winning models, we regularly found evidence for a difference in threshold parameters. Evidently, it appears that our hypothesis was supported, however, it is important to contextualise this finding within.
By contextualising this finding, we refer to discussions about different models and parameterisations, as well as thinking about the winning model (and parameter differences) in the context of any misfit. We may see very slight differences between parameterisations of models, so in these instances, we need to think about our research question. If the same effect is commonly observed across these very similar models, then we have more evidence on which to base our conclusion. However, if the parameterisations varied such that this was not the case, then we may be less confident in our inference.
Evidently, it is highly important to consider and test a variety of explanations, as well as discussing your inference within the context of the models and misfit.