5.1 Subspaces

We begin by considering our first question, about when subsets of a vector space stay invariant under the operations of our vector space, and define a linear subspace.

Definition 5.1: (Linear Subspace)

Let \(W\) be a vector space over \(\mathbb{F}\). A subset \(V\subseteq W\) is called a linear subspace of \(W\) if and only if the following three conditions hold:

1. \(V\neq \emptyset\), i.e., \(V\) is non-empty.

2. for all \(v,w\in V\), we have \(v+w\in V\), i.e., \(V\) is closed under addition.

3. for all \(\lambda\in \mathbb{F}\), \(v\in V\), we have \(\lambda v\in V\), i.e., \(V\) is closed under multiplication by scalars.

Note that this definition is equivalent to saying that \(V\) is itself a vector space over \(\mathbb{F}\) under the same operations as \(W\). The proof of this fact is left as an exercise.

When referring to linear subspaces we will often just say ‘subspace’ for short.

In order to determine whether a subset is a subspace, we must show that the subset satisfies all of the properties from the definition.

Example 5.2:

For any vector space \(W\) here are two trivial examples: \(V=\{\mathbf{0}\}\), the set containing only \(\mathbf{0}\), is a subspace, and \(V=W\) itself satisfies the conditions for a linear subspace.

Example 5.3:

Consider the real vector space \(\mathbb{C}^n\) over \(\mathbb{R}\). Then \(\mathbb{R}^n\) is a subspace since

1. \(\mathbb{0}\in \mathbb{R}^n\), so \(\mathbb{R}^n\) is non-empty.

2. If \(u,v \in \mathbb{R}^n\) then \(u+v \in \mathbb{R}^n\).

3. If \(v\in \mathbb{R}^n\) and \(\lambda \in \mathbb{R}\) then \(\lambda v \in \mathbb{R}^n\).

Exercise 5.4:

Consider the complex vector space \(\mathbb{C}^n\) over \(\mathbb{C}\). Is \(\mathbb{R}^n\) a subspace?

Example 5.5:

Let \(v\in \mathbb{R}^n\) be non-zero vector and let us take the set of all multiples of \(v\), i.e., \[V:=\{\lambda v: \lambda\in\mathbb{R}\}\] We show that this is a subspace by checking each of the conditions in the definition:

1. We have that \(V\neq \emptyset\), since, for example, \(v\in V.\)

2. If \(x,y\in V\) then there are \(\lambda_1,\lambda_2\in\mathbb{R}\) such that \(x=\lambda_1 v\) and \(y=\lambda_2 v\) (this follows from the definition of \(V\)). Hence \(x+y=\lambda_1v+\lambda_2v=(\lambda_1+\lambda_2)v\in V\), since \(\lambda_1 +\lambda_2 \in R.\)

3. If \(x\in V\) and \(\lambda \in \mathbb{R}\), then there exists \(\lambda_1 \in \mathbb{R}\) such that \(x=\lambda_1 v\) and \(\lambda x=\lambda\lambda_1v\in V\), since \(\lambda \lambda_1 \in \mathbb{R}\).

In geometric terms \(V\) is a straight line through the origin, e.g., if \(n=2\) and \(v=(1,1)\), then \(V\) is just the diagonal in \(\mathbb{R}^2\), as shown in Figure 5.1.

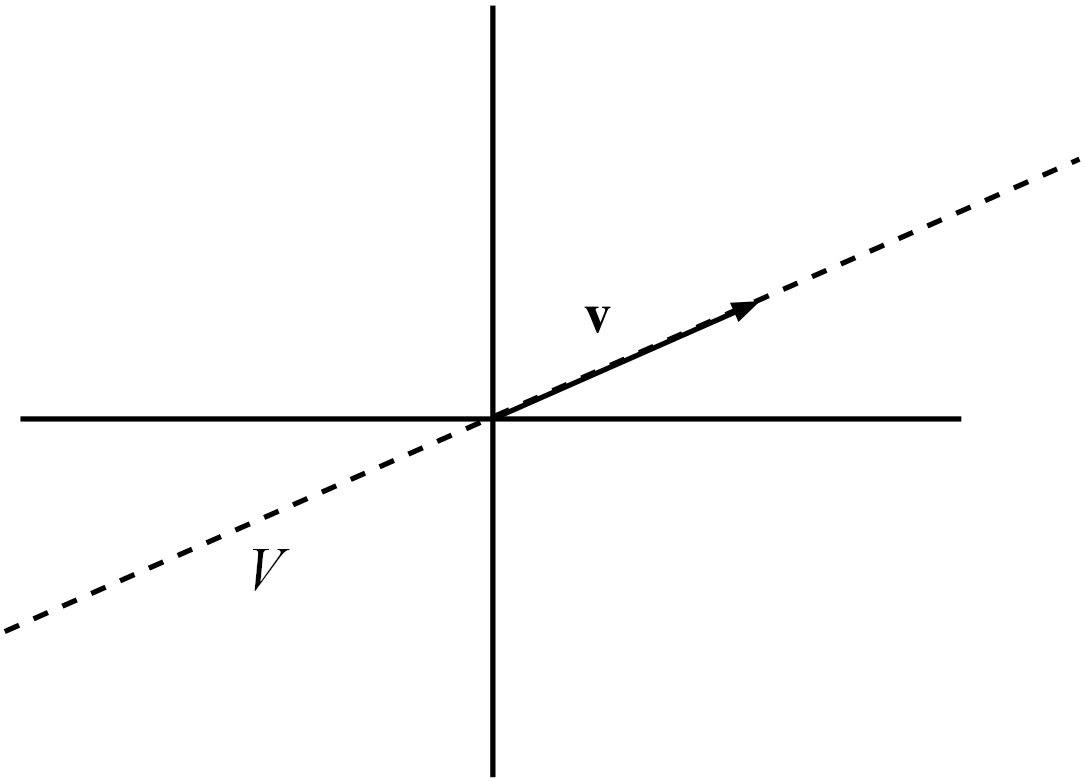
Figure 5.1: The subspace \(V\subseteq\mathbb{R}^2\) (a line) generated by a vector \(v \in \mathbb{R}^2\).

Theorem 5.6:

Let \(A\in M_{m,n}(\mathbb{R})\). Then \(S(A,\mathbf{0})\subseteq \mathbb{R}^n\) is a linear subspace.

Before proving this theorem let us consider in detail what this will mean for a homogeneous set of linear equations \(Ax=\mathbf{0}\):

• There is always at least one solution, namely \(x=\mathbf{0}\).

• The sum of any two solutions is again a solution.

• Any multiple of a solution is again a solution.

Proof.

We check the conditions of the definition and find that

1. \(S(A,\mathbf{0})\) is nonempty since \(A\mathbf{0}=\mathbf{0}\), hence \(\mathbf{0}\in S(A,\mathbf{0})\),

2. if \(x,y\in S(A,\mathbf{0})\), then \(A(x+y)=Ax+Ay=\mathbf{0}+\mathbf{0}=\mathbf{0}\), hence \(x+y\in S(A,\mathbf{0})\), and finally

3. if \(x\in S(A,\mathbf{0})\) then \(A(\lambda x)=\lambda Ax=\lambda \mathbf{0}=\mathbf{0}\) and therefore \(\lambda x\in S(A,\mathbf{0})\).

□

Example 5.7:

Consider the set \(V\) of vectors in \(\mathbb{R}^2\) of the form \((x,1)\), i.e. the second coordinate being fixed as \(1\). Is this a linear subspace? To answer this question we have to check the three properties in the definition:

1. Since, for instance, \((1,1)\in V\) we have \(V\neq\emptyset\).

2. Choose two elements in \(V\), e.g., \((1,1)\) and \((2,1)\), then \((1,1)+(2,1)=(3,2)\notin V\), hence the condition (ii) is not fulfilled and \(V\) is not a subspace.

Note that as soon as one of the three conditions of the definition fails then this set cannot possibly satisfy the definition, and so we do not need to check the third condition.

Example 5.8:

Now, for comparison to the previous example, choose \(V=\{(x,0) : x\in\mathbb{R}\}\). Then:

1. \(V\neq\emptyset\), since \((0.0)\in V\).

2. For any \((x,0),(y,0)\in V\) we have that \((x,0)+(y,0)=(x+y,0)\in V\) and so \(V\) is closed under addition.

3. For any \((x,0)\in V\) and \(\lambda \in \mathbb{R}\) we have that \(\lambda(x,0)=(\lambda x,0)\in V\), so \(V\) is closed under scalar multiplication.

Hence \(V\) satisfies all three conditions of the definition and is a linear subspace.

Exercise 5.9:

Consider the vector space \(\mathbb{C}^3\) over \(\mathbb{C}\). Is \(V=\left\{(x, iy, 0): x,y \in \mathbb{R} \right\}\) a linear subspace?

Exercise 5.10:

Consider the vector space \(\mathbb{C}^3\) over \(\mathbb{R}\). Is \(V=\left\{(x, iy, 0): x,y \in \mathbb{R} \right\}\) a linear subspace?

The following theorem provides a quick way of showing that something is not a linear subspace.

Theorem 5.11:

Let \(V\) be a linear subspace of a vector space \(W\). Then we must have \(\mathbf{0}\in V\).

The proof is left as an exercise. This theorem means that we can immediately say a subset is not a subspace if it does not contain the zero vector.

Exercise 5.12:

Does the converse hold? That is if \(0 \in V\) must \(V\) be a subspace?

Click for solution

No, this is not the case, for example \(V=\{(x, x^2): x \in \mathbb{R}\}\) is not a subspace of \(\mathbb{R}^2\) as \((1,1)\in V\) but \(2(1,1)=(2,2) \notin V\). However we do have that \((0,0)\in V\).

This means we can use Theorem 5.11 as a way to prove something is not a subspace, but it does not help us to show that something is a subspace.