5.2 Spans
Example 5.5 is related to the second question we asked at the start of the chapter. Here we fixed one vector and took all its multiples, and that gave us a straight line. Generalising this idea to two and more vectors and taking sums as well into account leads us to the following definition:
Let \(V\) be a vector space over \(\mathbb{F}\) and \(x_1,x_2,\cdots ,x_k\in V\) be \(k\) vectors. The span of this set of vectors is defined as \[\operatorname{span}_\mathbb{F}\{x_1,x_2,\ldots, x_k\}:=\{\lambda_1x_1+\lambda_2x_2+\cdots \lambda_kx_k : \lambda_1,\lambda_2,\cdots ,\lambda_k\in\mathbb{F}\}.\]
When \(\mathbb{F}=\mathbb{R}\) we call this an \(\mathbb{R}\)-span and when \(\mathbb{F}=\mathbb{C}\) we call this a \(\mathbb{C}\)-span.If the field that we are using is clear from context then we will often just say span, and omit the \(\mathbb{F}\) from the subscript.
We will call an expression like \[\lambda_1x_1+\lambda_2x_2+\cdots \lambda_kx_k\] a linear combination of the vectors \(x_1, \cdots ,x_k\) with coefficients \(\lambda_1, \cdots ,\lambda_k\). We may specify where the scalars in our linear combination come from by referring to an \(\mathbb{R}\)-linear combination (meaning that the scalars come from \(\mathbb{R}\)) or a \(\mathbb{C}\)-linear combination (meaning that the scalars come from \(\mathbb{C}\)).
So the span of a set of vectors is the set generated by taking all linear combinations of the vectors from the set. We have seen one example already in Example 5.5, where we took linear combinations of just one vector, but if we take for instance two vectors \(x_1,x_2\in\mathbb{R}^3\), and if they do point in different directions, then their span is a plane through the origin in \(\mathbb{R}^2\). The geometric picture associated with a span in Euclidean space is that it is a generalisation of lines and planes through the origin in \(\mathbb{R}^2\) and \(\mathbb{R}^3\) to \(\mathbb{R}^n\).
Consider the vector space \(\mathbb{R}^3\) over \(\mathbb{R}\). Let \(x_1=\begin{pmatrix} 1\\0\\0\end{pmatrix}\) and \(x_2=\begin{pmatrix}0\\1\\0\end{pmatrix}\). Then \[\operatorname{span}\{x_1,x_2\} =\left\{\lambda_1 \begin{pmatrix} 1\\0\\0\end{pmatrix}+\lambda_2\begin{pmatrix} 0\\1\\0\end{pmatrix}:\lambda_1,\lambda_2 \in \mathbb{R} \right\} =\left\{\begin{pmatrix}\lambda_1\\ \lambda_2\\ 0\end{pmatrix}:\lambda_1,\lambda_2 \in \mathbb{R} \right\}. \]
So in this case the span of these two vectors gives us the \(xy\)-plane.It turns out that Example 5.5 being a subspace was not a fluke; a span of vectors always gives us a subspace.
For a vector space \(V\) over \(\mathbb{F}\) and \(x_1,x_2,\cdots x_k\in V\) then \(\operatorname{span}\{x_1,x_2,\cdots , x_k\}\) is a linear subspace of \(V\).
The set is clearly non-empty. Now assume \(v,w\in \operatorname{span}\{x_1,x_2,\cdots , x_k\}\), i.e., there exist \(\lambda_1,\lambda_2,\cdots,\lambda_k\in \mathbb{F}\) and \(\mu_1,\mu_2,\cdots,\mu_k\in\mathbb{F}\) such that \[v=\lambda_1x_1+\lambda_2x_2+\cdots +\lambda_kx_k\quad \text{and} \quad w=\mu_1x_1+\mu_2x_2+\cdots +\mu_kx_k .\] Therefore \[v+w=(\lambda_1+\mu_1)x_1+(\lambda_2+\mu_2)x_2+\cdots +(\lambda_k+\mu_k)x_k\in \operatorname{span}\{x_1,x_2,\cdots , x_k\} ,\] and \[\lambda v=\lambda \lambda_1x_1+\lambda\lambda_2x_2+\cdots+\lambda\lambda_kx_k\in \operatorname{span}\{x_1,x_2,\cdots , x_k\} ,\] for all \(\lambda\in\mathbb{F}\). So \(\operatorname{span}\{x_1,x_2,\cdots , x_k\}\) is closed under addition and multiplication by numbers, hence it is a subspace.
□
In fact we have that \(\operatorname{span}\{x_1,x_2,\cdots , x_k\}\) will be the smallest linear subspace containing the vectors \(x_1,x_2,\cdots , x_k \in \mathbb{R}^n.\) The proof of this is left as an exercise.
We may want to check if a certain vector is in a given span. To do this we will once again need to solve systems of linear equations.
Consider \(\mathbb{R}^n\) over \(\mathbb{R}\) and let \(V=\operatorname{span}\{x_1,x_2\}\subseteq\mathbb{R}^n\) with \(x_1=(1,1,1)\) and \(x_2=(2,0,1)\).
The span is the set of all vectors of the form \[\lambda_1 x_1+\lambda_2x_2 ,\] where \(\lambda_1,\lambda_2\in\mathbb{R}\) can take arbitrary values. For instance if we set \(\lambda_2=0\) and let \(\lambda_1\) run through \(\mathbb{R}\) we obtain the line through \(x_1\), similarly by setting \(\lambda_1=0\) we obtain the line through \(x_2\). The set \(V\) is now the plane containing these two lines, as shown in Figure 5.2. To check if a vector is in this plane, i.e, in \(V\), we have to see if it can be written as a linear combination of \(x_1\) and \(x_2\).
Let us check if \((1,0,0)\in V\). We have to find \(\lambda_1,\lambda_2\) such that \[(1,0,0)=\lambda_1x_1+\lambda_2x_2=(\lambda_1+2\lambda_2, \lambda_1, \lambda_1+\lambda_2) .\] This gives us three equations, one for each component: \[1=\lambda_1+2\lambda_2 ,\quad \lambda_1=0 ,\quad \lambda_1+\lambda_2=0 .\] From the second equation we get \(\lambda_1=0\), then the third equation gives \(\lambda_2=0\) but the first equation then becomes \(1=0\), hence there is a contradiction and \((1,0,0)\notin V\).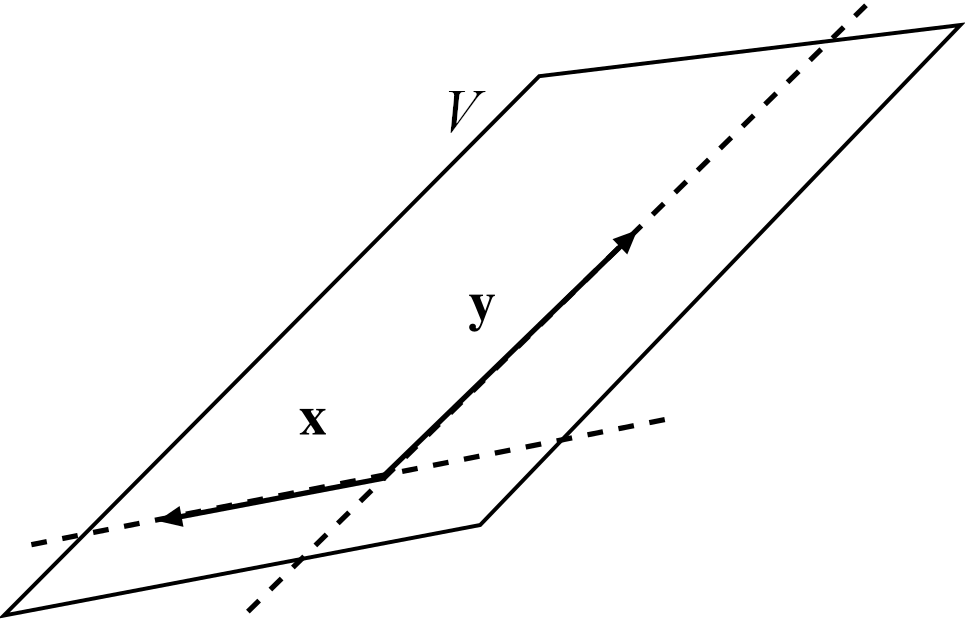
Figure 5.2: The subspace \(V\subseteq\mathbb{R}^3\) (a plane) generated by vectors \(x, y \in \mathbb{R}^3\). It contains the lines through \(x\) and \(y\), and is spanned by these.
Note that when checking whether a vector is in a span, we are solving a system of linear equations to find the coefficients \(\lambda_i\).To do this, we can make use of the methods we developed in Chapter 3.
Consider the vector space \(\mathbb{C}^2\) over \(\mathbb{C}\) and the subspace \(V=\operatorname{span}_\mathbb{C}\left\{\begin{pmatrix}i\\1\end{pmatrix}, \begin{pmatrix} 2\\1+i \end{pmatrix}\right\}\). We want to see if \(v=\begin{pmatrix}-3\\-1\end{pmatrix} \in V\), so we want to see if there exist \(\lambda_1, \lambda_2 \in \mathbb{C}\) such that \(v=\lambda_1\begin{pmatrix}i\\1\end{pmatrix}+\lambda_2 \begin{pmatrix} 2\\1+i \end{pmatrix}\).
This means we want to solve the system \[\begin{align*} i\lambda_1+ 2\lambda_2&=-3\\ \lambda_1+(1+i)\lambda_2&=-1. \end{align*}\] This gives the augmented matrix \[\begin{pmatrix}i&2&-3 \\1&1+i&2\end{pmatrix}.\] Performing row operations (multiplying row 1 by \(-i\) then subtracting row 1 from row 2) gives \[\begin{pmatrix}1&-2i&3i \\0&1+i&-1-3i\end{pmatrix},\] then back-substitution gives \(\lambda_2=-1\) and \(\lambda_1=2i\lambda_2+3i=i\).It also turns out that we can write any subspace of a vector space as a span of a finite set of vectors. We refer to such sets as spanning sets.
Note that this means that if we have a spanning set for a linear subspace, then we can construct any vector in the subspace from our spanning set and that taking linear combinations of our spanning set will give us only the vectors in our subspace and no others.