2.1 Operations on complex numbers

We can define addition and multiplication on the set of complex numbers in a natural way.

Definition 2.2: (Addition and multiplication of complex numbers)

Let $z_1=x_1+\mathrm{i}y_1$ and $z_2=x_2+\mathrm{i}y_2 \in \mathbb{C}$. Then we define $$z_1+z_2:=x_1+x_2+\mathrm{i}(y_1+y_2)$$ and $$z_1z_2:=x_1x_2-y_1y_2+\mathrm{i}(x_1y_2+x_2y_1).$$

Notice that the definition of multiplication just follows if we multiply $z_1z_2$ like normal numbers and then substitute in $\mathrm{i}^2=-1$: $$\begin{aligned} z_1z_2&=(x_1+\mathrm{i}y_1)(x_2+\mathrm{i}y_2)\\&=x_1x_2+\mathrm{i}x_1y_2+\mathrm{i}y_1x_2+\mathrm{i}^2y_1y_2\\ &=x_1x_2-y_1y_2+\mathrm{i}(x_1y_2+x_2y_1). \end{aligned}$$

A complex number is defined by a pair of real numbers, and so we can associate a vector in $\mathbb{R}^2$ with every complex number $z=x+\mathrm{i}y$ by $v(z)=( x, y)$. In other words, we associate a point in the plane with every complex number, and we then call this the complex plane, which is illustrated in Figure 2.1. For example, if $z=x$ is real, then the corresponding vector lies on the $x$-axis. If $z=\mathrm{i}$, then $v(\mathrm{i})=(0,1)$, and any purely imaginary number $z=\mathrm{i}y$ lies on the $y$-axis. So we sometimes call these the real and imaginary axes , respectively.

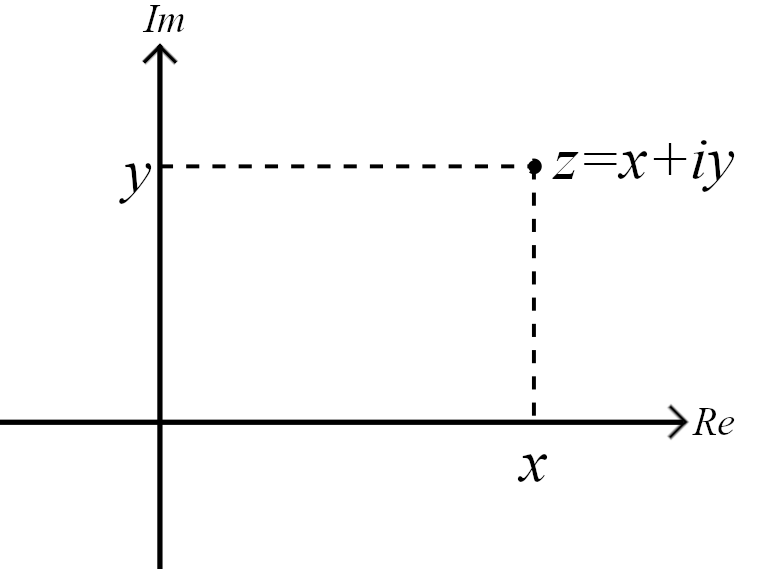
Figure 2.1: Complex numbers as points in the plane: with the complex number $z=x+\mathrm{i} y$ we associate the point $\mathbf(v)(z)= (x,y) \in \mathbb{R}^2$.

The addition of vectors corresponds to addition of complex numbers as we have defined it, that is $$v(z_1+z_2)=v(z_1)+v(z_2) ,$$ but will seldom use the notation $v(z)$ in favour of just $z$.

Multiplication of complex numbers is a new operation which had no correspondence for vectors. Therefore we want to study the geometric interpretation of multiplication a bit more carefully. To this end let us first introduce another operation on complex numbers, complex conjugation .

Definition 2.3:

For $z=x+\mathrm{i}y$ we define the complex conjugate of $z$ to be $$\bar z=x-\mathrm{i}y .$$

This corresponds to reflection across the $x$-axis. Using complex conjugation we find $$z\bar z=(x+\mathrm{i}y)(x-\mathrm{i}y)=x^2-\mathrm{i}xy+\mathrm{i}yx+y^2=x^2+y^2=\lVert v(z)\rVert^2.$$ So we can find the norm of the vector representation of $z$ by using the complex conjugate. In the complex number setting we usually call this the modulus of $z$ and denote it by $$\lvert z\rvert:=\sqrt{\bar z z}=\sqrt{x^2+y^2} .$$

Complex conjugation is useful when dividing complex numbers: for $z\neq 0$ we have $$\frac{1}{z}=\frac{\bar z}{\bar z z } =\frac{\bar z}{\lvert z\rvert^2}=\frac{x}{x^2+y^2}-\mathrm{i}\frac{y}{x^2+y^2} .$$ and so, for example $$\frac{z_1}{z_2}=\frac{\bar z_2z_1}{\lvert z_2\rvert^2} .$$

Example 2.4:

• We have $(2+3\mathrm{i})(4-2\mathrm{i})=8-6\mathrm{i}^2+12 \mathrm{i}-4\mathrm{i}=14+8\mathrm{i}$.

• We have $\displaystyle\frac{1}{2+3\mathrm{i}}=\frac{2-3\mathrm{i}}{(2+3\mathrm{i})(2-3\mathrm{i})}=\frac{2-3\mathrm{i}}{4+9}=\frac{2}{13}-\frac{3}{13} \mathrm{i}$.

• We have $\displaystyle \frac{4-2\mathrm{i}}{2+3\mathrm{i}}=\frac{(4-2\mathrm{i})(2-3\mathrm{i})}{(2+3\mathrm{i})(2-3\mathrm{i})}=\frac{2-10\mathrm{i}}{4+9}=\frac{2}{13}-\frac{16}{13} \mathrm{i}$.