5.3 Further examples of subspaces
Now that we have seen that once way of forming a subspace is taking the span of a set of vectors we will consider some other ways that we can build subspaces.
Click for solution
Yes, this is true for any subspace \(V\) of \(\mathbb{R}^n\), since as soon as we have some non-zero vector \(v\in V\) then \(\lambda V \in V\) for any \(\lambda \in \mathbb{R}\).
Similarly, subspaces of \(\mathbb{C}^n\) over \(\mathbb{C}\) or \(\mathbb{R}\) will be infinite. However, this is not true for all vector spaces and later in the course we will see examples of finite choices for \(\mathbb{F}\) which give rise to finite vector (sub)spaces.
Another way to create a subspace is by giving conditions on the vectors contained in it. For instance let us chose a vector \(a\in\mathbb{R}^n\) and let us look at the set \(W_a\) of vectors \(x\) in \(\mathbb{R}^n\) which are orthogonal to \(a\), i.e., which satisfy \(x\cdot a=0\) i.e., \[W_{a}:=\{x\in\mathbb{R}^n : x\cdot a=0\}.\] This is shown in Figure 5.3.
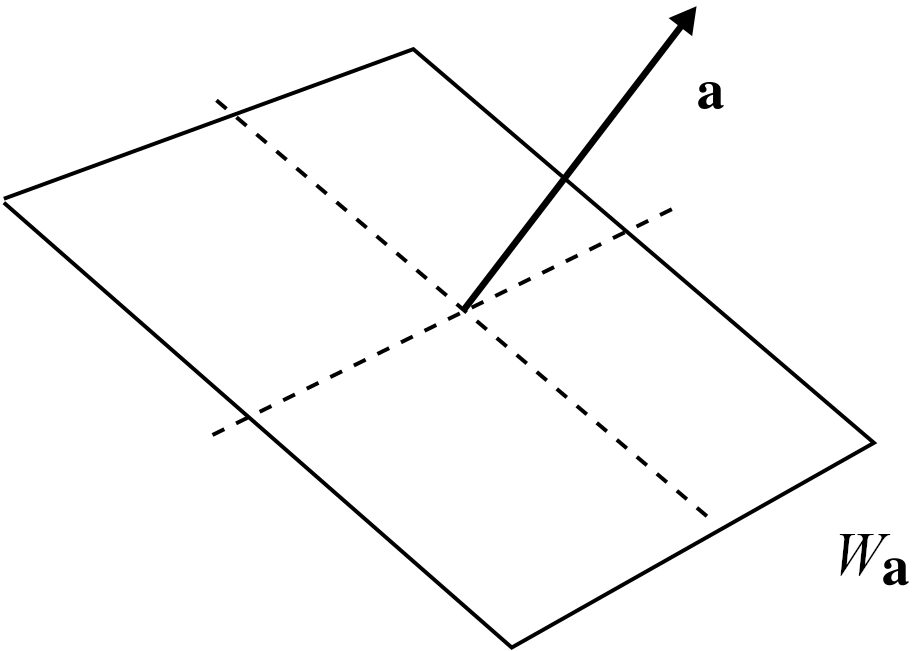
Figure 5.3: The plane orthogonal to a non-zero vector \(a\) is a subspace \(W_{a}\).
Let \(a\in \mathbb{R}^n\). Then \(W_{a}:=\{x\in\mathbb{R}^n: x\cdot a=0\}\) is a subspace of \(\mathbb{R}^n\).
Clearly \(\mathbf{0}\in W_{a}\), so \(W_{a}\neq\emptyset\). Let \(x, y\in W_a\) and \(\lambda \in \mathbb{R}^n\). So \(x\cdot a=0\) and \(y\cdot a=0\), and we have that \((x+y)\cdot a=x\cdot a+y\cdot a=0\) and \((\lambda x)\cdot a=\lambda x\cdot a=0\). Hence \(x+y\in W_{a}\) and \(\lambda x\in W_{a}\) so \(W_a\) is a linear subspace.
□
For instance if \(n=2\), then \(W_{a}\) is the line perpendicular to \(a\) (if \(a\neq \mathbf{0}\), otherwise \(W_{a}=\mathbb{R}^2\)) and if \(n=3\), then \(W_{a}\) is a plane perpendicular to \(a\) (if \(a\neq \mathbf{0}\), otherwise \(W_{a}=\mathbb{R}^3\)).
There can be different vectors \(a\) which determine the same subspace; in particular notice that since for \(\lambda\neq 0\) we have \(x\cdot a=0\) if and only if \(x\cdot (\lambda a)=0\) we get \(W_{a}=W_{\lambda a}\) for \(\lambda\neq 0\). In terms of the subspace \(V=\operatorname{span}\{a\}\) this means \[W_{a}=W_{b} ,\quad \text{for all} \quad b\in V\backslash\{\mathbf{0}\},\] and so \(W_{a}\) is actually perpendicular to the whole subspace \(V\) spanned by \(a\). This motivates the following definition:
So the orthogonal complement consists of all vectors \(x\in \mathbb{R}^n\) which are perpendicular to all vectors in \(V\). So, for instance, if \(V\) is a plane in \(\mathbb{R}^3\), then \(V^{\perp}\) is the line perpendicular to it.
Let \(V\) be a subspace of \(\mathbb{R}^n\). Then \(V^{\perp}\) is a subspace of \(\mathbb{R}^n\).
Clearly \(\mathbf{0}\in V^{\perp}\), so \(V^{\perp}\neq\emptyset\). If \(x\in V^{\perp}\), then for any \(v\in V\), \(x\cdot v=0\) and therefore \((\lambda x)\cdot v=\lambda x\cdot v=0\) and so \(\lambda x\in V^{\perp}\), so \(V^{\perp}\) is closed under multiplication by scalars. Finally if \(x,y\in V^{\perp}\), then \(x\cdot v=0\) and \(y\cdot v=0\) for all \(v\in V\) and hence \((x+y)\cdot v=x\cdot v+y\cdot v=0\) for all \(v\in V\), therefore \(x+y\in V^{\perp}\).
□
Note that if \(V=\operatorname{span}\{a_1,\cdots ,a_k\}\) is spanned by \(k\) vectors, then \(x\in V^{\perp}\) means that the \(k\) conditions \[\begin{align*} a_1\cdot x&=0,\\ a_2\cdot x&=0,\\ \vdots & \\ a_k\cdot x&=0 \end{align*}\] hold simultaneously.
To define an orthogonal complement, we have made use of the dot product as defined on vectors in \(\mathbb{R}^n\). We could also define such a structure for \(\mathbb{C}^n\) but using the dot product as defined on complex vectors instead. It is left as an excercise to convince yourself that the above proof will still hold. We will see later in the course how we can generalise these dot products to something called an inner product on a vector space in order to define these orthogonal complements more generally.
Given multiple subspaces of the same vector space, we can also combine them to make a new subspace.
Assume \(U, V\) are subspaces of a vector space \(W\), then
\(U\cap V=\{w \in W : w\in U \text{ and } w \in V\}\) is a subspace of \(W\)
\(U+W:=\{u+v: u\in U \text{ and } v\in V\}\) is a subspace of \(W\).
The proof of this result will be left as an exercise, as will the following generalisation:
Let \(W_1, W_2,\cdots W_m\) be subspaces of \(\mathbb{R}^n\), then \[W_1\cap W_2\cap \cdots\cap W_m\] is also a subspace of \(\mathbb{R}^n\).
Click for solution
No, in general the union of two subspaces is not another subspace.