11 Lab 9 - 11/12/2020

In questa lezione andremo ad introducce i concetti di leveraggio, residui studentizzati e osservazioni problematiche. Infine utilizzeremo i residui per verificare le assunzioni alla base del modello di regressione. Per i dettagli teorici di questi argomenti si rimanda alle lezioni teoriche.

Per questo laboratorio si considerano i dati contenuti nel file logret.csv e relativi ai rendimenti logaritmici dei seguenti titoli:

The Boeing Company (BA),
Caterpillar Inc. (CAT),
Cisco Systems Inc. (CSCO),
Nike Inc. (NKE),
The Walt Disney Company (DIS)
the Dow Jones Industrial Average index (DJI).

Iniziamo con l’importazione dei dati:

logret = read.csv("~/Dropbox/UniBg/Didattica/Economia/2020-2021/SAPF_2021/R_labs/lab9/logret.csv")
str(logret)

## 'data.frame':	1258 obs. of  6 variables:
##  $ BA  : num  -0.02662 0.03486 0.00429 -0.02535 0.01833 ...
##  $ CAT : num  -0.01279 0.00467 0.00675 0.00116 -0.0059 ...
##  $ CSCO: num  0.000985 -0.000492 0.006873 0.001955 0.023644 ...
##  $ NKE : num  -0.01063 0.000954 0.001905 0.010412 0.001694 ...
##  $ DIS : num  -0.004129 0.000394 0.000197 -0.004143 0.000197 ...
##  $ DJI : num  -0.00415 0.00462 0.00601 0.00128 0.0014 ...

Stimiamo quindi il modello di regressione multipla che considera come variabile dipendente i rendimenti di DJI; le altre variabili incluse nel dataframe logret sono incluse nel modello come regressori.

mod1 = lm(DJI ~ ., data=logret)

Il codice ~ . specifica che tutte le variabili, ad eccezione di DJI, devono essere incluse nel modello (in alternativa si possono specificare tutte le variabili separate da +).

Analizzando le informazioni contenute nel summary del modello

summary(mod1)

## 
## Call:
## lm(formula = DJI ~ ., data = logret)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0161881 -0.0022201 -0.0000164  0.0021291  0.0143476 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -4.066e-05  9.917e-05   -0.41    0.682    
## BA           1.628e-01  8.804e-03   18.50   <2e-16 ***
## CAT          1.531e-01  7.987e-03   19.17   <2e-16 ***
## CSCO         1.225e-01  8.582e-03   14.27   <2e-16 ***
## NKE          9.944e-02  8.120e-03   12.25   <2e-16 ***
## DIS          1.655e-01  1.021e-02   16.20   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.003501 on 1252 degrees of freedom
## Multiple R-squared:  0.7668,	Adjusted R-squared:  0.7659 
## F-statistic: 823.3 on 5 and 1252 DF,  p-value: < 2.2e-16

si può concludere che tutti i coefficeinti $\beta$ sono significativamente diversi da zero; non è quindi necessario rimuovere alcun regressore. La bontà di adattamento è piuttosto alta.

11.1 Osservazioni problematiche

Un’osservazione si definisce problematica in funzione di tre valori: leveraggio, residuo ed influenza (descritti separatamente nei seguenti paragrafi). Nei grafici contenuti in Figura 11.1 vengono riportati dei punti neri e un punto rosso che può rappresentare un’osservazione problematica. I punti neri vengono utilizzati per stimare la retta nera; la retta rossa invece viene stimata utilizzando i punti neri e il punto rosso. I seguenti quattro caso sono rappresentati:

alto-sinistra: il punto rosso ha un residuo elevato, un basso valore di leveraggio e risulta poco influente (infatti la retta rossa e quella nera sono molto vicine);
alto-destra: il punto rosso ha un residuo elevato, un alto leveraggio e risulta particolarmente influente (infatti la retta rossa è evidentemente diversa da quella nera, quest’ultima stimata senza il punto rosso);
basso-sinistra: il punto rosso ha un alto leveraggio ma un basso residuo e risulta poco influente (infatti la retta rossa e quella nera praticamente coincidono);
basso-destra: il punto rosso ha un residuo elevato, basso leveraggio ma risulta altamente influente (infatti le due rette differiscono).

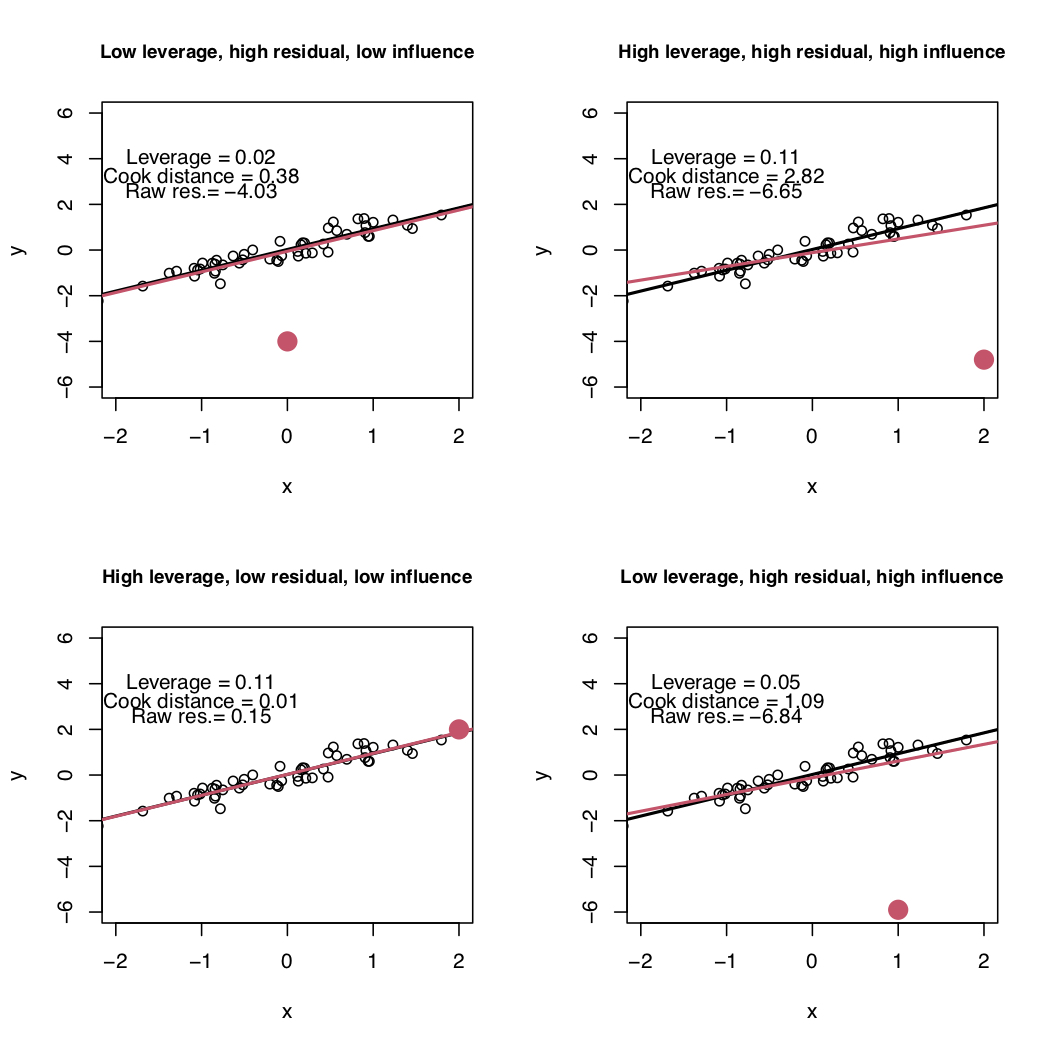
Figure 11.1: Modello di regressione semplice: quattro possibili casi rispetto al leveraggio, residui e influenza (distanza di Cook).

11.1.1 Leveraggio

Un punto ad alto leveraggio è un’osservazione con un valore della variabile indipendente $x$ lontano dalla media $\bar x$ (questo ovviamente si riferisce al caso in cui $p=1$ ma lo stesso concetto può essere esteso al caso in cui $p>1$). Il leveraggio si indica con $H_{ii}$ ($i=1,\ldots,n$) e misura l’influenza (o il peso) di $y_i$ sulla sua stessa previsione $\hat y_i$ sapendo che \[ \hat y_i = \sum_{j=1}^n H_{ij}y_j \] Il leveraggio è sempre un valore compreso tra 0 e 1. Inoltre, $\sum_{i=1}^n H_{ii}=p+1$; di conseguenza $\frac{p+1}{n}$ rappresenta il leveraggio medio. La soglia per identificare osservazioni ad alto leveraggio è $2(p+1)/n$, dove $n$ è la dimensione del campione di dati.

Calcoliamo quindi il leveraggio per le osservazioni utilizzate per stimare mod1 utilizzando la funzione hatvalues:

lev = hatvalues(mod1)

Il corrispondente grafico è dato dal seguente codice

plot(lev)

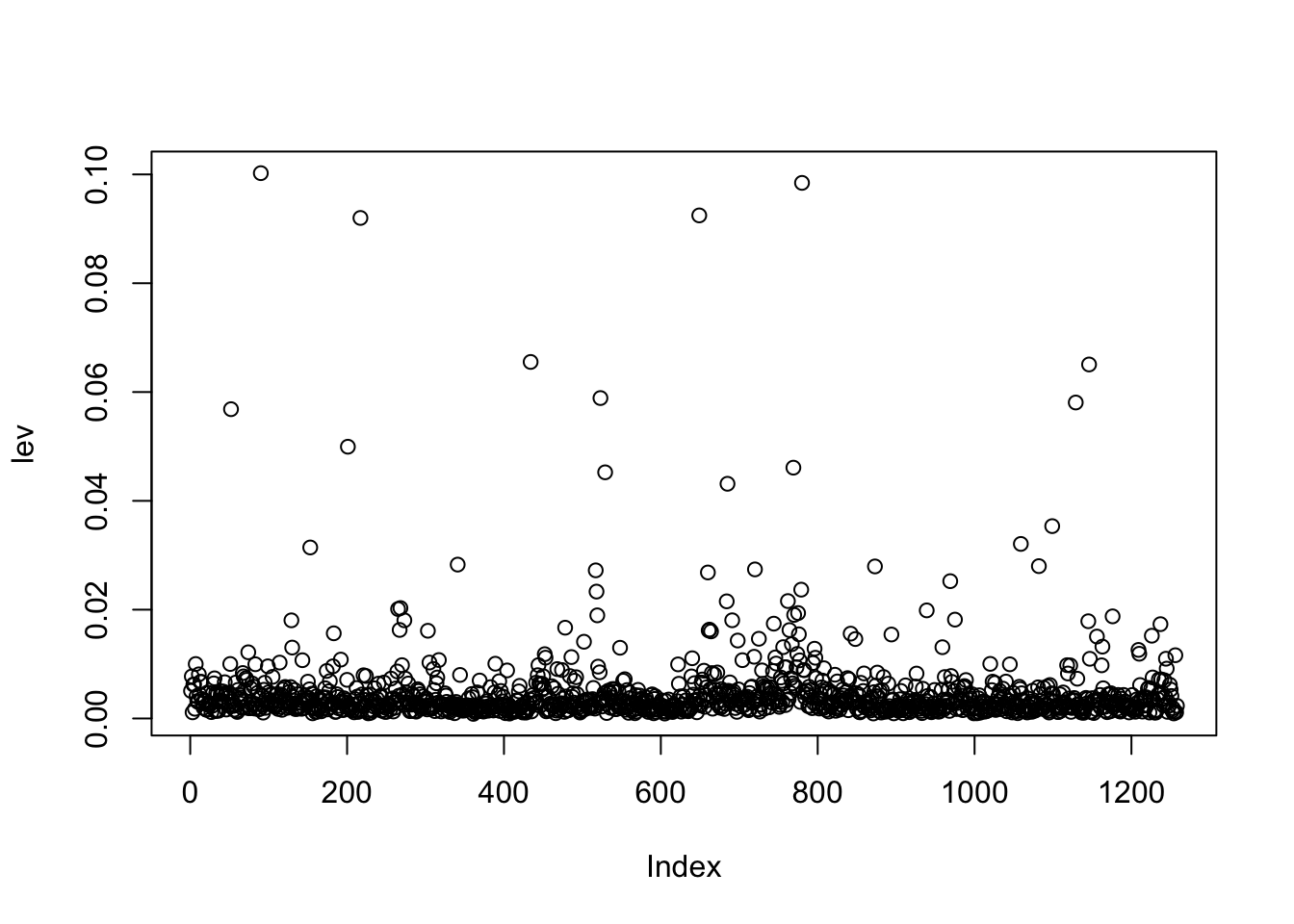dove sull’asse delle ascisse si riporta la variabile Index che assume valori interi da 1 a 1258 (rappresenta l’ordinamento delle osservazioni). Volendo includere nel grafico la soglia si procede come segue:

# salvare in 2 oggetti i valori di p e n
p = length(mod1$coefficients)-1
n = nrow(logret)
plot(lev)
abline(h=2*(p+1)/n, col="red")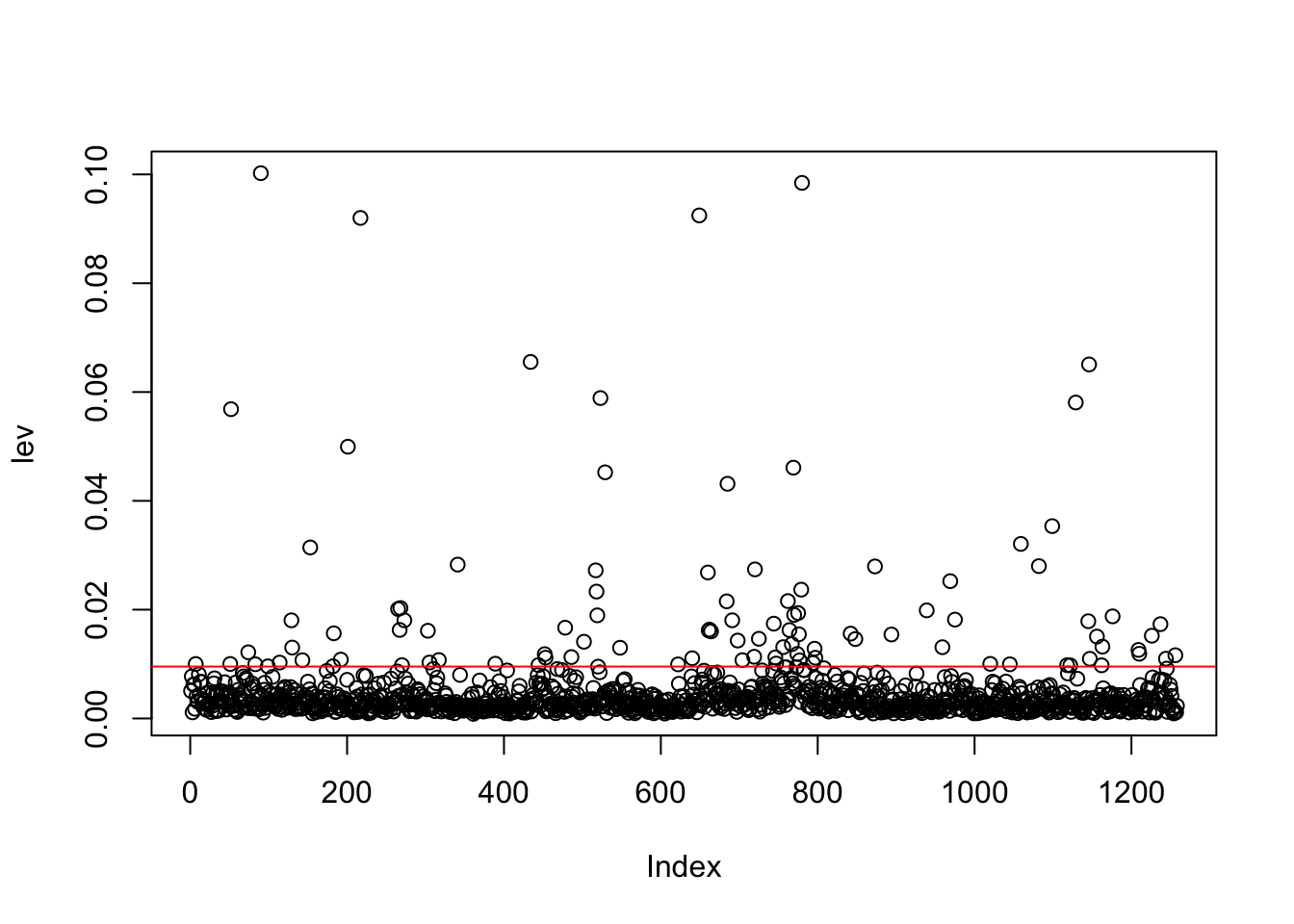

Per calcolare il numero e la percentuale di osservazioni ad alto leveraggio si utilizza il seguente codice:

sum(lev > 2*(p+1)/n)

## [1] 102

mean(lev > 2*(p+1)/n)*100

## [1] 8.108108

Come rappresentato nel grafico in basso a sinistra della Figura 11.1, avere un alto valore di leveraggio non necessariamente implica che l’osservazione sia altamente influente (sulle stime).

11.1.2 Residui e outliers

Un outlier è un’osservaizione con un valore estremo della variabile dipendente e perciò con un residuo elevato. Ci sono 3 diversi tipi di residui (si veda la teoria per i dettagli):

residui grezzi: $\hat \epsilon_i=y_i-\hat y_i$, ottenibili in R con mod1$residuals.
residui standardizzati: $\frac{\hat\epsilon_i}{\hat\sigma_\epsilon\sqrt{1-H_{ii}}}$, dati in R dalla funzione rstandard(model=...).
residui studentizzati esternamente (o sfrondati): $\frac{\hat\epsilon_i}{\hat\sigma_{\epsilon,_{-i}}\sqrt{1-H_{ii}}}$, dati in R da rstudent(model=...).

Calcoliamo quindi i residui studentizzati per il modello considerato:

res = rstudent(mod1)

I residui possono essere rappresentati graficamente utilizzando plot o hist:

plot(res)

hist(res)

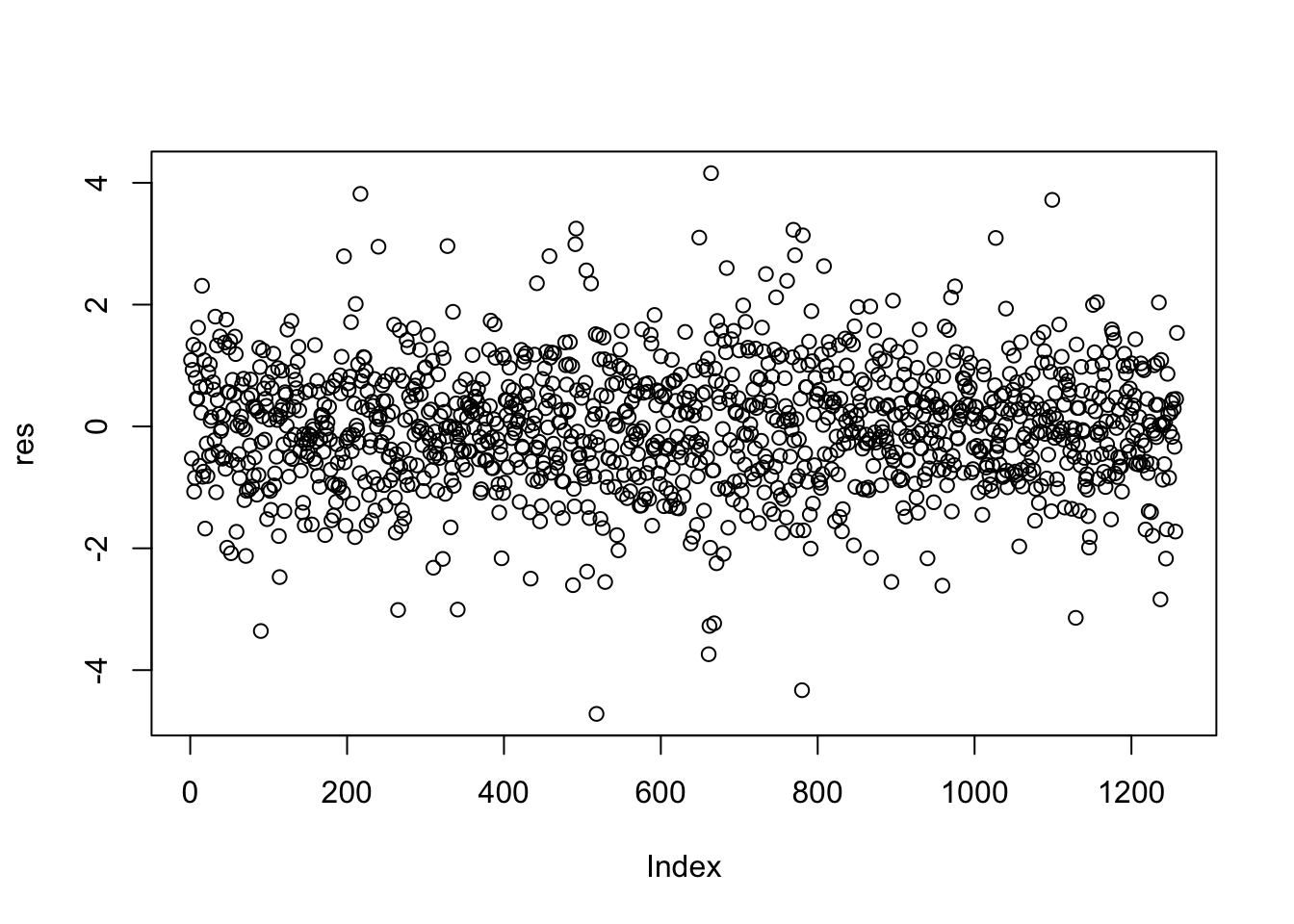
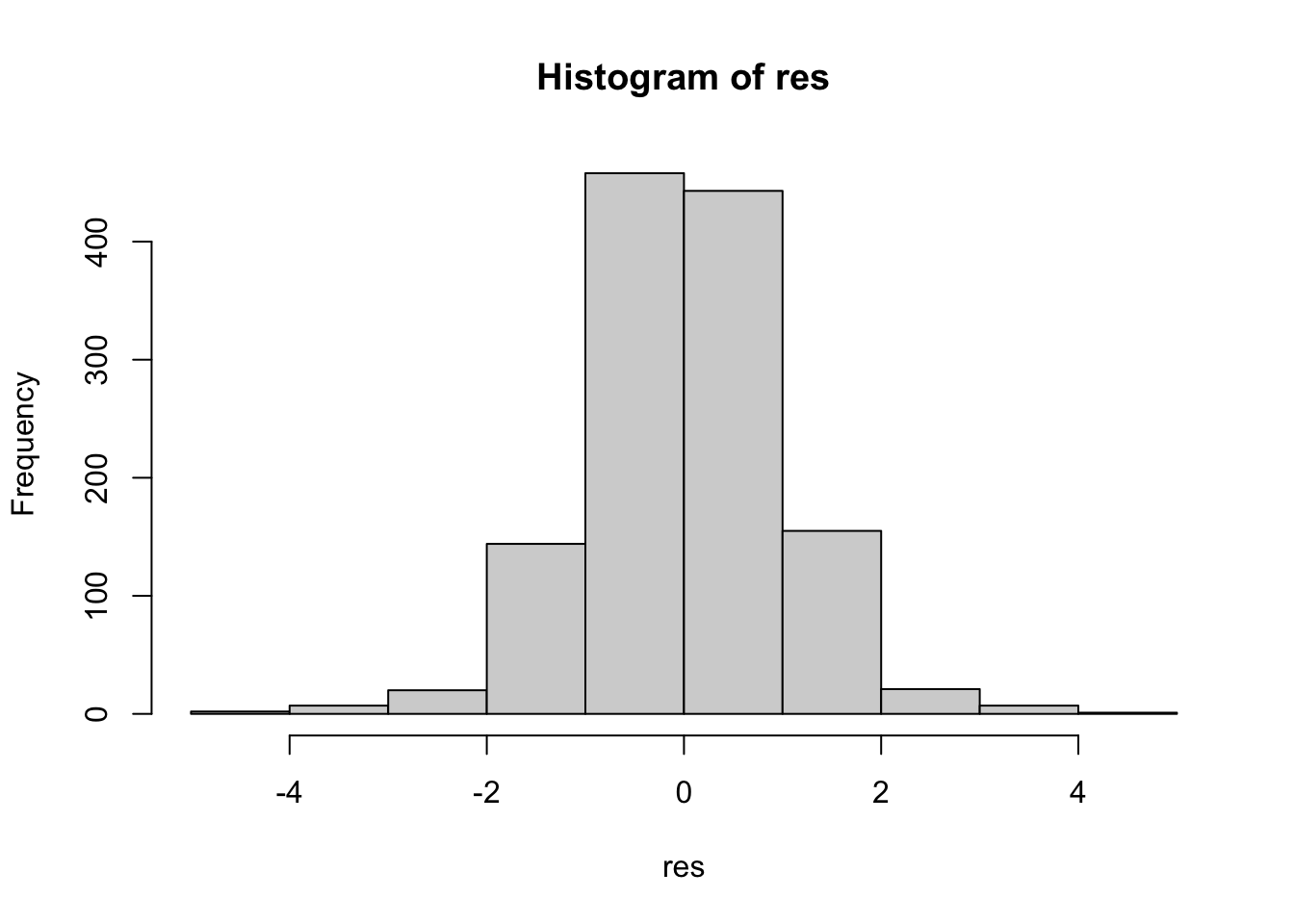I valori soglia per identificare gli eventuali outliers (i.e. osservazioni con residuo elevato) sono dati da -3 e +3 (o -2 e +2). Includiamo quindi questi valori soglia nel grafico:

plot(res)
abline(h=c(-3,+3),col="red")

hist(res)
abline(v=c(-3,+3),col="red")

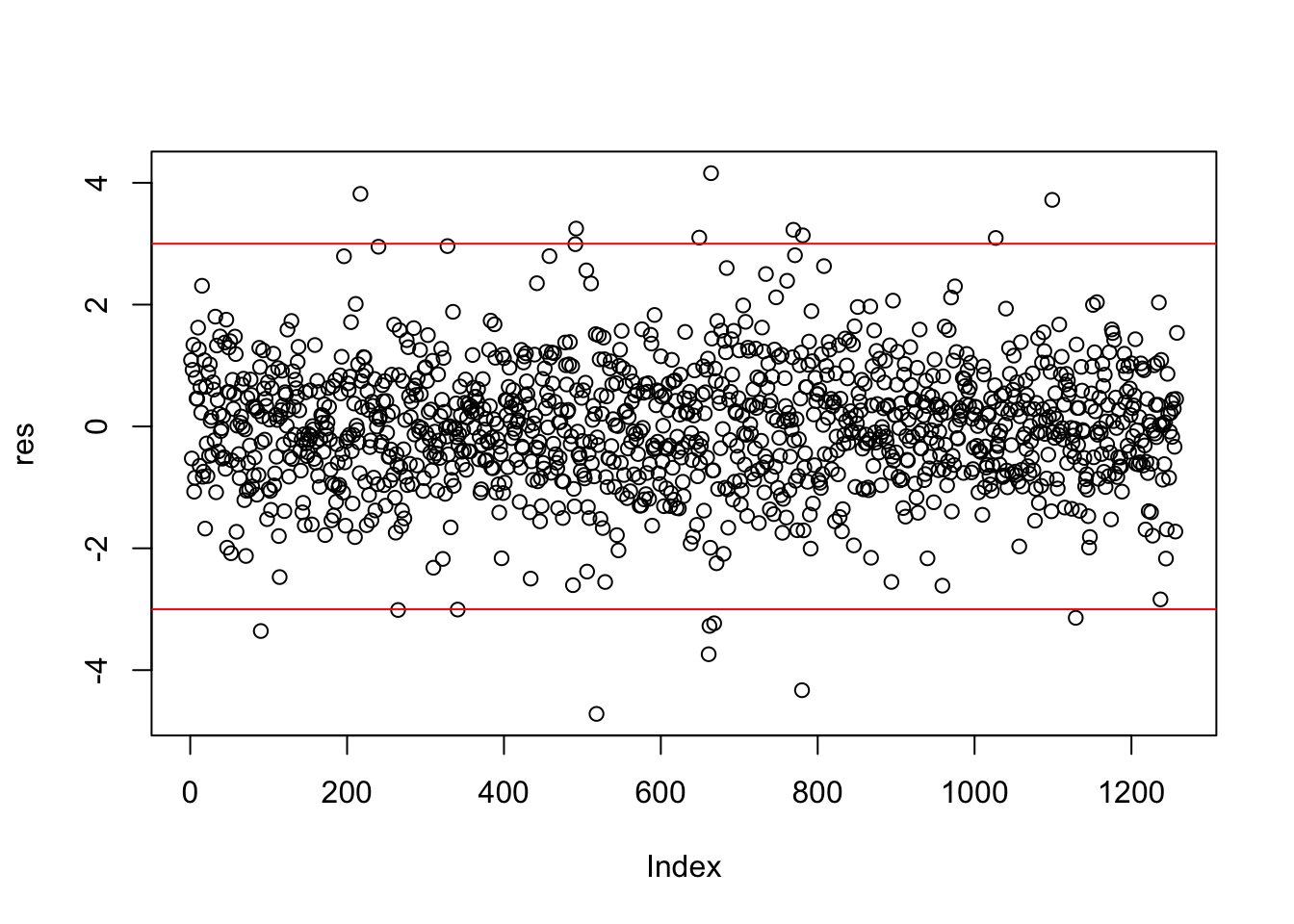
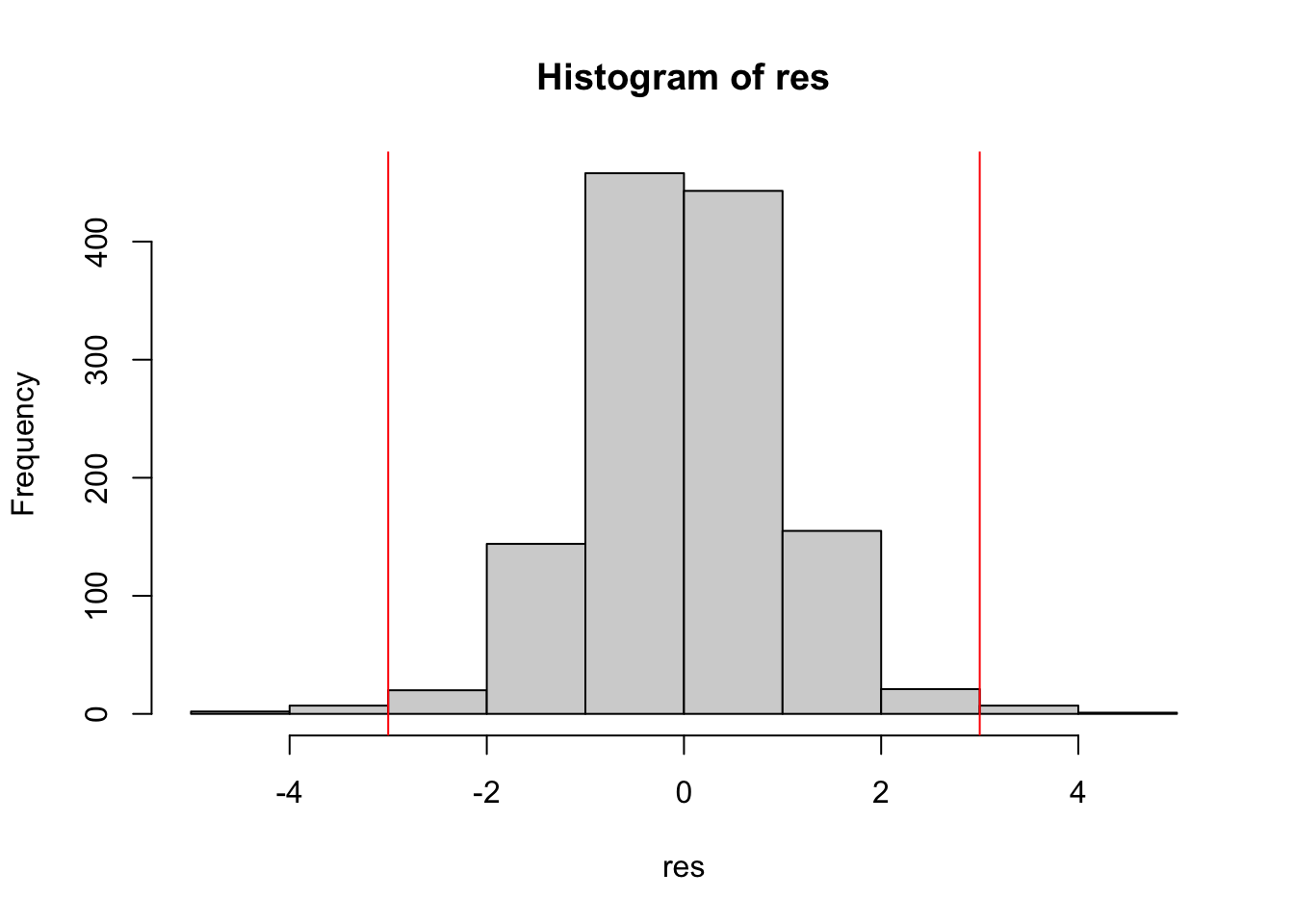Calcoliamo quindi la percentuale di outliers:

mean(res < -3 | res >+3)*100

## [1] 1.351351

Il simbolo | rappresenta l’operatore OR. Si noti che nel precedente codice è necessario scrivere separati da uno spazio i simboli < e -, altrimenti il simbolo <- viene interpretato da R come un’operazione di assegnazione (si ricordi infatti che <- può essere utilizzato al posto di =).

Come rappresento nel grafico in alto a sinistra della Figura 11.1, un’osservazione identificata come outlier non necessariamente è in grado di modificare le stime dei parameteri della retta (ed essere quindi altamente influente).

11.1.3 Distanza di Cook

Un punto influente è un’osservazione in grado di modificare le stime dei parametri del modello di regressione. La distanza di cook misura di quanto ogni valore fittato/previsto $\hat y_i$ cambia quando l’$i$-esima osservazione viene rimossa dal set di dati usato per la stima del modello. In R la distanza di Cook può essera calcolato per ogni osservazione usando al funzione cooks.distance(model=...).La soglia per individuare osservazioni influtenti è data da $4/n$.

cookdist = cooks.distance(mod1)

Il grafico, inclusa la soglia, è dato da:

plot(cookdist)
abline(h=4/n, col="red",lwd=2)

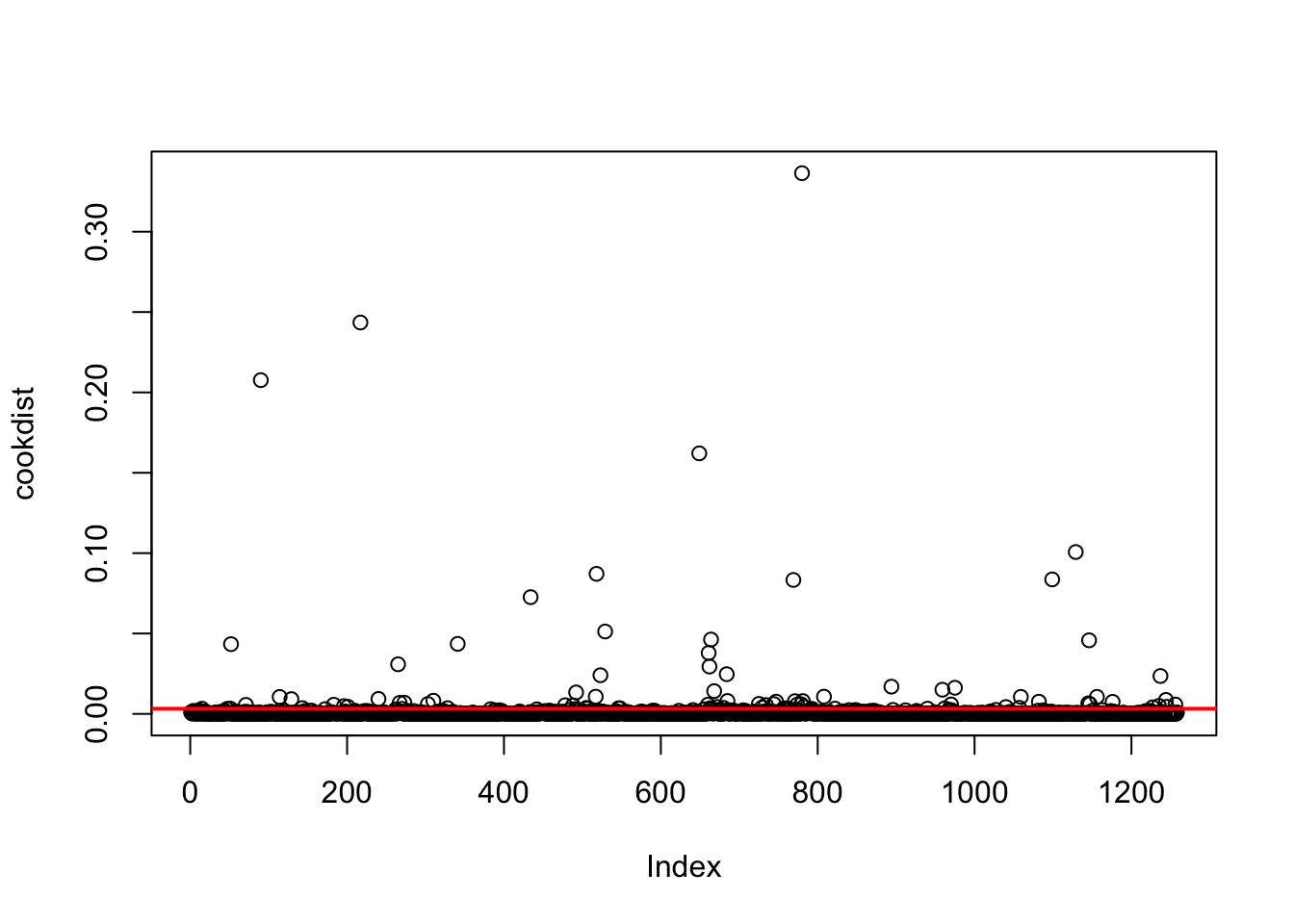
Come già fatto in prcedenza, la percentuale di osservazioni ad alta influenza si calcola come segue:

mean(cookdist > 4/n)*100

## [1] 6.518283

E’ importante investigare il motivo legato alla presenza di osservazioni ad alta influenza. Si tratta di errori nei dati? O di eventi straordinari nel mertcato finanziario?

11.1.4 Rappresentare insiem leveraggio, residui e distanza di Cook

La funzione influencePlot inclusa nella libreria car può essere utilizzata per rappresentare graficamente in un unico grafico le 3 quantità introdotte precedentemente (leveraggio, residui e distanza di Cook):

library(car) #load the library
influencePlot(mod1)

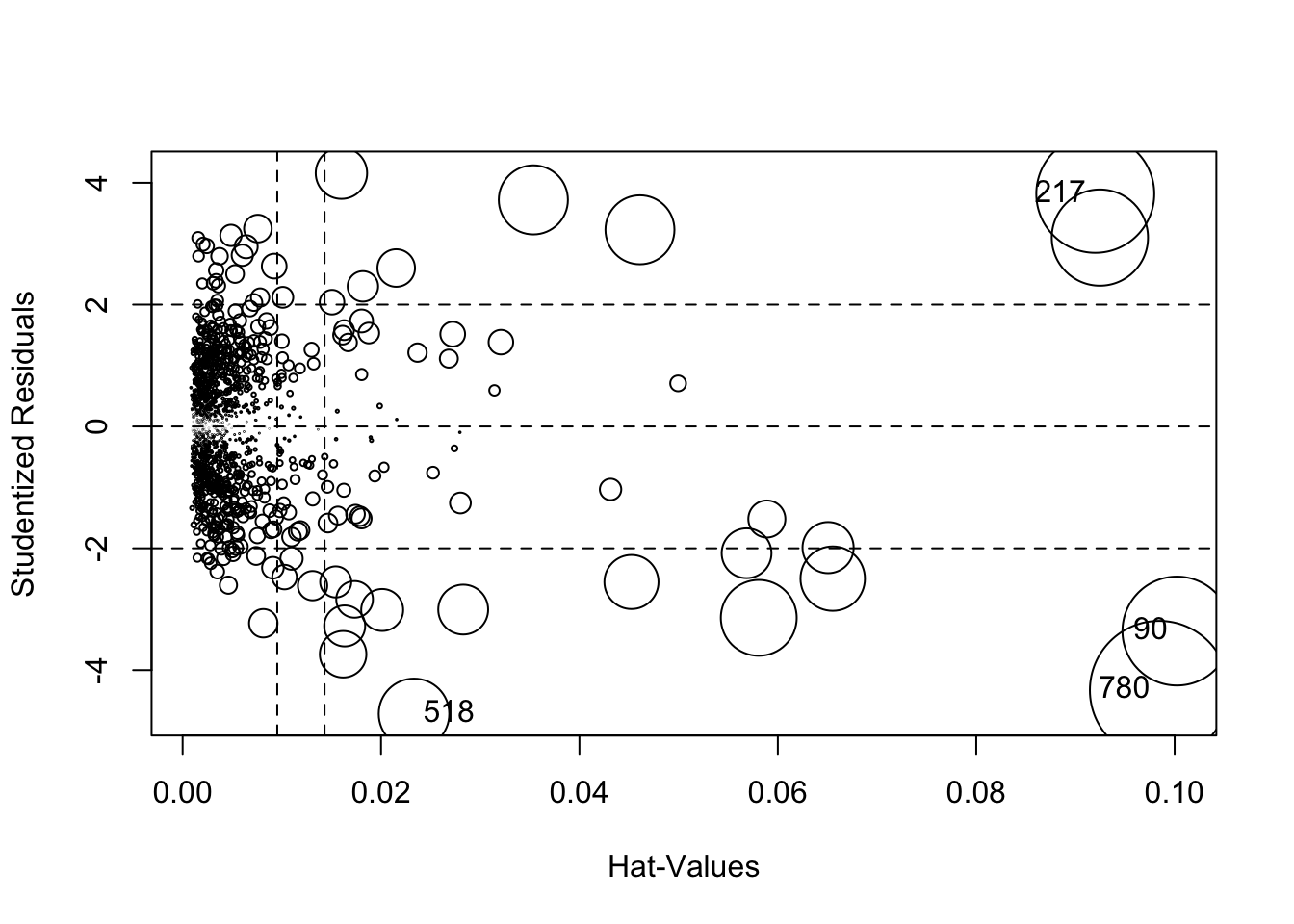
##       StudRes        Hat      CookD
## 90  -3.358004 0.10022960 0.20764693
## 217  3.817804 0.09199915 0.24349483
## 518 -4.718118 0.02332257 0.08711613
## 780 -4.329769 0.09844534 0.33640968

Come descritto nella pagina di help, questa funzione creare un grafico a bolle che rappresenta i residui studentizzati contro i valori di leveraggio. La dimensione delle bolle è proporzionale alla distanza di Cook. Le linee verticali di riferimento sono tracciate in corrispondenza di 2 e 3 volte il leveraggio medio; le linee orizzontali di riferimento in corrispondenza dei valori -2, 0, e 2. La funzione etichetta i punti con valori elevati delle tre quantità considerate (e i valori vengono riportati nella console). In questo caso vengono etichettate 4 osservazioni che possono essere considerate come le più problematiche.

11.2 Diagnostica dei residui

Dopo la stima del modello è necessario analizzare i residui per verificare le assunzioni alla base del modello (si vedano le lezioni di teoria). In particolare, le assunzioni riguardano:

varianza costante degli errore, nota anche come omoschedasticità ($Var(\epsilon_i)=\sigma^2_\epsilon$);
linearità dell’effetto delle covariate sulla variabile risposta;
normalità degli errori;
incorrelazione degli errori ($Cov(\epsilon_i,\epsilon_j)=0$ per ogni $i,j$.

11.2.1 Omoschedasticità?

Il fenomeno di varianza non costante è nota anche come eteroschedasticità e si riferisce al fatto che la variabilità degli errori, e quindi anche della variabile risposta, non è costante. In Figura 11.2 vengono riportati due scatterplot: nel grafico di sinistra si nota che la variabilità di $y$ cresce al crescere di $x$ (e la nuvola dei punti ha una forma a imbuto). Nel grafico di destra la variabilità invece appare uguale per tutti i valori di $x$.

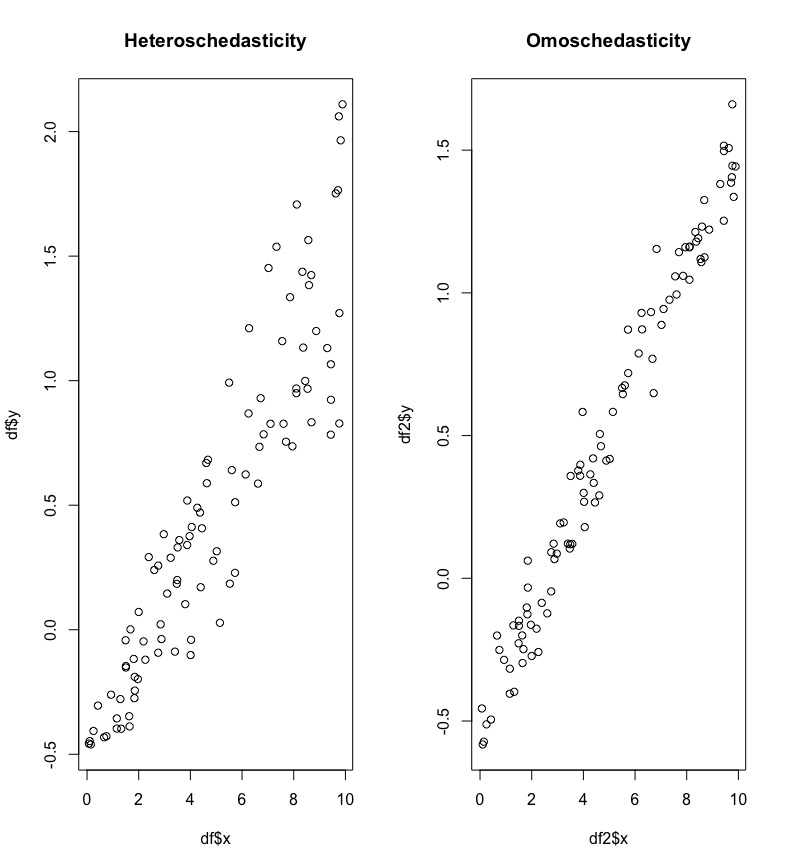
Figure 11.2: Scatterplot in caso di etero- ed omoschedasticità.

Si studia l’eventuale presenza di eteroschedasticità rappresentando graficamente i residui studentizzati in valore assoluto contro i valori previsti ($\hat y$). La presenza di un trend sistematico, come quello mostrato nel grafico a sinistra della Figura 11.3, è indicazione di varianza non costante.

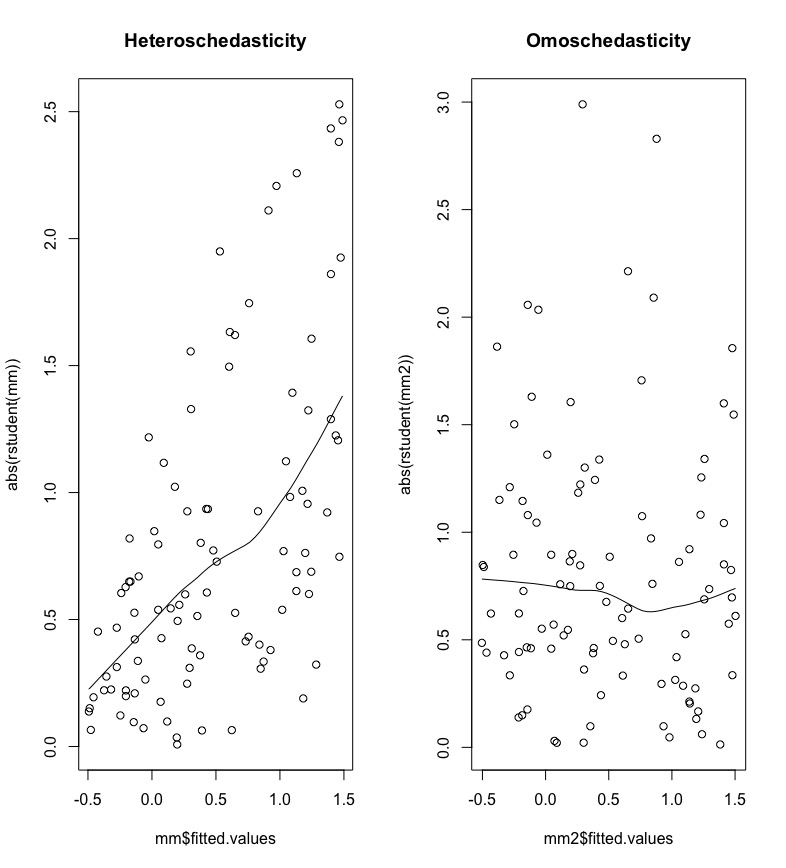
Figure 11.3: Residui studentizzati in valore assoluto contro valori previsti per lo studio dell’omoschedasticità.

Per i dati in analisi si ottiene il seguente grafico:

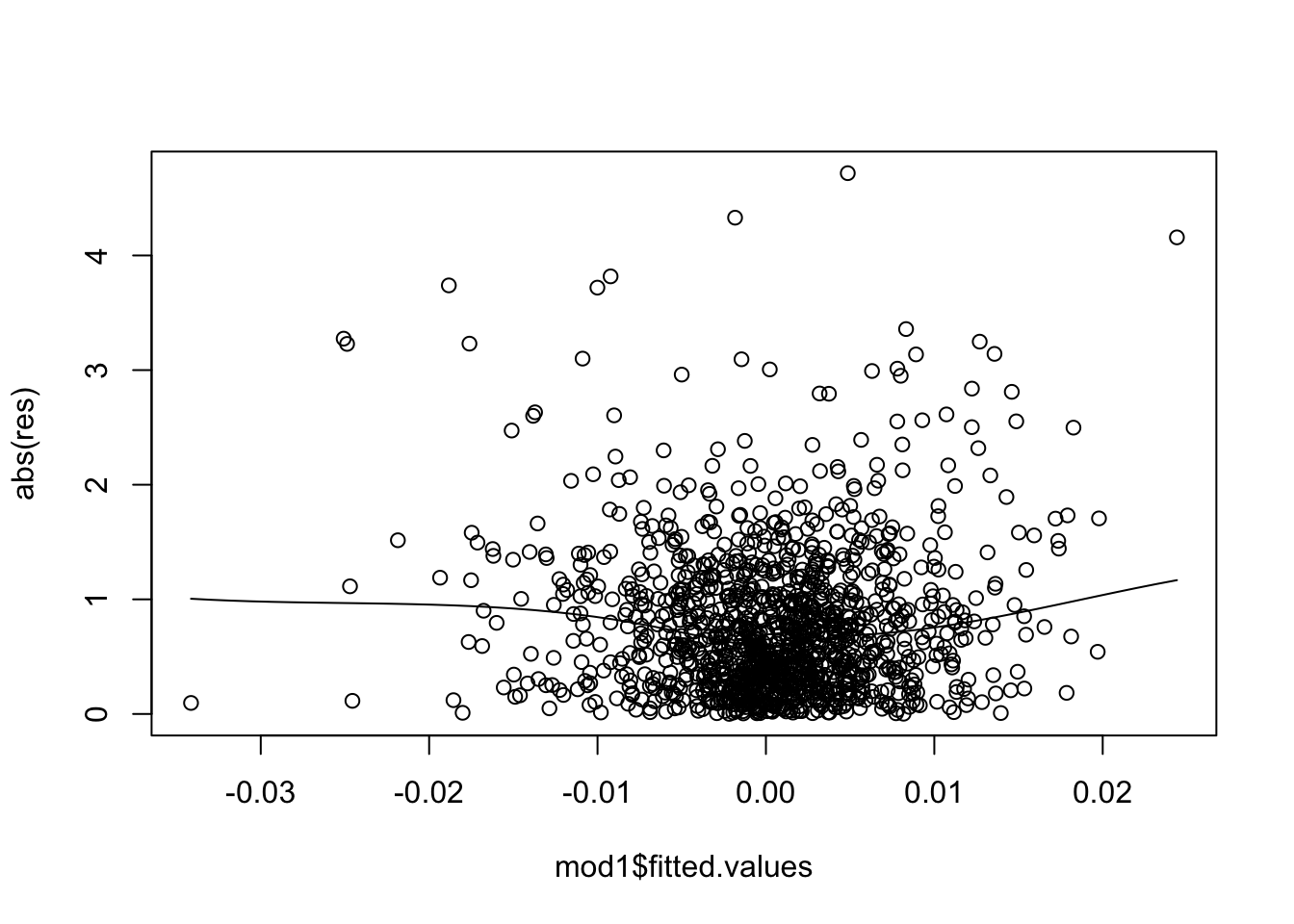
scatter.smooth(mod1$fitted.values,abs(res))

Si noti che viene usata la funzione scatter.smooth invece di plot; ciò permettere di includere nel grafico una linea che riassume la nuvola dei punti e permette una più facile lettura dell’andamento della nuvola dei punti. Il grafico non mostra un trend evidente e quindi è possibile concludere che non esiste un problema di eteroschedasticità.

11.2.2 Linearità?

La definizione stessa di modello di regressione lineare richiede che i predittori abbiano un effetto lineare sulla variable dipendente. Nel grafico di sinistra in Figura 11.4 si osserva un esempio di relazione non lineare tra $x$ e $y$ (sembra piuttosto una relazione quadratica).

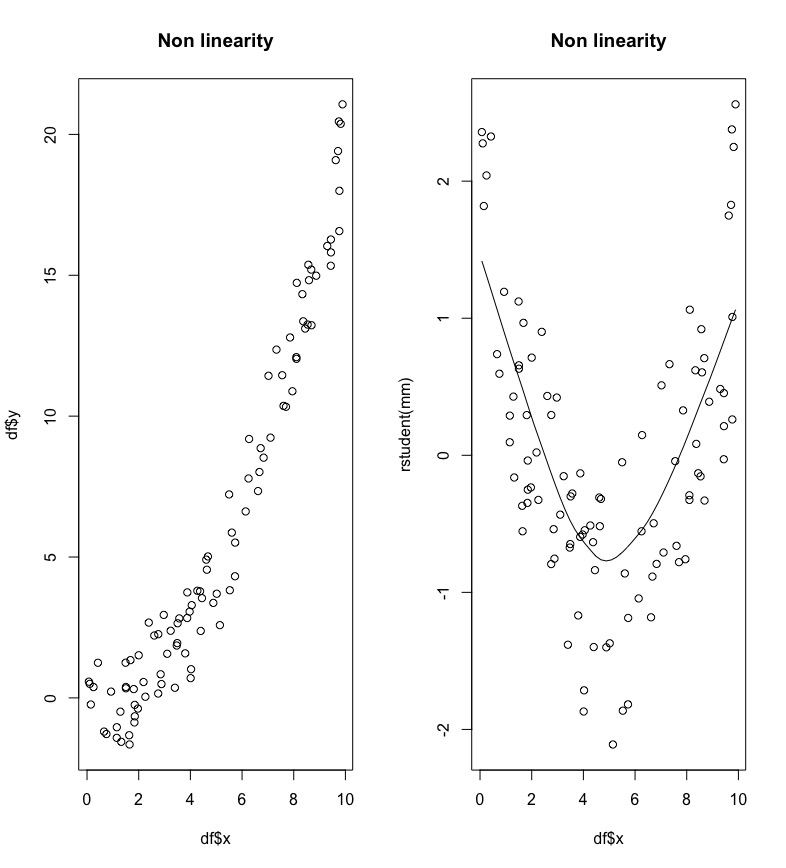
Figure 11.4: Un caso di non linearità tra x e y.

La non linerità può essere identificata con il grafico dei residui studentizzati contro i valori di ogni predittore incluso nel modello, come mostrato nel grafico di destra in Figura 11.4. Un andamento non lineare è sintomo di non linearità.

Il modello in esame mod1 utilizza $p=5$ regressori. E’ necessario quindi produrre 5 grafici:

scatter.smooth(logret$BA,res)

scatter.smooth(logret$CAT,res)

scatter.smooth(logret$CSCO,res)

scatter.smooth(logret$NKE,res)

scatter.smooth(logret$DIS,res)

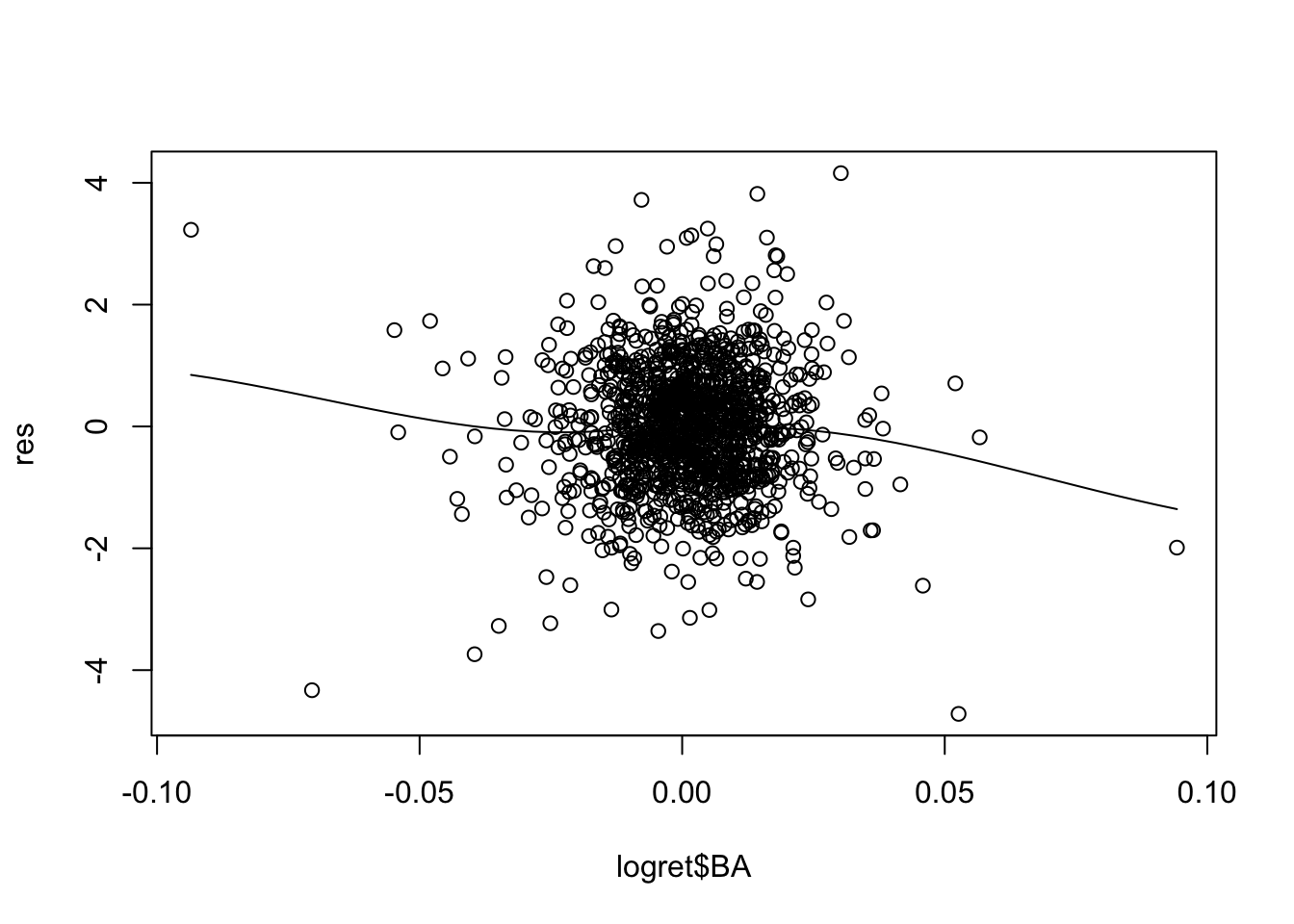
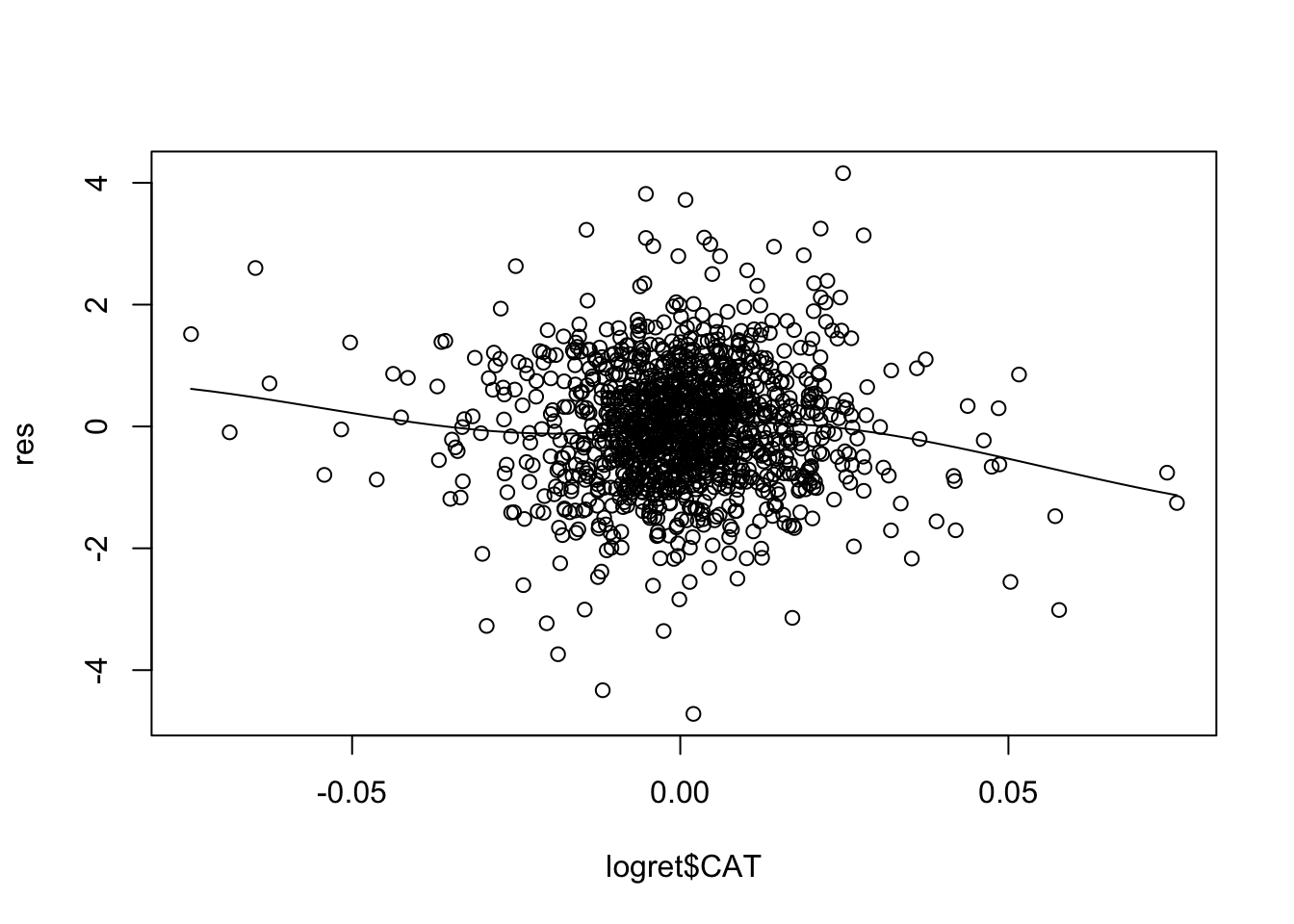
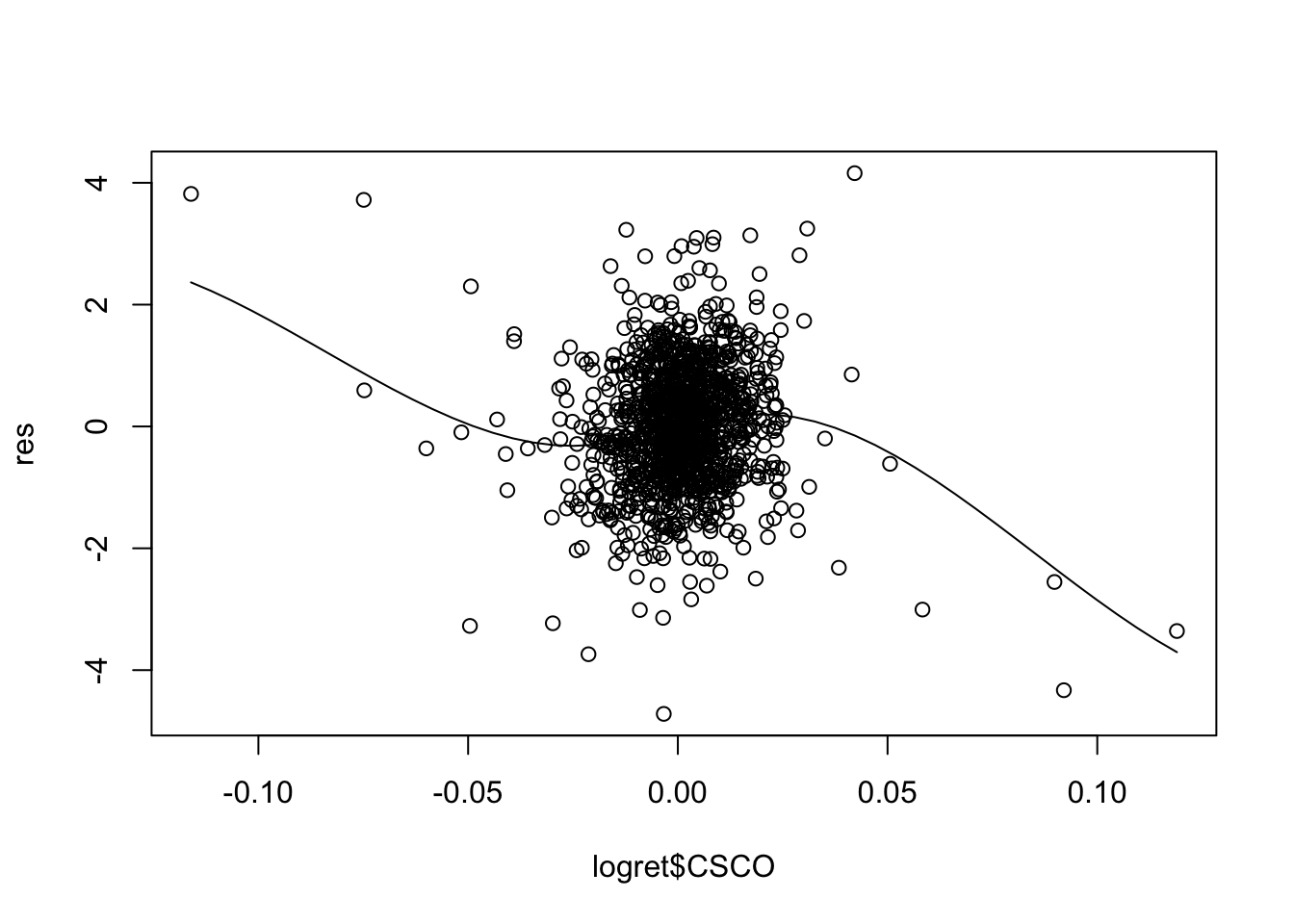
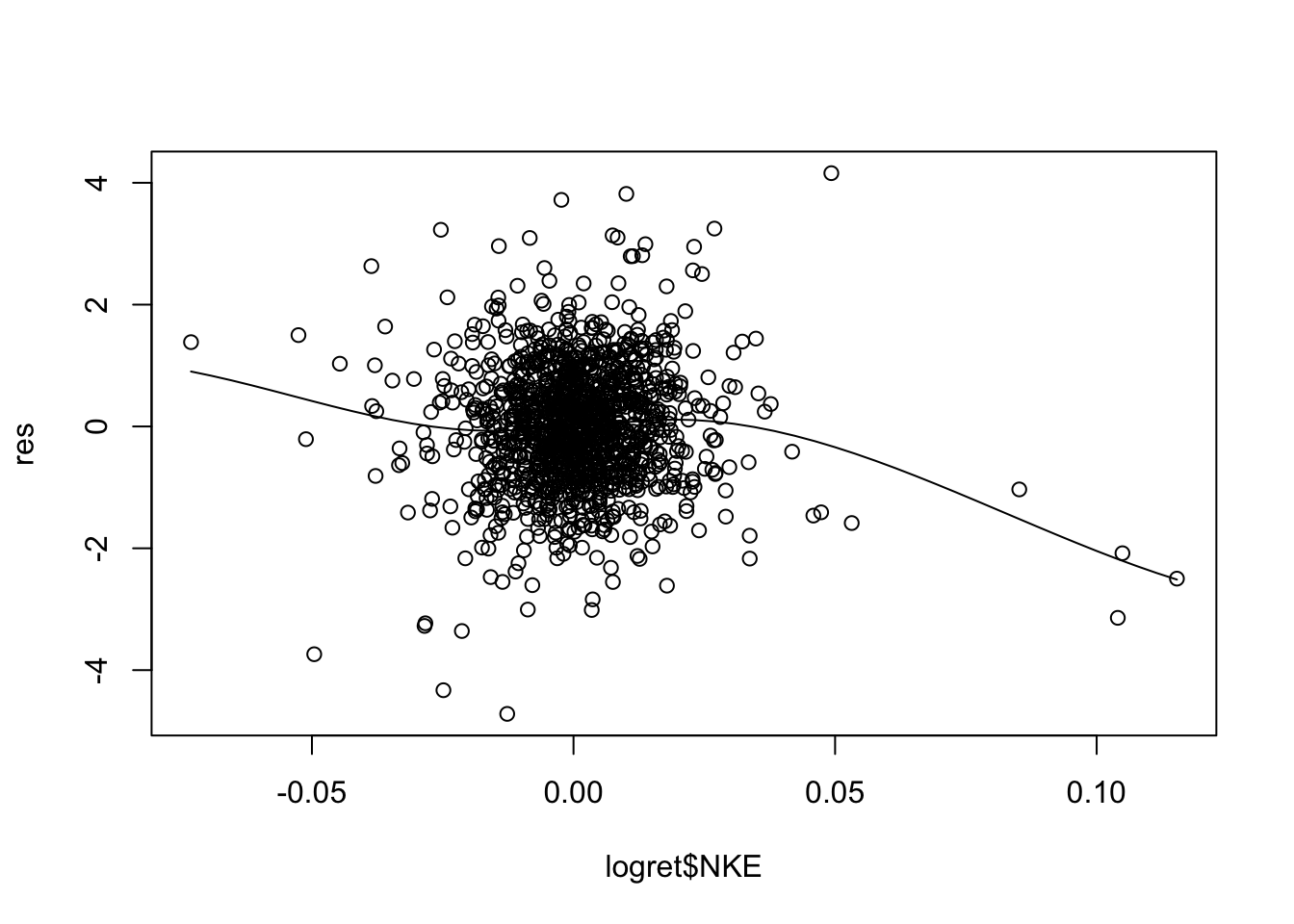
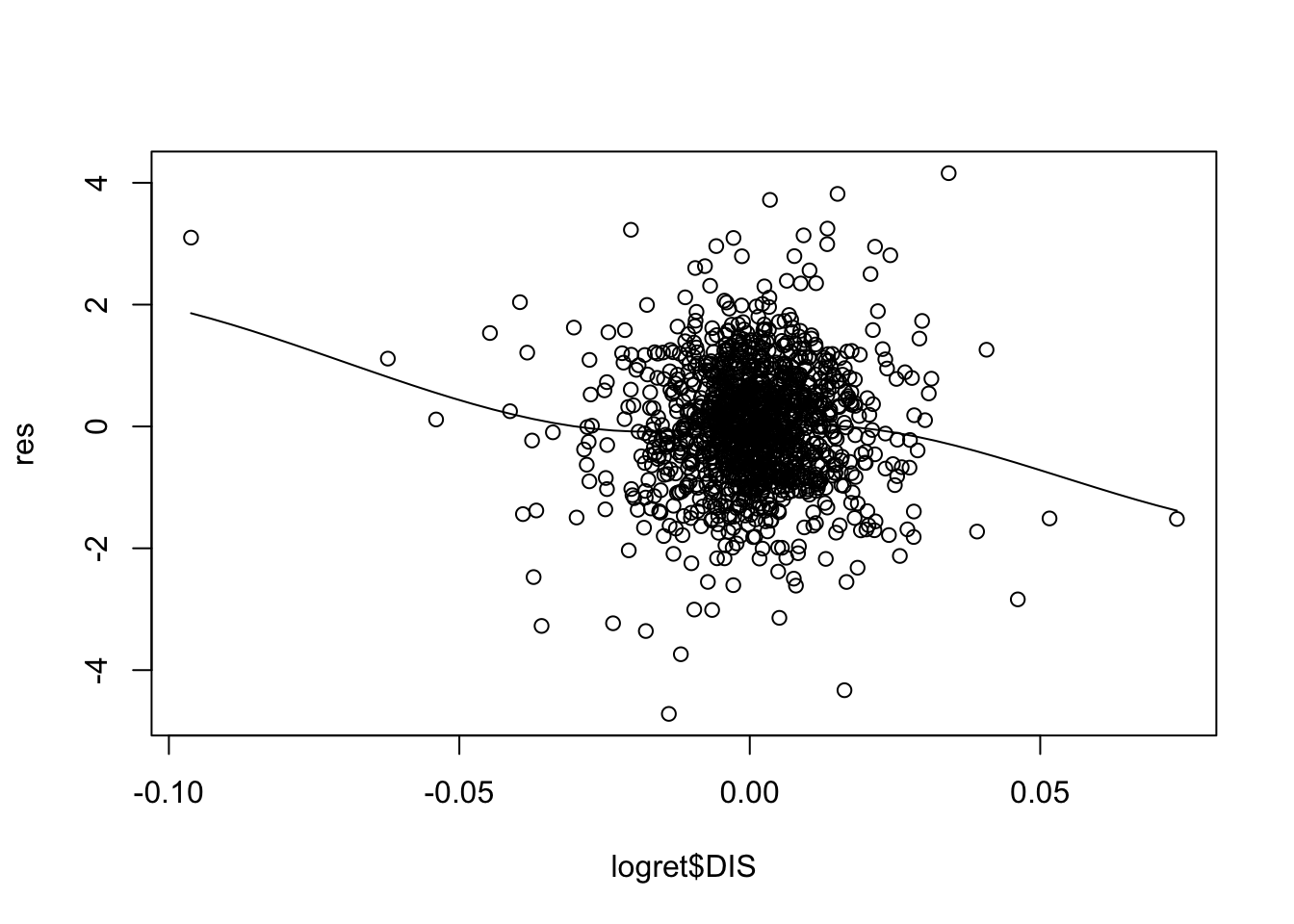
Per alcuni regressori si osservano andamenti non lineari (soprattutto per CSCO). Una possibile soluzione consiste nell’includere nel modello come regressore $X^2$ ed eventualmente anche $X^3$ (in questo caso si parla di regressione polinomiale).

11.2.3 Incorrelazione?

Per verificare l’eventuale presenza di correlazione nei residui si può utilizzare il correlogramma, grafico utilizzato diffusamente per l’analisi delle serie storiche. In R il correlogramma si produce utilizzando la funzione acf (autocorrelation function):

acf(res)

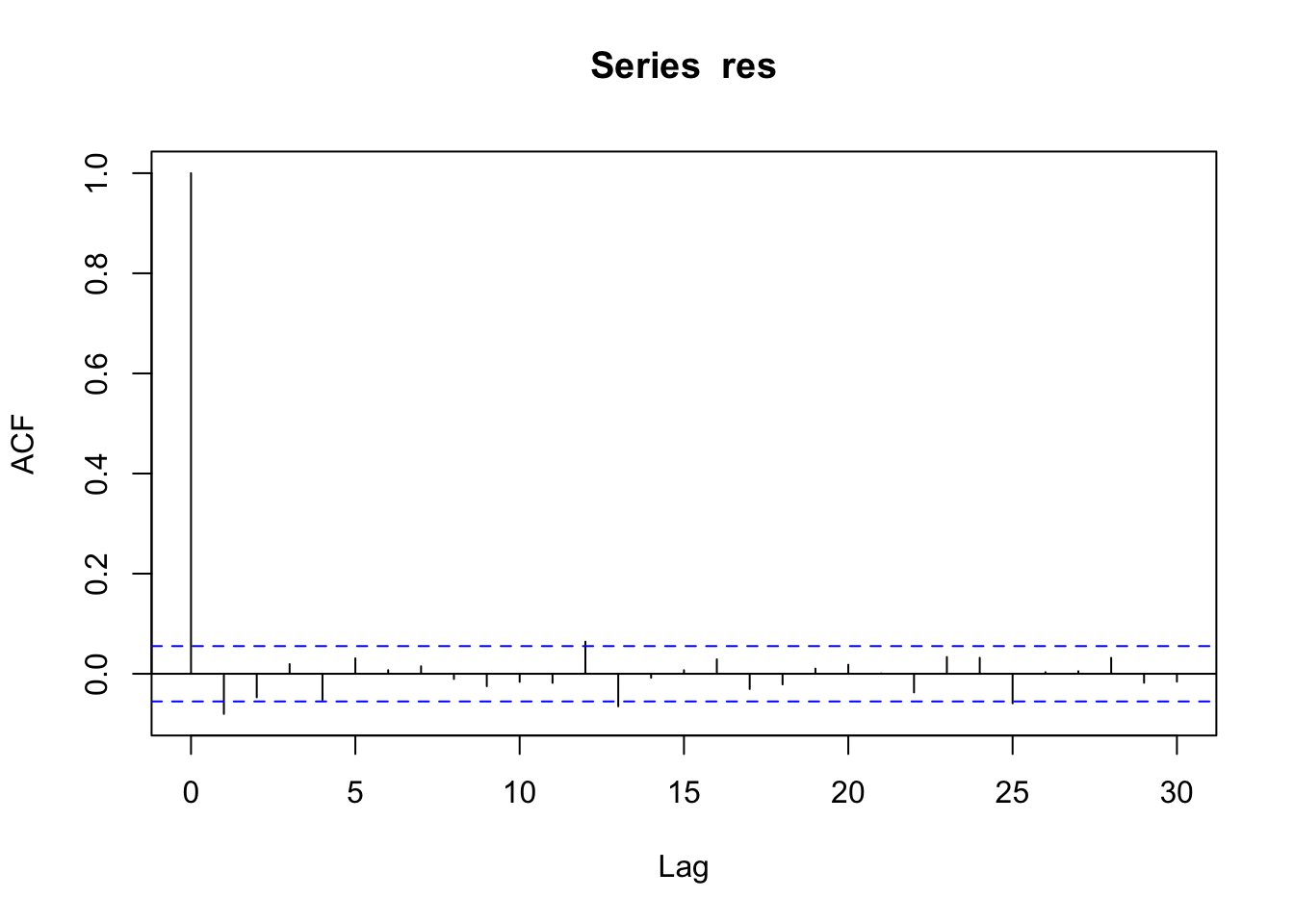
Il correlogramma rappresenta i valori di lag (distanza temporale) sull’asse delle ascisse e valori della correlazione su quello delle ordinate. La prima barra per $h=0$ è necessariamente uguale a 1 perchè corrisponde al caso di $Cor(y_t,y_t)$ con $t=1,\ldots,n$. La seconda barra per $h=1$ è negativa e significativamente diversa da zero (essendo al di furoi delle linee orizzontali blu). Perciò la correlazione $Cor(y_t,y_{t-1})$ è significativa. Questo ci porta a concludere che i residui non siano incorrelati. Questo ci suggerisce l’adozione di un modello specifico in grado di cogliere la correlazione che esiste nei dati (e.g. modelli ARIMA).

11.2.4 Normalità?

Per verificare l’ipotesi di normalità si possono utilizzare gli strumenti grafici e di verifica di ipotesi introdotti nei precedenti laboratori. Si può ad esempio utilizzare il normal probability plot:

qqnorm(res,datax = T)
qqline(res,datax = T)

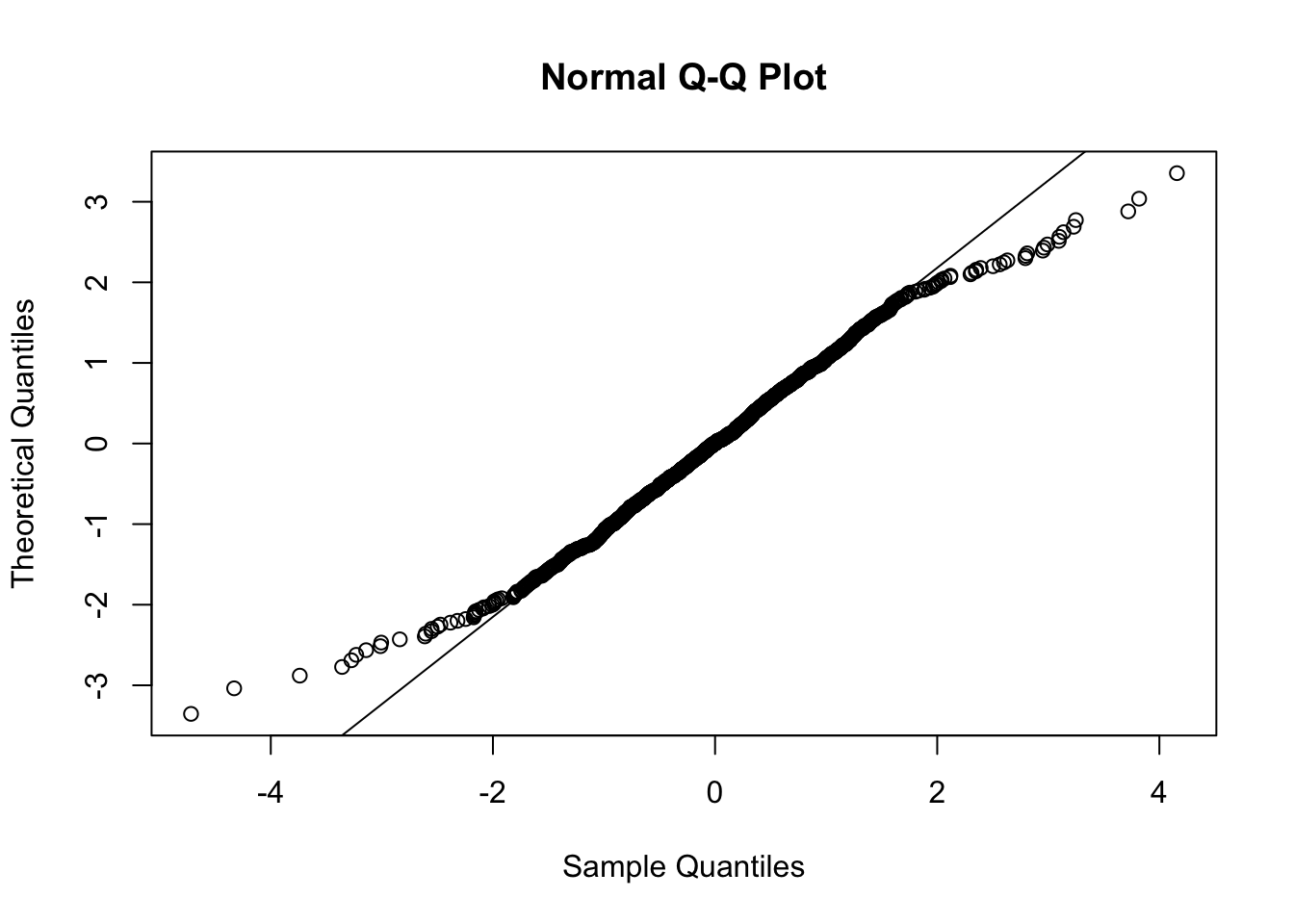
Il grafico mostra un andamento convesso-concavo, tipico di distribuzion con code più pesanti rispetto alla Normale. E’ anche possibile svolgere un test:

shapiro.test(res)

## 
## 	Shapiro-Wilk normality test
## 
## data:  res
## W = 0.98784, p-value = 9.853e-09

Dato il valore praticamente nullo del p-value, si rifiuta l’ipotesi di normalità.

11.3 Esercizi Lab 9

11.3.1 Esercizio 1

Considerare il dataset state.x77 già presente in R (digitare state.x77 per visionare il corrispondente oggetto).

Consultarne l’help per avere una descrizione delle variabili e delle unità statistiche.
Trasformare state.x77 in un data frame utilizzando la funzione data.frame (usare un nuovo nome per il data frame).
Ricavare la matrice di correlazione e la matrice degli scatterplot per le variabili Life.Exp, HS.Grad, Murder e Frost. Commentare.
Stimare il modello di regressione multipla che utilizza Life.Exp come variabile dipendente e HS.Grad e Murder come regressori. Commentare i risultati del modello. E’ necessario rimuovere qualche regressore?
Valutare la collinearità dei regressori. Commentari i valori.
Calcolare per ogni osservazione il leveraggio ($H_{ii}$) e rappresentarli graficamente. Inserire nel grafico la soglia. Commentare e cercare di identificare le osservazioni con alto leveraggio.
Calcolare per ogni osservazione la distanza di Cook e rappresentarla graficamente. Inserire nel grafico la soglia critica. Commentare e cercare di identificare le osservazioni influenti.
Rappresentare in un unico grafico leveraggio, distanza di Cook e residui studentizzati esternamente. Identificare nel grafico i punti influenti.
Ricavare i residui studentizzati esternamente e rappresentarli graficamente in uno scatterplot. Commentare il grafico.
Studiare la normalità dei residui. Commentare.
Verificare graficamente l’ipotesi di omoschedasticità. Commentare.
Verificare graficamente l’ipotesi di linearità. Commentare.
Verificare graficamente l’ipotesi di incorrelazione degli errori. Commentare.

11.3.2 Esercizio 2

Caricare la liberari faraway. Considerare poi il dataset savings presente nella libreria faraway.

Consultarne l’help per avere una descrizione delle variabili e delle unità statistiche.
Ricavare la matrice di correlazione per tutte le variabili. Commentare considerando sr come variabile dipendente.
Stimare il modello di regressione multipla che utilizza sr come variabile dipendente e le restanti come regressori come regressori. Commentare i risultati del modello. E’ necessario rimuovere qualche regressore? Se sì, procedere alla scelta del modello migliore.
Valutare la collinearità dei regressori. Commentari i valori. C’è qualche problema di collinearità? Se sì, risolvere eliminando qualche regressore.
Rappresentare graficamente insieme i valori di leveraggio e della distanza di Cook ed identificare eventuali punti influenti. A quali stati corrispondono?
Ricavare i residui studentizzati esternamente (rse) e rappresentarli graficamente in uno scatterplot.
Studiare la normalità dei rse. Commentare.
Verificare graficamente l’ipotesi di omoschedasticità. Commentare.
Verificare graficamente l’ipotesi di linearità. Commentare.
Verificare graficamente l’ipotesi di incorrelazione. Commentare.

11.3.3 Esercizio 3

Considerare il file simdata.csv che contiene dati simulati per una variabile risposta y e 2 regressori (x1 e x2) per $n=500$ osservazioni. Importare i dati in R.

Rappresentare graficamente la variabile risposta. Cosa si può concludere?
Stimare il modello completo.

Fornire il summary del modello stimato.
Si considerino i residui studentizzati e si verifichino le assunzioni del modello di regressione. Cosa si può concludere? Si osservano problemi?

Usare la trasformazione di Box-Cox per cercare di risolvere il problema di asimmetria della variabile risposta (aggiungere la nuova variabile trasformata al dataframe).

Rappresentare graficamente la nuova variabile risposta trasformata.
Stimare nuovamente il modello completo e fornirne l’output.
Si considerino i residui studentizzati e si verifichino le assunzioni del modello di regressione. Cosa si può concludere? Si osservano problemi?

Si consideri un effetto non lineare di $X_1$ nell’equazione del modello $Y = \beta_0+\beta_1X_1+\beta_2X_1^2+\beta_3X_2+\epsilon$ che verrà tradotto in R come segue: y ~ poly(x1,degree=2,raw = F)+x2.

Fornire il summary del modello completo con componenti non lineari per $X1$.
Si considerino i residui studentizzati e si verifichino le assunzioni del modello di regressione. Cosa si può concludere? Si osservano problemi?