5 Lab 3 - 29/10/2020

In questa lezione vedremo come aggiungere nuove colonne ad un data frame che già è presente nell’ambiente di lavoro. Impareremo poi a calcolare i rendimenti e a studiarne la distribuzione utilizzano boxplot e istogramma.

5.1 Aggiungere nuove colonne

Per questa lezione useremo lo stesso set di dati utilizzati per il Lab 2 (file Adjcloseprices.csv). Procediamo quindi con l’importazione dei dati come descritto nel Lab 2; l’oggetto fdata verrà creato quando si lancia il seguente codice:

fdata = read.csv("~/Dropbox/UniBg/Didattica/Economia/2020-2021/PSBF_2021/R_LABS/Lab02/Adjcloseprices.csv", sep=";", dec=".")

Si noti che uno degli input della funzione read.csv è il percorso del file (ovviamente questo è specifico per ogni computer). Se non siete sicuri di specificare nel modo corretto il percorso è possibile utilizzare l’opzione Import dataset di RStudio (pannello in alto a destra) come descritto nella sezione 4.1.

Si ipotizzi di voler creare una nuova variabile data dai prezzi del titolo N225 espressi in euro invece che dollari (si usa la trasformazione 1 dollaro = 0.85 euro). Il seguente codice calcola la nuova variabile (fdata$N225 * 0.85) e ne salva i valori in una nuova colonna di fdata denominata N225euro:

fdata$N225euro = fdata$N225 * 0.85
head(fdata) #si noti la nuova colonna
##         Date   N225      DJI     IXIC BTC.EUR    GSPC STOXX50E N225euro
## 1 2014-09-09 366.01 17013.87 15749.15 1988.44 4552.29  3245.43 311.1085
## 2 2014-09-10 368.35 17068.71 15788.78 1995.69 4586.52  3244.16 313.0975
## 3 2014-09-11 369.29 17049.00 15909.20 1997.45 4591.81  3237.76 313.8965
## 4 2014-09-12 367.49 16987.51 15948.29 1985.54 4567.60  3235.07 312.3665
## 5 2014-09-16 359.56 17131.97 15911.53 1998.98 4552.76  3221.73 305.6260
## 6 2014-09-17 353.98 17156.85 15888.67 2001.57 4562.19  3237.44 300.8830

Un approccio simile viene utilizzato per calcolare il valore di un portafoglio dato, per esempio, da DJI per il 70% e da GSPC per il 30%:

fdata$portfolio = fdata$DJI * 0.7 + fdata$GSPC * 0.3
head(fdata)
##         Date   N225      DJI     IXIC BTC.EUR    GSPC STOXX50E N225euro
## 1 2014-09-09 366.01 17013.87 15749.15 1988.44 4552.29  3245.43 311.1085
## 2 2014-09-10 368.35 17068.71 15788.78 1995.69 4586.52  3244.16 313.0975
## 3 2014-09-11 369.29 17049.00 15909.20 1997.45 4591.81  3237.76 313.8965
## 4 2014-09-12 367.49 16987.51 15948.29 1985.54 4567.60  3235.07 312.3665
## 5 2014-09-16 359.56 17131.97 15911.53 1998.98 4552.76  3221.73 305.6260
## 6 2014-09-17 353.98 17156.85 15888.67 2001.57 4562.19  3237.44 300.8830
##   portfolio
## 1  13275.40
## 2  13324.05
## 3  13311.84
## 4  13261.54
## 5  13358.21
## 6  13378.45

Si noti che la nuova variabile portfolio è stata correttamente aggiunta al data frame.

5.2 Calcolo dei rendimenti

Per comodità si consiglia di iniziare a calcolare i log rendimenti usando la seguente definizione: \[ r_t = \log\left(\frac{P_t}{P_{t-1}}\right) = \] per \(t=2, \ldots, n\).

In particolare sfrutteremo il fatto che i dati in R sono ordinati dai più antichi (prime righe del data frame) ai più recenti (ultime righe del data frame) e che i rendimenti logaritmici sono dati da differenze consecutive dei prezzi logaritmici (\(log(P_t) - log(P_{t-1})\)). I prezzi logaritmici sono facilmente calcolabili utilizzando la funzione log. Le differenze consecutive (per un vettore di prezzi) while differences posso essere ottenute utilizzando la funzione diff. Al fine di apprendere il funzionamento della funzione diff si consideri un piccolo vettore contenente i primi 5 prezzi di N225:

mini = fdata$N225[1:5]
mini
## [1] 366.01 368.35 369.29 367.49 359.56

Applicando la funzione diff all’oggetto (vettore) mini si ottiene il seguente vettore

diff(mini)
## [1]  2.339996  0.940003 -1.800019 -7.929992

il cui primo elemento è dato dalla differenza tra il secondo prezzo (368.350006) e il primo (366.01001). Analogamente la seconda differenza è data dalla differenza tra il terzo prezzo (369.290009) e il secondo (366.01001). Ripetendo la procedura per ogni giorno si otterrà un vettore di differenza la cui lunghezza è \(n-1\) (non è possibile calcolare la differenza per il primo giorno).

Per calcolare i rendimenti logaritmici è necessario calcolare prima i prezzi logaritmici di cui calcolarne poi le differenze con diff:

diff(log(mini))
## [1]  0.006372907  0.002548678 -0.004886187 -0.021815024

Il primo valore è il primo rendimento logaritmo. A titolo di controllo lo si può anche calcolare “manualmente”:

log(mini[2]/mini[1])
## [1] 0.006372907
log(mini[2])-log(mini[1])
## [1] 0.006372907

Lo stesso approccio può essere utilizzato per calcolare tutti i rendimenti logaritmici per N225; essi verranno salvato nel nuovo oggetto di nome N225logret:

N225logret = diff(log(fdata$N225)) 
length(N225logret)
## [1] 1057

Una volta calcolati i rendimenti logaritmici è possibile ottenere i rendimenti lordi con la seguente formula: \[ \frac{P_t}{P_{t-1}} = \exp(r_t) \] I rendimenti netti sono infine ricavabili con la seguente formula: \[ R_t = \frac{P_t}{P_{t-1}}-1 \]

Qui di seguito il codice di R per il calcolo dei rendimenti lordi e netti:

N225grossret = exp(N225logret)
N225netret = N225grossret - 1

Le tre serie storiche di rendimenti posso essere rappresentate graficamente come descritto nella Sezione ??:

plot(N225grossret, type="l", ylim=c(-0.5, 1.5),ylab="Returns")
lines(N225netret, col="blue")
lines(N225logret, col="red")
abline(h = 1, col="red")
abline(h = 0, col="green")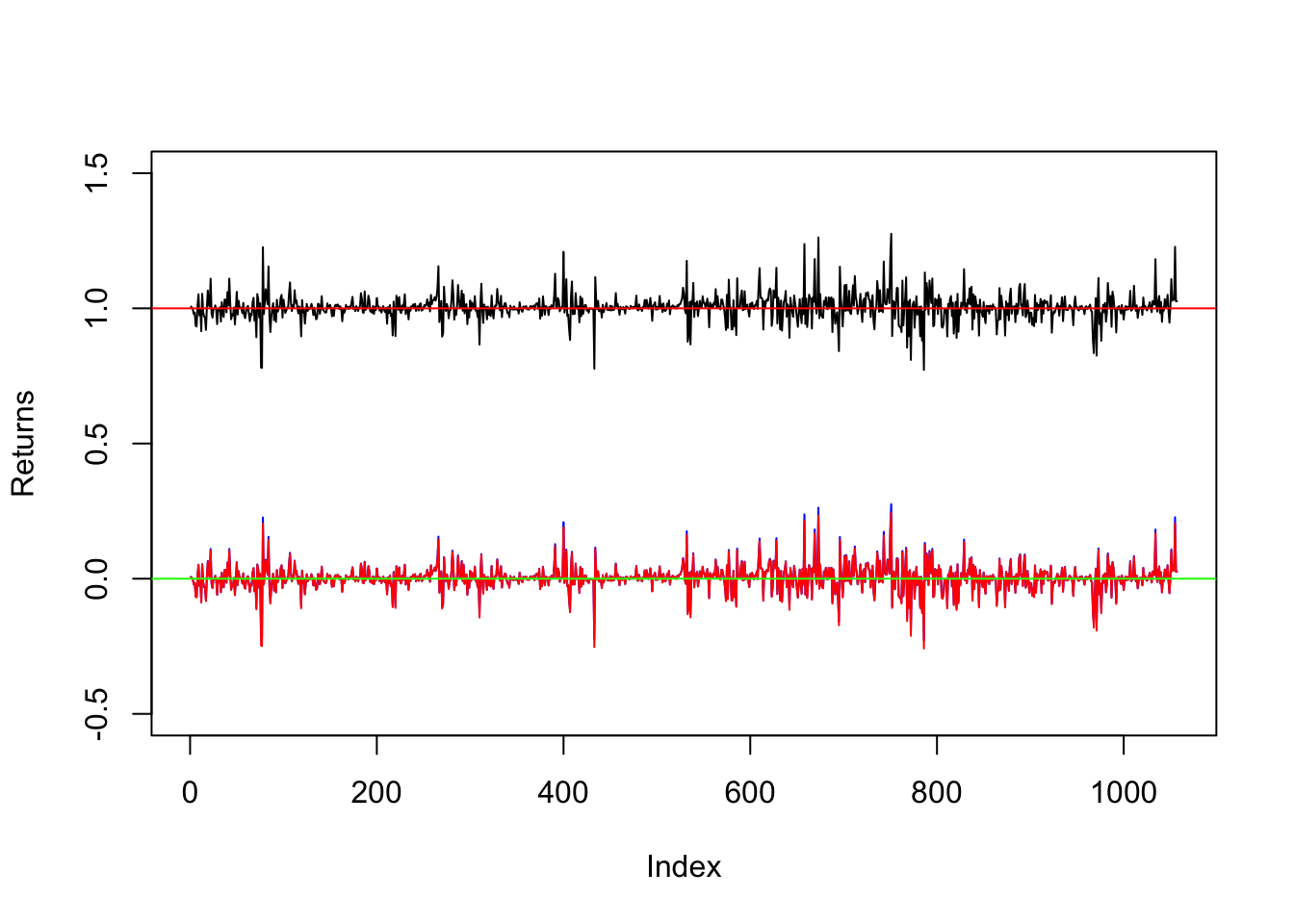

Si noti che la serie storica rossa di rendimenti logaritmici copre quasi interamente la serie storica blu dei rendimenti netti; questo è dovuto alle proprietà teoriche dei rendimenti e al fatto che \(r_t\simeq R_t\) per valri piccoli di \(R_t\).

La funzione abline aggiunge una linea costante orizzontale al grafico per \(y=1\) e \(y=0\) che rappresentano il valore di riferimento per i rendimenti lordi e netti/logaritmici (indicano nessun cambiamento nel prezzo).

Concludiamo questa sezione calcolando i rendimenti logaritmici per i rimanenti titoli in fdata;

DJIlogret = diff(log(fdata$DJI)) 
IXIClogret = diff(log(fdata$IXIC)) 
BTClogret = diff(log(fdata$BTC.EUR)) 
GSPClogret = diff(log(fdata$GSPC)) 
STOlogret = diff(log(fdata$STOXX50E))

Infine creiamo un nuovo data frame che contiene tutti i rendimenti logaritmici. Si userà la funzione data.frame andando a fornire come input i vettori da inserire come colonne nel nuovo data frame:

logretdf = data.frame(N225logret,
                      DJIlogret,
                      IXIClogret,
                      BTClogret,
                      GSPClogret,
                      STOlogret)
dim(logretdf)
## [1] 1057    6
head(logretdf)
##     N225logret    DJIlogret   IXIClogret     BTClogret   GSPClogret
## 1  0.006372907  0.003218174  0.002513158  0.0036394436  0.007491159
## 2  0.002548678 -0.001155467  0.007597992  0.0008815169  0.001152724
## 3 -0.004886187 -0.003613197  0.002454045 -0.0059804054 -0.005286370
## 4 -0.021815024  0.008467995 -0.002307595  0.0067461034 -0.003254333
## 5 -0.015640611  0.001451138 -0.001437749  0.0012948052  0.002069167
## 6 -0.066367068  0.006341196  0.011196703  0.0048792571  0.006824302
##       STOlogret
## 1 -0.0003914022
## 2 -0.0019746940
## 3 -0.0008311487
## 4 -0.0041321109
## 5  0.0048643997
## 6  0.0104260174

5.3 Boxplot

Il boxplot è un utile strumento grafico per lo studio di una distribuzione e per il confronto tra distribuzioni diverse. In questo caso si intende confrontare le diverse distribuzioni di rendimenti logaritmici:

boxplot(logretdf)

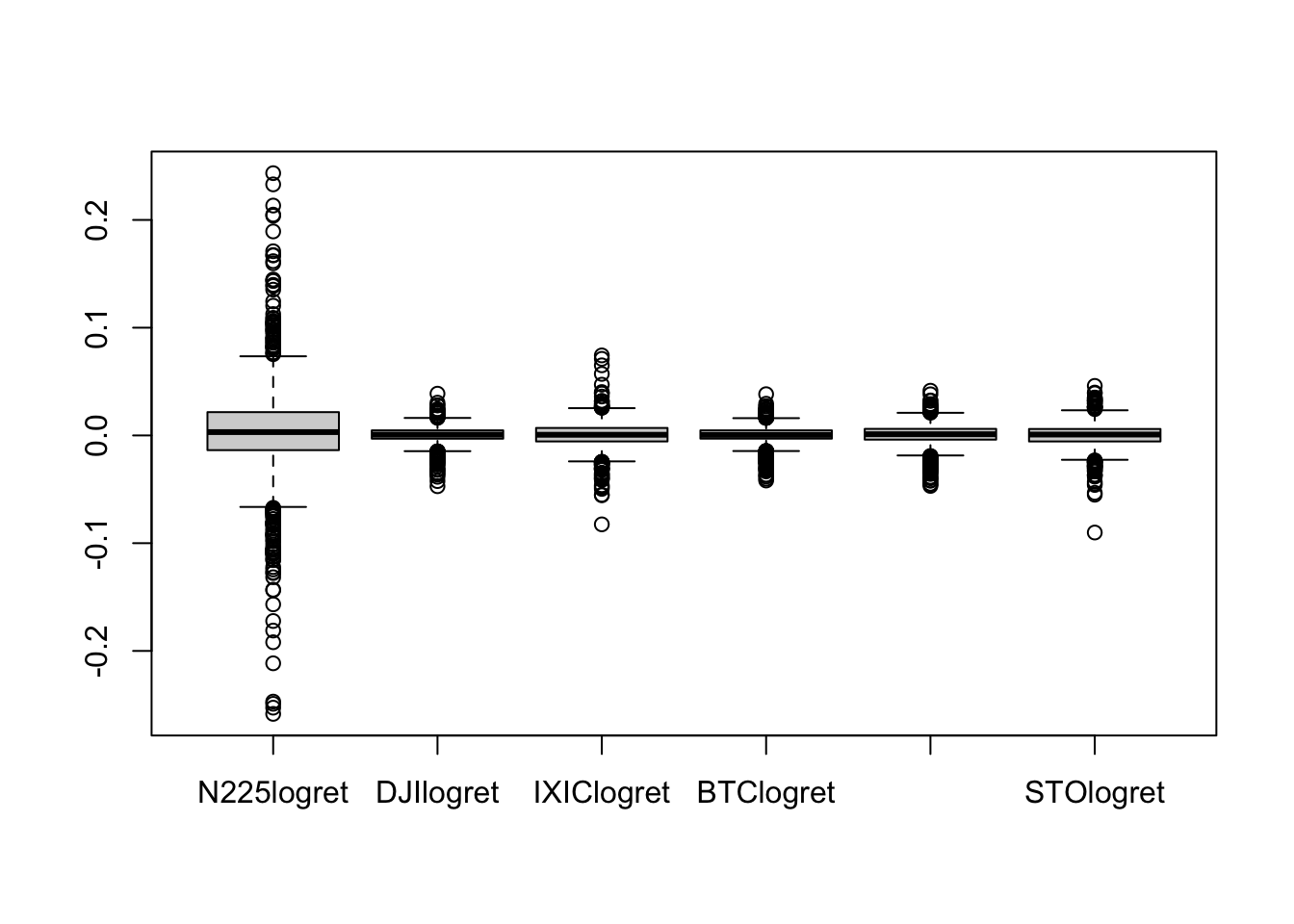Si nota che i rendimenti di N225 presentano una maggiore variabilità rispetto agli altri titoli, e sono inoltre caratterizzati da valori estremi (positivi e negativi). Per tutti i titoli la mediana è vicino a zero e i baffi risultano simmetrici rispetto alla scatola.

5.4 Indice di asimmetria

La formula per il calcolo dell’indice di asimmetria (skewness) è data da \[ sk = \frac{\frac{\sum_{i=1}^n (x_i-\bar x)^3}{n}}{\sigma^3} \] dove \(\bar x\) rappresenta la media aritmetica e \(\sigma\) la standard deviation (scarto quadratico medio) dei dati. In R l’indice può essere calcolato come segue:

mean((logretdf$N225logret - mean(logretdf$N225logret))^3) / sd(logretdf$N225logret)^3
## [1] -0.2690806

Si può quindi concludere che la distribuzione dei rendimenti logaritmici di N225 è caratterizzata da una lieve asimmetria negativa (coda lunga a sinistra).

5.5 Istogramma

L’asimmetria è evidente anche dalla rappresentazione grafica della distribuzione tramite istogramma:

hist(logretdf$N225logret)
abline(v=mean(logretdf$N225logret),col="blue")
abline(v=median(logretdf$N225logret),col="red")
abline(v=quantile(logretdf$N225logret,0.9),col="violet")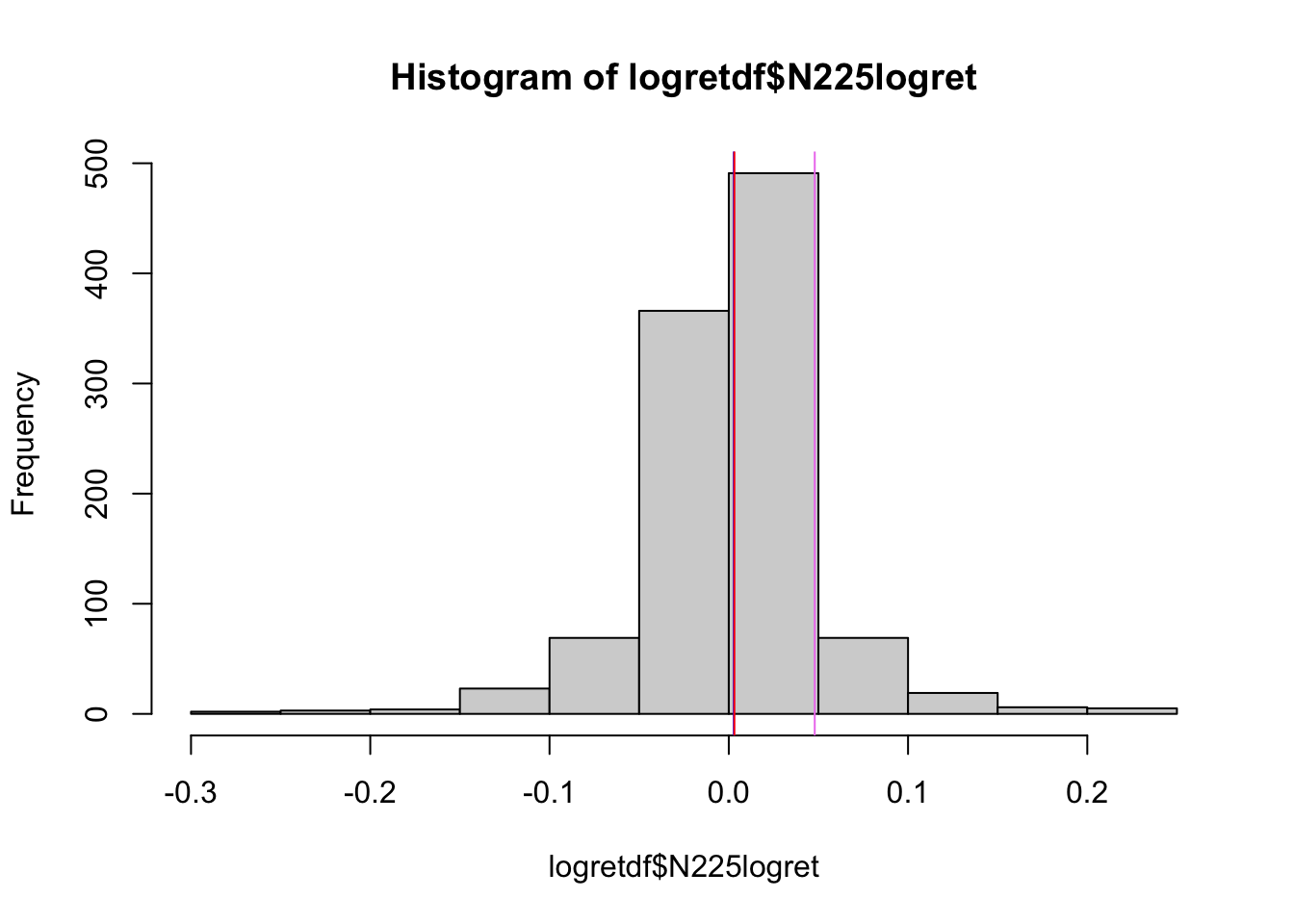

L’istogramma riporta sull’asse delle x i valori dei rendimenti in classi e sull’asse delle y le corrispondente frequenze (i.e. numero di giorni). La funzione abline è utilizzata qui per aggiungere 3 linee verticali costanti in corrispondenza della media, della mediana e del novantesimo quantile della distribuzione. In particolare,

quantile(logretdf$N225logret,0.9)
##        90% 
## 0.04795029

rappresenta il valore dei rendimenti logaritmici che divide in due la distribuzione, con 90% dei dati a sinistra e 10% a destra.

5.6 Esercizi Lab 3

5.6.1 Esercizio 1

Scaricare dall’e-learning i tre file CSV JNJ.csv, PFE.csv e NVS.csv (fonte dei dati: https://finance.yahoo.com/). Essi si riferiscono alle serie storiche dei prezzi dei seguenti titoli per il periodo 3/10/2013 - 3/10/2018: Johnson & Johnson (JNJ), Pfizer Inc. (PFE) e Novartis AG (NVS). Ogni file contiene le seguenti variabili:

  • Date: data
  • Open: prezzo di apertura
  • High: prezzo massimo registrato dal titolo nella giornata di negoziazione
  • Low: prezzo minimo registrato dal titolo nella giornata di negoziazione
  • Close: prezzo di chiusura
  • Adj.Close: prezzo di chiusura aggiustato per dividendi e frazionamenti
  • Volume: quantita’ complessiva di titoli scambiati nella giornata

Importare i 3 file in R creando 3 oggetti diversi con nomi JNJ, PFE e NVS. Fate attenzione al separatore di campo! Controllare le date dei 3 data frame per verificare che siano le stesse e abbiano lo stesso.

  1. Aggiungere al data frame NVS una nuova variabile (denominata Adj.Close.euro) data dai prezzi Adj.Close espressi in Euro (considerare che 1 Euro = 1.15 dollari).

  2. Usando la funzione plot rappresentare sullo stesso grafico le variabili Adj.Close (sull’asse delle x) e Adj.Close.euro (sull’asse delle y). Cosa si osserva?

  3. Calcolare per i tre titoli i rendimenti netti a partire dai prezzi Adj.Close. Calcolare, inoltre delle statistiche descrittive, per i rendimenti netti dei tre titoli.

  4. Costruire un nuovo data frame di nome mydata contenente i valori dei rendimenti netti per i tre titoli. Controllare la struttura e la dimensione del data frame.

  5. Rappresentare graficamente sullo stesso grafico le tre serie storiche dei rendimenti netti. Commentare il grafico.

  6. Rappresentare le tre distribuzioni dei rendimenti netti tramite boxplot. Commentare il grafico.

  7. Dal grafico precedente si dovrebbe osservare che PFE presenta un valore positivo estremo (superiore a 0.06). E’ possibile recuperare la data associata a questo valore (suggerimento: fare una selezione per condizione)?

  8. Nel boxplot i valori estremi sono indicati con dei punti. I valori estremi sono definiti tali se sono inferiore al valore \(Q_1-1.5*W\) o (OR) superiori al valore \(Q_3+1.5*W\), dove \(Q_1\) rappresenta il primo quartile, \(Q_3\) il terzo quartile e \(W=Q_3-Q1\) la differenza interquartile. Calcolare per ogni serie di rendimenti netti il numero di valori estremi (nella condizione l’operatore OR si traduce con |).

  9. Rappresentare la distribuzione dei rendimenti netti di ogni titolo tramite un istogramma (aggiungere al grafico media, mediana e quantili di ordine 0.1 e 0.9).

  10. Calcolare per le tre distribuzioni di rendimenti netti la percentuale di rendimenti superiori a 0.03 o inferiori a - 0.03.

  11. Calcolare l’indice di asimmetria per le tre distribuzion di rendimenti netti.