10 Lab 8 - 04/12/2020

In questa lezione andremo a studiare il modello di regressione multiplo dato dalla seguente equazione: $Y = \beta_0+\beta_1 X_1 +\beta_2X_2+\ldots+\beta_pX_p+ \epsilon$ dove $\beta_0$ è l’intercetta e $\beta_j$ è il coefficiente del regressore $X_j$ ( $j=1,\ldots,p$ ). Il termine $\epsilon$ rappresenta l’errore a media nulla e con variranza pari a $\sigma^2_\epsilon$ .

Utilizzeremo gli stessi dati del Lab 7 (file datareg_logreturns.csv) riguardanti i rendimenti logaritmici (log-returns) di:

the NASDAQ index
ibm, lenovo, apple, amazon, yahoo
gold
the SP500 index
the CBOE treasury note Interest Rate (10 Year)

Iniziamo con l’importazione dei dati:

data_logreturns = read.csv("~/Dropbox/UniBg/Didattica/Economia/2020-2021/SAPF_2021/R_labs/lab7/data_logreturns.csv", sep=";")
str(data_logreturns)

## 'data.frame':	1258 obs. of  10 variables:
##  $ Date  : chr  "27/10/11" "28/10/11" "31/10/11" "01/11/11" ...
##  $ ibm   : num  0.02126 0.00841 -0.01516 -0.01792 0.01407 ...
##  $ lenovo: num  -0.00698 -0.02268 -0.04022 -0.00374 0.07641 ...
##  $ apple : num  0.010158 0.000642 -0.00042 -0.020642 0.002267 ...
##  $ amazon: num  0.04137 0.04972 -0.01769 -0.00663 0.01646 ...
##  $ yahoo : num  0.02004 -0.00422 -0.05716 -0.04646 0.01132 ...
##  $ nasdaq: num  0.032645 -0.000541 -0.019456 -0.029276 0.012587 ...
##  $ gold  : num  -0.023184 0.006459 0.030717 0.043197 -0.000674 ...
##  $ SP    : num  0.033717 0.000389 -0.025049 -0.02834 0.015976 ...
##  $ rate  : num  0.0836 -0.0379 -0.0585 -0.0834 0.0025 ...

10.1 Regressione lineare multipla

Riprendiamo il modello di regressione semplice già mostrato nella Sezione 9.2, dove nasdq è la variabile dipendente e SP la variabile indipendente.

mod1 = lm(nasdaq ~ SP, data=data_logreturns)
summary(mod1)

## 
## Call:
## lm(formula = nasdaq ~ SP, data = data_logreturns)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0128494 -0.0018423  0.0002159  0.0020178  0.0115080 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 7.443e-05  8.777e-05   0.848    0.397    
## SP          1.085e+00  1.019e-02 106.471   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.003109 on 1256 degrees of freedom
## Multiple R-squared:  0.9003,	Adjusted R-squared:  0.9002 
## F-statistic: 1.134e+04 on 1 and 1256 DF,  p-value: < 2.2e-16

anova(mod1)

## Analysis of Variance Table
## 
## Response: nasdaq
##             Df   Sum Sq Mean Sq F value    Pr(>F)    
## SP           1 0.109579 0.10958   11336 < 2.2e-16 ***
## Residuals 1256 0.012141 0.00001                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Implmentiamo ora il modello completo utilizzando tutti le variabili disponibili nel data frame ( $p=8$ regressori). Nella funzione lm i regressori vanno specificati per nome e separati dal segno +:

mod2 = lm(nasdaq ~ ibm + lenovo + apple + amazon + yahoo + gold + SP + rate,
          data= data_logreturns)
summary(mod2)

## 
## Call:
## lm(formula = nasdaq ~ ibm + lenovo + apple + amazon + yahoo + 
##     gold + SP + rate, data = data_logreturns)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.011522 -0.001574  0.000089  0.001626  0.010487 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  6.097e-06  7.208e-05   0.085   0.9326    
## ibm         -9.625e-03  7.666e-03  -1.256   0.2095    
## lenovo       5.123e-03  3.361e-03   1.524   0.1277    
## apple        9.209e-02  5.008e-03  18.389   <2e-16 ***
## amazon       5.706e-02  4.285e-03  13.316   <2e-16 ***
## yahoo        3.901e-02  4.681e-03   8.333   <2e-16 ***
## gold        -5.936e-03  2.931e-03  -2.025   0.0431 *  
## SP           8.884e-01  1.462e-02  60.762   <2e-16 ***
## rate         2.604e-03  3.471e-03   0.750   0.4532    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.002547 on 1249 degrees of freedom
## Multiple R-squared:  0.9334,	Adjusted R-squared:  0.933 
## F-statistic:  2189 on 8 and 1249 DF,  p-value: < 2.2e-16

Nella tabella di summary vengono fornite le stime dei minimi quadrati dei parametri ( $\hat \beta_0,\hat \beta_1,\ldots,\hat\beta_p$ ) insieme alla stima della varianza data da $\sigma_\epsilon=\sqrt{\frac{SSE}{n-1-p}}$ ). In seconda colonna vengono riportati gli standard error delle stime che rappresentano una misura della precisione delle stime. Attraverso i valori t value (della statistica test t) e i corrispondenti p-value si può testare il seguente sistema di ipotesi: $H_0:\beta_j=0$ vs $H_1:\beta_j\neq 0$ separatamente per ogni coefficiente $\beta_j$ ( $j=1,\ldots,p$ ). Nel caso in esame non si rifiuta $H_0$ per le seguenti variabili: ibm, lenovo, rate (i.e. i corrispondenti parametri non sono significativamente diversi da zero e non c’è evidenza di un legame lineare con la variabile dipendente). Si noti che per la variabile gold c’è una debole evidenza empirica contro $H_0$ .

Quale è l’interpretazione del generico coefficiente $\hat\beta_j$ ? Per esempio si consideri apple: quando il rendimento logaritmico di apple aumenta di un’unità ci si aspetta un cambiamento pari a 0.0920924 per il rendimento logaritmico di nasdaq (tenendo fisse tutti gli altri regressori).

10.1.1 Analisi della varianza (test F sequenziali e globale)

Applichiamo ora la funzione anova per il modello di regressione multipla. In questo caso la funzione restituisce in output una serie di test F sequenziali sui singoli regressori (da intendersi inseriti uno ad uno). Questo tipo di analisi è utile per verificare l’effetto dell’inserimento di una nuova covariata (seguendo l’ordine utilizzando in lm).

anova(mod2)

## Analysis of Variance Table
## 
## Response: nasdaq
##             Df   Sum Sq  Mean Sq   F value Pr(>F)    
## ibm          1 0.040144 0.040144 6186.8396 <2e-16 ***
## lenovo       1 0.006941 0.006941 1069.7375 <2e-16 ***
## apple        1 0.020520 0.020520 3162.4311 <2e-16 ***
## amazon       1 0.013850 0.013850 2134.4469 <2e-16 ***
## yahoo        1 0.006197 0.006197  955.0328 <2e-16 ***
## gold         1 0.000006 0.000006    0.8585 0.3543    
## SP           1 0.025956 0.025956 4000.1962 <2e-16 ***
## rate         1 0.000004 0.000004    0.5629 0.4532    
## Residuals 1249 0.008104 0.000006                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Nella tabella ottenuta con anova il valore 0.0081042 rappresenta SSE (si noti che è inferiore rispetto al corrispondente valore ottenuto con mod1).

Come mostrato in Figura 10.1 e 10.2, il valore di SS riportatno in colonna Sum Sq rappresenta l’incremento di $SS_R$ quando una nuova variabile viene aggiunta ai regressori già inseriti. E’ importante sottolineare che l’ordine delle variabili (così come specificato nella formula di lm) determina i risultati presentati nell’output della funzione anova (cambiando l’ordine cambia l’output in questo cambia l’ordine con cui vengono inserite sequenzialmente le variabili).

Il valore 0.0401439 rappresenta l’incremento di SSR del modello $Y=\beta_0+\beta_1 ibm+\epsilon$ rispetto al modello senza covariate
$Y=\beta_0+\epsilon$ (per quest’ultimo SSR=0). Si noti che i due modelli differiscono per un solo parametero (ecco perchè df=1). Analizzando il corrispondente valore del p-value associato al test F (con 1 e 1249 gradi di libertà), possiamo concludere che il coefficiente di ibm è significativamente diverso da zero (e quindi ibm è un predittore utile). Allo stesso modo, il valore 0.0069411 rappresenta l’incremento di SSR per il modello $Y=\beta_0+\beta_1 ibm+\beta_2 lenovo + \epsilon$ rispetto al modello che contiene solo ibm: $Y=\beta_0+\beta_1 ibm+\epsilon$ . Anche in questo caso il p-value porta al rifiuto dell’ipotesi nulla e alla conclusione che lenovo sia una covariata utile. Lo stesso ragionamento può essere ripetuto per tutti i regressori che vengono inseriti uno ad uno. Alla fine summando tutti gli incrementi di SSR si ottiene il valore totale di SSR per il modello che contiene tutti i $p=8$ regressori:

mod2_an = anova(mod2)
SSR = sum(mod2_an$`Sum Sq`[1:8])
SSR

## [1] 0.1136159

SSE = mod2_an$`Sum Sq`[9]
SSE

## [1] 0.008104249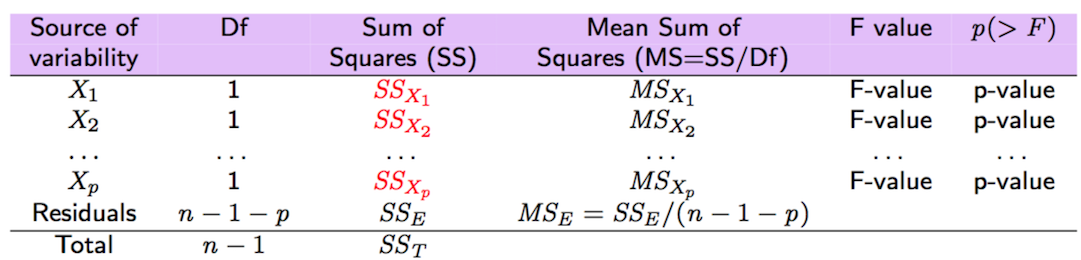

Figure 10.1: Test F sequenziali per modello di regressione multipla

Figure 10.2: Test F sequenziali per modello di regressione multipla

I valori di SSR e SSE possono poi essere utilizzati per eseguire il test F globale, i cui risultati sono riportati nell’ultima riga dell’output della funzione summary. Le ipotesi considerate sono: $H_0: \beta_1=\beta_2=\ldots=\beta_p=0$ (che corrisponde al modello $Y=\beta_0+\epsilon$ ) vs $H_1: \text{at least one } \beta\neq 0$ . Come riportato in Figura 10.3, la corrispondente statistica test è data da $\text{F-value}=\frac{SS_R/p}{SS_E/(n-1-p)}=\frac{MS_R}{MS_E}$ il cui valore è determinazione di una VC F di Fisher con $p$ e $n-1-p$ gradi di libertà. Si accetta per valori di F vicini a 0 (la zona di rifiuto è sulla coda di destra). Se si rifiuta l’ipotesi nulla significa che almeno una delle covariate ha potere predittivo, cioè è preferibile usare il modello di regressione multiplo piuttosto che la semplice media $\bar y$ (quest’ultima rappresenta il valore della previsione $\hat y$ nel caso di modelli senza regressori, $Y=\beta_0+\epsilon$ ).

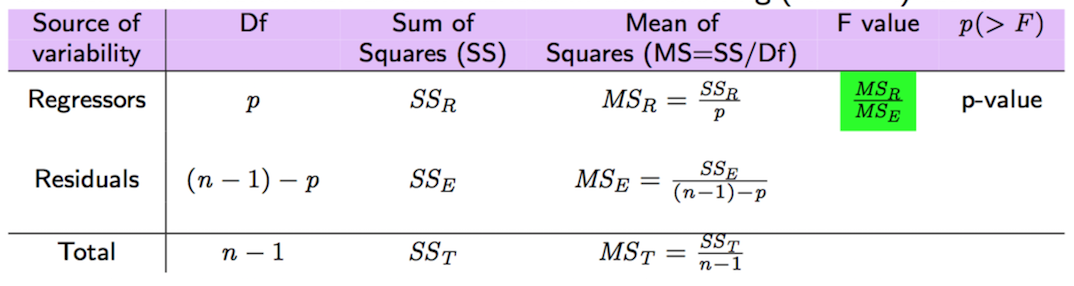
Figure 10.3: Test F globale per modello di regressione multipla

Il p-value del test F globale è riportato nell’ultima riga dell’output di summary (## F-statistic: 2189 on 8 and 1249 DF, p-value: < 2.2e-16). Come ci si aspettava, il p-values è praticamente nulla e porta al rifiuto di $H_0$ .

10.1.2 $R^2$ aggiustato

Utilizzando SSR, SSE, SST e i corrispondenti gradi di libertà (si veda in Figura 10.3), è possibile calcolare l’indice $R^2$ aggiusto (indice di bontà di adattamento): $adjR^2 =1- \frac{\frac{SS_E}{n-1-p}}{\frac{SS_T}{n-1}}=1-\frac{MS_E}{MS_T}$ Poichè nella formula di $adjR^2$ si include $p$ , c’è una penalizzazione per il numero di regressori inclusi nel modello. Di conseguenza $adjR^2$ , a differenza dell’indice $R^2$ introdotto in Sezione 9.2.3, può aumentare o dimunire. In particolare, l’indice aumenta solamente quando la variabile (o le variabili) aggiunte portano ad una decrescita del vaore di SSE sufficiente a compensare l’incremento di $p$ .

L’indice può essere calcolato manualmente come segue:

p = 8
n = nrow(data_logreturns)
SST = sum((data_logreturns$nasdaq - mean(data_logreturns$nasdaq))^2)
1 - (SSE/(n-1-p))/(SST/(n-1))

## [1] 0.9329925

Esso è riportato anche nell’output della funzione summary: Adjusted R-squared: 0.933. Questo valore indica un’ottima bontà di adattamento del modello ai dati.

10.1.3 Rimuove regressori non significativi

Dai t test riportai nel summary di mod2, si osserva che alcuni regressori non sono significativi. Per questa ragione andremo ora a rimuoverli, uno ad uno, iniziando dalla variabile con il p-value maggiore (rate). Si stima quindi un nuovo modello:

mod3 = lm(nasdaq ~ ibm + lenovo + apple + amazon + yahoo + gold + SP, data= data_logreturns)
summary(mod3)

## 
## Call:
## lm(formula = nasdaq ~ ibm + lenovo + apple + amazon + yahoo + 
##     gold + SP, data = data_logreturns)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0114711 -0.0015527  0.0000856  0.0016361  0.0104669 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.496e-06  7.204e-05   0.062   0.9502    
## ibm         -9.537e-03  7.664e-03  -1.244   0.2136    
## lenovo       5.244e-03  3.357e-03   1.562   0.1185    
## apple        9.211e-02  5.007e-03  18.396   <2e-16 ***
## amazon       5.692e-02  4.280e-03  13.298   <2e-16 ***
## yahoo        3.906e-02  4.680e-03   8.346   <2e-16 ***
## gold        -6.045e-03  2.927e-03  -2.066   0.0391 *  
## SP           8.913e-01  1.409e-02  63.258   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.002547 on 1250 degrees of freedom
## Multiple R-squared:  0.9334,	Adjusted R-squared:  0.933 
## F-statistic:  2502 on 7 and 1250 DF,  p-value: < 2.2e-16

Si noti che togliendo rate l’indice $R^2_{adj}$ non cambia (quindi includere rate non decresce SSE significativamente).Si procede rimuovendo ibm:

mod4 = lm(nasdaq ~  lenovo + apple + amazon + yahoo + gold + SP, data= data_logreturns)
summary(mod4)

## 
## Call:
## lm(formula = nasdaq ~ lenovo + apple + amazon + yahoo + gold + 
##     SP, data = data_logreturns)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0111649 -0.0015513  0.0000687  0.0016327  0.0108501 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  8.350e-06  7.199e-05   0.116   0.9077    
## lenovo       5.410e-03  3.355e-03   1.612   0.1071    
## apple        9.214e-02  5.008e-03  18.398   <2e-16 ***
## amazon       5.711e-02  4.278e-03  13.349   <2e-16 ***
## yahoo        3.941e-02  4.672e-03   8.435   <2e-16 ***
## gold        -5.886e-03  2.925e-03  -2.013   0.0444 *  
## SP           8.823e-01  1.208e-02  73.027   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.002547 on 1251 degrees of freedom
## Multiple R-squared:  0.9333,	Adjusted R-squared:  0.933 
## F-statistic:  2918 on 6 and 1251 DF,  p-value: < 2.2e-16

Di nuovo $R^2_{adj}$ non cambia. Si procede togliendo lenovo:

mod5 = lm(nasdaq ~  apple + amazon +
 yahoo + gold + SP, data= data_logreturns)
summary(mod5)

## 
## Call:
## lm(formula = nasdaq ~ apple + amazon + yahoo + gold + SP, data = data_logreturns)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0114026 -0.0015730  0.0000785  0.0016151  0.0107557 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  6.403e-06  7.202e-05   0.089    0.929    
## apple        9.191e-02  5.009e-03  18.348   <2e-16 ***
## amazon       5.702e-02  4.281e-03  13.321   <2e-16 ***
## yahoo        3.987e-02  4.666e-03   8.545   <2e-16 ***
## gold        -5.763e-03  2.925e-03  -1.970    0.049 *  
## SP           8.871e-01  1.171e-02  75.727   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.002549 on 1252 degrees of freedom
## Multiple R-squared:  0.9332,	Adjusted R-squared:  0.9329 
## F-statistic:  3496 on 5 and 1252 DF,  p-value: < 2.2e-16

Il valore del p-value di gold è molto vicino al valore soglia dato da alpha=0.05. Esiste quindi un’evidenza debole contro $H0:\beta_{gold}=0$ . Proviamo quindi a rimuovere gold e vedere che impatti ha questa scelta sulla bontà di adattamento:

mod6 = lm(nasdaq ~  apple + amazon +
yahoo  + SP, data= data_logreturns)
summary(mod6)

## 
## Call:
## lm(formula = nasdaq ~ apple + amazon + yahoo + SP, data = data_logreturns)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0114132 -0.0015924  0.0000558  0.0016247  0.0106998 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 7.367e-06  7.211e-05   0.102    0.919    
## apple       9.186e-02  5.015e-03  18.318   <2e-16 ***
## amazon      5.731e-02  4.283e-03  13.380   <2e-16 ***
## yahoo       3.964e-02  4.670e-03   8.489   <2e-16 ***
## SP          8.871e-01  1.173e-02  75.638   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.002552 on 1253 degrees of freedom
## Multiple R-squared:  0.933,	Adjusted R-squared:  0.9327 
## F-statistic:  4359 on 4 and 1253 DF,  p-value: < 2.2e-16

Si osserva che $R^2_{adj}$ per mod6 è molto simile a quello di mod5 (ed è un valore molto alto) ma mod6 è un modello più parsimonioso perchè ha un parametro in meno (è meno complesso). Per questa ragione mod6 è da preferire perchè, pur essendo parsimonioso, spiega una quota alta della variabilità della variabile risposta.

10.1.4 AIC

Per confrontare modelli diversi è possibile anche utilizzare l’indice Akaike Information Criterion (AIC) dato, nel caso di modello di regressione multipla, dalla seguente formula: $\text{AIC}=c + n \log({\hat\sigma^2_\epsilon})+2(1+p).$ dove $c$ è una costante che non influisce sul confronto tra modelli. Il criterio per AIC è: più piccolo è, migliore è il modello.

E’ possibile calcolare l’AIC usando la funzione extractAIC:

extractAIC(mod5)

## [1]      6.00 -15019.69

extractAIC(mod6)

## [1]      5.0 -15017.8

La funzione restituisce un vettore di lunghezza 2: il primo elemento è il numero totale di parametri ( $p$ + 1 (intercetta)), mentre il secondo numero è il valore di AIC. In questo caso mod5 presenta un valore inferiore di AIC. In realtà i due valore di AIC sono molto simili. Per questa ragione, considerando anche quanto detto precedentemente in merito all’alta bontà di adattamento, si continua a preferire mod6.

10.2 Variance Inflation Factor (VIF) - Collinearità

Il fattore di inflazione (crescita) della varianza (VIF) dice quanto la varianza di $\hat \beta_j$ (coefficiente del regressore $X_j$ ) viene incrementa avendo gli altri regressori nel modello ( $j=1,\ldots,p$ ). L’indice è definito come segue $VIF_j = \frac{1}{1-R^2_j}\geq 1$ dove $R^2_j$ è l’indice di bontà di adattamento del modello che ha $X_j$ come variabile dipendente e gli altri regressori come variabili indipendenti.

Si noti che l’indice $VIF_j$ non fornisce alcuna informazione circa la relazione esistente tra la variabile risposta e $X_j$ . Piuttosto ci informa di quanto $X_j$ sia correlato con gli altri regressori (collinearità). Si noti che nel caso di regressori indipendenti tutti i valori di VIF assumono il valore minimo pari ad 1. Si preferiscono, quindi, valori di VIF vicini ad 1. Valori superiori a 8 evidenziano problemi di collinearità.

La funzione vif contenuta nella libreria faraway permettono il calcolo dell’indice:

library(faraway)
vif(mod6)

##    apple   amazon    yahoo       SP 
## 1.335137 1.370225 1.381315 1.967353

In questo caso tutti i 4 valori di VIF (uno per ogni regressori) sono vicini ad 1. Si può quindi concludere che non ci sono problemi di collinearità.

10.3 Esercizi Lab 8

10.3.1 Esercizio 1

Un modello di regressione lineare con 3 regressori viene stimato per un dataset con 40 osservazioni. La correlazione tra valori osservati $y$ e valori previsti $\hat y$ è pari a 0.65. La somma totale dei quadrati (SST) è pari a 100.

Calcolare l’indice di bontà di adattamento (non aggiustato) $R^2$ e commentarne il valore.
Calcolare la somma dei quadrati degli errori (SSE).
Calcolare la somma dei quadrati della regressione (SSR).
Calcolare la stima di ${\sigma^2_\epsilon}$ .
Completare la seguente tabella ANOVA. Per il calcolo del p-value è possibile usare la funzione pf (vedere ?pf) che calcola le probabilità per la vc F dato un certo valore.

Source of variability	Df	Sum of Squares (SS)	Mean Sum of Squares (MS)	F value	p(>F)
Regressors	…	…	…	…	…
Residuals	…	…	…
Total	…	…

Commentare i risultati.

10.3.2 Esercizio 2

Completare la seguente tabella relativa al modello di regressione multipla $Y=\beta_0+\beta_1X_1+\beta_2X_2+\epsilon$ . Commentare tutti i passaggi eseguiti. Suggerimento: iniziare dai gradi di libertà e dal p-value. Il valore F-value si può ottenere usando la funzione qf (si veda ?qf) che restituisce i quantili della vc di F data una certa probabilità (è la funzione quantile).

Source of variability	Df	Sum of Squares (SS)	Mean Sum of Squares (MS)	F value	p(>F)
Regressors	…	…	…	…	0.04
Residuals	…	5.66	…
Total	15	…

Commentare i risultati.
Determinare il valore di $R^2$ e dell’ $R^2$ aggiustato. Commentare.

10.3.3 Esercizio 4

Il file “Adjcloseprice.csv” contiene i prezzi giornalieri (adjusted close prices) per i seguenti titoli/indici: The Boeing Company (BA), S&P 500 (GSPC), NASDAQ Composite (IXIC), Dow Jones Industrial Average (DJI), Best Buy Co., Inc. (BBY), Marriott International, Inc. (MAR) e Pfizer Inc. (PFE) per il periodo compreso tra 2010-11-15 e 2018-11-14 (fonte: Yahoo finance). Importare i dati in R.

Creare un nuovo data frame che contiene i rendimenti lordi per tutti i titoli.
Stimare il modello di regressione lineare completo che considera i rendimenti lordi di GSPC come variabile dipendente e tutti gli altri rendimenti come regressori. NB: nel modello di regressione dopo la tilde per indicare tutti i restanti regressori (senza doverli indicare uno ad uno) è possibile utilizzare un punto: lm(GSPCg ~ .). Questa semplificazione è utile soprattutto quando si hanno tanti regressori da inserire nella formula.
Commentare la significatività dei coefficienti. E’ necessario rimuovere qualche regressore?
Applicare la formula anova al modello completo e commentare l’output dei test sequenziali (il commento dipenderà ovviamente dall’ordine dei regressori nella formula).
Dalla tabella ANOVA calcolare SSR, SSE e SST.
Calcolare manualmente il valore della statistica test del test F globale. Verificare che coincida con quello riportato nel summary.
Calcolare manualmente il valore dell’ $R^2$ aggiustato. Verificare che coincida con quello riportato nel summary.
Calcolare l’AIC per il modello completo. Quanti parametri si stimano?
Rappresentare graficamente con uno scatterplot i valori osservati $y$ e i valori previsti $\hat y$ (fitted values). Calcolarne anche la correlazione. Commentare.