8 Lab 6 - 20/11/2020

In questa lezione verranno introdotti due test di normalità. Impareremo inoltre a fittare una distribuzione teorica a un campione di dati.

Utilizzeremo i dati contenuti nel file CPSch3.csv e relativi all’indagine Earnings from the Current Population Survey (CPS). Le seguenti variabili sono disponibili nel file:

year: anno dell’indagine (variabile quantitativa discreta)
ahe: guadagno medio orario (variabile quantitativa continua)
sex: genere (variabile qualitativa con due categorie

Si procede con l’importazione dei dati e la verifica della struttura del data frame:

CPSch3 = read.csv("~/Dropbox/UniBg/Didattica/Economia/2020-2021/SAPF_2021/R_labs/lab6/CPSch3.csv", sep=";")
str(CPSch3)

## 'data.frame':	11130 obs. of  3 variables:
##  $ year: int  1992 1992 1992 1992 1992 1992 1992 1992 1992 1992 ...
##  $ ahe : num  13 11.6 17.4 10.1 16.7 ...
##  $ sex : chr  "male" "male" "male" "female" ...

Per le variabili year e sex è possibile ricavare la distribuzione di frequenza che riporta per ogni categoria (o modalità) il corrispondente numero di osservazioni:

table(CPSch3$year)

## 
## 1992 1994 1996 1998 
## 2962 2956 2609 2603

table(CPSch3$sex)

## 
## female   male 
##   5174   5956

Si osserva per esempio che per l’anno 1992 sono disponibili 2962 osservazioni, corrispondenti al (26.61% del numero totale di osservazioni.

Inolte, anche la distribuzione di frequenza bivariata si può ottenere utilizzando la stessa funzione table:

table(CPSch3$year, CPSch3$sex)

##       
##        female male
##   1992   1371 1591
##   1994   1358 1598
##   1996   1235 1374
##   1998   1210 1393

Emerge che nell’anno 1992 ci sono 1371 osservazioni per il genere femminili, corrispondenti al 46.29% di tutte le osservazioni disponibili per il 1992, e al 26.5% di tutte le osservazion disponibili per le donne.

Di seguito andremo a considerare un sottoinsieme dal data frame originale, riferito solamente al genere maschile e agli anni dopo il 1994. Questa selezione può essere fatta fissando delle condizioni (logiche) così come mostrato nel Paragrafo 3.2. In alternativa è possibile usare la funzione subset come di seguito:

CPS = subset(CPSch3, sex=="male" & year>1994) 
dim(CPS)

## [1] 2767    3

head(CPS)

##      year       ahe  sex
## 5920 1996 11.660622 male
## 5922 1996 14.971988 male
## 5923 1996 25.958241 male
## 5924 1996  9.989918 male
## 5925 1996 13.451954 male
## 5926 1996 21.394132 male

str(CPS)

## 'data.frame':	2767 obs. of  3 variables:
##  $ year: int  1996 1996 1996 1996 1996 1996 1996 1996 1996 1996 ...
##  $ ahe : num  11.66 14.97 25.96 9.99 13.45 ...
##  $ sex : chr  "male" "male" "male" "male" ...

Il nuovo data frame denominato CPS contiene 2767 osservazioni.

Si considera quindi l’unica variabile quantativa continua e se ne rappresenta graficamente la distribuzione:

summary(CPS$ahe)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   2.159  12.009  16.233  17.416  21.377  52.467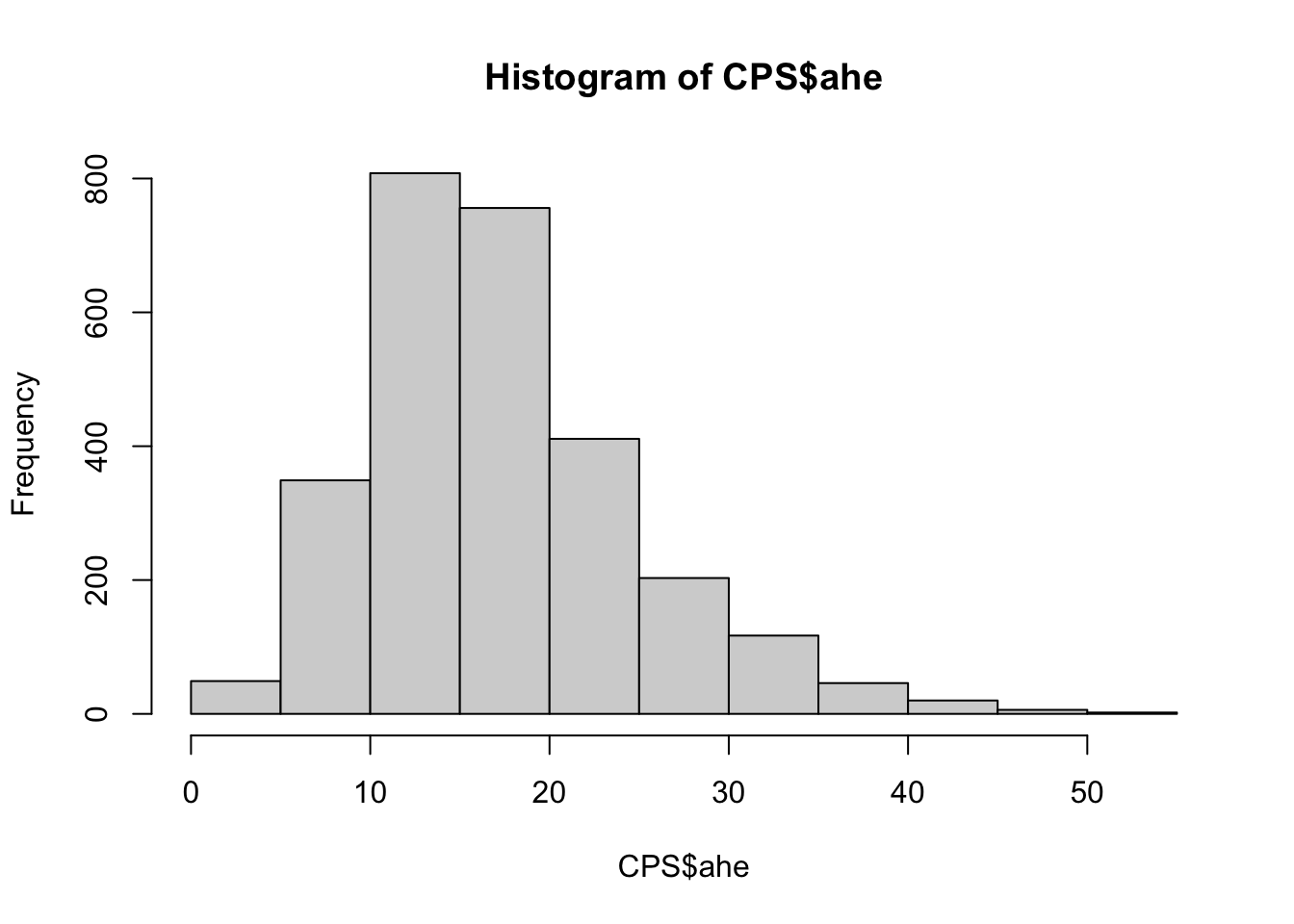

hist(CPS$ahe)

Si nota che la distribuzione è caratterizzata da asimmetria positiva, confermata anche dal fatto che la media è superiore alla mediana e dal seguente normal probability plot che risulta caratterizzato da concavità:

qqnorm(CPS$ahe,datax=T)
qqline(CPS$ahe,datax=T)

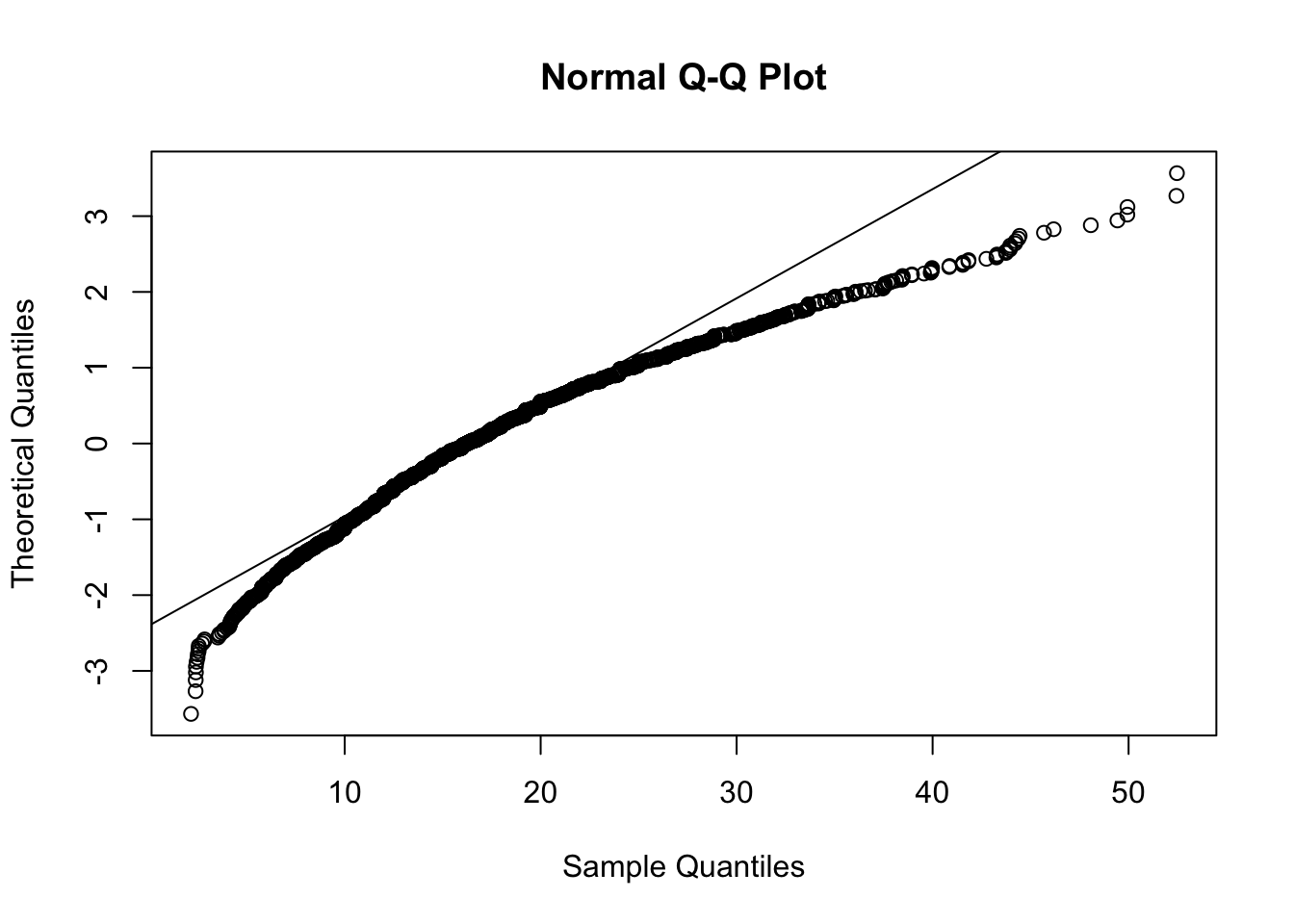
8.1 Test di normalità

In un test di normalità l’ipotesi nulla è data da: $H_0$: i dati provengono da una distribuzione Normale; l’ipotesi alternativa invece è definita come $H_1$: i dati non provengono da una distribuzione normale. Per prendere una decisione si utilizzerà il p-value, una probabilità che rappresenta l’evidenza empirica a favore/contro l’ipotesi nulla.

8.1.1 Test di Jarque-Bera

Il test di Jarque-bera utilizza la skewness campionaria $\hat{Sk}$ e la curtosi campionaria $\hat{Kur}$, che vengono confrontati con i corrispondenti valori di riferimento (0 e 3) nel caso di distribuzione Normale. La statistica test è data dalla seguente formula \[ JB = n\left(\frac{\hat{Sk}^2}{6}+\frac{(\hat{Kur}-3)^2}{24}\right) \] che, sotto l’ipotesi nulla, è distribuita approssimativamente come una variabile causale Chi-quadrato con 2 gradi di libertà ($\chi^2_2$). Sotto l’ipotesi nulla di normalità, ci aspettiamo un valore della statistica test vicino a zero.

Il test viene implementato in R tramite la funzione jarque.bera.test che è parte del pacchetto tseries.

Assumendo che il pacchetto tseries sia già stato installato (si veda il Paragrafo 7.3.1), lo carichiamo e lanciamo il test per la variabile ahe:

library(tseries)

## Registered S3 method overwritten by 'quantmod':
##   method            from
##   as.zoo.data.frame zoo

jarque.bera.test(CPS$ahe)

## 
## 	Jarque Bera Test
## 
## data:  CPS$ahe
## X-squared = 570.37, df = 2, p-value < 2.2e-16

Considerando il valore del p-value praticamente nullo rifiutiamo l’ipotesi nulla e concludiamo che il campione di dati fornisce una forte evidenza contro l’ipotesi nulla di normalità.

E’ anche possibile calcolare il valore della statistica test a mano, come segue:

n = length(CPS$ahe)
sk = mean((CPS$ahe-mean(CPS$ahe))^3)/sd(CPS$ahe)^3
kur = mean((CPS$ahe-mean(CPS$ahe))^4)/sd(CPS$ahe)^4
JB = n*(sk^2/6+(kur-3)^2/24)
JB

## [1] 569.0769

Si noti che il valore di JB ottenuto con il procedimento manuale non coincide esattamente con quello riportato nell’output della funzione jarque.bera.test (570.372621).

Questa differenza è dovuta al fatto che la funzione sd utilizzata nel denominatore del calcolo di sk e kur è la radice quadrata della varianza campionaria non distorta (quella calcolata dividendo per $n-1$). La funzione jarque.bera.test invece divide per $n$ per il calcolo della varianza. Per ottenere lo stesso valore di JB come la funzione jarque.bera.test si procede come segue (si noti come cambia il denominatore):

sk2 = mean((CPS$ahe-mean(CPS$ahe))^3)/(var(CPS$ahe)*(n-1)/n)^(3/2)
kur2 = mean((CPS$ahe-mean(CPS$ahe))^4)/(var(CPS$ahe)*(n-1)/n)^(4/2)
JB2 = n*(sk2^2/6+(kur2-3)^2/24)
JB2

## [1] 570.3726

Il valore di JB2 è ora uguale al valore della statistica test riportato nell’output di jarque.bera.test. Il corrispondente p-value può essere calcolato manualmente utilizzando la funzione
pchisq che fornisce il valore della CDF (i.e. $P(X\leq x)$) per una variabile casuale (VC) $X$ distribuita come una VC Chi-quadrato con df gradi di libertà. In questo caso df=2:

1-pchisq(JB2,df=2)

## [1] 0

Il complememnto a 1 è necessario perchè il p-value in questo caso rappresenta l’area a destra del valore JB2, mentre pchisq restituisce il valore a sinistra.

Come descritto nel Paragrafo 7.3, è possibile utilizzare la trasformazione di Box-Cox per risolvere il problema di asimmetria. La variabile trasformata, denominata ahe2, viene aggiunta al data frame, come descritto qui di seguito:

library(car)
bestpar = powerTransform(CPS$ahe)
bestpar$lambda

##   CPS$ahe 
## 0.3531166

CPS$ahe2 = bcPower(CPS$ahe,bestpar$lambda)
head(CPS)

##      year       ahe  sex     ahe2
## 5920 1996 11.660622 male 3.909613
## 5922 1996 14.971988 male 4.531714
## 5923 1996 25.958241 male 6.111130
## 5924 1996  9.989918 male 3.551352
## 5925 1996 13.451954 male 4.258539
## 5926 1996 21.394132 male 5.520853

La distribuzione della variabile trasformata viene studiata qui di seguito utilizzando diversi grafici:

hist(CPS$ahe2,freq=F)
lines(density(CPS$ahe2),col="red")

qqnorm(CPS$ahe2,datax = T)
qqline(CPS$ahe2,datax = T,col="red")

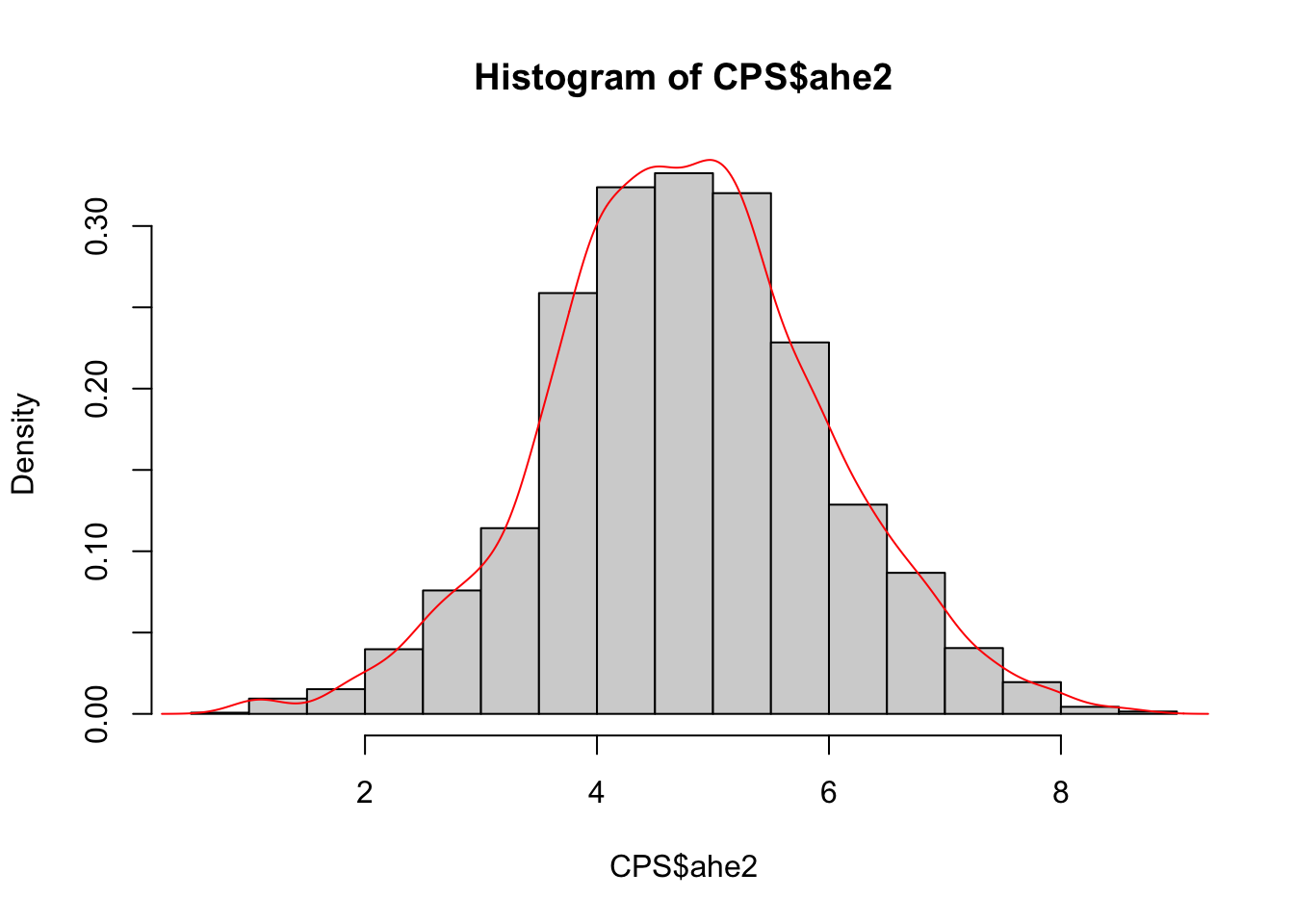
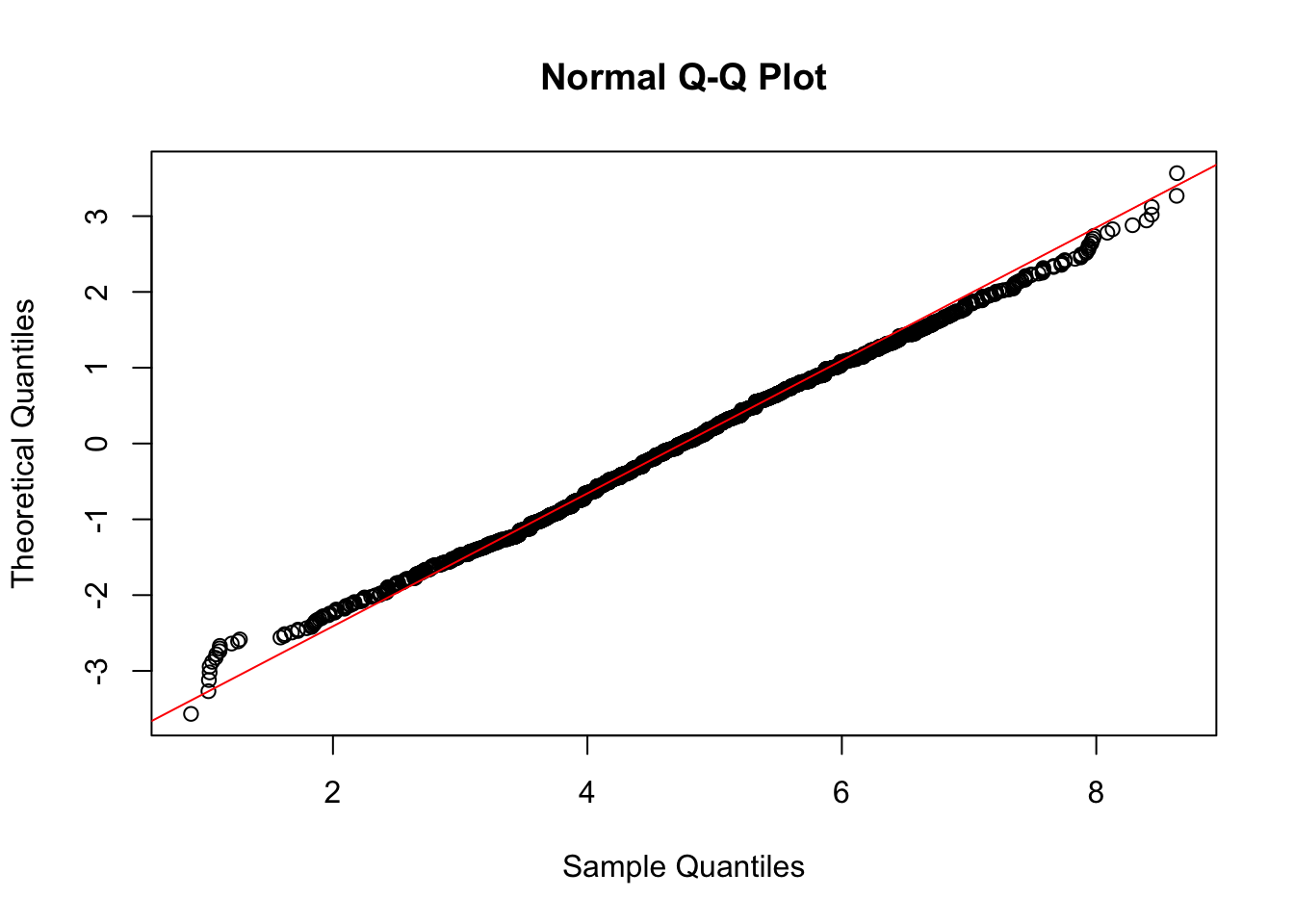
Figure 8.1: Normal probability plot della variabile trasformata ahe2

La distribuzione di ahe2 sembra essere simmetrica: la maggior parte dei punti sono localizzata lungo la linea di riferimento del normal probability plot anche se alcuni valori posizionati sulle cose si discostano dalla linea. E’ possibile concludere che i dati provengono da una distribuzione Normale? Per rispondere andremo ad utilizzare un (nuovo) test di normalità.

8.1.2 Test di Shapiro-Wilk

Il test di Shapiro-Wilk si basa sullo studio della correlazione tra i quantili empirici, dati da $y_{(i)}$, e i quantili teorici della Normale dati da $\Phi^{-1}(\frac{i}{n+1})$ per $i=1,\ldots,n$. Sotto l’ipotesi di normalità, la correlazione dovrebbe essere vicino a uno; al contrario l’ipotesi di normalità viene rigettata per valori piccoli di correlazione.

La funzione shapiro.test, che fa parte della versione base di R, fornisce il valore della statistica test (correlazione) e il corrispondente p-value. La funzione può essere utilizzata solo se la numerosità del campione di dati ($n$) è inferiore a 5000 osservazioni. E’ noto infatti che il test di Shapiro-Wilk sia molto sensibile e che, nel caso di $n$ grande, porti al rifiuto dell’ipotesi di normalità anche per piccoli scostamenti dalla distribuzione Normale.

shapiro.test(CPS$ahe2)

## 
## 	Shapiro-Wilk normality test
## 
## data:  CPS$ahe2
## W = 0.99775, p-value = 0.0005052

Nel caso considerato, anche se il valore della correlazione è piuttosto elevato (0.9977467), il p-value è piccolo e porta al rifiuto dell’ipotesi di normalità. Ciò è probabilmente dovuto ai valori presenti sulle code della distribuzione che si discostano dalla distribuzione Normale, così come mostrato in Figura 8.1.

Proviamo ad utilizzare il test di normalità di Jarque-Bera per gli stessi dati:

jarque.bera.test(CPS$ahe2)

## 
## 	Jarque Bera Test
## 
## data:  CPS$ahe2
## X-squared = 6.2297, df = 2, p-value = 0.04439

In questo caso il p-value non evidenzia una forte evidenza empirica contro l’ipotesi nulla (soprattutto se confrontato con il p-value del test di Shapiro-Wilk). In ogni caso, fissando il valore del livello di significatività a $\alpha=0.05$ (probabilità dell’errore di primo tipo), si andrà a rifiutare l’ipotesi di normalità anche in questo caso.

8.2 Fittare una distribuzione ai dati

Si intende fittare ai dati un modello teorico, la cui funzione di densità di probabilità (PDF) sia nota (e.g. distribuzione Normale o t di Student). I parametri della distribuzione teorica sono stimati tramite il metodo della massima verosimiglianza (ML).

Questo tipo di analisi può essere svolto in R utilizzando la funzione fitdistr contenuta nella libreria MASS. Quest’ultima è già disponibile nella release base di R e non è necessario installarla (ma solo caricarl con library(MASS)). Gli input della funzione fitdistr sono: i dati e il modello teorico da fittare ai dati (si veda ?fitdistr per l’elenco dei modelli teorici disponibili). Si consideri in prima battuta la distribuzione Normale (anche se sembra non essere particolarmente idoneo per i nostri dati visti i risultati dei test di normalità svolti precedentemente).

library(MASS)
fitN = fitdistr(x=CPS$ahe2,densfun="normal")
fitN

##       mean          sd    
##   4.76739792   1.19319427 
##  (0.02268332) (0.01603953)

L’output di fitN fornisce le stime di massima verosimiglianza provides per i due parametri della Normale (la media $\mu$ e la varianza $\sigma^2$) con i corrispondenti standard error forniti in parentesi che rappresentano una misura di accuratezza delle stime. Nel caso di modello Normale, la stima ML della media $\mu$è data dalla media campionaria $\bar x=\frac{\sum_{i=1}^n x_i}{n}$, mentre la stima ML della varianza è data dalla varianza campionaria distorta $s^2 =\frac{\sum_{i=1}^n (x_i-\bar x)^2}{n}$.

Si noti nel pannello in alto a destra che l’oggetto fitN è di tipo list (un nuovo tipo di oggetto che, come una scatola, può contenere al suo interno altri oggetti) contenente 5 oggetti il cui nome può essere ottenuto come segue:

names(fitN)

## [1] "estimate" "sd"       "vcov"     "n"        "loglik"

Per estrarre un generico elemento da una lista si utilizza il simbolo del dollaro; per esempio per estrarre da fitN l’oggetto che contiene le stime dei parametri si usa il seguente codice:

fitN$estimate #vettore delle stime

##     mean       sd 
## 4.767398 1.193194

fitN$estimate[1] #prima stima

##     mean 
## 4.767398

fitN$estimate[2] #seconda stima

##       sd 
## 1.193194

Un’altra distribuzione continua che può essere fittata ai dati è la distribuzione t standardizzata $t_\nu^{std}(\mu,\sigma^2)$. Si noti che in questo caso i parametri sono tre: media $\mu$, sd $\sigma$ e gradi di libertà $\nu$ (df). Si procede analogamente a prima andando a specificare "t" per l’argomento densfun:

fitT = fitdistr(CPS$ahe2,densfun="t")

## Warning in dt((x - m)/s, df, log = TRUE): NaNs produced

## Warning in log(s): NaNs produced

## Warning in log(s): NaNs produced

fitT

##         m             s            df     
##    4.76609084    1.13776818   21.78721404 
##  ( 0.02256787) ( 0.02553156) ( 8.46757670)

8.2.1 AIC e BIC

Quale è il miglior modello per i dati considerati? Per confrontare i due modelli fittati ai dati si può utilizzare il valore della funzione di log verosimiglianza (incluso con il nome loglik nell’output della funzione fitdistr): si andrà a preferire il modello con il valore più elevato di loglik.

fitN$loglik

## [1] -4414.949

fitT$loglik

## [1] -4411.569

In questo caso la distribuzioen di t ha un valore più elevato della funzione di log verosimiglianza. Una conclusione simile si ottiene analizzando il valore della devianza che rappresenta un indice di misfit da minimizzare (più piccola la devianza, migliore il fit). La devianza è definita come \[\text{deviance} = -2*\text{loglikelihood}\].

-2*fitN$loglik

## [1] 8829.898

-2*fitT$loglik

## [1] 8823.138

Anche in questo caso il modello t è da preferire. Ricordiamo però che esso è caratterizzato da un numero maggiore di parametri da stimare (ed è quindi da considerarsi come un modello più complesso). Per confrontare due modelli tenendo in considerazione anche la loro complessità è possibile utilizzare due indici: Akaike Information Criterion (AIC) e Bayes information criterion (BIC). Essi penalizzano la bontà di adattamento per il numero di parametri da stimare. Essi sono così definiti: \[ AIC = \text{deviance}+2p \]

\[ BIC = \text{deviance}+\log(n)p \] dove $p$ è il numero di parametri da stimare (2 per la Normale e 3 per la t) e $n$ la numerità del campione di dati. I termini $2p$ e $\log(n)p$ sono le penali legate alla complessità del modello. Entrambi gli indici AIC e BIC seguono il criterio smaller is better.

I due indici possono essere calcolati utilizzando le funzioni AIC e BIC come segue:

AIC(fitN)

## [1] 8833.898

AIC(fitT)

## [1] 8829.138

BIC(fitN)

## [1] 8845.749

BIC(fitT)

## [1] 8846.915

Confrontando i valori di AIC si preferisce il modello t; se invece si considerano i valori di BIC risulta preferibile il modello Normale. Si noti che solitamente $\log(n)>2$, per cui l’indice BIC penalizza di più rispetto all’AIC e per questo motivo porta alla scelta di modelli meno complessi. In ogni caso per i dati consideri i due valori di BIC sono molto simili e quindi la scelta può ricadere sul modello t.

8.2.2 Grafico della PDF della VC Normale

Si intende confrontare il grafico della stima Kernel della densità (KDE) per ahe2 con la funzione di densità della Normale fittata ai dati e riportata nella seguente formula (dove i parametri $\mu$ e $\sigma^2$ sono sostituiti dalle corrispondenti stime): \[ \hat f(x)=\frac{1}{\sqrt{2\pi s^2}}e^{-\frac{1}{s^2}(x-\bar x)^2} \]

Per calcolare i valori della PDF si utilizza la funzione dnorm(x,mean,sd) che restituisce i valori della PDF valutata per un set di valori x. Nel caso in analisi la KDE è data dal seguente grafico

plot(density(CPS$ahe2))

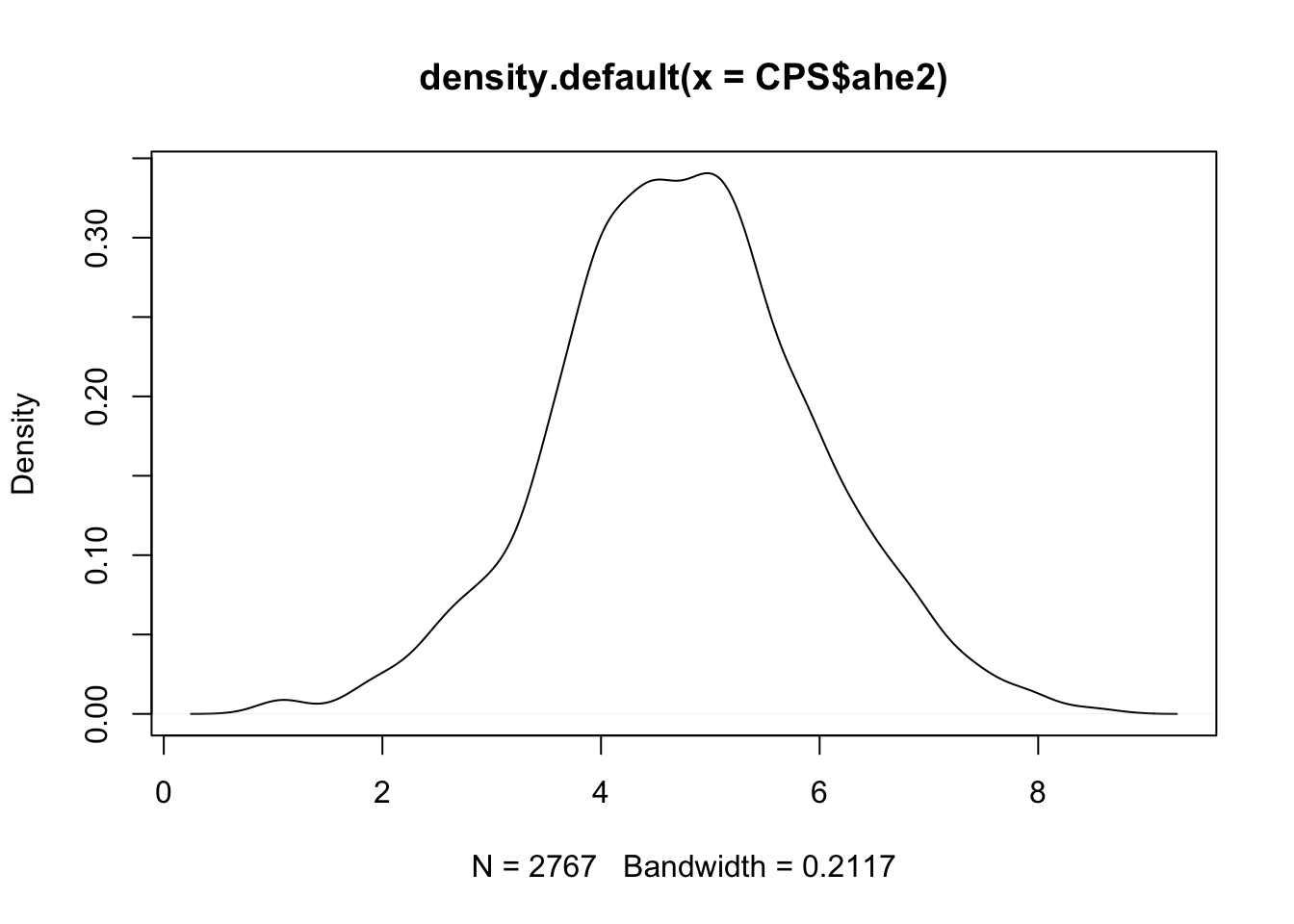e mostra valori sull’asse delle x compresi tra 0 e 9. Andremo quindi a costruire una sequenza regolare di 1000 valori tra 0 e 9 utilizzando la funzione seq:

xseq = seq(from=0,to=9, length=1000)
#parte iniziale della sequenza
head(xseq)

## [1] 0.000000000 0.009009009 0.018018018 0.027027027 0.036036036 0.045045045

#parte finale della sequenza
tail(xseq)

## [1] 8.954955 8.963964 8.972973 8.981982 8.990991 9.000000

Data la sequenza di valori per cui calcolare la PDF siamo ora pronti ad utilizzare la funzione dnorm. I valori del parametri saranno dati dalle stime ML contenute in fitN$estimates:

densN = dnorm(xseq,
          mean=fitN$estimate[1],
          sd=fitN$estimate[2])

Il vettore densN contiene 1000 valori per la PDF della Normale. Abbiamo ora tutti gli elementi per rappresentare graficamente la KDE insieme alla PFD della Normale fittata ai dati:

plot(density(CPS$ahe2),col="blue")
lines(xseq,densN,col="red")

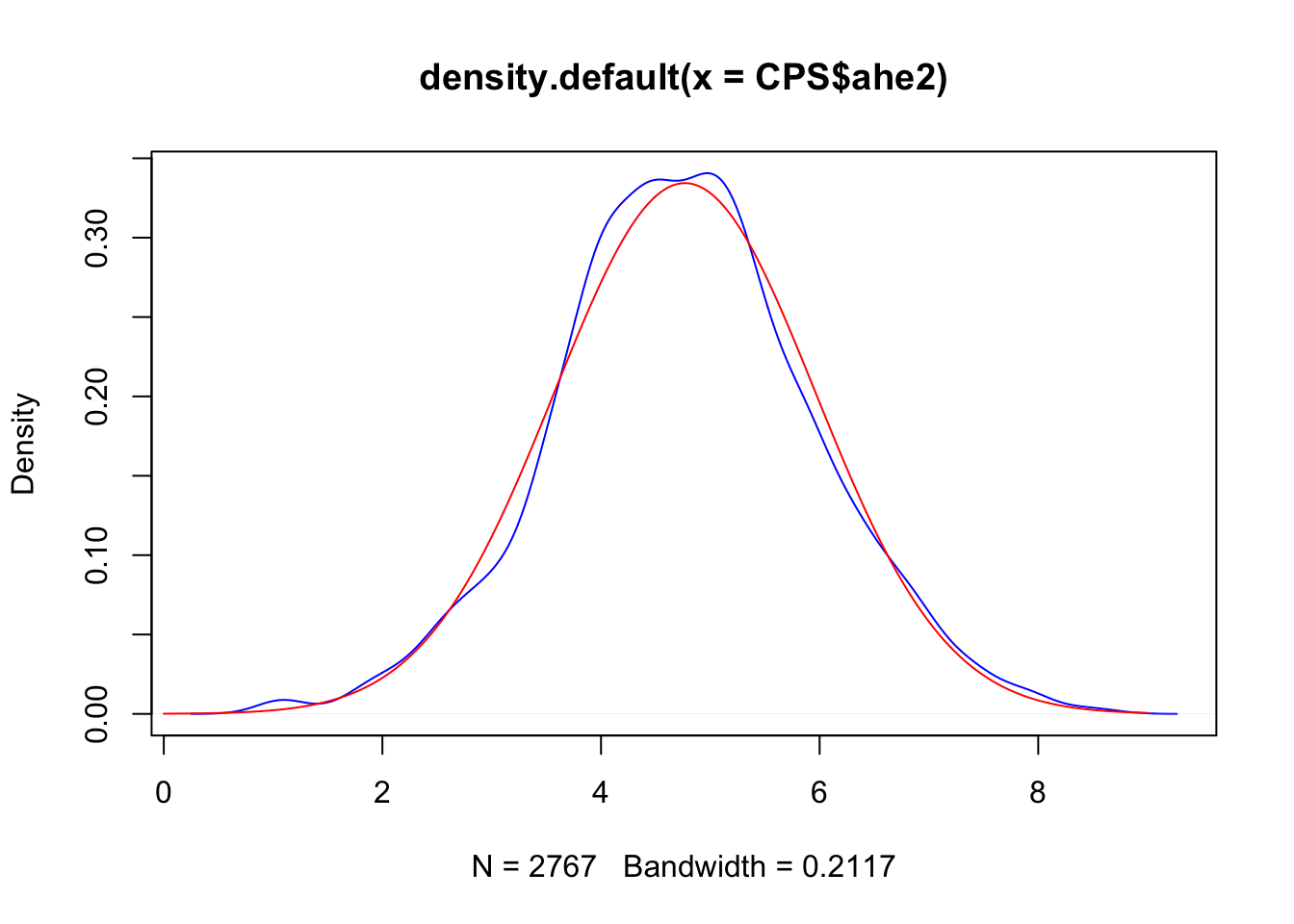
Si noti che sono evidente alcune differenza tra le due distribuzioni, responsabili molto probabilmente del rifiuto dell’ipotesi di normalità.

8.2.3 Grafico della PDF della t

La PDF della VC t standardizzata $t_\nu^{std}(\mu,\sigma^2)$ è implementata in R tramite la funzione dstd(x,mean,sd,nu) (si veda ?dstd) contenuta nella libreria fGarch. Si procede in maniera simile a quanto fatto precedentemente utilizzando la stessa sequenza di valori $x$ e le stime ML dei parametri contenute in fitT:

library(fGarch)
densT = dstd(xseq,
          mean=fitT$estimate[1],
          sd=fitT$estimate[2],
          nu=fitT$estimate[3])

Il grafico finale si ottiene come segue:

plot(density(CPS$ahe2),
     col="blue", ylim=c(0,0.4))
lines(xseq,densN,col="red")
lines(xseq,densT,col="orange")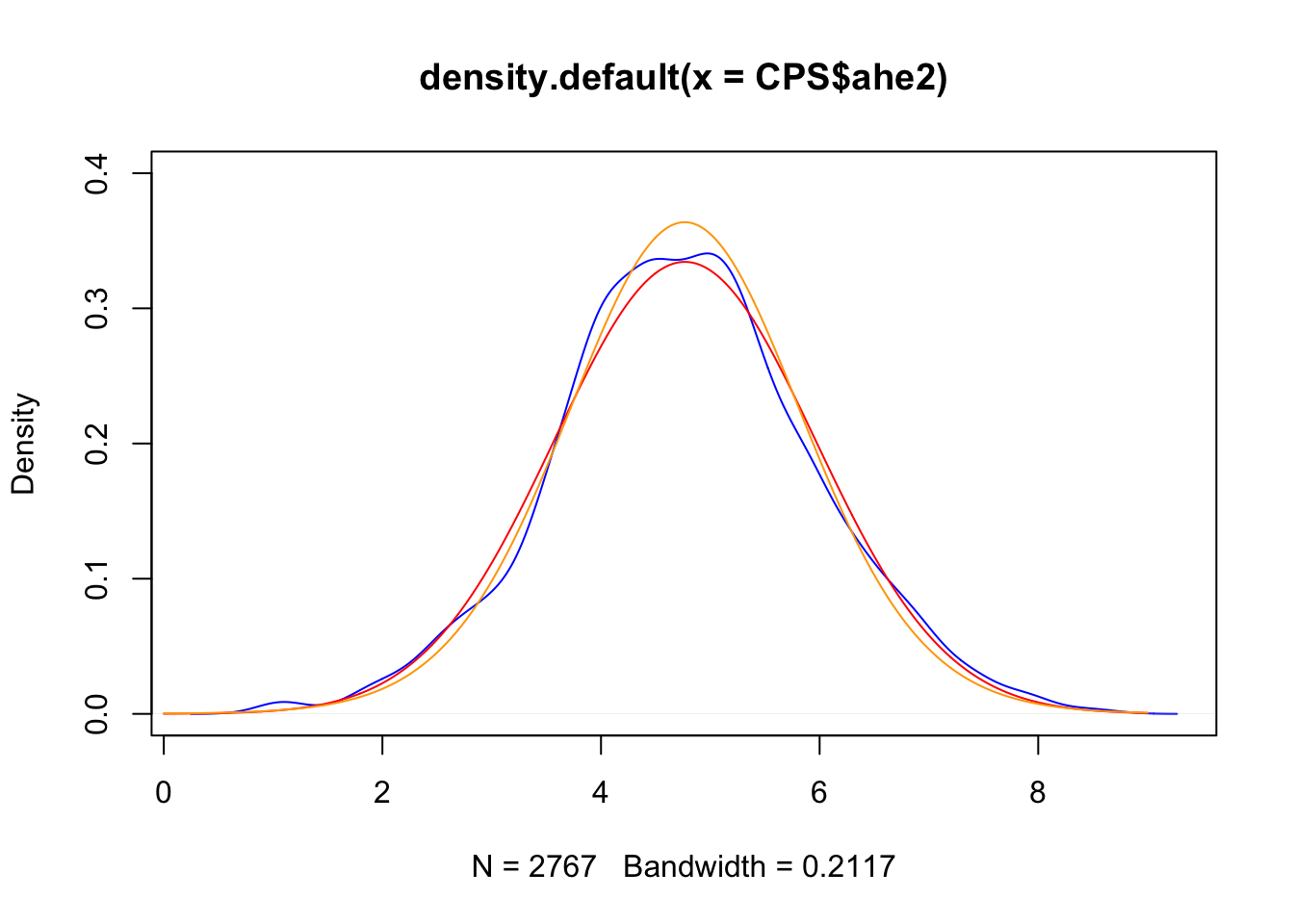

8.3 Esercizi Lab 6

8.3.1 Esercizio 1

Le serie giornalerie dei prezzi per il periodo dal 2012-11-09 al 2017-11-09 per il titolo ENI sono disponibili nel file E.csv. Importare i dati in R.

Calcolare i rendimenti lordi e rappresentarne graficamente la distribuzione con un istogramma.
Testare la normalità dei rendimenti lordi.
Stimare la distribuzione Normale e t di Student che meglio si adatta ai dati. Quale dei due modelli (Normale e t) è preferibile in termini di devianza, AIC e BIC?
Rappresentare graficamente la distribuzione dei dati con un istogramma a cui vengono aggiunte le funzioni di densità delle due distribuzioni fittate al punto precedente. Per calcolare la funzione di densità della t di Student è possibile utilizzare la funzione dstd che si trova nella libreria fGarch (da installare). Si veda l’help con ?dstd.
Quale è il valore della PDF (fittata ai dati) per la VC Normale e t di Student per il valore $x=0.9$? I valori sono uguali?

8.3.2 Esercizio 2

Simulare 1000 valori da una variabile casuale logNormale di parametri 15 (meanlog) e 0.5 (varlog). Usare come seme il valore 789.
Fittare ai dati la miglior (sapendo da dove arrivano i dati la scelta dovrebbe essere scontata) distribuzione per i dati considerati (vedere le distribuzioni disponibili in ?fitdistr). Quali sono i valori stimati dei parametri?
Rappresentare graficamente la distribuzione dei dati simulati tramite un istogramma. Aggiungere al grafico la linea della densità teorica stimata al punto precedente. Per calcolare la funzione di densità è possibile utilizzare la funzione dlnorm. Si veda l’help con ?dlnorm.
Fittare ai dati una distribuzione di tipo Esponenziale (densufun=exponential). In termini di devianza, AIC e BIC quale modello (logNormale o Esponenziale) è preferibile?