12 Lab 10 - 23/12/2020

In questo laboratorio utilizzeremo alcuni strumenti grafici per analizzare la dipendenza temporale presente in una serie storica. Impareremo poi a stimare modelli appartententi alla classe ARIMA. Per il laboratorio verrano utilizzati i seguenti dataset: logret.csv, già introdotto per il Lab. 9, e GNP.csv.

12.1 Studio della dipendenza temporale

Si procede con l’importazione del file logret.csv:

logret <- read.csv("~/Dropbox/UniBg/Didattica/Economia/2020-2021/SAPF_2021/R_labs/lab10/logret.csv")
head(logret)
##             BA          CAT          CSCO           NKE           DIS
## 1 -0.026622040 -0.012790378  0.0009849775 -0.0106301541 -0.0041285192
## 2  0.034863602  0.004669870 -0.0004920804  0.0009536113  0.0003940198
## 3  0.004289767  0.006754197  0.0068726044  0.0019048651  0.0001968674
## 4 -0.025354422  0.001156074  0.0019554610  0.0104117238 -0.0041431171
## 5  0.018325151 -0.005900466  0.0236439094  0.0016935999  0.0001974132
## 6  0.005081518  0.010930122  0.0004765842  0.0084245628  0.0098349702
##            DJI
## 1 -0.004150804
## 2  0.004615400
## 3  0.006009308
## 4  0.001276720
## 5  0.001399526
## 6  0.002038986
str(logret)
## 'data.frame':	1258 obs. of  6 variables:
##  $ BA  : num  -0.02662 0.03486 0.00429 -0.02535 0.01833 ...
##  $ CAT : num  -0.01279 0.00467 0.00675 0.00116 -0.0059 ...
##  $ CSCO: num  0.000985 -0.000492 0.006873 0.001955 0.023644 ...
##  $ NKE : num  -0.01063 0.000954 0.001905 0.010412 0.001694 ...
##  $ DIS : num  -0.004129 0.000394 0.000197 -0.004143 0.000197 ...
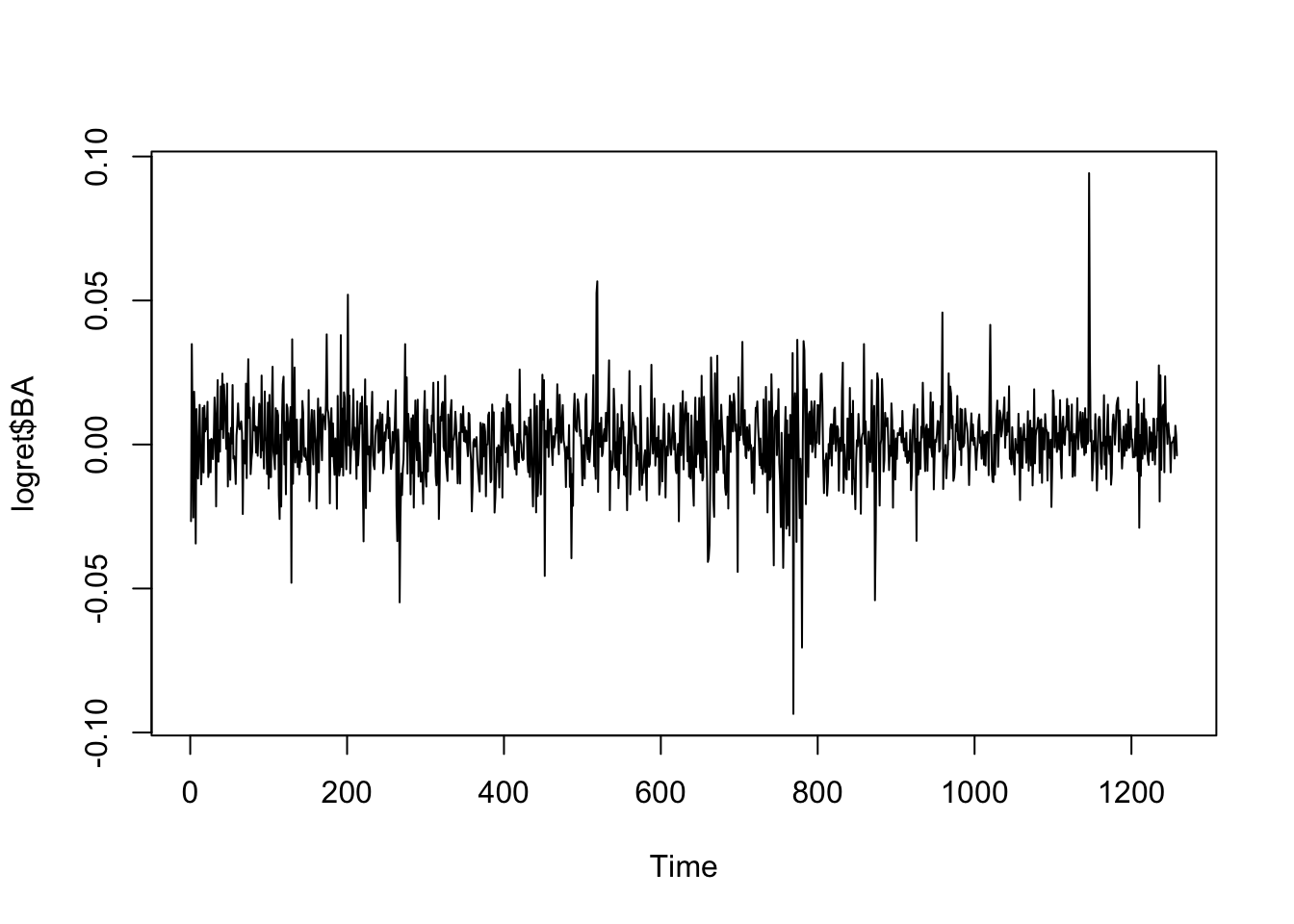
##  $ DJI : num  -0.00415 0.00462 0.00601 0.00128 0.0014 ...

Consideriamo i rendimenti logaritmici di BA la cui serie storica appare stazionaria rispetto alla media (non sono infatti presente trend crescenti o decrescenti). Si osservano episodi di valori estremi:

ts.plot(logret$BA)

Si intende ora studiare la struttura di dipendenza temporale della serie (autocorrelaizone). In particolare, utilizzando la funzione lag.plot è possibile rappresentare graficamente (con uno scatterplot) la serie storica in funzione di una sua versione ritardata (lagged). Questo concetto è rappresentato anche in Figura 12.1 in riferimento a un caso semplice con \(n=6\) osservazioni. E’ importante notare che quando il lag \(h\) cresce il numero di coppie di osservazioni usate per il calcolo dell’autocorrelazione diminuisce. In particolare, il valore massimo di \(h\) che può essere considerato è dato da \(n-1\). Ciò non rappresenta comunque un problema quando si dispone di una serie storica lunga, come il caso in analisi.

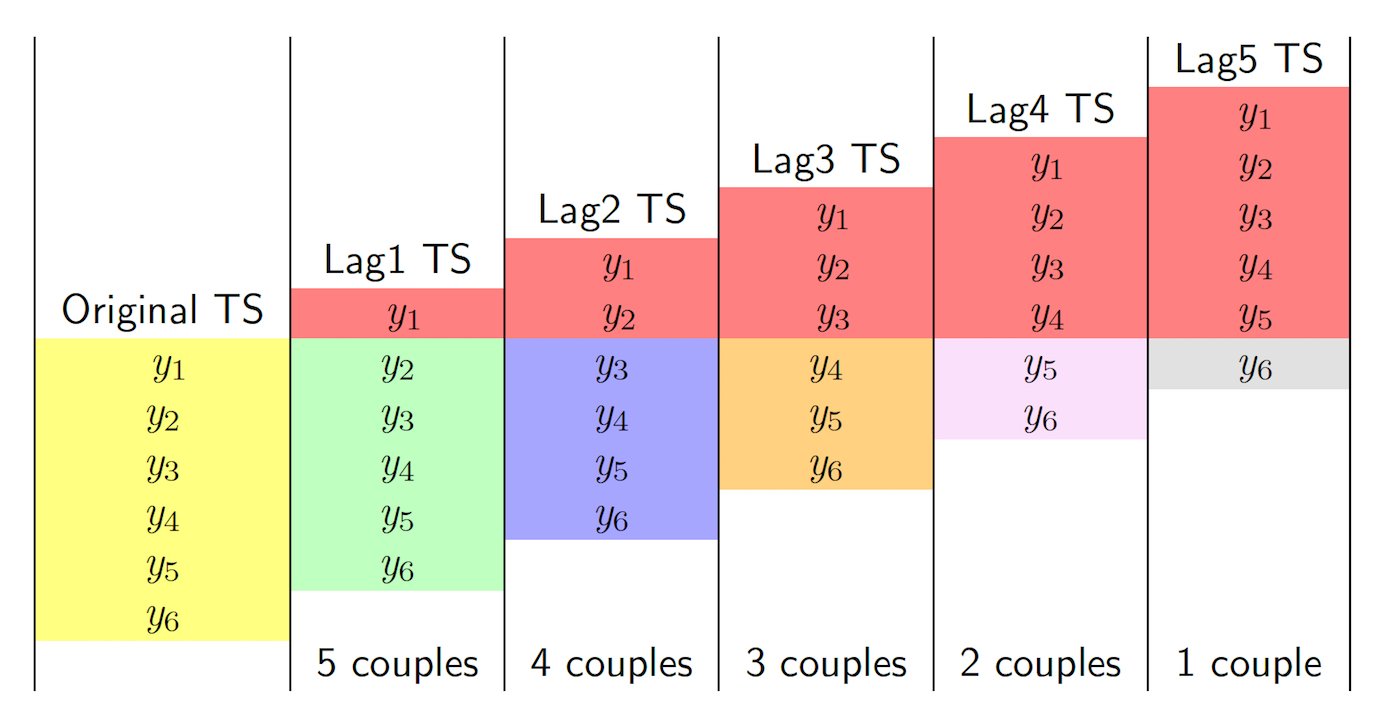
Il calcolo dell'autocorrelazione per diversi lag: il caso di $n=6$ osservazioni

Figure 12.1: Il calcolo dell’autocorrelazione per diversi lag: il caso di \(n=6\) osservazioni

Il seguente codice realizza lo scatterplot delle coppie di osservazioni a distanza (lag) di un giorno (i.e. \(y_t\) vs \(y_{t-1}\) per \(t=2,3, \ldots,\) 1258).

lag.plot(logret$BA, set.lags = 1) #h=1

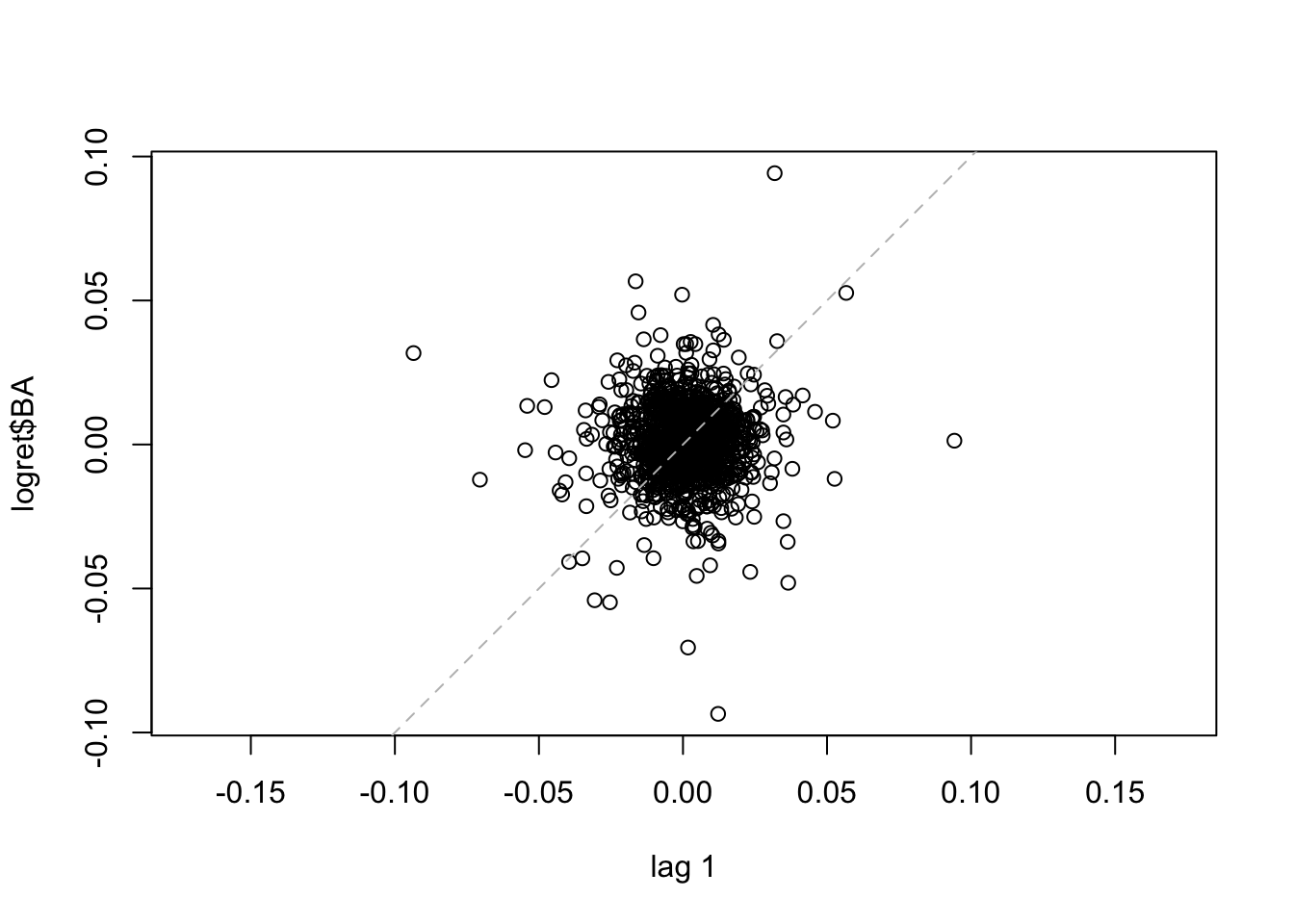La linea tratteggiata nel grafico rappresenta l’intercetta. Si osserva che i punti sono dispersi nei quattro quadranti del grafico, sintomo di una correlazione debole. Lo stesso grafico può essere ottenuto, per esempio, per il caso di \(h=2\) (per rappresentare \(y_t\) vs \(y_{t-2}\) per \(t=3, \ldots,\) 1258) ), 500 and 1000.

lag.plot(logret$BA, set.lags = 2) #h=2

lag.plot(logret$BA, set.lags = 500) #h=500

lag.plot(logret$BA, set.lags = 1000) #h=1000

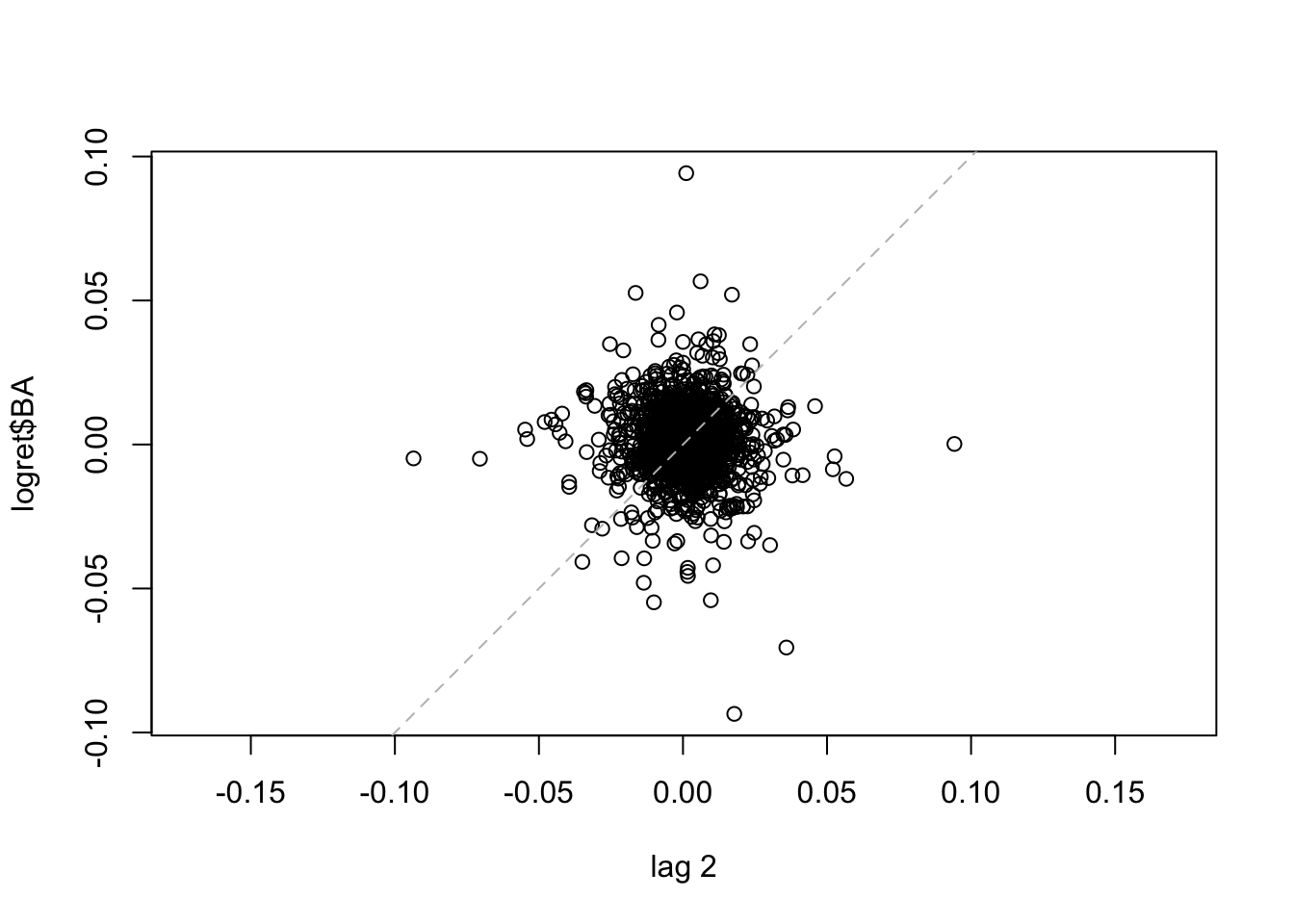
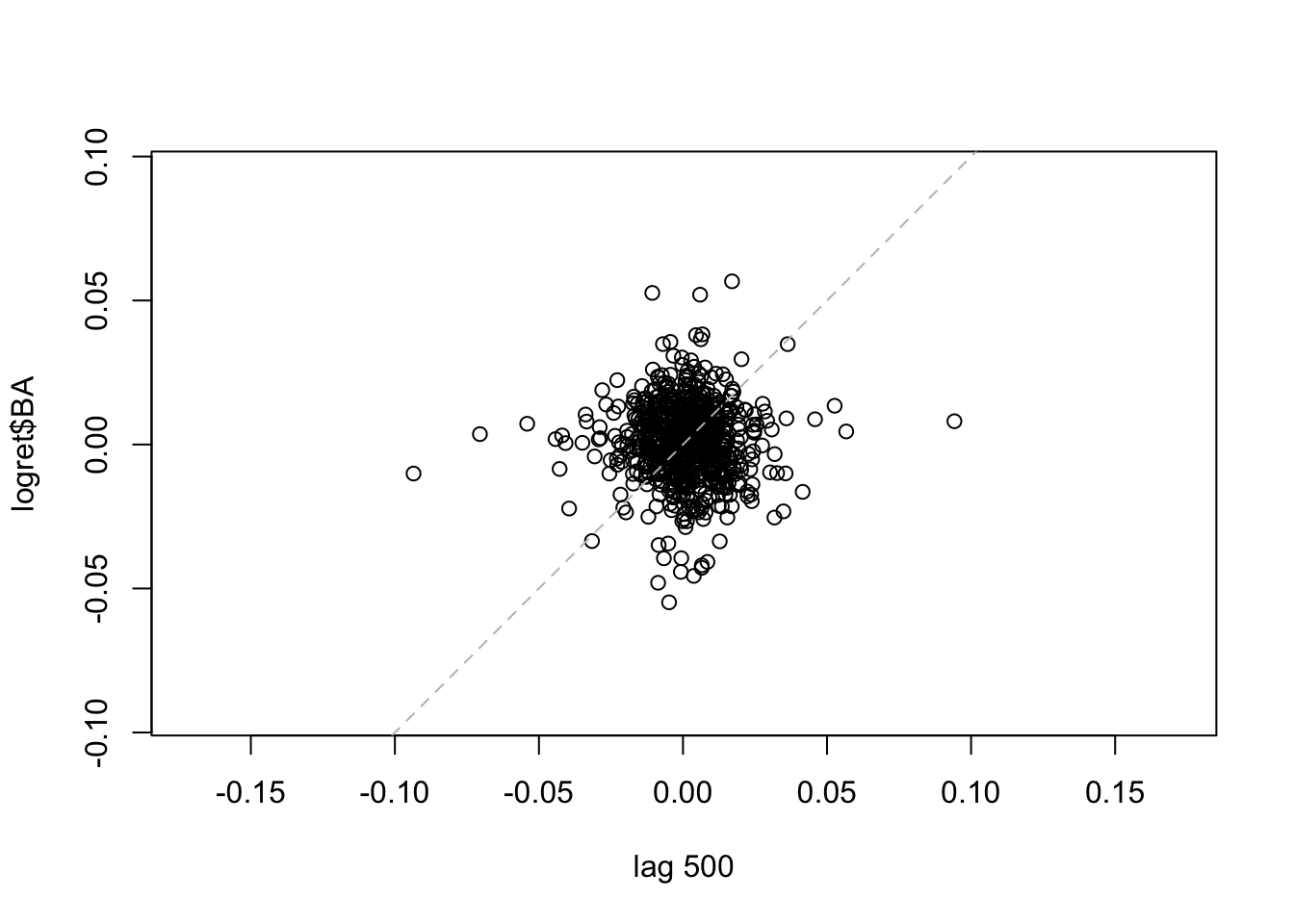
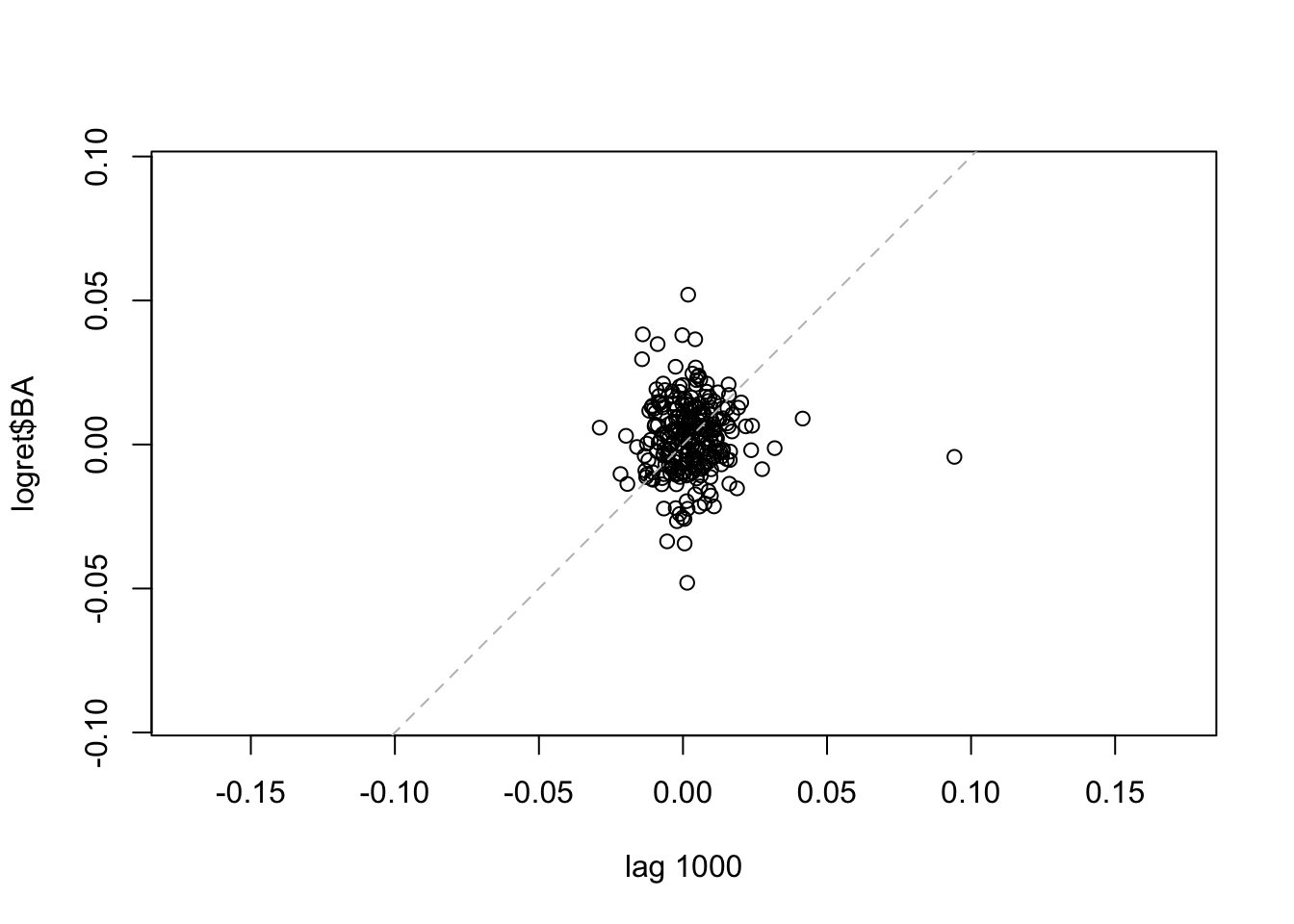Per i tre lag considerati si nota che il numero di punti diminuisce all’aumentare di \(h\); la correlazione appare comunque sempre debole. E’ anche possibile rappresentare graficamente più lag:

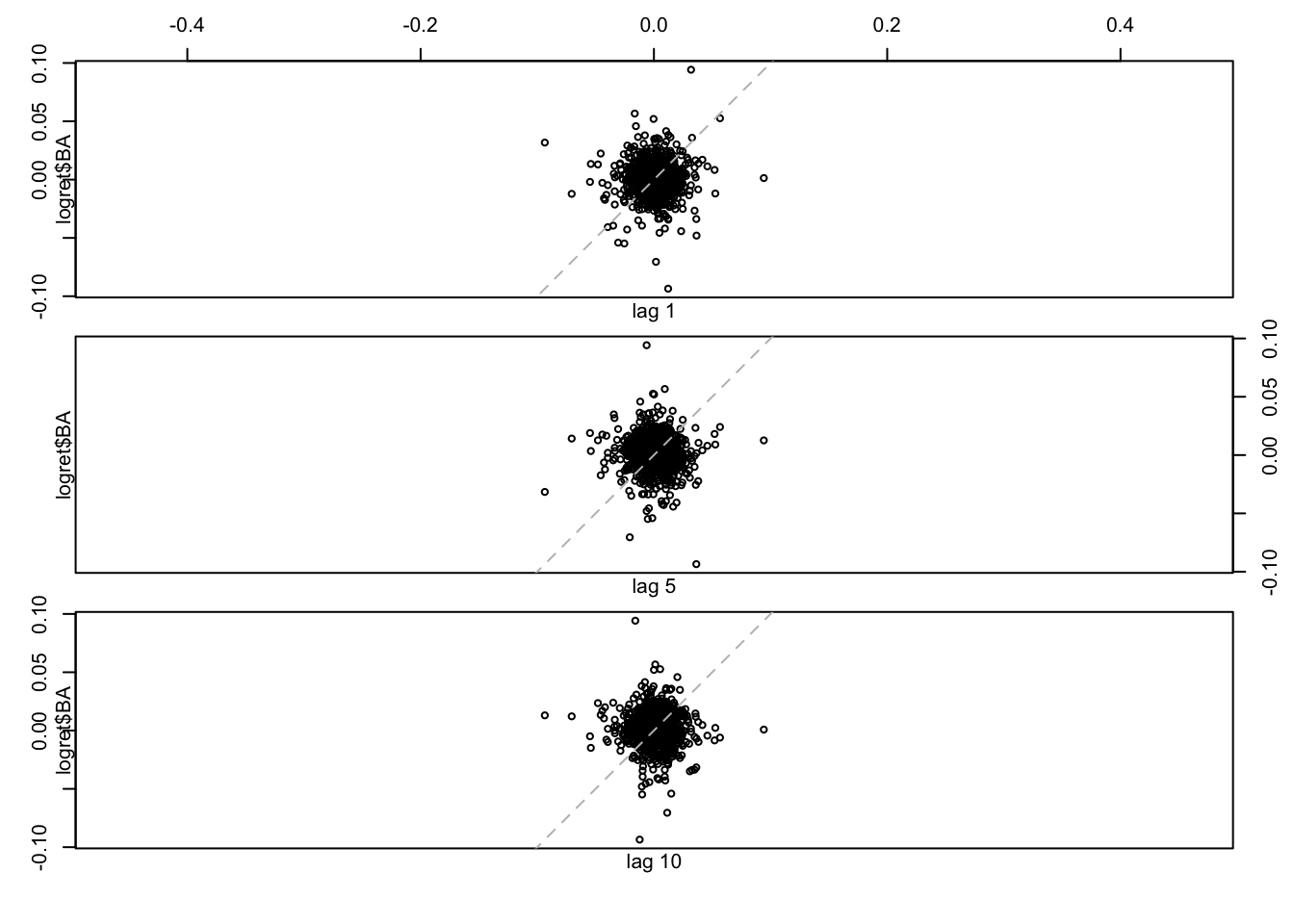
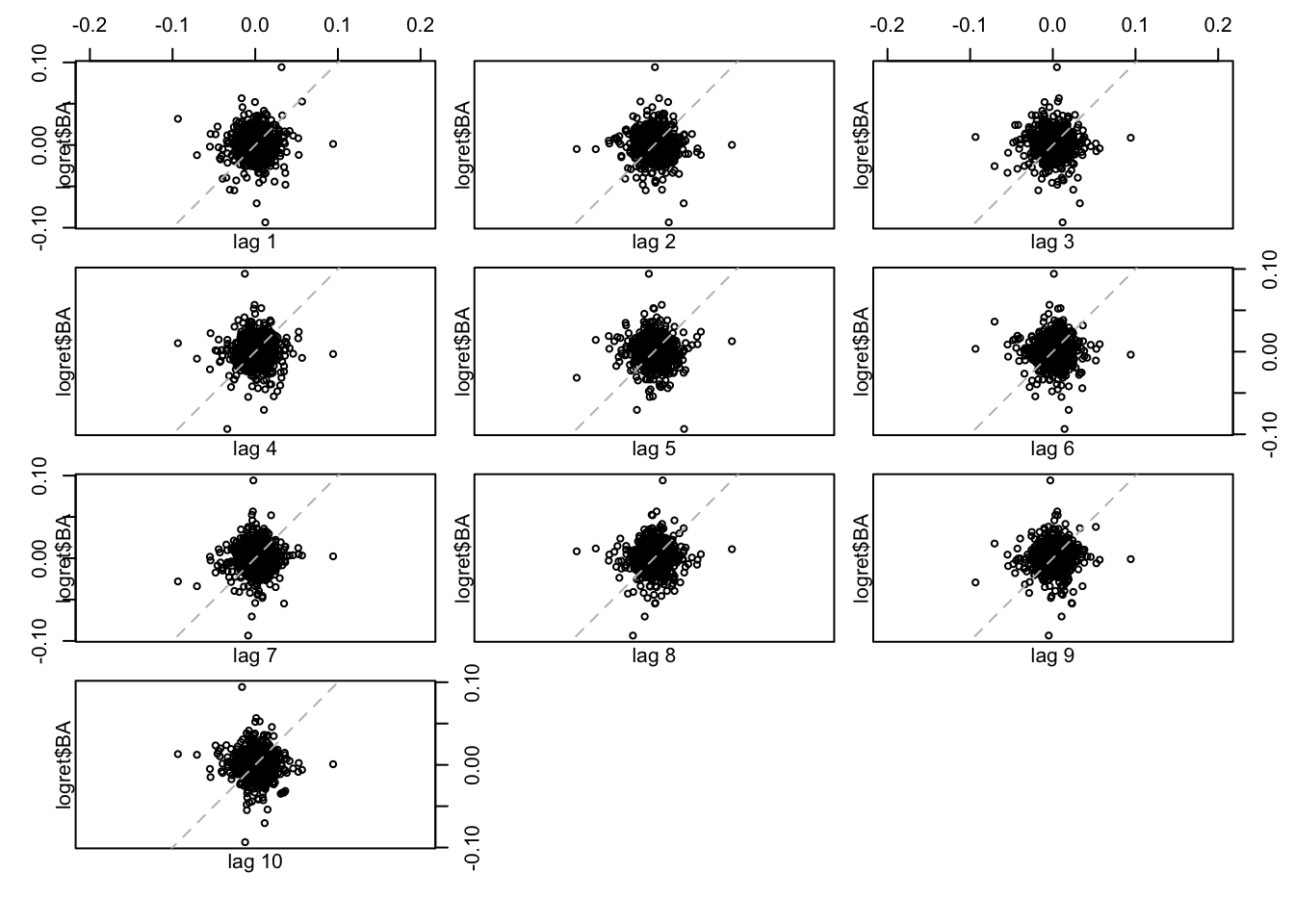lag.plot(logret$BA, set.lags = c(1,5,10)) #h=1,5,10

lag.plot(logret$BA, set.lags = 1:10) #i primi 10 lag

Tutti i 10 grafici mostrano una auto-correlazione debole. Per quantificarla è possibile calcolare i valori della funzione di autocorrelazione utilizzando la funzione acf:

acf(logret$BA, plot=FALSE)
## 
## Autocorrelations of series 'logret$BA', by lag
## 
##      0      1      2      3      4      5      6      7      8      9     10 
##  1.000  0.033 -0.032  0.006  0.005 -0.051 -0.008  0.012  0.019  0.026 -0.046 
##     11     12     13     14     15     16     17     18     19     20     21 
##  0.022  0.017 -0.012 -0.008 -0.031  0.037  0.013  0.005 -0.010  0.022  0.003 
##     22     23     24     25     26     27     28     29     30 
##  0.025  0.015  0.048  0.032 -0.002 -0.002 -0.016  0.024  0.013

L’opzione plot=FALSE permette di ottenere la tabella nella Console (ma non il grafico) con i valori della funzione di autocorrelazione, per i valori di \(h\) tra 1 e 30. Il valore massimo di \(h\) considerato è dato, di default, da \(10 \times log 10 \times n\) dove \(n\) è la lunghezza della serie (il alternativa il lag massimo può essere modificato con l’opzione lag.max).

Il grafico della funzione di autocorrelazione, detto anche correlogramma, può essere ottenuto con la stessa funzione acf ma con l’opzione plot=TRUE. Poichè questa è l’opzione di default non è necessario specificarla:

acf(logret$BA)

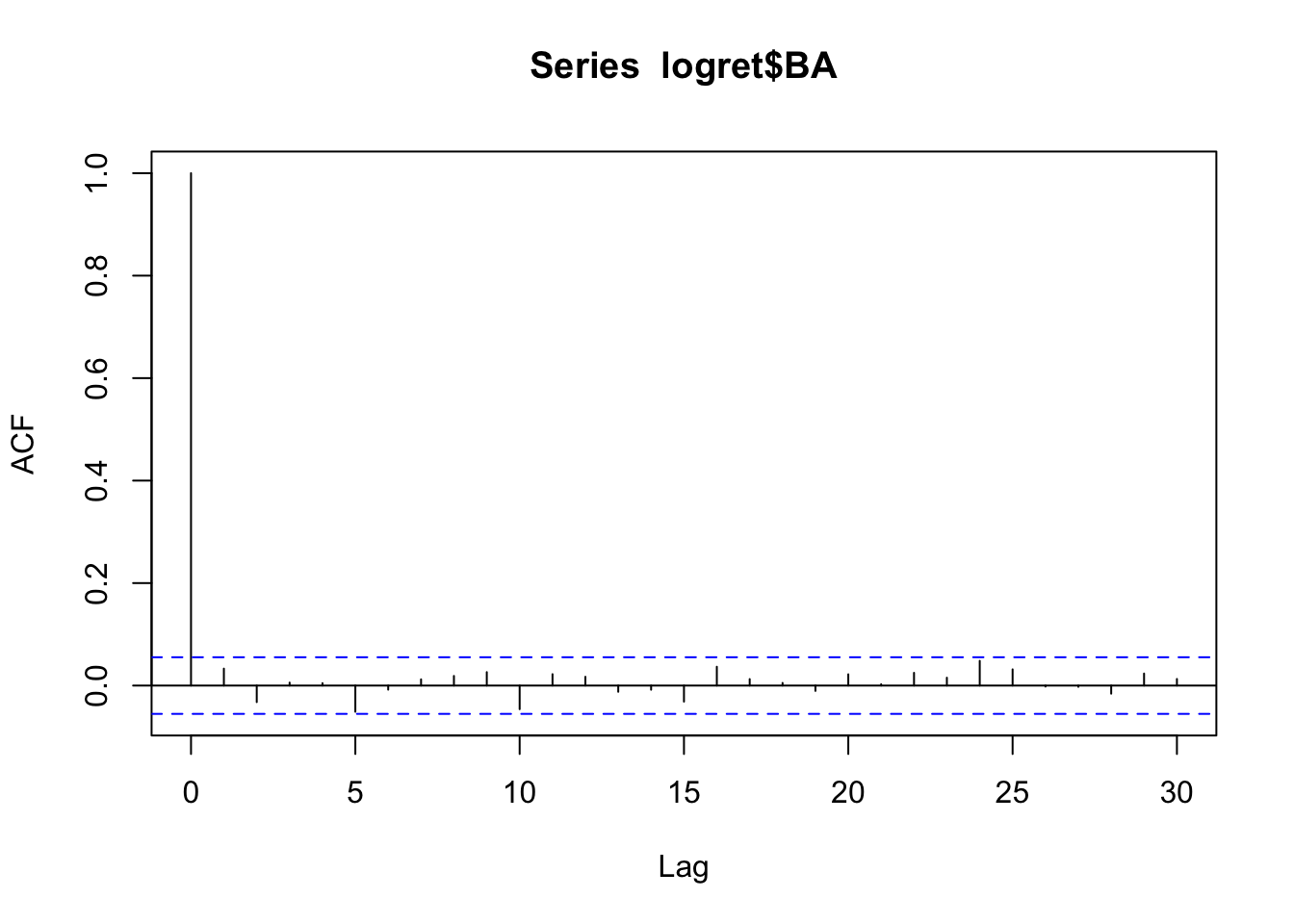Tutte le barre verticali sono contenute all’interno delle line blue. Ciò significa che non ci sono correlazione significativamente diverse da zero per alcun lag. I rendimenti considerati possono quindi essere considerati come una realizzazione di un processo di tipo white-noise a componenti incorrelate.

12.2 Test di Ljung-Box

Consideriamo ora il titolo CSCO e la corrispondente serie di log rendimenti.

ts.plot(logret$CSCO)

acf(logret$CSCO)

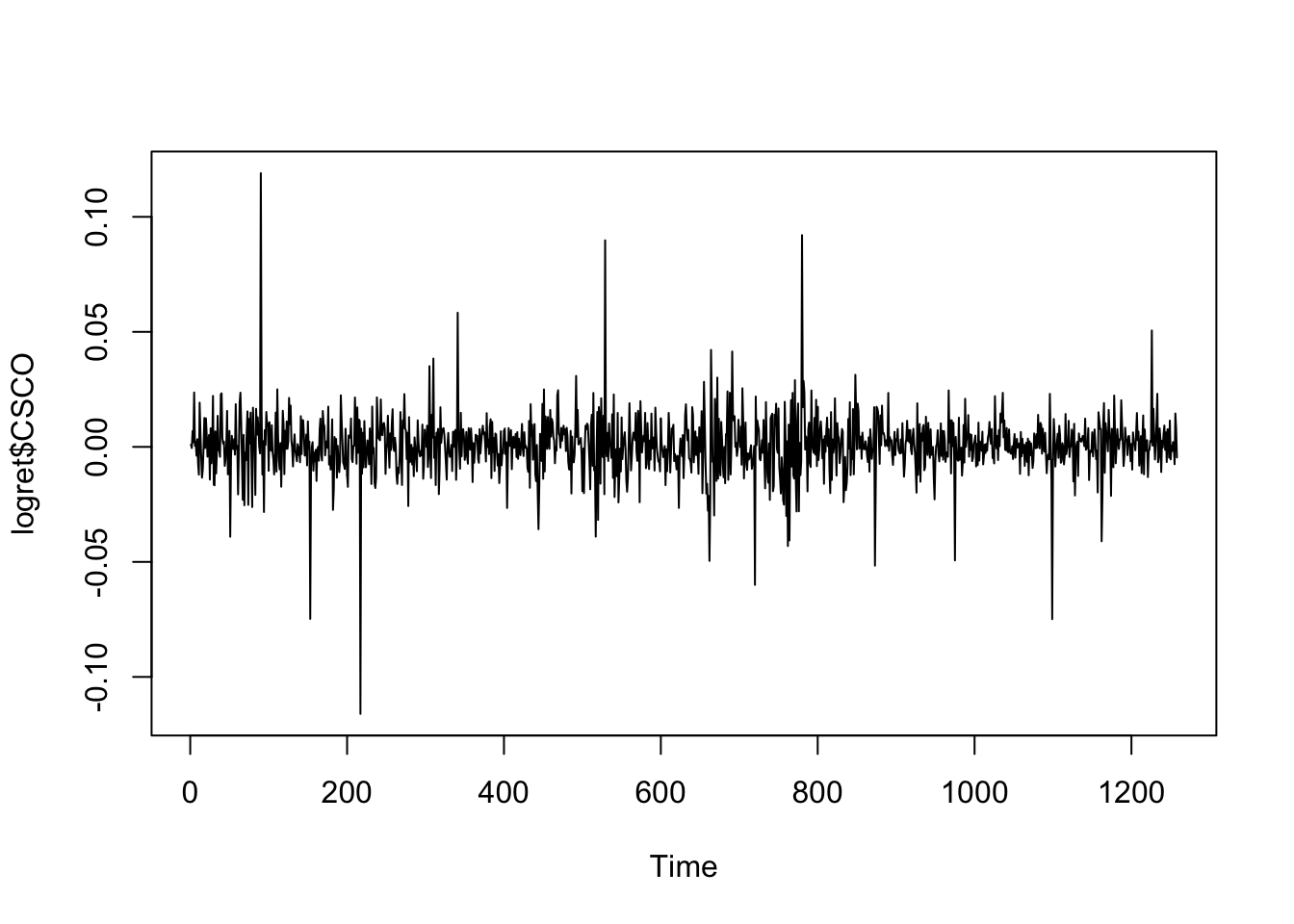
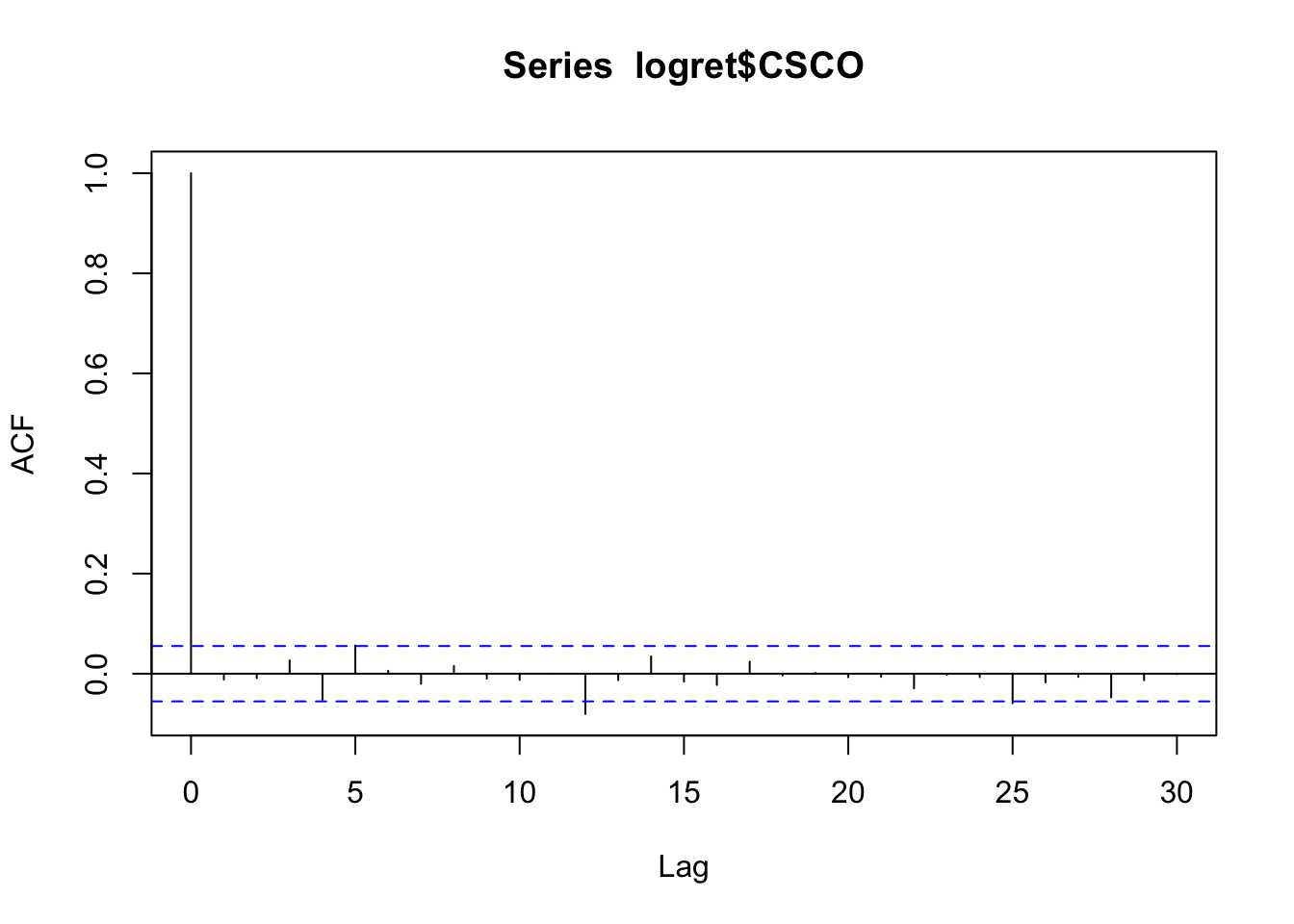Dall’analisi del correlogramma emerge che tutte le correlazioni, ad eccezione di quella per \(h=12\), non sono significativamente diverse da zero (the linee verticali sono contenute nelle linee blu e quindi non si rifiuta l’ipotesi nulla \(H_0:\rho(h)=0\)). Ci si domanda se il caso di \(h=12\) sia un falso positivo o una correlazione realmente diversa da zero? Per verificarlo è possibile utilizzare un test simultaneo come il test di Ljung-Box che può essere implementato utilizzando la funzione Box.test (si veda ?Box.test). Siamo in particolare interessati a testare l’ipotesi nulla \(H_0: \rho(1)=\rho(2)=\ldots=\rho(12)=0\) e quindi specificheremo nella funzione lag=12. E’ inoltre necessario specificare l’opzione type="L" per indicare il tipo di test che si intende implementare. La corrispondente statistica test è distributia come una variabile casuale \(\chi^2_{12}\).

Box.test(logret$CSCO,lag=12,type="L")
## 
## 	Box-Ljung test
## 
## data:  logret$CSCO
## X-squared = 17.969, df = 12, p-value = 0.1166

Dato il valore del p-value, non si rifiuta l’ipotesi nulla. Possiamo quindi considerare la correlazione che si osserva al lag 12 come uguale a zero; si tratta quindi di un falso positivo. Come per il precedente caso possiamo considerare i dati come provenienti da un processo white-noise debole.

12.3 Alla ricerca della stazionarietà

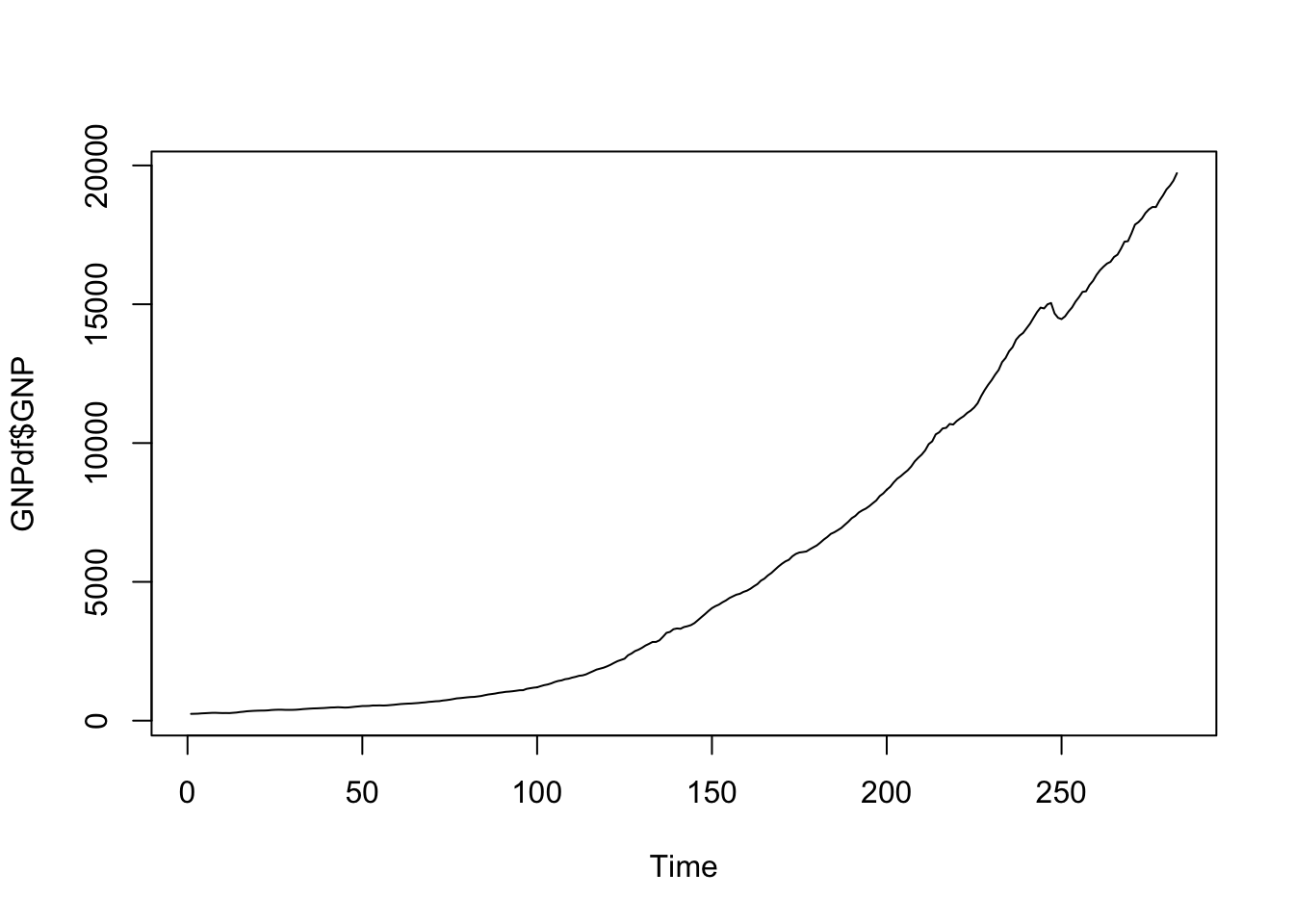
Importiamo ora i dati disponibili nel file GNP.csv. Essi si riferiscono alla serie storica del Gross National Product (GNP) americano (in billioni di dollari, dati trimestrali dal Gennaio 1947 al Luglio 2017).

GNPdf <- read.csv("~/Dropbox/UniBg/Didattica/Economia/2020-2021/SAPF_2021/R_labs/lab10/GNP.csv")
str(GNPdf)
## 'data.frame':	283 obs. of  2 variables:
##  $ DATE: chr  "1947-01-01" "1947-04-01" "1947-07-01" "1947-10-01" ...
##  $ GNP : num  244 247 251 262 268 ...
head(GNPdf)
##         DATE     GNP
## 1 1947-01-01 244.058
## 2 1947-04-01 247.362
## 3 1947-07-01 251.246
## 4 1947-10-01 261.545
## 5 1948-01-01 267.564
## 6 1948-04-01 274.376
tail(GNPdf)
##           DATE      GNP
## 278 2016-04-01 18733.02
## 279 2016-07-01 18917.47
## 280 2016-10-01 19134.46
## 281 2017-01-01 19271.96
## 282 2017-04-01 19452.41
## 283 2017-07-01 19722.06

La serie storica è caratterizzata da un trend crescente e non è quindi stazioaria:

ts.plot(GNPdf$GNP)

Calcoliamo quindi le differenze di primo ordine usando la funzione diff:

ts.plot(diff(GNPdf$GNP))

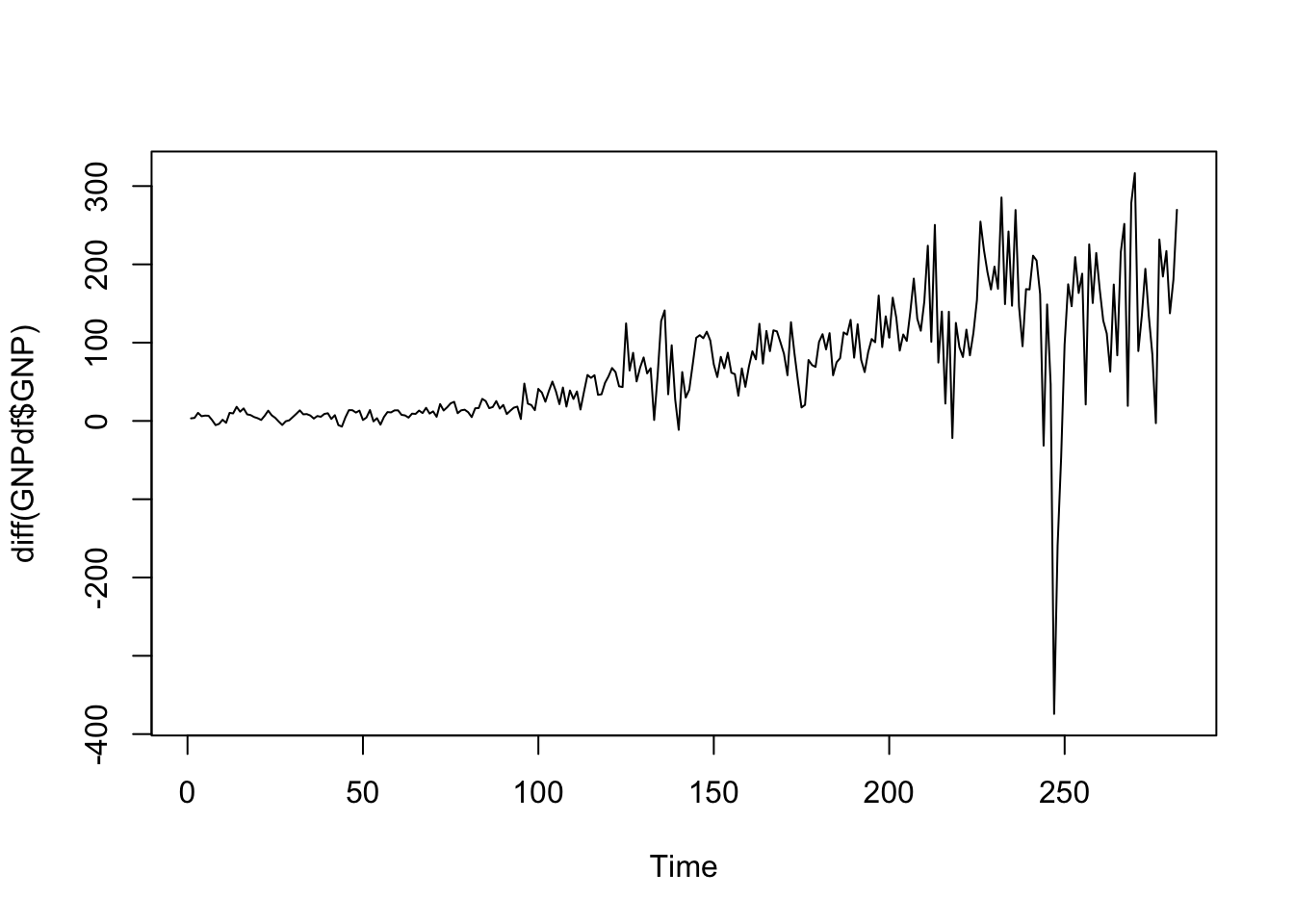La serie risulta ancora non stazionaria: si nota ancora un leggero trend positivo associato anche ad oscillazioni sempre più grandi della serie (sinonimo di un cambio della variabilità nel corso del tempo). Procediamo quindi con il calcolo delle differenze di secondo ordine, applicando per due volte la funzione diff:

ts.plot(diff(diff(GNPdf$GNP)))

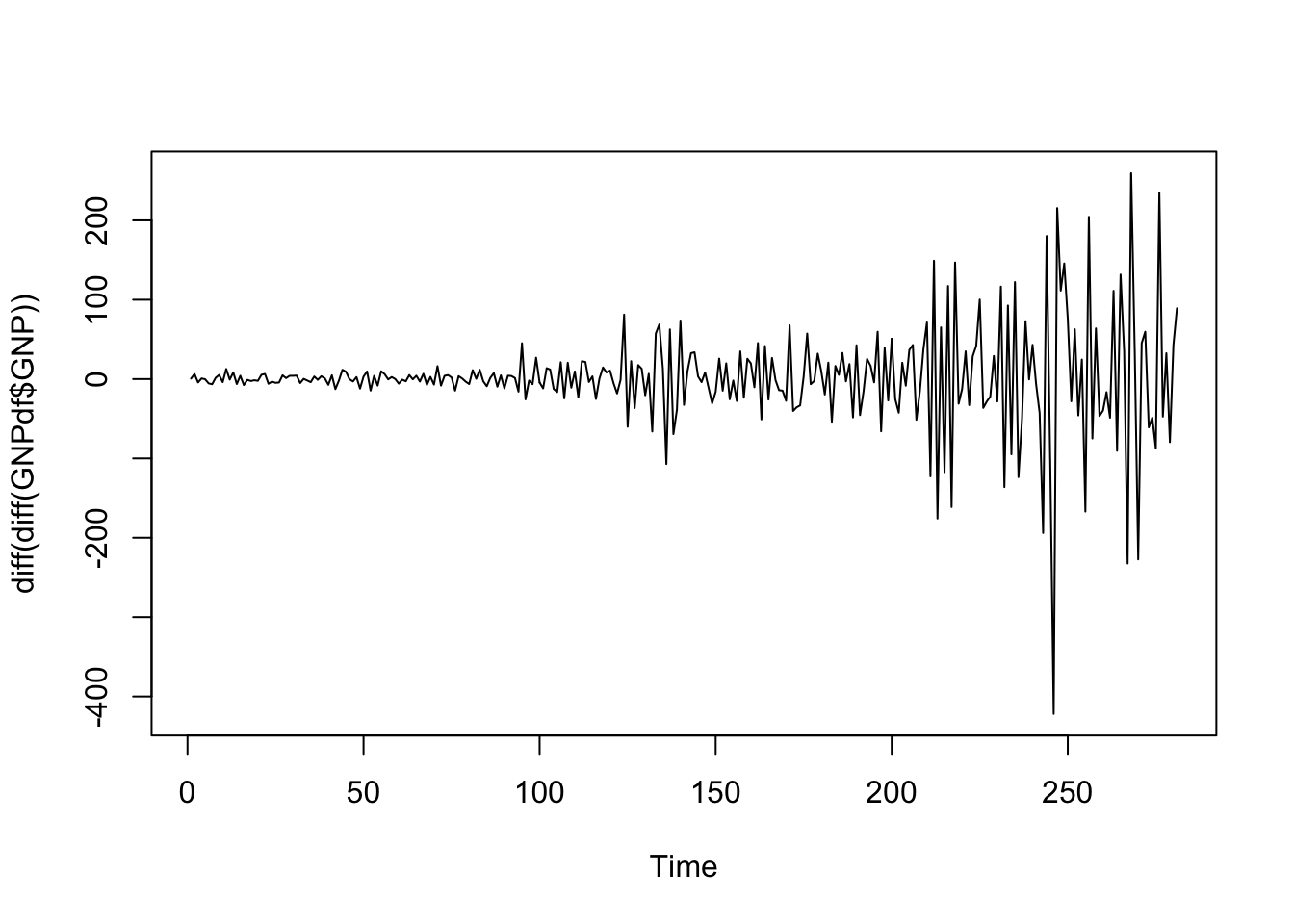La serie storica ora appare muoversi intorno al valore zero (non si osserva più alcun un trend). Rimane comunque ancora evidente il problema della variabilità che appare maggiore all’avanzare del tempo. Questo problema può essere affrontato utilizzando una trasformazione dei dati che stabilizza la varianza. si può ad esempio considerare la trasformazione logaritmica che appartiene alla famiglia delle trasformazioni di Box-Cox. La trasformazione logaritmica è inoltre associata ad una facile interpretazione: un cambio nei valori logaritmici corrisponde a un cambiamento relativo nella scala originale dei dati.

Applichiamo quindi la trasformazione logaritmica ai dati e poi ne rappresentiamo graficamente la serie storica (\(log(Y_t)\)):

ts.plot(log(GNPdf$GNP))

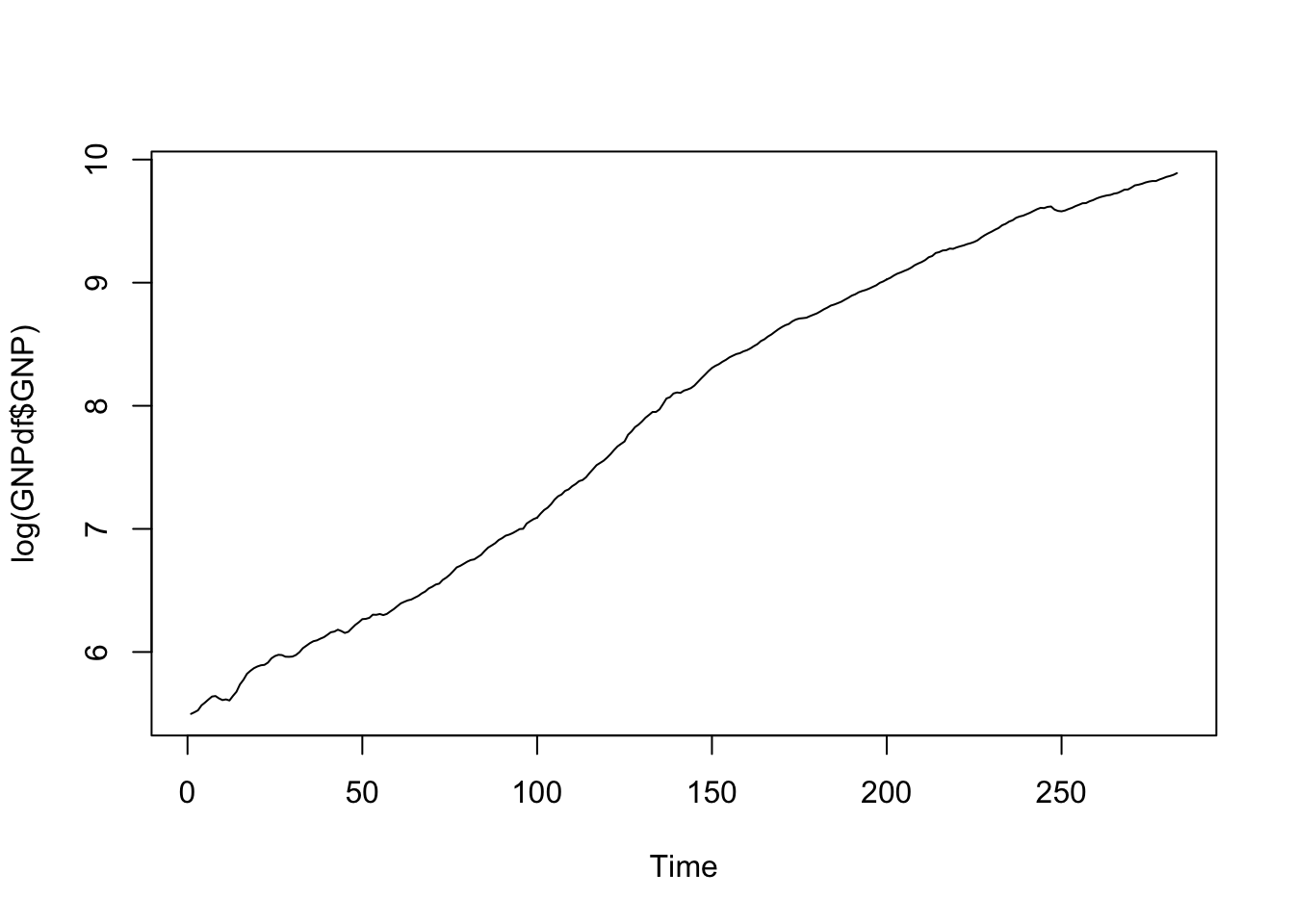Visto che la serie è non stazionario, utilizziamo le differenze di primo ordine (\(\Delta log(Y_t)\) e secondo ordine (\(\Delta^2 log(Y_t)\):

ts.plot(diff(log(GNPdf$GNP)))

ts.plot(diff(diff(log(GNPdf$GNP))))

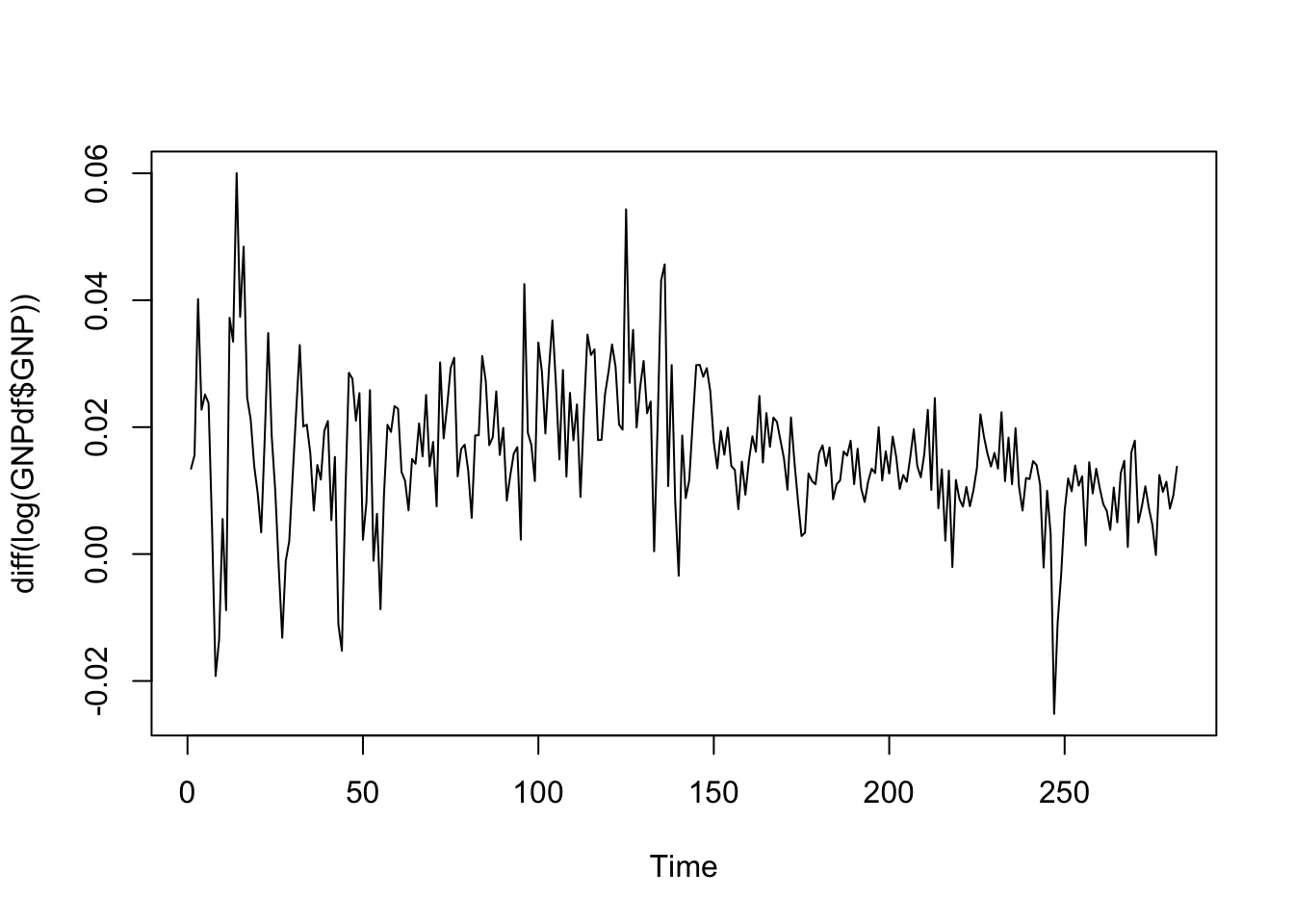
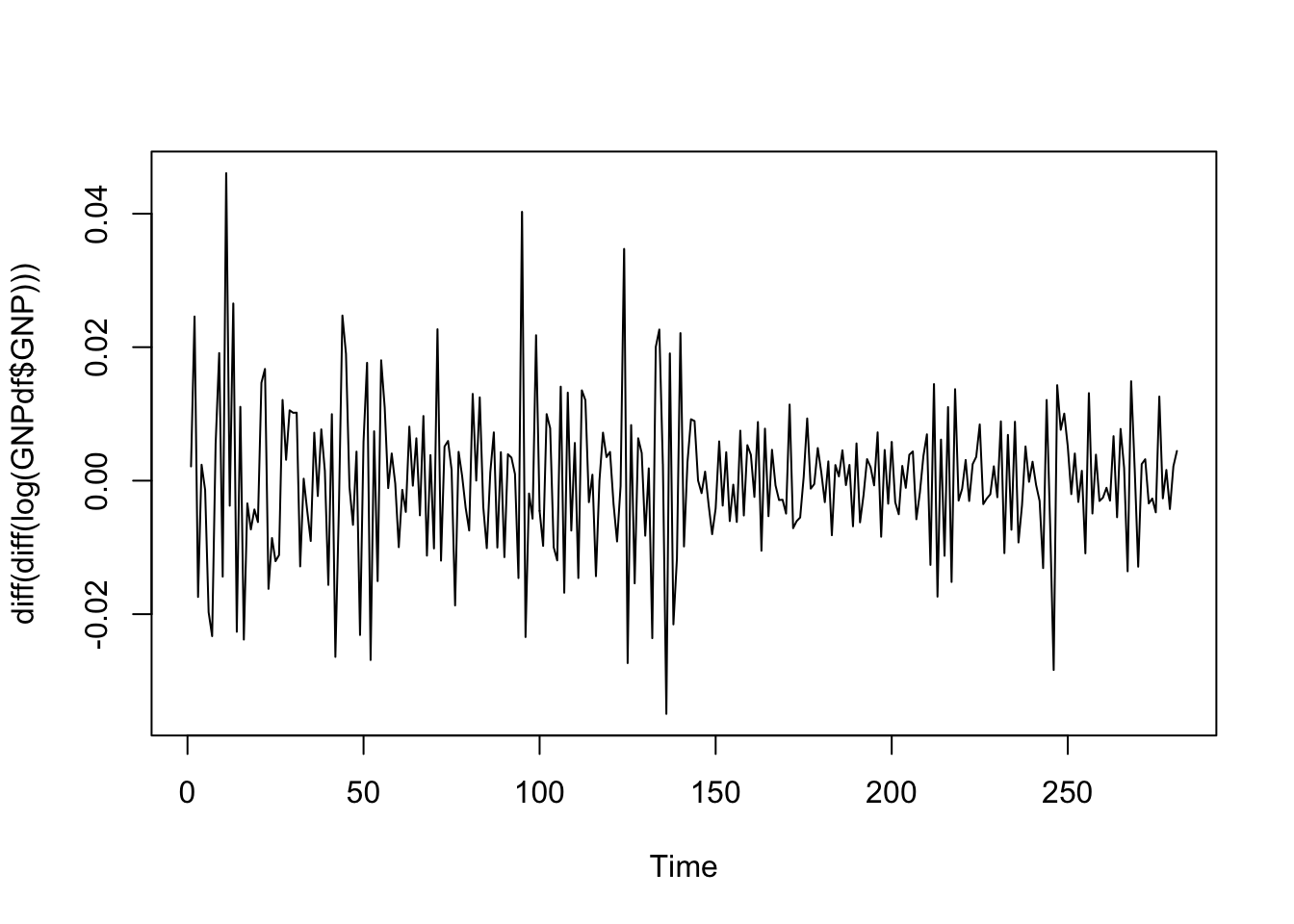La serie storica delle differenze di secondo ordine dei valori logaritmici appare stazionaria rispetto al valore zero. Apparentemente la variabilità sembra maggiore all’inizio del periodo. In questo caso è possibile utilizzare il test di Dickey Fuller per verificare l’ipotesi di stazionarietà (link). La funzione adf.test è inclusa nel pacchetto tseries e può essere utilizzata per verificare l’ipotesi nulla secondo la quale l’equazione caratteristica ha una soluzione unitaria root (i.e. non stazionarietà). Come ipotesi alternativa si può verificare che la serie sia stazionaria (ipotesi di default) oppure esplosiva.

#Salvo le differenze di secondo ordine (Delta^2 log(Y_t)) in un nuovo oggetto
diff2 = diff(diff(log(GNPdf$GNP)))
library(tseries)
adf.test(diff2, alternative = "stationary")
## Warning in adf.test(diff2, alternative = "stationary"): p-value smaller than
## printed p-value
## 
## 	Augmented Dickey-Fuller Test
## 
## data:  diff2
## Dickey-Fuller = -10.505, Lag order = 6, p-value = 0.01
## alternative hypothesis: stationary

Dato il p-value, si rifiuta H0 e si accetta l’ipotesi di stazionarietà per la serie denominata diff2. Procediamo quindi con lo studio della sua funzione di autocorrelazione totale (acf) e parziale (pacf):

acf(diff2) 

pacf(diff2)

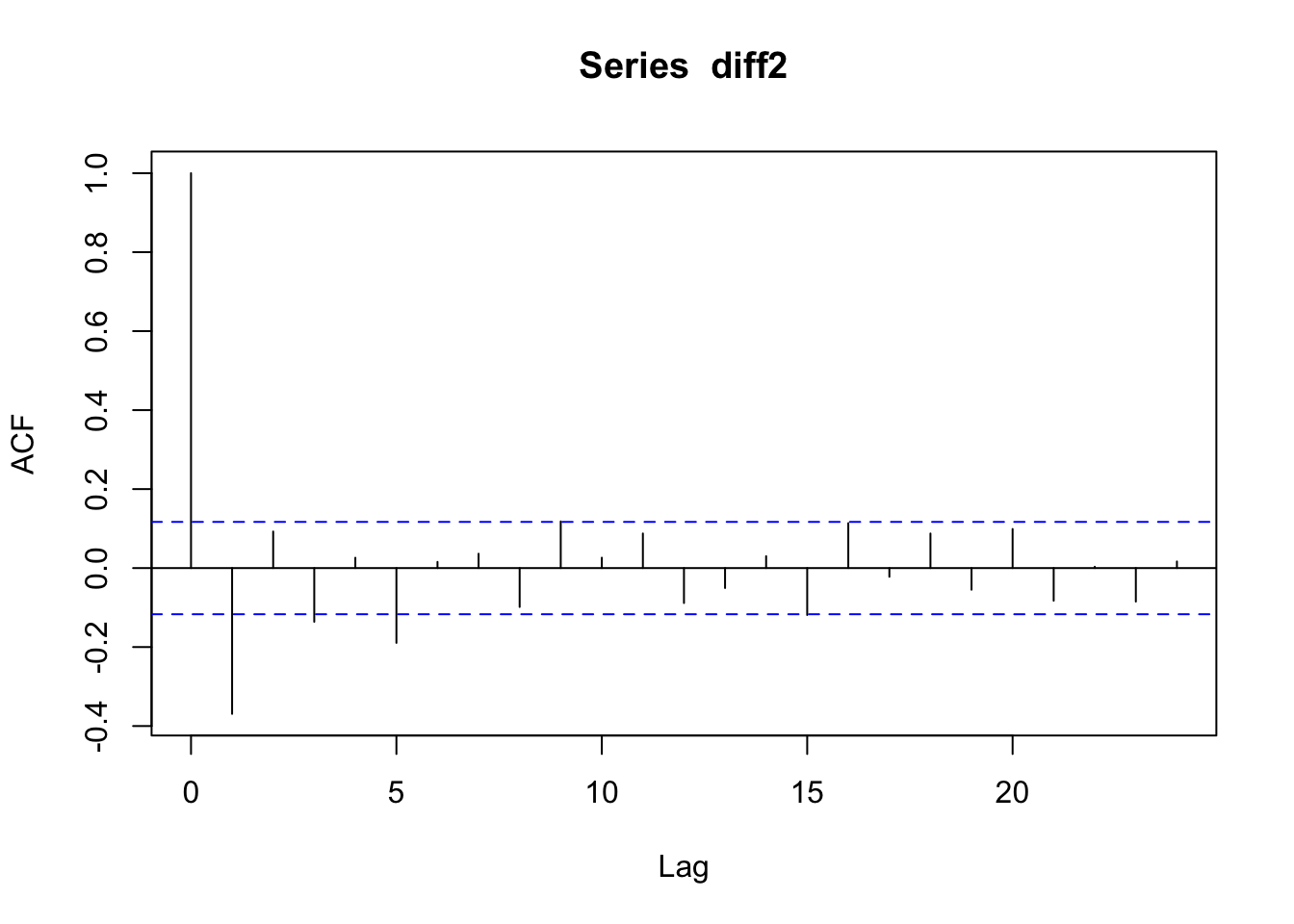
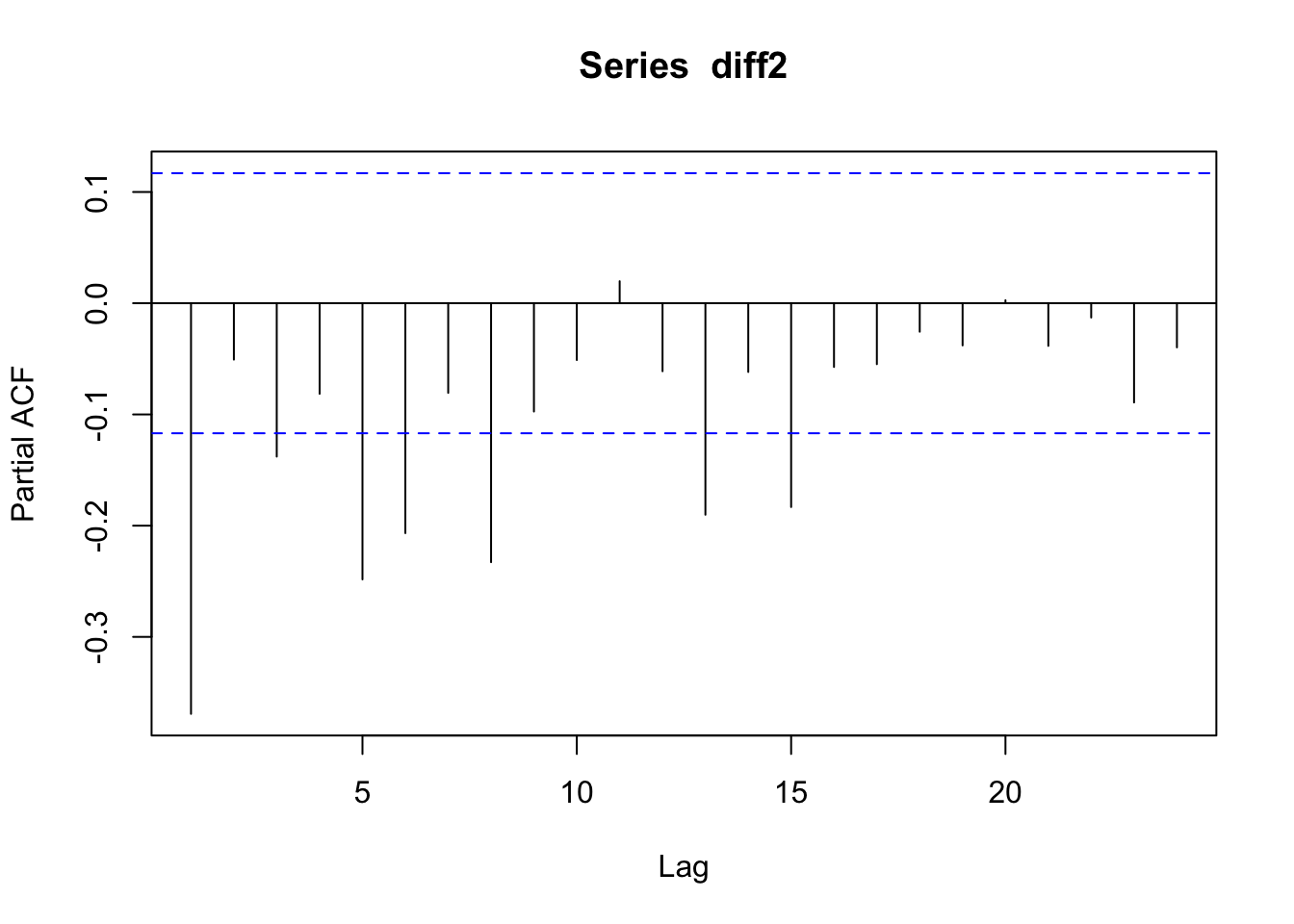E’ difficile riconoscere nei due grafici un comportamento noto: si tratta di un cut-off al lag 5 per la acf? Quello che si osserva nella pacf è un andamento di tipo tail-off con andamento ondivago? Sicuramente questi dati non sono stati generati da un processo puramente AR o MA (altrimenti avremmo trovato della caratteristica a noi note nei due grafici). Procediamo quindi a stimare diversi modelli ARMA che verranno confrontati utilizzando l’indice AIC; il modello migliore sarà quello più semplice e con residui incorrelati.

12.4 Stima di modelli ARIMA

Per la stima di modelli ARIMA si utilizza la funzione Arima disponibile nella libreria forecast. LA funzione utilizza il metodo della massima verosimiglianza per la stima dei parametri. La funzione riceve in input, oltre ai dati, il vettore \((p,d,q)\) che definisce l’ordine del modello. Inoltre, anche l’opzione include.constant=TRUE deve essere inclusa.

library(forecast)
mod1 = Arima(diff2, order=c(1,0,1),
             include.constant = TRUE)
summary(mod1)
## Series: diff2 
## ARIMA(1,0,1) with non-zero mean 
## 
## Coefficients:
##          ar1      ma1   mean
##       0.4161  -0.9623  0e+00
## s.e.  0.0589   0.0177  1e-04
## 
## sigma^2 estimated as 9.006e-05:  log likelihood=910.67
## AIC=-1813.33   AICc=-1813.19   BIC=-1798.78
## 
## Training set error measures:
##                        ME        RMSE         MAE      MPE     MAPE      MASE
## Training set 4.807754e-06 0.009439138 0.006820991 175.5431 236.4172 0.5016291
##                     ACF1
## Training set -0.04671616

Le stime dei parametri possono essere recuperate come segue:

mod1$coef
##           ar1           ma1     intercept 
##  4.160917e-01 -9.622901e-01 -2.993612e-05

Il modello stimato è dato da \(Y_t=\) 0.416 \(Y_{t-1}+\epsilon_t\) -0.962\(\epsilon_{t-1}\) (la media è omessa perchè molto piccola). Siamo interessati allo studio dei residui del modello per verificare se possono essere considerati come realizzazioni di un processo white-noise. E’ possibile utilizzare la funzione checkresiduals che fornisce dei grafici (incluso il correlogramma) e l’output del test di Ljung-Box:

checkresiduals(mod1)

## 
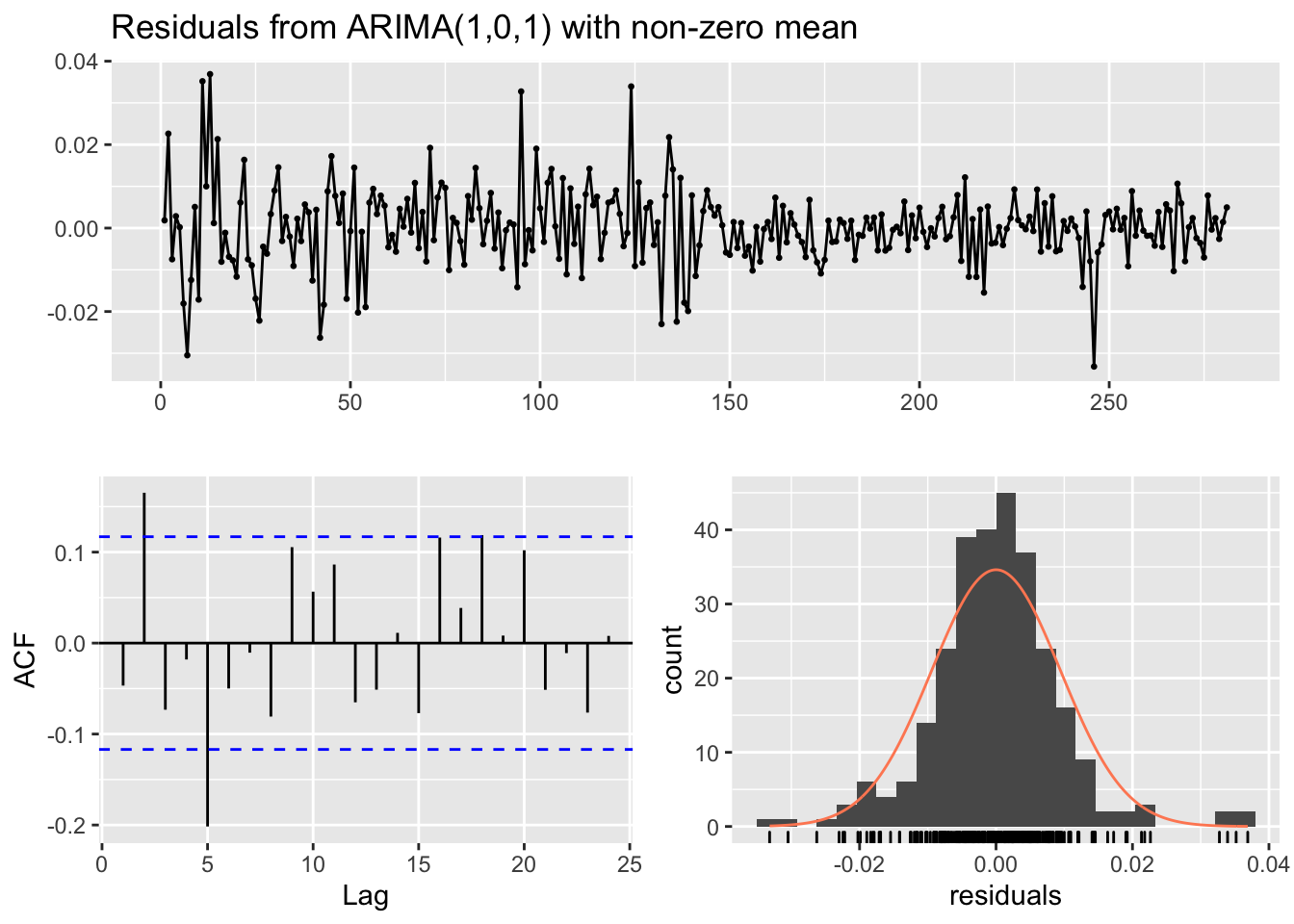
## 	Ljung-Box test
## 
## data:  Residuals from ARIMA(1,0,1) with non-zero mean
## Q* = 28.586, df = 7, p-value = 0.0001721
## 
## Model df: 3.   Total lags used: 10

Si noti che nel test di Ljung-Box test il numero di lag considerati è 10 (stiamo quindi verificando se le prime 10 correlazioni possono essere considerate tutte congiuntamente pari a zero). Se necessario è possibile cambiare il valore di \(K\) (lag massimo considerato) utilizzando l’argomento lag della funzione checkresiduals. Inoltre, il numero di gradi di libertà del modello è pari a 3 (dato dal numero di parametri stimati, \(\mu\), \(\phi\) e \(\theta\)) ed il numero di gradi di libertà della statistica test (vc \(\chi^2\)) è 7 (il numero di parametri stimati può anche essere definito manualmente con l’argomento df della funzione checkresiduals). Si ricordi che se si volessi usare la funzione Box.test per verificare l’incorrelazione dei residui è necessario specificare con l’opzione fitdf il numero di parametri stimati. Dato il valore del p-value si rifiuta l’ipotesi di incorrelazione dei residui e si conclude che la barra verticale che nel correlogramma fuoriesce dalla bande blu si riferisce ad una correlazione significativamente diversa da zero. Ciò significa che il modello ARMA(1,1) non è sufficiente per cogliere la correlazione presente nella serie storica. Andiamo quindi a provare un modello ARMA(2,1).

mod2 = Arima(diff2, order=c(2,0,1),
             include.constant = TRUE)
summary(mod2)
## Series: diff2 
## ARIMA(2,0,1) with non-zero mean 
## 
## Coefficients:
##          ar1     ar2      ma1   mean
##       0.3780  0.1184  -0.9706  0e+00
## s.e.  0.0618  0.0614   0.0176  1e-04
## 
## sigma^2 estimated as 8.919e-05:  log likelihood=912.53
## AIC=-1815.06   AICc=-1814.84   BIC=-1796.87
## 
## Training set error measures:
##                        ME        RMSE         MAE      MPE     MAPE      MASE
## Training set 2.931111e-05 0.009376612 0.006751608 207.9673 287.0736 0.4965266
##                    ACF1
## Training set 0.01841865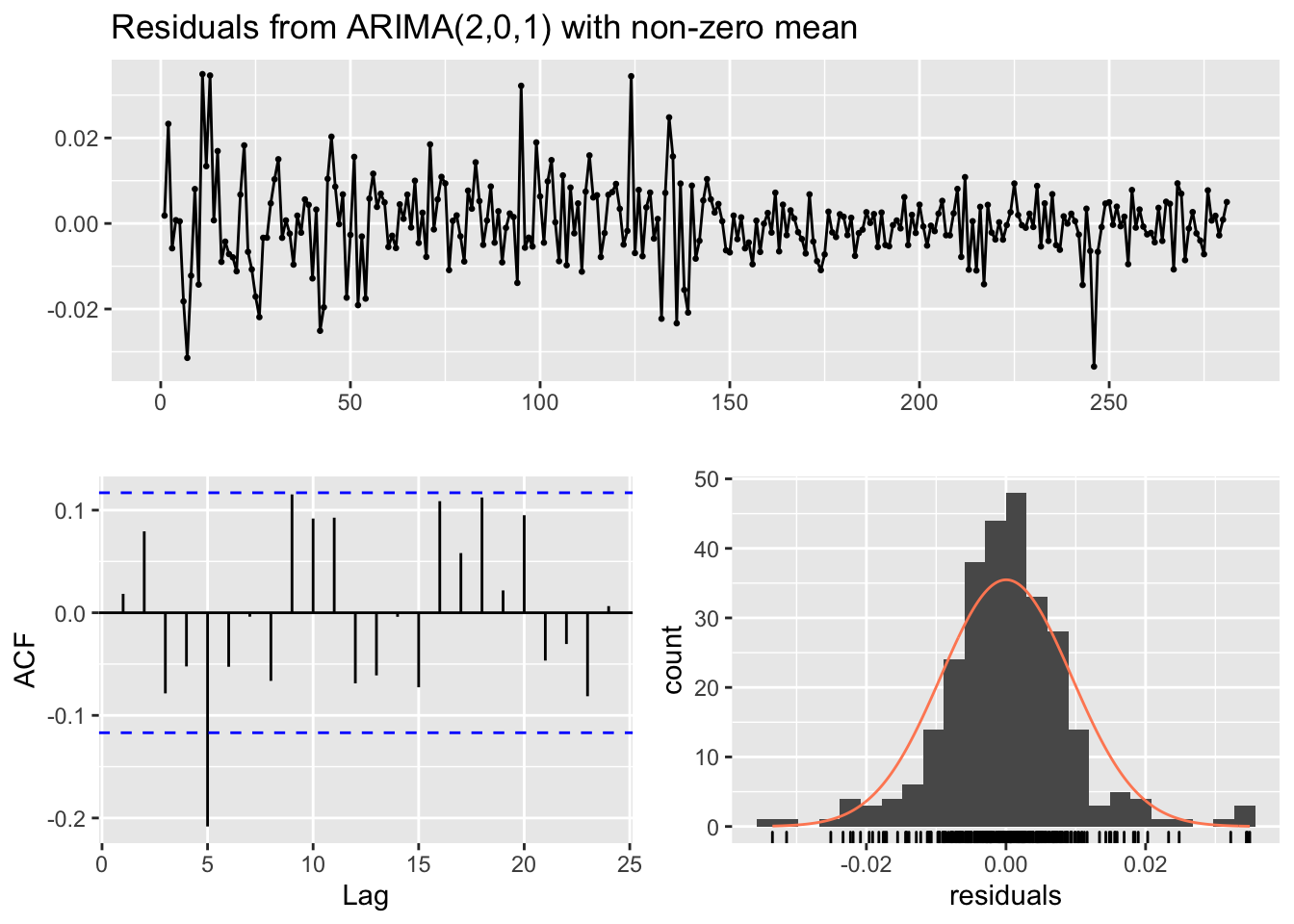
checkresiduals(mod2)

## 
## 	Ljung-Box test
## 
## data:  Residuals from ARIMA(2,0,1) with non-zero mean
## Q* = 25.384, df = 6, p-value = 0.0002898
## 
## Model df: 4.   Total lags used: 10

Nuovamente si conclude che i residui non sono incorrelati. Si procede quindi a stimare diversi modelli: ARMA(2,2), ARMA(3,1), ARMA(1,3), ARMA(2,3) e ARMA(3,2).

######### ARMA(2,2) #########
mod3 = Arima(diff2, order=c(2,0,2),
             include.constant = TRUE)
summary(mod3)
## Series: diff2 
## ARIMA(2,0,2) with non-zero mean 
## 
## Coefficients:
##           ar1     ar2      ma1      ma2   mean
##       -0.1836  0.3745  -0.4025  -0.5486  0e+00
## s.e.   0.1762  0.0787   0.1798   0.1712  1e-04
## 
## sigma^2 estimated as 8.815e-05:  log likelihood=914.67
## AIC=-1817.33   AICc=-1817.02   BIC=-1795.5
## 
## Training set error measures:
##                        ME        RMSE         MAE      MPE     MAPE     MASE
## Training set 2.827708e-05 0.009305174 0.006668397 213.8634 291.7492 0.490407
##                   ACF1
## Training set 0.0150511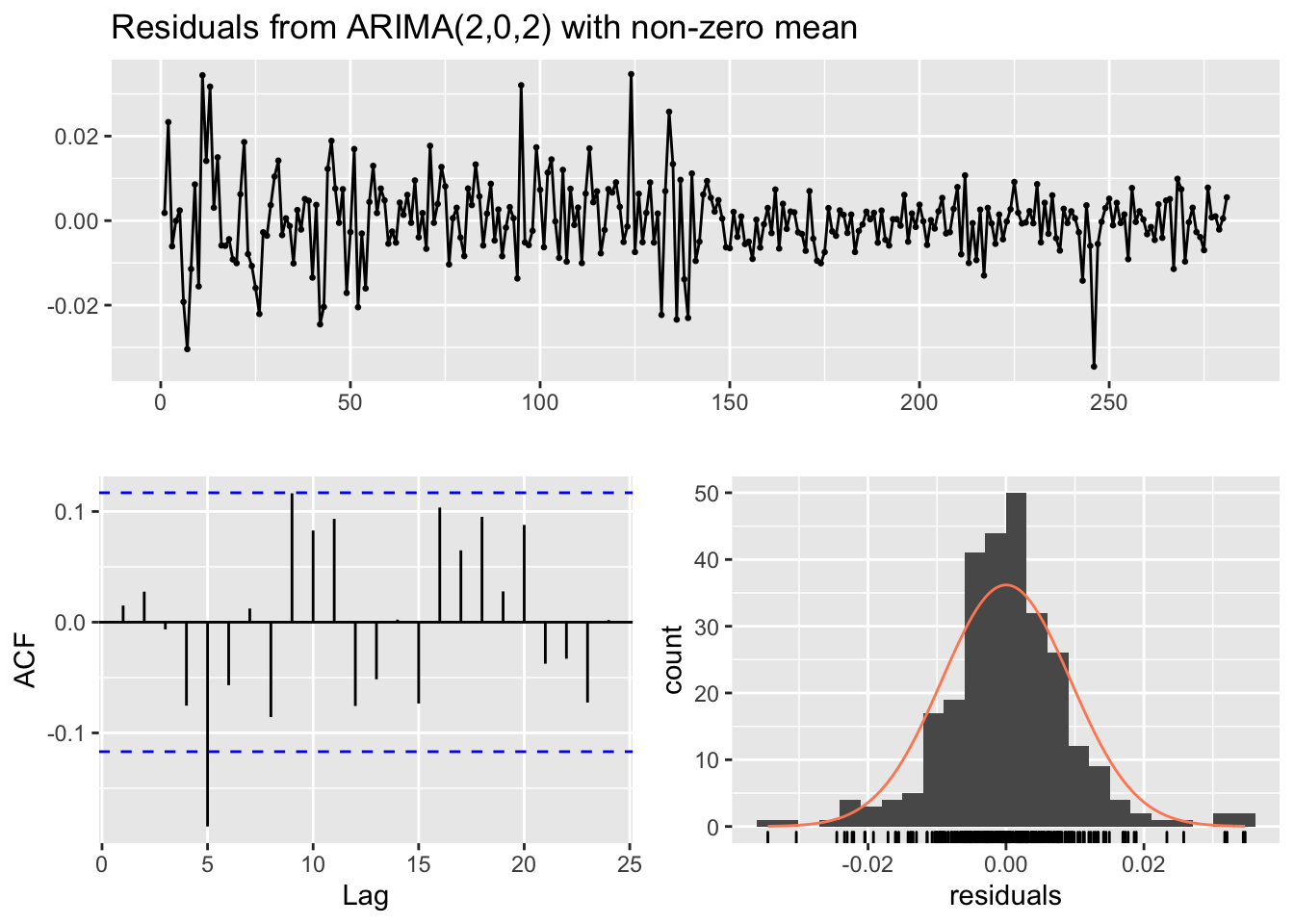
checkresiduals(mod3)

## 
## 	Ljung-Box test
## 
## data:  Residuals from ARIMA(2,0,2) with non-zero mean
## Q* = 20.823, df = 5, p-value = 0.0008749
## 
## Model df: 5.   Total lags used: 10
######### ARMA(3,1) #########
mod4 = Arima(diff2, order=c(3,0,1),
             include.constant = TRUE)
summary(mod4)
## Series: diff2 
## ARIMA(3,0,1) with non-zero mean 
## 
## Coefficients:
##          ar1     ar2      ar3      ma1   mean
##       0.3852  0.1708  -0.1725  -0.9577  0e+00
## s.e.  0.0606  0.0630   0.0607   0.0191  1e-04
## 
## sigma^2 estimated as 8.702e-05:  log likelihood=916.46
## AIC=-1820.93   AICc=-1820.62   BIC=-1799.1
## 
## Training set error measures:
##                        ME        RMSE         MAE      MPE     MAPE      MASE
## Training set 1.783105e-05 0.009245019 0.006574007 186.7293 252.9048 0.4834654
##                     ACF1
## Training set -0.01776276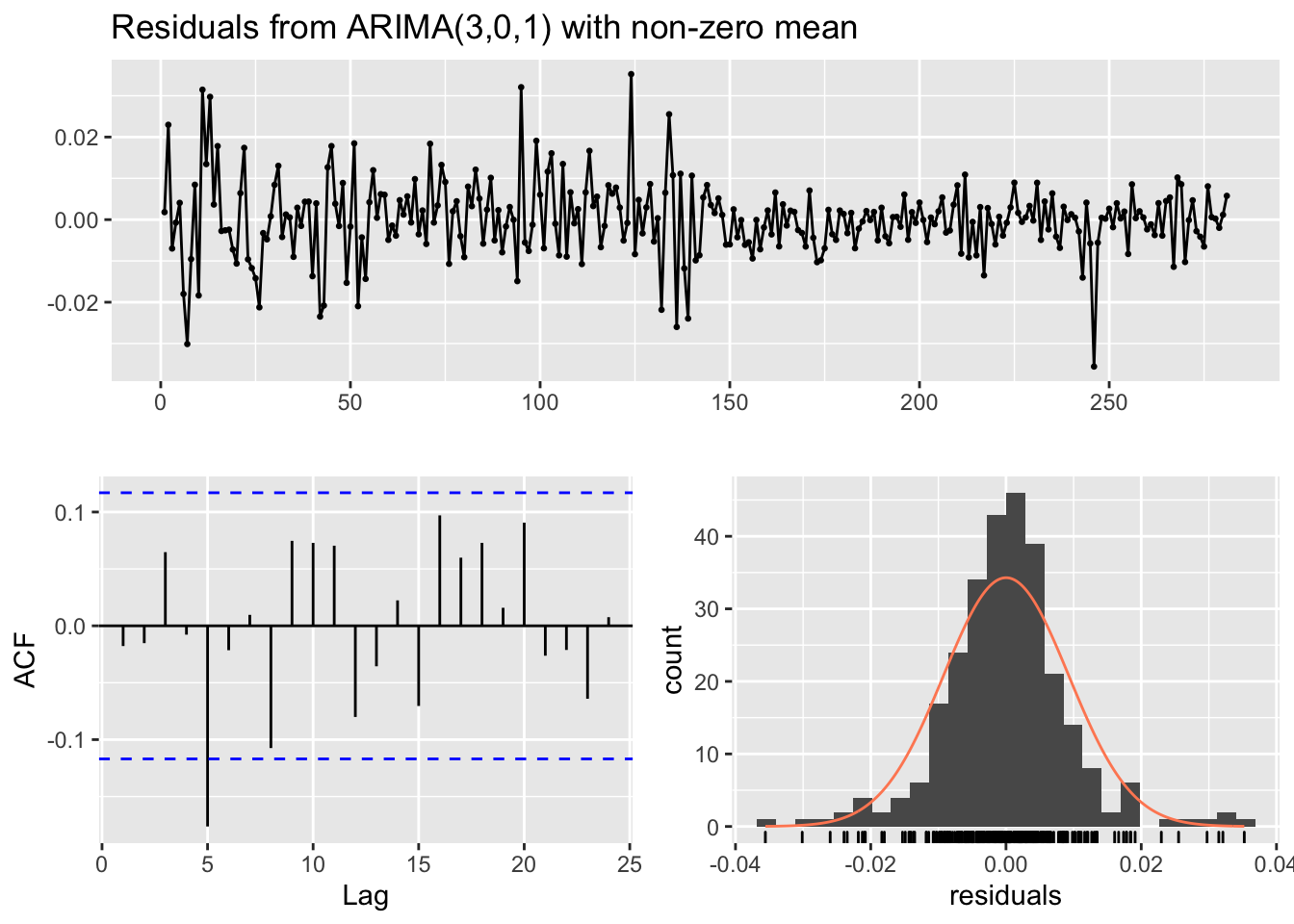
checkresiduals(mod4)

## 
## 	Ljung-Box test
## 
## data:  Residuals from ARIMA(3,0,1) with non-zero mean
## Q* = 17.037, df = 5, p-value = 0.00443
## 
## Model df: 5.   Total lags used: 10
######### ARMA(1,3) #########
mod5 = Arima(diff2, order=c(1,0,3),
             include.constant = TRUE)
summary(mod5)
## Series: diff2 
## ARIMA(1,0,3) with non-zero mean 
## 
## Coefficients:
##          ar1      ma1     ma2      ma3   mean
##       0.3332  -0.9211  0.1555  -0.1929  0e+00
## s.e.  0.1530   0.1532  0.1304   0.0652  1e-04
## 
## sigma^2 estimated as 8.787e-05:  log likelihood=915.13
## AIC=-1818.25   AICc=-1817.95   BIC=-1796.42
## 
## Training set error measures:
##                        ME        RMSE         MAE      MPE     MAPE    MASE
## Training set 2.647367e-05 0.009289874 0.006652528 211.2842 281.9028 0.48924
##                     ACF1
## Training set 0.003535468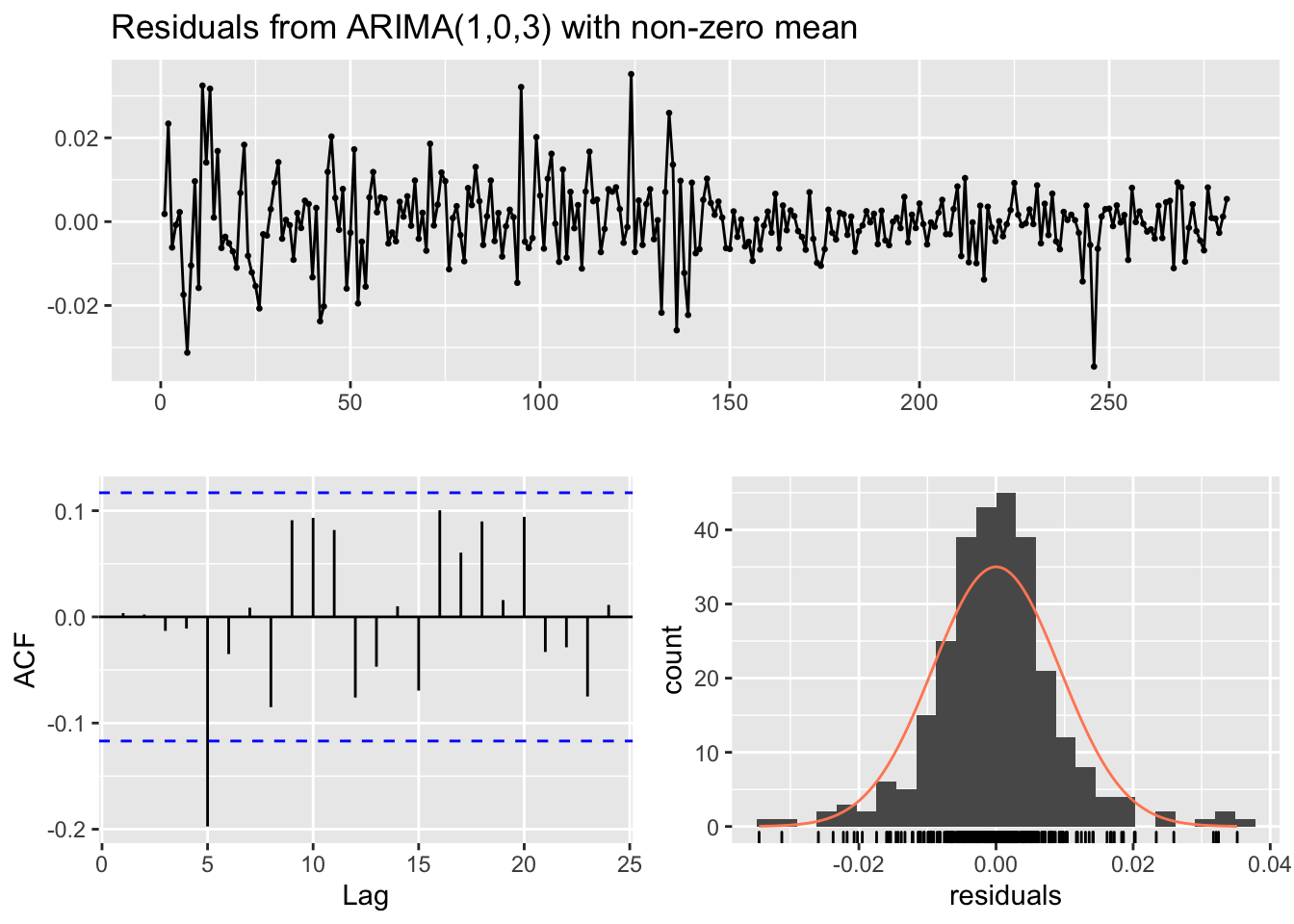
checkresiduals(mod5)

## 
## 	Ljung-Box test
## 
## data:  Residuals from ARIMA(1,0,3) with non-zero mean
## Q* = 18.776, df = 5, p-value = 0.002116
## 
## Model df: 5.   Total lags used: 10
######### ARMA(2,3) #########
mod6 = Arima(diff2, order=c(2,0,3),
             include.constant = TRUE)
summary(mod6)
## Series: diff2 
## ARIMA(2,0,3) with non-zero mean 
## 
## Coefficients:
##           ar1     ar2      ma1      ma2      ma3   mean
##       -0.1879  0.2820  -0.3862  -0.4622  -0.0948  0e+00
## s.e.   0.2221  0.1359   0.2277   0.2297   0.1023  1e-04
## 
## sigma^2 estimated as 8.822e-05:  log likelihood=915.07
## AIC=-1816.13   AICc=-1815.72   BIC=-1790.66
## 
## Training set error measures:
##                        ME        RMSE         MAE      MPE     MAPE      MASE
## Training set 2.382653e-05 0.009291752 0.006647268 200.0394 277.0012 0.4888531
##                       ACF1
## Training set -0.0003539481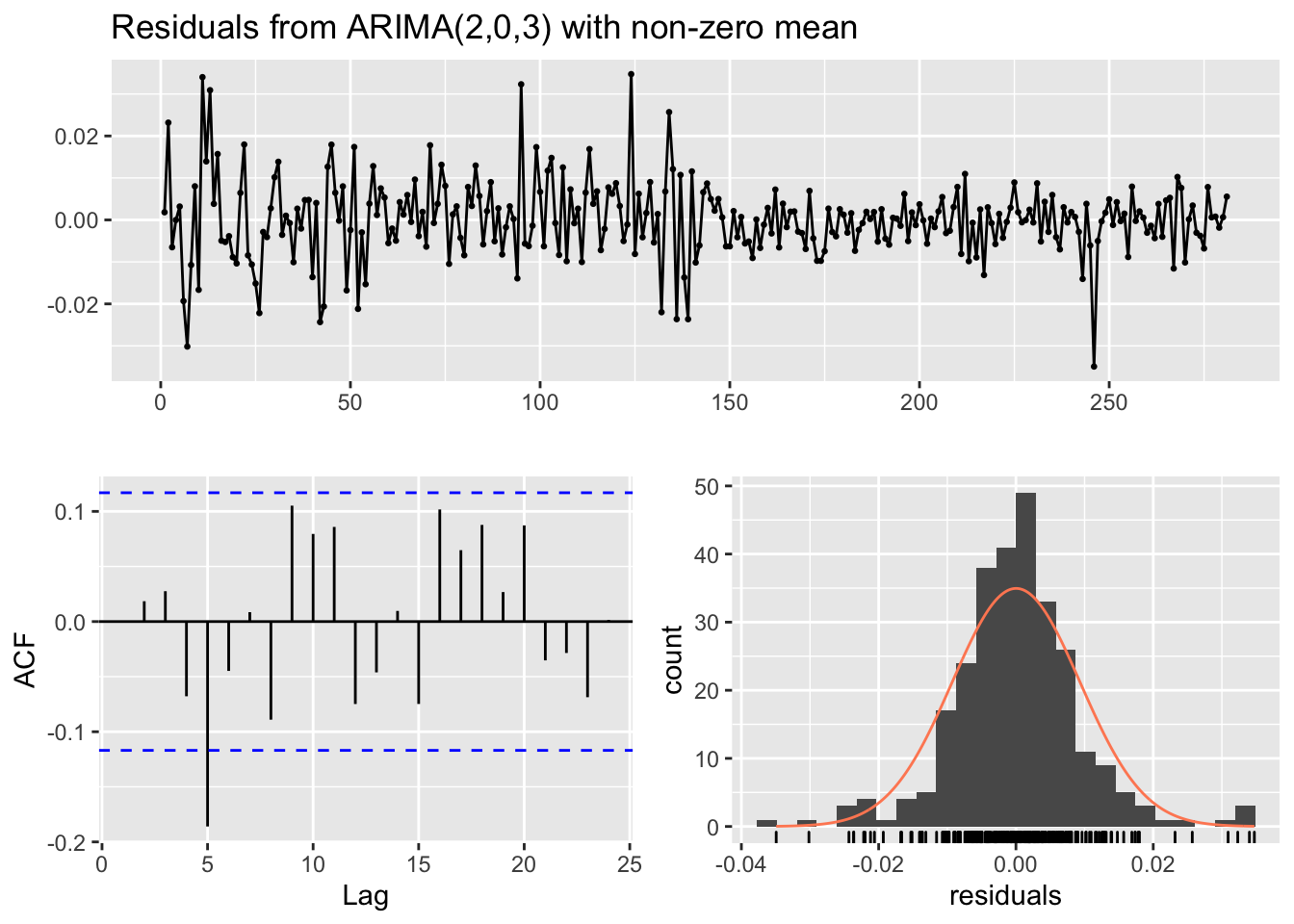
checkresiduals(mod6)

## 
## 	Ljung-Box test
## 
## data:  Residuals from ARIMA(2,0,3) with non-zero mean
## Q* = 19.605, df = 4, p-value = 0.0005974
## 
## Model df: 6.   Total lags used: 10
######### ARMA(3,2) #########
mod7 = Arima(diff2, order=c(3,0,2),
             include.constant = TRUE)
summary(mod7)
## Series: diff2 
## ARIMA(3,0,2) with non-zero mean 
## 
## Coefficients:
##          ar1      ar2      ar3      ma1     ma2   mean
##       1.0208  -0.0725  -0.2551  -1.6275  0.6548  0e+00
## s.e.  0.1686   0.1105   0.0613   0.1718  0.1652  1e-04
## 
## sigma^2 estimated as 8.514e-05:  log likelihood=919.95
## AIC=-1825.89   AICc=-1825.48   BIC=-1800.43
## 
## Training set error measures:
##                        ME        RMSE         MAE      MPE     MAPE      MASE
## Training set 4.601698e-05 0.009128333 0.006474332 139.5792 223.9337 0.4761351
##                      ACF1
## Training set -0.003316259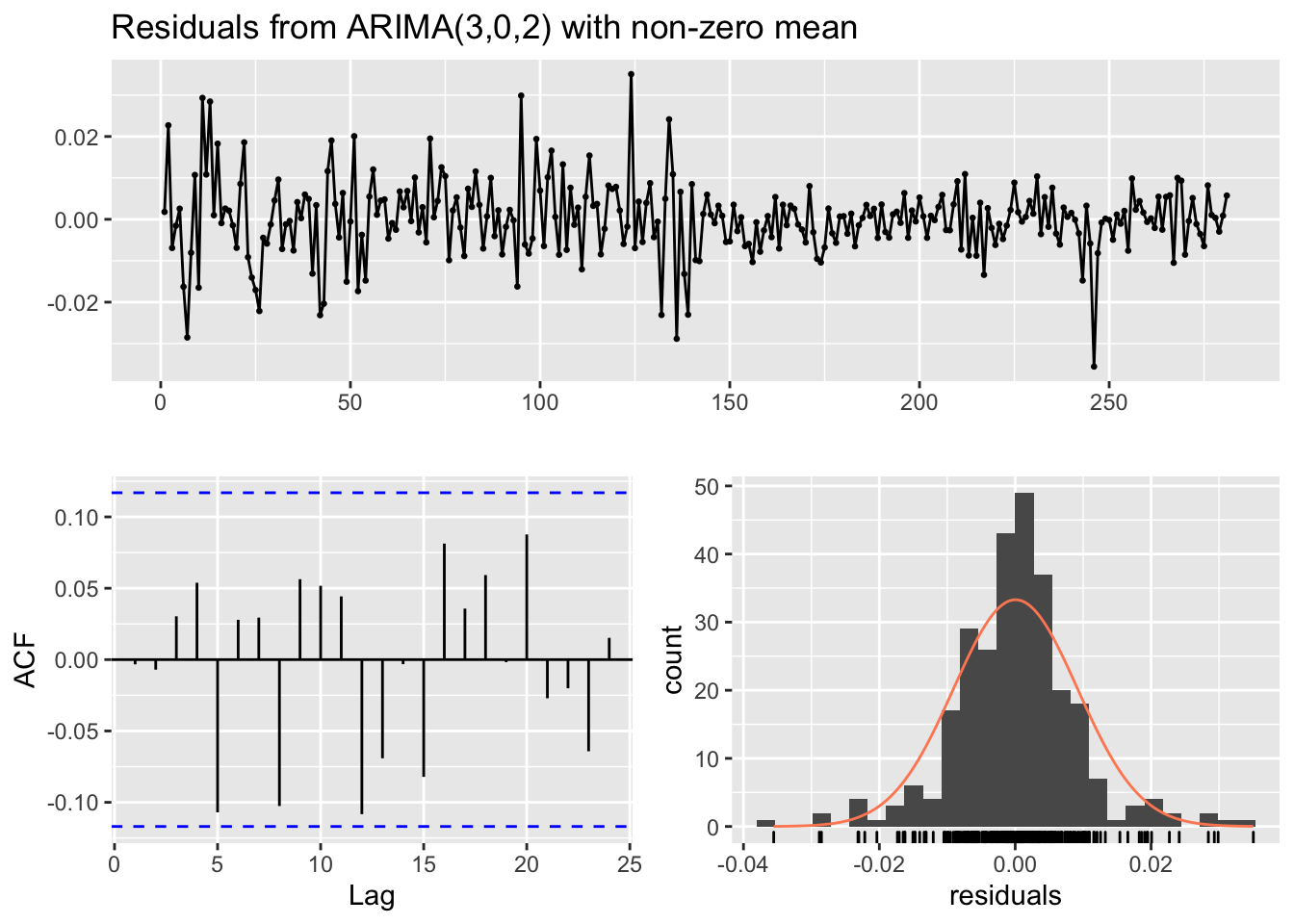
checkresiduals(mod7)

## 
## 	Ljung-Box test
## 
## data:  Residuals from ARIMA(3,0,2) with non-zero mean
## Q* = 9.666, df = 4, p-value = 0.04645
## 
## Model df: 6.   Total lags used: 10

I modelli possono essere confrontati utilizzando l’indice AIC:

all_aic = c(mod1$aic, mod2$aic, mod3$aic, mod4$aic,mod5$aic, mod6$aic, mod7$aic)
min(all_aic)
## [1] -1825.894
which.min(all_aic)
## [1] 7

Il modello con l’indice AIC più basso è mod7 (ARMA(3,2)). Inoltre, i residui di questo modello sono incorrelati (tutte le barre verticali sono contenute nelle linee blue). Ciò significa che non c’è altra correlazione temporale residua. L’equazione del modello stimato è la seguente: $Y_t=$1.021 \(Y_{t-1}\) -0.073 \(Y_{t-2}\) -0.255 \(Y_{t-3}+\epsilon_t\) -1.628 \(\epsilon_{t-1}\) +0.655 \(\epsilon_{t-2}\).

Una volta scelto il modello migliore è possibile rappresentare i valori osservati \(y_t\) (\(t=1,2,\ldots,n\)) e i corrispondenti valori previsti (fittati, \(\hat y_t\)) :

ts.plot(diff2, col="grey")
lines(mod7$fitted, col="blue")

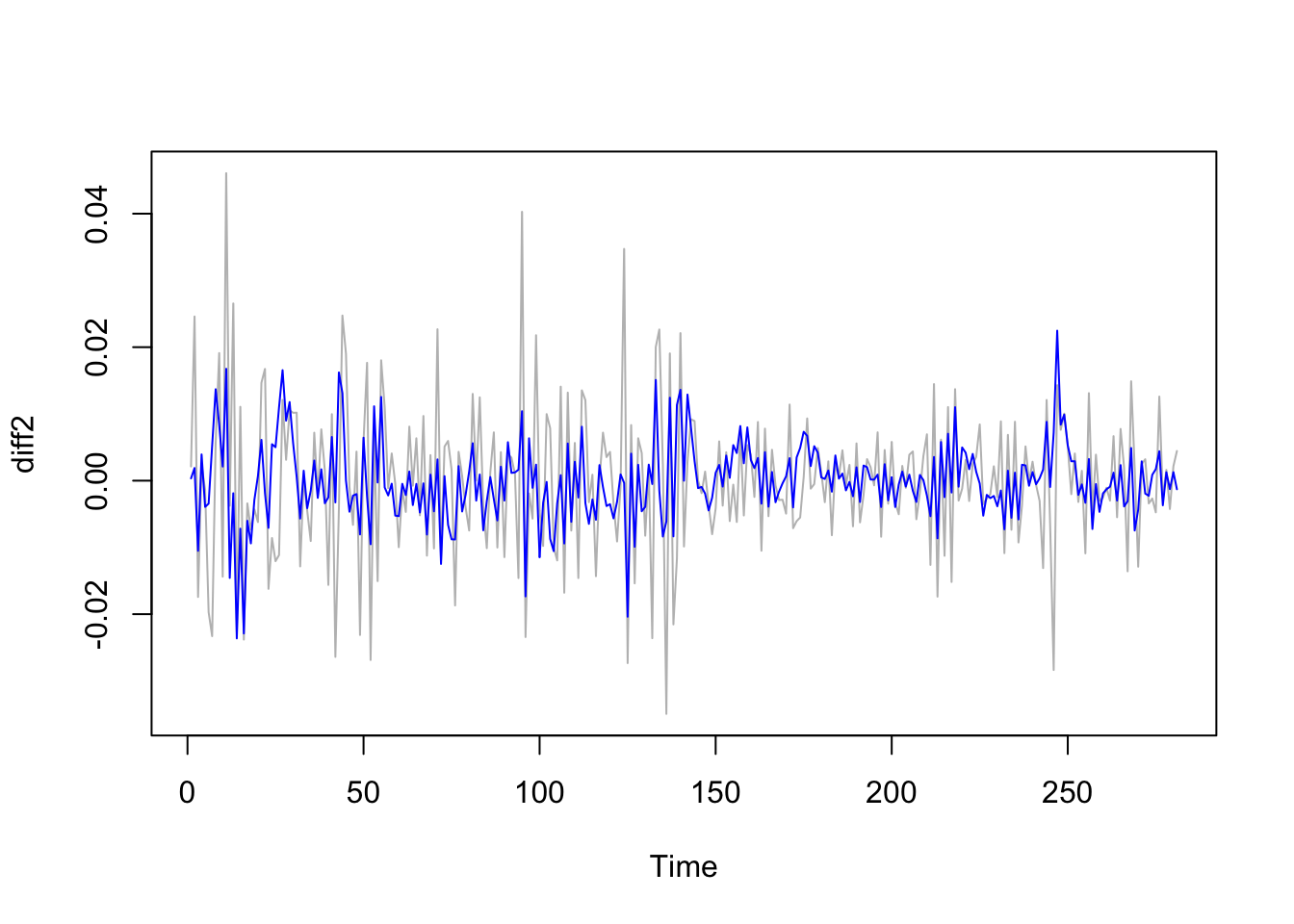
Si osserva che il modello non è in grado di cogliere i valori estremi della serie storica (servirebbe un altro tipo di famiglia di modelli…). Procediamo ora con la parte di previsione, con particolare riferimento ai 10 giorni successiva alla serie storica osservata. Per fare questo utilizziamo la funzione forecast:

forecast(mod7)
##     Point Forecast       Lo 80       Hi 80       Lo 95      Hi 95
## 282  -3.297003e-03 -0.01512236 0.008528357 -0.02138233 0.01478832
## 283  -4.933976e-04 -0.01432511 0.013338316 -0.02164718 0.02066038
## 284  -1.407692e-03 -0.01524636 0.012430972 -0.02257210 0.01975672
## 285  -5.687808e-04 -0.01471715 0.013579584 -0.02220684 0.02106928
## 286  -3.613323e-04 -0.01455580 0.013833140 -0.02206990 0.02134724
## 287   2.283446e-05 -0.01419656 0.014242231 -0.02172386 0.02176953
## 288   1.859326e-04 -0.01403349 0.014405352 -0.02156079 0.02193266
## 289   2.716382e-04 -0.01395154 0.014494819 -0.02148084 0.02202412
## 290   2.492921e-04 -0.01398453 0.014483118 -0.02151947 0.02201805
## 291   1.786564e-04 -0.01406558 0.014422894 -0.02160602 0.02196334

La tabella che si ottiene contiene le stime puntuali (previsioni puntuali) e i corrispondenti intervalli di previsione a livello \(1-\alpha\) pari a 0.80 e 0.95. Il corrispondente grafico è dato dalla combinazione della funzione plot e forecast:

plot(forecast(mod7))

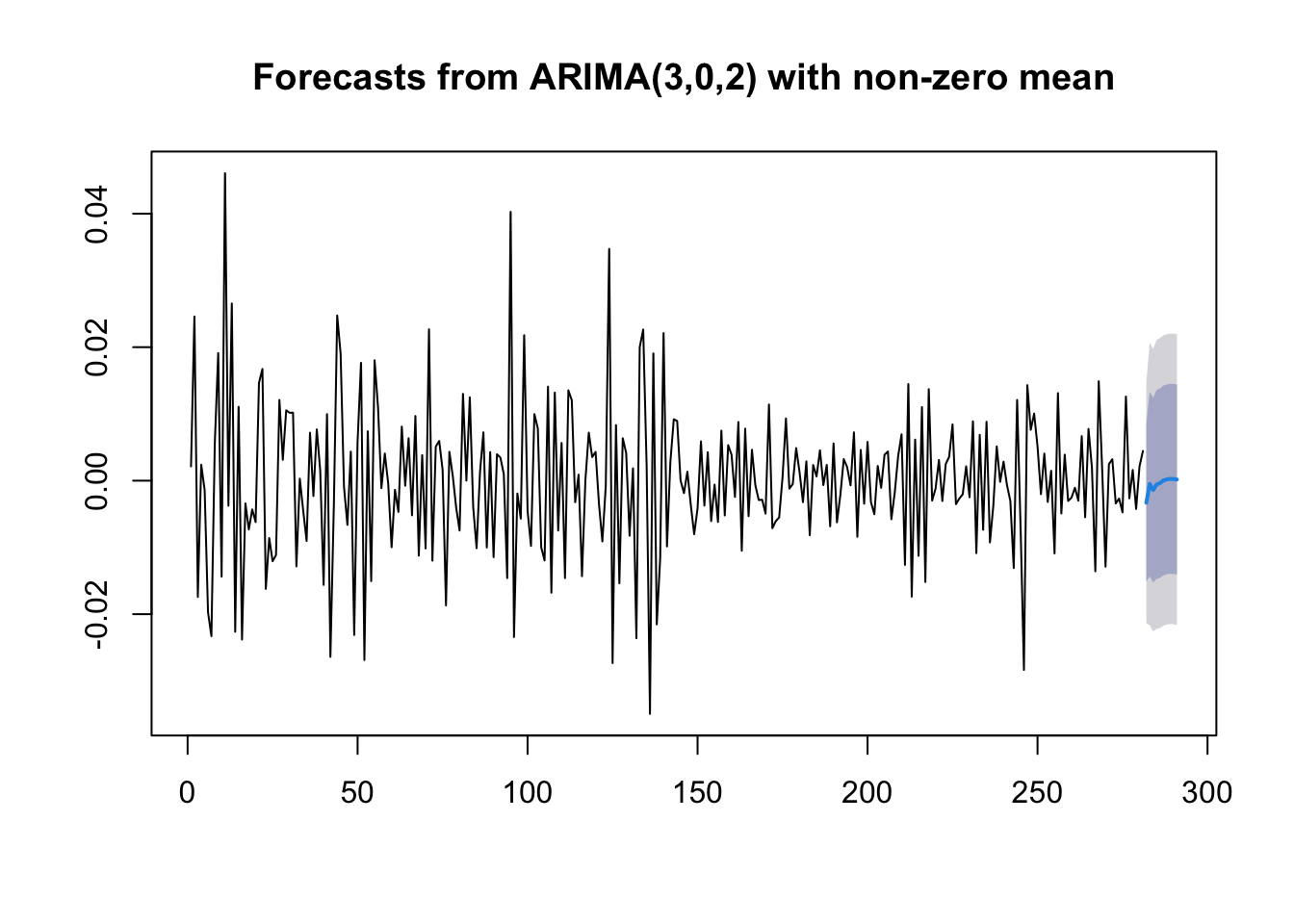Se siamo interessati ad ottenere delle previsioni per un periodo più lungo di 10 giorni possiamo utilizzare l’argomento h della funzione forecast:

plot(forecast(mod7, h=50))

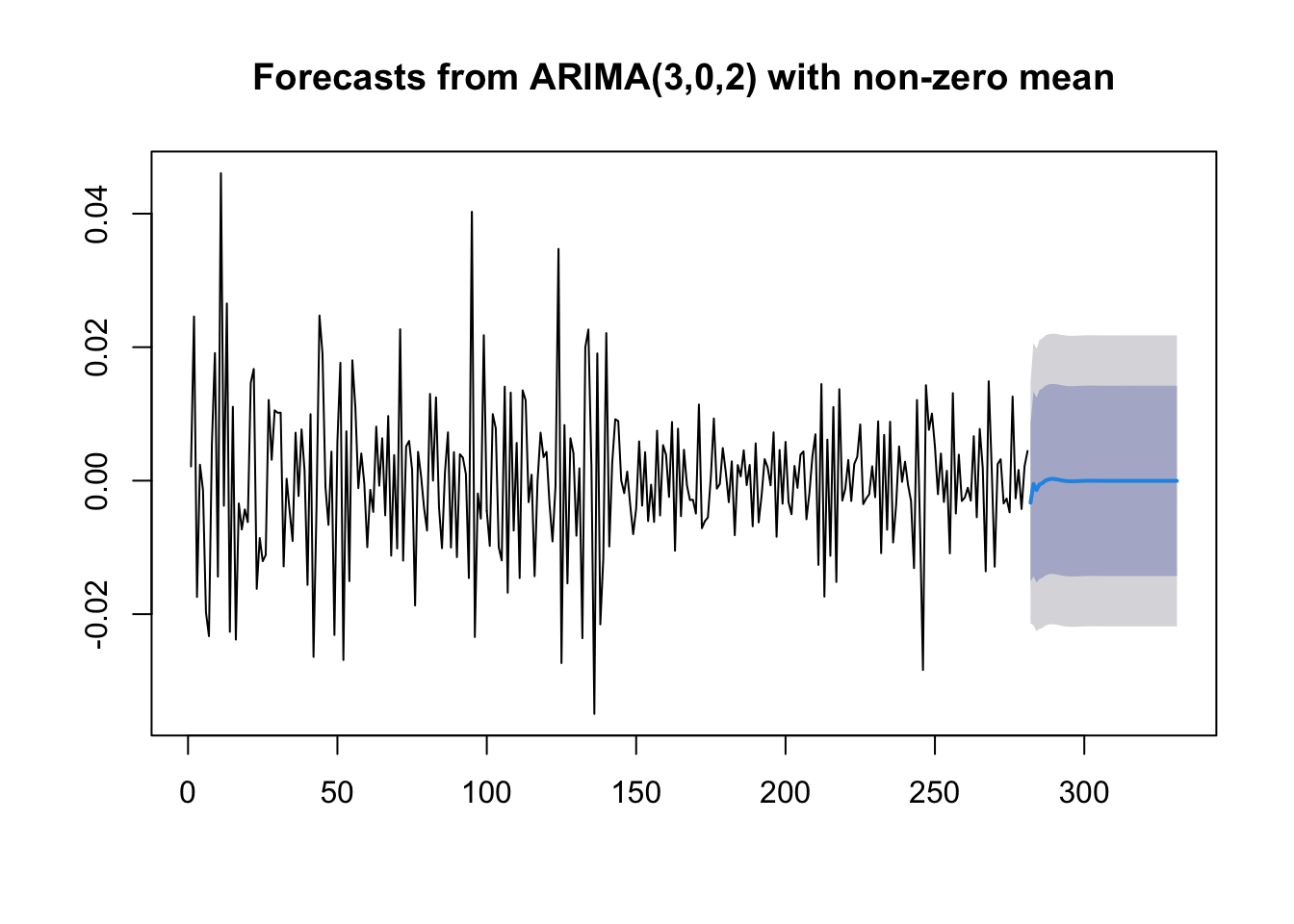Guardando le previsioni a 50 giorni, si nota che la previsione a \(k\) giorni, \(\hat y_{n+k}\), converge al valore medio \(\hat \mu\) per \(k\rightarrow +\infty\) (così come ci si aspetta per ogni modello stazionario). Inoltre, gli intervalli di previsione convergono a linee parallele (perchè la varianza della previsione converge a un valore finito).

12.5 Modello di regressione dinamico

Per illustrare l’implementazione di un modello di regressione dinamico, noto anche come ARIMAX, si utilizzano i dati usconsumption presenti nella libreria fpp. Essi si riferiscono alle differenze percentuali di due variabili: consumi e reddito. I dati si riferiscono agli Stati Uniti e al periodo dal 1970 al 2010.

library(fpp)
## Loading required package: fma
## 
## Attaching package: 'fma'
## The following objects are masked from 'package:MASS':
## 
##     cement, housing, petrol
## The following objects are masked from 'package:faraway':
## 
##     airpass, eggs, ozone, wheat
## Loading required package: expsmooth
## Loading required package: lmtest
## Loading required package: zoo
## 
## Attaching package: 'zoo'
## The following object is masked from 'package:timeSeries':
## 
##     time<-
## The following objects are masked from 'package:base':
## 
##     as.Date, as.Date.numeric
head(usconsumption)
##         consumption    income
## 1970 Q1   0.6122769  0.496540
## 1970 Q2   0.4549298  1.736460
## 1970 Q3   0.8746730  1.344881
## 1970 Q4  -0.2725144 -0.328146
## 1971 Q1   1.8921870  1.965432
## 1971 Q2   0.9133782  1.490757
tail(usconsumption)
##         consumption     income
## 2009 Q3   0.5740010 -1.3925562
## 2009 Q4   0.1093289 -0.1447134
## 2010 Q1   0.6710180  1.1871651
## 2010 Q2   0.7177182  1.3543547
## 2010 Q3   0.6531433  0.5611698
## 2010 Q4   0.8753521  0.3710579

Si noti che l’oggetto usconsumption disponibile ora nell’ambiente di lavoro è di tipo Time-Series. Per questo tipo di oggetto le variabili (colonne) vanno selezionate non usando il dollaro ma bensì le parentesi quadre. Si veda ad esempio qui di seguito la rappresentazione grafica delle due variabili:

#consumi (differenze%)
ts.plot(usconsumption[,1])

#reddito (differenze%)
ts.plot(usconsumption[,2])

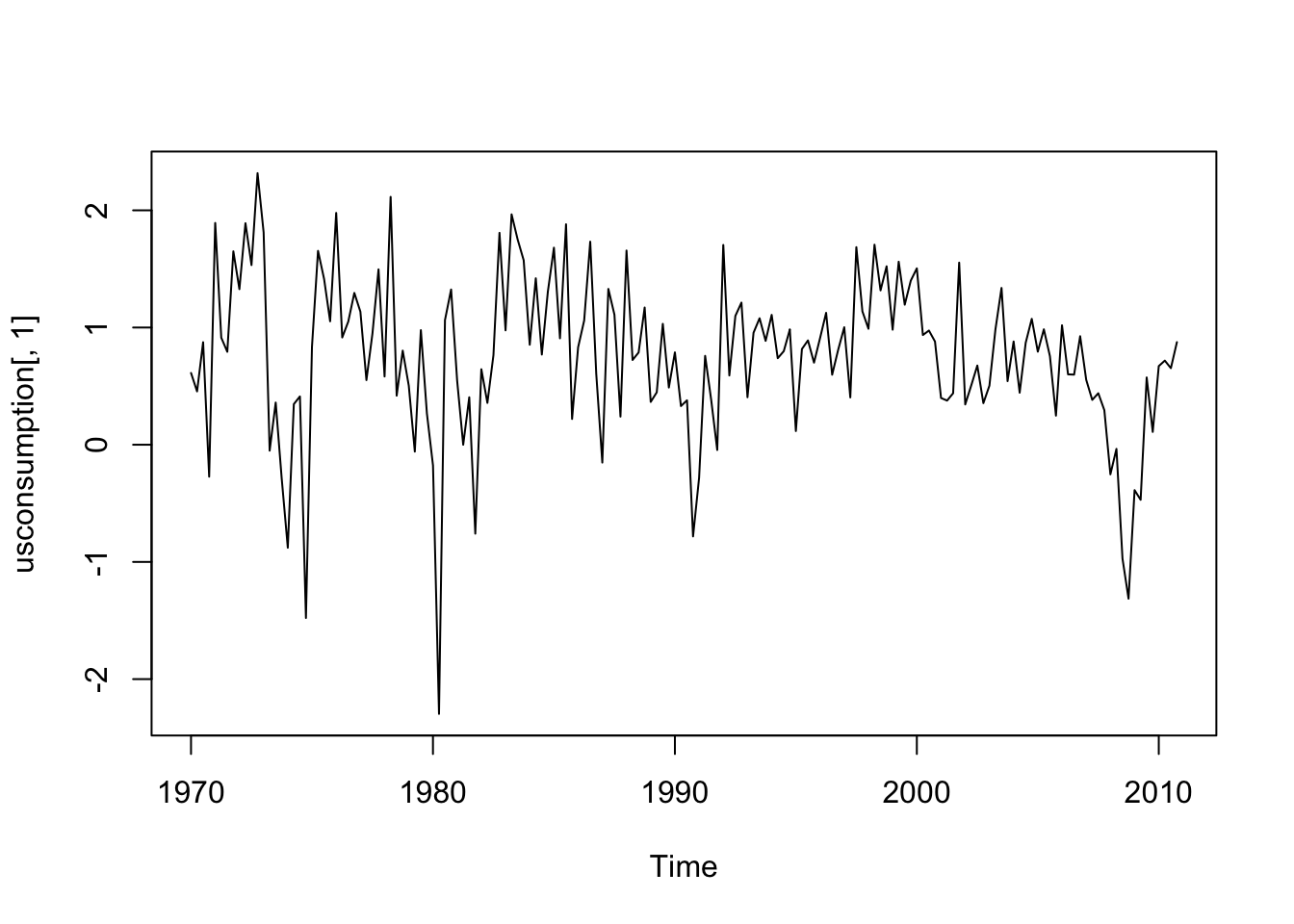
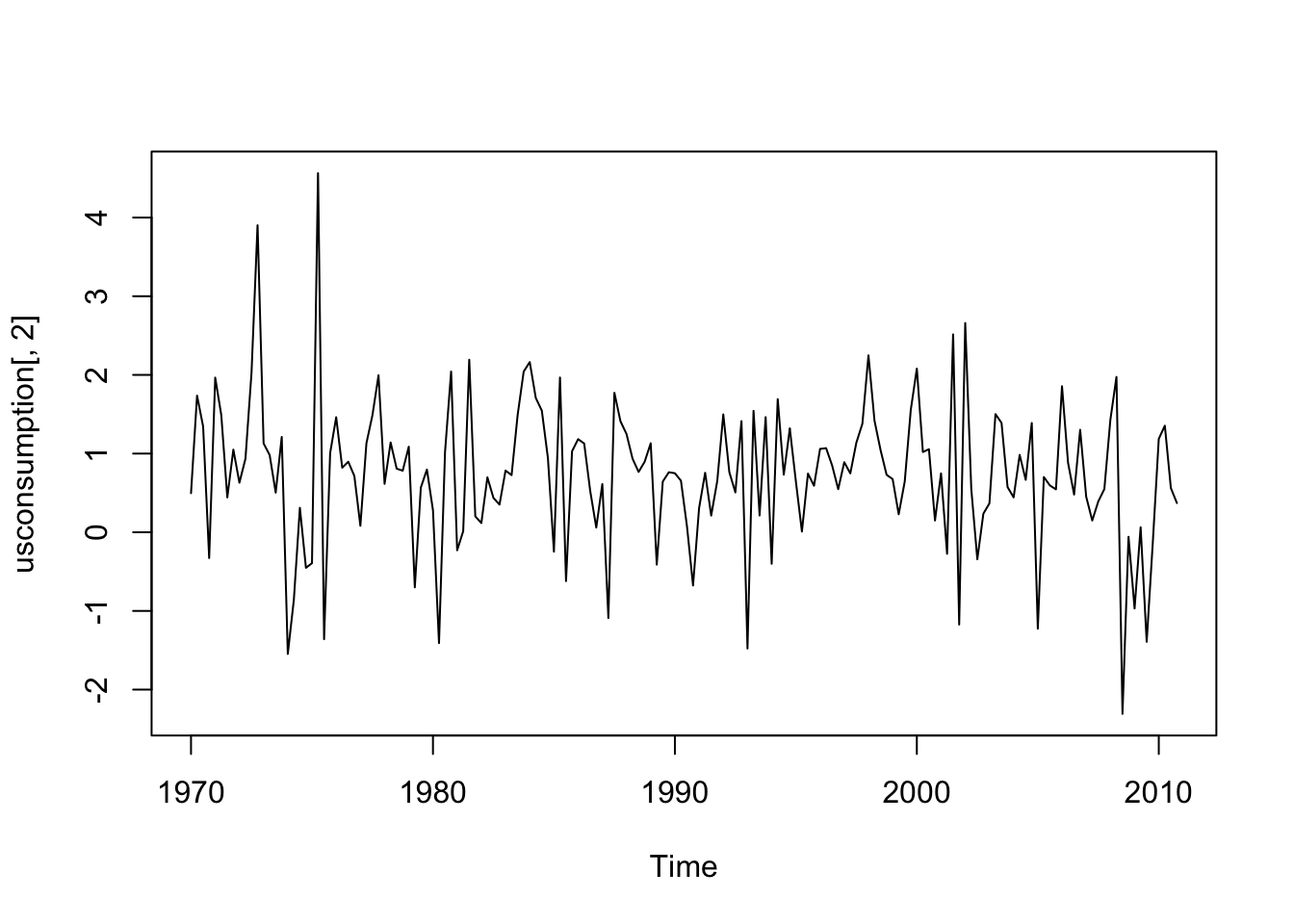
#le due variabili insieme
ts.plot(usconsumption[,1],ylim=range(usconsumption))
lines(usconsumption[,2],col="red")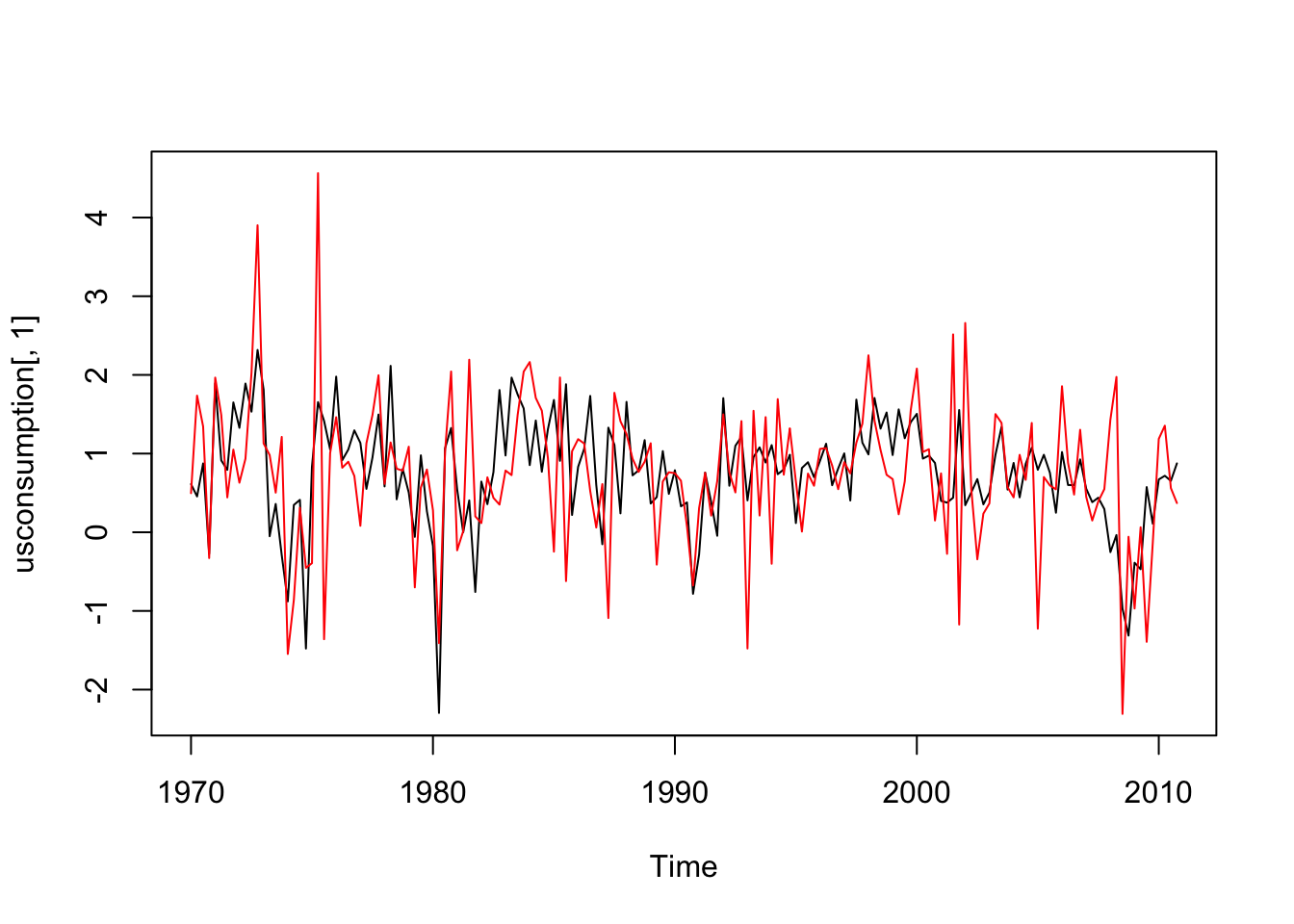

Entrambe le serie storiche appaiono stazionarie.

Si inizia quindi con la stima di un modello di regressione che utilizza come variabile risposta la variabile consumption e come regressore la variabile income:

modreg = lm(consumption ~ income, data=usconsumption)
summary(modreg)
## 
## Call:
## lm(formula = consumption ~ income, data = usconsumption)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.3681 -0.3237  0.0266  0.3436  1.5581 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.52062    0.06231   8.356 2.79e-14 ***
## income       0.31866    0.05226   6.098 7.61e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6274 on 162 degrees of freedom
## Multiple R-squared:  0.1867,	Adjusted R-squared:  0.1817 
## F-statistic: 37.18 on 1 and 162 DF,  p-value: 7.614e-09

Il parametro \(\beta\) che lega le due variabili è positivo e significativamente diverso da zero. Si procede con la verifica dell’ipotesi di incorrelazione dei residui:

acf(modreg$residuals) 

pacf(modreg$residuals)

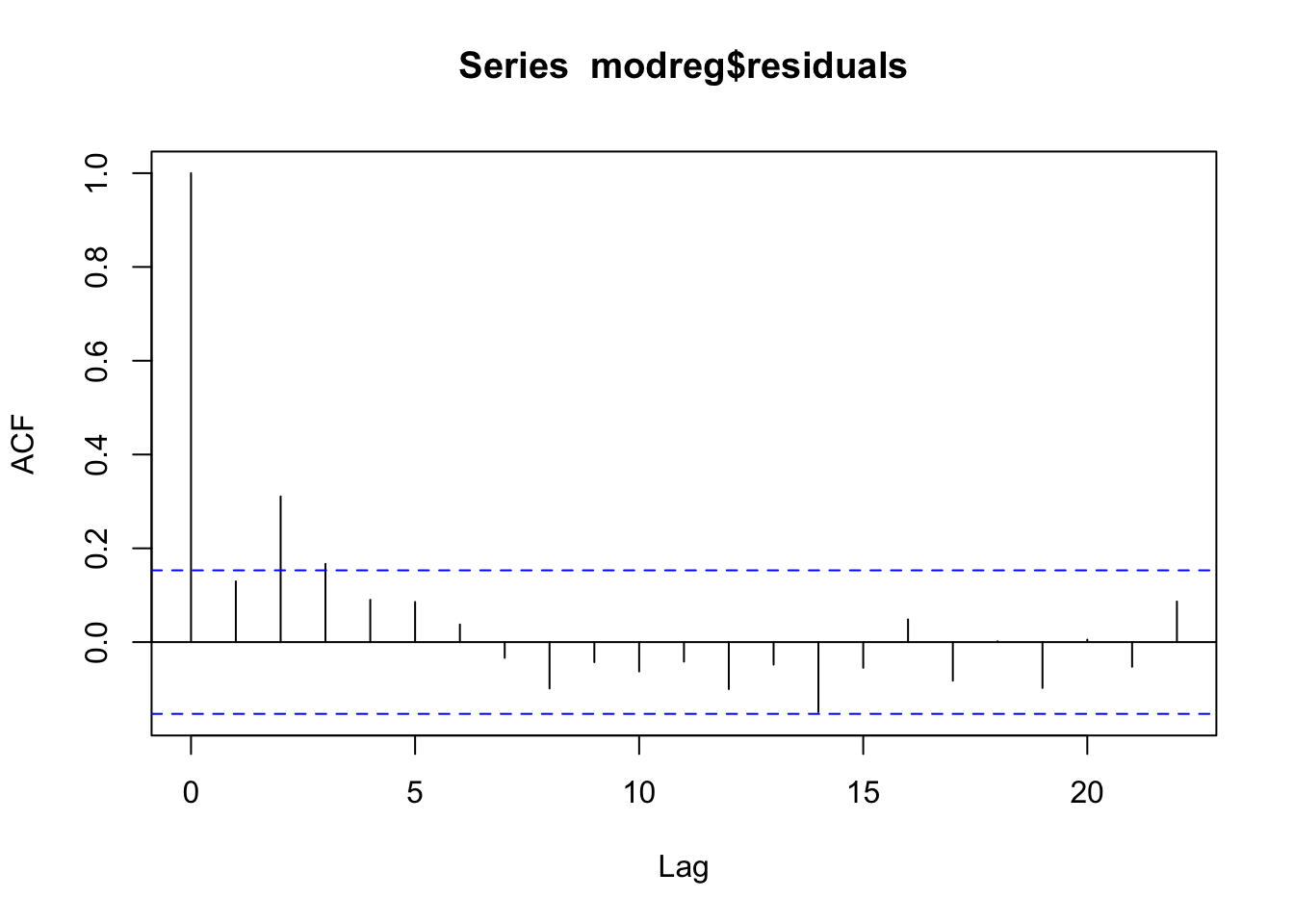
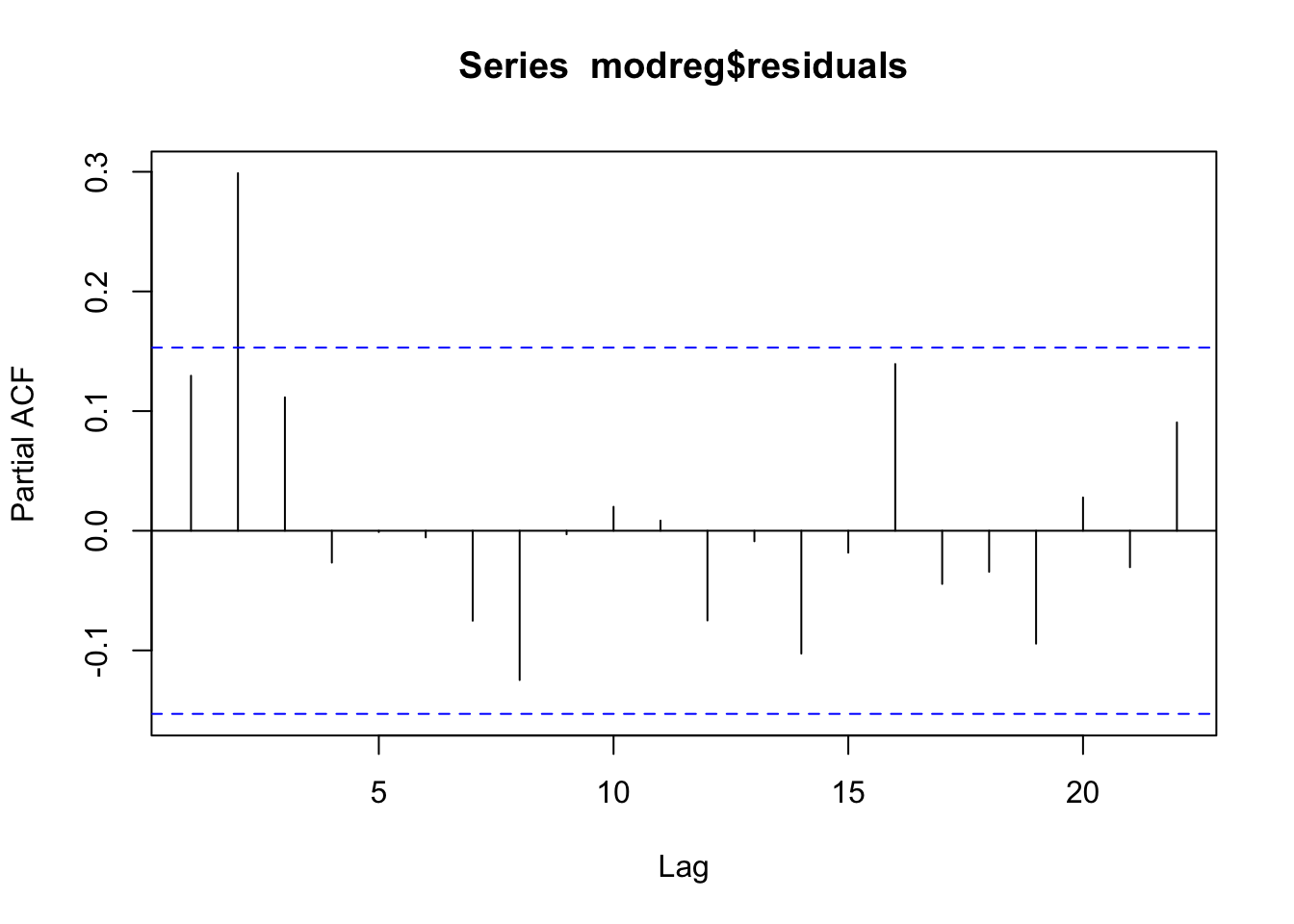Dall’analisi del correlogramma si nota che i residui non sono incorrelati; l’ipotesi di incorrelazione non può quindi essere accettata. La struttura che si osserva nei due grafici non è particolarmente chiara: si tratta di un cut-off a lag 3 per la acf? E di un cut-off a lag 2 per la pacf? Non è esattamente chiaro. Si procede quindi con la stima di diversi modelli nella classe dei modelli ARMA. Il modello migliore risulta essere il modello ARMA(1,2), implementato qui di seguito. In particolare, il regressore usconsumption[,2] andrà specificato nell’opzione xreg della funzione Arima:

modarimax = Arima(usconsumption[,1], order=c(1,0,2),
      xreg = usconsumption[,2], include.constant = TRUE)

summary(modarimax)
## Series: usconsumption[, 1] 
## Regression with ARIMA(1,0,2) errors 
## 
## Coefficients:
##          ar1      ma1     ma2  intercept    xreg
##       0.6516  -0.5440  0.2187     0.5750  0.2420
## s.e.  0.1468   0.1576  0.0790     0.0951  0.0513
## 
## sigma^2 estimated as 0.3502:  log likelihood=-144.27
## AIC=300.54   AICc=301.08   BIC=319.14
## 
## Training set error measures:
##                       ME      RMSE       MAE  MPE MAPE      MASE        ACF1
## Training set 0.001835782 0.5827238 0.4375789 -Inf  Inf 0.6298752 0.000656846
modarimax$coef
##        ar1        ma1        ma2  intercept       xreg 
##  0.6516382 -0.5440223  0.2186652  0.5749932  0.2419798

Il modello stimato è definito dalle seguenti due equazioni:

  • \(Y_t=\) 0.57+ 0.24 \(x_t+u_t\)
  • \(u_t\) = 0.65 \(u_{t-1}+\epsilon_t\) -0.54 \(\epsilon_{t-1}\) + 0.22 \(\epsilon_{t-2}\)

dove \(u_t\) sono gli errori della regressione (correlati) e \(\epsilon_t\) gli errori ARMA per i quali è necessario verificare l’ipotesi di incorrelazione. Si procede quindi come segue:

checkresiduals(modarimax, lag=14)

## 
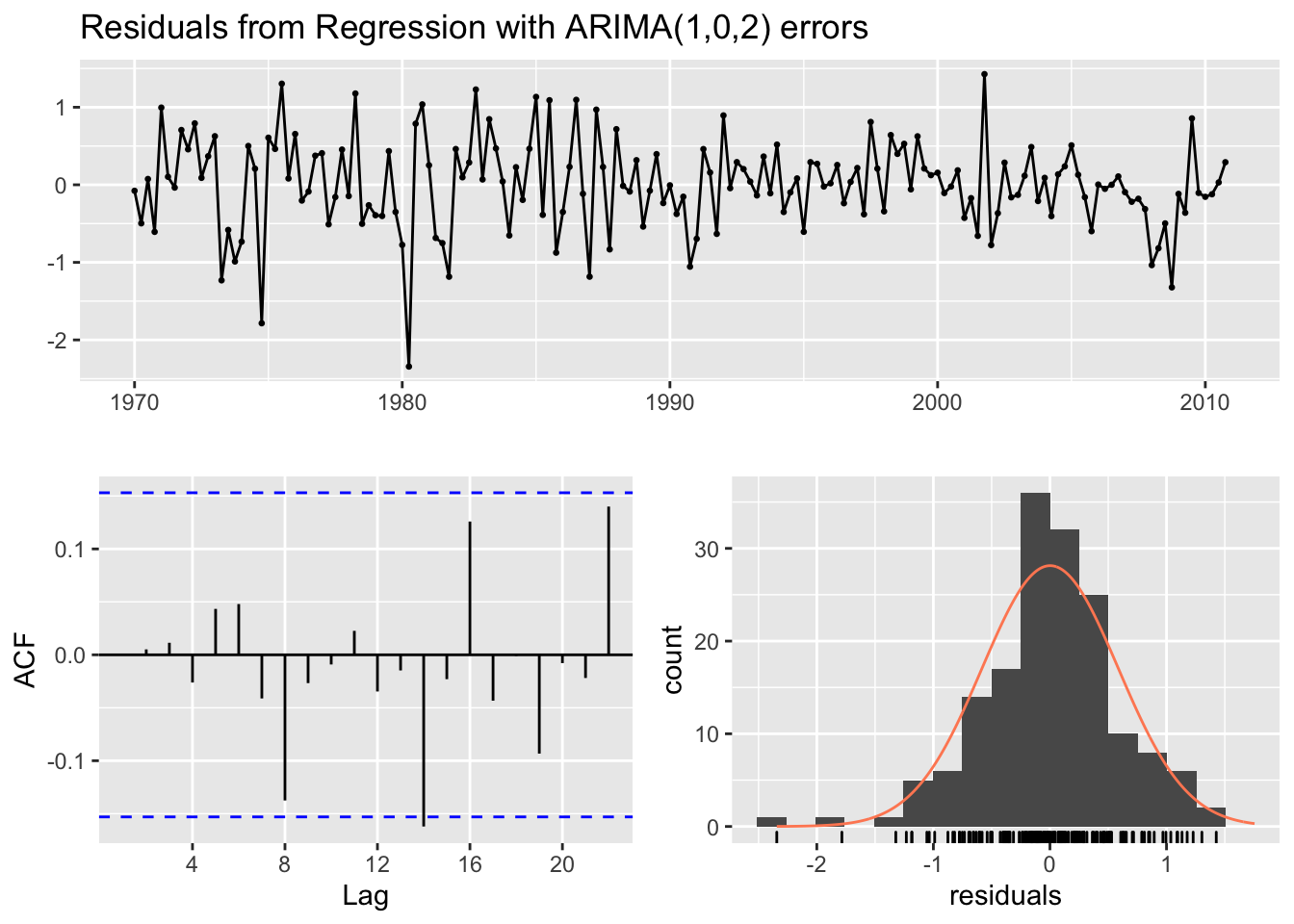
## 	Ljung-Box test
## 
## data:  Residuals from Regression with ARIMA(1,0,2) errors
## Q* = 9.7082, df = 9, p-value = 0.3746
## 
## Model df: 5.   Total lags used: 14

Si è in particolare interessati a verificare, con il test di Ljung-Box se la correlazione per \(h=14\) è un falso positivo (si sceglie quindi lag=14). Dato il valore del p-value (non si rifiuta l’ipotesi nulla di incorrelazione dei primi 14 lag) è possibile concludere che i residui ARMA possono essere considerati come incorrelati.

12.6 RMarkdown

RMarkdown è il miglior ambiente di lavoro per progetti di data science (official website: https://rmarkdown.rstudio.com/). Esso permette di ottenere report riproducibili che combinano testo codice di R ed il relativo output. Per un introduzione a RMarkdown si veda questo video: https://vimeo.com/178485416. Per utilizzare RMarkdown è necessario installare i pacchetti rmarkdown e knitr.

Per la parte di esercizi dell’esame di SAPF riceverete un documento di tipo RMarkdown, ovvero un file con estensione .Rmd extension (si veda ad esempio il file SAPF_Esame_FacSimile.Rmd disponibile nella pagina Moodle del corso). Il file può essere aperto con RStudio.

Nella parte in alto del file, come mostrato in Figura 12.2, dovete solamente scrivere il vostro nome, cognome e matricola. Il resto non deve essere modificato. E’ possibile compilare il file per ottenere un file html utilizzando il tasto Knit rappresentato dal gomitolo blu (si veda il cerchio giallo in Figura 12.2). Se la compilazione si conclude correttamente, si aprirà una pagina html con il contenuto del file. Inoltre il file SAPF_Esame_FacSimile.html verrà automaticamente creato nella stessa cartella dove si trova il file .Rmd. Se si vuole vedere il documento compilato nel pannello in basso a destra di Rstudio (e non in una pagina web separata) è possibile cliccare sul tasto con la rotella grigia (si veda il cerchio viola in Figura 12.2) e selezionare Preview in Viewer Pane. Si compili poi nuovamente il documento con il gomitolo Knit, you will see your document in the Viewer pane).

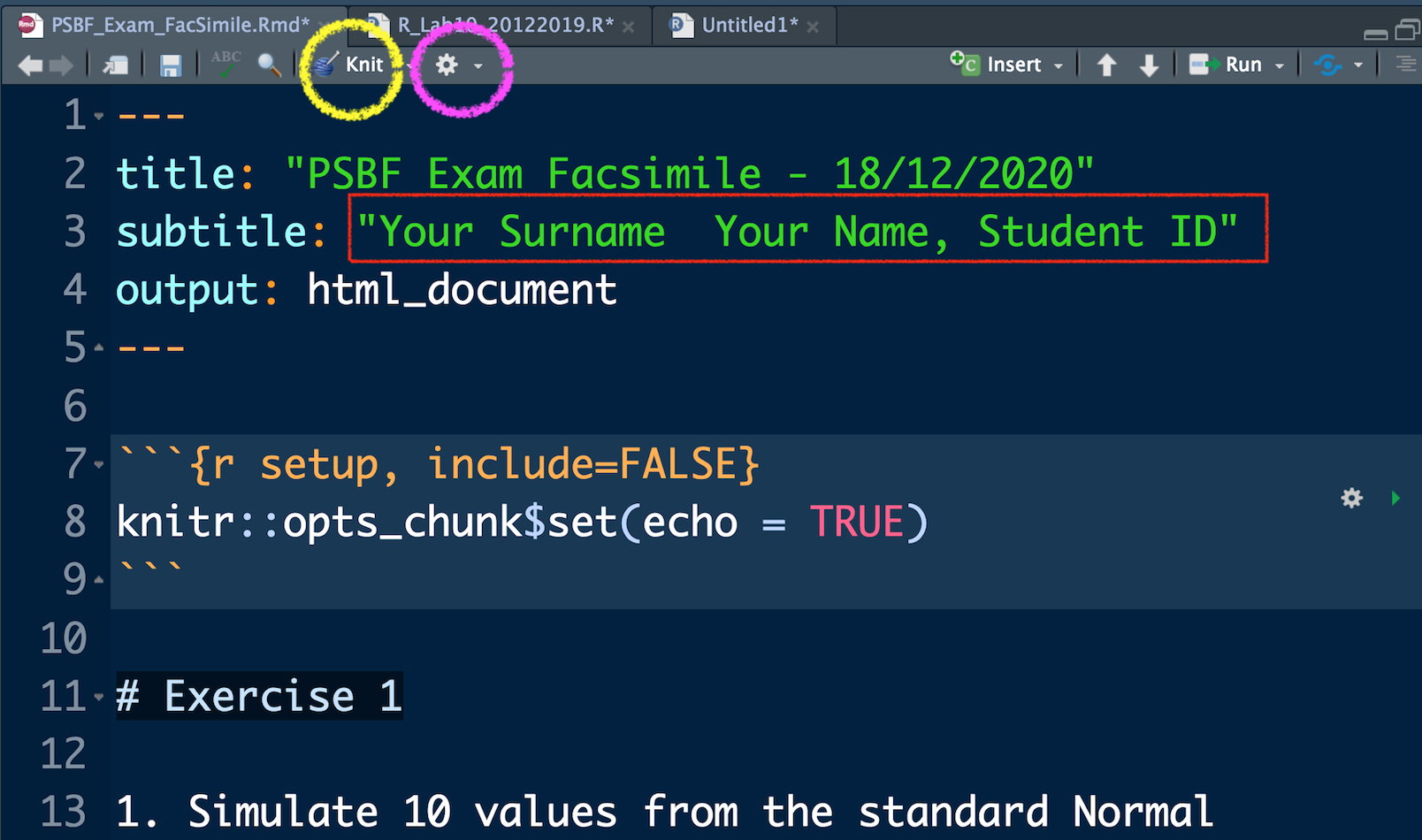
Parte iniziale del file RMarkdown

Figure 12.2: Parte iniziale del file RMarkdown

In Figura 12.3 è possibile vedere l’inizio del primo esercizio e del primo sotto-esercizio (rettangolo viola). Questa parte non deve assolutamente essere modificata. E’ invece possibile scrivere il proprio codice e i relativi commenti (ovviamente preceduti da #) nell’area (quadrato giallo) delimitata dai simboli ```{r} e ``` (questa area, che ha anche un coloro di sfondo diverso dal resto del documento, è anche chiamata code chunk). Per verificare cosa il proprio codice produce in output è possibile far girare separatamente ogni singola linea del codice utilizzando i tasti Ctrl/Cmd Enter. Questo è di fatto l’approccio che è stato utilizzato fino ad ora per far girare del codice. I risultati verranno mostrati nella console e i nuovi oggetti salvati nell’ambiente di lavoro (si veda il pannello in alto a destra).

E’ necessario in ogni caso compilare l’intero documento con il tasto del gomitolo alla fine di ogni sotto-esercizio. Questo vi permetterà di verificare passo per passo il documento che state creando e che consegnerete alla fine dell’esame. In particolare, dovrete consegnare il file .html e il file sorgente .Rmd (dovranno entrambi essere caricati sulla pagina Moodle del corso).

Se una parte del codice dà errore è sempre possibile lasciarla nel documento .Rmd andandola semplicemente a commentare con il cancelletto.

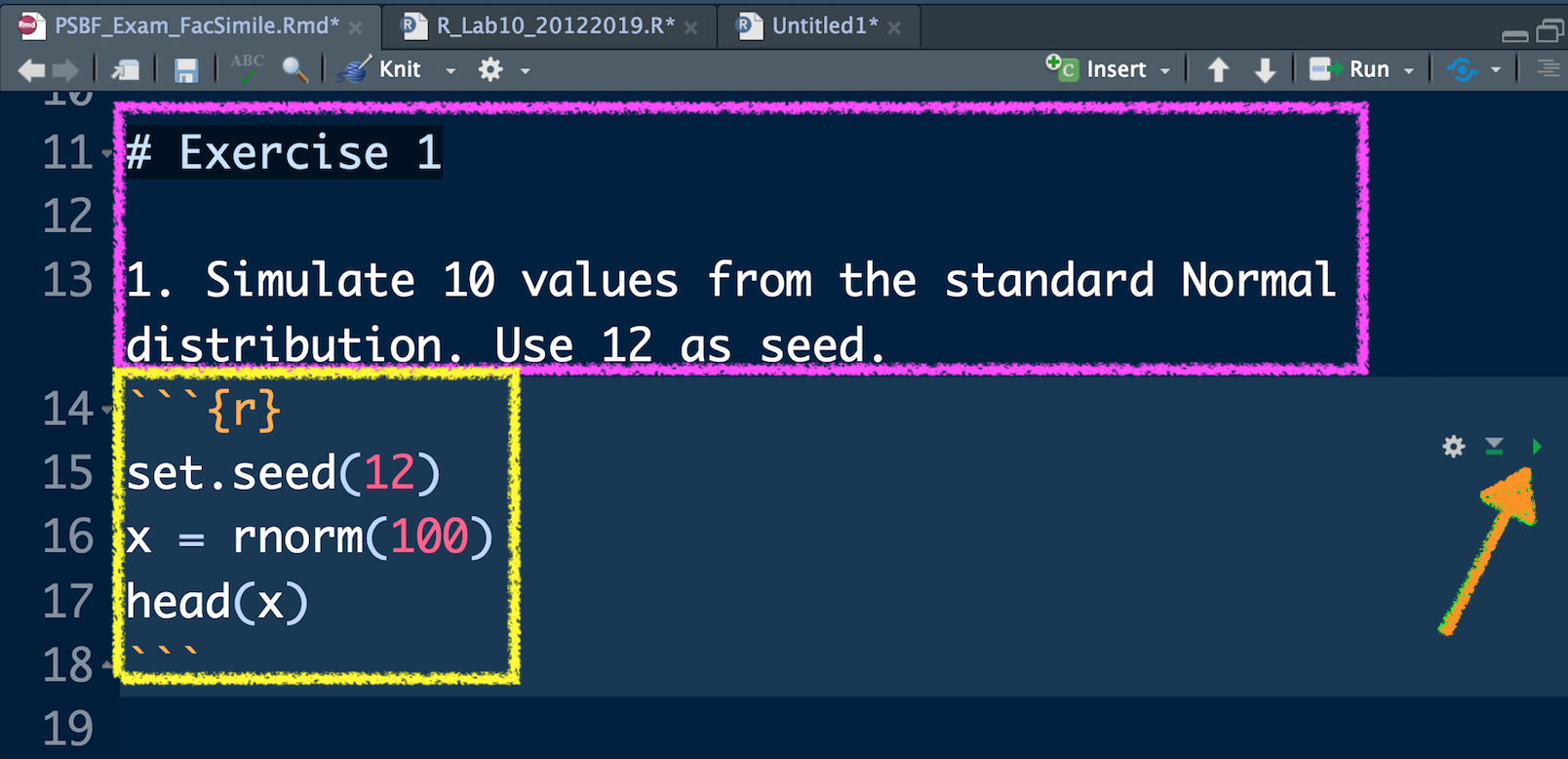
Testo di un esercizio in RMarkdown e relativo code chunk

Figure 12.3: Testo di un esercizio in RMarkdown e relativo code chunk

12.7 Esercizi Lab 10

Il testo degli esercizi sono disponibili nel file RMarkdown R_Lab10_esercizi_vuoto.Rmd. Usare questo file come se fosse un tema d’esame. Risolvere gli esercizi punto per punto e produrre un documento finale in formato html.