6 Lab 4 - 06/12/2020
In questa lezione impareremo ad eliminare alcune da un data frame righe contenenti valori mancanti, a rappresentare graficamente la stima kernel della densità e a simulare casualmente valori dalla variabile casuale Normale.
6.1 Rimuovere righe contenenti valori mancanti
Per questo laboratori useremo un nuovo set di dati disponibile nel file A2A.csv. Si procede quindi con l’importazione dei dati come mostrato nel laboratorio 2; l’oggetto di tipo data frame e denominato A2A verrà quindi creato:
A2A = read.csv("~/Dropbox/UniBg/Didattica/Economia/2020-2021/SAPF_2021/R_labs/lab4/A2A.csv", sep=";", dec=".")Si noti che uno degli input della funzione read.csv è il percorso del file (ovviamente questo è specifico per ogni computer). Se non siete sicuri di specificare nel modo corretto il percorso è possibile utilizzare l’opzione Import dataset di RStudio (pannello in alto a destra) come descritto nella sezione 4.1.
Controlliamo la struttura del data frame usando il seguente codice
## 'data.frame': 510 obs. of 4 variables:
## $ Date : chr "2018-10-31" "2018-11-01" "2018-11-02" "2018-11-05" ...
## $ Open : num 1.43 1.42 1.43 1.43 1.42 ...
## $ Close : num 1.42 1.42 1.43 1.41 1.43 ...
## $ Adjusted: num 1.28 1.27 1.28 1.26 1.28 ...dal cui output si nota che le variabili dei prezzi (Open, Close e Adjusted) sono di tipo num (i.e. variabili quantitative continue).
Inoltre la funzione summary può essere utilizzata per ottenere le principali statistiche descrittive per ogni variabile contenuta nel data frame:
## Date Open Close Adjusted
## Length:510 Min. :1.008 Min. :1.000 Min. :0.938
## Class :character 1st Qu.:1.261 1st Qu.:1.257 1st Qu.:1.253
## Mode :character Median :1.542 Median :1.543 Median :1.405
## Mean :1.481 Mean :1.480 Mean :1.389
## 3rd Qu.:1.623 3rd Qu.:1.622 3rd Qu.:1.509
## Max. :1.890 Max. :1.896 Max. :1.778
## NA's :2 NA's :2 NA's :2Si mette in evidenza che tutte le variabili relative ai prezzi presentano due valori mancanti indicati come NA (not available, non disponibili), ovvero due giorni per i quali i prezzi non sono disponibili.
Al fine di identificare in quali giorni sono presenti i dati mancanti, due diverse funzioni vengono utilizzate: is.na e which. La prima funzione restituisce, per ogni elemento in un vettore, T o F a seconda che l’elemento sia mancante oppure no. La seconda funzione invece restituisce come output la posizione degli elementi T nel vettore. Combinando insieme le due funzioni
## [1] 432 476## [1] 432 476## [1] 432 476si ottiene che i valori mancanti si verifano nel giorno 432 e 476. A ulteriore conferma di quanto trovato si vanno a selezionare esattamente queste due righe nel data frame, così come descritto nella Sezione ??:
## Date Open Close Adjusted
## 432 2020-07-20 NA NA NA
## 476 2020-09-18 NA NA NAAl fine di eliminare un elemento da un vettore o un’intera riga/colona da un data frame è possibile utilizzare il segno di meno - (minus), come segue:
## [1] 508 4Si noti che un nuovo oggetto di nome A2Ab è stato creato. Esso contiene due osservazioni in meno avendo eliminato i giorni con dati mancanti.
Dopo aver eliminato i dati mancanti è possibile ora procedere con il calcolo dei rendimenti logaritmici utilizzando i prezzi di chiusura aggiustati, così come descritto nella Sezione ??. Un nuovo oggetto di nome logret viene quindi creato:
6.2 Istogramma e funzione kernel della densità
La distribuzione di rendimenti logaritmici può essere rappresentata graficamente tramite un istogramma:
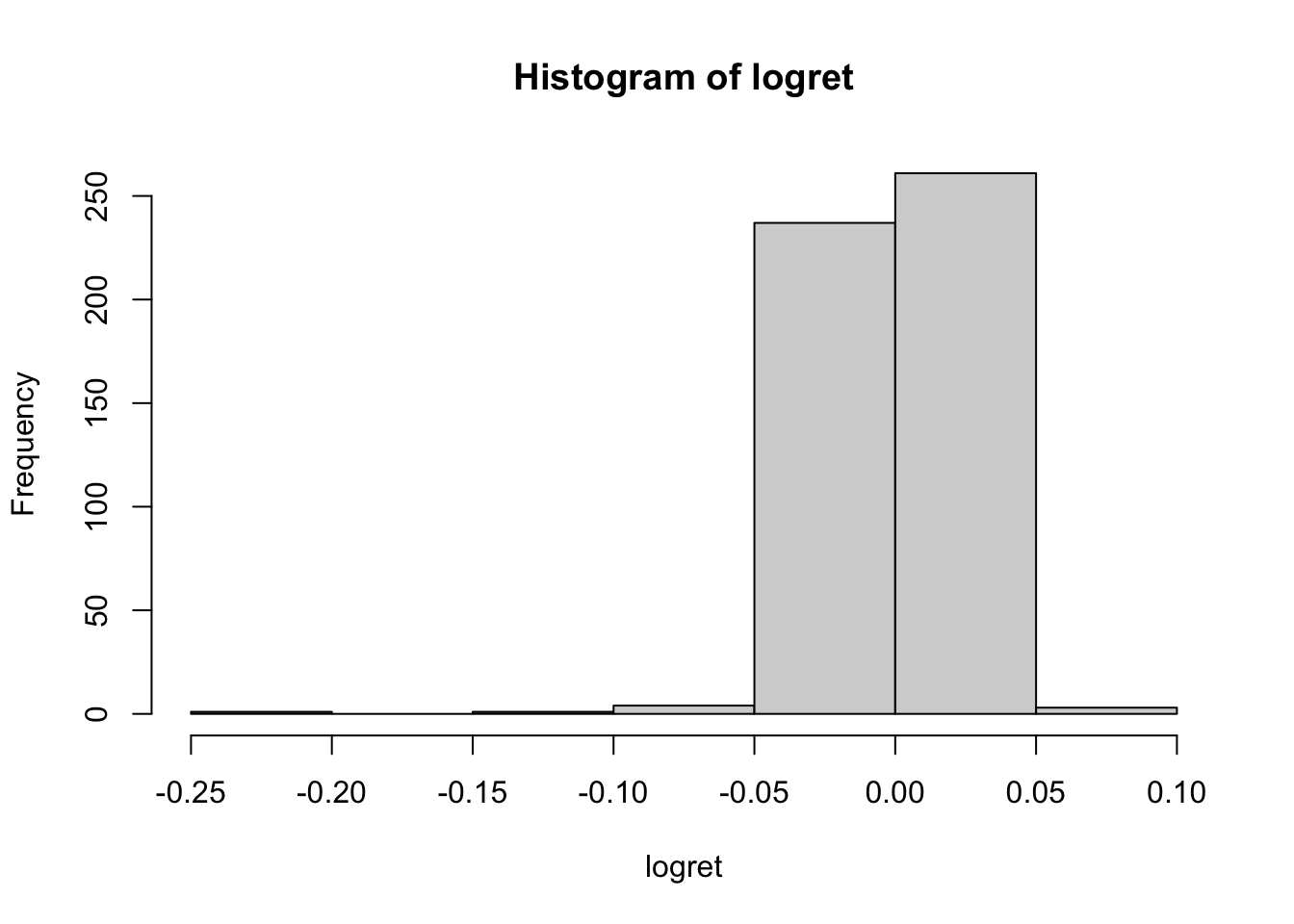
Utilizzando l’argomento breaks è possibile cambiare il numero di classi di valori nel grafico. In particolare, specificando un numero intero positivo la funzione hist calcolerà poi il numero ottimale di classi più vicino a quanto specificato (per questo motivo può succedere che il numero di classi nel grafico sia leggermento diverso rispetto a quanto specificato):
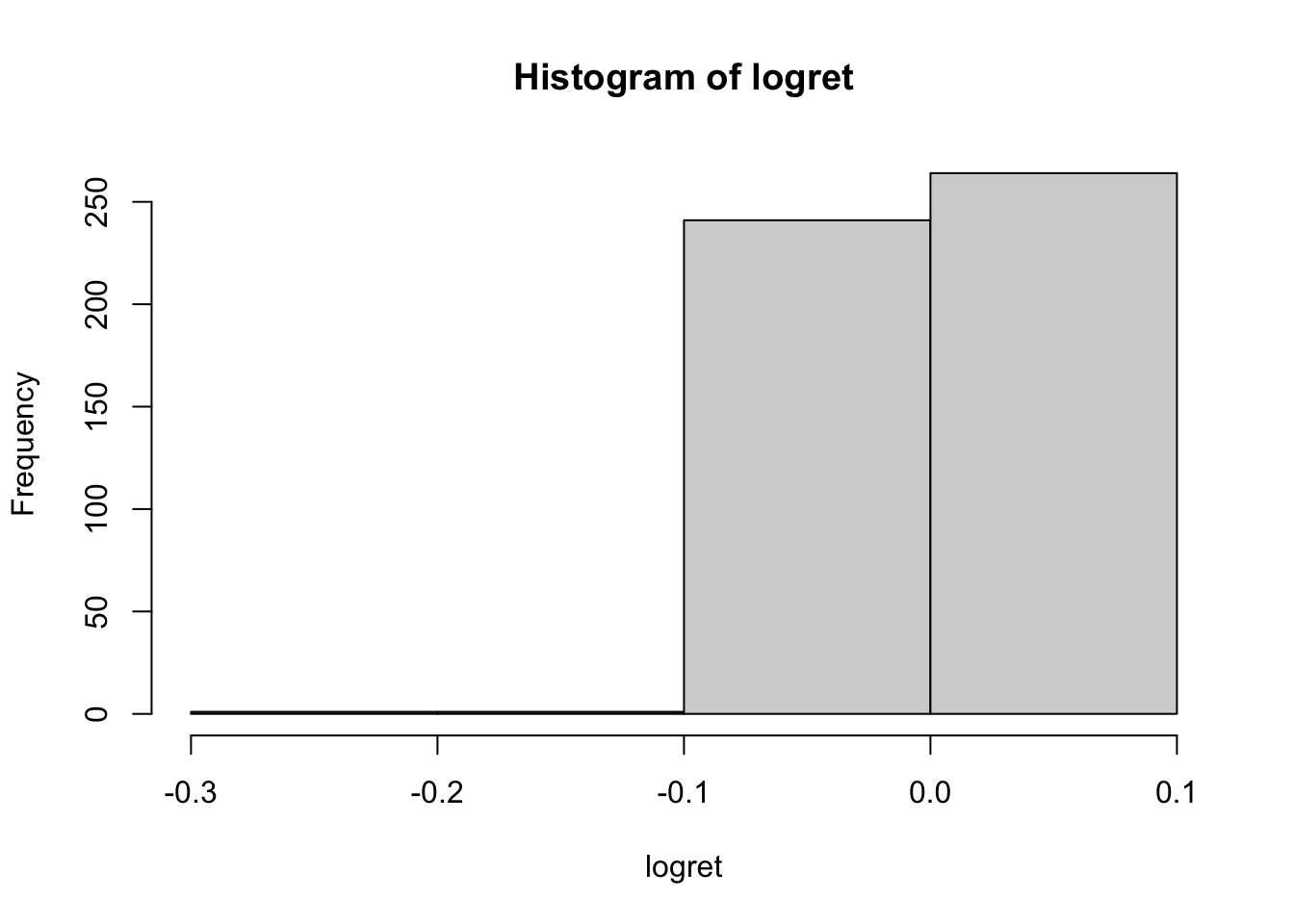
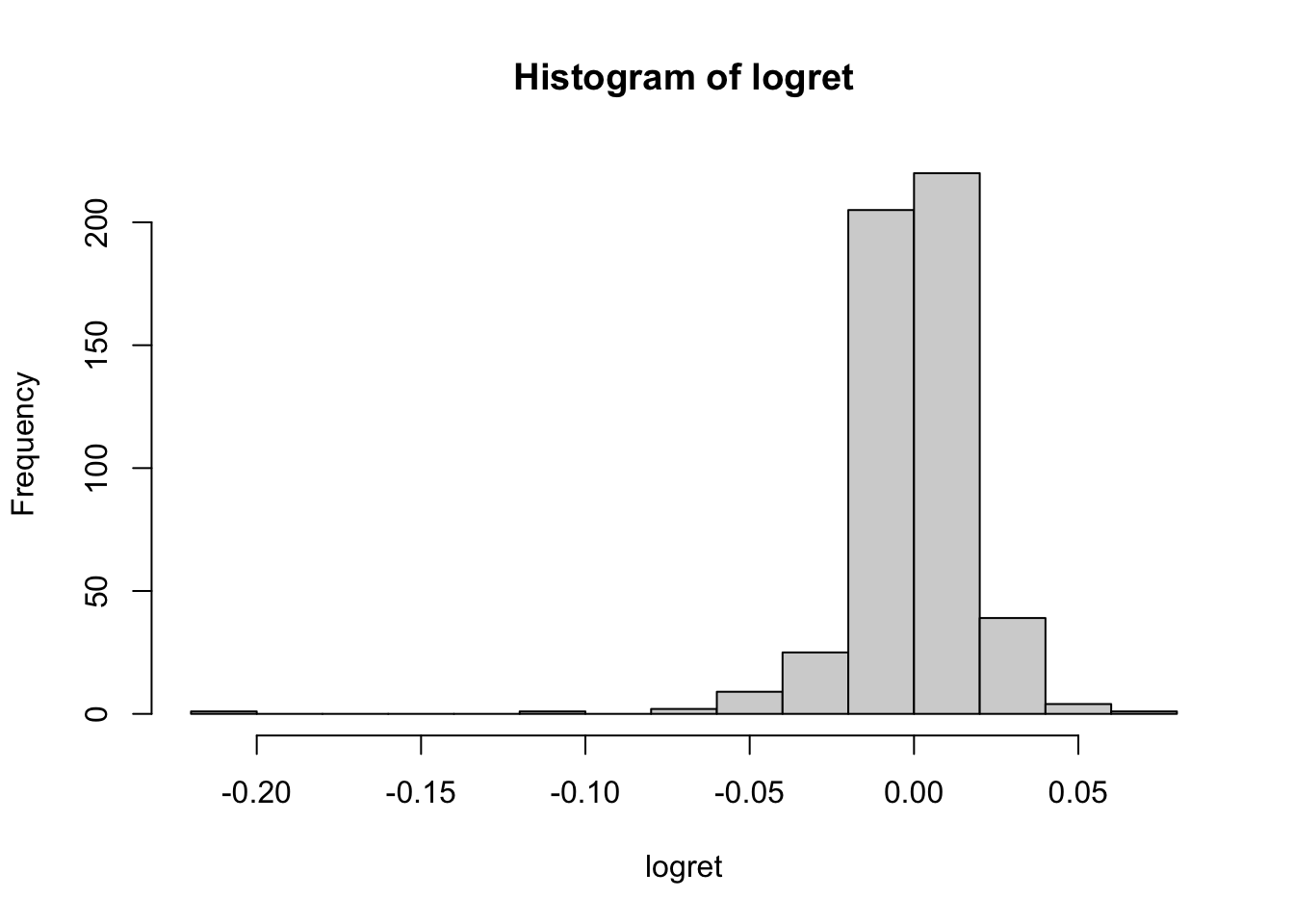 Dall’istogramma emerge una coda molto lunga a sinistra. Per studiare ulteriorment la distribuzione è possibile calcolare l’indice di asimmetria (skewness, si veda Sezione 5.4) e curtosi la cui formula è la seguente:
\[
kur = \frac{\frac{\sum_{i=1}^n (x_i-\bar x)^4}{n}}{\sigma^4}
\]
Dall’istogramma emerge una coda molto lunga a sinistra. Per studiare ulteriorment la distribuzione è possibile calcolare l’indice di asimmetria (skewness, si veda Sezione 5.4) e curtosi la cui formula è la seguente:
\[
kur = \frac{\frac{\sum_{i=1}^n (x_i-\bar x)^4}{n}}{\sigma^4}
\]
## [1] -3.152279## [1] 35.076Il valore dell’indice di skewness è negativo, sintomo di asimmetria negativa (coda lunga a sinistra). Il valore dell’indice di curtosi è notevolmente più grandi di 3 a significare una distribuzione leptocurtica.
Il grafo della stima kernel della densità (KDE) si può ottenere usando le funzioni plot e density:
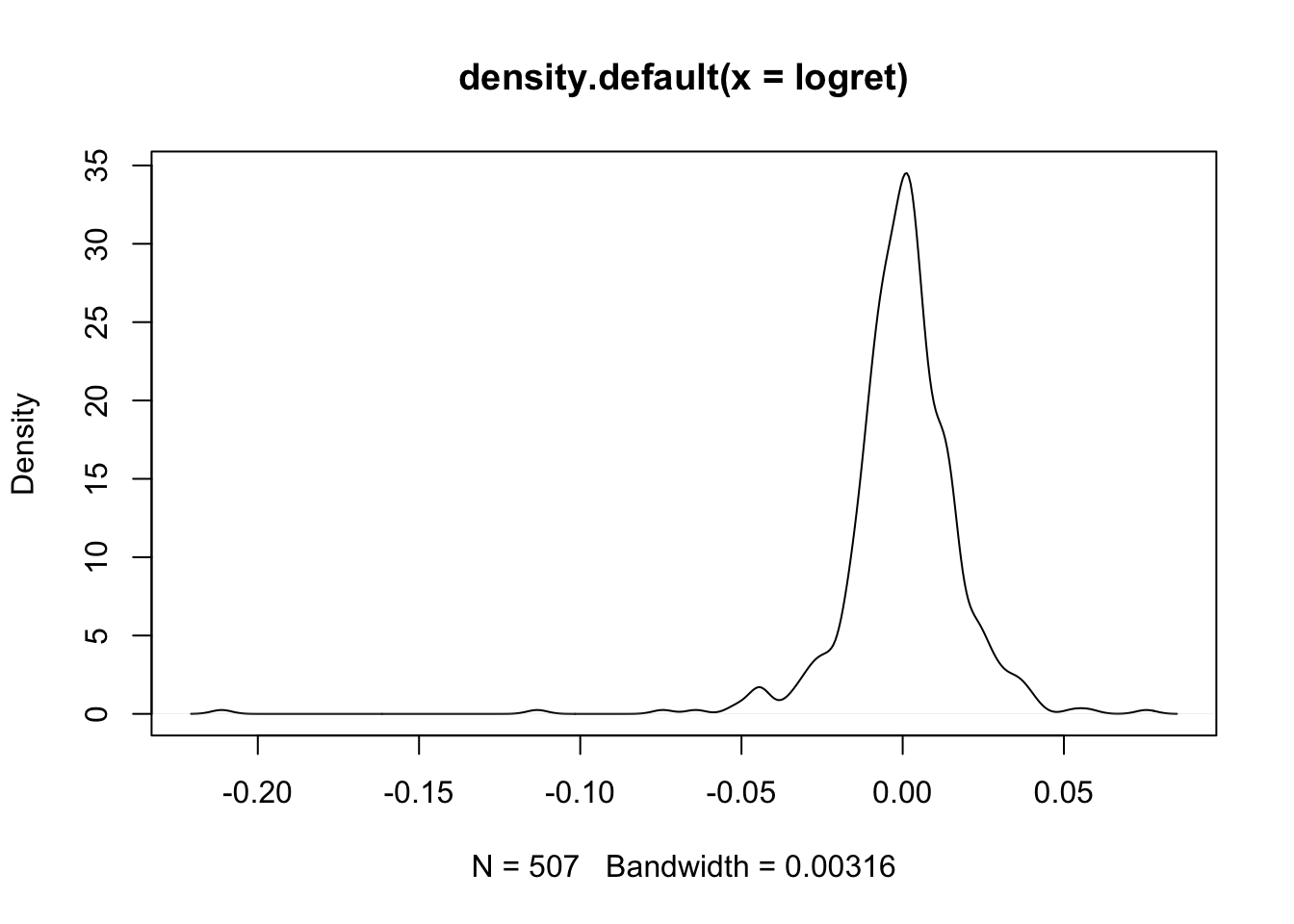 Si noti che R di default sceglie il miglior valore per l’ampiezza di banda (bandwidth, riportato in basso nel grafico). Con l’obiettivo di studiare l’effetto dell’ampiezza di banda sul grafico finale della KDE, possiamo ad esempio raddopiarne il valore utilizzando l’opzione
Si noti che R di default sceglie il miglior valore per l’ampiezza di banda (bandwidth, riportato in basso nel grafico). Con l’obiettivo di studiare l’effetto dell’ampiezza di banda sul grafico finale della KDE, possiamo ad esempio raddopiarne il valore utilizzando l’opzione adjust:
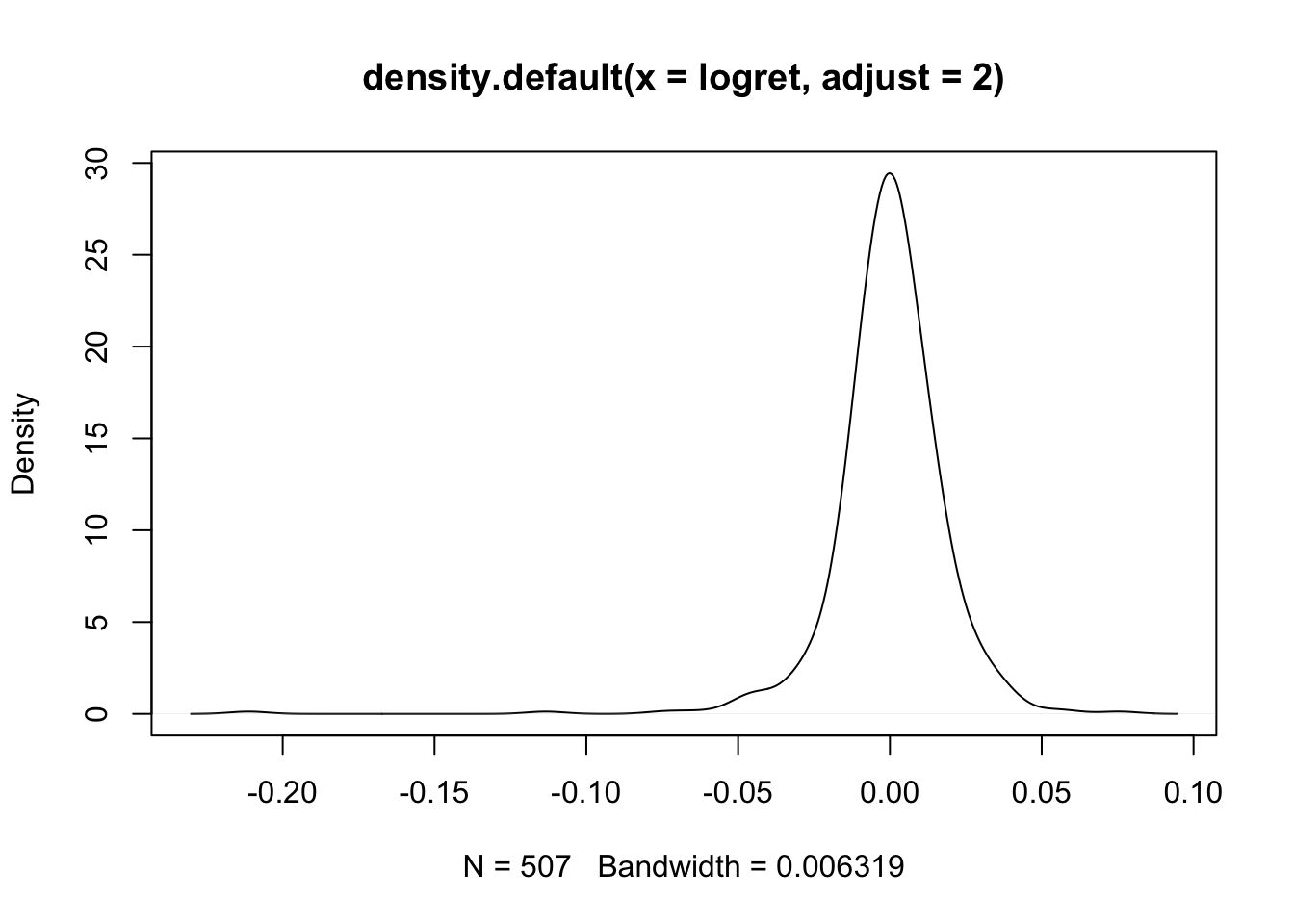
La costante moltiplicativa definita con adjust viene applicata al valore dell’ampiezza di banda scelta automaticamente da R. Quando l’ampiezza di banda raddoppia la curva è più liscia. Se invece l’ampiezza viene dimezzata
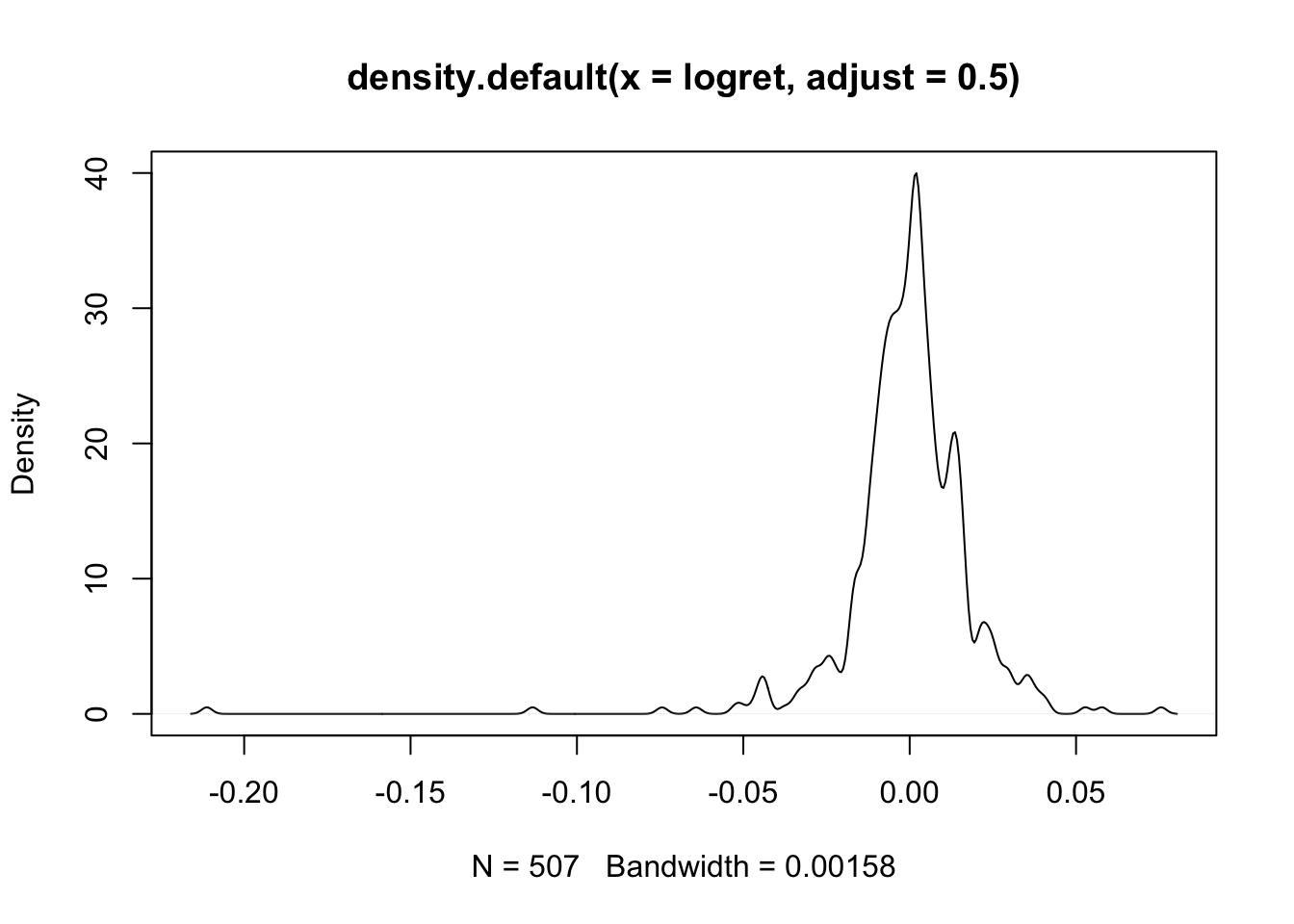 la KDE finale mostra più dettagli ed è meno liscia.
la KDE finale mostra più dettagli ed è meno liscia.
E’ anche possibile mostrare insieme l’istogramma e la linea della KDE:
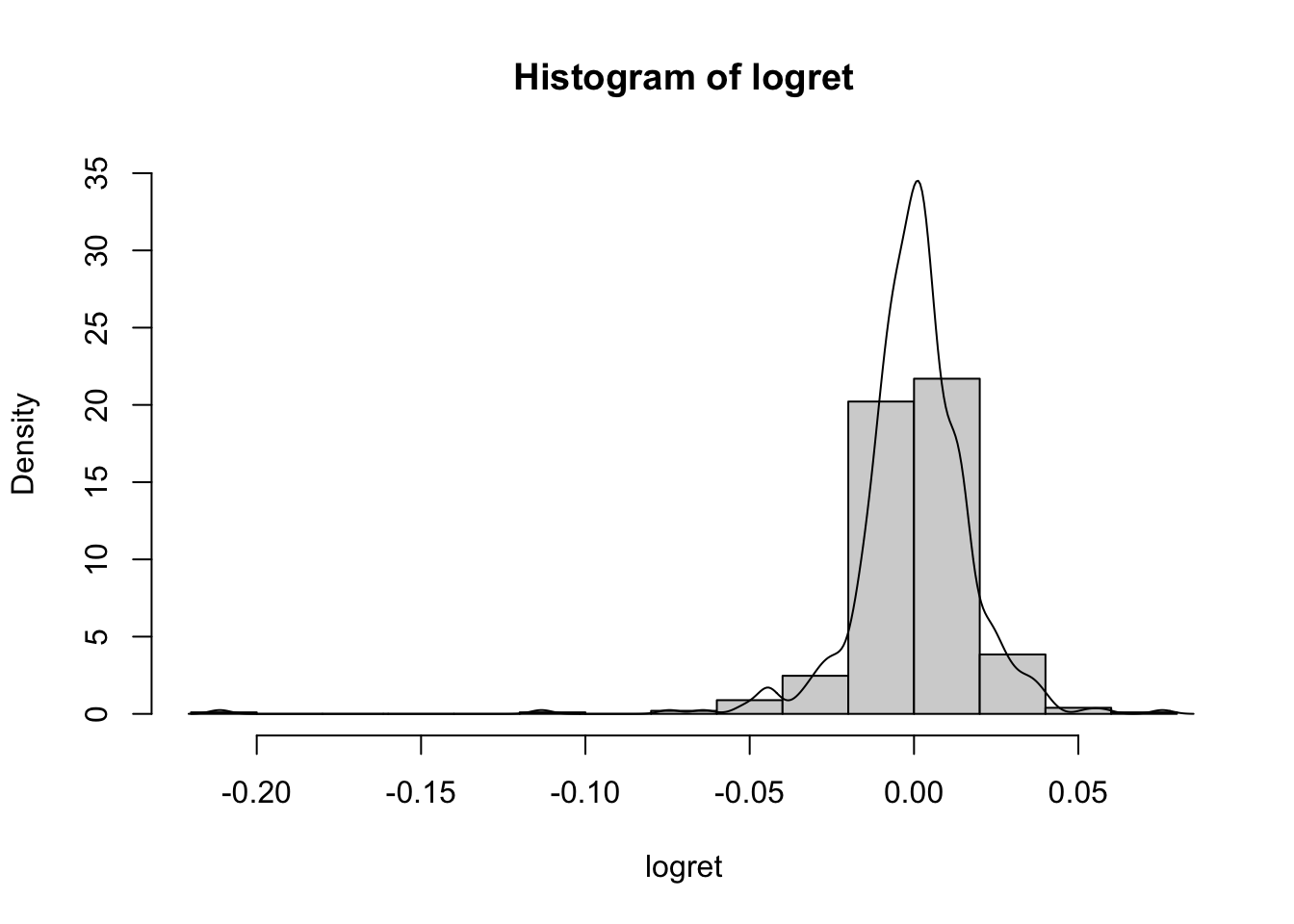
L’argomento freq=F serve per poter rappresentare sull’asse delle y le densità di frequenza invece delle frequenze assolute. In questo modo l’istogramma e la KDE sono comparabili e possono essere rappresentati insieme sullo stesso grafico. Quando si utilizza l’istogramma con densità di frequenza, l’area di ogni barra è data dalla frequenza assoluta della corrispondente classe di valori.
6.3 Simulazione di numeri casuali dalla distribuzione Normale
Un esempio di generazione casuale di numeri è dato dall’esperimento che consiste nel lanciare una moneta regolare per quattro volte. Una possibile sequenza ottenuta dall’esperimento è {T, C, C, T, T}, un’altra è {C, C, C, T, C}. Tutte le possibili sequenze casuali di T e C sono simulate dalla stessa distribuzione di probabilità che assegna probabilità 0.5 ad entrambe gli eventi. Procederemo ora in maniera simile per simulare valori dalla variabile casuale Normale. In questo caso la distribuzione è più complessa ed è necessario far ricorso ad un algoritmo. Nel caso di R si utilizza la funzione denominata rnorm (r... sta per random, casuale).
Per esempio per simulare casualmente 4 numeri da una Normale di media pari a 10 e standar deviation pari a 1 si procede come segue:
## [1] 9.289593 10.256884 9.753308 9.652457Il codice genera 4 numeri diversi ogni volta che viene fatto girare (perchè sono generati casualmente). Al fine di ottenere gli stessi numeri in un’ottica di riproducibilità dei risultati è necessario fissare il seme, ossia il valore del parametro che inizializza l’algoritmo che genera i numeri. A tal fine si utilizza la funzione set.seed che prende in input un numero intero positivo qualsiasi (456 nel seguente esempio):
## [1] 8.656479 10.621776 10.800875 8.611108In questo caso i 4 numeri sono salvati nell’oggetto di nome
x. Fissando il seme siamo tutti in grado di ottenere sempre gli stessi numeri.
Simuliamo ora 1000 valori dalla stessa distribuzione Normale e ne rappresentiamo la distribuzione usando istogramma e KDE.
## [1] 8.656479 10.621776 10.800875 8.611108 9.285643 9.675939 10.690643
## [8] 10.250548 11.007352 10.573235 9.084189 11.311097 10.988726 11.653929
## [15] 8.559195 11.947356 11.736936 10.387483 12.280034 11.537883 9.525396
## [22] 8.282691 8.573170 10.208236 9.964164 11.134285 9.537145 9.671616
## [29] 11.484539 8.910622 9.471206 9.406207 8.001084 10.296153 10.170625
## [36] 11.815652 9.339397 9.859748 9.576021 9.961264 9.971058 10.393037
## [43] 9.750386 10.083450 12.078875 10.120852 10.118149 10.770054 8.824598
## [50] 10.409039 9.335049 9.743475 10.678782 10.896845 10.618356 10.731454
## [57] 9.586825 11.557813 10.541699 10.577150 7.745290 9.017940 9.799432
## [64] 10.895930 9.956455 11.647308 11.563299 8.568622 9.455406 9.228746
## [71] 9.830012 9.959238 8.279460 11.444106 9.979985 10.270232 9.887066
## [78] 9.145112 8.966259 10.222027 8.920518 9.558626 12.020635 10.072856
## [85] 10.708817 10.850509 8.513803 10.920530 10.148329 9.763132 9.526764
## [92] 9.330794 11.358527 11.412918 9.267226 9.919448 10.810197 10.502588
## [99] 11.124023 9.828720 10.118151 10.869903 9.908064 10.068899 8.317573
## [106] 11.116956 8.648642 9.462833 9.629886 10.354012 9.190175 9.820275
## [113] 8.852340 10.096242 10.814700 10.982941 10.850843 11.207347 8.566222
## [120] 8.899054 9.722958 9.358637 10.856875 10.313843 11.222462 8.873672
## [127] 10.236297 8.727630 10.315683 10.355610 10.004052 11.149194 9.503386
## [134] 9.253203 8.717233 8.968228 7.927953 9.573933 9.223024 9.818188
## [141] 9.137693 9.817458 11.370695 11.342719 8.848238 10.748765 11.522148
## [148] 8.546980 11.210758 9.090654 11.200410 9.834584 9.505793 8.435431
## [155] 9.645632 8.978035 11.191806 10.229314 8.727421 10.691872 9.971245
## [162] 8.896168 8.964725 10.139953 10.682729 8.864441 11.772545 9.906074
## [169] 7.678812 10.151039 9.308853 10.830429 11.192598 10.309911 8.450616
## [176] 9.670239 8.587740 9.000240 7.689261 10.938619 8.611812 9.388313
## [183] 10.318495 9.764594 11.075052 9.899204 11.070153 11.035839 9.698027
## [190] 10.996494 9.302763 10.912898 11.232309 10.731207 9.536139 11.243934
## [197] 9.803887 8.937166 10.270078 9.520999 10.293886 11.052402 9.993564
## [204] 9.595477 9.919083 8.927576 9.432312 10.129383 10.094463 10.658378
## [211] 11.189112 10.661861 10.698721 9.449151 10.004792 11.378861 10.946054
## [218] 10.463952 10.122844 10.832728 8.267691 11.396030 9.573485 9.069970
## [225] 9.483635 10.600278 10.531420 8.510413 11.356649 10.669964 11.657759
## [232] 9.320082 10.888761 10.081891 9.824110 10.657728 9.241963 10.619467
## [239] 12.060492 8.852571 11.850409 9.145361 8.942086 10.774145 9.146757
## [246] 8.163557 11.006292 10.420103 8.975992 10.688506 9.750086 10.071306
## [253] 10.250064 8.771075 9.941358 9.636248 8.714266 9.784316 9.558692
## [260] 10.353911 11.084168 9.438790 10.430896 11.683946 10.896523 9.900024
## [267] 9.011004 11.699819 10.254250 10.820742 7.618343 10.151704 8.095561
## [274] 11.654265 10.498749 9.889566 10.847519 9.967179 8.861336 10.019051
## [281] 10.852940 10.007986 11.753788 10.112250 12.699447 9.422499 9.277398
## [288] 9.927689 8.989378 9.316947 9.043859 10.663697 10.823990 10.171773
## [295] 9.211259 10.340966 9.930660 9.161747 9.637589 11.239416 8.870149
## [302] 10.397409 9.314174 12.125640 9.713880 10.243458 8.916623 8.665777
## [309] 11.300328 9.822212 9.750756 10.865920 10.134130 10.449762 10.476889
## [316] 10.374626 10.954815 10.135659 10.744444 11.801724 9.950557 9.664505
## [323] 10.621241 9.747202 11.297262 10.154298 9.264297 10.085946 10.555347
## [330] 10.314166 11.113805 9.721423 11.177721 9.266785 12.134458 9.087392
## [337] 12.013392 10.338893 8.820051 9.678844 9.896896 9.616117 9.365149
## [344] 11.436316 8.559215 9.827798 10.132503 9.202160 10.294304 10.154591
## [351] 11.607784 10.103866 9.525351 11.357161 11.460983 10.403570 10.700763
## [358] 10.898184 10.833860 10.352225 10.813664 10.917774 9.331307 10.822370
## [365] 10.741375 9.163077 10.016555 9.404048 9.348592 8.817668 10.266647
## [372] 8.252141 10.779872 11.994766 9.833089 9.808333 11.044945 9.511135
## [379] 10.247030 10.496783 8.733866 11.607315 9.677428 8.667066 10.309669
## [386] 9.721970 10.939760 10.636812 9.859056 8.960641 9.004088 9.187897
## [393] 10.422906 8.798875 11.512315 9.975453 9.128568 10.503870 10.043902
## [400] 8.435457 10.717349 9.582663 9.968476 9.095188 9.999478 11.397854
## [407] 10.815535 11.035704 11.643277 10.944348 8.562225 11.691891 11.678378
## [414] 9.752141 12.506394 10.228024 10.415546 7.759581 9.041253 9.314783
## [421] 9.581293 9.363033 10.080680 9.722857 10.904960 10.138629 9.275736
## [428] 10.371864 10.785109 8.976383 10.449132 11.211041 11.017587 11.474395
## [435] 10.878696 10.527367 9.833182 10.068838 10.010037 9.990891 11.866595
## [442] 10.574696 10.399693 9.531603 10.124647 11.348965 11.451818 10.100393
## [449] 9.652122 11.006838 9.400970 11.048962 10.229073 9.185907 9.850207
## [456] 10.452858 10.489598 9.871836 10.543880 10.083568 10.869361 13.009402
## [463] 11.324411 9.315665 9.350322 9.833791 10.881449 12.533984 12.315229
## [470] 8.607062 8.829370 10.304693 8.930016 9.915033 10.526209 11.563843
## [477] 10.470956 9.008958 8.930869 12.157801 11.217489 10.650941 7.619365
## [484] 10.367709 9.100725 10.264468 10.796982 10.138972 9.855448 9.700854
## [491] 9.181914 8.898008 9.422036 10.590644 9.837442 9.891317 11.767232
## [498] 10.126790 9.458650 9.701577 10.145290 9.618181 9.437749 11.269368
## [505] 8.781486 8.811321 9.210153 10.217980 8.193908 10.697427 9.974094
## [512] 8.983178 9.452142 9.507733 11.780154 11.169700 8.983785 7.123714
## [519] 10.346815 8.630857 11.182300 11.123757 9.180261 10.410180 10.796245
## [526] 10.978053 10.206253 11.515845 10.584469 8.136053 10.568272 10.562538
## [533] 9.947060 10.083841 9.487423 9.772866 11.101168 8.830543 10.506190
## [540] 8.492843 10.151837 11.057101 9.903972 9.165033 9.777642 10.620698
## [547] 9.860194 9.954066 8.709419 8.395909 11.643621 10.277109 11.159464
## [554] 10.198909 10.998733 9.928053 7.707605 9.730014 11.166158 10.999719
## [561] 10.128578 9.331069 10.742269 11.399235 10.572057 10.052384 9.595543
## [568] 9.611919 9.018001 8.047012 8.941283 9.556748 11.384529 10.449732
## [575] 10.486966 9.096758 9.454850 10.321601 10.557025 9.548664 10.815534
## [582] 10.219334 9.903678 9.303513 9.083712 9.808553 8.714347 10.701996
## [589] 11.236431 10.987198 9.727079 10.123309 10.666883 10.983093 10.937910
## [596] 11.867081 12.017341 10.499767 10.201815 10.347301 9.862408 10.388813
## [603] 9.072332 9.367688 11.114506 9.725994 9.395172 13.057057 10.375956
## [610] 8.613711 11.067442 8.529290 10.034936 9.883877 10.789799 10.771003
## [617] 9.128507 11.747724 9.544831 9.709469 7.035740 9.476264 8.882424
## [624] 11.354183 10.054313 9.799694 9.390804 9.964877 10.835795 9.508490
## [631] 8.067418 8.799979 10.064625 9.221051 11.192417 10.699426 7.765637
## [638] 8.398241 9.831599 9.622871 11.140813 9.114096 9.641068 9.686837
## [645] 11.877538 8.485956 10.319708 9.623603 10.530076 9.977967 11.055110
## [652] 11.064050 10.661023 11.541681 10.354836 11.226550 9.957784 10.368364
## [659] 10.281193 10.896980 9.164963 10.878470 9.684406 8.328470 8.616938
## [666] 10.714498 10.453215 9.313808 10.325933 9.909374 9.335683 10.010137
## [673] 8.467343 9.796644 8.886213 10.942591 12.335059 11.102935 10.874354
## [680] 10.450949 10.050349 9.196810 9.664985 10.654803 8.776974 8.867388
## [687] 9.909012 9.345714 10.288572 8.738186 9.735155 9.931254 8.037704
## [694] 9.191214 9.409460 9.875135 10.342187 10.240254 9.569668 10.817045
## [701] 10.856308 9.185392 9.105367 12.518876 10.169326 9.039129 8.507953
## [708] 9.210669 9.799920 11.531129 10.955754 10.995681 8.969053 9.827849
## [715] 10.759192 10.492416 9.451688 11.043355 11.498383 8.737669 9.343636
## [722] 10.368355 10.630621 10.048710 10.904595 9.495916 8.941730 10.233247
## [729] 10.035499 10.292535 8.422017 11.071992 9.882351 9.068420 9.802569
## [736] 8.708614 10.110406 10.489301 10.951632 9.914317 10.763420 9.785278
## [743] 11.161861 8.925744 9.355152 11.719925 8.541065 10.378455 9.206147
## [750] 9.575333 9.919647 10.214707 8.325218 11.080880 10.934682 8.088188
## [757] 11.028050 9.381731 9.983127 8.676517 10.417492 11.203498 10.355101
## [764] 11.821398 10.389388 10.870536 12.138669 8.348151 9.661924 9.945547
## [771] 12.188610 9.215035 8.541597 9.746081 11.334711 10.156737 11.754497
## [778] 10.042060 9.403039 10.907710 9.502402 12.264397 10.050857 10.075698
## [785] 10.491177 10.109053 10.234350 10.005057 8.804774 9.544023 7.609112
## [792] 10.584359 9.576098 8.851080 11.356819 9.857165 9.375930 9.702782
## [799] 9.942088 9.003402 10.426999 11.480117 11.578533 10.221307 9.835955
## [806] 9.873502 10.277836 8.646085 12.229077 10.480303 11.126412 9.893474
## [813] 9.856708 8.275490 11.055977 9.710981 9.702553 9.225935 11.454520
## [820] 10.231117 10.208502 10.326736 9.381816 11.308794 9.260252 11.729780
## [827] 11.050599 7.767516 9.950737 9.888149 9.175856 9.349003 7.686567
## [834] 9.049780 10.475551 12.545495 10.850312 10.123935 10.736281 9.422766
## [841] 8.499521 10.022792 9.692923 11.001730 8.976440 9.974724 10.398645
## [848] 9.629062 10.740363 11.208125 12.478318 11.587460 8.265589 10.616447
## [855] 10.177435 9.024095 8.627053 9.760812 8.960006 8.701191 10.781863
## [862] 8.597403 8.266764 7.695247 9.662061 11.329749 10.367805 11.360846
## [869] 10.813664 9.712493 10.156507 10.536755 8.817474 8.618563 8.659587
## [876] 10.215515 9.722476 10.668524 9.763908 8.349692 10.406184 8.574791
## [883] 9.307851 8.808128 8.612064 10.083381 9.419063 9.679578 10.127443
## [890] 10.843464 11.764808 9.775700 9.218236 11.038376 11.949011 9.291408
## [897] 9.089396 10.570925 10.824330 10.674490 9.200025 8.218397 10.167175
## [904] 9.560706 11.165922 9.146477 10.836320 10.895685 9.738598 12.002294
## [911] 8.638028 9.999108 10.324158 10.071223 9.598167 10.859517 10.178909
## [918] 9.487706 8.877600 10.013708 9.770017 8.980036 10.910366 9.121254
## [925] 10.110045 11.140609 8.891715 10.583677 8.530582 9.854639 10.734482
## [932] 9.982678 10.332511 9.675909 10.465268 9.631842 10.424562 9.627676
## [939] 10.355039 10.108501 10.410568 10.786817 11.034012 9.601242 8.377763
## [946] 10.397978 11.354107 11.276313 9.764020 9.303540 10.737191 11.126466
## [953] 10.360221 12.024468 9.877439 9.948228 10.538721 8.652681 8.743485
## [960] 10.182912 9.061687 10.660311 9.868456 10.747388 10.881266 10.769281
## [967] 9.272967 9.677126 9.030675 10.684514 10.367473 11.491021 10.529991
## [974] 8.315680 8.554580 10.268119 10.267590 10.987654 10.322086 9.114308
## [981] 12.042712 11.269518 9.920299 8.541280 10.139597 9.766991 10.446159
## [988] 9.611280 9.965680 9.791479 10.447018 10.061575 11.605473 10.802708
## [995] 9.023753 9.677085 11.716167 9.436815 10.268763 11.295990
 I due grafici rappresentano la ben nota distribuzione a campana con le proprietà della Normale.
I due grafici rappresentano la ben nota distribuzione a campana con le proprietà della Normale.
Infine, simuliamo 1000 valori da una Normale con media e deviazione standard dati dai corrispodenti valori calcolati sulla serie di rendimenti logaritmici calcolati in precedenza:
Confrontiamo ora la KDE di logret con quella dei valori simulati contenuti in x:
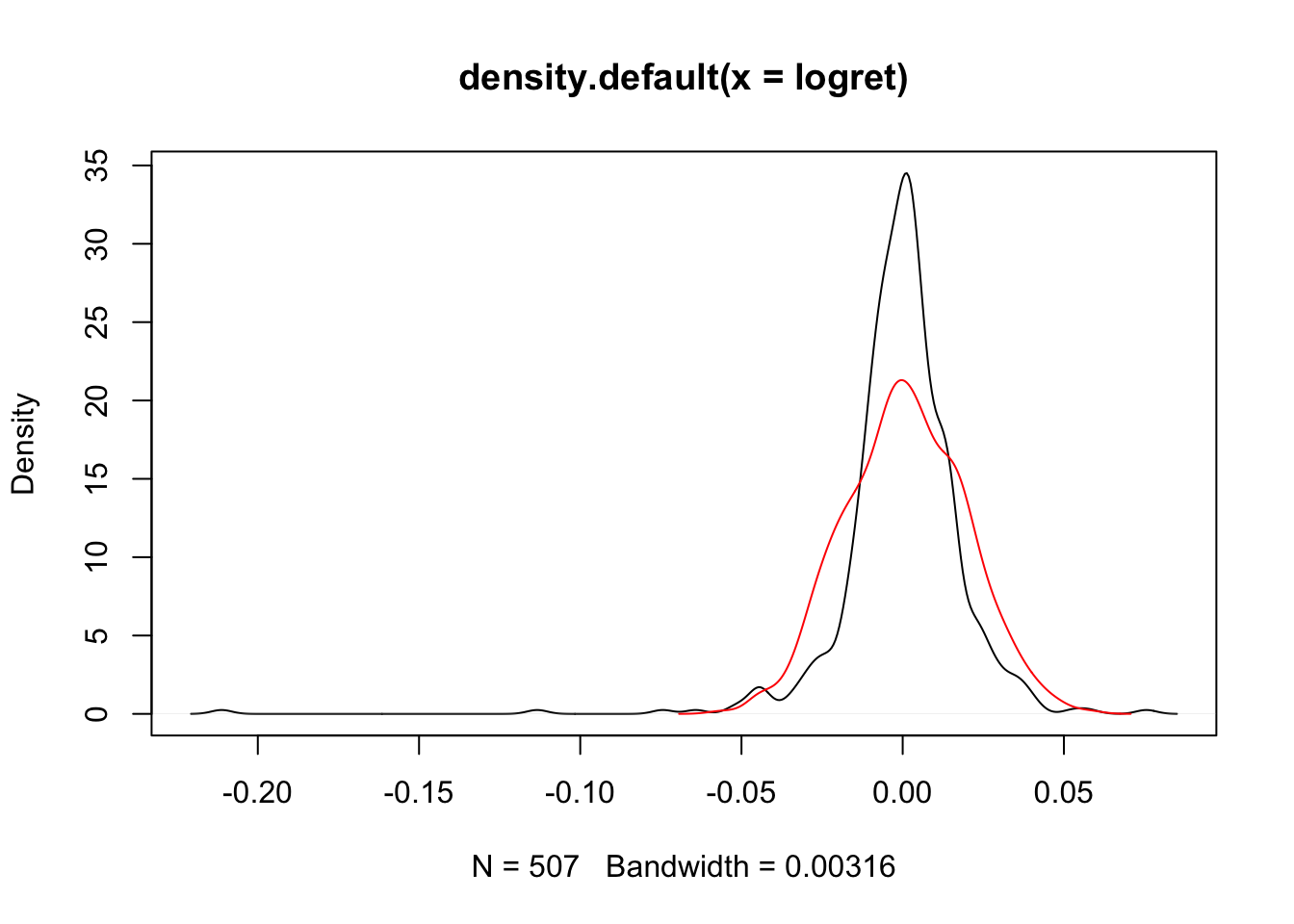
E’ chiaro che la distribuzione logret è caratterizzata da valori estremi (e che sarebbero molto rari nel modello Normale) e code pesanti (soprattutto nella coda di sinistra) che non sono tipiche della distribuzione Normale. Inoltre la linea di logret ha un evidente picco in zero e spalle più basse (i valori per i quali la linea nera è sotto la linea rossa).
6.4 Esercizi Lab 4
6.4.1 Esercizio 1
Il file AdjclosepricesLab4.csv contiene i prezzi giornalieri aggiustati per il periodo da 01-09-2016 a 27-08-2020 per i seguenti titoli: NASDAQ Composite (IXIC), Dow Jones Industrial Average (DJI), Gold (Gold) and CBOE Volatility Index (VIX). Fonte dei dati: Yahoo Finance.
Importare i dati in R e verificare la struttura dei dati. Ci sono dati mancanti?
Calcolare i rendimenti netti. Creare un nuovo data frame che contengo tutti i rendimenti.
Fornire il grafico che rappresenta i boxplot delle 4 distribuzioni di rendimenti. Commentare il grafico.
Rifare lo stesso grafico eliminando VIX. Cosa si può osservare? Suggerimento: per non selezionare una colonna di un data frame è possibile usare il simbolo di -; e.g.
mydata[,-1]omette la prima colonna dimydata.Rappresentare nello stesso grafico le 4 KDE per i rendimenti netti. Commentare il grafico.
Calcolare per le 4 distribuzioni di rendimenti netti l’indice di asimmetria. Commentare i valori.
Calcolare per le 4 distribuzioni di rendimenti netti l’indice di curtosi Commentare i valori.
Simulare casualmente 1000 da una Normale di media zero e varianza data dalla varianza campionaria per la serie di rendimenti IXIC (usare 887766 come seme). Salvare i valori simulati nell’oggetto
normsample. Calcolare inoltre l’indice di asimmetria e curtosi pernormsample. Che valori ci si attende?Rappresentare la distribuzionei di
normsampleusando un istogramma a cui aggiungere la curva KDE pernormsample(in rosso) e per JNJ (in blu). Commentare il grafico.Usare l’istogramma per rappresentare graficamente la distribuzione dei rendimenti netti di
Gold. Aggiungere al grafico due linee verticali in corrispondenza dei seguenti valori: \(\bar x - 2s\) e \(\bar x + 2s\) (\(\bar x\) è la media campionaria, \(s\) è la deviazione standard campionaria). Infine, calcolare quanti valori, in percentuale, si trovano tra i due valori soglia.