7 Lab 5 - 13/11/2020

In questa lezione apprenderemo come simulare data dalla variabile casuale Lognormale e come rappresentare graficamente la funzione di ripartizione empirica. Inoltre, introdurremo nuovi strumenti grafici, come il normal probability plot e l’half normal plot, per studiare graficamente una distribuzione di dati. Infine vedremo come è possibile utilizzare la trasformazione di Box-Cox per ridurre il grado di asimmetria dei dati.

7.1 Distribuzione Lognormale

Si indichi con $X$ una variabile casuale (VC) Normale di media parametri $\mu$ (media) e $\sigma^2$ (varianza). La trasformazione esponenziale di $X$ dà origine a una nuova variabile casuale $Y=e^{X}$ nota come Lognormale. La sua funzione di densità di probabilità (PDF) è data da \[ f_Y(y)=\frac{1}{y\sigma\sqrt{2\pi}}e^{-\frac{(\ln(y)-\mu)^2}{2\sigma^2}} \] per $y>0$ (e 0 altrove). Si noti che la PDF dipende da due parametri, $\mu$ e $\sigma$, noti come log media e log standard deviation. Essi vengono ereditati dalla distribuzione Normale $X$ ma hanno un significato diverso.

E’ possibile dimostrare empiricamente la relazione che esiste tra la VC Normale e Lognormale come segue:

si simulano 4 numeri dalla distribuzione Normale di media $\mu=4$ e standard deviation $\sigma= 0.5$, seguendo il procedimento illustrato nella Sezione 6.3:

set.seed(66)
x = rnorm(4, mean=4, sd=0.5)
x

## [1] 5.161987 4.108489 4.209096 3.904504

Si applica la trasformazione esponenziale ai valori contenuti nel vettore $x$:

exp(x)

## [1] 174.51092  60.85467  67.29570  49.62544

Si verifica che i valori trasformati sono gli stessi che si ottengono utilizzando rlnorm, la funzione di R che simula valori dalla VC Lognormale di parametri $\mu$ e $\sigma$ (denominati dalla funzione meanlog e sdlog, si veda ?rlnorm):

set.seed(66)
y = rlnorm(4, meanlog=4, sdlog=0.5)
y

## [1] 174.51092  60.85467  67.29570  49.62544

Si noti che i valori di exp(x) e y coincidono.

Si simulino ora 1000 valori dalla VC Lognormale di parametri $\mu=0.1$ e $\sigma=0.5$:

set.seed(66)
y = rlnorm(1000, meanlog=0.1, sdlog=0.5)
head(y)

## [1] 3.5324346 1.2318148 1.3621936 1.0045137 0.9441982 0.7993718

e si rappresentino graficamente i valori simulati

hist(y, freq=F)
lines(density(y))

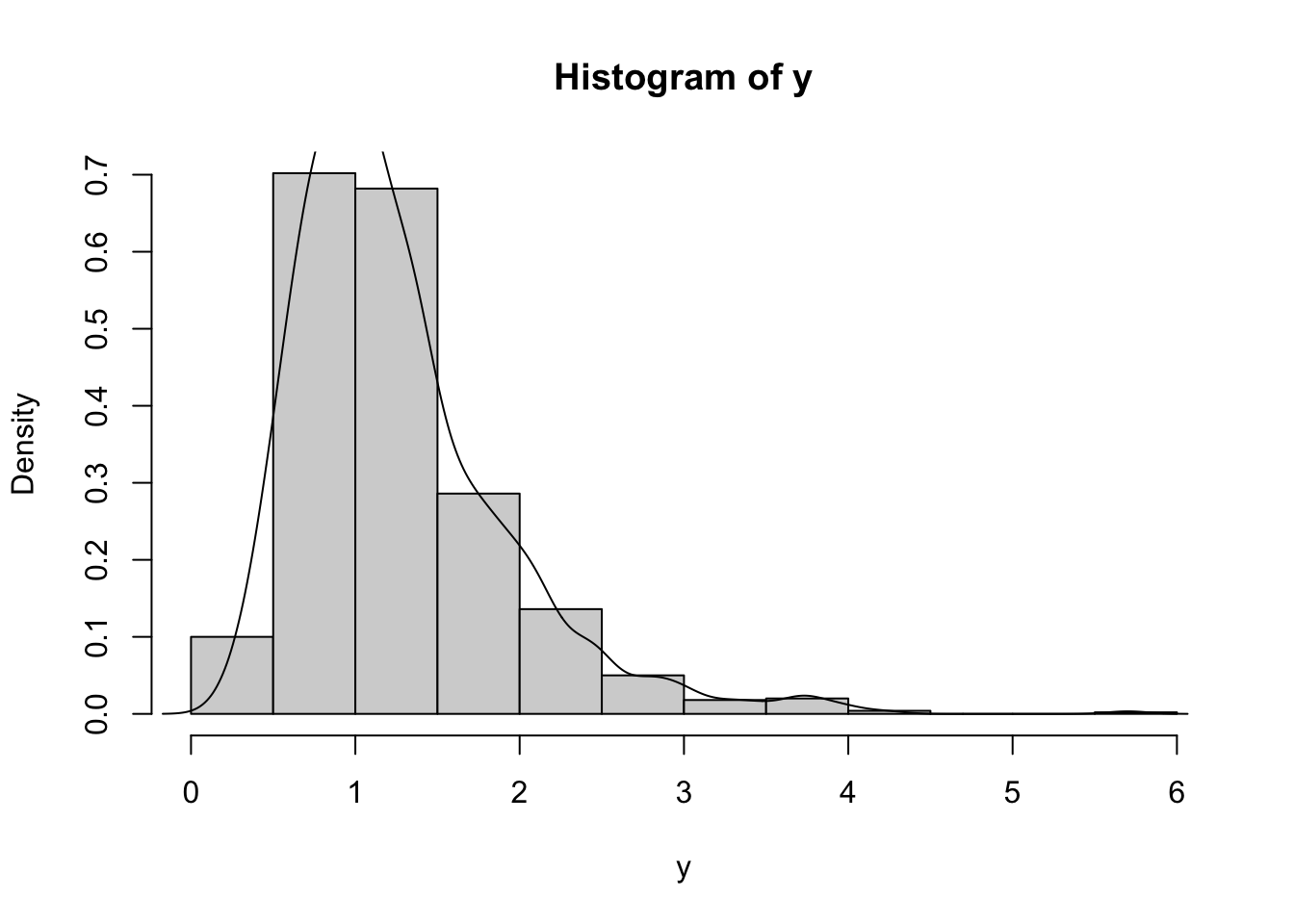
Si osserva che la distribuzione ha una coda lunga verso destra ed è pertanto caratterizzata da asimmetria positiva. Ciò è confermato anche dal fatto che la media è maggiore della mediana:

summary(y)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.1913  0.8111  1.1060  1.2574  1.5288  5.7015

Questo è dovuto al fatto che la media, a differenza della mediana, non è un indice robusta ed è quindi influenzato dai valori estremi positivi che ne trascinano il valore verso destra.

Inoltre, l’indice di skewness

mean((y-mean(y))^3)/sd(y)^3

## [1] 1.632364

è notevolmente maggiore di zero, come ci si aspetta.

E’ interessante notare che la media empirica del campione di dati è data da

mean(y)

## [1] 1.25742

Questo valore è vicino al valore medio atteso, dato dalla media della VC Lognormale, data da \[ E(Y)=e^{\mu+\frac{\sigma^2}{2}} \]

exp(0.1+0.5^2/2)

## [1] 1.252323

I due valori non coincidono esattamente a causa della variabilità campionaria legata al processo di simulazione dei dati. Ovviamente più il campione è grande e più ci si la media campionaria sarà vicina alla media teorica.

7.2 Funzione di ripartizione empirica

La funzione di ripartizione empirica (EDF) restituisce la proporzione di valori in un vettore di dati minori o uguali ad un dato numero reale $y$. La EDF è definita da \[ F_n(y)=\frac{\sum_{i=1}^n \mathbb I(Y_i\leq y)}{n} \] dove $\mathbb I(\cdot)$ è la funzione indicatarice che vale uno se $Y_i\leq y$ o zero altrimenti (di fatto si calcola il rapporto tra il numero totale di osservazioni $\leq y$ ed il totale $n$ delle osservazioni).

In R la EDF si può ottenere salvando l’output della funzione ecdf in un nuovo oggetto qui di seguito denominato myecdf (qualsiasi nome può essere scelto per il nuovo oggetto):

myecdf = ecdf(y)

L’oggetto myecdf appartiene alla classe function è può essere utilizzato come una normale altra funzione. In questo caso la funzione, valutata in un certo valore reale, restituirà la proporzione di valori uguali o inferiori al valore scelto. Ad esempio, utilizzando 2.68:

myecdf(2.68)

## [1] 0.961

si ottiene che il 96.1% dei valori in y è minore o uguale a 2.68. Si ricordi che il numero utilizzato in input della funzione myecdf può essere qualsiasi numero reale. Ovviamente per il caso in esame ci si aspetta che la EDF valutata in un numero negativo sia 0 e che sia 1 per qualsiasi valore superiore a 5.7015488. Ad esempio:

myecdf(-1.4)

## [1] 0

myecdf(7.9)

## [1] 1

La EDF può essere rappresentata graficamente usando la funzione plot:

plot(myecdf)

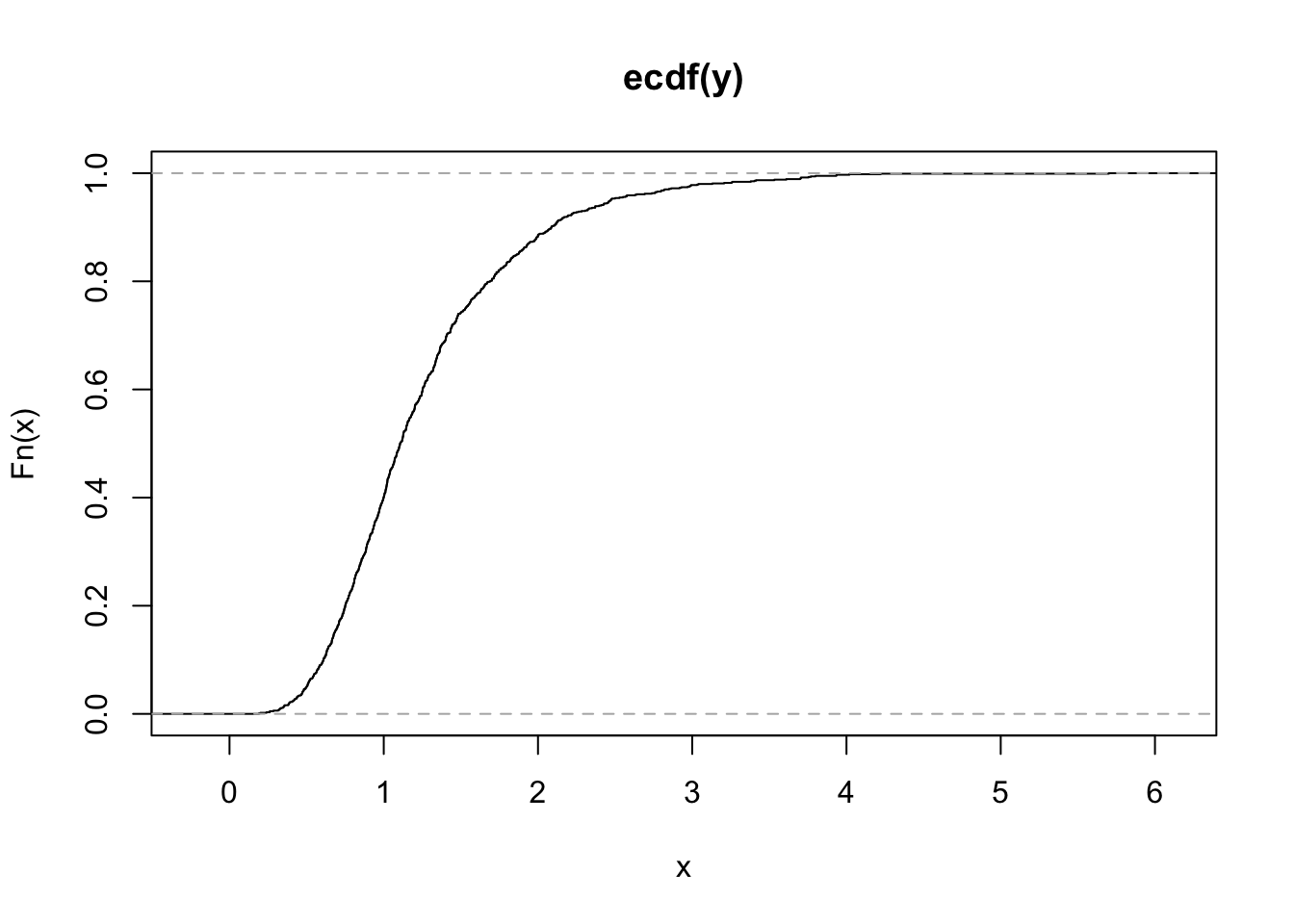L’asse delle x si riferisce all’intervallo da $-\infty$ a $+\infty$; ovviamente vengono visualizzati i valori compresi tra il minimo e il massimo di y rappresentando essi l’intervallo di interesse). Sull’asse delle y vengono riportati i valori della EDF, e quindi proporzioni comprese tra 0 e 1.

Analizzando il grafico è possibile ottenere, per qualsiasi valore sull’asse delle x, il corrispondente valore della EDF. Per una migliore visualizzazione dell’andamento della linea della EDF è opportuno fare uno zoom sui valori mostrati sull’asse delle x tra 1.8 e 2.2.

plot(myecdf, xlim = c(1.8, 2.2))

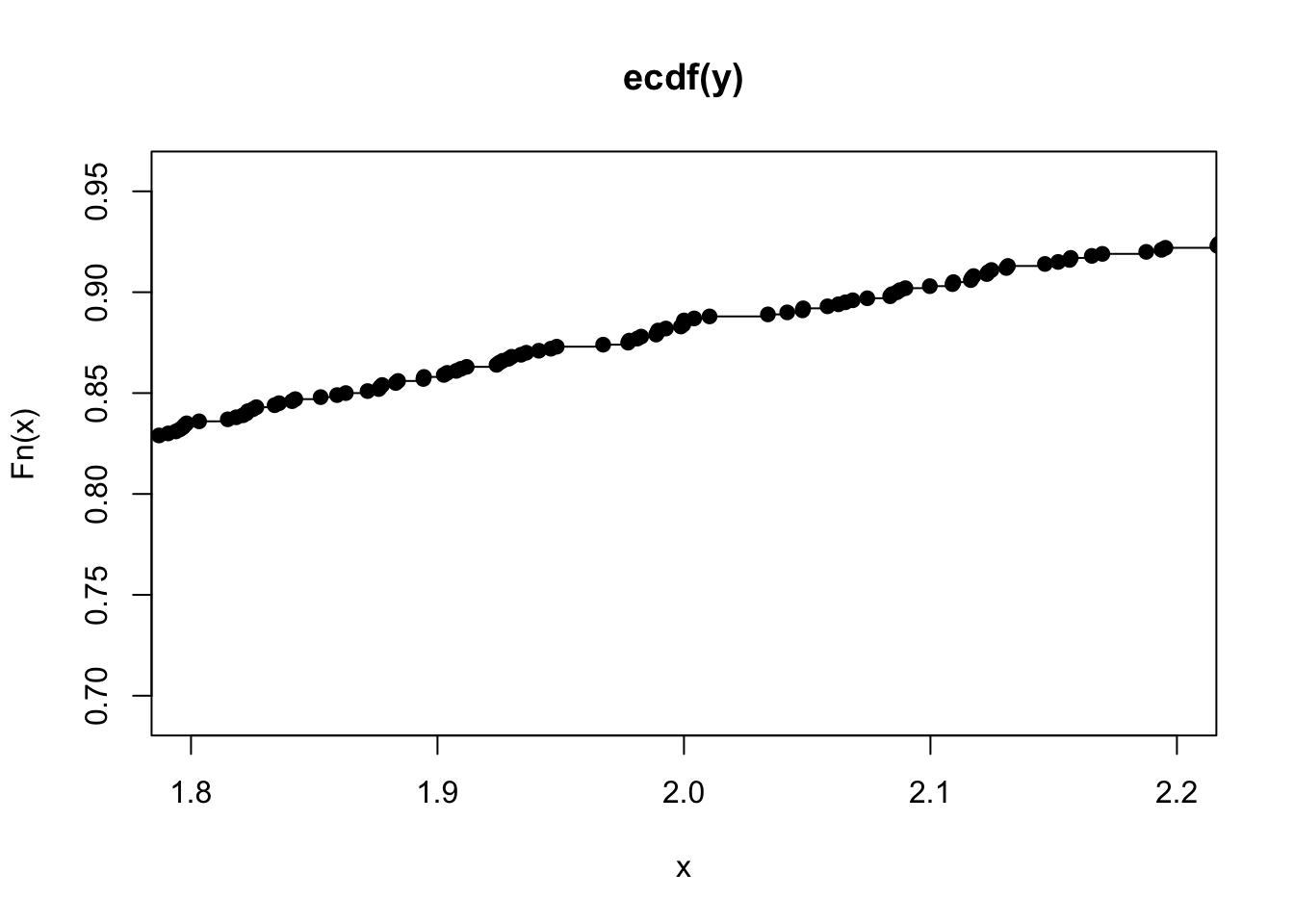
Dal grafico è evidente che la EDF è definita per tutti i valori reali (anche quelli non osservati nel campione) ed è una funzione non decrescente. E’ una funzione a gradini: in particolare, i gradini sono localizzati in corrispondenza dei valori inclusi nel vettore y (e l’altezza del salto è dato da $1/n$). La pendenza della EDF fornisce importanti informazioni circa la distribuzione analizzata: una curva molto pendenza indica poca variabilità dei dati, mentre una curva con poca pendenza indica una distribuzione caratterizzata da maggiore variabilità.

7.2.1 Normal probability plot

Il normal probability plot (NPP) è uno strumento grafico (uno scatterplot) utile per verificare l’ipotesi di normalità dei dati. Esso si basa sul confronto dei quantili empirici (solitamente rappresentati in ascissa) e quelli teorici della Normale (solitamente rappresentati in ordinata).

Se l’assunzione di normalità è verificata i punti sono linearmente distribuiti. In caso contrario, quattro possibili situazioni si possono verificare come riportato in Figura 7.1.

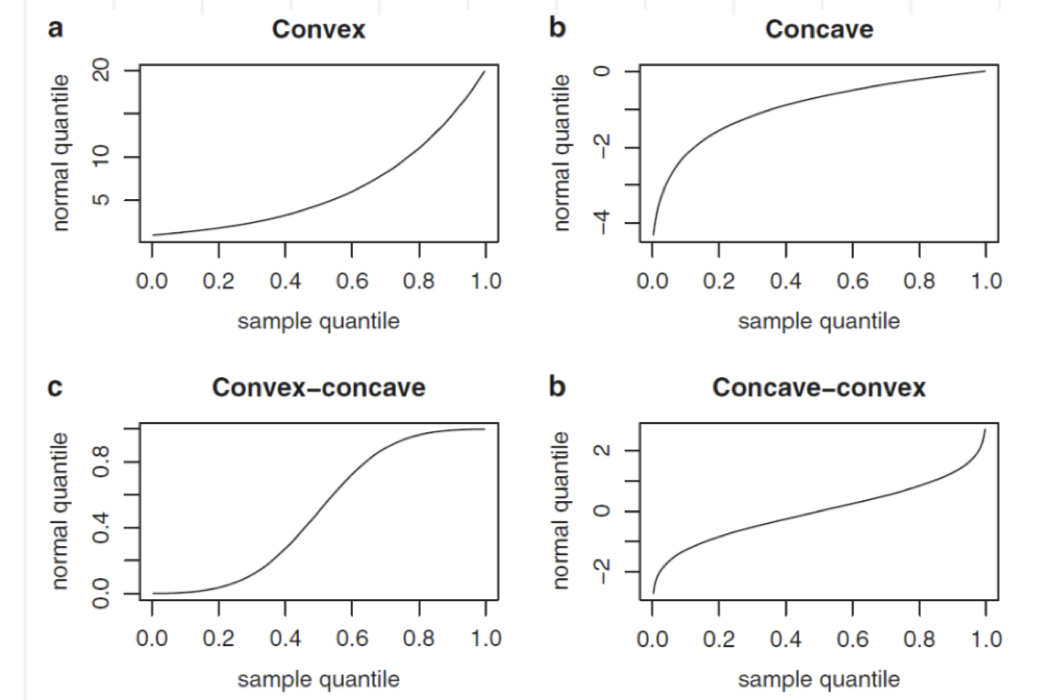
Possibili casi di non normalità: a = asimmetria negativa, b = asimmetria positiva, c = code più pesanti della Normale, d = code più leggere della Normale.

Figure 7.1: Possibili casi di non normalità: a = asimmetria negativa, b = asimmetria positiva, c = code più pesanti della Normale, d = code più leggere della Normale.

In R la funzione per ottenere il NPP è qqnorm:

qqnorm(y)

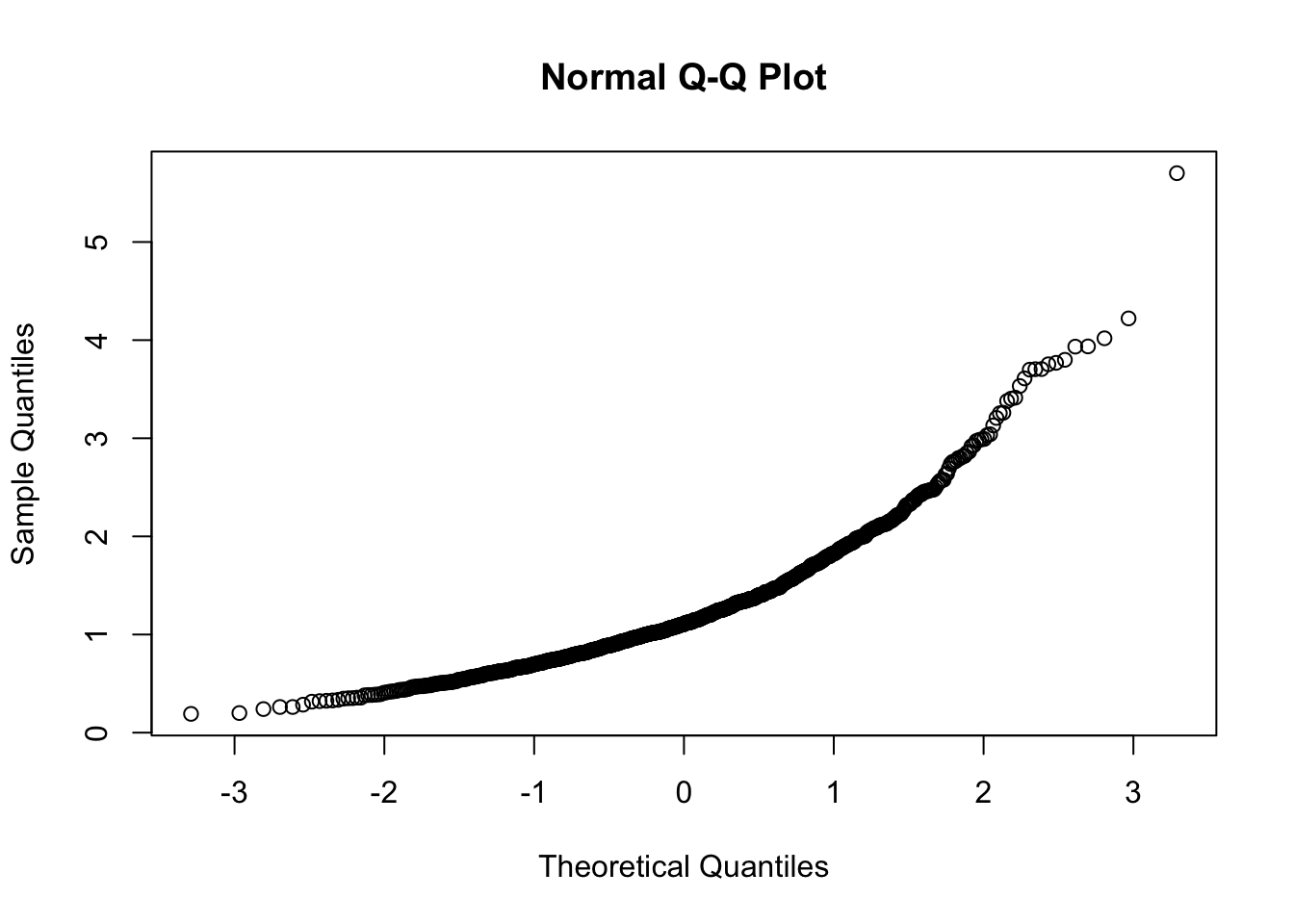Si noti che questo grafico, a differenza di quanto riportato in Figura 7.1, riporta in ascissa i quantili teorici e in ordinata quelli empirci. E’ necessario quindi, ai fini interpretativi, porre attenzione alle quantità riportate sui due assi (altrimenti si rischia di commentare in maniera sbagliata i risultati come in figura 7.2 😄.

Figure 7.2: Attenzione agli assi!

Al fine di scambiare gli assi è possibile utilizzare l’argomento datax della funzione qqnorm. E’ inoltre utile includere nel grafico una linea di riferimento utilzzando qqline.

qqnorm(y, datax=T)
qqline(y, datax=T)

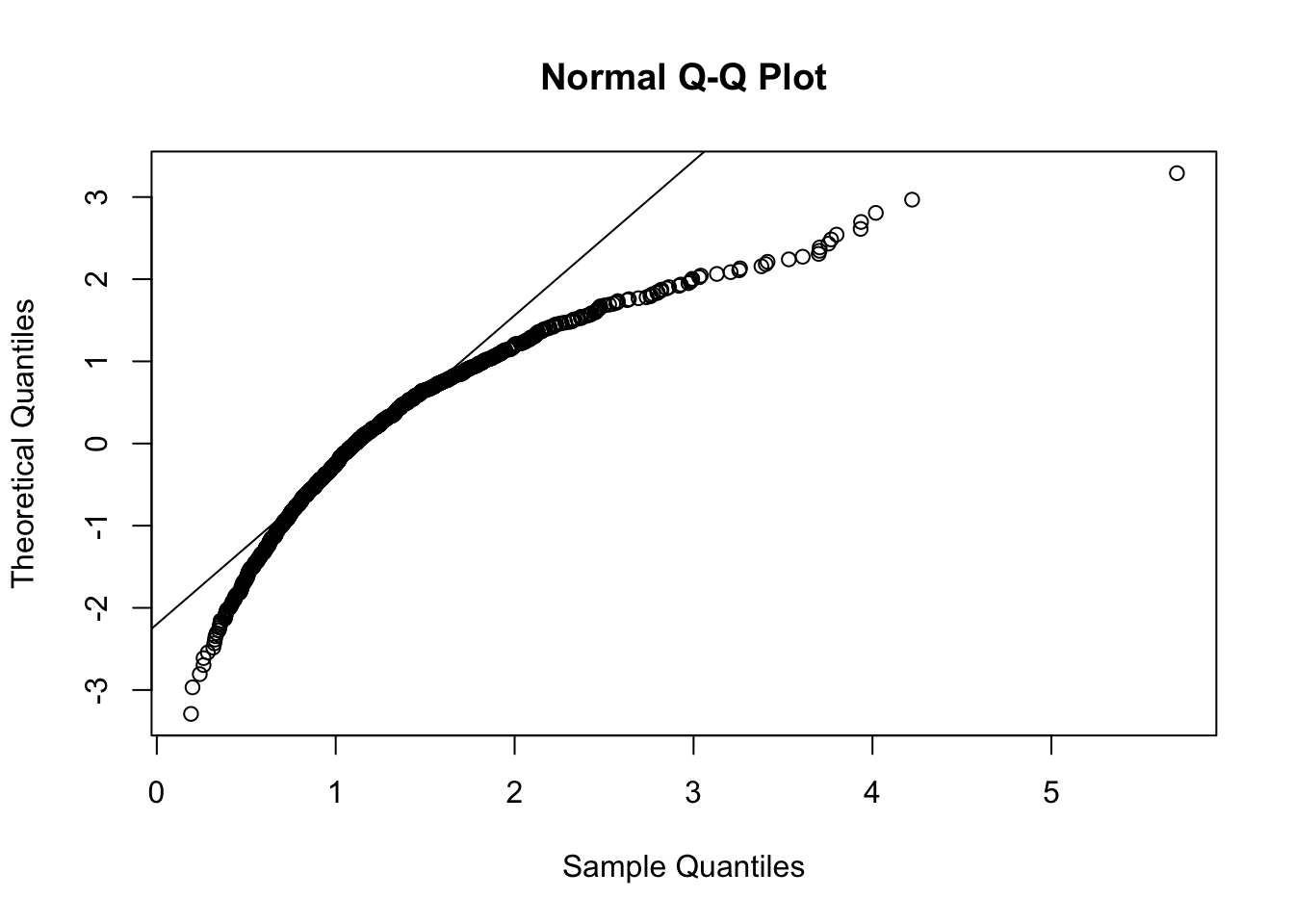
Figure 7.3: Normal probability plot per i dati del vettore y

La retta di riferimento passa per le coppie di coordinate $(I_{emp},I_{teo})$ e $(III_{emp},III_{teo})$ dove $I$ e $III$ rappresentano rispettivamente il primo e terzo quartile (empirico e teorico). I dati ordinati $y_{(1)},\ldots,y_{(n)}$ definiscono i quantili empirici, mentre i quantili teorici sono dati da $\Phi^{-1}\left(\frac{i-0.5}{n}\right)$ (per $i=1,\ldots, n$), dove $\Phi^{-1}$ rappresenta la funzione quantile della VC Normale.

In Figura 7.3 si osserva chiaramente una non linearità dei punti che sono invece caratterizzati da una concavità verso il basso che è tipica di dati caratterizzati da asimmetria positiva. Si conclude che i dati non possono essere assunti come proveniente da una distribuzioen Normale (il commento risulta ovviamente banale esseno noi a conoscenza del fatto che i dati sono stati simulati da una VC Lognormale).

7.3 Trasformazione di Box-Cox

Cercheremo di risolvere il problema di asimmetria di y utilizzando la trasformazione di Box-Cox data dalla seguente formula: \[ y^{(\alpha)}=\frac{y^\alpha-1}{\alpha} \tag{7.1} \] per $y>0$ e $\alpha\in\mathbb R$. Il caso $\alpha=0$ rappresenta un caso particolare e corrisponde alla trasformazione logaritmica dei dati, i.e. $y^{(0)}=\log(y)$. In R la funzione da utilizzare è bcPower che è inclusa nel pacchetto car (link). Un pacchetto di R è un’estensione della versione base di R e può essere scaricato dal CRAN (a tale proposito si veda anche la Sezione ??).

7.3.1 Installare e caricare un pacchetto

Prima di iniziare ad utilizzare un pacchetto è necessario seguire due passaggi:

**installare* il pacchetto: questa procedura deve essere eseguita solamente una volta (a meno che decidiate di reinstallare R, di cambiare o resettare il computer). E’ come decidere di comprare una lampadina e di montarla (si veda la Figura @ref(fig:install_load): questa azione viene fatta solamente una sola volta e non ogni volta che è necessario avere luce in una stanza.

La procedura di installazione può essere fatta utilizzando il menù di RStudio seguendo il percorso Tools - Install package, come mostrato in Figura 7.5. E’ utile sapere che tramite il menù di RStudio si sta usando la funzione install.packages("car").

caricare il pacchetto: questa azione corrisponde all’azione di accendere con l’interrutore la luce in una stanza ogni qual volta sia necessario (si veda la Figura @ref(fig:install_load)). Allo stesso modo, un pacchetto può essere caricato più volte, ogni qual volta sia necessario utilizzare una delle funzion incluse nel pacchetto. Per caricare il pacchetto car, dopo averlo installato, si utilizza il seguente codice:

library(car)

## Loading required package: carData

Figure 7.4: Installare e caricare un pacchetto

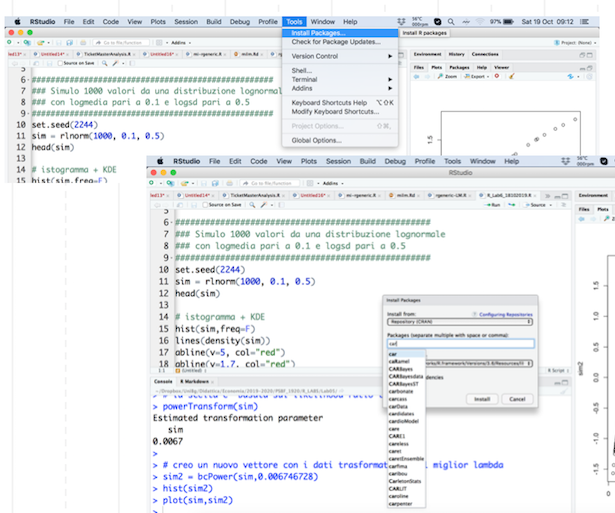
Figure 7.5: Il menù di RStudio per installare nuovi pacchetti

Una volta che il pacchetto car è caricato, è possibile utilizzare la funzione bcPower in esso contenuta. Questa funzione ha bisogno di due input: i dati e il valore denominato $\alpha$ in Eq.(7.1) e lambda dalla funzione bcPower. Per esempio con il seguente codice

y2 = bcPower(y, lambda=1.5)

viene creato un nuovo vettore di nome y2 contenente i data trasformati di y usando l’equazione di Box-Cox con $\alpha=1.5$. Ovviamente la lunghezza di y e y2 sono uguali. E’ anche possibile rappresentare graficamente i dati trasformati utilizzando, per esempio, un istogramma:

hist(y2)

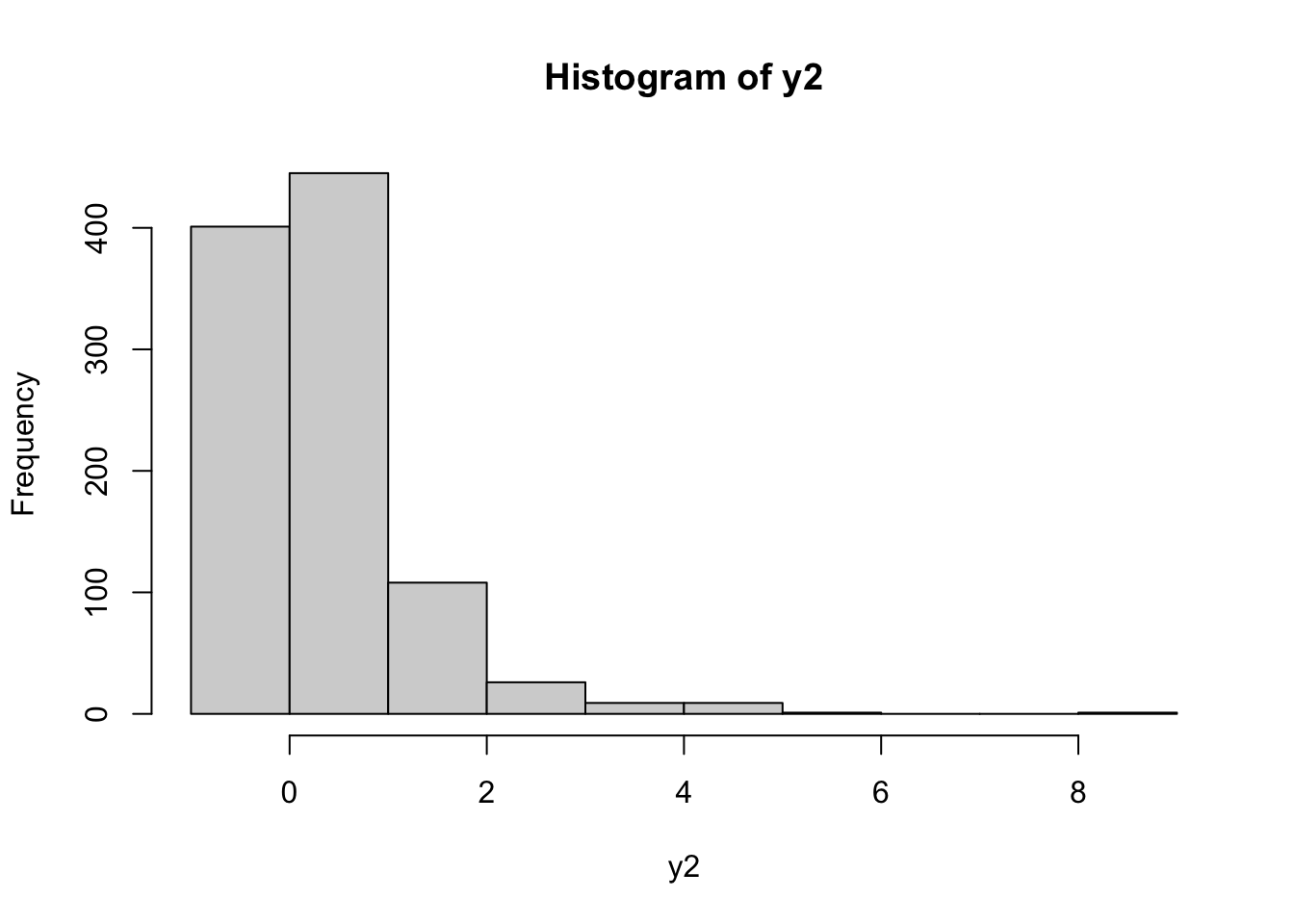
Si osserva che la distribuzione è ancora asimmetrica. E’ quindi possibile provare ad utilizzare un valore diverso di $\alpha$ (si ricordi che $\alpha\in \mathbb R$):

y2 = bcPower(y, lambda=-1.5)
hist(y2)

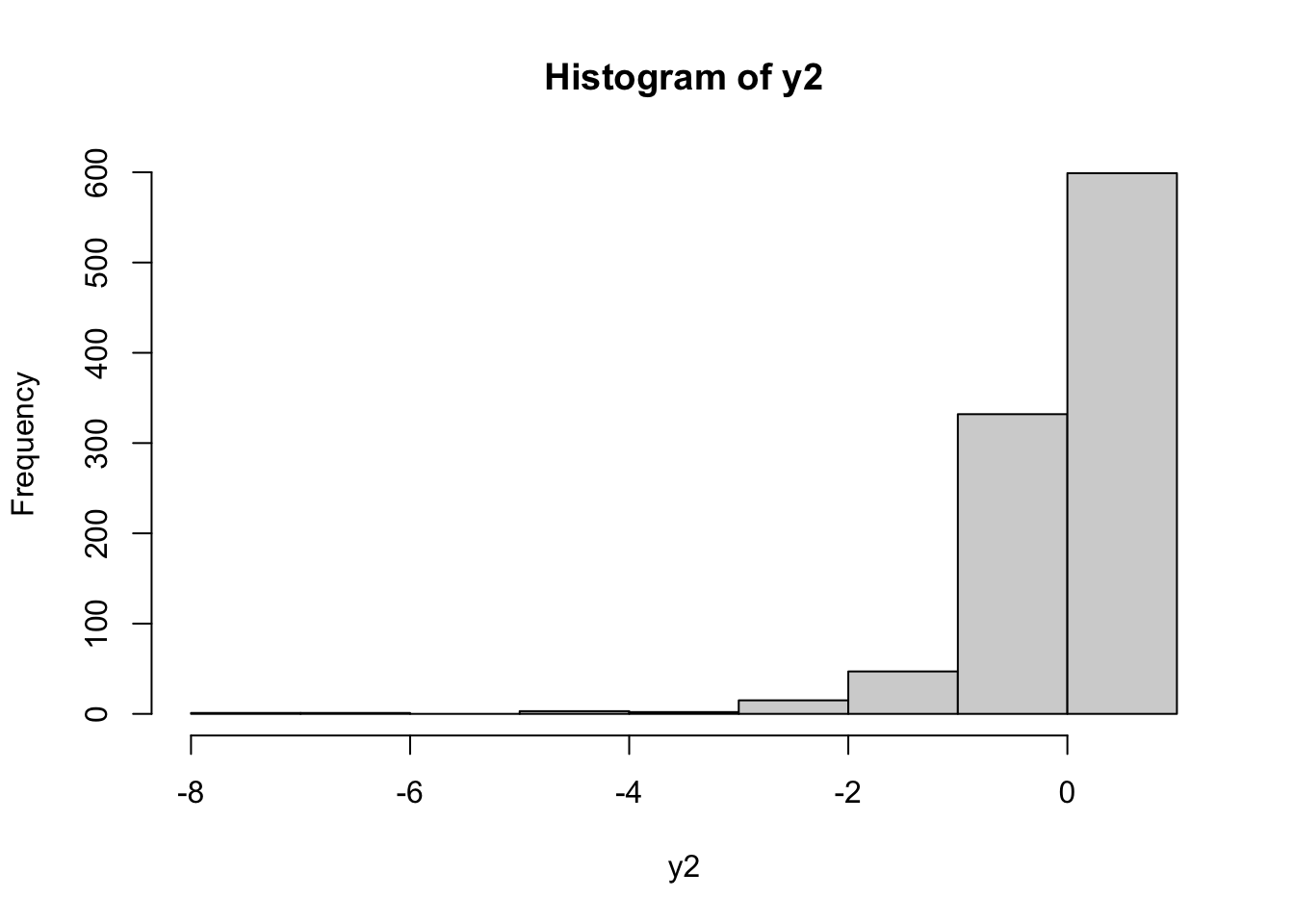
In questo caso la distribuzione ha un coda lunga a sinistra ed è quindi caratterizzata da asimmetria negativa. Per trovare il migliore valore di $\alpha$ (al fine di ottenere una distribuzione simmetrica) è possibile utilizzare la funzione powerTransform inclusa nel pacchetto car (si veda ?powerTransform per ulteriori dettagli):

powerTransform(y)

## Estimated transformation parameter 
##          y 
## 0.04165664

Il valore ottenuto come output rappresenta il migliore valore di $\alpha$ da utilizzare nella formula della trasformazione di Box-Cox. Al fine di utilizzare questo valore direttamente come input di bcPower si può procedere come segue: salvare l’output di powerTransform in un nuovo oggetto e poi estrarre da questo oggetto il valore del coefficiente usando $lambda:

bestpower = powerTransform(y)
bestpower$lambda

##          y 
## 0.04165664

In questo modo si può passare direttamente il valore di $\alpha$ a bcPower senza dover utilizzare copia-incolla o doverlo ricopiare manualmente:

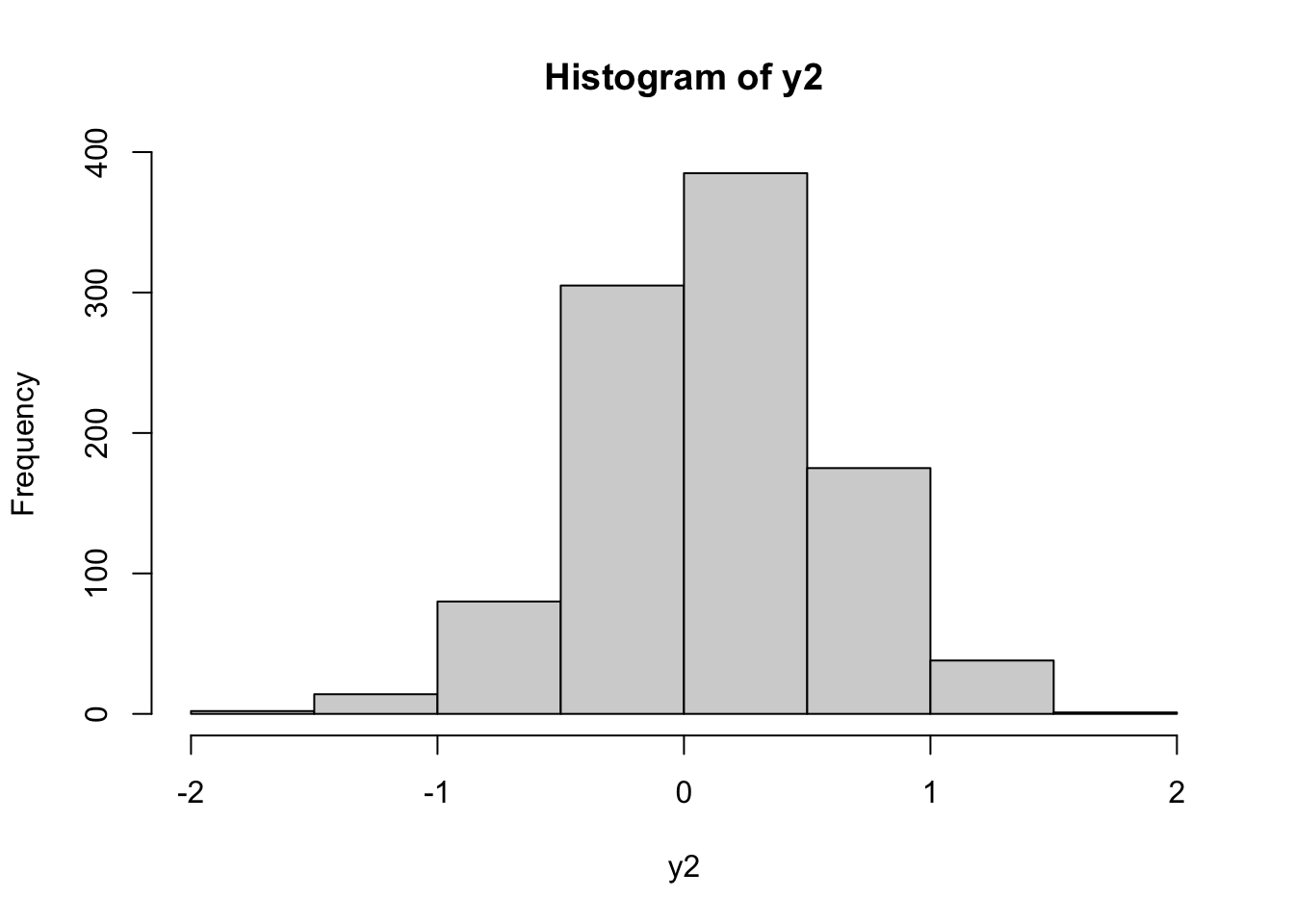
y2=bcPower(y, lambda=bestpower$lambda)
hist(y2)

Dall’istrogramma si vede che ora la distribuzione è simmetrica. A titolo di verificare utilizziamo il NPP per studiare la distribuzione dei dati trasformati:

qqnorm(y2,datax=T)
qqline(y2,datax=T)

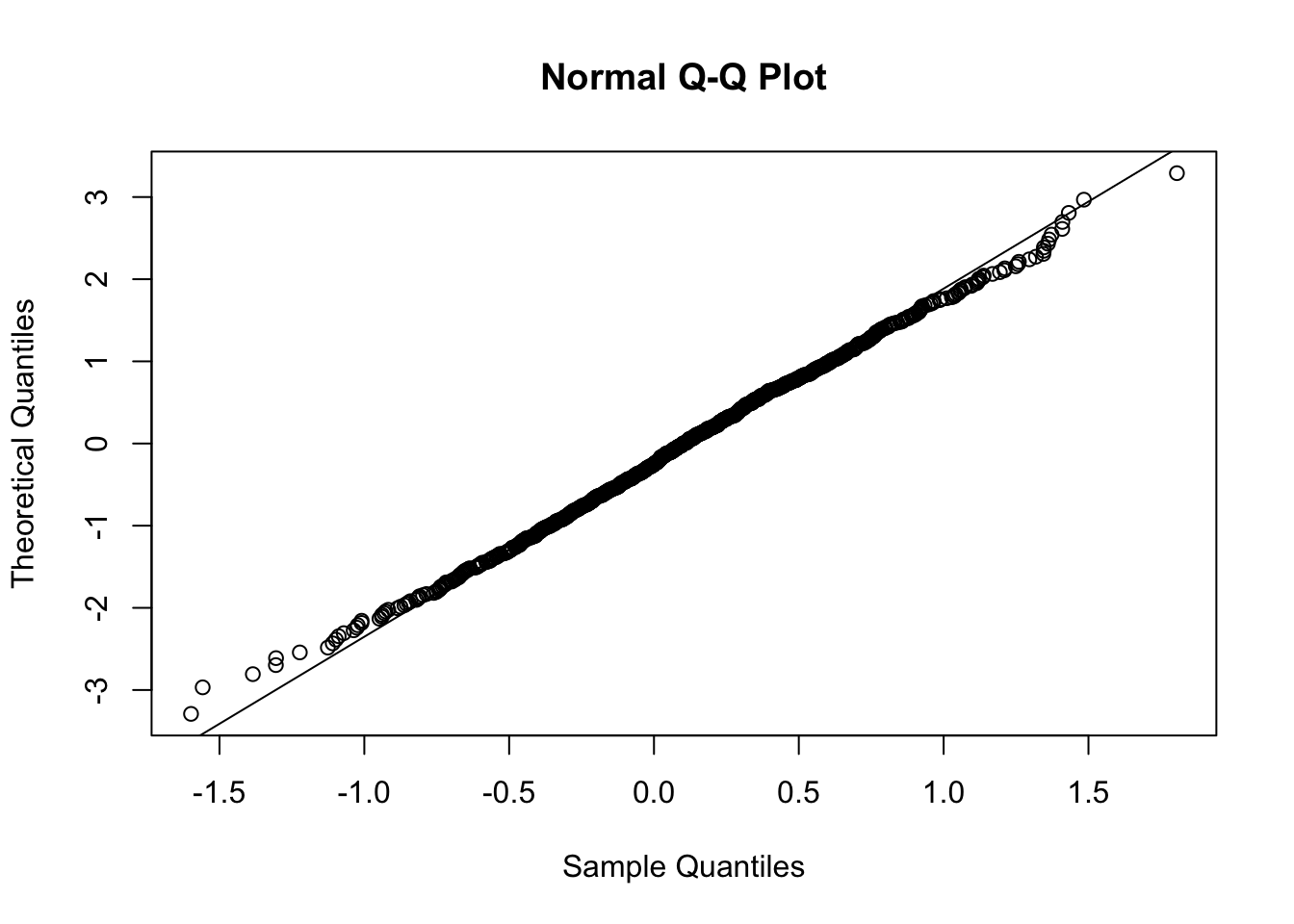
In questo caso quasi tutti i dati sono allineati lungo la retta di riferimento. Solo poche osservazioni situate sulle code si discostano dalla retta. Anche l’indice di skewness risulta vicino a zero:

mean((y2-mean(y2))^3) / sd(y2)^3

## [1] 0.001726087

7.3.2 Half-Normal plot

L’half-Normal plot confronta i quantili empirici con i quantili teorici al fine di rilevare la presenza di outliers. Il modello teorico di riferimento è $|Z|$ (half-Normal), ovvero il valore assoluto di una VC Normale standard (in questo caso non si è quindi interessati al segno dei valori estremi ma solo alla loro posizione nelle code della distribuzione).

La funzione di R da utilizzare è halfnorm, inclusa nel pacchetto faraway (link). Per installare e caricare il pacchetto si proceda come descritto nella Sezione 7.3.1:

library(faraway)

## Registered S3 methods overwritten by 'lme4':
##   method                          from
##   cooks.distance.influence.merMod car 
##   influence.merMod                car 
##   dfbeta.influence.merMod         car 
##   dfbetas.influence.merMod        car

## 
## Attaching package: 'faraway'

## The following objects are masked from 'package:car':
## 
##     logit, vif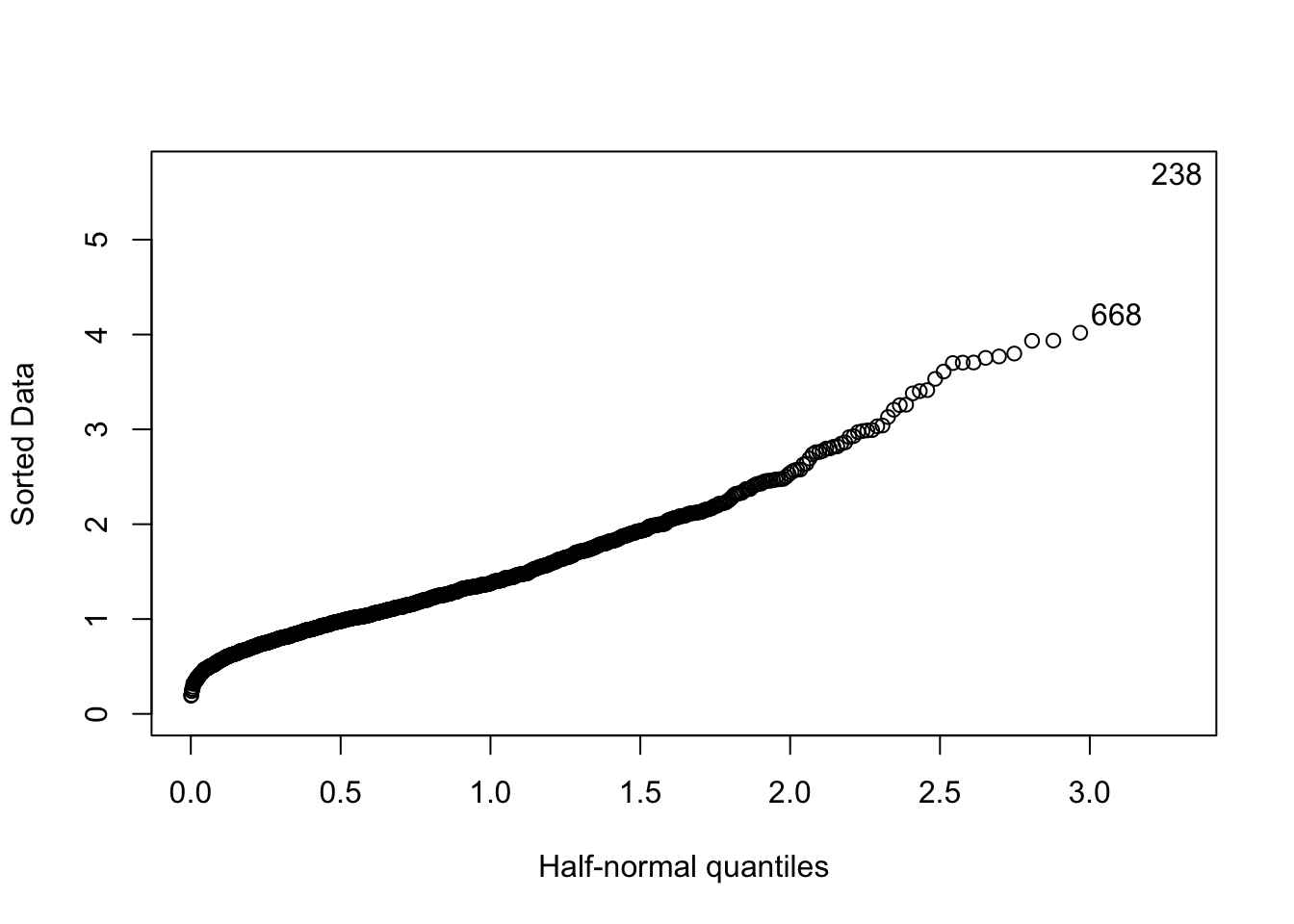

halfnorm(y)

Sull’asse delle ascisse si riportano i quantili di $|Z|$ dati da $\Phi^{-1}\left(\frac{n+i}{2n+1}\right)$ con $i=1,\ldots,n$. Sull’asse delle ordinate vengono invece utilizzati i dati ordinati in valore assoluto. Nel grafico le due osservazioni più estreme vengono etichettate con le rispettive posizioni nel vettore. Utilizzando le posizioni è possibile recuperare i corrispondenti valori dei due valori più estremi:

y[238]

## [1] 5.701549

y[668]

## [1] 4.221412

L’argomento nlab della funzione halfnorm può essere utilizzato per cambiare il numero di valori che vengono etichettati (di default 2).

7.4 Esercizi lab 5

7.4.1 Esercizio 1

Simulare 1000 valori da una Normale di parametri 0.5 e varianza=0.3 (usare come seme il valore 99). Salvare i valori in un oggetto di nome norm_sim.
Calcolo l’esponenziale dei valori simulati (exp) e rappresentarli graficamente con un istogramma. A quale distribuzione teorica possono essere associati i valori esponenziati?
Calcolare la media empirica (calcolata con i dati simulati) e confrontarla con la media teorica (vedi teoria) della distribuzione di riferimento.

7.4.2 Esercizio 2

Si supponga che i log-returns (rendimenti lordi) $X$ di un certo titolo siano distribuiti come una vc Normale di media pari a 0.005 e varianza pari a 0.1.

Simulare 1000 log-returns da $X$ (usare come seme il valore 789) e rappresentarli tramite un boxplot. Commentare il grafico.
Calcolare – tramite la corretta trasformazione matematica – il corrispondente vettore dei gross-returns (rendimenti lordi). Rappresentare tramite istogramma + KDE la distribuzione dei gross-returns. Che distribuzione può essere associata ai gross-returns?
Calcolare la skewness per il campione di gross-returns. Cosa si può concludere circa la simmetria?
Produrre il normal probability plot per il campione di gross-returns. Cosa si può concludere circa la normalità?
Utilizzare la trasformazione di Box-Cox per cercare di rendere i dati simmetrici. Quale valore di $\alpha$ (lambda per R) conviene usare?
Rappresentare graficamente i dati trasformati tramite KDE.Aggiungere al grafico la KDE per 1000 dati simulati da una VC Normale con media e varianza pari ai corrispondenti valori empirici stimati per i dati trasformati (usare 1000 come seme). Commentare il grafico.
Calcolare la skewness e curtosi empirica dei dati trasformati.

7.4.3 Esercizio 3

Simulare 1000 valori da una variabile casuale Chi-quadrato con 5 gradi di libertà (si veda qui per maggiori dettagli) utilizzando il seguente codice. Creare un nuovo oggetto di nome simdatachisq contenente i dati simulati.

?rchisq
set.seed(543)
simdatachisq = rchisq(1000, 5)

Rappresentare graficamente la distribuzione dei valori simulati simdatachisq con un istogramma a cui viene aggiunta anche la linea della KDE (stima Kernel della densità).
Calcolare la stima campionaria dell’indice di skewness. Dal valore ottenuto e dal grafico ottenuto al punto precedente cosa si può concludere?
Rappresentare la distribuzione dei valori simdatachisq con un normal probability plot. Cosa si osserva?
Trovare la miglior trasformazione di Box-Cox per i dati simulati. Quale è la trasformazione da applicare ai dati (riportare la formula)?
Rappresentare graficamente i dati trasformati tramite un normal probability plot. Cosa si può concludere osservando dal grafico?
Rappresentare graficamente la funzione di ripartizione empirica (EDF) dei dati trasformati.

7.4.4 Esercizio 4

Si considerino le tre seguenti variabili casuali:

$X_1\sim Normale(\mu=10, \sigma=1)$
$X_2\sim Normale(\mu=10, \sigma=2)$
$X_2\sim Normale(\mu=10, \sigma=0.5)$

Simulare 1000 valori da $X_1$ (seme=1), da $X_2$ (seme=2) e da $X_3$ (seme=3).

Rappresentare in uno stesso grafico le 3 KDE (utilizzare opportunamente xlim e ylim). Commentare il grafico.

Rappresentare sullo stesso grafico le 3 funzioni di distribuzione empirica. Aggiungere al grafico una linea (costante) in corrispondenza della mediana e un in corrispondenza del valore di probabilità (frequenza relativa) pari a 0.5. Commentare il grafico.

Si considerino le tre seguenti variabili casuali:

$X_4\sim Normale(\mu=-10, \sigma=1)$
$X_5\sim Normale(\mu=0, \sigma=1)$
$X_6\sim Normale(\mu=10, \sigma=1)$

Simulare 1000 valori da $X_4$ (seme=4), da $X_5$ (seme=5) e da $X_6$ (seme=6).

Rappresentare in uno stesso grafico le 3 KDE (utilizzare opportunamente xlim). Commentare il grafico.

Rappresentare sullo stesso grafico le 3 funzioni di distribuzione empirica. Aggiungere al grafico una linea (costante) in corrispondenza delle tre mediane e in corrispondenza del valore di probabilità (frequenza relativa) pari a 0.5. Commentare il grafico (settare oppportunamente xlim).

7.4.5 Esercizio 5

Si considerino i due seguenti grafici (A e B). Entrambi riportano le stime kernel della densità per tre distribuzioni empiriche (curva nera, rossa e blu). In merito al grafico A cosa si può commentare circa la simmetria delle distribuzioni? E per il grafico B cosa si può dire circa la kurtosi?
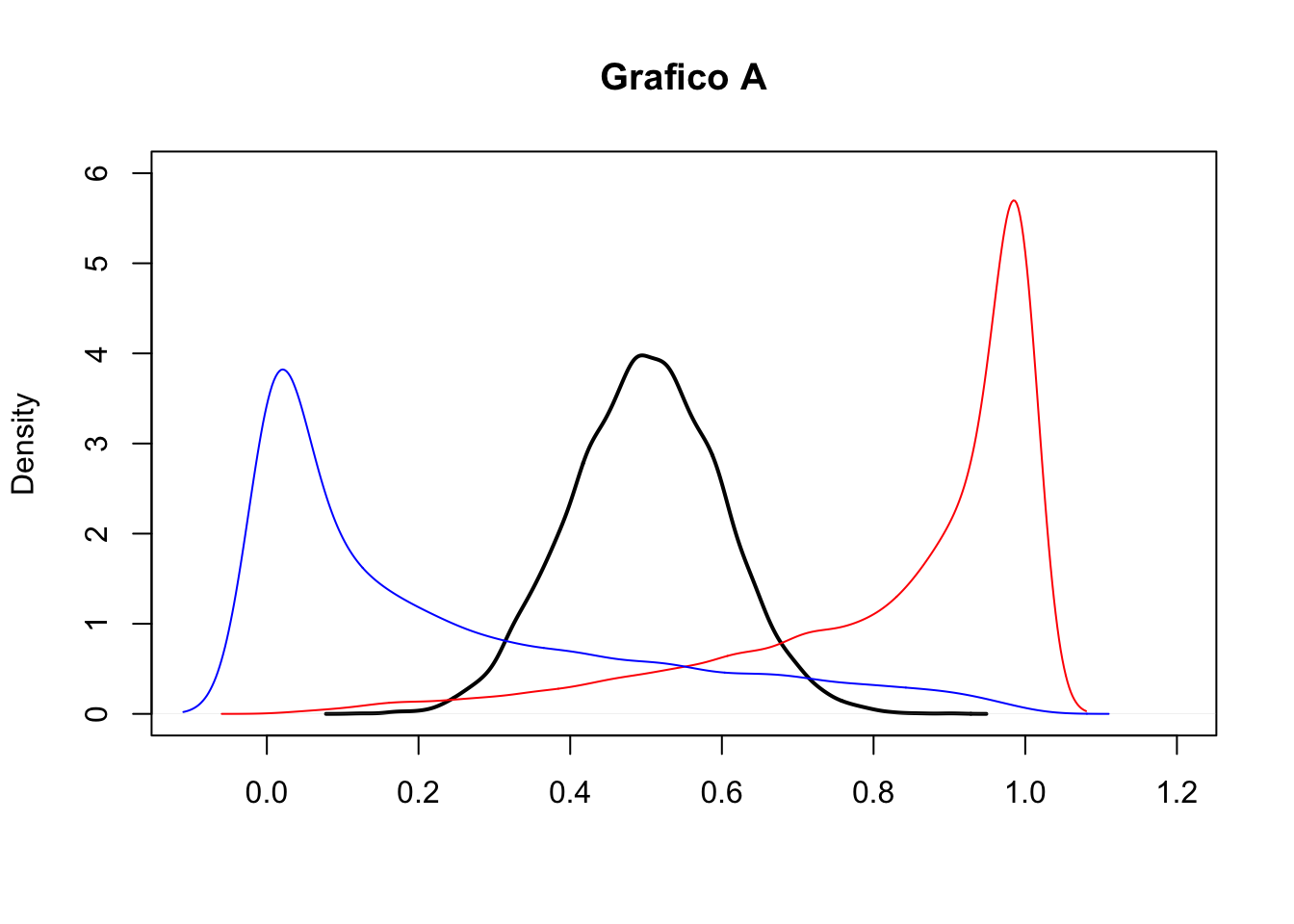
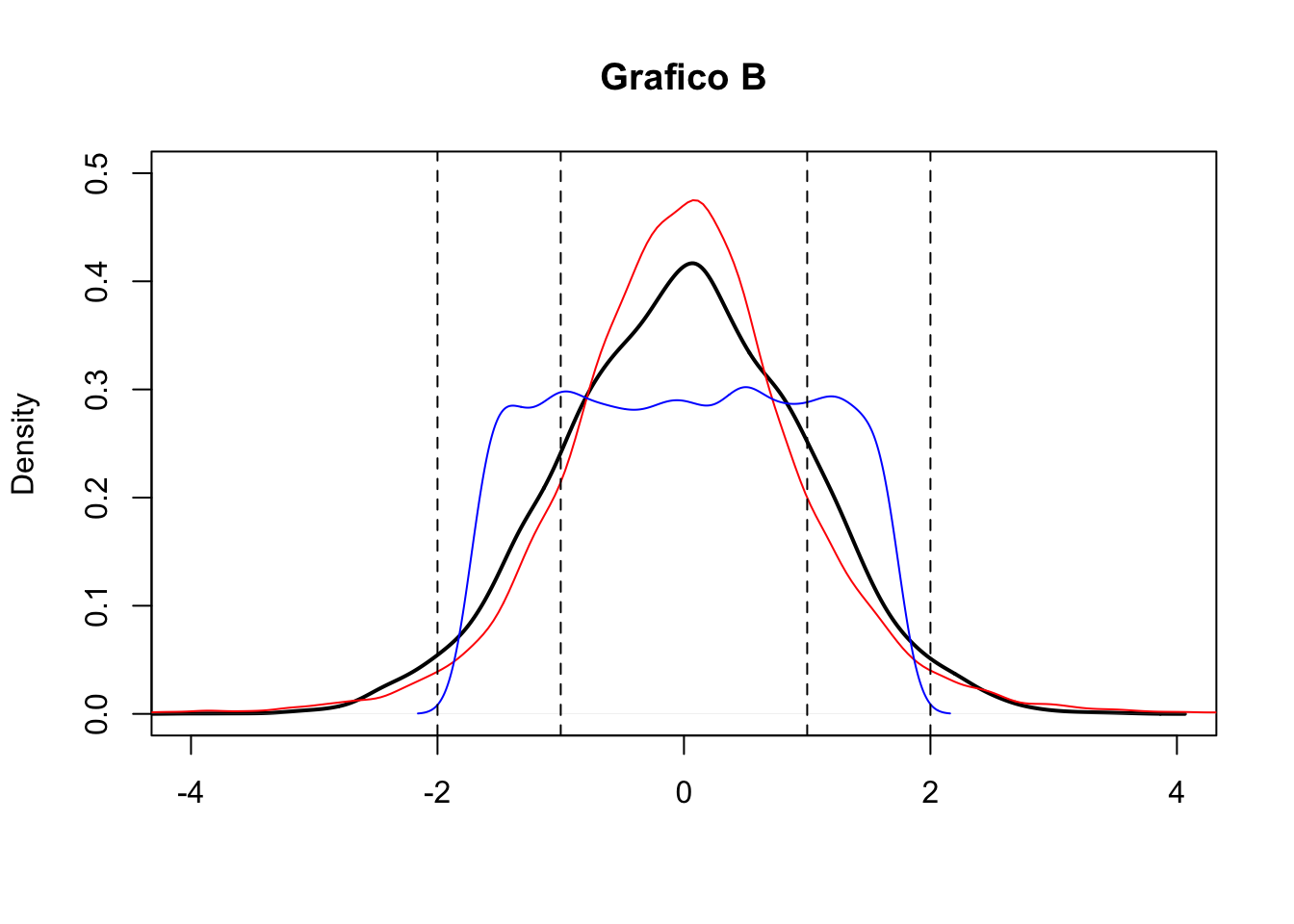
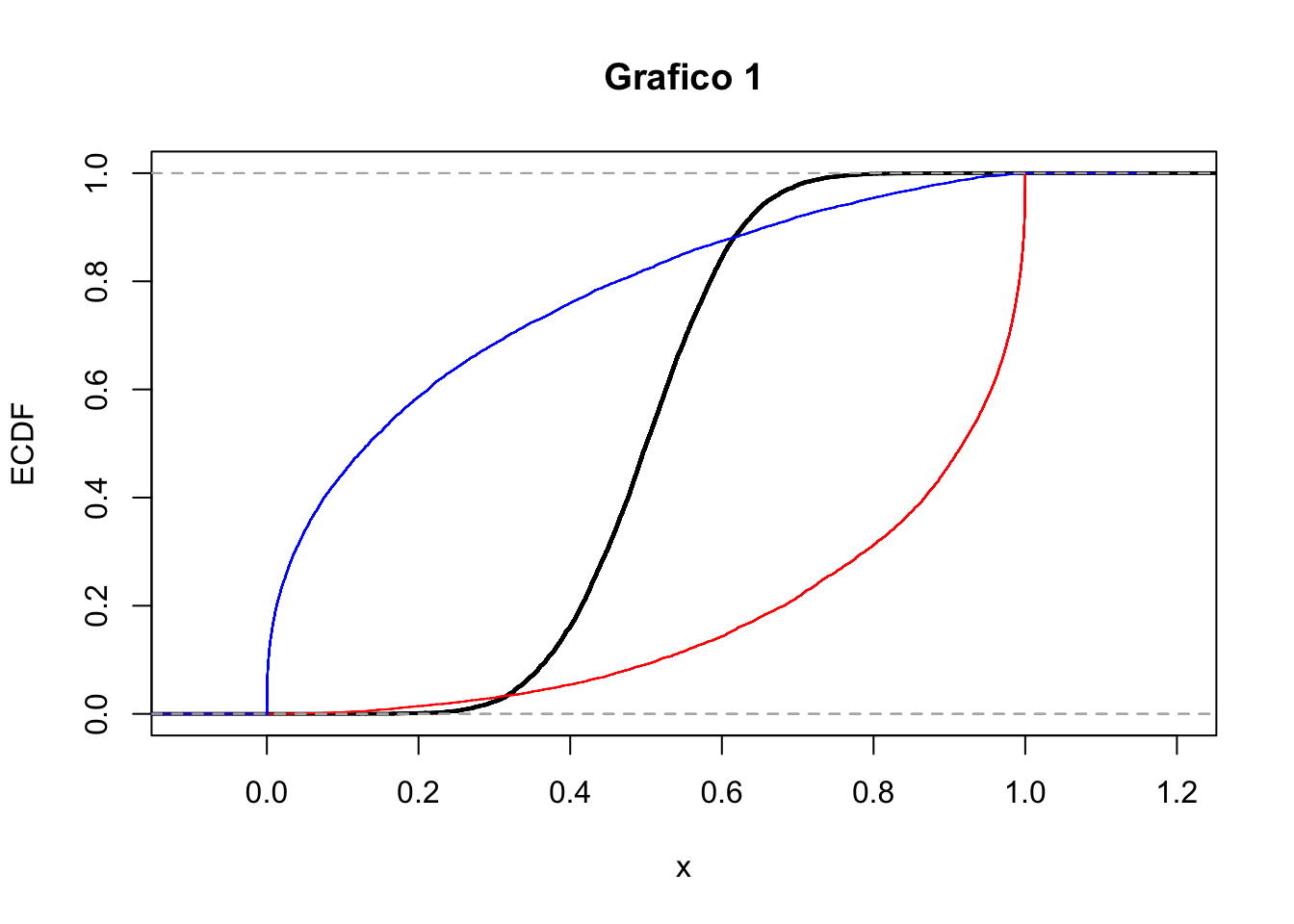
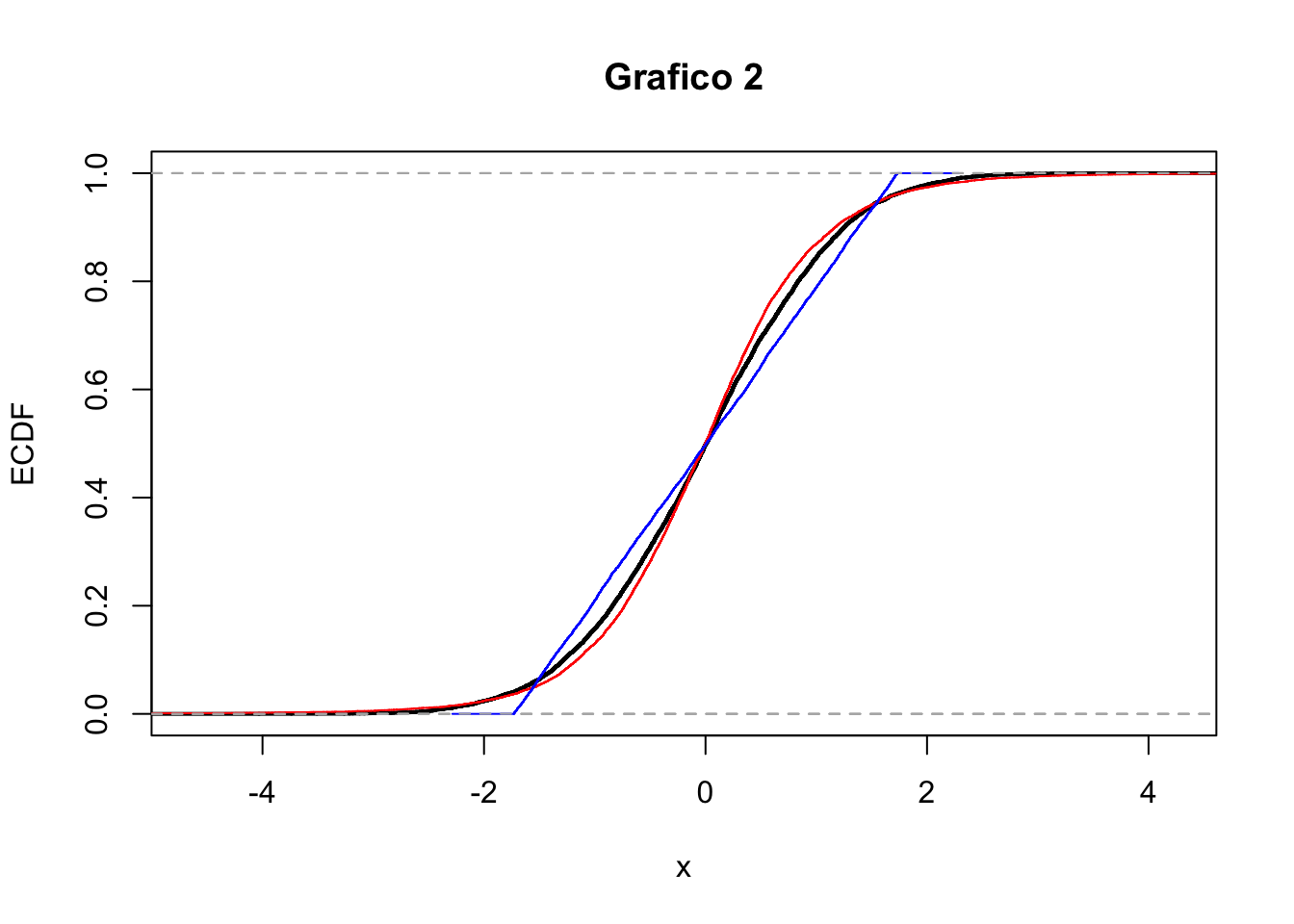
Si considerino ora i due seguenti grafici (grafico 1 e 2) che riportano le funzioni di ripartizioni empiriche (EDF). Il grafico 1 si riferisce alle distribuzioni riportate nel grafico A o a quelle del grafico B? Motivare.