9 Lab 7 - 27/11/2020

In questa lezione verrà introdotto il test di Kolmogorov-Smirnov per verificare la normalità di una distribuzione. Andremo poi ad introdurre i concetti di covarianza, correlazione ed infine il modello di regressione semplice (con un solo regressore).

Useremo i dati contenuti nel file datareg_logreturns.csv e relativi ai rendimenti logaritmici giornalieri di:

indice NASDAQ
ibm, lenovo, apple, amazon, yahoo
oro (gold)
indice SP500
il tasso di interesse a 10 anni CBOE

Come al solito iniziamo con l’import dei dati ed il check della loro struttura;

datareg = read.csv("~/Dropbox/UniBg/Didattica/Economia/2020-2021/SAPF_2021/R_labs/lab7/data_logreturns.csv", sep=";")
str(datareg)

## 'data.frame':	1258 obs. of  10 variables:
##  $ Date  : chr  "27/10/11" "28/10/11" "31/10/11" "01/11/11" ...
##  $ ibm   : num  0.02126 0.00841 -0.01516 -0.01792 0.01407 ...
##  $ lenovo: num  -0.00698 -0.02268 -0.04022 -0.00374 0.07641 ...
##  $ apple : num  0.010158 0.000642 -0.00042 -0.020642 0.002267 ...
##  $ amazon: num  0.04137 0.04972 -0.01769 -0.00663 0.01646 ...
##  $ yahoo : num  0.02004 -0.00422 -0.05716 -0.04646 0.01132 ...
##  $ nasdaq: num  0.032645 -0.000541 -0.019456 -0.029276 0.012587 ...
##  $ gold  : num  -0.023184 0.006459 0.030717 0.043197 -0.000674 ...
##  $ SP    : num  0.033717 0.000389 -0.025049 -0.02834 0.015976 ...
##  $ rate  : num  0.0836 -0.0379 -0.0585 -0.0834 0.0025 ...

Nel seguito considereremo nasdaq come la nostra variabile dipendente.

9.1 Test di Kolmogorov-Smirnov

Il test confronta la funzione di ripartizione empirica $F_n(t)$ (ECDF, si veda il paragrafo 7.2) con la funzione di ripartizione teorica $F(t)$ di una variabile casuale continua i cui parametri sono noti. La statistica test è data dalla distanza in valore assoluto tra le due funzioni: \[ D_n=\sup_t |F_n(t)-F(t)| \]

Sotto l’ipotesi nulla di ugualinza delle due funzioni ci aspettiamo un valore relativamente basso di $D_n$. In R la funzione ks.test(x,y,...) può essere utilizzata per il test di Kolmogorov-Smirnov. I seguenti input devono essere specificati:

x è il vettore di dati di cui verificare la normalità;
y è “character string naming a cumulative distribution function or an actual cumulative distribution function”. Di fatto è una stringa di testo che definisce la funzione teorica utilizzata $F(t)$. In R ci si riferisce alle funzioni che definiscono le CDF come ad esempio pnorm, plnorm.
… è per i parametri della distribuzione specificata con y (per esempio mean e sd se si usa pnorm).

In realtà l’utilizzo della funzione ks.test può dar luogo a un problema qualora i parametri della distribuzione non siano noti e debbano essere stimati. Come riportato nell’help della funzione “the parameters specified in … must be pre-specified and not estimated from the data”. Il punto è che quando si utilizzano i dati per stimare i parametri della distribuzione, la statistica test $D_n$ risulta essere più “vicina” all’ipotesi nulla rispetto al caso in cui i parametri della distribuzione sono noti. Ciò si traduce in un incremento della probabilità dell’errore di secondo tipo (ovvero della probabilità di non rifiutare $H_0$ quando non è vera). Si veda ad esempio il seguente caso di 200 valori simulati da una variabile casuale Uniforme(0,1) (si veda qui per la definizione di VC Uniforme) utilizzando la funzione runif:

set.seed(4)
x = runif(200)
hist(x)

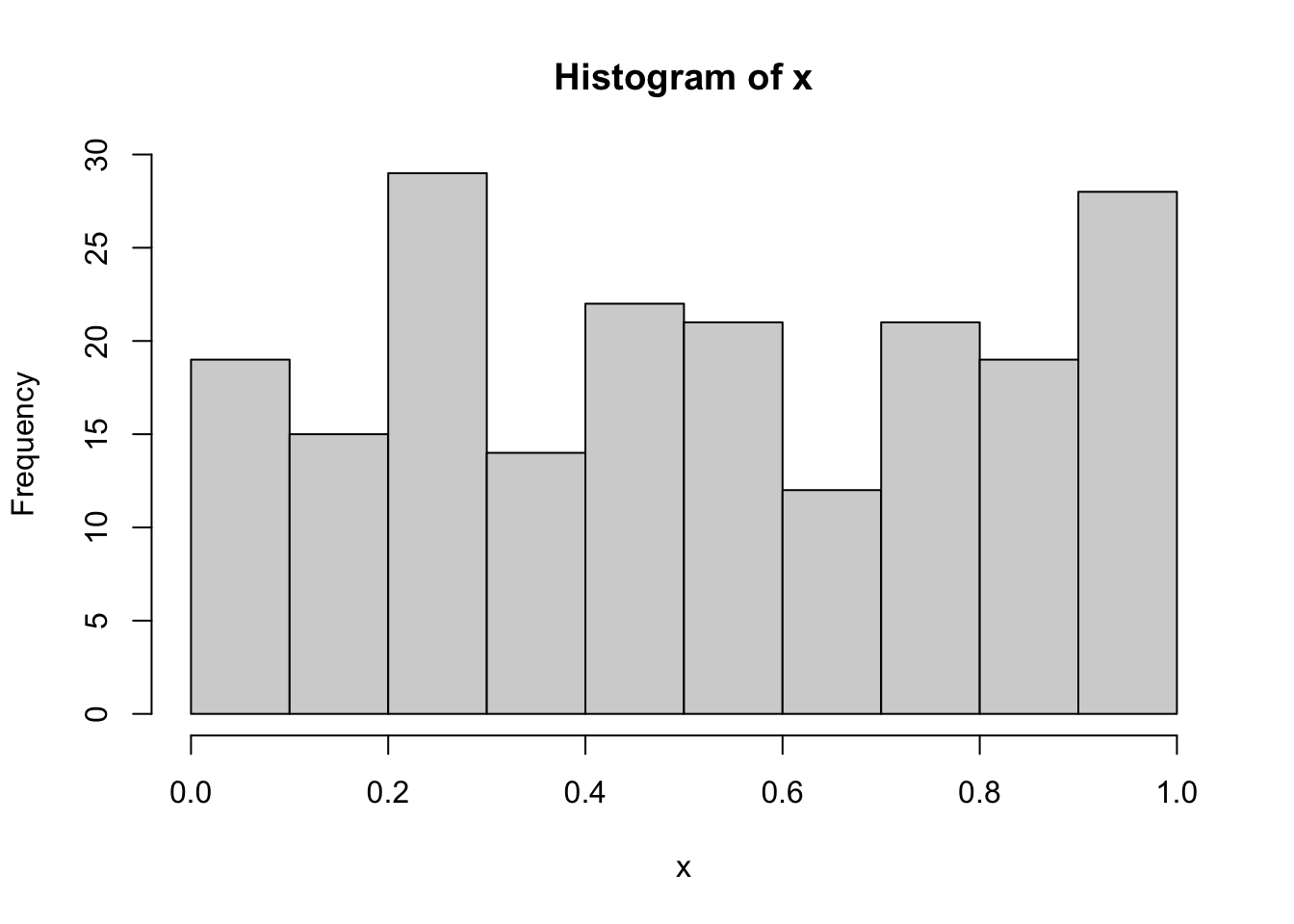
I dati non sono sicuramente normalmente distribuiti, essendo stati generati da una VC Uniforme. Eppure quando si va ad utilizzare la funzione ks.test utilizzando la media e varianza campionaria come stime dei parametri della normale

ks.test(x, "pnorm",
        mean=mean(x),
        sd=sd(x))

## 
## 	One-sample Kolmogorov-Smirnov test
## 
## data:  x
## D = 0.089686, p-value = 0.08011
## alternative hypothesis: two-sided

si ottiene un p-value pari a 0.0801094. Considerando una soglia $\alpha= 0.05$, si conclude che i dati non suggeriscono di rifiutare l’ipotesi nulla (e ovviamente questa è una decisione sbagliata).

Per superare questo problema è possibile usare la funzione corretta del test di Kolmogorov-Smirnov implementato nella funzione LcKS contenuta nella libreria KScorrect (che deve essere installata e caricata):

library(KScorrect)
ks2 = LcKS(x,"pnorm")
ks2$p.value

## [1] 0.001

In questo caso il p-value porta a rifiutare, correttamente, l’ipotesi di normalità.

Si consideri ora una delle variabili quantitative continue contenute nel dataframe datareg e se ne verifichi l’ipotesi di normalità:

nasdaq_KS = LcKS(datareg$ibm,"pnorm")
nasdaq_KS$p.value

## [1] 2e-04

Dato il valore del p-value praticamente nullo si va a rifiutare l’ipotesi di normalità. La conclusione è coerente con quanto emerge dai seguenti grafici:

plot(density(datareg$ibm))

qqnorm(datareg$ibm, datax=T)
qqline(datareg$ibm, datax=T)

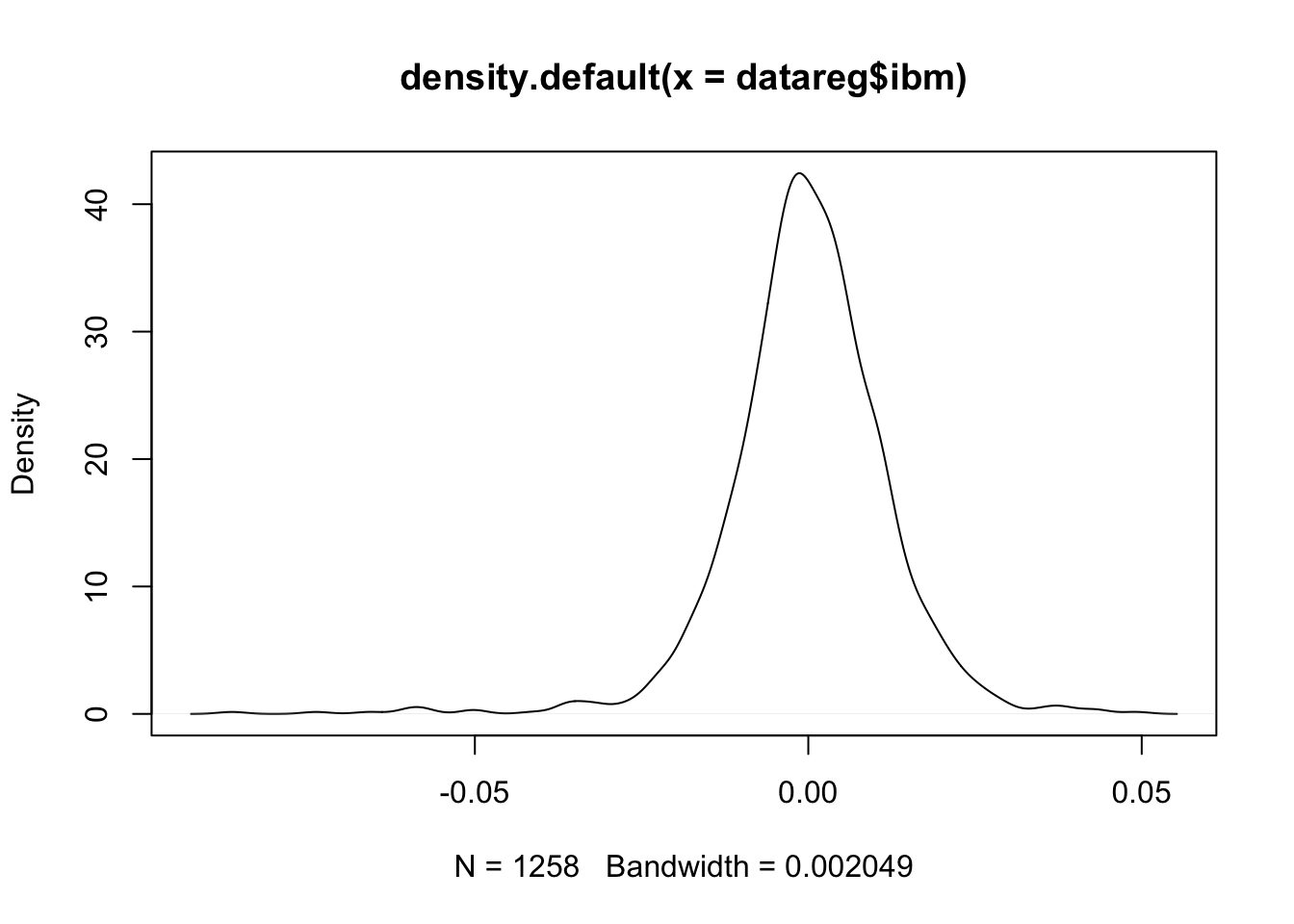
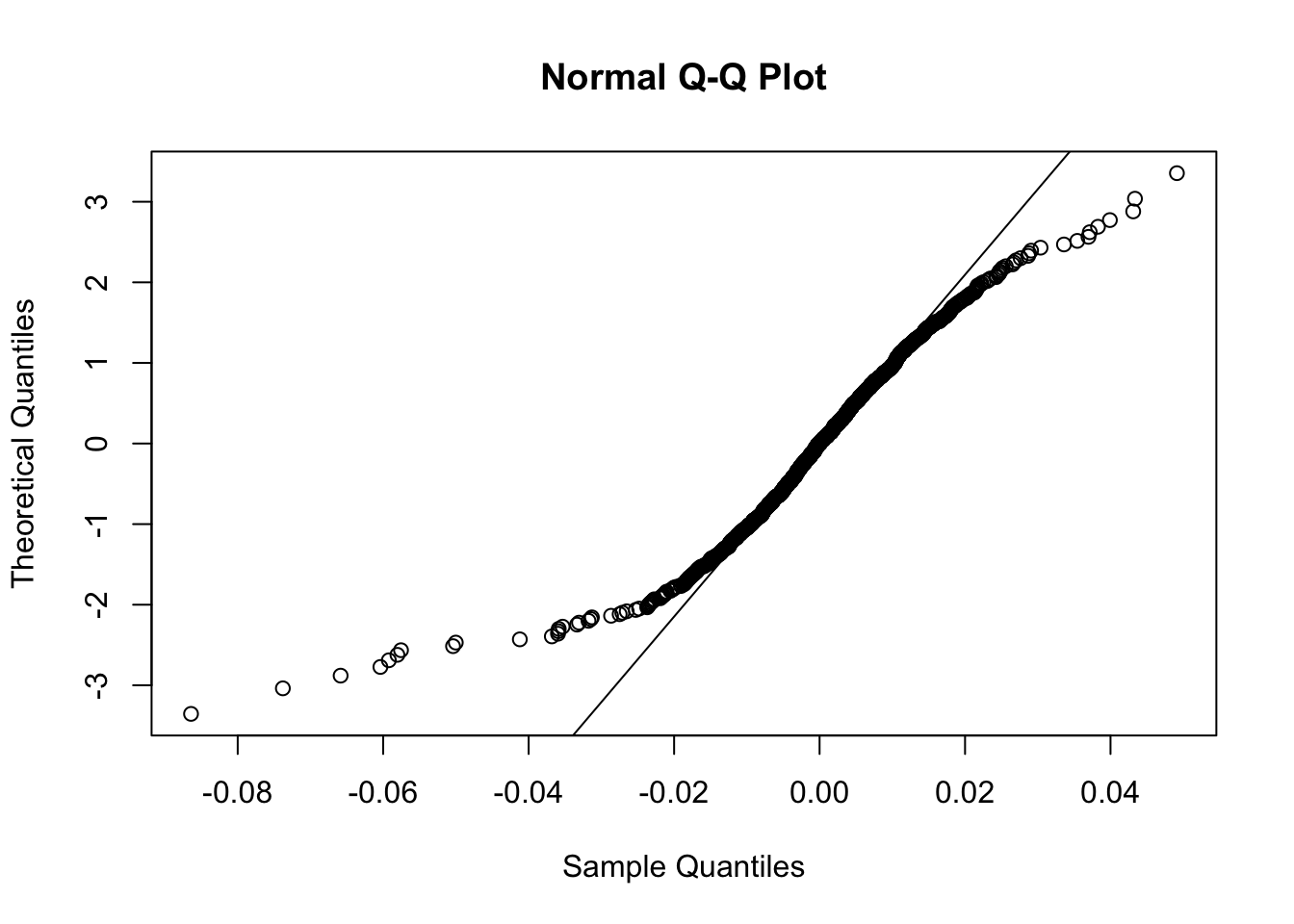
9.2 Modello di regressione lineare semplice

9.2.1 Covarianza e correlazione

La relazione lineare esistente tra due variabili quantitative può essere studiata utilizzando un grafico a dispersione (scatterplot); inoltre gli indici di covarianza e correlazione possono aiutare nel quantificare la forza del legame lineare. Il seguente codice può essere utilizzato per rappresentare nello stesso grafico due variabili (ibm - variabile indipendente - e nasdaq - variabile dipendente):

plot(datareg$ibm, datareg$nasdaq)

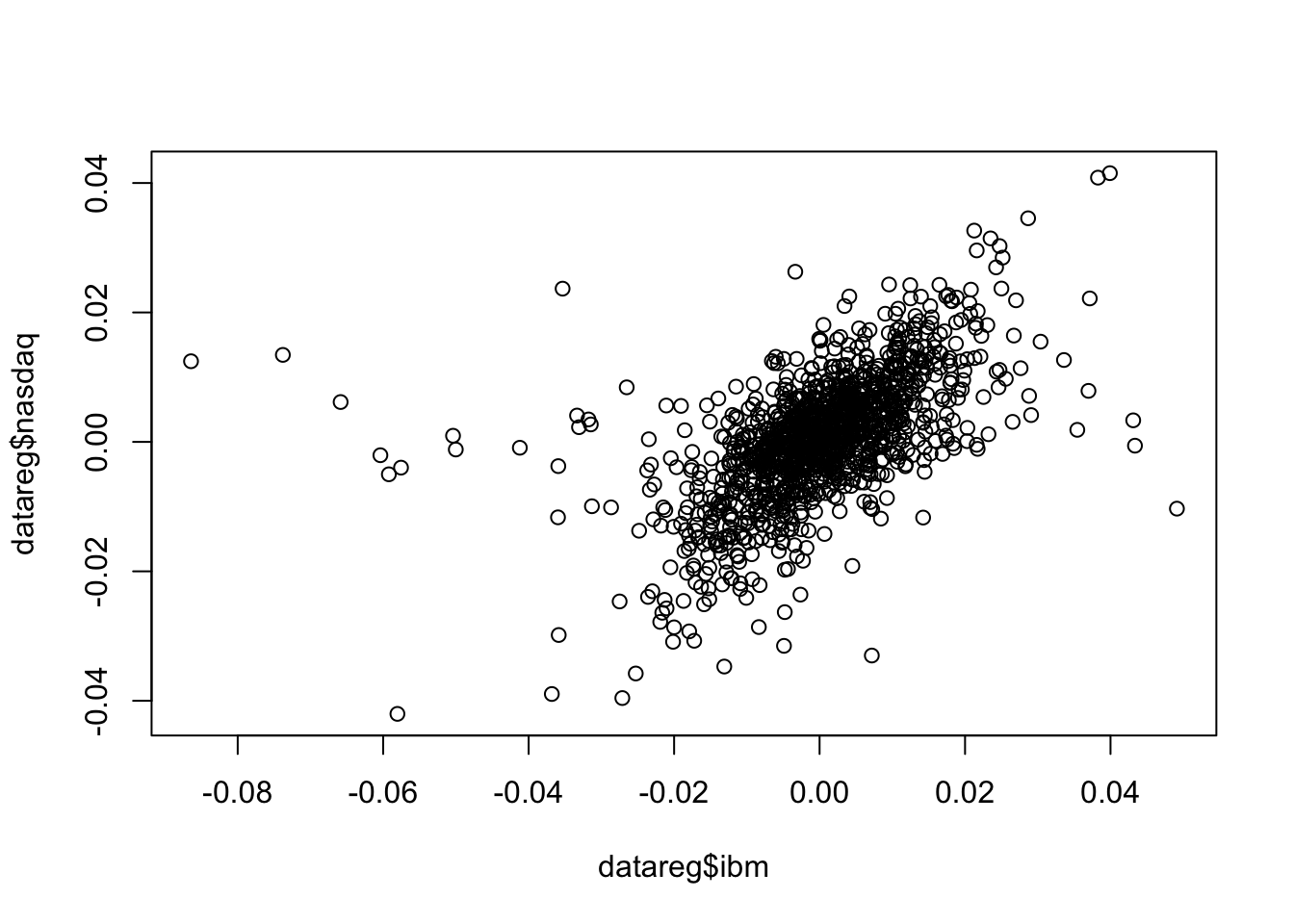
Dall’andamento della nuvola di punti emerge che tra le due variabile esiste una relazione positiva (all’aumentare/diminuire di una variabile ci si aspetta un cambiamento concorde anche per l’altra variabile). Nel grafico si osserva anche dipendenza delle code (alti/bassi valori di ibm si verificano congiuntamente ad alti/bassi valori di nasdaq). Allo stesso tempo per alcune osservazioni si può parlare di indipenza delle code (si vedano in particolare i punti a sinistra del grafico corrispondenti a valori estremamente negativi per ibm per i quali corrispondono valori positivi o vicini a zero per nasdq). Le funzioni cov e cor possono essere utilizzate per il calcolo degli indici di covarianza e correlazione:

cov(datareg$ibm, datareg$nasdaq)

## [1] 6.783533e-05

cor(datareg$ibm, datareg$nasdaq)

## [1] 0.5742862

Entrambi gli indici sono positivi, come ci si aspettava dato il grafico. In particolare, il valore 0.57 rappresenta un livello medio di correlazione (positiva) esistente tra le due variabili. Si ricordi infatti che l’indice di correlazione è compreso tra -1 e +1.

E’ anche possibile considerare tutte le variabili insieme e calcolare la matrice di varianza-covarianza e la matrice di correlazion utilizzando nuovamente le funzioni cov(x) e cor(x), dove in questo caso x rappresenta un dataframe o una selezione delle sue colonne. Prima di procedere è necessario rimuovere la prima colonna del dataframe che contiene le date (e che non è un carattere quantitativo). Andiamo in particolare a sovrascrivere l’oggetto datareg con un nuovo dataframe con una colonna in meno (si selezionano tutte le colonne tranne la prima):

datareg = datareg[,-1] 
cov(datareg) #matrice di varianza-covarianza

##                  ibm       lenovo        apple        amazon        yahoo
## ibm     1.440880e-04 5.018175e-05 6.154061e-05  6.708451e-05 5.879838e-05
## lenovo  5.018175e-05 5.243653e-04 5.723924e-05  7.734088e-05 9.423343e-05
## apple   6.154061e-05 5.723924e-05 2.750300e-04  7.906427e-05 7.324756e-05
## amazon  6.708451e-05 7.734088e-05 7.906427e-05  3.869414e-04 1.287336e-04
## yahoo   5.879838e-05 9.423343e-05 7.324756e-05  1.287336e-04 3.281435e-04
## nasdaq  6.783533e-05 7.653079e-05 9.610814e-05  1.105234e-04 9.789117e-05
## gold   -1.043981e-05 1.450081e-05 1.706496e-06 -1.298227e-05 7.818512e-06
## SP      6.406188e-05 6.842926e-05 7.147921e-05  8.565277e-05 7.978556e-05
## rate    7.738766e-05 1.000652e-04 8.378584e-05  8.419878e-05 9.519658e-05
##               nasdaq          gold            SP          rate
## ibm     6.783533e-05 -1.043981e-05  6.406188e-05  7.738766e-05
## lenovo  7.653079e-05  1.450081e-05  6.842926e-05  1.000652e-04
## apple   9.610814e-05  1.706496e-06  7.147921e-05  8.378584e-05
## amazon  1.105234e-04 -1.298227e-05  8.565277e-05  8.419878e-05
## yahoo   9.789117e-05  7.818512e-06  7.978556e-05  9.519658e-05
## nasdaq  9.683385e-05 -3.823920e-06  8.037427e-05  9.373488e-05
## gold   -3.823920e-06  6.049650e-04 -7.393048e-08 -2.435893e-05
## SP      8.037427e-05 -7.393048e-08  7.410393e-05  8.577946e-05
## rate    9.373488e-05 -2.435893e-05  8.577946e-05  5.306421e-04

cor(datareg) #matrice di correlazione

##               ibm     lenovo       apple      amazon      yahoo      nasdaq
## ibm     1.0000000 0.18256390 0.309141875  0.28410946 0.27040797  0.57428618
## lenovo  0.1825639 1.00000000 0.150725539  0.17169970 0.22717272  0.33962969
## apple   0.3091419 0.15072554 1.000000000  0.24236375 0.24382108  0.58892032
## amazon  0.2841095 0.17169970 0.242363747  1.00000000 0.36127453  0.57097612
## yahoo   0.2704080 0.22717272 0.243821083  0.36127453 1.00000000  0.54915892
## nasdaq  0.5742862 0.33962969 0.588920320  0.57097612 0.54915892  1.00000000
## gold   -0.0353601 0.02574602 0.004183599 -0.02683262 0.01754798 -0.01579902
## SP      0.6199620 0.34713968 0.500690167  0.50582255 0.51164856  0.94881773
## rate    0.2798703 0.18969900 0.219320776  0.18581568 0.22813327  0.41351071
##                 gold            SP        rate
## ibm    -0.0353601041  0.6199619759  0.27987034
## lenovo  0.0257460172  0.3471396840  0.18969900
## apple   0.0041835993  0.5006901672  0.21932078
## amazon -0.0268326183  0.5058225541  0.18581568
## yahoo   0.0175479795  0.5116485609  0.22813327
## nasdaq -0.0157990161  0.9488177268  0.41351071
## gold    1.0000000000 -0.0003491707 -0.04299245
## SP     -0.0003491707  1.0000000000  0.43257539
## rate   -0.0429924489  0.4325753882  1.00000000

Si noti che entrambe le matrici hanno dimensione 9X9 e sono simmetriche (e quindi ad esempio $Cor(ibm,nasdaq)=Cor(nasdaq,ibm)$ matrix. Inoltre, i valori sulla diagonale principale della matrice di correlazione sono uguali a uno.

E’ possibile anche rappresentare graficamente tutte le variabili a coppie di due. Il comando pairs(x) (dove x rappresenta un dataframe o una selezione delle sue colonne) permette di ottenere una matrice di scatterplot (di dimensione 9X9):

pairs(datareg)

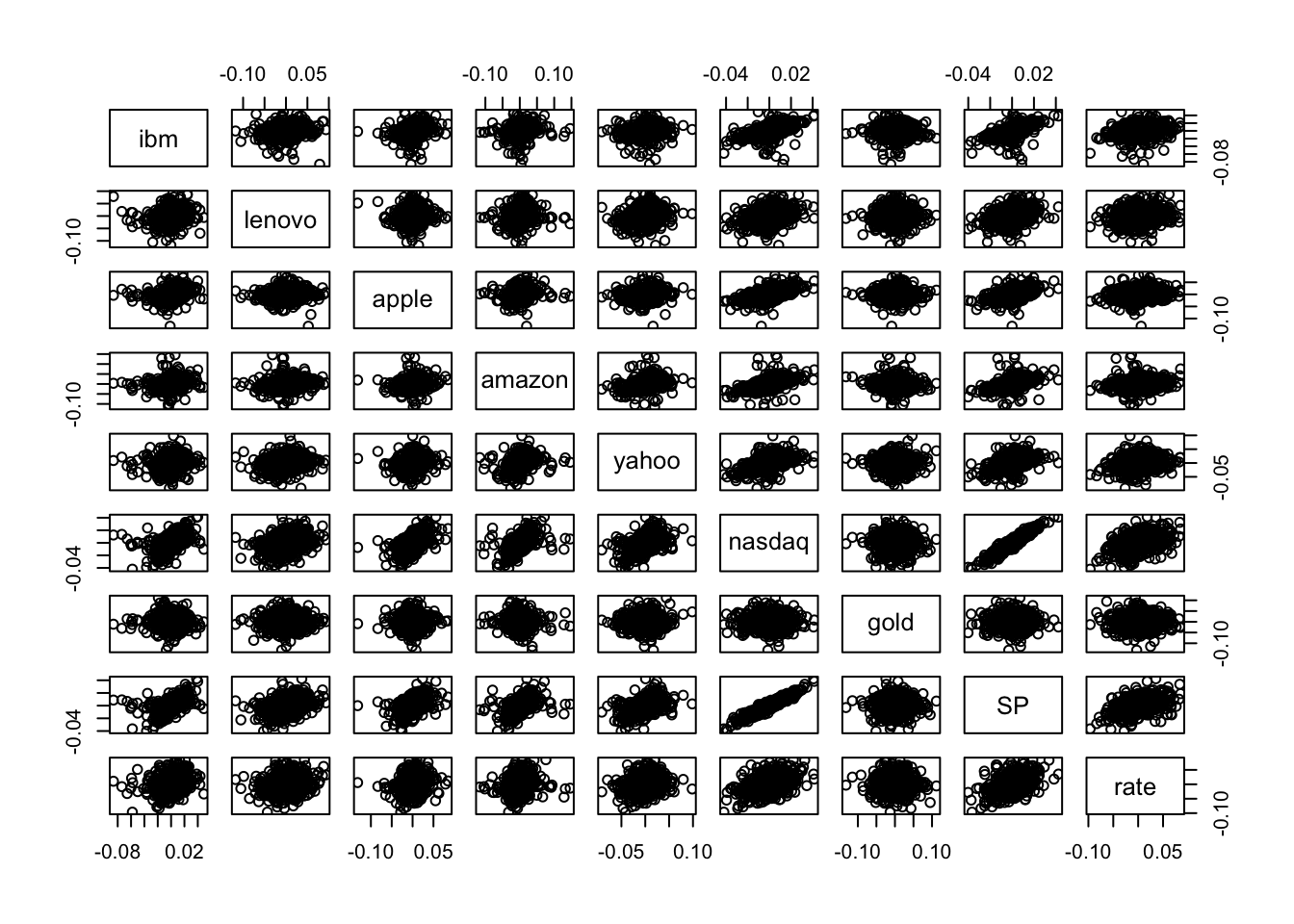
Si noti che la matrice di scatterplot non è simmetrica. Ad esempio il grafico in seconda riga e prima colonna non è uguale al grafico in prima riga e seconda colonna: gli assi infatti sono scambiati; nel primo grafico lenovo è sull’asse delle y, mentre nel secondo grafico è rappresentato sull’asse delle x).

Nella matrice degli scatterplot solamente due grafici presentano una nuvola dei punti molto “stretta”, sintomo di una forte relazione lineare: si tratta dei grafici riferiti a nasdaq e SP. Come riportato anche nella matrice di correlazione, l’indice di correlazione tra queste due variabili è pari a

cor(datareg$nasdaq,datareg$SP)

## [1] 0.9488177

Essendo questa la variabile maggiormente correlata con la variabile dipendente nasdaq, utilizzeremo SP come regressore nel modello di regressione lineare che andremo a stimare qui di seguito.

9.2.2 Simple linear regression model

Si consideri nasdq come variabile risposta (dipendente) e SP come variabile indipendente (o covariata o regressore); in questo caso quindi il numero di regressori è $p=1$. L’equazione del modello di regressione linear è \[ Y = \beta_0+\beta_1 X + \epsilon \] dove $\beta_0$ è l’intercetta e $\beta_1$ la pendenza. Il termine $\epsilon$ rappresenta l’errore a media nulla e varianza pari a $\sigma^2_\epsilon$.

La funzione da utilizzare in R per la stima del modello lineare è lm (linear model):

lm(nameofy ~ nameofx, data=nameofdataframe)

Il simbolo $\sim$ (tilde) si può ottenere come segue:

Mac: digitare ALT e 5
Windows con tastierino numerico: digitare ALT (tenere premuto) 1, 2 e 6 (in sequenza)
Windows senza tastierino numerico: digitare ALT Fn (tenere premuto) e 1, 2, 6 (in sequenza)

Nel caso in esame si procede come segue

mod1 = lm(nasdaq ~ SP, data=datareg)

L’oggetto mod1 è una lista contenente i seguenti 12 oggetti:

names(mod1)

##  [1] "coefficients"  "residuals"     "effects"       "rank"         
##  [5] "fitted.values" "assign"        "qr"            "df.residual"  
##  [9] "xlevels"       "call"          "terms"         "model"

In particolare siamo interessati ai seguenti oggetti di mod1:

le stime dei minimi quadrati $\hat\beta_0$ e $\hat \beta_1$:

mod1$coefficients

##  (Intercept)           SP 
## 7.443203e-05 1.084615e+00

La stima della pendenza (1.085) indica che ad un aumento unitario del rendimento logaritmico di SP ci si aspetta un aumento pari a 1.085 per i rendimenti logaritmici di nasdaq. Il modello stimato $\hat y=\hat\beta_0+\hat\beta_1 x$ (retta con pendenza crescente) si può anche rappresentare graficamente come segue:

plot(datareg$SP, datareg$nasdaq)
abline(mod1,col="red",lwd=2)

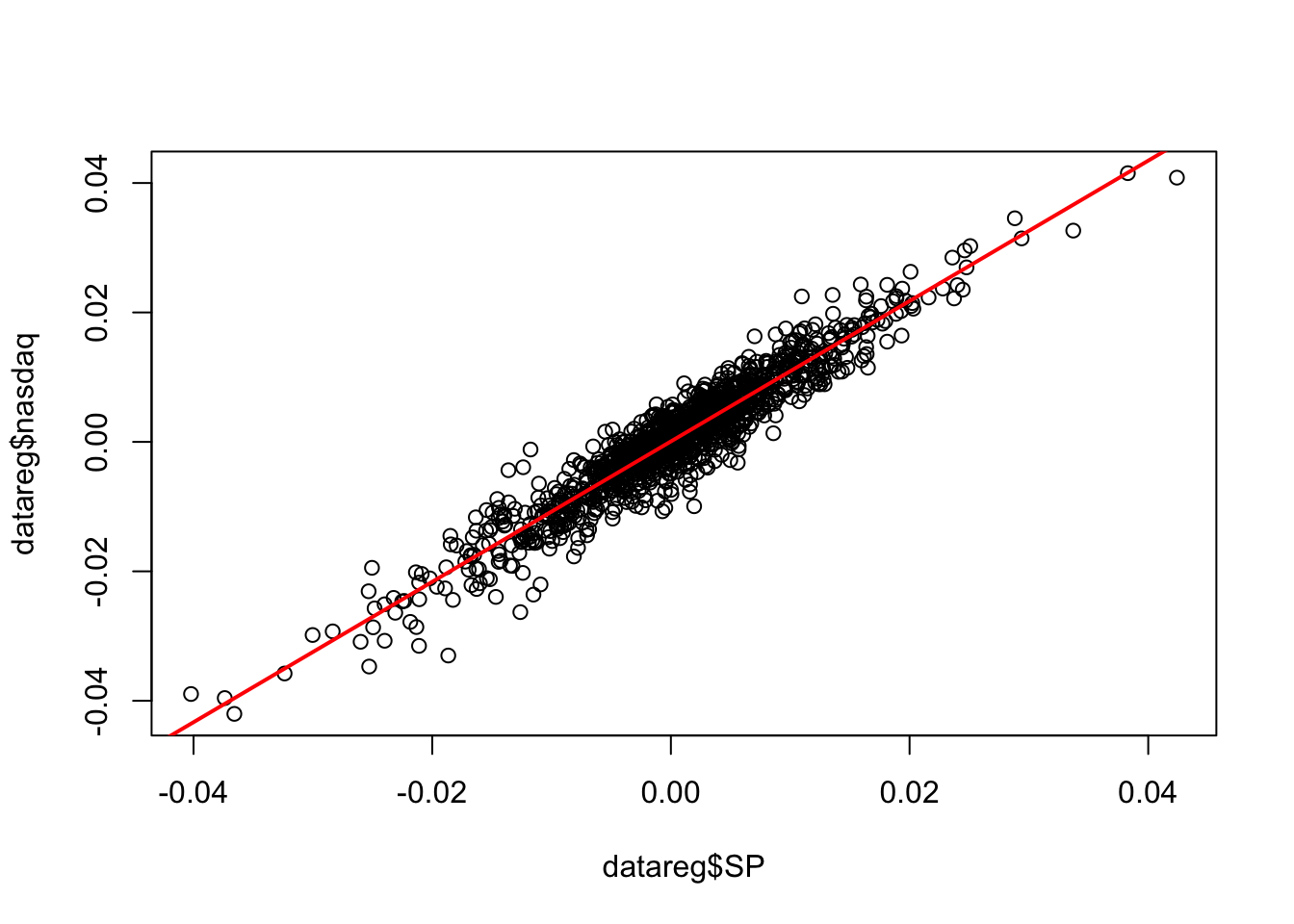
i valori fittati della variabile risposta (o previsti secondo il modello stimato) sono dati da $\hat y_i=\hat\beta_0+\hat\beta_1 x_i$ ($i=1,\ldots,n$ con $n=$1258) e si ottengono come segue:

head(mod1$fitted.values)

##             1             2             3             4             5 
##  0.0366439651  0.0004965144 -0.0270936832 -0.0306636329  0.0174026410 
##             6 
##  0.0202565287

i residui calcolati come differenza tra valori osservati e valori previsti: $y_i -\hat y_i$ ($i=1,\ldots,n$ con $n=$1258):

head(mod1$residuals)

##            1            2            3            4            5            6 
## -0.003998621 -0.001037069  0.007637417  0.001387478 -0.004816084  0.001471765

Tutte le informazioni importanti relative al modello di regressione si possono ottenere usando la funzione summary:

summary(mod1)

## 
## Call:
## lm(formula = nasdaq ~ SP, data = datareg)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0128494 -0.0018423  0.0002159  0.0020178  0.0115080 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 7.443e-05  8.777e-05   0.848    0.397    
## SP          1.085e+00  1.019e-02 106.471   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.003109 on 1256 degrees of freedom
## Multiple R-squared:  0.9003,	Adjusted R-squared:  0.9002 
## F-statistic: 1.134e+04 on 1 and 1256 DF,  p-value: < 2.2e-16

Nella parte centrale dell’output di summary (denominata Coefficients) sono riportate le seguenti informazioni:

Estimate (stime dei minimi quadrati) ($\hat \beta_0$ indicato con (Intercept) e $\hat \beta_1$ indicato con SP);
Std.Error (errore standard): stima della standard deviation di $\hat\beta_0$ e $\hat\beta_1$ (questa è una misura di precisione delle stime);
t.value: valore della statitica test del test t ottenuto come rapporto tra Estimate e Std.Error. E’ una realizzazione della VC t di Studente con $n-p-1$=nrow(datareg)-2 gradi di libertà;
Pr(>|t|): questa probabilità corrisponde al p-value del test t che verifica la nullità del coefficiente.

Nel caso considerato si rifiuta l’ipotesi $H_0:\beta_1=0$ (quindi SP è un regressore significativo) ma non si rifiuta l’ipotesi $H_0:\beta_0=0$ (ma in ogni caso teniamo l’intercetta nel modello anche se può essere considerata pari a zero).

9.2.3 Scomposizione della devianza

Nel seguito vengono introdotte le quantità (somme dei quadrati) relative alla scomposizione della devianza della variabile dipendente ($SST=SSR+SSE$); si veda anche la Figura 9.1 per le relative formule.

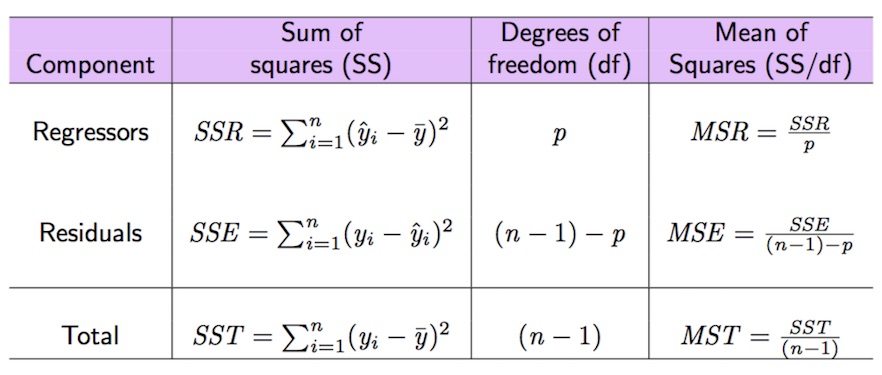
Figure 9.1: Quantità notevoli della scomposizione della devianza della variabile dipendente

La variabilità totale di nasdaq è data da $SST$ (somma totale dei quadrati) che può essere calcolata come segue:

SST = sum((datareg$nasdaq - mean(datareg$nasdaq)) ^2)
SST

## [1] 0.1217202

La somma dei quadrati degli errori SSE si calcola come segue:

SSE = sum(mod1$residuals^2)
SSE

## [1] 0.01214097

#SSE = sum((datareg$nasdaq-mod1$fitted.values)^2)

Dato che $SST=SSR+SSE$, $SSR$ si ottiene come segue:

SSR = SST-SSE
#SSR=sum((mod1$fitted.values-mean(datareg$nasdaq))^2)

Date queste tre quantità notevoli è possibile calcolare l’indice di bontà di adattamento $R^2$ dato dal rapporto tra $SSR$ e $SST$ (essendo una parte sul totale si ottiene un numero compreso tra zero e uno):

SSR/SST

## [1] 0.9002551

1-SSE/SST

## [1] 0.9002551

In questo caso si ottiene che il SSR/SST*100% della variabilità totale di nasdaq è spiegata da SP. Considerando che il range dell’indice $R^2$ è l’intervallo $[0,1]$: si conclude quindi che in questo caso il modello ha un’ottima performance. Si noti che l’indice $R^2$ è riportato anche nell’output della funzione summary come Multiple R-squared: 0.9003.

Tutte le quantità notevoli introdotte qui sopra e riportate anche in Figura 9.2 possono essere ottenute utilizzando la funzione anova:

anova(mod1)

## Analysis of Variance Table
## 
## Response: nasdaq
##             Df   Sum Sq Mean Sq F value    Pr(>F)    
## SP           1 0.109579 0.10958   11336 < 2.2e-16 ***
## Residuals 1256 0.012141 0.00001                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1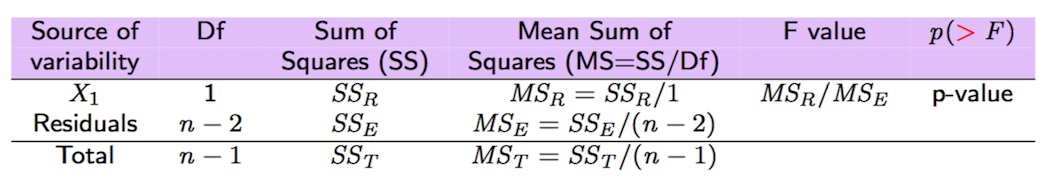

Figure 9.2: Tabella Anova con test F

9.2.4 Test F

Il test F riportato nell’output della funzione anova considera, nel caso in esame con $p=1$, le seguenti ipotesi: $H_0: \beta_1=0$ vs $H_0: \beta_1\neq 0$. La corrispondente statistica test è data dalla seguente formula: \[ \text{F-value}=\frac{SS_R/1}{SS_E/(n-2)}=\frac{MS_R}{MS_E} \]

che si distribuisce come una VC F di Fisher (si veda qui) con 1 e $n-2$ gradi di libertà. Ci si aspetta un valore elevato della statistica test se il regressore è altamente significativo. Nel caso di regressione lineare semplice ($p=1$) il test F porta alla stessa conclusione del test t effettuato sul coefficiente $\beta_1$ dell’unico regressore incluso nel modello. Infatti, dato il valore praticamente null del p-value riportato nell’output di anova si può concludere, come già fatto in precedenza, che SP è un regressore significativo e che esiste una relazione lineare significativa tra le due variabili. Si noti che l’output del test F è riportato anche nell’output della funzione summary (si veda l’ultima riga: F-statistic: 1.134e+04 on 1 and 1256 DF, p-value: < 2.2e-16).

9.2.5 Stima della varianza dell’errore

La stima della varianza dell’errore $\sigma^2_\epsilon$ è data da $\hat\sigma^2_\epsilon=\frac{SSE}{n-p-1}$ e può essere calcolata come segue

SSE/(nrow(datareg)-length(mod1$coefficients))

## [1] 9.666375e-06

La corrispondente stima di $\sigma_\epsilon$ (standard error)

sqrt(SSE/(nrow(datareg)-2))

## [1] 0.003109079

è riportata anche nell’output di summary con la dicitura Residual standard error: 0.003109 on 1256 degrees of freedom.

9.3 Esercizi Lab 7

9.3.1 Esercizio 1

I dati nel file prices_5Y.csv si riferiscono ai prezzi (Adj.Close) per il periodo 05/11/2012-03/11/2017 e per i seguenti titoli: Apple (AAPL), Intel (INTC), Microsoft (MSFT) e Google (GOOGL). Importare i dati in R.

Rappresentare graficamente la serie storica di GOOGL (usare le date sull’asse delle x). Commentare il grafico.
Creare un nuovo data frame che contiene i rendimenti netti per tutti i titoli.
Rappresentare graficamente la serie storica dei rendimenti netti di GOOGL (si riportino sull’asse delle x le date. Attenzione che avrete bisogno di eliminare la prima data). Commentare il grafico
Utilizzare il normal probability plot ed il test di Kolmogorov-Smirnov per studiare la normalità dei rendimenti netti di GOOGL. Commentare.
Si considerino nuovamente tutte le variabili. Calcolare la matrice di correlazione e commentarne i valori.
Costruire la matrice degli scatterplot e commentare la dipendenza-indipendenza delle code per la coppia GOOGL-MSFT.
Stimare il modello di regressione lineare semplice che considera GOOGL come variabile dipendente e MSFT come variabile indipendente. Commentare il valore della pendenza.
Rappresentare graficamente le due variabili insieme alla retta di regressione dei minimi quadrati.
Calcolare le seguenti quantità notevoli: SST, SSE, SSR.
E’ possibile usare una funzione di R per calcolare SSE, SSR e SST?
Determinare, in 4 modi diversi, il coefficiente $R^2$ e commentare il valore della bontà di adattamento della retta ai dati.
Calcolare la stima della varianza degli errori $\sigma^2$.
Stimare il rendimento netto di GOOGL qualora il rendimento netto di MSFT sia pari a 0.0007.
Come cambierebbe la correlazione tra GOOGL e MSFT se si usassero i lordi anzichè i rendimenti netti? E la pendenza della retta come cambierebbe?