13  Erwartungswerttests

Das allgemeine Vokabular aus Kapitel 12.2 wird leichter verständlich, wenn man konkrete Tests im Detail durchspielt. In diesem Abschnitt sehen wir uns mehrere Variationen von Tests für Erwartungswerte an.

13.1 t-Test

Der t-Test (engl. t-test) ist ein Test für den unbekannten Erwartungswert \(\mu\) einer Zufallsvariable \(X\). Wir gehen zunächst davon aus, dass wir nichts weiter über die Verteilung von \(X\) wissen. Das ist offensichtlich eine sehr realistische Annahme Die Null- und Alternativhypothesen des zweiseitigen t-Tests lauten

\[\begin{align*} H_0: \mu&=\mu_0\\ H_1: \mu&\neq\mu_0. \end{align*}\]

Dabei ist \(\mu_0\in\mathbb{R}\) der (hypothetische) Wert, gegen den getestet werden soll. Um etwas über den Erwartungswert zu lernen, bietet es sich an, eine Stichprobe \(X_1,\ldots,X_n\) aus \(X\) zu ziehen und das Stichprobenmittel \(\bar X\) zu berechnen. Wenn das Stichprobenmittel “weit weg” von \(\mu_0\) liegt, spricht das gegen die Nullhypothese. Was aber ist mit “weit weg” gemeint? Um das zu beantworten, brauchen wir Informationen darüber, wie sehr das Stichprobenmittel um den wahren Erwartungswert herum streut. Dafür berechnen wir die Stichprobenstandardabweichung \(S\) (oder die Stichprobenvarianz \(S^2\)).

Aus dem zentralen Grenzwertsatz (Kapitel 8.3) folgt, dass bei großen Stichproben approximativ \[ \sqrt{n}\frac{\bar X-\mu}{S}\sim N(0,1) \] gilt (da die Approximation für große \(n\) sehr genau ist, wird im folgenden nicht mehr jedesmal extra darauf hingewiesen, dass es sich nur um eine Approximation handelt). Die Formel hilft jedoch nicht weiter, weil \(\mu\) unbekannt ist. Nun folgt ein Trick: Unter der Nullhypothese ist der Erwartungswert bekannt! Er beträgt dann natürlich \(\mu_0\). Unter der Nullhypothese gilt also \[ \sqrt{n}\frac{\bar X-\mu_0}{S}\sim N(0,1). \] Diese Größe nutzen wir als Teststatistik, d.h. \[ T=\sqrt{n}\frac{\bar X-\mu_0}{S}. \] Da die Teststatistik unter der Nullhypothese einer Standardnormalverteilung folgt, liegt sie mit einer Wahrscheinlichkeit von \((1-\alpha)\) in dem Intervall \([-u_{1-\alpha/2},u_{1-\alpha/2}]\) (vgl. Kapitel 11). Für das typische Signifikanzniveau \(\alpha=0.05\) sind die Intervallgrenzen

alpha <- 0.05
-qnorm(1-alpha/2)

[1] -1.959964

qnorm(1-alpha/2)

[1] 1.959964

Der kritische Bereich ist also \[ K=(-\infty,-u_{1-\alpha/2}]\cup [u_{1-\alpha/2},\infty). \] Mit anderen Worten: Wenn die Nullhypothese gilt, dann ist es nicht weiter verwunderlich, wenn die Teststatistik in dem Intervall \([-1.96,1.96]\) liegt. Wenn die Teststatistik dagegen aus diesem Intervall herausfällt, dann spricht das (auf einem Signifikanzniveau von 5 Prozent) gegen die Gültigkeit der Nullhypothese. In diesem Fall verwirft man \(H_0\).

Die Wahrscheinlichkeit, dass die Nullhypothese abgelehnt wird, obwohl sie wahr ist, beträgt

\[\begin{align*} P(T\in K||H_0\text{ ist wahr}) &= P\left(T<-u_{1-\alpha/2})+P(T> u_{1-\alpha/2}\right)\\ &= P\left(T<-u_{1-\alpha/2})+1-P(T\le u_{1-\alpha/2}\right)\\ &= \frac{\alpha}{2}+1-\left(1-\frac{\alpha}{2}\right)\\ &= \alpha. \end{align*}\]

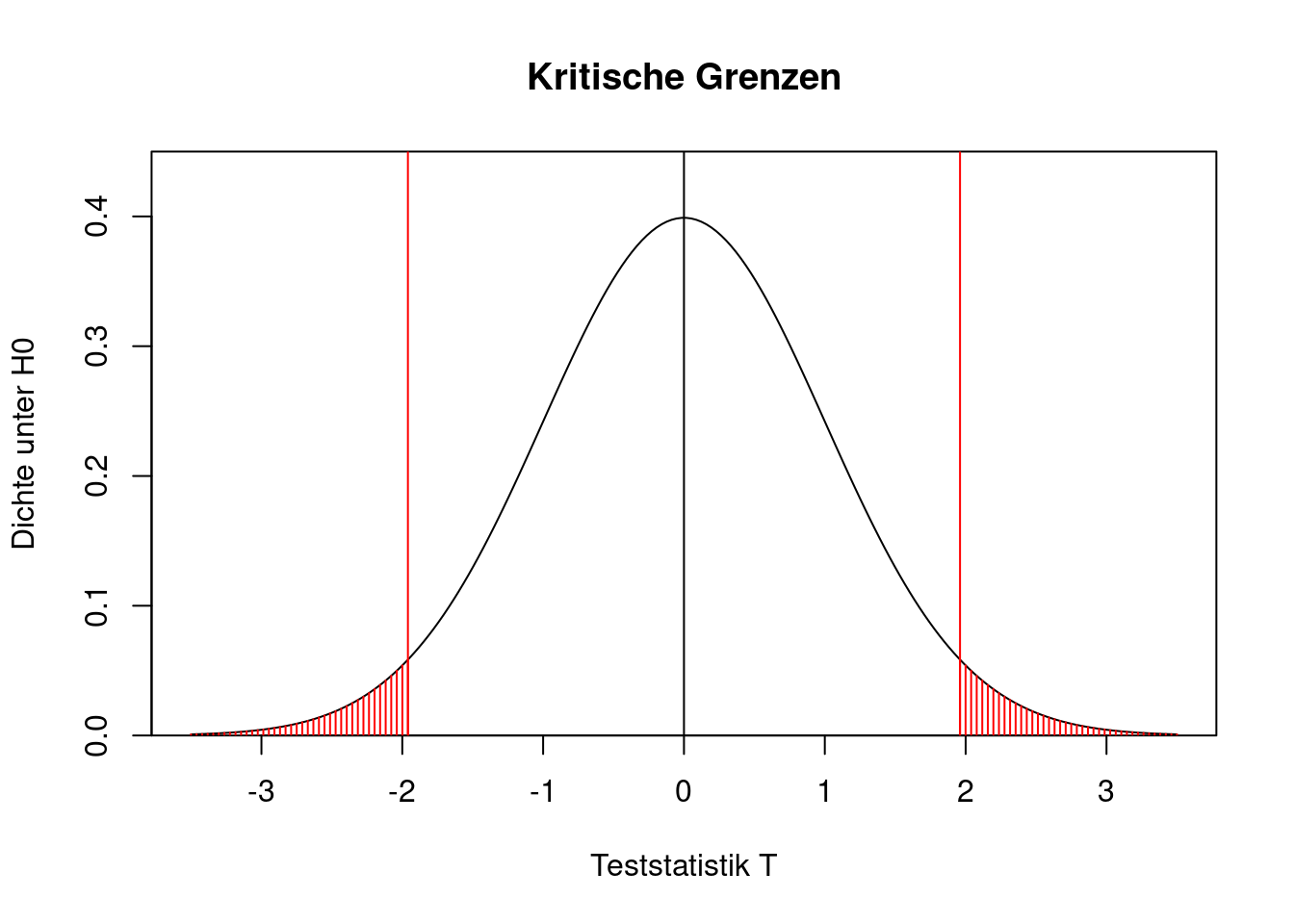
Die Fehlerwahrscheinlichkeit erster Art entspricht also in der Tat dem vorgegebenen Signifikanzniveau. Das lässt sich auch grafisch darstellen. In der folgenden Grafik sind die beiden kritischen Grenzen \(u_{0.025}\) und \(u_{0.975}\) durch die senkrechten roten Linien gekennzeichnet. Die rot schraffierte Fläche ist die Wahrscheinlichkeit, dass die Teststatistik unter \(H_0\) in den kritischen Bereich fällt. Sie setzt sich zusammen aus zwei Teilfläche mit jeweils 2.5 Prozent Wahrscheinlichkeit.

x <- seq(from=-3.5, to=3.5, length=200)
plot(x, dnorm(x),
     type="l",
     main="Kritische Grenzen",
     xlab="Teststatistik T",
     ylab="Dichte unter H0",
     yaxs="i", ylim=c(0,0.45))

abline(v=0)
abline(v=qnorm(c(0.025,0.975)),col="red")

for(x in seq(from=qnorm(0.975), to=3.5, length=40)){
  lines(c(x,x), c(0,dnorm(x)), col="red")
  lines(-c(x,x), c(0,dnorm(x)), col="red")
}

Wie bestimmt man den p-Wert des Tests? Dazu nehmen wir an, dass die Teststatistik \(T\) einen (positiven oder negativen) Wert \(t\) annimmt. Der p-Wert ist die Wahrscheinlichkeit, dass die Teststatistik unter der Nullhypothese “noch stärker” gegen \(H_0\) spricht als \(t\). Da wir einen zweiseitigen Test untersuchen, kann “noch stärker” heißen, dass die Teststatistik besonders klein oder besonders groß ist, d.h.

\[\begin{align*} \text{p-Wert}&=P(T < -|t| \text{ oder }T > |t|)\\ &= P(T< -|t|)+P(T>|t|)\\ &= P(T< -|t|)+1-P(T\le |t|)\\ &= \Phi(-|t|)+1-\Phi(|t|)\\ &= 1-\Phi(|t|)+1-\Phi(|t|)\\ &= 2(1-\Phi(|t|)). \end{align*}\]

Grafisch lässt sich das wie folgt veranschaulichen.

x <- seq(from=-3.5, to=3.5, length=200)
plot(x, dnorm(x),
     type="l",
     main="p-Wert",
     xlab="Teststatistik T",
     ylab="Dichte unter H0",
     yaxs="i", ylim=c(0,0.45))

abline(v=0)

mtext("|t|",1,0.5,at=1.5)
mtext("-|t|",1,0.5,at=-1.5)

lines(c(1.5,1.5), c(0,dnorm(1.5)), col="red", lwd=3)
lines(c(-1.5,-1.5), c(0,dnorm(1.5)), col="red", lwd=3)

for(x in seq(1.5,3.5,length=40)){
  lines(c(x,x), c(0,dnorm(x)),col="red")
  lines(-c(x,x), c(0,dnorm(x)),col="red")
}

text(-2.9,0.11,
     expression(Phi(-group("|",t,"|"))))
text(2.9,0.1,
     expression(1-Phi(group("|",t,"|"))))
arrows(-2.7,0.08,-2,0.03,length=0.1)
arrows(2.7,0.08,2,0.03,length=0.1)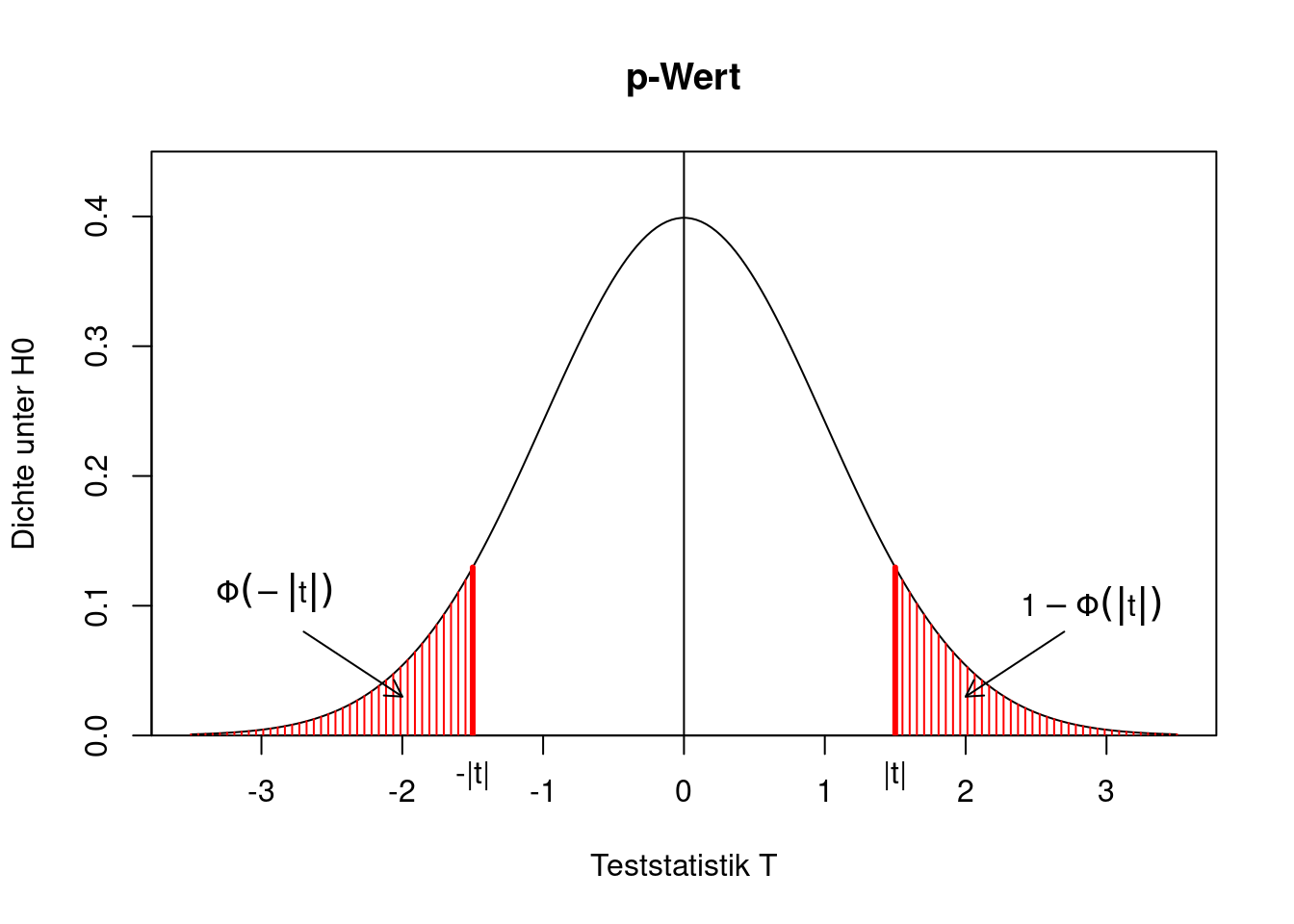

Wenn die gesamte rote Fläche kleiner als das Signifikanzniveau ist, spricht das gegen die Nullhypothese und man verwirft sie.

Beispiel: Versicherungsschäden

Um zu evaluieren, ob die Prämien für eine Hausratversicherung angemessen sind, will ein Versicherungsunternehmen testen, ob der Erwartungswert der Schäden \(\mu_0=25000\) Euro beträgt. Die Prämien sollen möglichst selten angepasst werden. Das Unternehmen möchte die Prämienhöhe nur anpassen, wenn der Erwartungswert signifikant von 25000 Euro abweicht. Als Signifikanzniveau setzt das Unternehmen \(\alpha=0.05\). Für die Evaluation wird eine einfache Stichprobe aus den Schadensmeldungen gezogen. Die Daten werden als Dataframe in R eingelesen. Aus dem Dataframe wird mit dem $-Zeichen die Schadensvariable herausgezogen und unter dem Namen schaden abgelegt.

daten <- read.csv("../data/versicherungsschaeden.csv")
schaden <- daten$schaden
mu0 <- 25000
alpha <- 0.05

Die konkrete Stichprobe schaden umfasst

n <- length(schaden)
print(n)

[1] 270

Schadensmeldungen. Die ersten Werte sind

head(schaden)

[1] 51603 31468 50127 20078 32118 12072

(die restlichen Werte 264 werden hier nicht abgedruckt).

Aus der konkreten Stichprobe schaden errechnet man das realisierte Stichprobenmittel

mean(schaden)

[1] 29609.24

und die realisierte Stichprobenstandardabweichung \(s\),

sd(schaden)

[1] 25020.17

(beide in Euro). Damit ergibt sich als Wert der Teststatistik

teststat <- sqrt(n) * (mean(schaden) - mu0)/sd(schaden)
teststat

[1] 3.027058

Das 0.975-Quantil der \(N(0,1)\) beträgt

qnorm(1-alpha/2)

[1] 1.959964

Der Wert der Teststatistik liegt also über dem oberen kritischen Wert. Die Nullhypothese wird abgelehnt. Die mittlere Schadenshöhe ist signifikant höher als 25000 Euro. Das Unternehmen sollte seine Prämienhöhe anpassen.

Beispiel: Test auf Anteil

Häufig geht man vereinfachend davon aus, dass Neugeborene mit einer Wahrscheinlichkeit von je 50 Prozent männlich bzw. weiblich sind. Ist diese Vereinfachung wirklich korrekt? Das soll für Münster überprüft werden. Kann man davon ausgehen, dass ein (zufällig ausgewähltes) in Münster neugeborenes Kind mit einer Wahrscheinlichkeit von 50 Prozent männlich ist? Das Geschlecht kann durch eine bernoulli-verteilte Zufallsvariable beschrieben werden (z.B. 0=weiblich, 1=männlich). Der unbekannte Parameter \(\pi\) ist dann die Wahrscheinlichkeit, dass ein Neugeborenes männlich ist. Die Hypothesen lauten

\[\begin{align*} H_0: \pi &= 0.5\\ H_1: \pi &\neq 0.5. \end{align*}\]

Als Signifikanzniveau setzen wir \(\alpha=0.01\). Um die Nullhypothese zu testen, werten wir Daten der Statistikabteilung der Stadt Münster zum Jahr 2021 aus. Dort findet man in der Jahres-Statistik 2021 (auf S. 106) die Angabe, dass im Jahr 2021 in Münster 1594 Jungen und 1431 Mädchen zur Welt kamen. Wir interpretieren das als Realisation einer einfachen Stichprobe vom Umfang 3025.

Das Stichprobenmittel \(\bar X\) entspricht bei einer Bernoulli-Verteilung dem Stichprobenanteil und wird meist mit \(\hat\pi\) notiert. Der Stichprobenanteil der Jungen ist etwas höher als 50 Prozent, nämlich \[ \hat\pi = \frac{1594}{3025}=0.52694. \] Die Stichprobenstandardabweichung kann im Fall der Bernoulli-Verteilung auch als \(\sqrt{\hat\pi(1-\hat\pi)}\) berechnet werden (anstelle von \(S\)). Damit ergibt sich als Teststatistik \[ T=\sqrt{n}\frac{\hat\pi-0.5}{\sqrt{\hat\pi(1-\hat\pi)}}. \] Als Wert der Teststatistik ergibt sich \[ t=\sqrt{3025}\cdot\frac{0.52694-0.5}{\sqrt{0.52694\cdot (1-0.52694)}} =2.9677. \] Die obere kritische Werte ist

alpha <- 0.01
qnorm(1-alpha/2)

[1] 2.575829

Da der Wert der Teststatistik die obere kritische Grenze überschreitet, wird die Nullhypothese verworfen. Im Jahr 2021 wich die Wahrscheinlichkeit einer Jungengeburt auf einem Niveau von 0.01 in Münster signifikant von 50 Prozent ab.

13.2 t-Test bei Normalverteilungen

In manchen Anwendungen weiß man, dass die Verteilung von \(X\) durch eine Normalverteilung modelliert werden kann. In so einer Situation ist die Verteilung der Teststatistik nicht nur approximativ, sondern exakt bekannt, und zwar selbst dann, wenn die Stichprobe klein ist. Wir haben in Kapitel 11.2 gesehen, dass für eine normalverteilte Population \(X\) gilt \[ \sqrt{n}\frac{\bar X-\mu}{S} \sim t_{n-1}, \] d.h. das standardisierte Stichprobenmittel folgt einer t-Verteilung mit \(n-1\) Freiheitsgraden. Das ist auch der Grund, warum man von einem t-Test spricht. Unter der Nullhypothese gilt \[ \sqrt{n}\frac{\bar X-\mu_0}{S} \sim t_{n-1}. \] Als Teststatistik dient daher \[ T=\sqrt{n}\frac{\bar X-\mu_0}{S}. \] Der kritische Bereich ist \[ K=(-\infty,-t_{n-1,1-\alpha/2}]\cup [t_{n-1,1-\alpha/2},\infty). \] Die Quantile sind abhängig vom Stichprobenumfang. Beispielsweise gilt für \(n=8\)

n <- 8
alpha <- 0.05
qt(1-alpha/2, df=n-1)

[1] 2.364624

Je kleiner \(n\), desto weiter von der Null entfernt sind die Quantile. Für wachsendes \(n\) nähern sich die Quantile den Quantilen der Standardnormalverteilung an. So gilt z.B. für \(n=100\)

n <- 100
alpha <- 0.05
qt(1-alpha/2, df=n-1)

[1] 1.984217

Zum Vergleich: Das \((1-\alpha/2)\)-Quantil der \(N(0,1)\) ist

qnorm(1-alpha/2)

[1] 1.959964

Die Nullhypothese \(H_0:\mu=\mu_0\) wird auf dem Signifikanzniveau \(\alpha\) verworfen, wenn die Teststatistik im kritischen Bereich liegt, also betragsmäßig größer als das \((1-\alpha/2)\)-Quantil der t-Verteilung ist.

Beispiel: Qualitätskontrolle

Mit der Zufallsvariable \(X\) bezeichnen wir das Gewicht (in g) einer zufällig aus der laufenden Produktion ausgewählten 200g-Tafel Schokolade. Bei der Produktion treten immer kleinere Abweichungen von der nominalen Menge auf, d.h. die 200g-Tafeln sind nicht immer exakt 200g schwer. Wir gehen davon aus, dass das tatsächliche Gewicht einer Normalverteilung folgt mit einem unbekannten Erwartungswert \(\mu\) und einer unbekannten Varianz \(\sigma^2\).

Um zu überprüfen, ob die Produktionsanlage korrekt justiert ist, wird eine einfache Stichprobe vom Umfang \(n=10\) aus der laufenden Produktion gezogen. Die Werte der konkreten Stichprobe sind:

x <- c(199.47,197.19,197.02,197.53,198.78,
       202.52,195.74,199.11,200.3,195.74)

Das Stichprobenmittel beträgt

mean(x)

[1] 198.34

Dieser Wert ist kleiner als der Zielwert. Könnte das Zufall sein? Ist es noch plausibel, ein so kleines Stichprobenmittel aus einer Stichprobe vom Umfang 10 zu erhalten, wenn die Maschinen korrekt eingestellt sind?

Es soll die Hypothese getestet werden, dass das mittlere Gewicht \(\mu_0=200\)g ist. Das Signifikanzniveau wird auf \(\alpha=0.1\) gesetzt.

alpha <- 0.1
mu0 <- 200
n <- length(x)

Der Wert der Teststatistik ist

teststat <- sqrt(n) * (mean(x) - mu0)/sd(x)
print(teststat)

[1] -2.470973

Für die Testentscheidung wird der Wert der Teststatistik mit den kritischen Grenzen verglichen. Sie sind

k_unten <- -qt(1-alpha/2, df=n-1)
k_oben <- qt(1-alpha/2, df=n-1)
print(paste(round(k_unten,4), "; ", round(k_oben,4)))

[1] "-1.8331 ;  1.8331"

Der Wert der Teststatistik liegt außerhalb dieses Intervalls, also in dem kritischen Bereich. Folglich wird die Nullhypothese verworfen. Das mittlere Gewicht weicht auf dem Niveau \(\alpha=0.1\) statistisch signifikant vom Zielwert 200g ab. Die Maschinen sollten neu eingestellt werden.

13.3 Einseitige Tests

Bei einseitigen Tests wird in der Nullhypothese kein eindeutiger fester Wert für den unbekannten Parameter postuliert, sondern nur eine Ungleichheit. Die Nullhypothese lautet dann entweder \[ H_0:\mu\le\mu_0 \] oder \[ H_0:\mu\ge\mu_0. \] Die Alternativhypothese ist jeweils das Gegenteil davon.

Da die Nullhypothese keinen eindeutigen Wert festlegt, kann man die Frage “Wie ist die Teststatistik unter der Nullhypothese verteilt?” nicht mehr so leicht beantworten. Es ist ja nicht klar, welcher Wert aus der Nullhypothese gemeint sein könnte.

Um zu entscheiden, für welchen Wert unter der Nullhypothese die Verteilung der Teststatistik betrachtet wird, hilft es sich die “Philosophie” der Hypothesentests in Erinnerung zu rufen. Mit dem Test wird untersucht, ob die Daten einer Stichprobe noch “einigermaßen vereinbar” sind mit der Nullhypothese oder ob sie sehr deutlich gegen die Nullhypothese sprechen. Damit ein Fehler erster Art, also eine fälschliche Ablehnung einer korrekten Nullhypothese, nur mit einer kleinen Wahrscheinlichkeit vorkommt, wird der kritische Bereich geeignet gewählt.

Der kritische Bereich muss folglich so festgelegt werden, dass auch im “worst case” die Fehlerwahrscheinlichkeit erster Art das vorgegebene Signifikanzniveau nicht überschreitet. Der “worst case” tritt ein, wenn man sich zwar noch innerhalb des Parameterraums der Nullhypothese befindet, aber den minimalen Abstand zum Parameterraum der Alternativhypothese hat. Deswegen betrachtet man bei einseitigen Tests die Verteilung der Teststatistik unter Gültigkeit von \(\mu=\mu_0\), also exakt wie bei den zweiseitigen Tests! Wenn der wahre Erwartungswert nicht an der Grenze zwischen der Null- und der Alternativhypothese liegt, sondern deutlich innerhalb der Nullhypothese, dann ist die Fehlerwahrscheinlichkeit erster Art sogar kleiner als das vorgegebene Signifikanzniveau.

Im nächsten Schritt überlegen wir uns, wie der kritische Bereich bei einem einseitigen Test aussieht. Exemplarisch spielen wir das für die folgende Null- und Alternativhypothese durch,

\[\begin{align*} H_0: \mu&\le\mu_0\\ H_1: \mu&> \mu_0. \end{align*}\]

Die Teststatistik ist \[ T=\sqrt{n}\frac{\bar X-\mu_0}{S}. \] An der Grenze zwischen Null- und Alternativhypothese (also für \(\mu=\mu_0\)) folgt die Teststatistik (approximativ) einer Standardnormalverteilung. Welchen Bereich wählen wir nun als kritischen Bereich? Welche Werte der Teststatistik sprechen eklatant gegen die Nullhypothese?

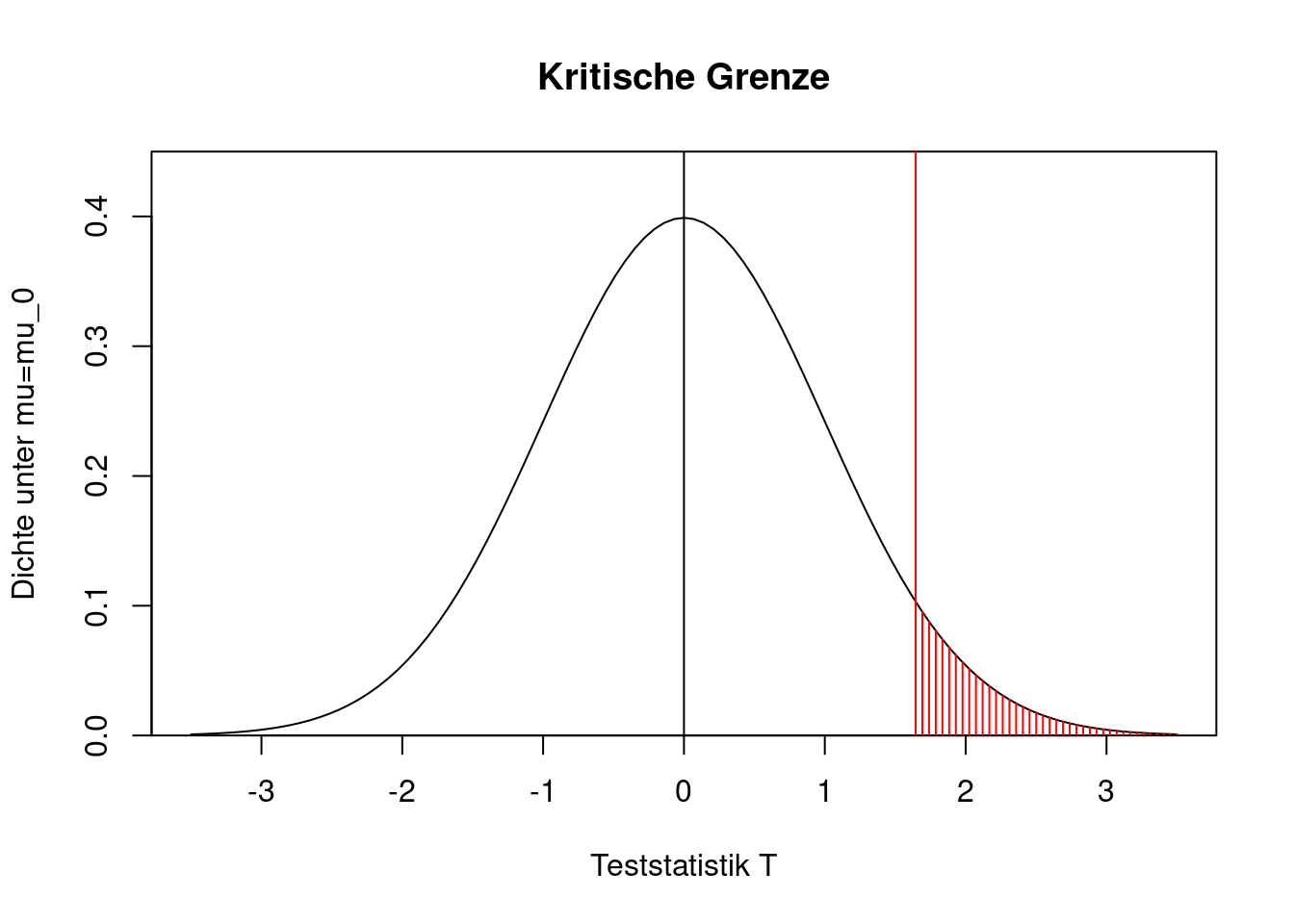
Da die Nullhypothese \(H_0:\mu\le\mu_0\) lautet, sind besonders kleine Werte der Teststatistik (z.B. \(-4\)) gut mit der Nullhypothese vereinbar. Auch leicht positive Werte könnten unter der Nullhypothese noch plausiblerweise auftreten. Nur sehr große positive Werte der Teststatistik sprechen gegen die Gültigkeit von \(H_0\). Wenn unter \(\mu=\mu_0\) die Wahrscheinlichkeit einer Ablehnung der (korrekten) Nullhypothese gerade \(\alpha\) betragen soll, dann müssen wir das \((1-\alpha)\)-Quantil als kritische Grenze setzen. Der kritische Bereich ist dann \([u_{1-\alpha},\infty)\). Die Grafik zeigt diesen Zusammenhang für \(\alpha=0.05\), die kritische Grenze ist 1.6449.

curve(dnorm(x),from=-3.5,to=3.5,
      main="Kritische Grenze",
      xlab="Teststatistik T",
      ylab="Dichte unter mu=mu_0",
      yaxs="i", ylim=c(0,0.45))
abline(v=0)
abline(v=qnorm(0.95),col="red")
for(x in seq(qnorm(0.95),3.5,length=40)){
  lines(c(x,x),c(0,dnorm(x)),col="red")
}

Wie bestimmt man bei diesem einseitigen Test den p-Wert? Zur Erinnerung: Der p-Wert ist die Wahrscheinlichkeit, dass die Teststatistik noch stärker gegen die Nullhypothese spricht als der tatsächliche Wert der Teststatistik. Bei einem einseitigen Test mit der Nullhypothese \(H_0: \mu\le\mu_0\) und der Alternative \(H_1: \mu>\mu_0\) bedeutet “noch stärker”, dass die Teststatistik einen noch größeren Wert annimmt (denn das spricht gegen die Nullhypothese). Also ist \[ \text{p-Wert} = P(T>t) = 1-\Phi(t). \]

Der einseitige Test in die andere Richtung mit den Hypothesen

\[\begin{align*} H_0: \mu&\ge\mu_0\\ H_1: \mu&< \mu_0 \end{align*}\]

wird vollkommen analog durchgeführt. Der kritische Bereich liegt nun links. Man lehnt \(H_0\) ab, wenn die Teststatistik kleiner ist als das \(\alpha\)-Quantil der Standardnormalverteilung (also kleiner als \(-1.6449\), wenn das Signifikanzniveau 5 Prozent ist). Der p-Wert ist die Wahrscheinlichkeit, dass die Teststatistik (noch) kleiner ist als der tatsächliche Wert der Teststatistik, \[ \text{p-Wert} = P(T<t) = \Phi(t). \]

Eine Besonderheit der einseitigen Erwartungswerttests besteht darin, dass man frei ist, wie die Nullhypothese formuliert werden soll. Man kann sowohl \(\mu\ge\mu_0\) als auch \(\mu\le\mu_0\) in die Nullhypothese schreiben. Die Alternativhypothese behauptet jeweils das Gegenteil davon. Es ist nicht gleichgültig, in welche Richtung die Nullhypothese formuliert wird, denn die Belastbarkeit der Testentscheidungen ist nicht symmetrisch. Eine Ablehnung der Nullhypothese ist eine belastbare statistische Untermauerung der Alternativhypothese (für ein gegebenes Signifikanzniveau). Hingegen ist die Nichtablehnung keine statistische Untermauerung der Nullhypothese. Wird die Nullhypothese nicht abgelehnt, können wir nur schlussfolgern, dass die Daten (noch) mit der Nullhypothese vereinbar sind.

Wenn man mit den Daten seiner Stichprobe gern einen Sachverhalt statistisch signifikant untermauern möchte, sollte man darum die Aussage, die man zeigen will, in die Alternativhypothese schreiben. Das Gegenteil davon ist dann die Nullhypothese.

Beispiel: Pünktlichkeit im Fernverkehr

Eine (fiktive) Regulierungsbehörde gibt eine Pünktlichkeitsquote von mindestens 95 Prozent für Reisen (inkl. Umstiege) im Fernverkehr vor. Ob das Verkehrsunternehmen die Vorgabe erfüllt, soll getestet werden. Aus den möglichen Reiserouten wird eine einfache Stichprobe vom Umfang \(n=80\) gezogen. Anschließend wird für jede ausgewählte Route ein Testfahrer losgeschickt, um festzustellen, ob das Reiseziel pünktlich erreicht wird. Die Zufallsvariable \(X\): “Für eine zufällig ausgewählte Reiseroute wird das Ziel pünktlich erreicht” ist Bernoulli-verteilt. Der Parameter \(\pi\) ist die Pünktlichkeitsquote. Sie wird geschätzt durch den Anteil der pünktlich erreichten Ziele der Testfahrten. Von den (fiktiven) Testfahrten waren 71 pünktlich, also eine Quote von \[ \hat\pi=\frac{71}{80}=0.8875. \] Die Mindestquote wird also nicht erreicht. Könnte es sein, dass dieser Wert bei den Testrouten nur zufällig niedriger als 0.95 ist, obwohl die Pünktlichkeitsquote von der Gesamtheit aller Reiserouten eingehalten wird? Die Regulierungsbehörde möchte (auf einem Signifikanzniveau von 5 Prozent) zeigen, dass die Zielvorgabe statistisch signifikant nicht eingehalten wurde. Die Null- und Alternativhypothesen lauten

\[\begin{align*} H_0: \pi&\ge 0.95\\ H_1: \pi& <0.95. \end{align*}\]

Der Wert der Teststatistik ist

\[\begin{align*} t&=\sqrt{n}\frac{\hat\pi-0.95}{\sqrt{\hat\pi (1-\hat\pi)}}\\ &=\sqrt{80}\cdot\frac{0.8875-0.95}{\sqrt{0.8875(1-0.8875)}}\\ &= -1.7692. \end{align*}\]

Der kritische Bereich des einseitigen Tests liegt wegen der Alternativhypothese \(H_1:\pi<0.95\) am unteren Ende der Standardnormalverteilung. Das 0.05-Quantil ist

qnorm(0.05)

[1] -1.644854

Diese kritische Grenze wird vom Wert der Teststatistik unterschritten. Die Nullhypothese wird verworfen. Das Fernverkehrsunternehmen erreicht die vorgegebene Pünktlichkeitsquote von 0.95 statistisch signifikant nicht.

Das Fernverkehrsunternehmen hätte die Nullhypothese vermutlich anders herum formuliert, nämlich

\[\begin{align*} H_0: \pi&\le 0.95\\ H_1: \pi& >0.95. \end{align*}\]

Der kritische Bereich wäre dann am oberen Ende der Standardnormalverteilung, also auf einem Niveau von 5 Prozent oberhalb von 1.6449. Die Teststatistik und auch der Wert der Teststatistik bleiben unverändert. Da der Wert der Teststatistik mit \(t=-1.7692\) kleiner als die kritische Grenze ist, wird \(H_0\) nicht verworfen. Die Daten sind vereinbar mit der Nullhypothese einer Pünktlichkeit von 0.95 oder weniger. Bei einer beobachteten Quote von \(\hat\pi=0.8875\) ist das natürlich offensichtlich und auch ohne einen formalen Hypothesentest sofort erkennbar.

Für das Fernverkehrsunternehmen wäre die Formulierung

\[\begin{align*} H_0: \pi&\le 0.95\\ H_1: \pi& >0.95. \end{align*}\]

vor allem dann empfehlenswert, wenn es zeigen will (und kann!), dass die Pünktlichkeitsquote statistisch signifikant besser als die vorgegebene Mindestquote ist.

In vielen Lehrbüchern zu Data Science oder Statistik wird auch der sogenannte Gauß-Test ausführlich behandelt. Als Gauß-Test bezeichnet man einen t-Test, wenn die Varianz \(\sigma^2\) der Population nicht aus der Stichprobe geschätzt werden muss, sondern bekannt ist. Häufig wird zusätzlich angenommen, dass \(X\) eine normalverteilte Zufallsvariable ist. Da diese Situation jedoch extrem unrealistisch ist, wird sie in diesem eLehrbuch ausgelassen. Wann weiß man schon von der Zufallsvariable \(X\), dass sie normalverteilt ist mit einer Varianz \(\sigma^2\), weiß aber nicht, wie hoch ihr Erwartungswert \(\mu\) ist?

13.4 Vergleich zweier Erwartungswerte

Sehr häufig interessiert man sich nicht nur für einen Erwartungswert, sondern für zwei Erwartungswerte. Ist der mittlere Lohn von Gruppe A höher als der mittlere Lohn von Gruppe B? Erreicht Produktionsverfahren A eine niedrigere Fehlerquote als Produktionsverfahren B? Kann man mit der Wärmepumpe der Firma A effizienter heizen als mit der Pumpe von Firma B? Kaufen Kunden, die einer Werbemaßnahme ausgesetzt waren, mehr von dem beworbenen Produkt als Kunden, die keine Werbemaßnahme gesehen haben?

Derartige Fragen lassen sich immer durch Erwartungswerte von zwei Zufallsvariablen ausdrücken, \(X\) und \(Y\). Wir gehen direkt von der realistischen Situation aus, dass \(X\) und \(Y\) beliebig verteilt sein können und dass ihre Varianzen \(\sigma_X^2\) und \(\sigma_Y^2\) nicht bekannt sind. Um etwas über die beiden Erwartungswerte \(\mu_X\) und \(\mu_Y\) zu lernen, brauchen wir Daten. Dazu werden zwei Stichproben erhoben. Im folgenden nehmen wir an, dass die beiden Stichproben unabhängig voneinander gezogen werden. Sie müssen nicht gleich groß sein. Die beiden einfachen Stichproben \[ X_1,X_2,\ldots,X_m \] und \[ Y_1,Y_2,\ldots,Y_n \] bestehen aus Zufallsvariablen.

Wenn \(m\) und \(n\) groß sind, greift der zentrale Grenzwertsatz für die beiden Stichprobenmittel \(\bar X\) und \(\bar Y\). Es gilt dann approximativ (vgl. Kapitel 8.3)

\[\begin{align*} \bar X &\stackrel{appr}{\sim} N\left(\mu_X,\frac{\sigma_X^2}{m}\right)\\ \bar Y &\stackrel{appr}{\sim} N\left(\mu_Y,\frac{\sigma_Y^2}{n}\right). \end{align*}\]

Im folgenden wird darauf verzichtet, jedesmal explizit zu schreiben, dass es sich nur um einen approximativen Zusammenhang handelt. Auf einem vorgegebenen Signifikanzniveau von \(\alpha\) soll

\[\begin{align*} H_0:\mu_X&=\mu_Y\\ H_1:\mu_X&\neq \mu_Y \end{align*}\]

getestet werden. Es handelt sich um einen zweiseitigen Test. Das wird noch deutlicher, wenn man die Hypothesen umformuliert,

\[\begin{align*} H_0:\mu_X-\mu_Y &=0\\ H_1:\mu_X-\mu_Y&\neq 0. \end{align*}\]

Die Differenz der Erwartungswerte schätzen wir durch die Differenz der Stichprobenmittel \(\bar X-\bar Y\). Wegen der Unabhängigkeit der Stichproben gilt für diese Differenz \[ \bar X-\bar Y \sim N\left(\mu_X-\mu_Y,\frac{\sigma_X^2}{m}+\frac{\sigma_Y^2}{n}\right). \] Zur Begründung des Varianzausdrucks: Es handelt sich bei der Differenz der Stichprobenmittel um eine Linearkombination von zwei Zufallsvariablen, nämlich \(a\bar X+b\bar Y\) mit \(a=1\) und \(b=-1\). Nach den Regeln aus Kapitel 7.2 ist die Varianz der Summe \(a^2 Var(\bar X)+b^2 Var(\bar Y)\). Die Kovarianz fällt weg, weil die Stichprobenmittel unabhängig voneinander sind.

Folglich gilt unter der Nullhypothese für die standardisierte Differenz \[ \frac{\bar X-\bar Y}{\sqrt{\frac{\sigma_X^2}{m}+\frac{\sigma_Y^2}{n}}} \sim N(0,1). \] Als Teststatistik ist der Bruch noch nicht geeignet, weil die beiden Varianzen nicht bekannt sind. Ersetzt man sie durch die Schätzer \(S_X^2\) und \(S_Y^2\), dann ergibt sich als Teststatistik \[ T=\frac{\bar X-\bar Y}{\sqrt{\frac{S_X^2}{m}+\frac{S_Y^2}{n}}}. \] Für große Stichproben folgt die Teststatistik wegen des zentralen Grenzwertsatzes unter der Nullhypothese einer Standardnormalverteilung. Man lehnt die Nullhypothese ab, wenn die Teststatistik im kritischen Bereich liegt. Der kritische Bereich ist (bei einem Signifikanzniveau von 5 Prozent) der Bereich links und rechts von dem üblichen Intervall \([-1.96,1.96]\).

In dem Spezialfall zweier Bernoulli-verteilter Zufallsvariablen mit den Parametern \(\pi_X\) und \(\pi_Y\) hat es sich durchgesetzt, die Stichprobenmittel als \(\hat\pi_X\) und \(\hat\pi_Y\) zu notieren. Die geschätzten Varianzen schreibt man als \(\hat\pi_X(1-\hat\pi_X)\) und \(\hat\pi_Y(1-\hat\pi_Y)\). In dieser Notation ist die Teststatistik \[ T=\frac{\hat\pi_X-\hat\pi_Y}{\sqrt{\frac{\hat\pi_X(1-\hat\pi_X)}{m} +\frac{\hat\pi_Y(1-\hat\pi_Y)}{n}}}. \] Die Teststatistik erscheint auf den ersten Blick anders als oben, das liegt aber nur an der anderen Art der Notation.

Beispiel: Verdiensterwartungen von Männern und Frauen

Eine mögliche Erklärung für den großen Unterschied im Lohneinkommen von Männern und Frauen in Deutschland lautet, dass Frauen niedrigere Lohnforderungen stellen. Das könnte damit zusammenhängen, dass sie im Mittel niedrigere Verdiensterwartungen haben als Männer. Um das zu testen, definieren wir die Populationen \(X\) (Verdiensterwartung von Studentinnen der Wirtschaftswissenschaften) und \(Y\) (Verdiensterwartung von Studenten der Wirtschaftswissenschaften). Die mittleren Erwartungen seien \(\mu_X=E(X)\) und \(\mu_Y=E(Y)\). Die Nullhypothese lautet \[ H_0: \mu_X=\mu_Y \] und die Alternativhypothese behauptet das Gegenteil.

In einer großen Vorlesung (Data Science 1 im Sommersemester 2023) wurden die Studierenden unter anderem zu ihren Verdiensterwartungen befragt. Wir gehen im folgenden davon aus, dass die Antworten als Realisation einer einfachen Stichprobe angesehen werden können. Wir tun also so, als seien die Studierenden der Vorlesung repräsentativ für die Population aller Studierenden der Wirtschaftswissenschaften in Deutschland.

Die Daten werden in R eingelesen. Die ersten Beobachtungen sind:

Umfrage <- read.csv("../data/verdiensterwartungen.csv")
head(Umfrage)

  Geschlecht ErwartetesGehalt Nebenjob
1   männlich            84000        0
2   männlich            36000        0
3   weiblich            50000        0
4   weiblich            50000        5
5   männlich            40000        0
6   männlich            36000        0

In dem Datensatz wurden offensichtliche Fehler (vor allem die Verwechselung von Monats- und Jahreseinkommen) bereits bereinigt. Fehlende Werte wurden entfernt. Entfernt wurden auch zwei Beobachtungen mit der Geschlechtsangabe “divers”. Da der Test nur durchgeführt werden kann, wenn die Zahl der Beobachtungen ausreichend groß ist, können Ausprägungen nicht berücksichtigt werden, die nur sehr selten auftreten.

Die Anzahl an Beobachtungen von Frauen ist

m <- sum(Umfrage$Geschlecht == "weiblich")
m

[1] 204

Die Zahl der Beobachtungen von Männern ist

n <- sum(Umfrage$Geschlecht == "männlich")
n

[1] 386

Die Zahlen sind ausreichend groß, um einen Test auf Gleichheit der Erwartungswerte durchzuführen. Mit Hilfe der logischen Indizierung werden die beiden Vektoren x und y mit den Verdiensterwartungen der Frauen und Männer aus dem Dataframe Umfrage herausgelesen.

x <- Umfrage$ErwartetesGehalt[Umfrage$Geschlecht=="weiblich"]
y <- Umfrage$ErwartetesGehalt[Umfrage$Geschlecht=="männlich"]

Das Stichprobenmittel der Frauen ist

mean(x)

[1] 42733.33

und für die Männer ergibt sich

mean(y)

[1] 56632.05

Der Unterschied ist recht hoch, aber ist er auch statistisch signifikant? Das Signifikanzniveau setzen wir auf

alpha <- 0.05

Der Wert der Teststatistik ist

teststat <- (mean(x) - mean(y))/sqrt(var(x)/m + var(y)/n)
teststat

[1] -6.545493

Der untere kritische Wert von \(-1.96\) wird also deutlich unterschritten. Die Verdiensterwartungen von männlichen und weiblichen Studierenden unterscheiden sich statistisch signifikant.

Zu dem gleichen Ergebnis kommt man über den p-Wert:

2*(1-pnorm(abs(teststat)))

[1] 5.929945e-11

Dieser Wert ist kleiner als jedes vernünftige Signifikanzniveau. Die Nullhypothese wird also verworfen.

Selbstverständlich lassen sich auch einseitige Tests für zwei Erwartungswerte durchführen. Dann geht es nicht um die Frage, ob zwei Erwartungswerte statistische signifikant unterschiedlich sind, sondern ob der eine Erwartungswert statistisch signifikanz größer (oder kleiner) ist als der andere. Die kritischen Grenzen werden analog zum t-Test für einen einzelnen Erwartungswert angepasst. Auch hier sollte man klug auswählen, welche Ungleichung in die Nullhypothese und welche in die Alternativhypothese geschrieben wird. Nur eine Ablehnung der Nullhypothese ist eine belastbare statistische Untermauerung der Alternativhypothese. Eine nicht abgelehnte Nullhypothese ist keine statistische Bestätigung für die Richtigkeit von \(H_0\).

Beispiel: Randomisiertes Experiment

Um den Effekt von Politikmaßnahmen (oder anderen Arten von Maßnahmen) zu messen, werden idealerweise randomisierte Experimente durchgeführt. In einem solchen Experiment werden aus der Population zwei Stichproben gezogen. Die Mitglieder der einen Stichprobe werden einem Treatment unterzogen, die Mitglieder der anderen Stichprobe sind die Kontrollgruppe. Anschließend untersucht man, ob zwischen den beiden Gruppen ein statistisch signifikanter Unterschied besteht.

In einem Feldexperiment hat Falk (2007, Econometrica, vol. 75, S. 1501-1511) untersucht, ob eine Wohltätigkeitsorganisation höhere Spenden bekommt, wenn sie ihren Briefen mit Spendenaufforderungen ein (kleines oder großes) Geschenk beilegt. Im folgenden testen wir anhand der Daten von Fehr (2007), ob ein kleines Geschenk die Spendenbereitschaft signifikant erhöht. Mit \(X\) bezeichnen wir eine Bernoulli-verteilte Zufallsvariable, die angibt, ob eine Person ohne Geschenk spendet. Die Zufallsvariable \(Y\) gibt an, ob eine Person spendet, die ein kleines Geschenk erhalten hat. Die (unbekannten) Spendenwahrscheinlichkeiten werden als \(\pi_X\) und \(\pi_Y\) geschrieben.

Da wir eine Erhöhung der Spendenbereitschaft statistisch untermauern wollen, behauptet die Nullhypothese, dass es durch das kleine Geschenk nicht zu einer Erhöhung kommt, d.h. dass die Spendenwahrscheinlichkeit ohne Geschenk mindestens genauso hoch ist wie mit einem kleinen Geschenk, \[ H_0:\pi_X\ge \pi_Y. \] Die Alternativhypothese behauptet das Gegenteil, \[ H_1: \pi_X < \pi_Y. \] In dem Artikel von Fehr (2007) sind die folgenden Zahlen gegeben:

	kein Geschenk	kleines Geschenk
Anzahl Anschreiben	3262	3237
Anzahl Spenden	397	465

Daraus ergeben sich die beiden Stichprobenmittel (Anteile),

\[\begin{align*} \hat\pi_X &= \frac{397}{3262}=0.1217\\ \hat\pi_X &= \frac{465}{3237}=0.1437. \end{align*}\]

Der Wert der Teststatistik ist folglich

\[\begin{align*} t &=\frac{\hat\pi_X-\hat\pi_Y}{\sqrt{\frac{\hat\pi_X(1-\hat\pi_X)}{m} +\frac{\hat\pi_Y(1-\hat\pi_Y)}{n}}}\\[2ex] &= \frac{0.1217-0.1437)}{\sqrt{\frac{0.1217\cdot(1-0.1217)}{3262} +\frac{0.1437\cdot (1-0.1437)}{3237}}}\\[2ex] &= -2.615. \end{align*}\]

Der p-Wert dieses Tests entspricht der Wahrscheinlichkeit, dass eine standardnormalverteilte Zufallsvariable kleiner ist als der Wert der Teststatistik. In R erhält man

pnorm(-2.615)

[1] 0.004461373

Der p-Wert ist also kleiner als die üblichen Signifikanzniveaus (0.05 oder 0.01). Die Nullhypothese wird abgelehnt. Ein kleines Geschenk erhöht die Spendenbereitschaft also statistisch signifikant.

13.5 Monte-Carlo-Simulation

Für ein tieferes Verständnis von Hypothesentests ist es hilfreich, Monte-Carlo-Simulationen zu programmieren und durchzuführen. Am Beispiel des Tests auf Gleichheit von zwei Erwartungswerten mit

\[\begin{align*} H_0: \mu_X &= \mu_Y\\ H_1: \mu_X &\neq \mu_Y \end{align*}\]

wird das im folgenden vorgestellt. Es gibt zwei Zufallsvariablen \(X\) und \(Y\), deren Verteilung für die Simulationen vorgegeben ist. Beide Zufallsvariablen folgen einer Exponentialverteilung, jedoch mit unterschiedlichen Parametern,

\[\begin{align*} X &\sim Exp(0.25)\\ Y &\sim Exp(0.28) \end{align*}\]

Die wahren Erwartungswerte sind (vgl. Kapitel 5.3.2)

\[\begin{align*} \mu_X &= 1/0.25 =4\\ \mu_Y &= 1/0.28 =3.571. \end{align*}\]

Die Nullhypothese ist also tatsächlich falsch, denn der wahre Erwartungswert von \(X\) ist größer als der von \(Y\). Mit Hilfe einer Monte-Carlo-Simulation können wir leicht ermitteln, wie hoch die Wahrscheinlichkeit ist, dass die falsche Nullhypothese von dem Test korrekt als falsch erkannt wird, d.h. wie hoch die Power des Tests in der gegebenen Situation ist.

Für die Simulation tut man so, als seien wahren Erwartungswerte unbekannt. Die Simulation läuft auf ähnliche Weise ab wie die Monte-Carlo-Simulation von Konfidenzintervallen in Kapitel 11.3. Die Kernidee ist, dass nicht nur einmal zwei Stichproben vom Umfang \(m\) und \(n\) gezogen werden, sondern sehr oft. Wir setzen für das Beispiel \(m=200\) und \(n=300\). Sei \(R=10000\) die Zahl der Schleifendurchläufe. In jedem Schleifendurchlauf

• wird eine Stichprobe x der Länge m aus \(X\) und eine Stichprobe y der Länge n aus \(Y\) gezogen

• wird aus den beiden Stichproben x und y der Wert der Teststatistik teststat berechnet

• wird kontrolliert, ob teststat in den kritischen Bereich fällt. Wenn ja, wird ein Zähler um 1 erhöht.

So sieht das R-Programm aus:

lambda_X <- 0.25
lambda_Y <- 0.28
m <- 200
n <- 300

alpha <- 0.05
R <- 10000

# (1-alpha/2)-Quantil der N(0,1)
qnt <- qnorm(1-alpha/2)

# Initialisierung eines Zählers
z <- 0

for(r in 1:R){
  
  # Ziehung der Stichproben
  x <- rexp(m, rate=lambda_X)
  y <- rexp(n, rate=lambda_Y)
  
  # Berechnung der Teststatistik
  teststat <- (mean(x)-mean(y)) / sqrt(var(x)/m + var(y)/n)
  
  # Liegt die Teststatistik im krit. Bereich?
  if(teststat < -qnt | teststat > qnt){
    z <- z+1
  }
}

Der Anteil der Ablehnungen von \(H_0\) konvergiert nach dem Gesetz der großen Zahl gegen die theoretische Power (für die festgelegten Parameter und Stichprobenumfänge). In dieser Simulation ergab sich als Power

print(z/R)

[1] 0.2201

Mit einer Wahrscheinlichkeit von 22 Prozent wird die falsche Nullhypothese von dem Test als falsch erkannt. Umgekehrt heißt das natürlich auch, dass mit einer recht großen Wahrscheinlichkeit von 78 Prozent ein Fehler zweiter Art auftritt. Dass der Test in der gegebenen Situation nicht über eine besonders hohe Power verfügt, liegt daran, dass die beiden Erwartungswerte nicht sehr weit auseinander liegen. Die Power wäre höher, wenn die Differenz der wahren Erwartungswerte höher wäre. Die Power steigt auch an, wenn die Stichproben größer sind. Spielen Sie diese Fälle in weiteren eigenen Simulationen durch, um ein Gefühl für das Verhalten des Testverfahrens zu entwickeln.

In einer zweiten Simulation untersuchen wir, wie gut die Fehlerwahrscheinlichkeit erster Art eingehalten wird. Dazu wiederholen wir die Simulation, wenn die Nullhypothese tatsächlich korrekt ist, d.h. \(\lambda_X=\lambda_Y\) ist. Wir setzen

lambda_X <- 1/0.25
lambda_Y <- 1/0.25

und lassen den restlichen Code unverändert. Als Ergebnis der Simulation unter \(H_0\) ergibt sich eine Fehlerwahrscheinlichkeit erster Art in Höhe von

[1] 0.0462

Das vorgegebene Signifikanzniveau (0.05) wird also gut eingehalten. Eine Wiederholung der Simulation würde ein leicht anderes Ergebnis liefern. Je höher \(R\) gesetzt wird, desto präziser ist die Schätzung der Fehlerwahrscheinlichkeit, allerdings dauert es dann auch länger.