gewicht <- c(509.2,504.6,492.8,508.0,500.2,
508.4,502.6,518.0,494.4,487.1,
510.8,504.2,519.9,488.3,509.2,
513.8,511.2,506.1,505.7,493.3)
n <- length(gewicht)10 Punktschätzung
Alle Verteilungen, für die man sich in den Wirtschaftswissenschaften interessiert, können durch Zufallsvariablen repräsentiert werden. Eine Zufallsvariable \(X\) kann beispielsweise die Dauer bis zur nächsten Transaktion an einer Aktienbörse darstellen; \(X\) kann die Einkommensverteilung in der Population darstellen; \(X\) kann eine Fehlerverteilung sein, die durch eine Normalverteilung beschrieben wird etc.
Wir interessieren uns oft für bestimmte Aspekte der Verteilung von \(X\), zum Beispiel für den Erwartungswert, ein Quantil oder die Standardabweichung. Diese interessierenden Größen nennt man auch “Parameter” von \(X\). Leider ist es normalerweise nicht möglich, die interessierenden Parameter exakt zu berechnen, weil wir die Verteilungsfunktion oder die Dichtefunktion von \(X\) bei realen Anwendungen praktisch nie kennen.
Was jedoch möglich ist: Wir können den unbekannten Parameter, für den wir uns interessieren, aus einer Stichprobe berechnen. Die Stichprobe dient also dazu, etwas über die Verteilung der Zufallsvariable zu lernen. Da die Stichprobe immer einem Zufallseinfluss unterliegt, lernt man zwar nicht die wahre Verteilung von \(X\), aber man kann zumindest Aussagen darüber machen, in welchem Bereich der Parameter liegen könnte, für den man sich interessiert. Intuitiv klar ist auch, dass man aus einer großen Stichprobe mehr über eine Verteilung lernen kann als aus einer kleinen Stichprobe.
In diesem Kapitel wird erklärt, wie man eine Punktschätzung für einen Parameter finden kann. Im nachfolgenden Kapitel 11 geht es dann darum, Konfidenzintervalle zu bestimmen, in denen der Parameter mit einer hohen Wahrscheinlichkeit liegt.
10.1 Schätzer
Den Parameter, für den wir uns interessieren, bezeichnen wir allgemein mit \(\theta\) (“theta”). Es kann sich bei \(\theta\) um den Erwartungswert einer Verteilung handeln, um die Varianz, ein Quantil, den Wert der Verteilungsfunktion an einer bestimmten Stelle usw. Um etwas über den unbekannten Wert von \(\theta\) zu lernen, wird eine einfache Stichprobe \(X_1,\ldots,X_n\) vom Umfang \(n\) erhoben. Die Stichprobe besteht aus Zufallsvariablen, die identisch und unabhängig verteilt sind (vgl. Kapitel 9)
Mit Hilfe der Stichprobe wird nun eine Aussage über den Wert des unbekannten Parameters \(\theta\) getroffen. Dazu benutzt man eine Statistik (im Sinne von Kapitel 9.2).
Da die Stichprobe aus Zufallsvariablen besteht, handelt es sich auch bei dem Schätzer um eine Zufallsvariable. Ersetzt man die Stichprobe durch die konkrete (realisierte) Stichprobe \(x_1,\ldots,x_n\), erhält man eine Realisation des Schätzers. Sie heißt Schätzwert (engl. estimate). Der Schätzwert ist keine Zufallsvariable. In der Notation wird gewöhnlich nicht zwischen dem Schätzer und dem Schätzwert unterschieden, beides wird mit \(\hat\theta\) bezeichnet. Die richtige Bedeutung ergibt sich meist aus dem Kontext. Wenn die Bedeutung nicht eindeutig ist, sollte man \(\hat\theta(X_1,\ldots,X_n)\) für den Schätzer und \(\hat\theta(x_1,\ldots,x_n)\) für den Schätzwert schreiben.
Auch wenn die Standardabweichung eines Schätzers nur geschätzt wird, spricht man vom Standardfehler. In der Notation unterscheiden wir nicht zwischen der exakten Standardabweichung eines Schätzers und seiner geschätzten Standardabweichung. Beides notieren wir als \(se(\hat\theta)\).
10.2 Wichtige Schätzer
Im folgenden werden Schätzer für die beiden Parameter vorgestellt, die in den Wirtschaftswissenschaften besonders oft von Interesse sind, nämlich Erwartungswert und Varianz.
10.2.1 Erwartungswert
Der Erwartungswert einer Verteilung ist vermutlich der Parameter, der mit Abstand am häufigsten von Interesse ist. Da er so wichtig ist, hat er ein eigenes Symbol und wird nicht als \(\hat\theta\), sondern als \(\bar X\) notiert. Der Schätzer ist \[ \bar X=\hat\theta(X_1,\ldots,X_n)=\frac{1}{n}\sum_{i=1}^n X_i, \] also das Stichprobenmittel. Der zugehörige Schätzwert \[ \bar x=\hat\theta(x_1,\ldots,x_n)=\frac{1}{n}\sum_{i=1}^n x_i \] ist das arithmetische Mittel der konkreten Stichprobe.
Der Standardfehler des Schätzers ist die Standardabweichung der Zufallsvariable \(\bar X\). Wir haben sie bereits in Kapitel 8.1 hergeleitet, und zwar \[ se(\bar X)=\sqrt{Var(\bar X)}=\frac{\sigma}{\sqrt{n}}. \]
In R berechnet man das Stichprobenmittel mit der Funktion mean. Wenn die konkrete Stichprobe als Vektor x (der Länge n) vorliegt, dann ergibt mean(x) den Schätzwert für den Erwartungswert.
Beispiel: Erwartungswertschätzung
In einem Supermarkt werden Erdbeeren in Pappschalen angeboten. Ausgeschildert sind die Schalen mit einem Gewicht von 500g. Natürlich wiegt nicht jede Schale wirklich exakt 500g, es gibt kleinere Abweichungen von dem Soll-Gewicht. Im Mittel muss das Gewicht der Schalen aber (mindestens) dem ausgeschilderten Gewicht entsprechen. Um herauszufinden, wie hoch der Erwartungswert des Gewichts einer Schale ist, werden in dem Supermarkt daher zufällig \(n=20\) Schalen ausgewählt und gewogen. Die Ergebnisse der Messungen werden in R als Vektor gewicht zusammengefasst.
Der Schätzwert \(\bar x\) für den Erwartungswert \(E(X)\) des Gewichts einer Schale Erdbeeren beträgt
mean(gewicht)[1] 504.39Der Schätzwert für das mittlere Gewicht ist also tatsächlich etwas höher als das angegebene Gewicht. Würde man eine neue Stichprobe (wieder vom Umfang 20) ziehen, ergäbe sich ein anderer Schätzwert. Wie sehr die Schätzung von Stichprobe zu Stichprobe streuen würde, lässt sich mit Hilfe des Standardfehlers beurteilen. Dazu brauchen wir aber eine Schätzung der Standardabweichung von \(X\), die im nächsten Beispielblock folgt.
10.2.2 Spezialfall: Anteile
Ein wichtiger Spezialfall der Erwartungswertschätzung betrifft die Bernoulli-Verteilung (Kapitel 5.2.1). Die Bernoulli-Verteilung tritt in den Wirtschaftswissenschaften oft auf, nämlich immer dann auf, wenn es um Anteile geht. Wie hoch ist der Anteil in der Population mit einer “interessierenden Eigenschaft”? Mögliche Beispiele: Wie hoch ist der Anteil der Firmen, die eine Verlagerung ihrer Produktion ins Ausland planen? Wie hoch ist der Anteil der fehlerhaften Produkte eines Betriebs? Wie hoch ist der Anteil der SPD-Wähler in NRW? Wie hoch ist der Anteil der Studierenden, die mit ihrem Studium unzufrieden sind?
Eine bernoulli-verteilt Zufallsvariable hat nur die beiden Ausprägungen 0 (=interessierende Eigenschaft liegt nicht vor) und 1 (=Eigenschaft liegt vor). Aus einer gegebenen Population wird zufällig eine Person (eine Firma, ein Haushalt, …) ausgewählt. Die Wahrscheinlichkeit, dass sie die Eigenschaft hat, entspricht gerade dem Populationsanteil. Der Parameter \(\pi\) der Bernoulli-Verteilung ist also der Populationsanteil, für den man sich interessiert.
Nur in seltenen Fällen ist eine Vollerhebung für die gesamte Population machbar. Normalerweise muss eine Stichprobe ausreichen, um etwas über den Populationsanteil zu lernen. Dazu zieht man aus der Population eine einfache Stichprobe \(X_1,\ldots,X_n\). Das Stichprobenmittel \(\bar X\) ist bei einer Bernoulli-Verteliung der Anteil der Stichprobenelemente mit der Eigenschaft. Um in der Notation deutlich zu machen, dass das Stichprobenmittel der geschätzte Populationsanteil ist, schreibt man in diesem Spezialfall daher oft \(\hat\pi\) anstelle von \(\bar X\), \[ \hat\pi = \frac{1}{n}\sum_{i=1}^n X_i =\frac{\text{Anzahl }X_i \text{ mit der Eigenschaft}}{n}. \] Da die Varianz der Bernoulli-Verteilung \(\pi(1-\pi)\) ist, erhält man den Standardfehler von \(\hat\pi\) durch \[ se(\hat\pi)=\sqrt{\frac{\hat\pi(1-\hat\pi)}{n}}. \]
Beispiel: Wahlumfrage
Durch eine Wahlumfrage soll ermittelt werden, wie hoch aktuell der Anteil der Wahlberechtigten in NRW ist, der die SPD wählen will. Die “interessierende Eigenschaft” ist also: “die befragte Person will die SPD wählen”. Aus der Wahlpopulation wird eine einfache Stichprobe vom Umfang \(n=1000\) erhoben. Jede Person wird befragt, ob sie die SPD wählen will. Die (fiktive) Anzahl an Personen, die angeben, die SPD wählen zu wollen, betrage 273. Der Anteil der SPD-Wähler in der konkreten Stichprobe ist folglich \(\hat\pi=0.273\). Der geschätzte Anteil der SPD-Wähler in der Population ist also rund 27 Prozent.
10.2.3 Varianz
Als Schätzer für die Varianz verwendet man \[ S^2=\hat\theta(X_1,\ldots,X_n)=\frac{1}{n-1}\sum_{i=1}^n (X_i-\bar X)^2, \] also die Stichprobenvarianz. Die Realisation ist der Schätzwert \[ s^2=\hat\theta(x_1,\ldots,x_n)=\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar x)^2, \] also die Varianz der konkreten Stichprobenelemente, allerdings nicht mit \(n\), sondern mit \(n-1\) im Nenner. Schätzer und Schätzwert für die Standardabweichung sind \[ S=\sqrt{\frac{1}{n-1}\sum_{i=1}^n (X_i-\bar X)^2} \] und \[ s=\sqrt{\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar x)^2}. \] Auch für die Schätzer von Varianz und Standardabweichung, \(S^2\) und \(S\), gibt es Standardfehler, \(se(S^2)\) und \(se(S)\). In diesem Kurs leiten wir sie jedoch nicht theoretisch her, sondern ermitteln in Kapitel 10.4 beispielhaft den Standardfehler \(se(S)\) durch Monte-Carlo-Simulationen.
Die Schätzung der Standardabweichung \(S\) bzw. die Realisation \(s\) kann man nutzen, um den Standardfehler des Stichprobenmittels \(se(\bar X)\) zu schätzen. Man erhält dann den (geschätzten) Standardfehler \[
se(\bar X)=\frac{S}{\sqrt{n}}.
\] In R berechnet man die Stichprobenvarianz \(S^2\) und die Stichprobenstandardabweichung \(S\) mit den Funktionen var und sd (standard deviation). Wenn die konkrete Stichprobe als Vektor x (der Länge n) vorliegt, dann ergibt var(x) den Schätzwert \(s^2\) für die Varianz und sd(x) den Schätzwert \(s\) für die Standardabweichung.
10.3 Unverzerrtheit
Man kann sich einen Schätzer als Bogenschützen vorstellen, der auf eine Zielscheibe schießt, auch wenn die Analogie Grenzen hat. Der wahre Parameter \(\theta\) liegt im Zentrum der Zielscheibe. Der Bogenschütze trifft natürlich nicht bei jedem Schuss exakt ins Zentrum, er liegt manchmal zu weit oben oder unten, zu weit links oder rechts. Die Einschlagstelle des Pfeils in der Zielscheibe entspricht dem Schätzer bzw. dem Schätzwert \(\hat\theta\).
In einem Gedankenexperiment können wir uns vorstellen, dass nicht nur eine Stichprobe vom Umfang \(n\) gezogen wird, sondern dass unabhängig voneinander mehrere Stichproben jeweils vom Umfang \(n\) gezogen werden.
Die Analogie des Bogenschützen wären mehrere Schüsse auf die Zielscheibe.
Die folgende Abbildung zeigt die Einschläge von vier Bogenschützen, die jeweils 20 Pfeile mit dem Ziel abschießen, möglichst dicht an dem schwarzen Punkt in der Mitte zu landen.
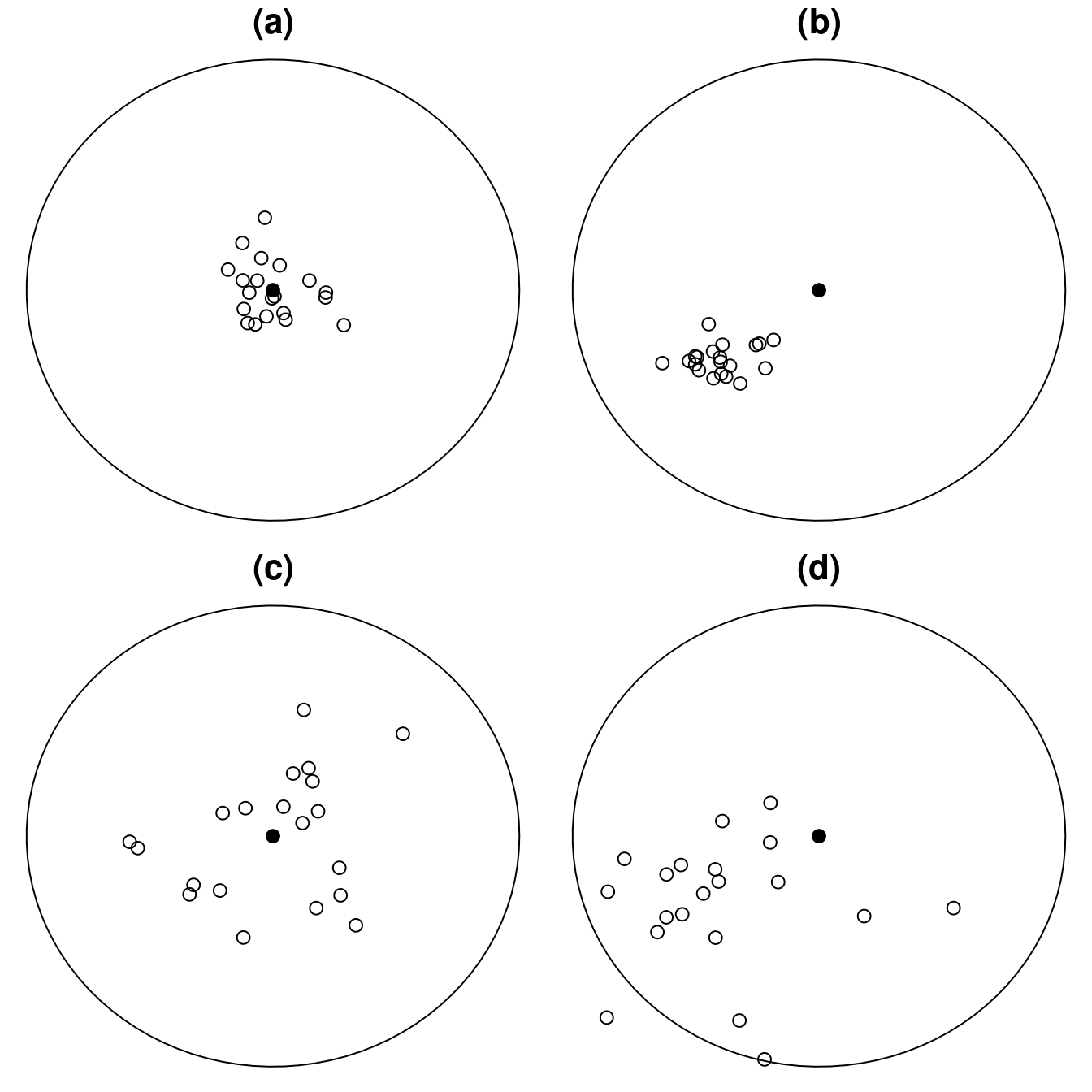
Welcher Schütze ist der beste? Offenbar trafen die Pfeile von (a) besonders nahe am Zielpunkt. Der Schütze (a) hat zwar das Ziel nicht exakt getroffen, aber seine Pfeile lagen nicht systematisch zu hoch oder niedrig oder zu weit links oder rechts. Außerdem liegen alle Pfeile nahe beieinander. Im Gegensatz dazu hat (b) zwar auch alle Pfeile nahe beieinander platziert, aber sie liegen systematisch zu weit links unten. Die Pfeile der Schützen (c) und (d) streuen deutlich mehr. Während (c) gleichmäßig um das Ziel herum getroffen hat, liegt (d) systematisch zu weit links unten.
Diese Überlegungen lassen sich auf Schätzer übertragen. Ein Qualitätskriterium für Schätzer ist die Erwartungstreue (oder Unverzerrtheit).
Der Schätzer \(\hat\theta\) darf zwar um den wahren Wert \(\theta\) herum streuen, aber er soll im Erwartungswert nicht zu hoch oder zu niedrig sein, sondern den wahren Wert “im Mittel” treffen. Die Schützen (a) und (c) wären in Analogie erwartungstreu, die Schützen (b) und (d) hingegen nicht. Der Schütze in (a) hat einen kleineren Standardfehler als (c), denn die Einschläge streuen weniger.
Im folgenden untersuchen wir, ob die Schätzer \(\bar X\) und \(S^2\) erwartungstreu für den Erwartungswert \(\mu\) und die Varianz \(\sigma^2\) sind. Den Erwartungswert von \(\bar X\) haben wir bereits in Kapitel 8.1 hergeleitet (dort mit der leicht abgewandelten Notation \(\bar X_n\)), er ist \[ E(\bar X)=\mu. \] Folglich ist \(\bar X\) ein erwartungstreuer Schätzer für \(E(X)\).
Nun betrachten wir den Varianzschätzer \[ S^2=\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar X)^2. \] Die Herleitung ist recht komplex. Wir beginnen mit einem Trick: In die Definition des Schätzers fügen wir den Ausdruck \(-\mu+\mu\) ein. Dadurch verändert sich das Ergebnis natürlich nicht, aber der Term unter dem Quadrat lässt sich auf eine neue Art schreiben.
\[\begin{align*} E(S^2) &= E\left(\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar X)^2\right)\\ &= E\left(\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\mu+\mu-\bar X)^2\right)\\ &= E\left(\frac{1}{n-1}\sum_{i=1}^{n}[(X_i-\mu)+(\mu-\bar X)]^2\right)\\ &= E\left(\frac{1}{n-1}\sum_{i=1}^{n}\left[(X_i-\mu)^2+ (\mu-\bar X)^2+2(X_i-\mu)(\mu-\bar X) \right] \right)\\ &= \left(\frac{1}{n-1}\sum_{i=1}^{n}E((X_i-\mu)^2)\right)+ \frac{1}{n-1}\sum_{i=1}^{n}E((\mu-\bar X)^2)\\ &\quad -\frac{2}{n-1}\sum_{i=1}^{n}E((X_i-\mu)(\bar X-\mu))\\ &= \underbrace{\left(\frac{1}{n-1}\sum_{i=1}^{n}E((X_i-\mu)^2)\right)}_{(I)} \\[2ex] &\quad +\underbrace{\frac{n}{n-1}E((\bar{X}-\mu)^2)}_{(II)} \\[2ex] &\quad -\underbrace{\frac{2}{n-1}\sum_{i=1}^{n}E((X_i-\mu)(\bar{X}-\mu))}_{(III)}. \end{align*}\]
Der Schritt von Zeile 3 zu Zeile 4 ist eine Anwendung der ersten binomischen Formel. Danach werden die üblichen Rechenregeln für Erwartungswerte angewendet. Die drei Summanden werden nun einzeln weiter betrachtet. Der erste Summand ist
\[\begin{align*} (I)&= \frac{1}{n-1}\sum_{i=1}^{n}E((X_i-\mu)^2)\\ &=\frac{1}{n-1}\sum_{i=1}^{n}Var(X_i) \\ &=\frac{1}{n-1}\sum_{i=1}^{n}\sigma^2 \\ &=\frac{n}{n-1}\sigma^2. \end{align*}\]
Dabei wurde die Definition der Varianz (vgl. Kapitel 4.7) genutzt.
Der zweite Summand ist
\[\begin{align*} (II)&=\frac{n}{n-1}E((\bar{X}-\mu)^2) \\ &=\frac{n}{n-1}Var(\bar{X}) \\ &=\frac{n}{n-1}\frac{\sigma^2}{n}\\ &=\frac{\sigma^2}{n-1}. \end{align*}\]
Die Varianz des Stichprobenmittels wurde bereits in Kapitel 8.1 hergeleitet.
Der dritte Summand ist
\[\begin{align*} (III)&=\frac{2}{n-1}\sum_{i=1}^{n}E((X_i-\mu)(\bar{X}-\mu)) \\ &= \frac{2n}{n-1} E((X_1-\mu)(\bar{X}-\mu)) \\ &= \frac{2n}{n-1} Cov(X_{1},\bar{X}) \\ &= \frac{2n}{n-1} Cov\left( X_{1},\frac{1}{n}\sum_{i=1}^{n}X_i\right) \\ &= \frac{2}{n-1}\sum_{i=1}^{n}Cov(X_1,X_i) \\ &= \frac{2}{n-1}\sigma^2. \end{align*}\]
Hier ist der erste Schritt der schwierigste. Da alle Stichprobenelemente \(X_i\) identisch verteilt sind, ist der Ausdruck \[ E((X_i-\mu)(\bar{X}-\mu)) \] für alle \(i\) gleich. Er hängt also nicht im Laufindex \(i\) ab, und man darf folglich anstelle von \(X_i\) auch (z.B.) \(X_1\) schreiben. Dieser Ausdruck wird in der Summe \(n\) Mal addiert. Im nächsten Schritt wird die Definition der Kovarianz verwendet (vgl. Kapitel 7). Schließlich wird im letzten Schritt ausgenutzt, dass \(Cov(X_1,X_1)=Var(X_1)=\sigma^2\) und \(Cov(X_1,X_i)=0\) für \(i\neq 1\). Die Kovarianzen sind 0, weil die Stichprobenelemente annahmegemäß unabhängig voneinander sind.
Führt man die drei Terme wieder zusammen, ergibt sich
\[\begin{align*} E(S^2) &= (I)+(II)-(III)\\ &=\frac{n}{n-1}\sigma^2+\frac{\sigma^2}{n-1}-\frac{2}{n-1}\sigma^2 \\ &= \left(\frac{n}{n-1}+\frac{1}{n-1}-\frac{2}{n-1}\right)\sigma^2 \\ &= \left(\frac{n+1-2}{n-1}\right)\sigma^2 \\ &= \sigma^2. \end{align*}\]
Der Schätzer \(S^2\) ist also erwartungstreu für die Varianz \(\sigma^2\). Diese Herleitung erklärt auch, warum der Varianzschätzer im Nenner \(n-1\) stehen hat. Würde durch \(n\) geteilt werden, dann wäre der Varianzschätzer verzerrt.
Beachten Sie, dass der Schätzer \(S\) für die Standardabweichung nicht erwartungstreu ist für die wahre Standardabweichung \(\sigma\). Die Wurzel ist keine lineare Funktion. In Kapitel 4.8 wurde gezeigt, dass der Erwartungswert bei nichtlinearen Funktionen nicht aus der Funktion “herausgezogen” werden darf.
Erwartungstreue ist ein gut verständliches Qualitätskriterium für einen Schätzer, denn Schätzer, die systematisch neben dem wahren Wert landen, sind schlechter als erwartungstreue Schätzer. In dem Wahlpflichtmodul Advanced Statistics werden weitere wichtige Qualitätskriterien für Schätzer (z.B. Konsistenz und Effizienz) eingeführt und ausführlich diskutiert.
10.4 Simulation in R
Das Gedankenexperiment einer sehr oft wiederholten Stichprobe kann als Monte-Carlo-Simulation tatsächlich real im Computer durchgeführt werden. Dafür legt man die Verteilung der Zufallsvariable \(X\) fest, tut aber anschließend so, als ob man sie nicht kennt, und schätzt dann den interessierenden Parameter.
Konkret wird als Beispiel im folgenden gezeigt, wie man die Erwartungstreue der Stichprobenstandardabweichung als Schätzer für die Populationsstandardabweichung mit Hilfe einer Monte-Carlo-Simulation überprüfen kann. Die Frage ist also, ob \[ E(S)=\sigma \] ist. Die Standardabweichung dient hier als Beispiel, weil wir ja bereits theoretisch gezeigt haben, dass die üblichen Schätzer für den Erwartungswert und die Varianz erwartungstreu sind - da wäre eine Monte-Carlo-Simulation, die das nur bestätigen kann, nicht sehr ergiebig.
Zuerst wird die Verteilung der Zufallsvariable \(X\) festgelegt. In diesem Beispiel wird \(X\) als exponentialverteilt mit Parameter \(\lambda=0.25\) angenommen. Der Standardabweichung von \(X\) ist also (vgl. Kapitel 5.3.2) \[ \sigma=\sqrt{Var(X)}=\sqrt{\frac{1}{0.25^2}}=4. \] Die Anzahl der Simulationsdurchläufe wird auf \(R=10000\) gesetzt. Bei der Wahl von \(R\) muss man zwischen Gewschwindigkeit und Genauigkeit abwägen. Je größer \(R\), desto genauer sind die Ergebnisse, aber desto länger dauern die Berechnungen. Der Stichprobenumfang wird mit \(n=8\) sehr klein gewählt, damit die wiederholten Stichproben zu einer deutlich spürbaren Streuung des Schätzers \(S\) führen.
lambda <- 0.25
R <- 10000
n <- 8Nun wird ein Vektor s der Länge R initialisiert, in dem die Schätzergebnisse der \(R\) Schleifendurchläufe gesammelt werden können. Welche Werte zu Beginn in s stehen, ist gleichgültig, weil sie ohnehin überschrieben werden. Hier werden alle Werte auf Null gesetzt:
s <- rep(0, R)Jetzt folgt eine for-Schleife. Innerhalb der Schleife wird in jedem Durchlauf neue eine Stichprobe vom Umfang \(n\) aus \(X\) gezogen. Mit Hilfe der Stichprobe wird die Populationsstandardabweichung \(\sigma\) durch die Stichprobenstandardabweichung \(S\) geschätzt (und als ein Element des Vektors s gespeichert).
for(r in 1:R){
x <- rexp(n, lambda)
s[r] <- sd(x)
}Das Histogramm zeigt, dass die im Vektor s gesammelten Schätzergebnisse stark streuen, was auch nicht verwunderlich ist, weil die Stichproben nur einen Umfang von \(n=8\) haben. Aus so kleinen Stichproben kann die Standardabweichung natürlich nicht sehr präzise geschätzt werden. Das Histogramm zeigt außerdem, dass die Verteilung schief ist: Eine Mehrheit der Schätzwerte ist etwas kleiner als der wahre Wert (gekennzeichnet durch die vertikale rote Linie), manchmal gibt es jedoch Werte, die viel zu groß sind.
hist(s, breaks=50)
abline(v=1/lambda, col="red")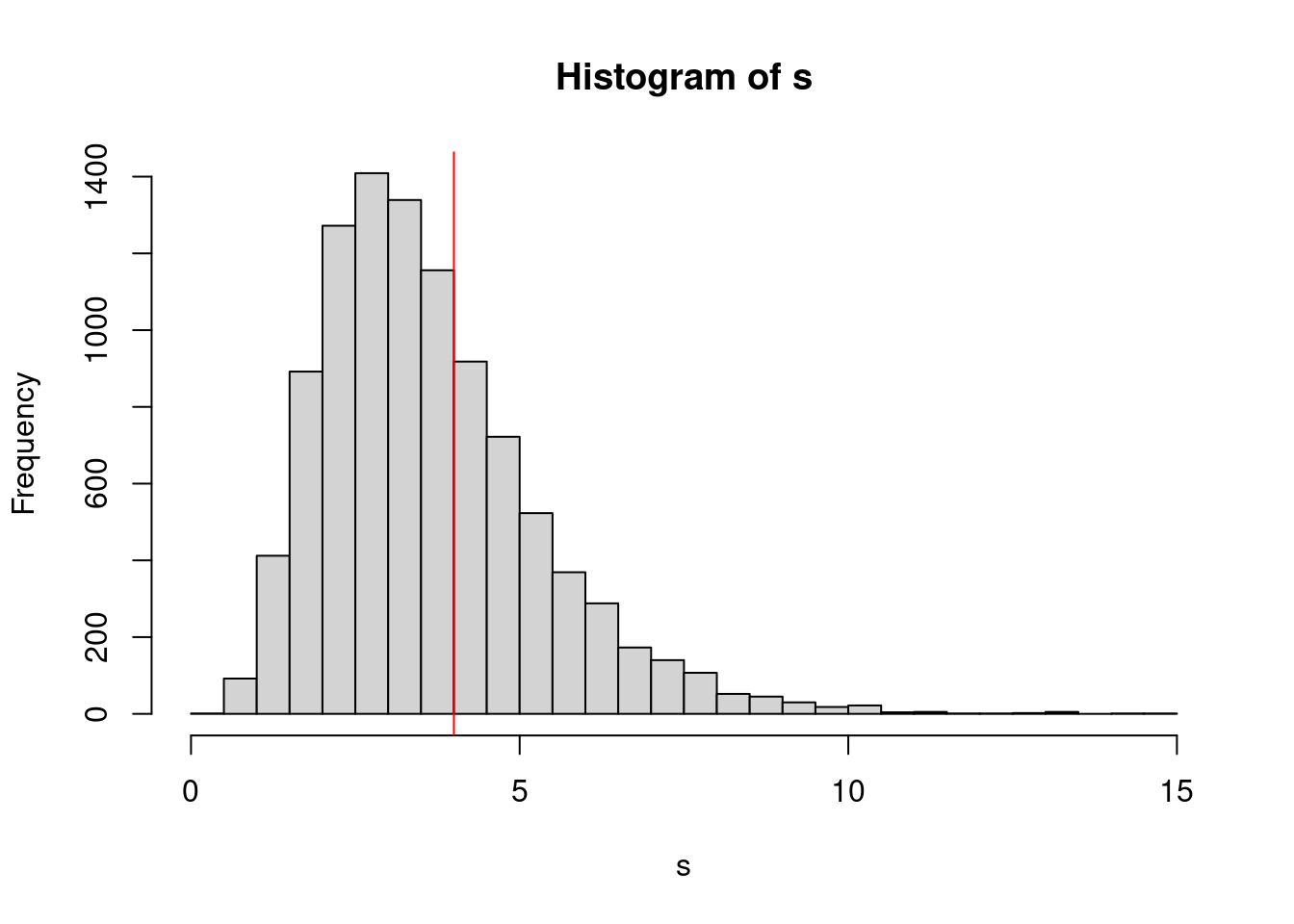
par(cex=0.7)
hist(s, breaks=50)
abline(v=1/lambda, col="red")
Der Erwartungswert des Schätzers für die Standardabweichung, \(E(S)\), wird durch
mean(s)[1] 3.616054approximiert. Dieser Wert ist substantiell kleiner als die wahre Standardabweichung \(\sigma=4\). Der Standardfehler des Schätzers, \(se(S)\), ist mit
sd(s)[1] 1.658843sehr hoch. Die Monte-Carlo-Simulation zeigt also (für das konkrete Beispiel einer Exponentialverteilung und eines Stichprobenumfangs von nur 8), dass die Stichproben-Standardabweichung \(S\) als Schätzer für die Populations-Standardabweichung \(\sigma\) verzerrt ist. Der Erwartungswert des Schätzers \(E(S)\) ist kleiner als der wahre Wert \(\sigma\). Außerdem zeigt sich, dass der Standardfehler des Schätzers \(se(S)\) groß ist.
Es ist für das Verständnis von Monte-Carlo-Simulationen hilfreich, sie mit anderen Werten zu wiederholen. Insbesondere sollte man nachprüfen, was mit der Erwartungstreue passiert, wenn der Stichprobenumfang erhöht wird, z.B. auf \(n=100\).
10.5 Schätzmethoden
Eine Frage wurde in diesem Kapitel bisher verschwiegen: Woher kommen eigentlich die Schätzer? Warum wird der Erwartungswert durch durch das Stichprobenmittel \(\bar X\) geschätzt? Warum schätzt man die Varianz durch die Stichprobenvarianz \(S^2\)? Was macht man, wenn man Parameter einer neu entwickelten Verteilung oder eines ökonomischen Modells schätzen will, für die es noch keine Schätzer gibt?
Es gibt einige allgemeine Konstruktionsprinzipien für Schätzer (z.B. Maximum-Likelihood-Methode, Momenten-Methode, Generalized Method of Moments). In diesem Kurs setzen wir jedoch einfach voraus, dass die Formeln für die Schätzer vorliegen. Ausführlicher behandelt werden Schätzmethoden in dem Bachelor-Wahlpflichtmodul Advanced Statistics.