2 Zufallsvorgänge
In diesem Kurs geht es um Zufall. Die Frage, was man unter Zufall eigentlich zu verstehen hat, ist schwierig zu beantworten. Sie gehört eher in den Bereich der Philosophie als den der Wirtschaftswissenschaften. Voltaire meinte dazu:
Le hasard est un mot vide de sens; rien ne peut exister sans cause.
(Zufall ist ein Wort ohne Sinn; nichts kann ohne Ursache existieren.)
Wir definieren in diesem Kurs Zufall darum auf eine sehr pragmatische Art.
Mit Zufallsvorgängen hat man es also unentwegt zu tun. Wir wissen nicht, wie sich der DAX-Index im Laufe des nächsten Monats entwickeln wird, aber wir wissen, dass er einen Wert zwischen 0 und unendlich haben wird. Die Entwicklung des DAX-Index ist also im Sinne unserer Definition zufällig. Wir wissen nicht, ob eine bestimmte Person im nächsten Jahr arbeitslos sein wird, aber wissen, dass sie es sein könnte oder auch nicht. Der Arbeitslosigkeitsstatus dieser Person ist also ebenfalls zufällig im Sinne unserer Defintion. Entscheidend für unser Verständnis von Zufall ist also nicht, dass ein Vorgang ohne erkennbare Ursache auf ein bestimmtes Ergebnis zuläuft, sondern dass wir als Beobachter nicht genau vorhersehen können, was passieren wird, selbst wenn wir wissen, dass es Faktoren gibt, mit denen man das Ergebnis erklären könnte, wenn man mehr Informationen hätte.
Oft wird bei der Definition von Zufallsvorgängen gefordert, dass sie unter identischen Bedingungen wiederholbar sind. In den Wirtschaftswissenschaften betrachten wir fast immer Zufallsvorgänge, die nicht unter identischen Bedingungen wiederholt werden können. Trotzdem werden wir in diesem Kurs, zumindest am Beginn, aus didaktischen Gründen oft wiederholbare Zufallsvorgänge betrachten, die jedoch nichts mit wirtschaftlichen Fragestellungen zu tun haben. Als Beispiel dienen vor allem Würfelwürfe. Solche Zufallsvorgänge, die sich unter praktisch identischen Bedingungen wiederholen lassen, nennt man auch Zufallsexperimente.
Damit wir einen Zufallsvorgang präzise beschreiben und vernünftig mit ihm arbeiten können, brauchen wir einen formalen Rahmen und eine geeignete Terminologie. Die Wahrscheinlichkeitstheorie bietet einen solchen Rahmen. In den folgenden Abschnitten lernen wir ihn kennen.
2.1 Mengen
Für die Wahrscheinlichkeitstheoriebraucht man einige einfache Grundbegriffe aus der Mengenlehre. Sie werden hier auf nicht formale Weise kurz dargestellt. Die Beschreibung orientiert sich an Kapitel 2.5 des Lehrbuchs “Probability Theory and Statistical Inference” (2019), 2nd ed., von Aris Spanos.
Die Objekte in einer Menge können reale physische Objekte oder imaginäre Objekte sein. Die Elemente einer Menge können Zahlen sein, aber es müssen keine Zahlen sein. Wichtig ist, dass die Objekte einer Menge unterscheidbar sind.
Die Elemente einer Menge kann man explizit aufzählen oder durch ihre Eigenschaften definieren. In beiden Fällen werden die Elemente einer Menge durch geschweifte Klammern umfasst. Die Reihenfolge der Elemente in der Menge spielt keine Rolle. Mengen dürfen auch Mengen enthalten.
Wenn ein Objekt \(x\) Elemente einer Menge \(A\) ist, schreibt man \(x\in A\) (“\(x\) ist Element von \(A\), engl. \(x\) belongs to \(A\)). Wenn \(x\) kein Element ist, schreibt man \(x\not\in A\).
Eine Menge kann endlich (engl. finite) viele oder unendliche (engl. infinite) viele Elemente enthalten. Bei Mengen mit unendlich vielen Elementen unterscheidet man verschiedene “Stufen” von Unendlichkeit. Wenn die Elemente im Prinzip mit den natürlichen Zahlen durchnummeriert werden können, nennt man die Menge abzählbar (engl. countable) unendlich. Wenn das nicht geht, heißt sie überabzählbar (engl. uncountable) unendlich. Die Mengen \(\mathbb{N}\) (natürliche Zahlen), \(\mathbb{Z}\) (ganze Zahlen), \(\mathbb{B}\) (Brüche) sind abzählbar unendlich. Die Menge der reellen Zahlen \(\mathbb{R}\) oder Intervalle von reellen Zahlen sind überabzählbar unendlich.
Eine Menge darf auch leer sein. Man nennt sie dann die leere Menge und schreibt \(\{\}\) oder \(\emptyset\).
Eine Menge \(A\) heißt Teilmenge (engl. subset) der Menge \(B\), wenn alle Elemente von \(A\) auch Element von \(B\) sind. Man schreibt dann \(A\subset B\). Nach dieser Definition gilt auch \(A\subset A\). Auch die leere Menge ist immer Teilmenge einer Menge. Wenn \(A\) keine Teilmenge von \(B\) ist, schreibt man \(A\not\subset B\).
Die Definition der Teilmenge benutzt man auch, um die Gleichheit zweier Mengen zu definieren. Zwei Mengen \(A\) und \(B\) sind gleich, wenn \(A\subset B\) und \(B\subset A\). Man schreibt \(A=B\). Will man explizit deutlich machen, dass bei \(A\subset B\) auch die Gleichheit mitgemeint ist, wird manchmal die (eigentlich redundante) Notation \(A\subseteq B\) verwendet.
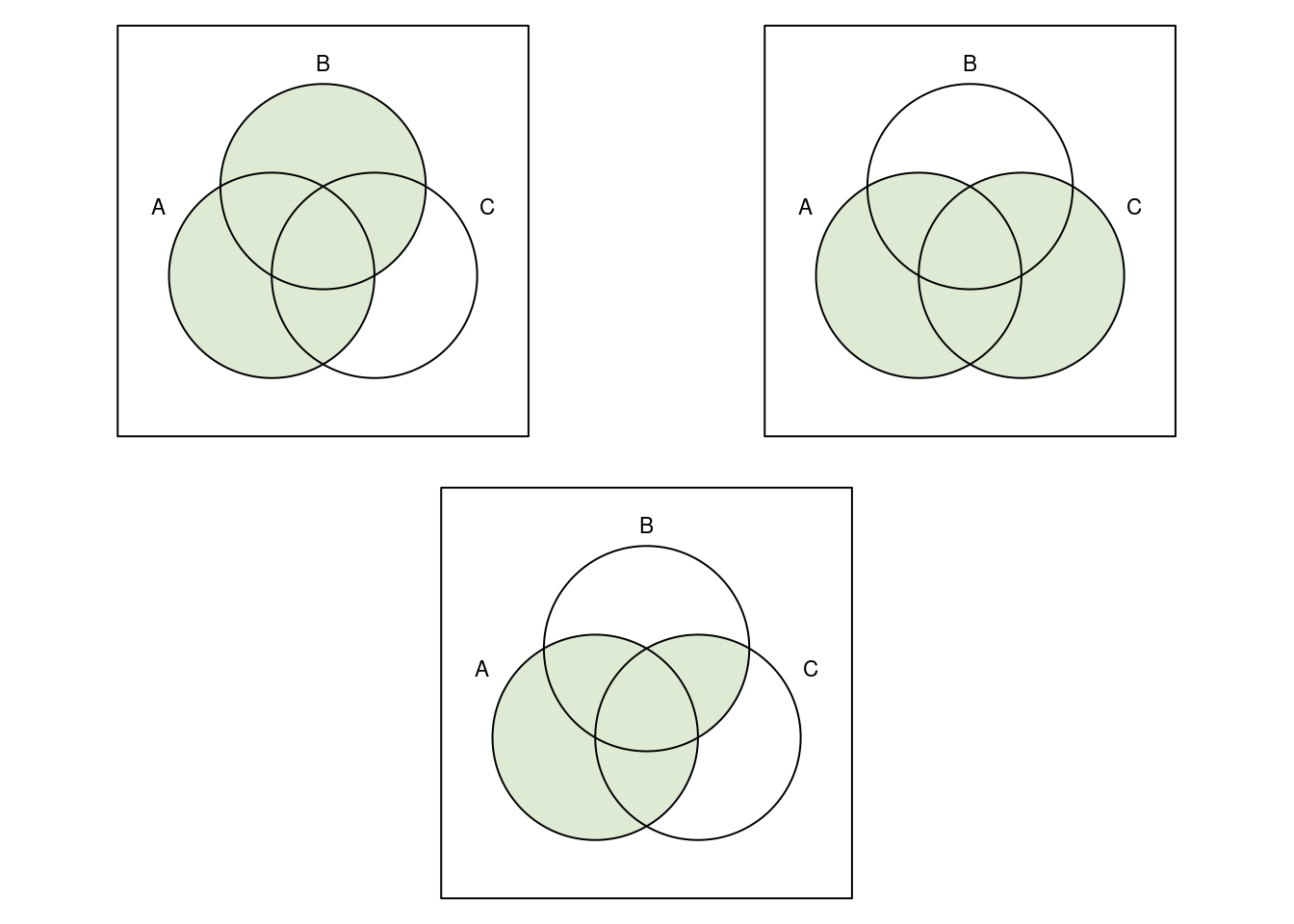
Die Vereinigungsmenge (engl. union) von zwei Mengen \(A\) und \(B\) enthält alle Elemente, die in \(A\) oder \(B\) (oder in beiden) enthalten sind. Man schreibt \(A\cup B\). Da alle Elemente einer Menge unterscheidbar sein müssen, kommen Elemente, die sowohl in \(A\) als auch in \(B\) enthalten sind, in der Vereinigungsmenge nur einmal vor.
Die Schnittmenge (engl. intersection) von zwei Mengen \(A\) und \(B\) enthält alle Elemente, die sowohl in \(A\) als auch in \(B\) enthalten sind. Man schreibt \(A\cap B\).
Sowohl die Vereinigungsmenge als auch die Schnittmenge kann auf mehr als zwei Mengen verallgemeinert werden. Beispielsweise schreibt man \(A\cup B\cup C\) für die Vereinigungsmenge von \(A\), \(B\) und \(C\) und entsprechend \(A\cap B\cap C\) für die Schnittmenge. Wenn sehr viele Mengen vereinigt oder geschnitten werden, nutzt man eine Notation, die dem Summenzeichen ähnelt, nämlich \[ \bigcup_{i=1}^n A_i \] für die Vereinigung der Mengen \(A_1,A_2,\ldots, A_n\) und \[ \bigcap_{i=1}^n A_i \] für ihre Schnittmenge.
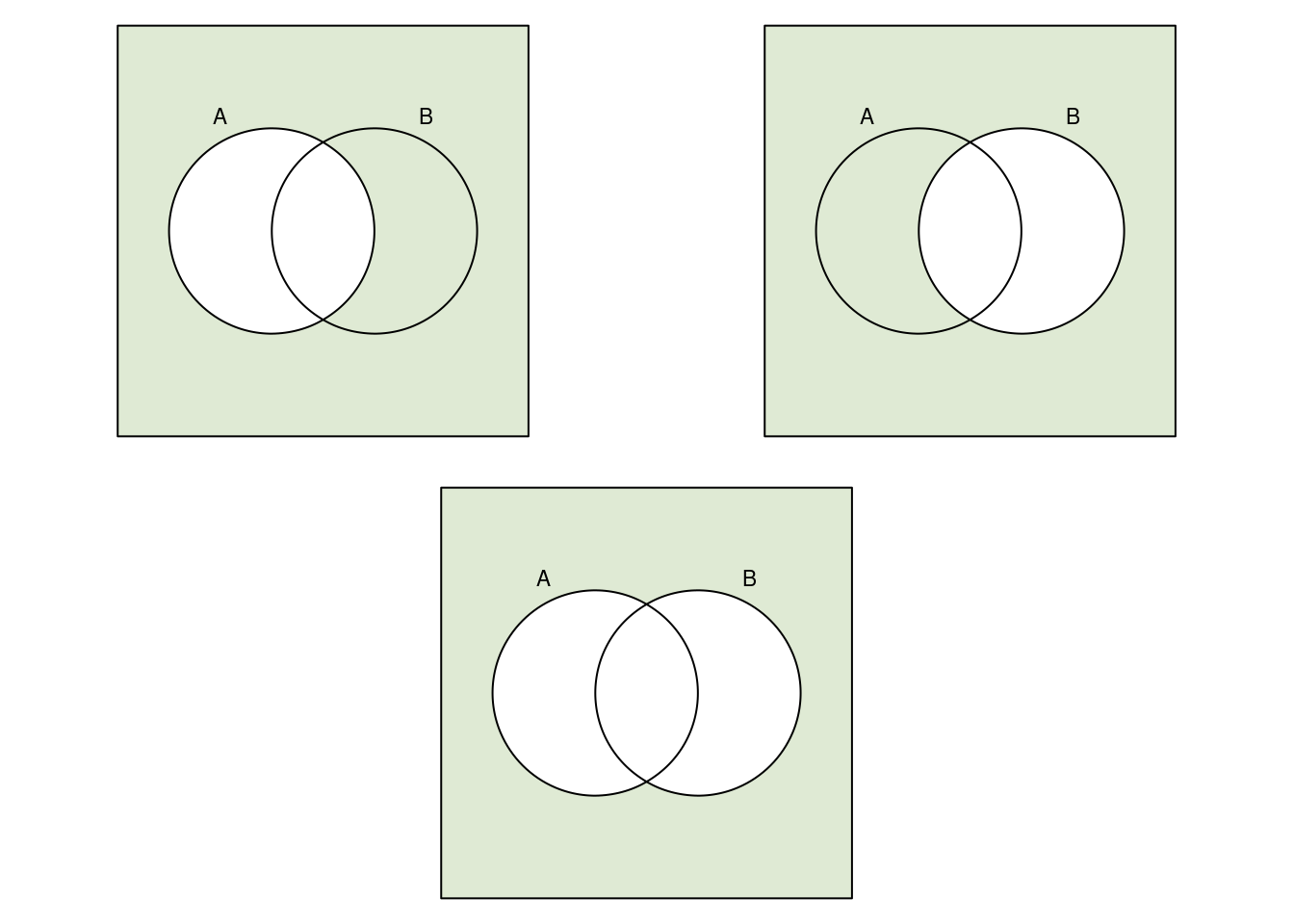
Als Komplementärmenge (engl. complementation) einer Menge \(A\) relativ zu einer Menge \(\Omega\) bezeichnet man alle Elemente aus \(\Omega\), die nicht in \(A\) enthalten sind. Man schreibt \(\bar A\) und spricht “nicht \(A\)” (die Menge \(\Omega\) wird also nicht explizit erwähnt, sie muss sich aus dem Kontext ergeben).
Sowohl Vereinigungs- als auch Schnittmenge sind kommutativ, d.h. \[\begin{align*} A\cup B &= B\cup A\\ A\cap B &= B\cap A. \end{align*}\]
Außerdem sind sie assoziativ, d.h. \[\begin{align*} A\cup (B \cup C)&= (A\cup B) \cup C\\ A\cap (B \cap C)&= (A\cap B) \cap C. \end{align*}\]
Auch das Distributivgesetz gilt, \[\begin{align*} A\cup (B \cap C)&= (A\cup B) \cap (A\cup C)\\ A\cap (B \cup C)&= (A\cap B) \cup (A\cap C). \end{align*}\]
Als Rechenregel nützlich ist oft die Regel von de Morgan. Sie zeigt, wie die Komplementärmenge einer Vereinigungsmenge oder Schnittmenge aussieht, \[\begin{align*} \overline{A \cup B} &= \bar A \cap \bar B\\ \overline{A \cap B} &= \bar A \cup \bar B. \end{align*}\] Es ist also möglich, die Schnittmengenbildung durch die Vereinigung zusammen mit der Komplementärbildung auszudrücken.
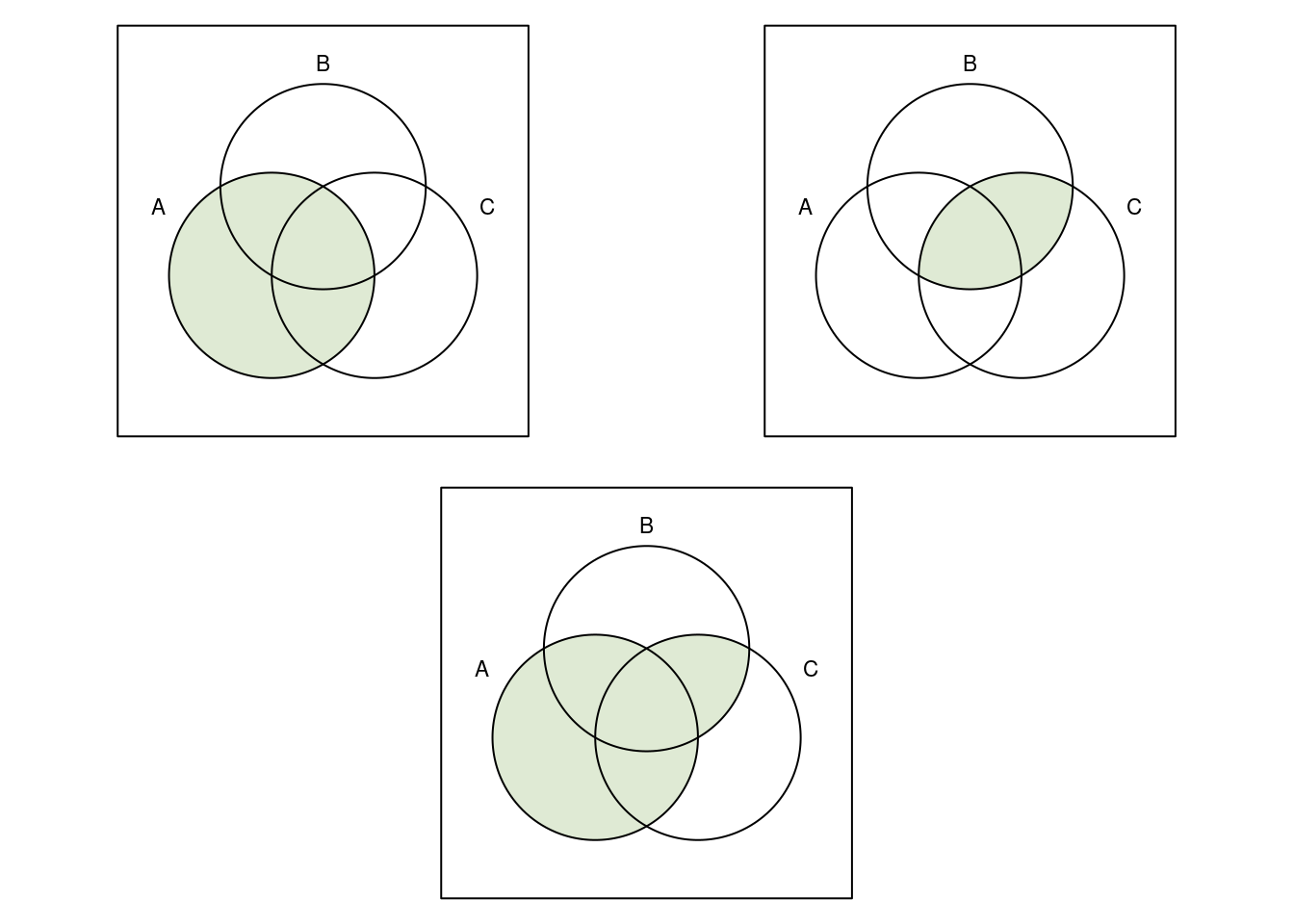
Mengen - und vor allem Mengenoperationen - können auch grafisch repräsentiert werden. Eine oft genutzte Methode sind die sogenannten Venn-Diagramme. In einem Venn-Diagramm werden Mengen durch Flächen dargestellt, oft durch Kreise. Die Elemente der Mengen können dann in die Flächen eingetragen werden. Oft interessieren einen jedoch die einzelnen Elemente gar nicht so, sondern man möchte nur die Funktionsweise der Mengenoperationen veranschaulichen.
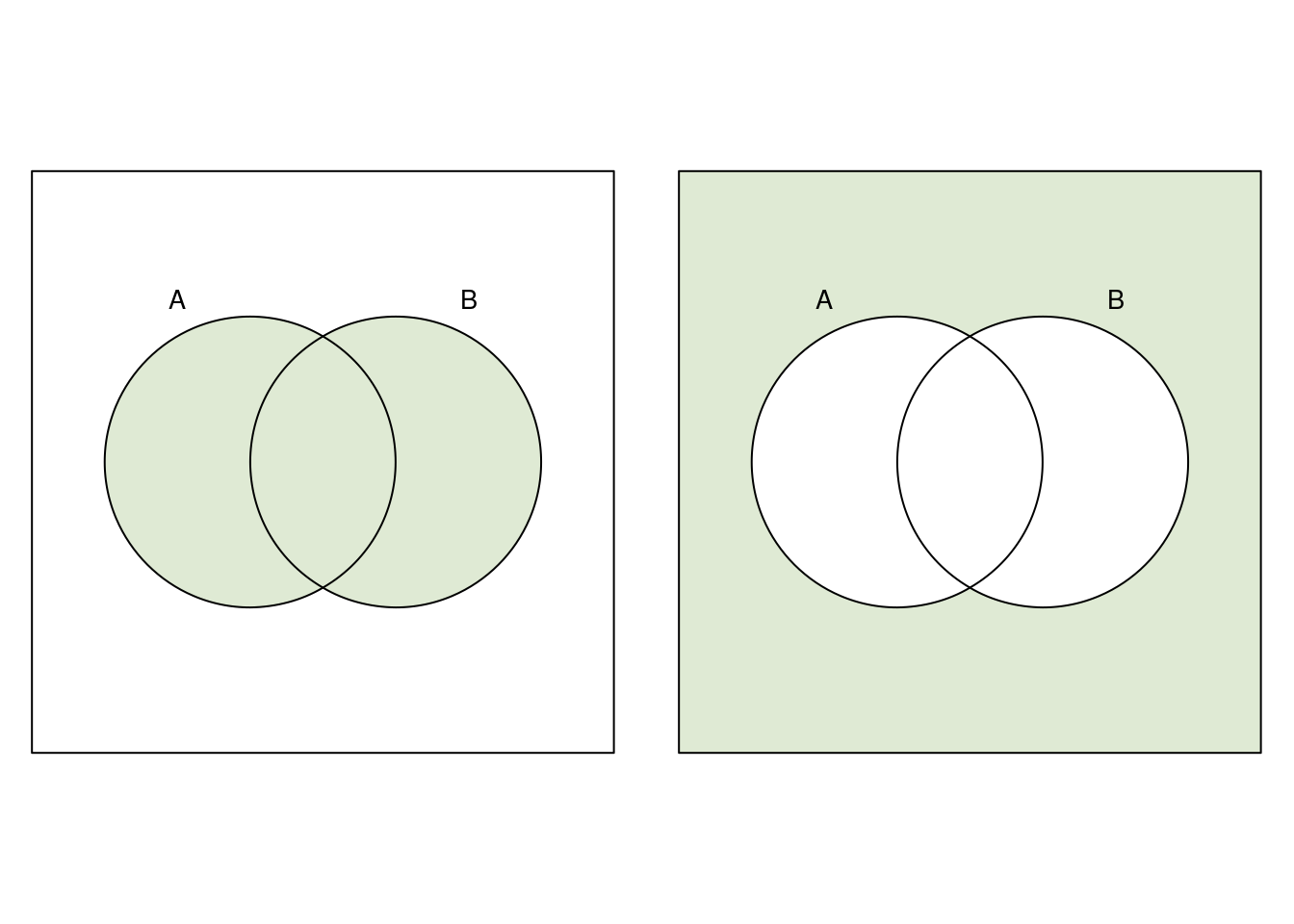
Am Beispiel von zwei Mengen \(A\) und \(B\) ist das gut zu sehen. Die beiden Mengen werden durch Kreise repräsentiert, der sie umgebende Kasten steht für die Menge \(\Omega\), die für die Komplementärmengen relevant ist.
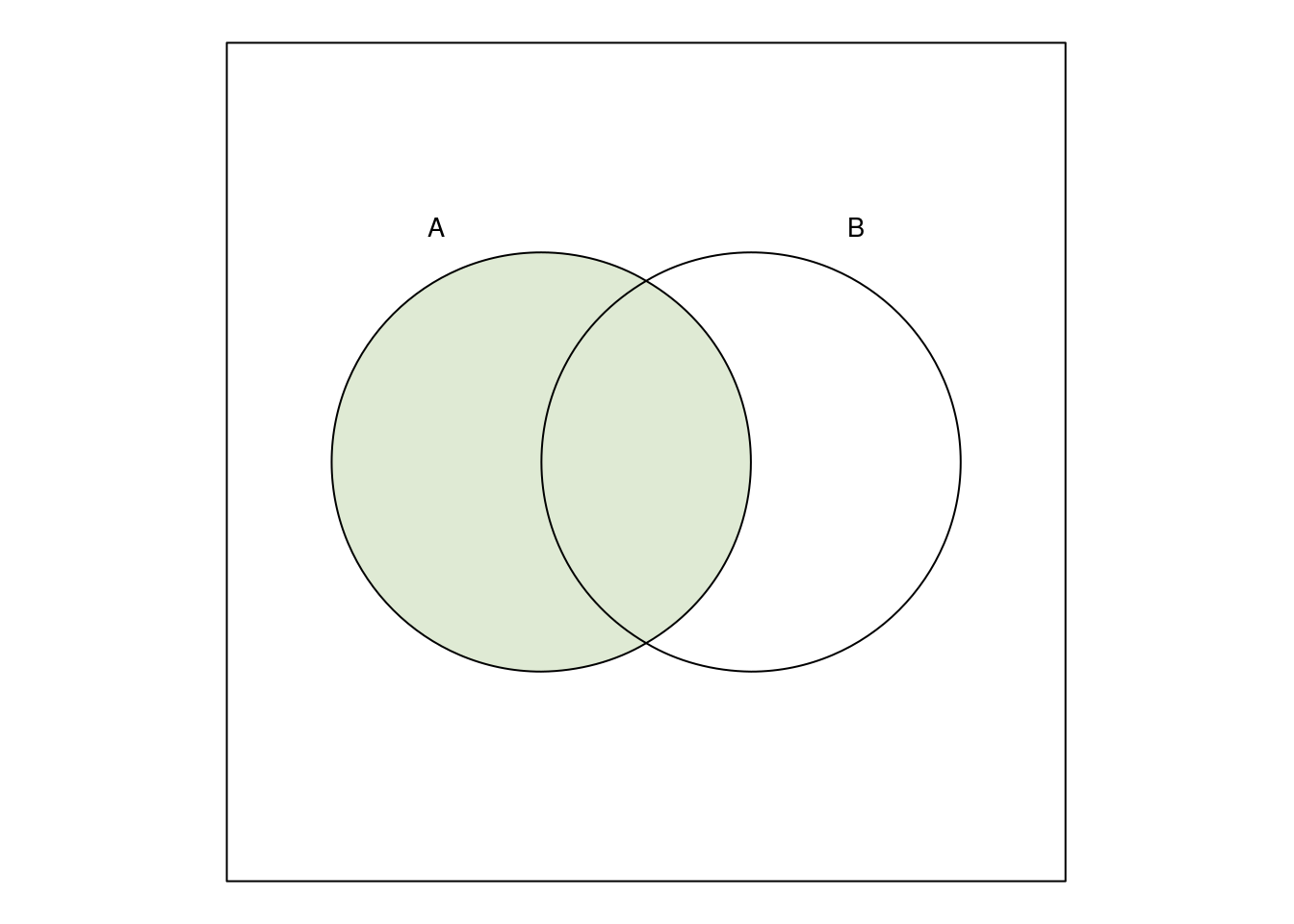
Will man ausdrücklich \(A\) zeigen, zeichnet man
Entsprechend zeigt
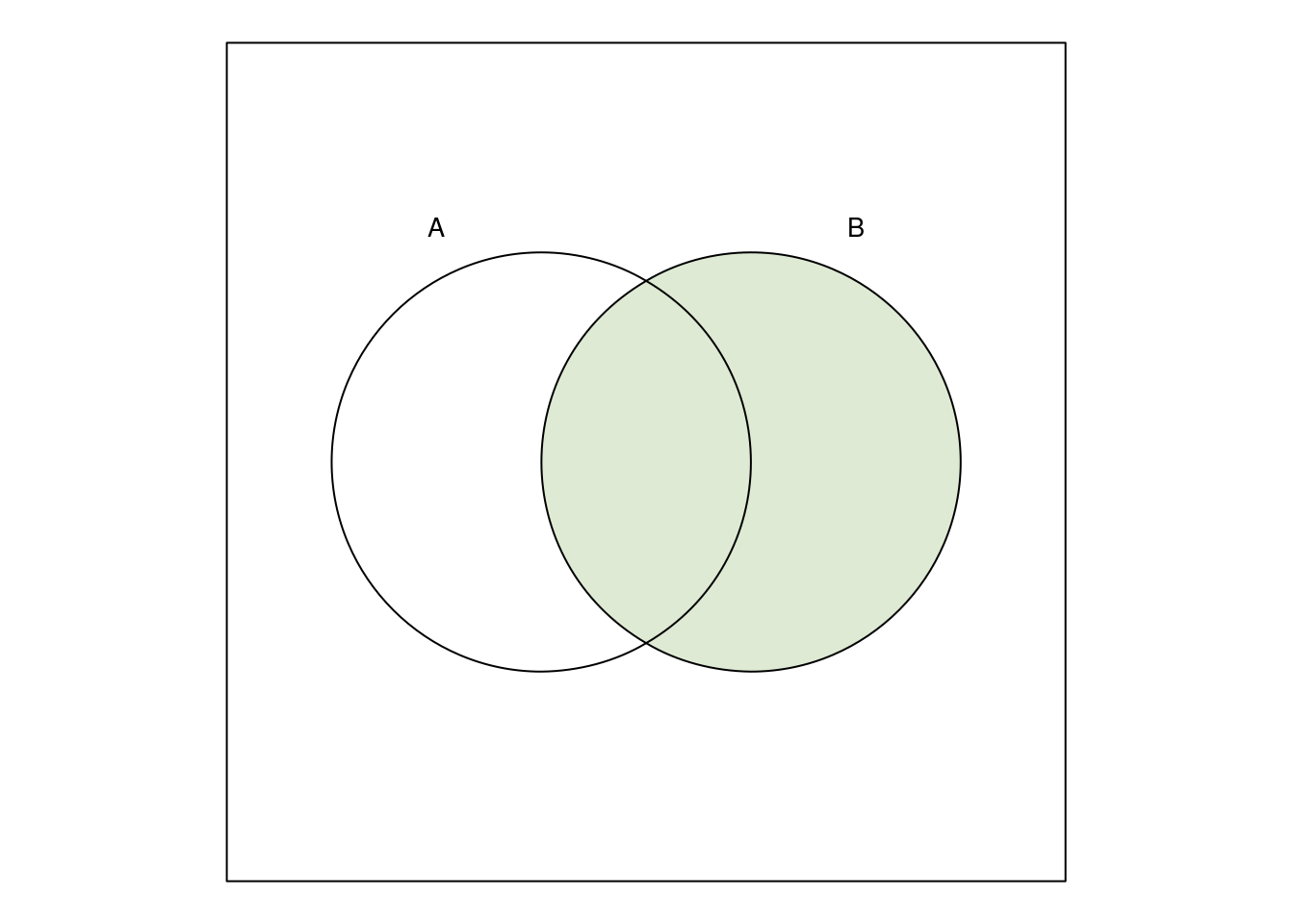
nur die Menge \(B\). Die Vereinigungsmenge \(A\cup B\) ist
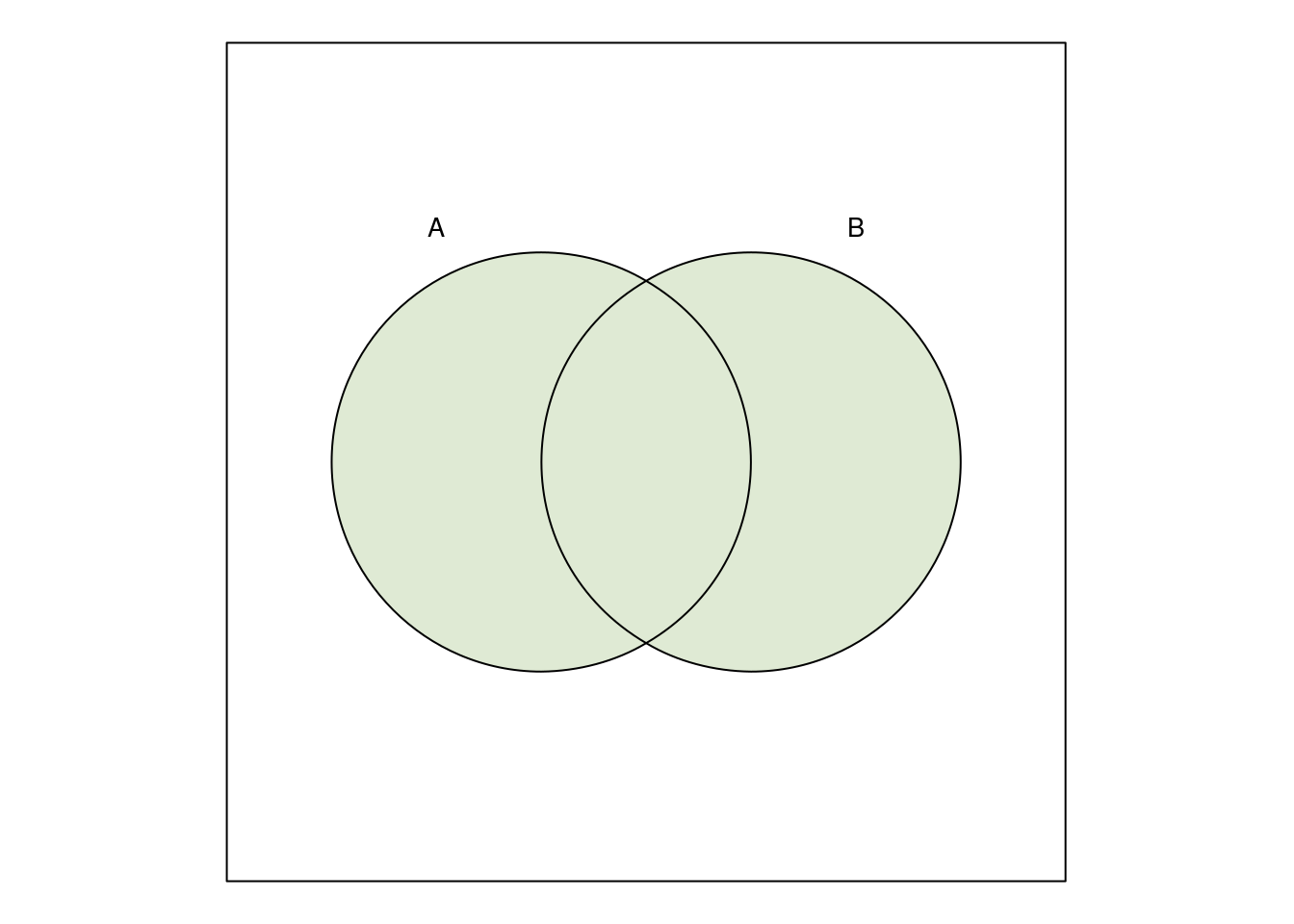
Die Schnittmenge \(A\cap B\) ist
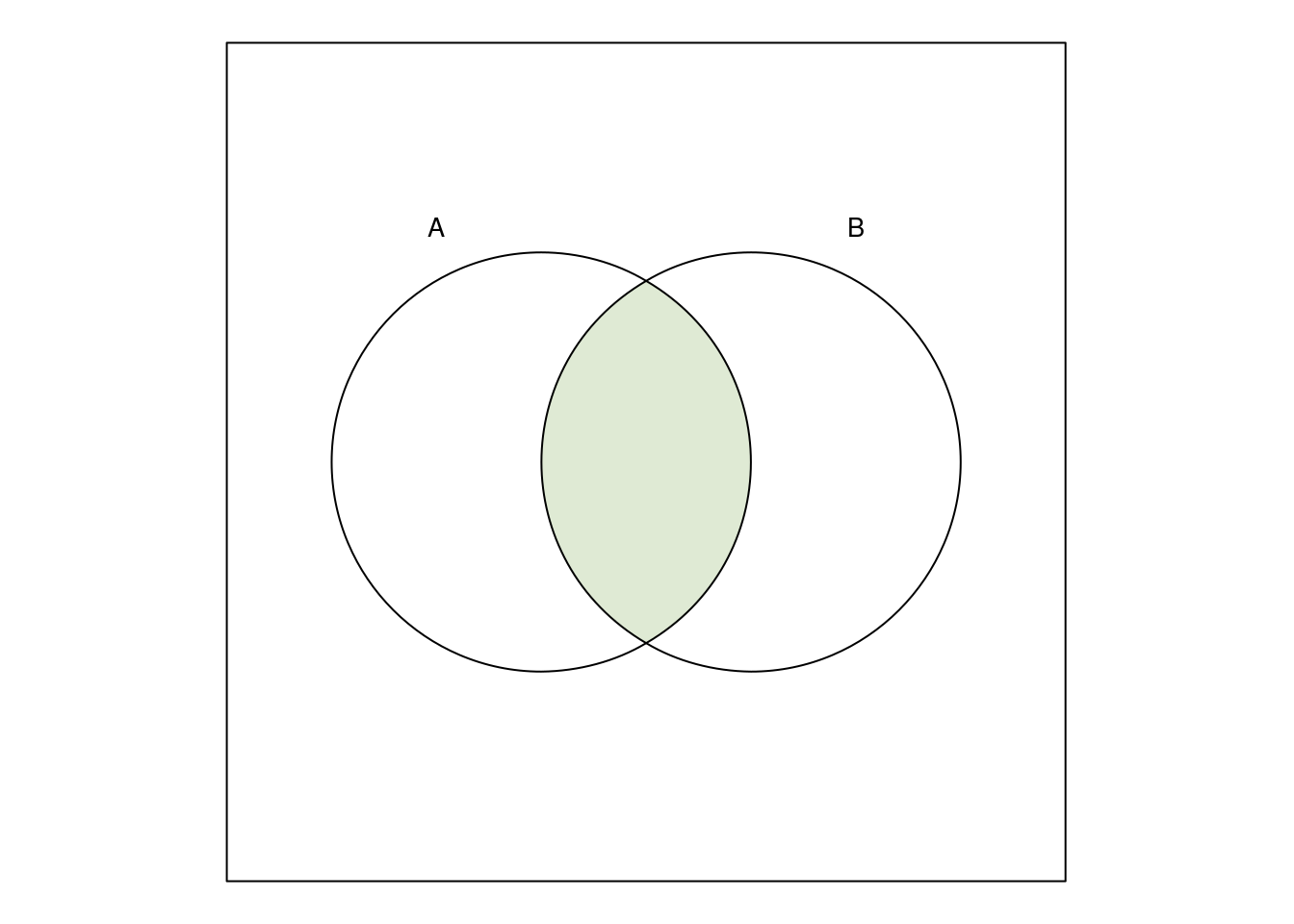
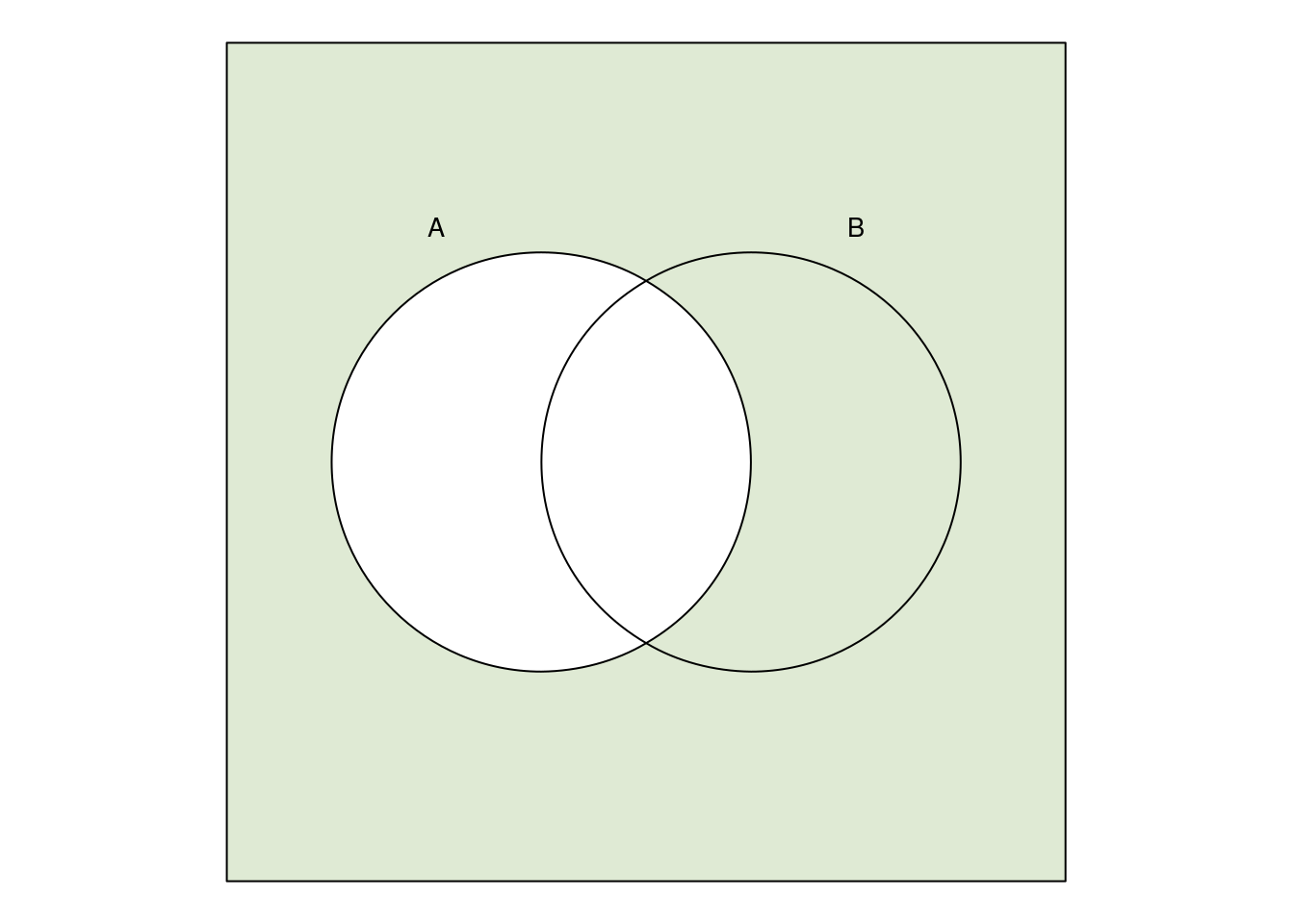
Die Komplementärmenge \(\bar A\) ist
Beispiel: Venn-Diagramm und Distributivgesetz
Die grafische Darstellung durch Venn-Diagramme kann man auch nutzen, um etwas komplexe Zusammenhänge zu illustrieren, z.B. das Distributivgesetz \[ A\cup (B \cap C)= (A\cup B) \cap (A\cup C). \] Zuerst zeichnen wir die beiden Ausdrücke auf der linken Seite der Gleichung: In der linken oberen Grafik sieht man \(A\), rechts oben \(B\cap C\). In der Mitte darunter ist die Vereinigungsmenge zu sehen.
Auf der rechten Seite der Gleichung stehen ebenfalls zwei Ausdrücke, nämlich \(A\cup B\) und \(A\cup C\). Sie sind in den folgenden beiden oberen Abbildungen zu sehen. Darunter sieht man die Schnittmenge.
Beispiel: Venn-Diagramm und de Morgansche Regel
Auf ähnliche Weise kann man sich die de Morgansche Regel \[ \overline{A \cup B} = \bar A \cap \bar B \] veranschaulichen. Wir beginnen mit der linken Seite der Gleichung. Die Vereinigung \(A\cup B\) ist im linken Bild zu sehen. Das Komplement dazu steht rechts.
Nun betrachten wir die rechte Seite der Gleichung, also \(\bar A \cap \bar B\). Oben links ist \(\bar A\) abgebildet, oben rechts \(\bar B\). Ihre Schnittmenge ist im unteren Bild gezeigt.
2.2 Ergebnisraum
Um einen Zufallsvorgang formal zu erfassen, schreiben wir alle möglichen Ergebnisse des Zufallsvorgangs in eine Menge. Dabei spielt es keine Rolle, ob der Eintritt eines Ergebnisses als wahrscheinlich oder unwahrscheinlich angesehen wird. Alle Ergebnisse, die eintreten können, werden in die Menge aufgenommen. Im Kapitel 2.1 finden Sie eine kurze Zusammenfassung zu Mengen und Mengenoperationen.
Der Ergebnisraum wird meist mit dem griechischen Buchstaben \(\Omega\) (großes Omega) bezeichnet. Die Elemente des Ergebnisraums werden allgemein als \(\omega_1,\omega_2,\ldots\) (kleine Omegas) notiert.
2.3 Ereignisse
Aussagen über Wahrscheinlichkeiten beziehen sich nicht immer nur auf einzelne Ergebnisse aus der Ergebnismenge, sondern oft auf mehrere Ergebnisse. Zusammenfassungen von Ergebnissen nennt man Ereignisse. Sie werden meist mit großen lateinischen Buchstaben bezeichnet \((A, B, C, \ldots)\).
Zu den Ereignissen gehören auch die leere Menge \(\emptyset\) und \(\Omega\) selber. Das Ereignis \(\emptyset\) nennt man das unmögliche Ereignis, weil es nie eintreten kann. Das Ereignis \(\Omega\) nennt man das sichere Ereignis, weil es mit Sicherheit eintritt. Wenn ein Ereignis nur ein einziges Ergebnis enthält (z.B. \(A=\{\omega_1\}\)), dann spricht man von einem Elementarereignis.
Weil Ereignisse Mengen sind, lassen sie sich nach den normalen Regeln der Mengenlehre verknüpfen. Dadurch lassen sich aus Ereignissen neue Ereignisse definieren.
Vereinigungsmenge (engl. union): Das Ereignis \(A\cup B\) tritt ein, wenn \(A\) oder \(B\) eintritt (oder beide).
Schnittmenge (engl. intersection): Das Ereignis \(A\cap B\) tritt ein, wenn \(A\) und \(B\) eintreten.
Komplementärmenge (engl. complementary set): Das Ereignis \(\bar A\) tritt ein, wenn \(A\) nicht eintritt.
Zwei Ereignisse heißen disjunkt (oder unvereinbar), wenn sie nicht gemeinsam eintreten können, d.h. wenn \(A\cap B=\emptyset\) ist.
Bei einem Zufallsvorgang tritt immer nur ein Ergebnis ein, da aber dieses Ergebnis Element mehrerer Ereignisse sein kann, können durchaus mehrere Ereignisse eintreten. Die Unterscheidung zwischen Ergebnis und Ereignis mag zunächst etwas haarspalterisch erscheinen, sie ist aber wichtig und nützlich, denn sie erleichtert später den Umgang mit Wahrscheinlichkeiten. Über Wahrscheinlichkeiten wurde bisher noch nichts gesagt, das folgt in Kapitel 3.
Die folgenden Rechenregeln für Mengen sind oft nützlich, wenn man mit Ereignissen arbeitet:
- Distributivgesetz:
\[\begin{align*} A\cup (B\cap C)&=(A\cup B)\cap (A\cup C)\\ A\cap (B\cup C)&=(A\cap B)\cup (A\cap C). \end{align*}\]
- Regeln von de Morgan:
\[\begin{align*} \overline{A\cup B} &= \overline{A}\cap \overline{B}\\ \overline{A\cap B} &= \overline{A}\cup \overline{B}. \end{align*}\]
Die Kardinalität oder Mächtigkeit der Ergebnismenge bezeichnen wir mit \(|\Omega|\). Wenn \(\Omega\) nur endlich viele Elemente hat, ist die Kardinalität schlicht und einfach die Anzahl der Elemente. Es ist aber auch möglich (und in vielen ökonomischen Anwendungen auch üblich), dass die Ergebnismenge unendlich viele Elemente enthält. In solchen Fällen kann es zu einigen mathematisch-technischen Schwierigkeiten kommen, die wir in diesem Kurs aber ignorieren. Eine sorgfältigere Behandlung findet in dem Bachelor-Wahlpflichtmodul Advanced Statistics statt.