R-Code zeigen
x <- c(0, 3, 4, 9)
y <- c(0, 0.3, 0.4, 0.6, 1)
plot(stepfun(x, y),
verticals=FALSE,
pch=19,
xlab="x",
ylab="F(x)",
main="Verteilungsfunktion")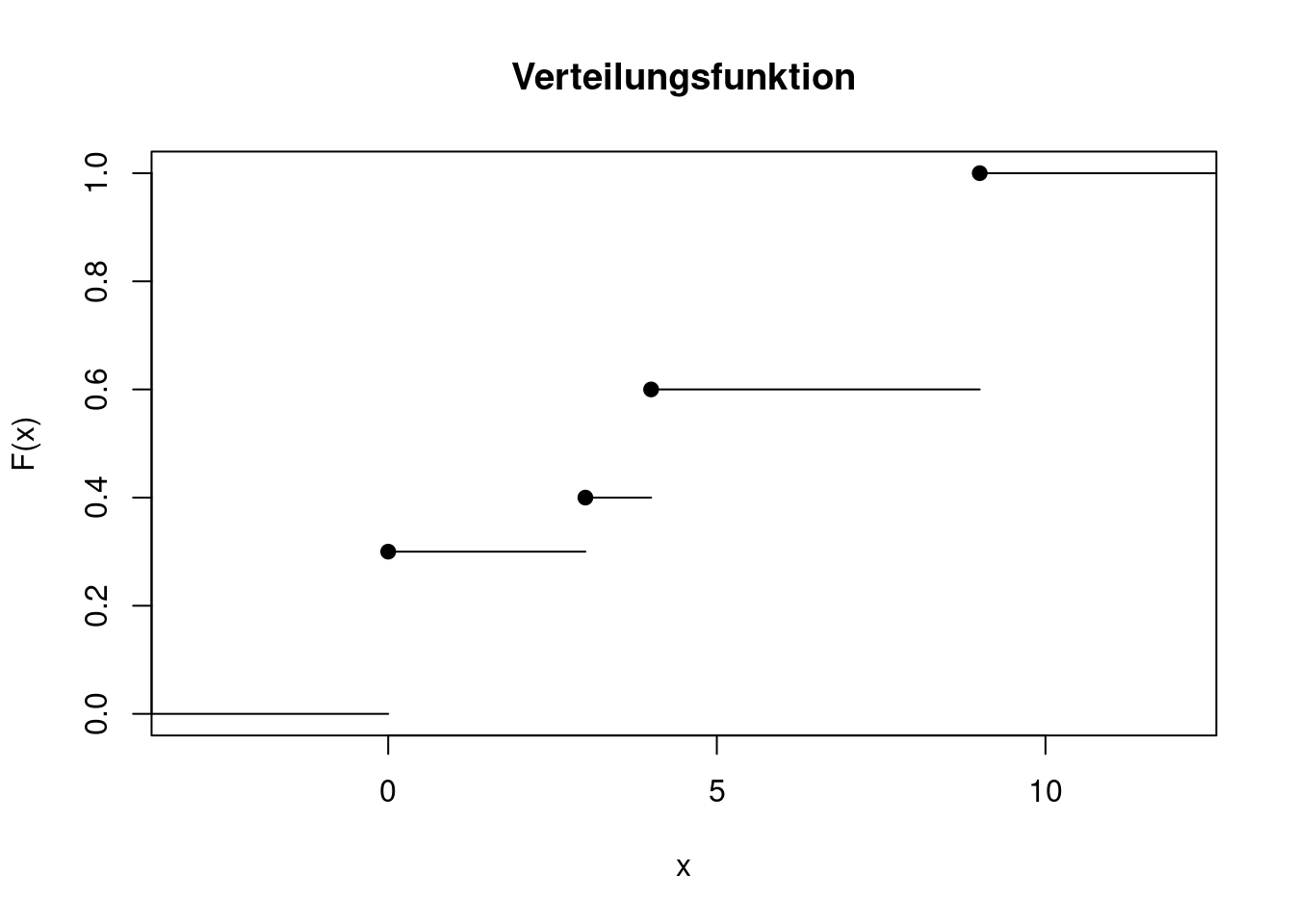
4 Zufallsvariablen
Die wichtigsten formalen Grundlagen der Wahrscheinlichkeitstheorie sind nun gelegt. Darauf aufbauend definieren wir Zufallsvariablen. Zufallsvariablen sind - intuitiv gesprochen - Zahlen, deren Wert man noch nicht kennt, deren Wert sich aber (irgendwann) realisiert. Die formale Definition von Zufallsvariablen bezieht sich auf die Ergebnismenge.
Eine Zufallsvariable kann man sich zwar als eine Zahl vorstellen, deren Wert man noch nicht kennt. Formal gesehen handelt es sich jedoch um eine Funktion, die jedem Element der Ergebnismenge genau eine reelle Zahl zuordnet.
Wenn die Zufallsvariable sich realisiert, bezeichnet man die Realisation gewöhnlich mit einem Kleinbuchstaben. Beispielsweise ist \(x\) die Realisation der Zufallsvariable \(X\). Allerdings werden Kleinbuchstaben auch in ihrer sonstigen Funktion als Variablennamen verwendet, man muss also auf den Kontext achten. Gedanklich ist es oft hilfreich, sich \(X\) (also die Zufallsvariable) als die Situation ex ante und \(x\) (also die Realisierung) als die Situation ex post vorzustellen.
Beachten Sie den großen Unterschied zwischen einer Zufallsvariable und ihrer Realisation. Die Zufallsvariable ist eine Funktion, die Realisation ist eine reelle Zahl. Wahrscheinlichkeitsaussagen lassen sich nur über Zufallsvariablen treffen, nicht über ihre Realisation.
Um mit Zufallsvorgängen in der Ökonomik zu arbeiten, sind Zufallsvariablen eine große Hilfe. Praktisch alle Vorgänge, bei denen der Zufall oder Unwissenheit eine Rolle spielen, lassen sich gut mit Hilfe von Zufallsvariablen beschreiben. In fast allen Fällen wird die Funktion \(X:\Omega\to\mathbb{R}\) nicht explizit angegeben, sondern implizit als vorhanden vorausgesetzt. Auch die Ergebnismenge wird im allgemeinen nicht ausdrücklich aufgeschrieben. Trotzdem ist es wichtig zu erkennen, dass Zufallsvariablen auf dem mengentheoretischen Fundament aufbauen, das wir in den vorangegangenen Kapiteln gelegt haben, und deshalb eine saubere mathematische Grundlage haben.
4.1 Verteilungsfunktion
Wir wissen zwar nicht, welchen Wert eine Zufallsvariable annehmen wird, aber oft wissen wir, dass bestimmte Werte mit einer höheren Wahrscheinlichkeit vorkommen als andere Werte. So wissen wir zum Beispiel, dass beim Werfen mit zwei Würfeln die Augensumme 2 weniger wahrscheinlich ist als die Augensumme 7, denn für die Augensumme 2 müssen beide Würfel eine 1 zeigen, für die Augensumme 7 gibt es dagegen viel mehr Möglichkeiten (nämlich 16, 25, 34, 43, 52 und 61). Um die Verteilung einer Zufallsvariable zu beschreiben, gibt es mehrere Möglichkeiten. Eine besonders wichtige ist die Verteilungsfunktion.
In der Definition wird die Verteilungsfunktion einer Zufallsvariable zurückgeführt auf Wahrscheinlichkeiten von Ereignissen. Dabei werden ganz spezielle Ereignisse betrachtet, nämlich \(\{\omega:X(\omega)\le x\}\). Es gibt also für jedes beliebige \(x\in\mathbb{R}\) ein solches Ereignis. Für ein gegebenes \(x\) enthält das Ereignis alle Ergebnisse, die dazu führen, dass die Zufallsvariable den Wert \(x\) nicht überschreitet. Die kompliziertere Notation, in der das Ereignis ausdrücklich hingeschrieben wird, benutzt man in der Praxis sehr viel seltener als die Kurzschreibweise. Man sollte sie trotzdem kennen und vor allem verstehen, damit die enge Verbindung zwischen Zufallsvariablen und Ereignissen klar ist. Die Verteilungsfunktion einer Zufallsvariable ist sehr nützlich, weil durch sie die Verteilung der Zufallsvariable eindeutig charakterisiert wird. Kennt man die Verteilungsfunktion, dann weiß man alles über die Verteilung, was wichtig ist.
Die Verteilungsfunktion ist - wie der Name schon sagt - eine Funktion. Ihr Definitionsbereich ist die Menge der reellen Zahlen \(\mathbb{R}\). Man darf also jede beliebige Zahl in die Funktion einsetzen. Der Wertebereich der Verteilungsfunktion ist das Intervall \([0,1]\), da es sich um eine Wahrscheinlichkeit handelt. Verteilungsfunktionen sind (wegen ihrer Konstruktion) immer monoton wachsend. Sie verlaufen niemals fallend, es kann jedoch sein, dass sie in einigen Bereichen flach verlaufen und nicht steigen. Verteilungsfunktionen können stetig sein, sie können aber auch Sprünge aufweisen.
Wenn man die Verteilungsfunktion \(F_X(x)\) für immer kleinere Werte von \(x\) auswertet, dann erreicht man (zumindest als Grenzwert) die 0, d.h. \[ \lim_{x\to -\infty} F_X(x)=0. \] Für immer größere Werte von \(x\) erreicht man (zumindest als Grenzwert) die 1, d.h. \[ \lim_{x\to\infty} F_X(x)=1. \] Für praktisch alle Anwendungen reicht es aus, sich auf zwei Klassen von Verteilungsfunktionen einzuschränken:
Die eine Klasse sind Treppenfunktionen (Stufenfunktionen), d.h. die Verteilungsfunktion hat Sprünge und verläuft zwischen den Sprüngen waagerecht. Zufallsvariablen, die eine solche Verteilungsfunktion haben, nennt man diskrete Zufallsvariablen.
Die andere Klasse sind stetige Verteilungsfunktionen (d.h. ohne Sprünge). Zufallsvariablen mit einer stetigen Verteilungsfunktion nennt man stetige Zufallsvariablen.
Im folgenden wird genauer definiert, wann Zufallsvariablen diskret oder stetig sind und was für Eigenschaften diskrete und stetige Zufallsvariablen haben.
4.2 Diskrete Zufallsvariablen
Ohne tiefer in die Mengenlehre einzusteigen, sei hier nur erwähnt, dass eine Menge abzählbar unendlich ist, wenn man ihre Elemente mit den natürlichen Zahlen durchnummerieren kann. Abzählbar unendlich sind zum Beispiel die Menge der natürlichen Zahlen \(\mathbb{N}\), die Menge der ganzen Zahlen \(\mathbb{Z}\) und die Menge aller Brüche \(\mathbb{B}\), nicht jedoch die Menge der reellen Zahlen \(\mathbb{R}\) oder ein Intervall reeller Zahlen. Letztere nennt man überabzählbar unendlich.
Die Menge aller Werte, die eine diskret verteilte Zufallsvariable annehmen kann, nennt man den Träger (engl. support) der Verteilung. Für endliche viele Ausprägungen ist der Träger \[ T_X=\{x_1,\ldots,x_J\}, \] und für (abzählbar) unendlich viele Ausprägungen ist er \[ T_X=\{x_1,x_2,x_3,\ldots\}. \] Die Funktion \[ f_X(x)=\left\{\begin{array}{ll} p_j & \text{ wenn }x=x_j\\ 0 &\text{ sonst} \end{array}\right. \] heißt Wahrscheinlichkeitsfunktion. Gelegentlich finden Sie auch die Bezeichnung Dichte für die Wahrscheinlichkeitsfunktion einer diskreten Zufallsvariable. Den Subindex lässt man weg und schreibt \(f(x)\), wenn aus dem Kontext hervorgeht, zu welcher Zufallsvariable die Wahrscheinlichkeitsfunktion gehört.
Die Verteilungsfunktion einer diskreten Zufallsvariable ist eine Treppenfunktion. Der Träger der Zufallsvariable gibt an, an welchen Stellen die Treppenstufen liegen. Die erste Stufe ist an der Stelle \(x_1\), die zweite an der Stelle \(x_2\) etc. Die Stufenhöhen sind \(p_1, p_2,\ldots,\).
Die folgende Abbildung zeigt die Verteilungsfunktion einer Zufallsvariablen \(X\). Hier und bei den folgenden Abbildungen im Rest dieses eLehrbuchs können Sie den R-Code, mit dem die Grafiken erzeugt werden, aufklappen. Er wird jedoch nicht näher erklärt und ist zum Verständnis des Inhalts auch nicht notwendig.
An dieser Verteilungsfunktion lässt sich ablesen, dass
- \(X\) diskret verteilt ist, denn die Verteilungsfunktion ist eine Treppenfunktion,
- \(X\) den Wert \(x_1=0\) mit einer Wahrscheinlichkeit von 0.3 annimmt, denn an der Stelle 0 springt die Verteilungsfunktion um 0.3 nach oben,
- \(X\) den Wert \(x_2=3\) mit einer Wahrscheinlichkeit von 0.1 annimmt, denn an der Stelle 3 springt die Verteilungsfunktion um 0.1 nach oben,
- den Wert \(x_3=4\) mit einer Wahrscheinlichkeit von 0.2 annimmt
- und den Wert \(x_4=9\) mit einer Wahrscheinlichkeit von 0.4 annimmt.
Die schwarzen Punkte zeigen, dass der Funktionswert an einer Sprungstelle immer der obere Wert ist. Man nennt die Treppenfunktion rechts-stetig, denn wenn man von der Sprungstelle ein winziges Stück nach rechts wandert, ändert sich der Funktionswert nicht. Wandert man ein winziges Stück nach links, springt man auf die tiefere Stufe zurück.
Beispiel: Anzahl der Sechsen bei zwei Würfeln
Zwei Würfel werden geworfen. Die Zufallsvariable \(X\) sei die Anzahl der Sechsen. Sie kann also nur die Wert 0, 1 oder 2 annehmen (Träger). Die Wahrscheinlichkeitsfunktion ist \[ f(x)=\left\{ \begin{array}{ll} 25/36 & \text{ für }x=0\\ 10/36 & \text{ für }x=1\\ 1/36 & \text{ für }x=2\\ 0 & \text{ sonst.} \end{array} \right. \] Die zugehörige Verteilungsfunktion lautet \[ F(x)=\left\{ \begin{array}{ll} 0 & \text{ für }x<0\\ 25/36 & \text{ für }0\le x<1\\ 35/36 & \text{ für }1\le x<2\\ 1 & \text{ für }x\ge 2. \end{array} \right. \] bzw. als Grafik
R-Code zeigen
x <- c(0, 1, 2)
y <- c(0, 25/36, 35/36, 1)
plot(stepfun(x,y),
verticals=FALSE,
pch=19,
xlab="x",
ylab="F(x)",
main="Verteilungsfunktion")
4.3 Stetige Zufallsvariablen
Wenn aus dem Kontext hervorgeht, zu welcher Zufallsvariable eine Dichte gehört, lässt man den Subindex gewöhnlich weg und schreibt einfach \(f(x)\). Die Dichte hat folgende Eigenschaften:
Die Dichte kann nicht negativ sein, da sonst die Verteilungsfunktion nicht mehr monoton wachsend wäre. Es gilt also \(f(x)\ge 0\) für alle \(x\in\mathbb{R}\).
Die Fläche unter der Dichte muss 1 ergeben, da jede Verteilungsfunktion \(F(x)\) für \(x\to\infty\) gegen 1 konvergiert. Es gilt also \[ \int_{-\infty}^\infty f(x)dx=1. \]
Die Dichte gibt an, wie steil die Verteilungsfunktion verläuft. Für alle Stellen, an denen die Verteilungsfunktion differenzierbar ist, gilt daher \[ f(x)=F'(x). \] Es ist jedoch nicht unbedingt nötig, dass die Verteilungsfunktion überall differenzierbar ist, sie darf nicht differenzierbare Knicke enthalten. Wenn es nicht differenzierbare Stellen in der Verteilungsfunktion gibt, dann weist die Dichte an diesen Stellen einen Sprung auf.
Der Wert der Dichte an einer Stelle \(x\) ist keine Wahrscheinlichkeit. Hingegen ist die Fläche unter der Dichte eine Wahrscheinlichkeit. So gilt beispielsweise \[ P(a<X\le b)=\int_a^b f(x)dx. \]
Die Wahrscheinlichkeit, dass eine stetige Zufallsvariable exakt den Wert \(x\) annimmt, ist also (für jedes \(x\in\mathbb{R}\)) \[ P(X=x)=0. \] Das impliziert, dass es (im Gegensatz zu diskreten Zufallsvariablen) bei stetigen Zufallsvariablen keine Rolle spielt, ob in einer Ungleichung die Gleichheit enthalten ist oder nicht, d.h. \[ P(X\le x)=P(X<x),\qquad P(X\ge x)=P(X>x) \]
Die Menge \(T_X=\{x: f_X(x)>0\}\) ist der Träger (engl. support) der Zufallsvariable \(X\). Der Träger enthält alle Werte, die die Zufallsvariable im Prinzip annehmen könnte.
Obwohl die Dichte selbst keine Wahrscheinlichkeit ist, hilft sie beim intuitiven Verständnis einer Verteilung trotzdem sehr. Man erkennt an einem Dichte-Plot sofort, in in welchen Bereichen die Zufallsvariable mit großer Wahrscheinlichkeit liegen wird und wo es eher unwahrscheinlich ist.
Beispiel: Dichte- und Verteilungsfunktion
Die Dichte der Zufallsvariable \(X\) sei \[ f(x)=\left\{ \begin{array}{ll} 0 & \text{ wenn }x < -0.56\\ -x^4+x^2+0.5 & \text{ wenn }-0.56 \le x < 1.1\\ 0 & \text{ wenn }x \ge 1.1. \end{array} \right. \] Der Plot der Dichte zeigt, dass die Realisation der Zufallsvariable \(X\) mit Sicherheit in dem Intervall \([-0.56, 1.1]\) liegen wird. Es ist eher unwahrscheinlich, dass ein Wert sehr nah an der rechten Grenzen realisiert wird. Auch der Bereich um die 0 herum ist etwas weniger wahrscheinlich als die Bereiche um die 0.75 herum oder nah an der linken Grenze.
R-Code zeigen
x <- c(-1, -0.56, NA,
seq(-0.56, 1.1, length=100),
NA, 1.1, 1.8)
f <- 0.5-x^4+x^2
f[c(1, 2, 105, 106)] <- 0
plot(x, f, t="l", lwd=3,
xlab="x", ylab="f(x)",
main="Dichte")
Wie hoch ist die Wahrscheinlichkeit, dass die Zufallsvariable \(X\) in dem Intervall \([0.1,0.8]\) liegt? Um diese Frage zu beantworten, berechnen wir das Integral
\[\begin{align*} \int_{0.1}^{0.8} f(x)dx&=\int_{0.1}^{0.8} (-x^4+x^2+0.5) dx\\ &= \left. -\frac{1}{5}x^5+\frac{1}{3}x^3+\frac{1}{2}x \right|_{0.1}^{0.8}\\[2ex] &= 0.4548. \end{align*}\]
Die Verteilungsfunktion erhält man durch Integration der Dichte. \[ F(x)=\left\{ \begin{array}{ll} 0 & \text{ wenn }x < -0.56\\ -\frac{1}{5}x^5+\frac{1}{3}x^3+\frac{1}{2}x+0.3275 & \text{ wenn }-0.56 \le x < 1.1\\ 1 & \text{ wenn }x \ge 1.1. \end{array} \right. \] Die Konstante (0.3275) muss so gewählt werden, dass die Verteilungsfunktion am Punkt -0.56 bei 0 startet und am Punkt 1.1 bei 1 endet. Der Plot der Verteilungsfunktion macht deutlich, dass Verteilungsfunktionen für das schnelle Erfassen der Eigenschaften einer Verteilung nicht so gut geeignet sind wie Dichtefunktionen. Die Realisation der Zufallsvariable liegt mit höherer Wahrscheinlichkeit in einem Bereich, in dem die Verteilungsfunktion steil ist, als in einem Bereich, in dem sie flacher verläuft. Bereiche, in denen die Verteilungsfunktion gar nicht ansteigt, gehören nicht zum Träger der Zufallsvariable.
R-Code zeigen
x <- c(-1, -0.56,
seq(-0.56, 1.1, length=100),
1.1, 1.8)
f <- x^3/3-x^5/5+x/2+0.3275
f[1:2] <- 0
f[103:104] <- 1
plot(x, f, t="l", lwd=3,
xlab="x", ylab="F(x)",
main="Verteilungsfunktion")
4.4 Numerische Integration
Nicht immer ist es möglich, Integrale in geschlossener Form zu berechnen. In manchen Fällen ist es vielleicht möglich, aber so mühsam, dass sich der Aufwand nicht lohnt, wenn eine Approximation des Ergebnisses ausreicht. In solchen Fällen lassen sich die Integrale durch numerische Verfahren berechnen. Auch für die Plausibilitätskontrolle eines analytischen Ergebnisses eignet sich die numerische Integration. Die numerische Mathematik liefert ausgefeilte Algorithmen für die numerische Integration. In diesem Kurs lernen Sie nur eine “Holzhammer-Methode” kennen, mit der Sie eine grobe Approximation eines Integrals schnell und einfach bestimmen können.
Das Integral einer Funktion \(f(x)\) von \(a\) bis \(b\) ist die Fläche zwischen der Funktion und der x-Achse, \[ \int_a^b f(x)dx. \]
Die Fläche lässt sich annähern, indem man viele schmale Rechtecke in die Funktion einschmiegt. Die Graphik illustriert das beispielhaft für das Integral von 0.1 bis 0.8 der Dichtefunktion \[ f(x)=0.5-x^4+x^2. \]
R-Code zeigen
x <- c(-1, -0.56, NA,
seq(-0.56, 1.1, length=100),
NA, 1.1, 1.8)
f <- function(x){
return(0.5-x^4+x^2)
}
ff <- f(x)
ff[c(1, 2, 105, 106)] <- 0
plot(x, ff, t="l", lwd=3,
xlab="x", ylab="f(x)",
main="Approximation des Integrals von 0.1 bis 0.8")
abline(h=0)
dx <- 0.05
g <- seq(0.1,0.8,by=dx)
for(i in 1:(length(g)-1)){
lines(c(g[i], g[i], g[i]+dx, g[i]+dx),
c(0, f(g[i]), f(g[i]), 0))
}
Die Fläche der Rechtecke lässt sich sehr leicht bestimmen, selbst wenn es viele sind. Wenn die Gitterpunkte zwischen \(a\) und \(b\) mit \(x_1,\ldots,x_R\) bezeichnet werden und der Abstand zwischen zwei benachbarten Gitterpunkten mit \(\Delta\), dann ist die gesamte Fläche aller Rechtecke \[ \sum_{i=1}^R f(x_i)\Delta. \] Je feiner die Rechtecke (d.h. je größer \(R\) bzw. je kleiner \(\Delta\)) sind, desto genauer wird das Integral approximiert. Die Breite der Rechtecke entspricht (im Grenzwert) dem Symbol \(dx\) des Integrals.
Diese Berechnung kann wie folgt in R umgesetzt werden. Zuerst wird ein feines Gitter von \(a=0.1\) bis \(b=0.8\) erzeugt. Die Gitterpunkte werden in einem Vektor x abgelegt. Der Vektor wird durch die Funktion seq erzeugt (s. Kapitel A.1). Dabei können Sie entweder mit der Option length die Anzahl der Gitterpunkte festlegen oder alternativ mit der Option by den Abstand der Gitterpunkte voneinander vorgeben. In dem folgenden Code wird der Abstand vorgegeben und mit dx bezeichnet, um die Analogie zum Integral deutlich zu machen.
dx <- 0.001
x <- seq(from=0.1, to=0.8, by=dx)Nun werden die Funktionwerte an allen Gitterpunkten x ermittelt und in dem Vektor f gespeichert. Da R vektor-orientiert arbeitet, geschieht das sehr einfach mit einem einzigen Befehl.
f <- 0.5 - x^4 + x^2Der Wert des Integrals kann nun angenähert werden durch
sum(f*dx)[1] 0.4554194Der analytisch hergeleitete Wert des Integrals beträgt 0.4548. Der Fehler der numerischen Approximation ist also sehr klein.
4.5 Quantilfunktion
Die Quantilfunktion ist das Gegenstück zur Verteilungsfunktion. Während die Verteilungsfunktion auf die Frage antwortet “Wie hoch ist die Wahrscheinlichkeit, dass die Zufallsvariable den Wert \(x\) nicht übersteigt?”, beantwortet die Quantilfunktion die Frage “Welcher Wert wird mit einer Wahrscheinlichkeit von \(p\) nicht überschritten?”. Da es einige Fälle gibt, in denen diese Frage nicht eindeutig beantwortet werden kann, ist die formale Definition der Quantilfunktion etwas komplizierter:
Den Subindex kann man weglassen, wenn sich die Zufallsvariable aus dem Kontext ergibt. Gelegentlich findet man auch die alternative Notation \(Q_X(p)\) oder \(Q(p)\) für die Quantilfunktion. Das 0.5-Quantil heißt auch Median (engl. median).
Aus einer gegebenen Verteilungsfunktion lässt sich die Quantilfunktion durch Invertieren finden. Das geht leicht, wenn die Verteilungsfunktion streng monoton steigend verläuft. Aufpassen muss man jedoch, wenn sie Sprünge aufweist oder in einigen Bereichen flach verläuft.
Beispiel: Anzahl der Sechsen bei zwei Würfeln
Zwei Würfel werden geworfen. Die Zufallsvariable \(X\) sei die Anzahl der Sechsen. Die Verteilungsfunktion ist eine Treppenfunktion mit den Sprungstellen 0, 1 und 2, die hier noch einmal gezeigt wird.
R-Code zeigen
x <- c(0, 1, 2)
y <- c(0, 25/36, 35/36, 1)
plot(stepfun(x, y),
verticals=FALSE,
pch=19,
xlab="x",
ylab="F(x)",
main="Verteilungsfunktion")
Wie sieht die zugehörige Quantilfunktion aus? Um das zu beantworten, wandern wir langsam die y-Achse hoch und schauen jeweils, welches Quantil zu dem Wert gehört. Für Werte von \(0<p\le 25/36\) landet man auf dem Quantil 0. Für \(25/36<p\le 35/36\) ergibt sich das Quantil 1 und für \(p>35/36\) ist das Quantil 2. Also ist \[ F^{-1}(p)=\left\{ \begin{array}{ll} 0 & \text{ wenn }0 < p \le 25/36\\ 1 & \text{ wenn }25/36 < p \le 35/36\\ 2 & \text{ wenn }p>35/36 \end{array} \right. \] bzw. als Grafik
R-Code zeigen
p <- c(0, 25/36, 35/36, 1)
Q <- c(0, 1, 2)
plot(p[1:2], Q[c(1,1)],
t="l",
xlab="x",
ylab="F(x)",
xlim=c(0,1),
ylim=c(0,2),
main="Quantilfunktion")
for(i in 2:length(Q)){
lines(p[c(i,i+1)], Q[c(i,i)])
}
points(p[2:3], Q[1:2], pch=19)
Im Gegensatz zur Verteilungsfunktion ist die Quantilfunktion nicht rechtsstetig, sondern linksstetig. Der Funktionswert an einer Sprungstelle ist gleich dem Grenzwert, wenn man sich von links der Sprungstelle nähert.
4.6 Erwartungswert
Der Erwartungswert einer Verteilung gibt Auskunft darüber, wo der “Schwerpunkt” der Verteilung liegt.
Beachten Sie, dass der Erwartungswert einer Zufallsvariablen keine Zufallsvariable, sondern eine reelle Zahl ist. Wir werden später in Kapitel 8.1 sehen, dass der Erwartungswert derjenige Wert ist, gegen den der Durchschnitt von sehr vielen Realisierungen der Zufallsvariable (in einem gewissen Sinn) konvergiert. Wirft man z.B. einen Würfel sehr oft (eigentlich unendlich oft), dann ergibt sich als Durchschnitt der (unendlich) vielen Realisationen der Erwartungswert.
Wie der Erwartungswert einer Zufallsvariable berechnet wird, hängt davon ab, ob es sich um eine diskrete oder eine stetige Zufallsvariable handelt.
4.7 Varianz
Die Varianz einer Zufallsvariable gibt an, wie stark die Verteilung streut bzw. wie sehr man mit großen Abweichungen vom Erwartungswert rechnen sollte.
Ebenso wie der Erwartungswert ist auch die Varianz einer Zufallsvariable eine reelle Zahl. Für diskrete und stetige Zufallsvariablen lässt sich die Varianz folgendermaßen schreiben: \[ Var(X)=\left\{ \begin{array}{ll} \sum\limits_{j:x_j\in T_X} (x_j-E(X))^2 f(x_j) & \text{ wenn } X\text{ diskret}\\[2ex] \int\limits_{-\infty}^\infty (x-E(X))^2 f(x)dx & \text{ wenn } X\text{ stetig} \end{array} \right. \]
Für die Berechnung der Varianz ist manchmal die folgende Formel hilfreich: \[ Var(X)=E(X^2)-(E(X))^2. \]
4.8 Lineare Transformationen
Eine lineare Transformation einer Zufallsvariable ergibt wieder eine Zufallsvariable. Für zwei reelle Zahlen \(a\) und \(b\) ist \[ Y=aX+b \] eine lineare Transformation von \(X\). Welche Eigenschaften hat die transformierte Zufallsvariable \(Y\)? Wir sehen uns an, wie sich die Transformation auf die Verteilungsfunktion, den Erwartungswert und die Varianz auswirkt.
Die Verteilungsfunktion von \(Y\) ist für \(a>0\)
\[\begin{align*} F_Y(y) &= P(Y\le y)\\ &= P(aX+b \le y)\\ &= P(aX \le y-b)\\ &= P\left(X \le \frac{y-b}{a}\right)\\ &= F_X\left(\frac{y-b}{a}\right). \end{align*}\]
Für \(a<0\) dreht sich die Ungleichung bei der Division durch \(a\) um, also gilt dann
\[\begin{align*} F_Y(y) &= P(Y\le y)\\ &= P(aX+b \le y)\\ &= P(aX \le y-b)\\ &= P\left(X \ge \frac{y-b}{a}\right)\\ &= 1-P\left(X <\frac{y-b}{a}\right). \end{align*}\]
Wie die Beziehung des letzten Terms zur Verteilungsfunktion von \(X\) aussieht, lässt sich nicht einfach allgemein beantworten. Wenn \(X\) stetig verteilt ist, macht es keinen Unterschied, ob in der Ungleichung ein “\(<\)” oder ein “\(\le\)” steht, dann ist also \[ F_Y(y)=1-F_X\left(\frac{y-b}{a}\right). \] Wie wirkt sich eine lineare Transformation \(Y=aX+b\) auf den Erwartungswert aus? Wir untersuchen diskrete und stetige Zufallsvariablen getrennt voneinander. Zuerst betrachten wir eine diskrete Zufallsvariable \(X\) und \(a,b\in\mathbb{R}\). Der Erwartungswert von \(Y\) ist
\[\begin{align*} E(Y) &= E(aX+b)\\ &= \sum_{j\in T_X}(ax_j+b)f(x_j)\\ &= \sum_{j\in T_X}ax_j f(x_j) + \sum_{j\in T_X}b f(x_j)\\ &= a\sum_{j\in T_X}x_j f(x_j) + b\sum_{j\in T_X}f(x_j)\\ &= aE(X)+b, \end{align*}\]
denn \(\sum_{j\in T_X}f(x_j)=1\). Wenn \(X\) eine stetige Zufallsvariable ist, dann gilt für den Erwartungswert der linearen Transformation
\[\begin{align*} E(Y) &= E(aX+b)\\ &= \int_{-\infty}^\infty (ax+b)f(x)dx\\ &= \int_{-\infty}^\infty ax f(x)dx + \int_{-\infty}^\infty b f(x)dx\\ &= a\int_{-\infty}^\infty x f(x)dx + b\int_{-\infty}^\infty f(x)dx\\ &= aE(X)+b, \end{align*}\]
weil \(\int_{-\infty}^\infty f(x)dx=1\).
Es gilt also sowohl für diskrete als auch für stetige Zufallsvariablen, dass der Erwartungswert der linearen Transformation der Zufallsvariable der linearen Transformation des Erwartungswerts entspricht. Kurz gesagt, kann man den Erwartungswert in eine lineare Funktion “hineinziehen” oder ihn aus ihr “herausziehen”. Man sagt auch, dass der Erwartungswert ein “linearer Operator” ist.
Achtung: Den Erwartungswert darf man im allgemeinen nicht aus anderen (nichtlinearen) Funktionen herausziehen oder ihn dort hineinziehen. So ist beispielsweise im allgemeinen \[
E(X^2) \neq E(X)^2.
\] Die Ergebnisse zum Erwartungswert können wir nun benutzen, um die Varianz einer linear transformierten Zufallsvariable zu untersuchen. Es gilt
\[\begin{align*} Var(Y) &= E((Y-E(Y))^2)\\ &= E((aX+b-E(aX+b))^2)\\ &= E((aX+b-(aE(X)+b))^2)\\ &= E((aX+b-aE(X)-b)^2)\\ &= E((aX-aE(X))^2)\\ &= E(a^2(X-E(X))^2)\\ &= a^2 E((X-E(X))^2)\\ &= a^2 Var(X). \end{align*}\]
Diese Herleitung gilt sowohl für diskrete als auch für stetige Zufallsvariablen. Offensichtlich wirkt sich eine additive Verschiebung um \(b\) überhaupt nicht auf die Varianz aus. Eine Multiplikation mit \(a\) verändert die Varianz jedoch, und zwar um den Faktor \(a^2\). Wenn \(a>1\) ist, wird die Varianz also größer, wenn \(0<a<1\) ist, wird sie kleiner. Beachten Sie, dass es für die Varianz keine Rolle spielt, ob \(a\) positiv oder negativ ist. Insbesondere bleibt die Varianz unverändert, wenn \(X\) mit \((-1)\) multipliziert wird.
4.9 Standardisierung
Eine lineare Transformation, die dazu führt, dass der Erwartungswert der transformierten Zufallsvariable 0 und die Varianz 1 ist, nennt man Standardisierung. Die transformierte Zufallsvariable heißt standardisiert. Vergleicht man zwei standardisierte Zufallsvariablen miteinander, dann wird sowohl die Lage (Erwartungswert) als auch die Streuung (Varianz) beim Vergleich ausgeblendet. Welche lineare Transformation muss für eine Standardisierung durchgeführt werden? Wie erreicht man, dass der Erwartungswert nach der Transformation 0 ist und die Varianz 1? Wir gehen in zwei Schritten vor. Im ersten Schritt subtrahieren wir von der Zufallsvariablen \(X\) ihren Erwartungswert \(E(X)\) (also eine reelle Zahl), \[
X-E(X).
\] Die Zufallsvariable \(X-E(X)\) hat den Erwartungswert \[
E(X-E(X))=E(X)-E(X)=0.
\] Die Varianz von \(X-E(X)\) ist gleich der Varianz von \(X\), denn die Varianz verändert sich nicht, wenn eine reelle Zahl addiert oder subtrahiert wird. Der Erwartungswert ist eine reelle Zahl. Man nennt die Zufallsvariable \(X-E(X)\) auch zentriert.
Im zweiten Schritt dividieren wir \(X-E(X)\) durch die Standardabweichung von \(X\), \[ \frac{X-E(X)}{\sqrt{Var(X)}}. \] Dadurch verändert sich der Erwartungswert nicht, er bleibt weiterhin 0. Wie groß ist die Varianz? Um das zu beantworten, nutzen wir die Ergebisse zu Varianzen von linearen Transformationen, insb. das Ergebnis, dass eine multiplikative Konstante aus der Varianz herausgezogen werden kann, dann aber ins Quadrat gesetzt werden muss. Also ergibt sich \[ Var\left( \frac{X-E(X)}{\sqrt{Var(X)}} \right)= \frac{1}{Var(X)}Var(X-E(X))=1. \] Im letzten Schritt wird ausgenutzt, dass der Erwartungswert eine reelle Zahl ist, so dass \(X-E(X)\) nur eine Verschiebung der Zufallsvariable ist. Das hat keinen Einfluss auf die Varianz, sie ist weiterhin \(Var(X)\). Fassen wir zusammen: Wenn \(X\) eine Zufallsvariable mit Erwartungswert \(E(X)\) und Varianz \(Var(X)\) ist, dann hat die linear transformierte Zufallsvariable \[ Y=\frac{X-E(X)}{\sqrt{Var(X)}} \] den Erwartungswert \(E(Y)=0\) und die Varianz \(Var(Y)=1\). In der Schreibweise des vorhergehenden Abschnitts erreicht man eine Standardisierung von \(X\) durch die lineare Transformation \(Y=aX+b\) mit \(a=1/\sqrt{Var(X)}\) und \(b=-E(X)/\sqrt{Var(X)}\).