Clase 3: ¿y la estacionalidad? ¿y la inercia de la propia serie? ¿y la incertidumbre?
Como vimos antes, una serie temporal puede presentar estacionalidad. Si esto es así, y esta es marcada, podría enmascarar la capacidad predictiva del indicador adelantado si este no tiene estacionalidad. En este caso, la inflación la presenta. ¿Cómo se puede mejorar el modelo?
- Hay muchas maneras de tratar la estacionalidad. Nosotros vamos a utilizar una muy sencilla que consiste en introducir una dummy para cada mes del año (excepto uno, recuerde)
\[ \Delta IPC_{t}=\alpha+\beta_1 \Delta UNC_{t-1}+\beta_2\Delta UNC_{t-2}+...+\beta_k\Delta UNC_{t-k}+ \alpha_1 E_t+\alpha_2 F_t+...\alpha_{11}N_t+ u_{t}, \]
donde, \(E_t\) es el mes de enero, \(F_t\) es el mes de febrero, y \(N_t\) es el mes de noviembre.
Recuerde ¿Donde se recoge diciembre?
A continuación introducimos la estacionalidad en el modelo. Pero, antes…
Por otro lado, una serie temporal, en general, tiene un comportamiento suave. Esto quiere decir que no suele exhibir cambios bruscos: el pasado de esta ayuda a explicar parte del presente. Esto se conoce como parte autorregresiva de la serie. Podemos incluir un término autorregresivo de la siguiente manera:
Lo que aquí proponemos es una simplificación, dado que los objetivos que tenemos es mostrar modelos sencillos a este respecto (aunque hay toda una teoría disponible al respecto: modelos ARIMA, modelos RegARIMA, modelos de función de transferencia y modelos ARDL.). En nuestro caso, proponemos este modelo sencillo:
\[ \Delta IPC_{t}=\alpha+\beta_1 \Delta UNC_{t-1}+\beta_2\Delta UNC_{t-2}+...+\beta_k\Delta UNC_{t-k}+ \phi_1\Delta IPC_{t-1}+ u_{t}, \]
como ve, el propio pasado de la serie (\(\Delta IPC_{t-1}\)) ayuda a explicar el presente. Veamos cómo incluir ambas cosas en un modelo y hacer validación cruzada
install.packages("forecast")
library(forecast)
library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)
install.packages("dynlm")
library(dynlm)
inflacion<- read_excel("TS_INF_UNC.xlsx")
IPC.t=ts(inflacion[,2],frequency=12,start=c(2002,1))
SEAS<-seasonaldummy(IPC.t) #creamos la variable de dummies estacionales (gracias al paquete forecast)
UNC.t=ts(inflacion[,3],frequency=12,start=c(2002,1))
#introducimos diferencias en todas las series con las que vamos a trabajar
d_IPC.t=diff(IPC.t)
d_UNC.t=diff(UNC.t)
d_SEAS=diff(SEAS)
#finalmente, usaremos la función "auto.arima" que especifica la parte dinámica del modelo (la parte autorregresiva). Para ello, creamos previamente un vector de variables predictoras:
Predictores<- cbind(c(NA,d_UNC.t[2:dim(d_UNC.t)[1]]),
c(NA,NA,d_UNC.t[2:(dim(d_UNC.t)[1]-1)]),
c(NA,NA,NA,d_UNC.t[2:(dim(d_UNC.t)[1]-2)]),
c(NA,NA,NA,NA,d_UNC.t[2:(dim(d_UNC.t)[1]-3)]))
colnames(Predictores)<-paste("UNCLag",1:4,sep="")
Predictores_F<-cbind(Predictores,d_SEAS)
fit0<- auto.arima(d_IPC.t[5:dim(d_UNC.t)[1]], xreg=Predictores_F[5:dim(d_UNC.t)[1],],stationary=TRUE)
pred<-predict(fit0,newxreg=Predictores_F[5:dim(d_UNC.t)[1],])
#################################################################3
#Elijo cuantos datos quiero tener para empezar
T <- 100
#obtengo el total de datos de la muestra
n<-length(d_IPC)
#genero dos vectores vacíos para almacenar errores
errorn<-vector()
errorn2<-vector()
#Creo un bucle que va a ir elaborando predicciones a horizonte 1
for(i in 1:(n-T-5)) {
#extrae la muestra con la que entrenará
IPCshort <- d_IPC[5:(T+i)]
Pred_short <- Predictores_F[5:(T+i),]
#extrae el dato real con el que comparar
IPCnext <- d_IPC[(T+i+1)]
IPCshort = ts(IPCshort, frequency = 12, start=c(2002,06))
# fit 1: modelo ARMA automático con los retardos de d_UNC y estacionalidad
# fit 3: modelo ARMA automático sin los retardos de d_UNC y estacionalidad
fit1 <-auto.arima(IPCshort,xreg=Pred_short,stationary=TRUE)
fit2 <-auto.arima(IPCshort,stationary=TRUE,seasonal=TRUE)
#obtengo las predicciones (a mano) de cada modelo.
forecast1<-predict(fit1,newxreg=Predictores_F[(T+i+1):(T+i+2),])
forecast2<-predict(fit2,h=1)
#obtengo los errores de predicción (porcentuales en valor absoluto )
errorn[i]<-abs((IPCnext-forecast1$pred[1])/IPCnext)
errorn2[i]<-abs((IPCnext-forecast2$pred[1])/IPCnext)
}
assign("error1_new",errorn,envir = globalenv())
assign("error2_new",errorn2,envir = globalenv())
hgm1 <- hist(errorn, breaks = 20, plot = FALSE)
hgm2 <- hist(errorn2, breaks = 30, plot = FALSE)
c1 <- rgb(173,216,230,max = 255, alpha = 80)
c2 <- rgb(180,150,30,max = 255, alpha = 80)
plot(hgm1, col = c1,main="Errores de los modelos", xlab="errores")
plot(hgm2, col = c2, add = TRUE) En este caso, hemos usado una función “auto.arima” que determina el número de retardos de la variable dependiente y permite incluir diferentes especificaciones para la variable predictora.
Ejercicio comparemos la habilidad predictiva de estos modelos frente a los anteriores
finite1<-is.finite(error1)
error1<-error1[finite1]
#modelo sólo con indicador adelantado
summary(error1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.01784 0.59126 0.86404 1.62145 1.35779 34.51434
#modelo con indicador adelantado, dinámica (AR) y estacionalidad
finiten<-is.finite(errorn)
errorn<-errorn[finiten]
summary(errorn)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00689 0.24270 0.58927 2.21977 1.30488 91.05349
#modelo con dinámica AR y estacionalidad (sin indicador adelantado)
finiten2<-is.finite(errorn2)
errorn2<-errorn2[finiten2]
summary(errorn2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000 0.3057 0.6946 2.2258 1.5058 78.2290
- Parece que, en general, respecto al primer, segundo y tercer cuartiles, el modelo con indicador adelantado, AR y estacionalidad, muestra errores ligeramente inferiores que los otros modelos. Esto es un punto a favor del indicador adelantado. Por sí sólo no tiene un poder predictivo alto pero, al introducir dinámica y estacionalidad (que podrían enmascarar la relación) esta parece más clara.
- Ahora bien, deberá analizar con sus clientes, si el error que propone el modelo es adecuado. Para ello, es bueno que conozca qué error cometen ellos y si usted, con su nuevo modelo, podría prometer mejoras. Esto, como ve, es algo que hay que hacer con mucho cuidado porque pone en juego su prestigio. Haga cuantos más ejercicios pueda de evaluación del error.
Clase 4 Elaboración de predicciones probabilísticas
Uno de los intereses que tiene un ejercicio de predicción es ser capaces de otorgar una probabilidad (o verosimilitud) a un escenario. Esto le permitirá entrar en un debate más sano que aquel en el que se proporciona una predicción central sin dar información sobre la incertidumbre que se tiene sobre dicha predicción.
Una manera de poder hacer esto es mediante la técnica del bootstrapping. Usted, a partir de un modelo inicial, podrá generar un conjunto grande de estimaciones alternativas de los parámetros de los modelos sin tener que asumir distribuciones (generalmente rígidas) sobre la distribución de los errores o de los parámetros de los modelos.
Sin embargo, el bootstrapping con series temporales tiene una particularidad: no debe mueestrear (con reemplazamiento) directamente en la serie temporal, puesto que una de las características de máximo interés en una serie temporal es el orden. Es decir, si su serie temporal es esta:
un muestreo con reemplazamiento erróneo sería, por ejemplo, hacer esto:
de repente, el orden de la serie se ha perdido…y podrían pasar cosas desastrosas como esto:
es decir, sería equivalente a tener datos de paro (inflación, beneficios, ventas, etc…) y juntar mezclarlos aleatoriamente ¿qué podría analizar de eso? nada, puesto que en una serie temporal su tendencia es uno de los componentes más importantes.
La idea del bootstrapping en series temporales es la siguiente:
- Usted parte de su modelo de series temporales
- Ajuste el modelo que corresponda
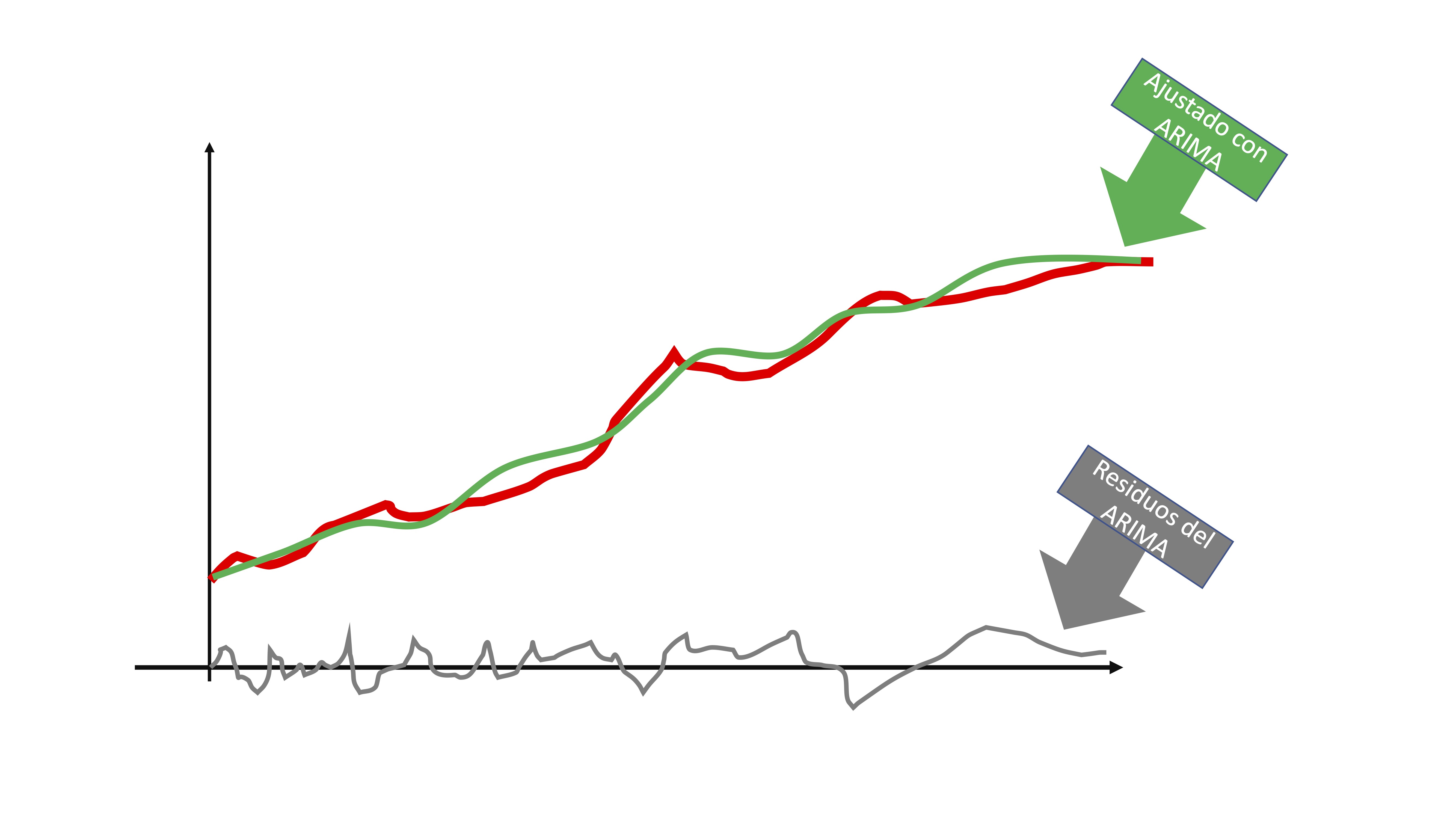
entonces, obtendrá dos elementos: la línea verde de la FIG5 que sería la serie que es capaz de predecir con su modelo y la línea gris que son los residuos. Puede interpretar los residuos, al ser i.i.d, como una secuencia de shocks o sorpresas que no puede captar el modelo por ser completamente aleatorio.
- Remuestree con reemplazamiento esos residuos
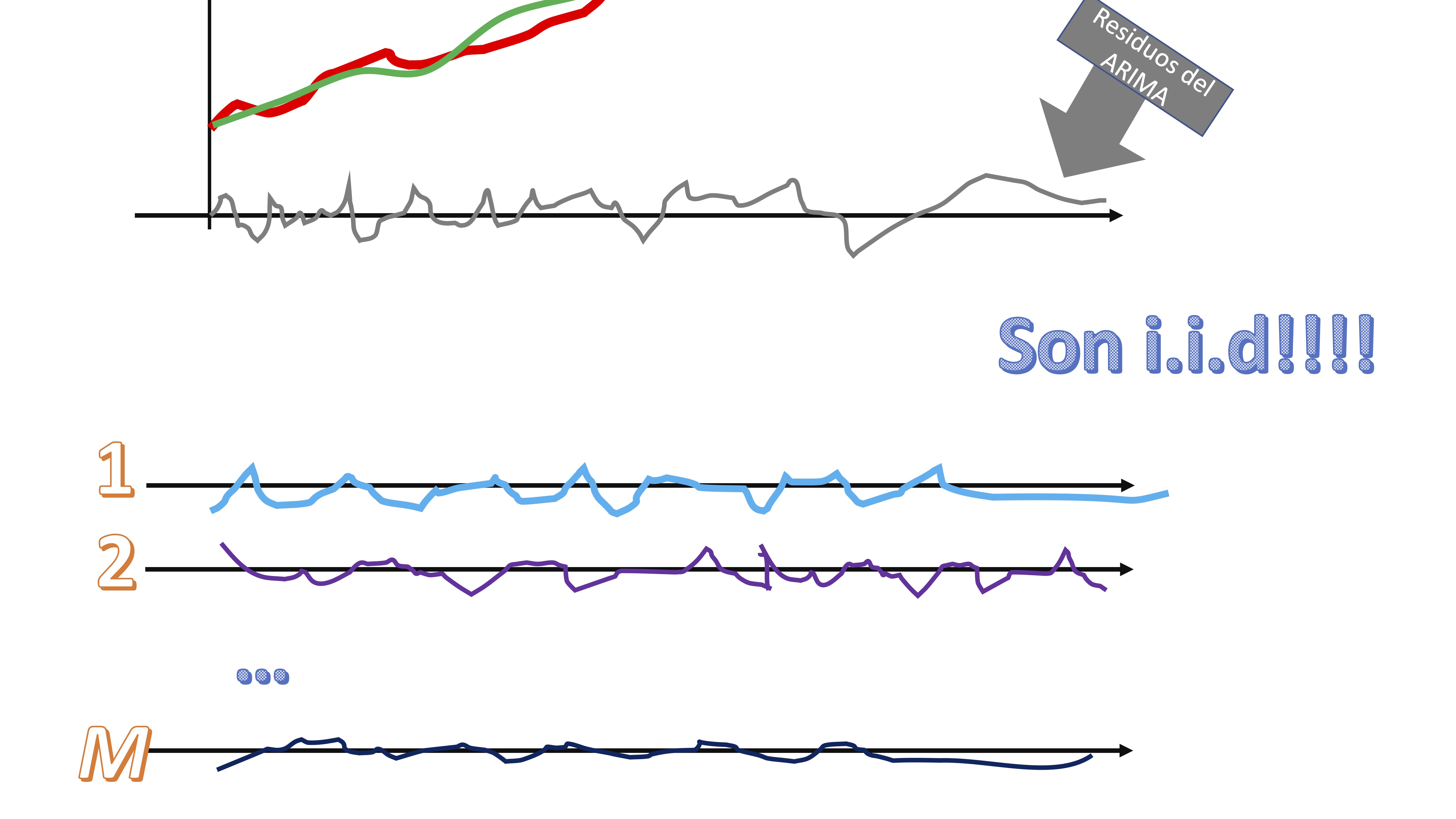
claro, los residuos, al ser i.i.d, su orden nos da igual. Tendremos, entonces \(M\) secuencias de “shocks” que podrían haber ocurrido a la serie original.
- Súmele cada secuencia de shocks a la serie ajustada por el modelo ARIMA y tendrá diferentes versiones de la serie original, afectadas por shocks alternativos
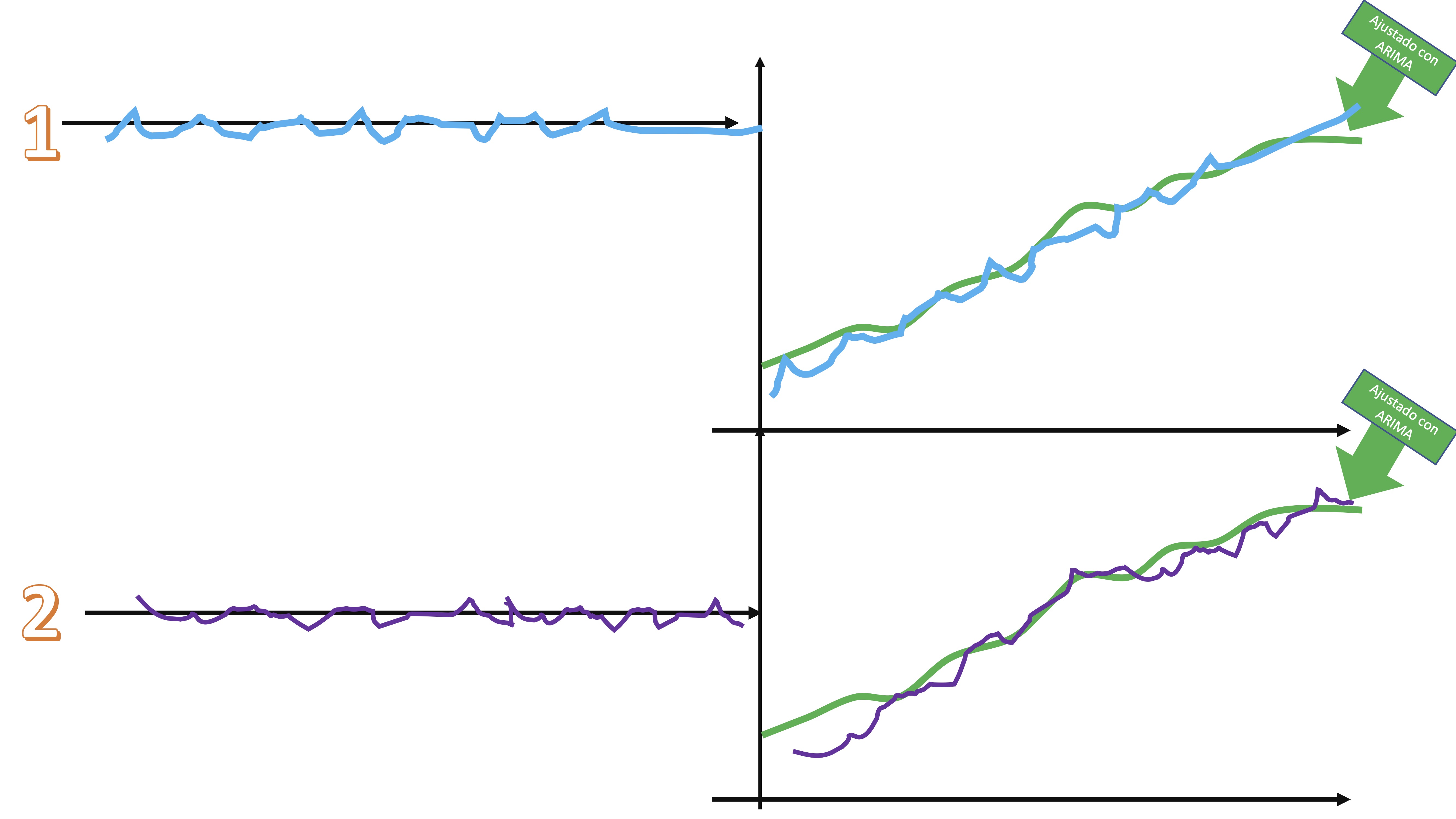
Las características principales de la serie no se pierden, pero sí son versiones “perturbadas” de la serie original.
Estime los correspondientes \(M\) modelos y obtenga las predicciones. De esta manera, al finalizar, podrá tener distribuciones de la variable aleatoria prevista.
Así puede hacerse en R. Vamos a generar una predicción dos meses adelante (recuerde que la predicción con modelos ARIMA sólo está justificada para horizontes cortoplacistas)
Supongamos que queremos predecir la inflación para el mes siguiente con el primer modelo estimado anteriormente (por simplificación)
library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)
install.packages("forecast")
library(forecast)
#cargamos los datos hasta la última observación disponible
inflacion<- read_excel("TS_INF_UNC.xlsx")
IPC.t=ts(inflacion[,2],frequency=12,start=c(2002,1))
SEAS<-seasonaldummy(IPC.t) #creamos la variable de dummies estacionales (gracias al paquete forecast)
UNC.t=ts(inflacion[,3],frequency=12,start=c(2002,1))
#introducimos diferencias en todas las series con las que vamos a trabajar
d_IPC.t=diff(IPC.t)
d_UNC.t=diff(UNC.t)
d_SEAS=diff(SEAS)
#finalmente, usaremos la función "auto.arima" que especifica la parte dinámica del modelo (la parte autorregresiva). Para ello, creamos previamente un vector de variables predictoras:
Predictores<- cbind(c(NA,d_UNC.t[2:dim(d_UNC.t)[1]]),
c(NA,NA,d_UNC.t[2:(dim(d_UNC.t)[1]-1)]),
c(NA,NA,NA,d_UNC.t[2:(dim(d_UNC.t)[1]-2)]),
c(NA,NA,NA,NA,d_UNC.t[2:(dim(d_UNC.t)[1]-3)]))
colnames(Predictores)<-paste("UNCLag",1:4,sep="")
# generamos una matriz donde guardaremos los 1000 posibles escenarios para el horizonte temporales que vamos a usar
FORECAST<-matrix(0,1000,1)
#estimamos el modelo de indicadores adelantados
AM1<- auto.arima(d_IPC.t[5:dim(d_UNC.t)[1]], xreg=Predictores[5:dim(d_UNC.t)[1],],stationary=TRUE, seasonal=TRUE)
#obtenemos los datos ajustados
fitted<-AM1$fitted
fitted<-ts(fitted,frequency=12,start=c(2002,1))
#obtenemos los residuos, que es lo que remuestrearemos
res<-AM1$residuals
n<-length(res)
n_d_IPC.t<-d_IPC.t
for (i in 1:(1000)){
AM1<-auto.arima(n_d_IPC.t[5:dim(d_UNC.t)[1]], xreg=Predictores[5:dim(d_UNC.t)[1],],stationary=TRUE,seasonal=TRUE)
#almacenamos las predicciones para horizonte 1
newreg<-tail(Predictores,n=1)
FORECAST[i]<-predict(AM1,newxreg=newreg)$pred
#remuestreamos el error a través de los residuos
new_error<-sample(res, n+1, replace = TRUE)
#importante: para no sesgar los resultados, nos aseguramos que
#el error tenga media cero
m_error<-mean(new_error)
new_error<-new_error-m_error
#damos estructura de serie temporal al nuevo error
new_error.t=ts(new_error,frequency=12,start=c(2002,1))
#generaamos la nueva serie temporal
n_d_IPC.t<-fitted+new_error.t
}
hist(FORECAST)Entonces, tenemos una distribución de posibles valores de la inflación de un mes al siguiente (FIG8)
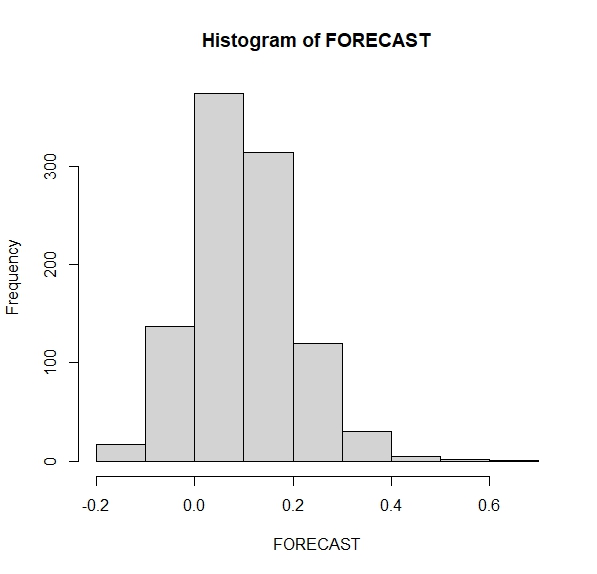De aquí podemos hacernos preguntas. Por ejemplo,
- ¿Qué probabilidad hay de que la inflación en el mes siguiente caiga?
- ¿qué probabilidad hay de que la inflación en el mes siguiente sea mayor que 0.20?
- ¿qué probabilidad hay de que la inflación en el mes siguiente sea el doble que la de este mes?
Deberemos contar cuántas veces la predicción está en esa zona y dividirlo por el total de simulaciones (1000 en este caso)
Prob1<-sum(FORECAST<=0)/length(FORECAST)
Prob2<-sum(FORECAST>=0.20)/length(FORECAST)
Prob3<-sum(FORECAST>=0.62)/length(FORECAST)Ahora bien, ¿Cómo interpreta las probabilidades de cada escenario? Este hilo de Twitter de Kiko Llaneras lo explica muy bien: https://twitter.com/kikollan/status/1294926143758508033