BLOQUE 4: Simulación de variables aleatorias

En este bloque vamos a aprender técnicas de simulación de números aleatorios. De esta forma, aprenderemos-mediante la experimentación- conceptos de variables aleatorias, y veremos una nueva técnica de estimación paramétrica llamada “bootstrap”, muy relacionada con la simulación de variables aleatorias.

Clase 1. Introducción a los generadores de números aleatorios

¿Cómo generan las máquinas números aleatorios? ¿Para qué los necesitamos? Como ha visto en este texto, algunos de los algoritmos más famosos con los que ha trabajado tienen, como punto de partida, una selección aleatoria de elementos de la muestra. Para poder hacer eso, [R] necesita saber cómo buscar dichos números aleatorios. Para ello, vamos a aprender un método de generación de números “al azar” que se denomina generador congruencial.

Repaso de aritmética modular

Como seguro que ya sabe, en informática, la operación módulo \((mod)\) obtiene el resto de la división de un número entre otro. Dados dos números positivos, \(a\) (el numerador) y \(b\) (el denominador), \(a\) \(mod\) \(b\) es el resto de la división de a entre b. Por ejemplo, la expresión \(5\) \(mod\) \(2\) se evalúa como 1, porque 5 dividido entre 2 da un cociente de 2 y un resto de 1 (es decir \({\color{red}5}=2\times{\color{blue}2}+1)\), mientras que \(9\) \(mod\) \(3\) se evaluaría a 0. porque la división de 9 entre 3 tiene un cociente de 3 y da un resto de 0. ¿Y cómo se evalúa \(3\:mod\;9?\) En este caso, \(3=0\times9+3\), por lo que cuando el numerador es menor que el denominador, el módulo es el numerador.

Un generador congruencial

Queremos tener una máquina que simule a un niño de San Ildefonso. Imagine que tiene el conjunto \(\{0,1,2,3,4,5,6,7,8\}\) y le gustaría tener un niño de San Ildefonso autómata que fuera extrayendo números al azar. ¡Hay una manera muy sencilla!

\[\begin{equation} X_{n+1}=(aX_{n}+c)\:mod\:m\label{eq:congruencial} \end{equation}\]

donde

\(m>0\) es el módulo

\(0<a<m\) es el multiplicador

\(0\leq c<m\) es el incremento

\(0\leq X_{0}<m\) es la semilla.

Supongamos que \(a=2,m=9\) y \(c=0\). Supongamos, además, que \(X_{0}=1.\) ¿Cómo obtenemos el resto de números aleatorios?

\[ X_{1}=(2X_{0}+0)\:mod\:9 \]

es decir, \(X_{1}=2\:mod\:9=2\)

¿Y el siguiente?

\[ X_{2}=(2\times2+0)\:mod\:9=4 \]

Ejercicio Complete el siguiente script para que [R] genere los números aleatorios

 #parámetros iniciales
m <- 9 
a <- 2 
c <- 0  
x <- 1  
aleat<-rep(0,20) #queremos obtener 20 resultados
aleat[1]<-1 #inicializamos el vector resultados
for (i in 2:20) {   
 $ x <- (a * x + c) %% m
  aleat[i] <- x }   #almacenamos los números

Si imprime la salida, obtendrá lo siguiente

1 2 4 8 7 5 \({\color{red}{1 2 4 8 7 5}}\)\({\color{green}{1 2 4 8 7 5}}\)\({\color{blue}{1 2...}}\)

Como ve, esta salida tiene

los seis primeros son, efectivamente, valores aleatorios

Hay una estructura cíclica, lo que imposibilita que sea “lo aleatorio” que desearíamos

Cada vez que ejecute el script, saldrá exactamente lo mismo (uhm, ¿es eso aleatoriedad?)

¿Qué podemos hacer?

El resultado obtenido depende de los valores para \(m\),\(a\),\(c\) y la semilla. De esta forma, este generador de números aleatorios no es tan “aleatorio”. En realidad, no es aleatorio en el sentido “puro” de la palabra. Es más bien “pseudoaleatorio” porque:

Si empieza con la misma semilla y parámetros, obtendrá los mismos valores

Si pide una cantidad suficiente de extracciones “aleatorias” volverá a repetirse el ciclo como ocurrió anteriormente.

Hay, documentados, algunos valores famosos para estos parámetros (puede encontrarlos en Wikipedia, por ejemplo, al buscar “generador congruencial”).

Ejercicio propuesto

Investigue cómo genera un ordenador números aleatorios. ¿De dónde saca la semilla? Diseñe un algoritmo para obtener números aleatorios de una uniforme (0,1). Para ello, complete este código

 #parámetros iniciales

m <- 2 ** 32 
a <- 1103515245 
c <- 12345  #parámetros iniciales
x <- 1234 
aleat<-rep(0,20) 
aleat[1]<-x #inicializamos el vector resultados
for (i in 1:20) {   
  x <- (a * x + c) %% m 
  aleat[i] <- x/m } #almacenamos los números

Fíjese que, si genera una cantidad grande de estos números, obtendrá lo que esperamos teóricamamente: una distribución donde cualquier valor en el intervalo \(0\leq x \leq 1\) tiene la misma probabilidad de ser elegido. Compruébelo.

Como habrá observado, la semilla (es decir, el valor inicial elegido) modificará la secuencia que obtenga. Esto quiere decir que si queremos obtener la misma secuencia, por motivos relacionados con el experimento que estemos llevando a cabo, entonces deberemos utilizar la misma semilla.

En [R] puede simular una uniforme mediante la función runif. Observará que, cada vez que lo lance, el resultado será distinto. Eso es así porque [R] usa como semilla un código obtenido mediante la señal horaria de su PC. Si quiere obtener siempre la misma simulación, deberá establecer una semilla (con la secuencia set.seed())

Esta instrucción le proporcionará siempre la misma secuencia "pseudoaleatoria" de valores distribuidos según una uniforme (0,1).


set.seed(1234)
runif(10)

Clase 2: La distribución normal. Entendiendo el Teorema Central del Límite

Ya hemos aprendido a simular distribuciones uniformes. Muchas de las distribuciones de probabilidad conocidas se pueden simular a través de la uniforme. Por ejemplo, la distribución normal (0,1), puede simularse de forma muy sencilla mediante la transformación de Box-Muller. Puede probarse, no está al alcance de este curso, que la normal se genera a través de dos uniformes (\(u_1\),\(u_2\)\(\rightarrow U(0,1)\)) mediante la expresión

\[ N=\sqrt{-2log(u_1)}\times \cos(2\pi u_2) \] donde \(N\) será un valor, aleatorio, proveniente de una normal \(N(0,1)\), y \(u_1\),\(u_2\) son realizaciones aleatorias de sendas distribuciones uniformes \(U(0,1)\).

Así podría hacerlo en [R]

u1<-runif(100)
u2<-runif(100)
N<-sqrt(-2*log(u1))*cos(2*pi*u2)

En el siguiente ejercicio, se puede ver cómo la simulación, según aumenta el tamaño muestral, es más precisa y se acerca más a lo esperado.

par(mfrow=c(2,2))
u<-runif(100)
v<-runif(100)
N<-sqrt(-2*log(u))*cos(2*pi*v)
hist(N, main="n=100")

u<-runif(1000)
v<-runif(1000)
N<-sqrt(-2*log(u))*cos(2*pi*v)
hist(N,main="n=1000")

u<-runif(10000)
v<-runif(10000)
N<-sqrt(-2*log(u))*cos(2*pi*v)
hist(N,main="n=10000")

u<-runif(100000)
v<-runif(100000)
N<-sqrt(-2*log(u))*cos(2*pi*v)
hist(N,main="n=100000")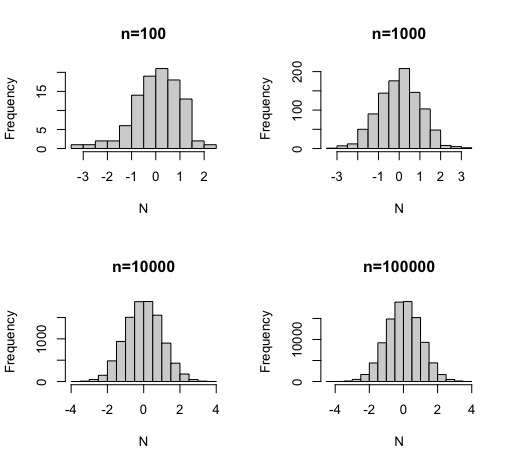

FIG 1: simulación de una normal con diferentes tamaños muestrales

¡Ya sabe cómo generar números aleatorios y, además, cómo generar observaciones que provienen de una distribución poblacional! Con esto, más adelante, podrá hacer muchas cosas. Ahora, vamos a seguir explorando ideas que seguro que le suenan de años anteriores.

Piense por un momento: ¿Cómo explicaría en qué consiste exactamente el Teorema Central del Límite?

El Teorema Central del Límite

En general, suele haber cierta confusión con la interpretación del Teorema Central del Límite, uno de los más famosos, celebrados e importantes en Estadística. Por simplificación, mucha gente cree que este teorema dice algo así como si una muestra es muy grande, la distribución de los datos será normal . Lo cual, se mire como se mire, es incorrecto.

Por si le interesa, aquí puede ver un vídeo sobre el TCL que, quizá le enseñe algo y le entretenga:

De hecho,lo puede comprobar muy fácilmente

Ejercicio: Simule distribuciones uniformes (0,1) para muestras cada vez mayores. Obtenga el histograma y discuta si la distribución, según aumenta la muestra, está normalmente distribuida

par(mfrow=c(2,2))

U<-runif(100)
hist(U, main="n=100")

U<-runif(1000)
hist(U, main="n=1000")

U<-runif(10000)
hist(U, main="n=10000")


U<-runif(100000)
hist(U, main="n=100000")

como verá, por mucho que amplíe la muestra la distribución uniforme… seguirá siendo una distribución uniforme

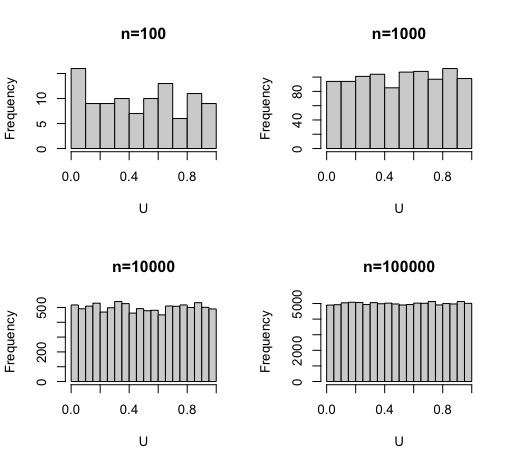
FIG 2: simulación de una normal con diferentes tamaños muestrales

Veamos, entonces, qué resultado proporciona el teorema.

TCL

Sean \(X_{1},...,X_{n}\) \(n\) variables aleatorias independientes e idénticamente distribuidas de media \(\mu\) y varianza, \(\sigma\), finita. Sea \(\overline{X}_{n}=\frac{X_{1}+X_{2}+...+X_{n}}{n}\) la media muestral, entonces, si \(n\rightarrow\infty\) se cumple que \[ \overline{X}_{n}\approx N\left(\mu,\frac{\sigma^{2}}{n}\right) \]

donde \(\approx\) significa se aproxima . Este teorema, entonces, quiere decir de una manera más coloquial:

No importa la distribución de partida de la variable aleatoria \(X\) (valen tanto continuas (exponencial, uniforme, etc…) como discretas (binomial, Poisson, etc…) si el muestreo es aleatorio, se satisface el teorema.

Es importante el se aproxima del texto . Esto quiere decir, que la distribución de la media no es normal, sino que puede utilizarse la distribución normal como un resultado aproximado para lo que se necesite calcular, en contextos de muestras grandes.

Quizás esta infografía le sirva para entender, básicamente, la idea del teorema

FIG 3: El TCL(1)

FIG 4: El TCL(2)

FIG 5: El TCL(3): aquí es importante ver que tenemos dos tamaños que nos importan: \(n\) se refiere la cantidad de individuos que hay en cada submuestra y \(N\) se refiere al número de submuestras

FIG 6: El TCL(4)

Esto mismo, lo puede simular utilizando [R]. Para ello:

simule \(N\) muestras de tamaño fijo (en general, \(N\) debe ser grande para poder ver el histograma adecuadamente) (\(n={1,5,100,500}\)) de uniformes \(U(0,1)\). -A continuación, obtenga los promedios muestrales de cada una y dibuje el histograma. Pruebe que, según \(n\) se hace grande, la distribución de los promedios muestrales se acerca a una normal.

Puede escribir el script generando una matriz como esta:

De esta forma, obtendrá la FIG7 donde se puede ver cómo la campana de Gauss se empieza a conformar con una muestra superior a 100 elementos

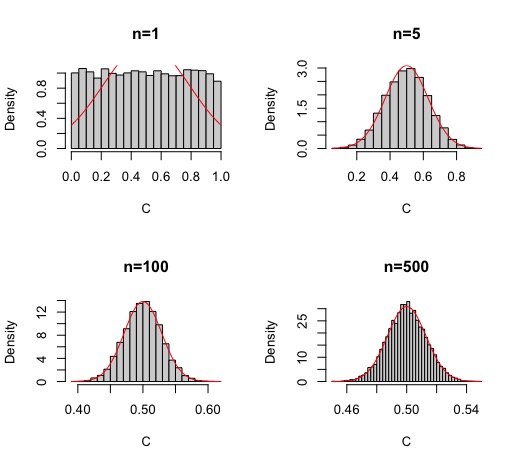
FIG 7: El TCL simulado con una uniforme como distribución original de la variable aleatoria con \(n=10\)

Para ello, habrá tenido que escribir un código similar a este

par(mfrow=c(2,2))
M1<-matrix(runif(10000*1),nrow=1)
C<-colMeans(M1)    
hist(C,breaks=30,prob=TRUE,main="n=1")
curve( dnorm(x,mean=0.5,sd=sqrt(1/(12*1))), add=TRUE, col='red' )


M1<-matrix(runif(10000*5),nrow=5)
C<-colMeans(M1)    
hist(C,prob=TRUE,main="n=5",breaks=30)
curve( dnorm(x,mean=0.5,sd=sqrt(1/(12*5))), add=TRUE, col='red' )

M1<-matrix(runif(10000*100),nrow=100)
C<-colMeans(M1)    
hist(C,prob=TRUE,main="n=100",breaks=30)
curve( dnorm(x,mean=0.5,sd=sqrt(1/(12*100))), add=TRUE, col='red' )


M1<-matrix(runif(10000*500),nrow=500)
C<-colMeans(M1)    
hist(C,prob=TRUE,main="n=500",breaks=50)
curve( dnorm(x,mean=0.5,sd=sqrt(1/(12*500))), add=TRUE, col='red' )

Por cierto, este no es el código más eficiente, pero pensamos que es didáctico porque puede ver la matriz donde, cada columna es una réplica del experimento (queremos muchas para verlo bien gráficamente) y cada fila es un individuo de la muestra.

Por otro lado, como sabemos que \(X\rightarrow U(a,b)\), entonces \(E(X)=\frac{b+a}{2}\) y que \(V(X)=\frac{\left(b-a\right)^{2}}{12}\), entonces,

\[ \overline{X}_{n}\approx N\left(\frac{b+a}{2},\frac{\left(b-a\right)^{2}}{12\times n}\right) \] en este caso, pruebe que \[ \overline{X}_{N}\approx N\left(0.5,\frac{1}{12\times n}\right) \]

Para ello, tendrá que obtener la media y la varianza de lo que ha simulado y cercionarse de que se obtiene dicho resultado. En la FIG7 se ha incluido dicha curva.

Clase 3: Usos de la simulación (1): entender conceptos de estadística y probabilidad

En esta clase, vamos a discutir dos ideas centrales en estadística y probabilidad que, es probable, que siga interpretando con errores o no sea capaz de definir de manera adecuada.

Antes de nada, intente responder este cuestionario: ¿cuántas preguntas cree que son verdaderas?

FIG 1: El test del Professor Bumbledorf: tranquilo, no se descuenta un punto por errónea.

IMPORTANTE

Puede ver este vídeo donde se muestra cómo simular cuestiones: 1.- por qué hay que descontar en un “tipo test”. ¿Se atreve a pensarlo analíticamente una vez visto el vídeo? 2.- ¿Cómo interpretar un intervalo de confianza? Es menos sexy de lo que parece.

El intervalo de confianza

Suponga que quiere estimar el valor promedio de una variable aleatoria \(X\) de una población, es decir, quiere estimar \(\mu\), utilizando un intervalo de confianza. Asuma que la población se distribuye como una normal \(X\rightarrow N(\mu,\sigma^{2})\) entonces, según la teoría de muestreo tradicional, para una muestra de tamaño \(n\), el intervalo de confianza (a un nivel \((1-\alpha)\) para la media poblacional será:

Si la muestra es “pequeña” (en este contexto, menor que 50)

\[ IC\left(\mu\right)_{\left(1-\alpha\right)\%}\equiv\left(\overline{x}-t^{\alpha/2}_{n-1}\sqrt{\frac{s^2}{n}},\overline{x}+t^{\alpha/2}_{n-1}\sqrt{\frac{s^2}{n}}\right), \]

donde se utiliza la distribución \(t\) de student y \(s^2\) denota a la varianza muestral.

Si la muestra es grande, la distribución converge a una normal vía el TCL

\[ IC\left(\mu\right)_{\left(1-\alpha\right)\%}\equiv\left(\overline{x}-N(0,1)\sqrt{\frac{s^2}{n}},\overline{x}+N(0,1)\sqrt{\frac{s^2}{n}}\right) \]

donde el \(N(0,1)\) es el percentil correspondiente de la normal dado el nivel de significación \(\alpha\) (o de confianza \(1-\alpha\). ¿Qué cosas son importantes del intervalo?

Ejercicio Piense, por un momento, cómo definiría usted la idea de intervalo de confianza.

Es un intervalo aleatorio : eso quiere decir que, por cada muestra que recoja, el valor de los límites inferior y superior de este va a cambiar

Como ve en la FIG 1, cada muestra que utilice sobre un mismo experimento, le permitirá obtener un intervalo diferente. En algunos de esos intervalos, el parámetro poblacional estará contenido en este y en otros, no.

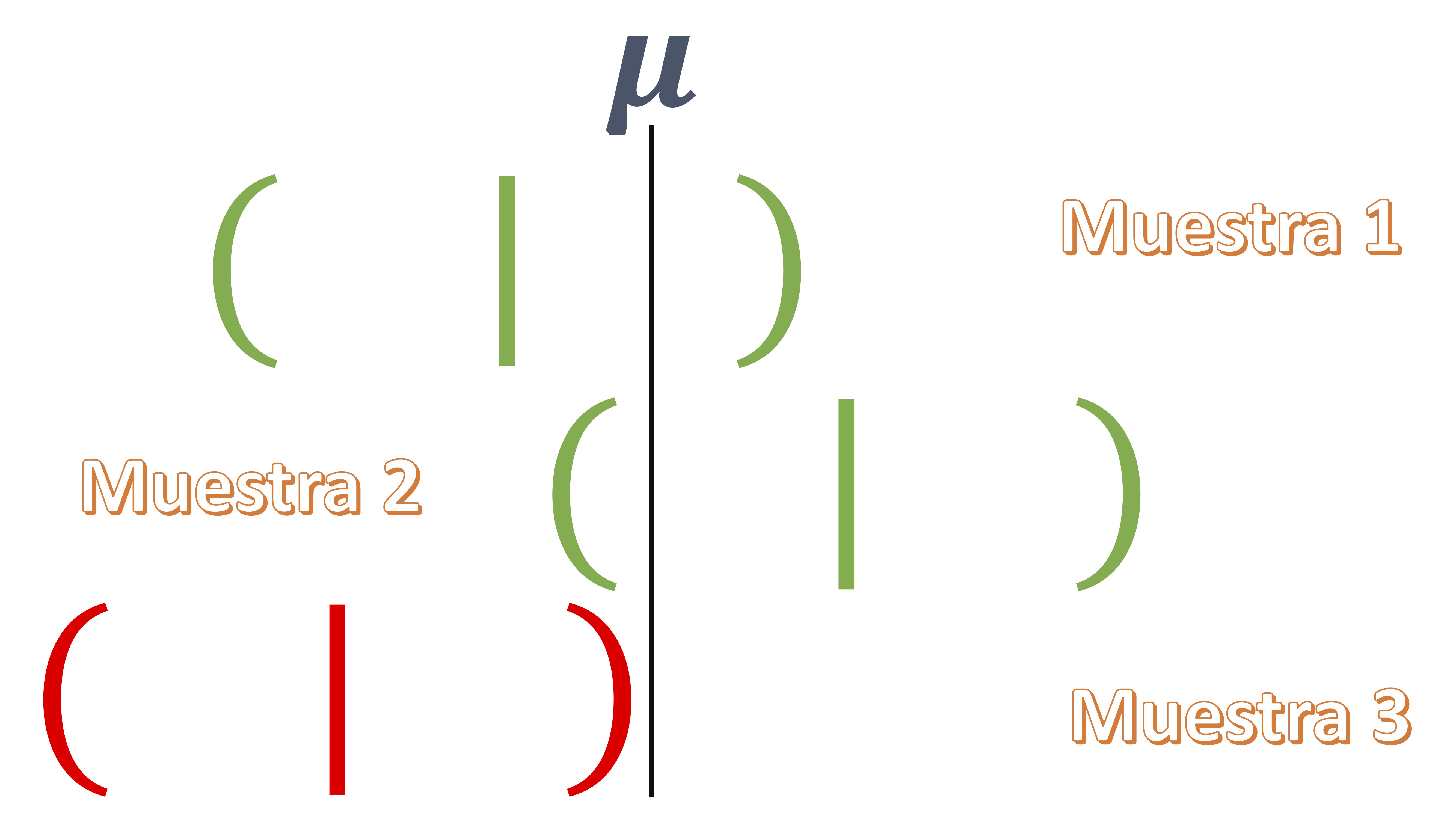
FIG 1: La idea de construir diferentes intervalos de confianza para un mismo parámetro poblacional

Entonces, lo que queremos decir es que:

La idea de intervalo de confianza-al 95%, por ejemplo- implica que de cada 100 experimentos que realice en las mismas condiciones, en 95 de ellos estará el verdadero parámetro poblacional desconocido.

En la vida real, se cuenta con una sola muestra (debido a lo caro que resulta la extracción de esta) y, por tanto, usted nunca sabrá si está ante el intervalo que contiene al verdadero parámetro poblacional o no.

Por eso se llama de confianza. Porque usted confía en que el intervalo contenga el parámetro. Claro, ante mayor valor de la confianza, más ancho será el intervalo y, por tanto, más frecuente será que esté dicho parámetro poblacional dentro del intervalo. Sin embargo, cuanto más ancho sea un intervalo, menos informativo será para usted (es como decir que un intevalo de confianza al 99% de la nota de la asignatura está entre 1 y 9.5)

Ejercicio Simule muestras aleatorias (por ejemplo, 50) de una población normal con la media y desviación típica deseadas. Calcule los límites inferior y superior de cada uno de los 50 intervalos de confianza (al 95%, por ejemplo) que genere y obtenga una variable dicotómica que tome valor 1 si el valor de la media poblacional elegido está contenido o no en el intervalo. Obtenga el porcentaje de veces que está contenido. Esa es la confianza.

n<-50
vec<-vector()
N<-200
for (i in 1:N){
y <- rnorm(n,mean=1,sd=0.5)  #generamos muestras de 50 individuos normales con media 1 y desv típica 0.5
x_bar<-mean(y)  #obtenemos la media muestral de cada muestra
sd_bar<-sd(y)/sqrt(n) #obtenemos la desviación típica de la media muestral (error estándar)
CI_low<-x_bar-1.96*sd_bar #obtenemos el límite inferior del intervalo
CI_high<-x_bar+1.96*sd_bar #obtenemos el límite superior del intervalo
vec[i]<-CI_low<1 & CI_high>1} #generamos una variable que nos dice si el valor poblacional está o no dentro del intervalo

¿Qué ha aprendido?

La interpretación del intervalo de confianza es más sutil y, quizás, menos práctica de lo que pensaba. En realidad, cuando calcula un intervalo con una sola muestra, la probabilidad de que el verdadero parámetro poblacional esté dentro del intervalo es 1 o 0. Esto es poco útil, en realidad. Puede pensarlo de una manera más relajada: “un intervalo de confianza nos proporciona un conjunto de valores compatibles con el parámetro poblacional desconocido”. Obviamente, cuanto más ancho sea el intervalo, más imprecisa será su inferencia. Cuanto más estrecho, más riesgo corre de excluir al verdadero parámetro poblacional. Esto entronca con lo aprendido en capítulos anteriores: la inferencia no debería consistir en una dicotomía entre “rechazar” y “no rechazar” hipótesis.

Es decir, entonces esta pregunta es de interés:

¿Cómo interpretamos un intervalo de confianza si en la vida real sólo tenemos UNA MUESTRA?

Después de analizar la esperanza de vida en España, se concluye que un intervalo de confianza al 95% para dicho parámetro es \(\left(77.8,79.1\right)\) años. ¿Podemos decir, entonces, decir:

En torno al 95% de la gente en Españaa tiene una esperanza de vida entre 77.8 y 79.1 años

No, pese a que es muy común interpretar así el intervalo de confianza. Recuerde que 77.8 y 79.1 son valores aleatorios. Si hubiéramos contado con otra muestra, esos límites habrían cambiado (por ejemplo, \(\left(77.3,80.2\right)\) . Tampoco sabemos cuál es el verdadero parámetro, por lo que no podemos obtener qué porcentaje de gente, en la población, tiene como esperanza de vida entre 77.8 y 79.1 años.

Hay una probabilidad del 95% de que la esperanza de vida promedio valga entre 77.8 y 79.1 años?

La esperanza de vida, como parámetro poblacional, es desconocida, y determinista (es decir, no hay probabilidad asociada con ella: es un valor único). De nuevo, no podemos asociar una probabilidad a dicho parámetro.

Entonces, lo que en realidad podemos decir, que es lo que hemos simulado, es que:

De cada 100 posibles intervalos, 95 de ellos contendrán el verdadero parámetro, es decir, hay un 95% de probabilidad de que el intervalo aleatorio (77.8,79.1) cubra al verdadero parámetro poblacional.

Entonces, trate de evitar excesivas “sobreinterpretaciones” de un intervalo de confianza: al final nunca sabrá si está utilizando el intervalo que contiene el verdadero valor del parámetro o no.

De manera más gráfica, puede ejecutar el siguiente script de regalo, donde se simulan muestras provenientes de poblaciones \(N(1,\sigma=0.5)\). El objetivo es obtener 100 intervalos y ver cuántos de ellos no contienen a la media poblacional (que conocemos, porque la hemos impuesto nosotros).

install.packages("BSDA")
library(BSDA)
N = 100
curve(expr = dnorm(x, mean = 1, sd = 0.5), from = -1, to = 3,
      main = "95% Simulación de intervalos de confianza",
      xlab = "valores x", ylab = "densidad",
      lwd=2, col="blue") #creamos una curva normal
abline(v = 1, col = "purple", lwd = 2) #esta línea indica el valor de la media poblacional (que es 1)
contador <- 0
#el siguiente bucle genera N intervalos de confianza basados en N muestras aleatorias
#y marca con rojo aquellos intervalos que no contienen la media poblacional
for (i in 1:N) {
  col <- rgb(0,0,0,0.5)
  simula.interv <- rnorm(n = 20, mean = 1, sd = 0.5) 
  myCI <- z.test(simula.interv, sigma.x = 0.5, conf.level = 0.95)$conf.int
  if (min(myCI) > 1 | max(myCI) < 1) {
    contador <- contador + 1
    col <- rgb(1,0,0,1)
  }
  segments(min(myCI), 1.5 * i / N,
           max(myCI), 1.5 * i / N,
           lwd = 1, col = col)
}

del que obtendrá la FIG2

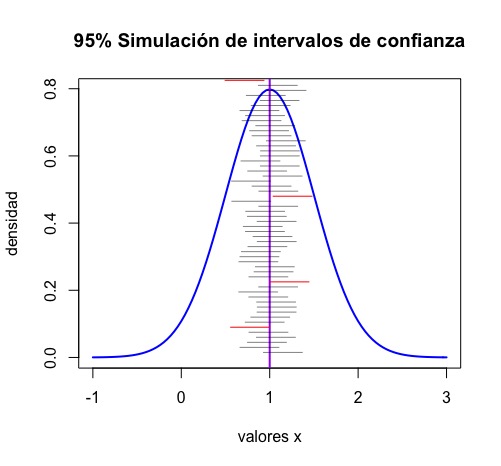
FIG 2: La idea de construir diferentes intervalos de confianza para un mismo parámetro poblacional

fíjese cómo, en rojo, se mustran los intervalos de confianza (de los 100 generados) que no contienen al verdadero parámetro poblacional. Es una aproximación, en teoría deberíamos haber obtenido 5, ya que la confianza es del 95%. Si lo repite con \(N\) mayor, verá cómo según crece \(N\), más se acerca al resultado teórico.

El p valor

Piense en el caso anterior, en el que queríamos estimar el valor promedio de una variable aleatoria \(X\), es decir, quiere estimar \(\mu\), utilizando un intervalo de confianza. Asuma que la población se distribuye como una normal \(X\rightarrow N(\mu,\sigma^{2})\).

Quiere testar la hipótesis típica:

\[ H_{0}:\mu=0 \] \[ H_{1}:\mu\neq0 \]

Para ello, dadas las asunciones que hemos hecho antes, tendremos que el estadístico de contraste, \(t\), será

\[ t=\frac{\bar{x}-\mu_{H_{0}}}{\frac{s}{\sqrt{n}}}\approx N(0,1) \]

donde \(s\) es la desviación típica muestral. El p-valor del contraste se obtiene como

\[ 2\times Pr\left(N(0,1)\geq\left|\frac{\bar{x}-\mu_{H_{0}}}{\frac{s}{\sqrt{n}}}\right|\right) \]

es decir, es la probabilidad de encontrar un estadístico \(t\) más extremo (en valor absoluto) que el obtenido con esta muestra, asumiendo que la hipótesis nula es cierta. ¿Qué significa lo de asumiendo que la hipótesis nula es cierta? Pues que en la expresión del estadístico

\(\left(\frac{\bar{x}-{\color{red}\mu_{H_{0}}}}{\frac{s}{\sqrt{n}}}\right)\)

se introduce el valor de la nula (en este caso, cero). En el fondo, estamos tratando de medir el grado de compatibilidad de nuestros datos con nuestro modelo (el modelo aquí es tan sencillo como decir que \(\mu=0\)). De nuevo, el p-valor necesita una interpretación probabilística que, consiste en:

p-valor

El p-valor es también una variable aleatoria. Nos permite analizar cómo de compatible es la muestra con la hipótesis que se contrasta. Sin embargo, tenga en cuenta que detrás de una hipótesis hay una selección de un modelo concreto (con sus correspondientes restricciones) y la elección de unos datos concretos. De hecho, volvemos a la situación de partida: cuando obtiene el p-valor de un contraste- y bajo los supuestos de que el modelo es el adecuado- no sabe si ha obtenido aquella muestra donde rechazaría la hipótesis de manera correcta o lo contrario.

Puede recordar todo esto en estos dos vídeos:

https://youtu.be/Cl8ETtmzakA

https://youtu.be/dfBcajUg7LI

Ejercicio Simule un conjunto de muestras de tamaño \(n\) a su elección y con distribución normal de parámetros \(\mu\neq0\) y \(\sigma^2\), también a su elección. Obtenga los p valores de dos contrastes: el de media poblacional nula (que deberá rechazar puesto que su media poblacional es distinta de cero) y el de media poblacional cero (que no deberá rechazar). Analice la distribución del p valor en ambos casos y, por tanto, la frecuencia con la que rechaza indebidamente o no rechaza indebidamente.

n<-50
p_value<-vector()
N<-200
for (i in 1:N){
  y <- rnorm(n,mean=1,sd=4)  #generamos muestras de 50 individuos normales con media 0 y desv típica 0.5
  x_bar<-mean(y)  #obtenemos la media muestral de cada muestra
  sd_bar<-sd(y)/sqrt(n) #obtenemos la desviación típica de la media muestral (error estándar)
  tstat<-(x_bar-0)/(sd_bar) #calculamos el t-stadístico con la nula mu=0
 p_value[i]<-2*(1-pnorm(abs(tstat), mean=0, sd=1))} #obtenemos el p valor



hist(p_value,main="Aquí deberíamos rechazar")
abline(v = 0.05, col = "purple", lwd = 2)

mean(p_value>0.05)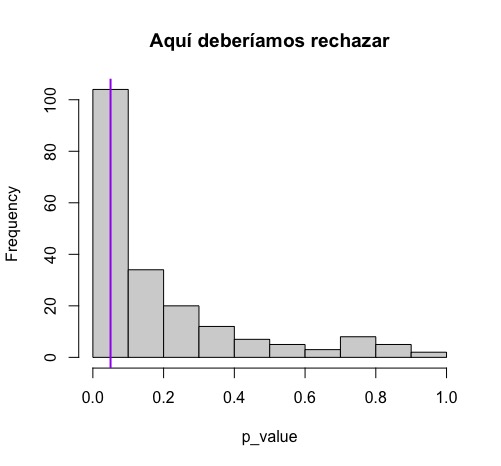

FIG 3: Distribución de los diferentes p valores cuando deberíamos rechazar la nula

Como verá en la FIG3, en el 59% de las veces, no rechazaríamos la nula de que \(\mu=0\), al 5% de significación, esto es, obtenemos en el 59% de los contrastes un p-valor mayor al 0.05. Sin embargo, deberíamos rechazarla siempre. Esto se debe, entonces, a un alto “error de tipo 2” (no rechazar la nula cuando es falsa) y estamos en un caso de baja potencia. El p-valor no detecta baja potencia en el contraste.

p-valor

Por eso, en el primer semestre discutimos el riesgo de utilizar el p-valor como único dato para la toma de decisiones. Recuerde el gráfico de p-valores que realizábamos para entender qué conjunto de hipótesis no habríamos rechazado.

Por lo tanto:

El p-valor debe tomarse como una medida-informal-de compatibilidad de nuestros datos con el modelo.

El p-valor no es un criterio sólido científico que pueda sustituir cualquier otro análisis en favor de “rechazar” o “no rechazar” una hipótersis

La propia construcción y definición del p-valor debería hacerle reflexionar sobre su uso indiscriminado.

Ejercicio

Mire el ejercicio 3 de la clase 2 del primer cuatrimestre. Ahora va a tratar de simular esas distribuciones y a discutir la importancia del tamaño muestral en el p-valor.

Caso 1: simule observaciones procedentes de dos distribuciones normales. Elija un tamaño de muestra grande (por ejemplo, \(n=10000\)) y utilice una media \(\mu_1=6\) y otra media \(\mu_2=5.9\). Por otro lado, elija una desviación típica poblacional de 2.5

Haga un gráfico de ambas distribuciones y observará que son prácticamente iguales (pues la media se diferencia en 0.1 puntos y las desviaciones típicas son iguales)

Haga el experimento tantas veces como quiera y compruebe que, casi siempre, rechazará la hipótesis nula de que las medias son iguales al 5% de significación. ¡Pero si sólo se diferencian en 0.1 puntos!

Haga el mismo experimento ahora con una muestra de 50 elementos. ¿Qué concluye aplicándolo a datos “reales”?

set.seed(1)

#crea los datos
df <- data.frame(var1=rnorm(10000, mean=6, sd=2.5),
                 var2=rnorm(10000, mean=5.9, sd=2.5))



#convierte el formato de manera que tengas dos columnas
data <- melt(df)

#dibuja las distribuciones
ggplot(data, aes(x=value, fill=variable)) +
  geom_density(alpha=.25)

#haz el test de hipótesis

t.test(df$var1, df$var2, paired = FALSE, alternative = "two.sided")

Caso 2. Ahora simule dos distribucines normales donde las medias sean bastante distintas. Por ejemplo, \(\mu_1=6\), \(\mu_2=5\). Por otro lado, \(\sigma=2.5\). Si el tamaño muestral es, por ejemplo, \(n=50\), compruebe el resultado que obtiene frente al que obtendría si \(n=500\) ¿Qué concluye?

Interesante Que cada alumno lance su resultado y se toman nota de los p-valores del test cuando \(n=50\). ¿Cuántas veces nos hemos equivocado al no rechazar la nula de igualdad de medias?

Clase 4: Simulación de un modelo de regresión

Está cerca de entender un método que requiere de la simulación para la obtención de resultados. Sin embargo, antes va a aprender a simular datos sintéticos para poner a prueba ciertos resultados que conoce de los modelos de regresión lineal. ¿En qué consistirá esta simulación? Vayamos paso a paso.

Usted cuenta con una población que-en la vida real-suele estar formada por infinitos individuos y que, para R va a ser un modelo. En este caso, es un modelo de regresión lineal, por ejemplo:

\[ y=3+5x+u, \]

donde \(u\rightarrow N(0,\sigma=3)\). Usted no puede crear los infinitos elementos de esa población. Sin embargo, puede simular una muestra de dicha población. Por ejemplo, puede simular \(n=50\) elementos de dicha población. Es decir, su marco conceptual es el de la FIG1

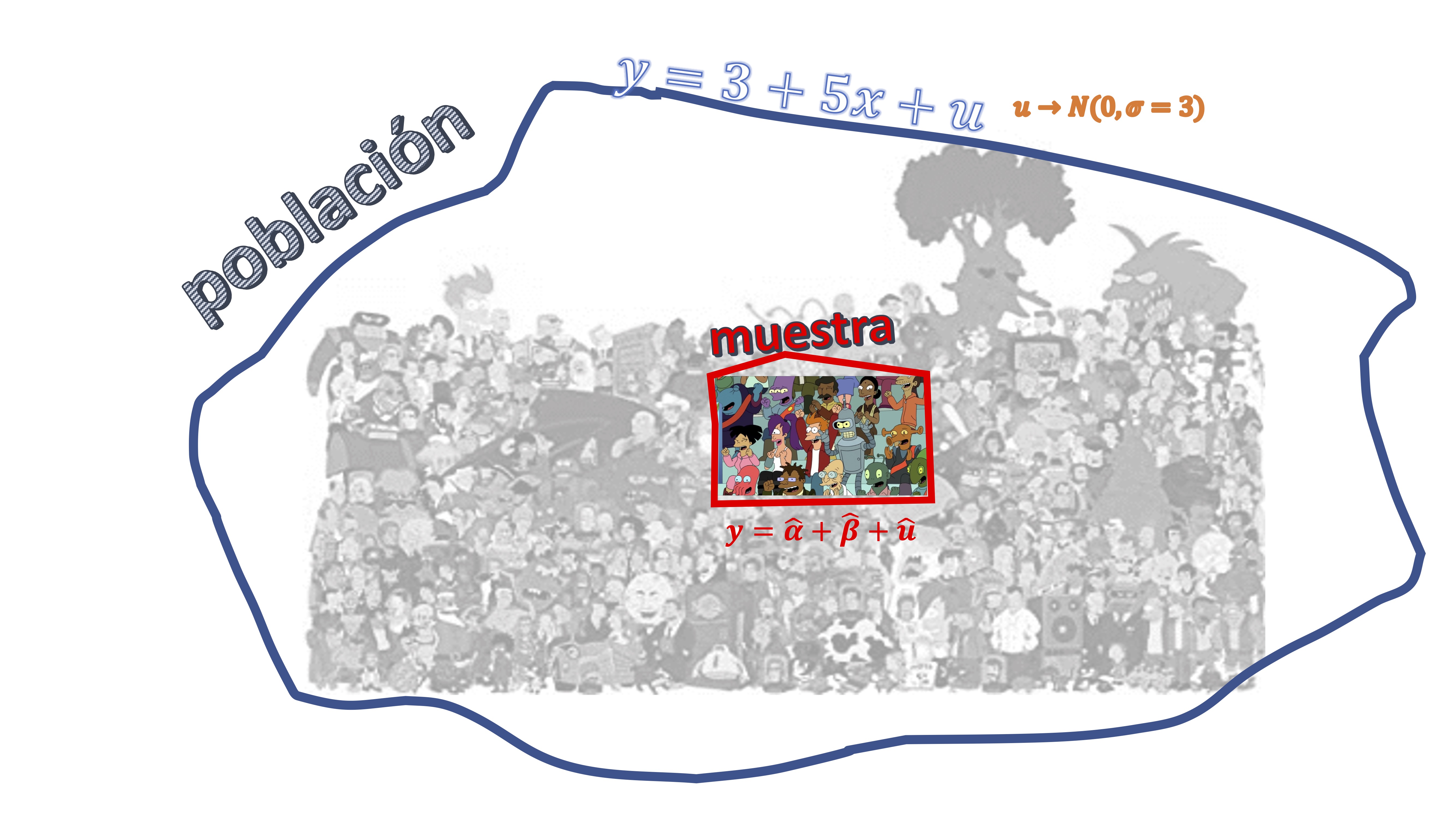FIG 1: la idea de “muestra” y “población” en un modelo de regresión Para ello, explore el siguiente:

Experimento 1

Simule primero el error del modelo (mediante una normal de media cero y varianza 3)

u<-rnorm(n,0,sd=3)

-Simule valores para la variable \(x\). Recuerde que, bajo los supuestos generales del modelo de regresión lineal, \(x\) no es aleatoria y-por tanto, para fines de simulación-puede fijar los números de esa variable como desee.

x<-runif(n)

Escriba la ecuación de regresión y ya tiene 50 elementos extraídos al azar de dicha población.

y<-3+5*x+u

A continuación, puede utilizar el estimador de mínimos cuadrados (lm, en R) para tratar de recuperar los coeficientes del modelo poblacional

M0<-lm(y~x)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.6615     0.7422   3.586 0.000785 ***
x             4.8682     1.2149   4.007 0.000213 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.547 on 48 degrees of freedom
Multiple R-squared:  0.2507,    Adjusted R-squared:  0.2351 
F-statistic: 16.06 on 1 and 48 DF,  p-value: 0.0002132

¿Qué ha ocurrido?

Como verá, los coeficientes que obtiene, no tienen por qué ser

\[ \alpha=3,\beta=5 \]

puesto que usted ha cogido una única muestra al azar-representativa de la población- y, por tanto, lo que ha obtenido es una posible realización del experimento. Entonces ¿la estadística no me promete que-cada vez que haga el experimento- obtenga el verdadero valor de los parémetros? ¡No! la estadística lo que le promete es que, bajo ciertas propiedades de (en este caso, de la más importante es que la \(x\) y la \(u\) no estén relacionadas, esto es, sean independientes y el error aleatorio sea i.i.d) el estimador lineal de los parámetros será insesgado, es decir,

\[ E\left[\widehat{\alpha}\right]=\alpha \]

\[ E\left[\widehat{\beta}\right]=\beta \]

O lo que es lo mismo, si usted pudiera hacer este experimento infinitas veces, en promedio, las estimaciones que obtendría le proporcionarían el verdadero parámetro poblacional. Es decir, como ve en la FIG2,

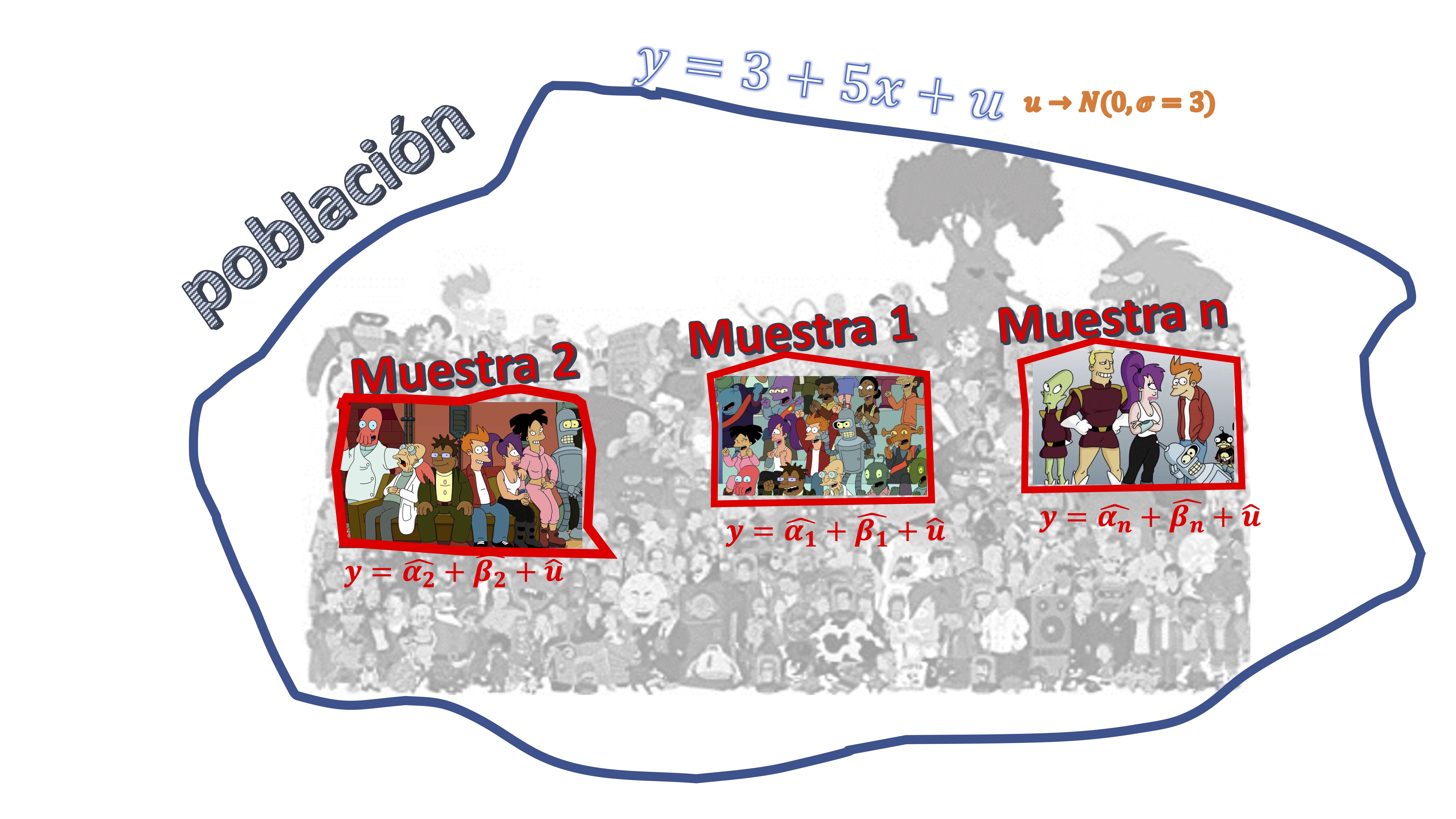
FIG 2: la idea de diferentes “muestras” y “población” en un modelo de regresión

sería lo equivalente en nuestro experimento a tomar un conjunto de muestras de tamaño \(n\) de nuestra población y hacer (en este caso hemos decidido 10.000 veces) el mismo experimento que antes para obtener 10000 posibles realizaciones de \(\widehat{\alpha},\widehat{\beta}.\)

Experimento 2 Este es el código que le permite obtener los 10.000 posibles valores paramétricos

b<-vector()
a<-vector()
n<-50
for(i in 1:10000) {
  u<-rnorm(n,0,sd=3)
  x<-runif(n)
  y<-3+5*x+u
  M1<-lm(y~x)
  a[i]<-M1$coefficients[1]
  b[i]<-M1$coefficients[2]
  
}

par(mfrow=c(1,2))
hist(a, main="histograma para a")
abline(v =3, col = "purple", lwd = 2)
hist(b, main="histograma para b")
abline(v =5, col = "blue", lwd = 2)

De esta forma, obtendrá los histogramas de la FIG3,

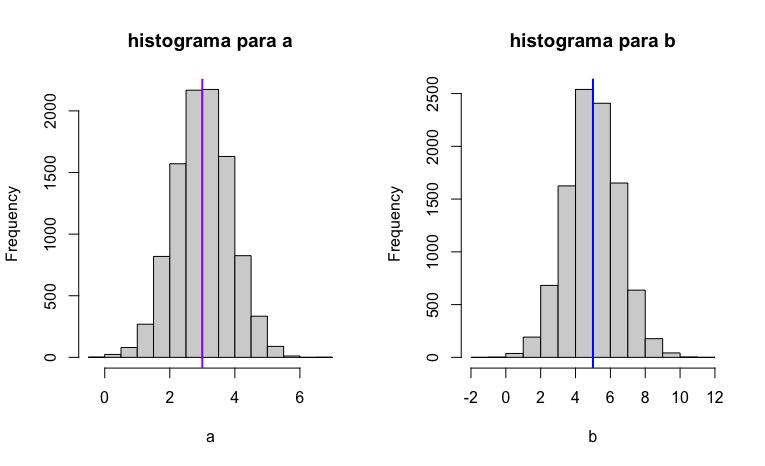FIG 3: obtención de los coeficientes insesgados que representan la idea de la insesgadez: en promedio, nuestros estimadores están apuntando al verdadero valor poblacional, aunque-como ya sabe- lo normal es obtener el resultado de una única muestra (es decir, una única realización del experimento aleatorio) y utilizar dichos valores como si fueran los poblaciones. Ya que es la mejor estimación que puede tener.

¿Qué ha aprendido?

Este ejercicio de simulación le ha permitido comprobar cómo se comporta un estimador de un modelo de regresión si satisface las hipótesis habituales. Pese a que-en teoría- la propiedad de insesgadez es deseable y funciona, en la práctica usted sólo ha estimado el posible valor del parámetro utilizando una única muestra (que es lo equivalente al experimento 1) pese a que lo desesable, pero imposible, es el experimento 2.

Ahora bien, como se habrá dado cuenta, hemos especificado que-para que este experimento salga bien- debemos asegurarnos de que la variable \(x\) y la variable \(u\) sean independientes. Si no lo son, entonces, en general

\[ E\left[\widehat{\beta}\right]\neq\beta \]

es decir, los estimadores de las pendientes son sesgados. Esto es un problema, puesto que no podemos confiar, entonces, en la estimación obtenida.

Ejercicio resuelto. Investigue cómo generar una normal multivariante para las variables \(x,u\) de tal manera que, indicando la correlación deseada entre \(x,u\) pueda evaluar cómo es el tamaño del sesgo según dicha correlación es mayor (por ejemplo, hágalo para correlación de un 10%, de un 30% y de un 70% entre el error y la variable explicatova)

solución

install.packages("dplyr")
install.packages("tidyr")
install.packages("faux")


library(dplyr)
library(tidyr)
library(faux)


#correlación del 10%#

#usamos cmat para introducir la correlación. Se hace en los dos valores
#centrales del vector

a10<-vector()
b10<-vector()
n<-50
for(i in 1:10000) {
  
  cmat <- c(1, .1,.1, 1)
  bvn <- rnorm_multi(n, 2, 0, 1, cmat, 
                     varnames = c("x", "u"))
  x<-bvn$x
  u<-bvn$u
  y<-3+5*x+u
  M1<-lm(y~x)
  a10[i]<-M1$coefficients[1]
  b10[i]<-M1$coefficients[2]
}




#correlación del 30%#
a30<-vector()
b30<-vector()
n<-50
for(i in 1:10000) {
  
  cmat <- c(1, .3,.3, 1)
  bvn <- rnorm_multi(n, 2, 0, 1, cmat, 
                     varnames = c("x", "u"))
  x<-bvn$x
  u<-bvn$u
  y<-3+5*x+u
  M1<-lm(y~x)
  a30[i]<-M1$coefficients[1]
  b30[i]<-M1$coefficients[2]
}

#correlación del 70%#
a70<-vector()
b70<-vector()
n<-50
for(i in 1:10000) {
  
  cmat <- c(1, .7,.7, 1)
  bvn <- rnorm_multi(n, 2, 0, 1, cmat, 
                     varnames = c("x", "u"))
  x<-bvn$x
  u<-bvn$u
  y<-3+5*x+u
  M1<-lm(y~x)
  a70[i]<-M1$coefficients[1]
  b70[i]<-M1$coefficients[2]
}


par(mfrow=c(3,2))
hist(a10, xlim = c(2,6), main="histograma para a, corr=0.1")
abline(v =3, col = "purple", lwd = 2)
hist(b10,xlim=c(2,6), main="histograma para b,corr=0.1")
abline(v =5, col = "blue", lwd = 2)

hist(a30,xlim=c(2,6), main="histograma para a,corr=0.3")
abline(v =3, col = "purple", lwd = 2)
hist(b30,xlim=c(2,6), main="histograma para b,corr=0.3")
abline(v =5, col = "blue", lwd = 2)


hist(a70,xlim=c(2,6), main="histograma para a,corr=0.7")
abline(v =3, col = "purple", lwd = 2)
hist(b70,xlim=c(2,6), main="histograma para b,corr=0.7")
abline(v =5, col = "blue", lwd = 2)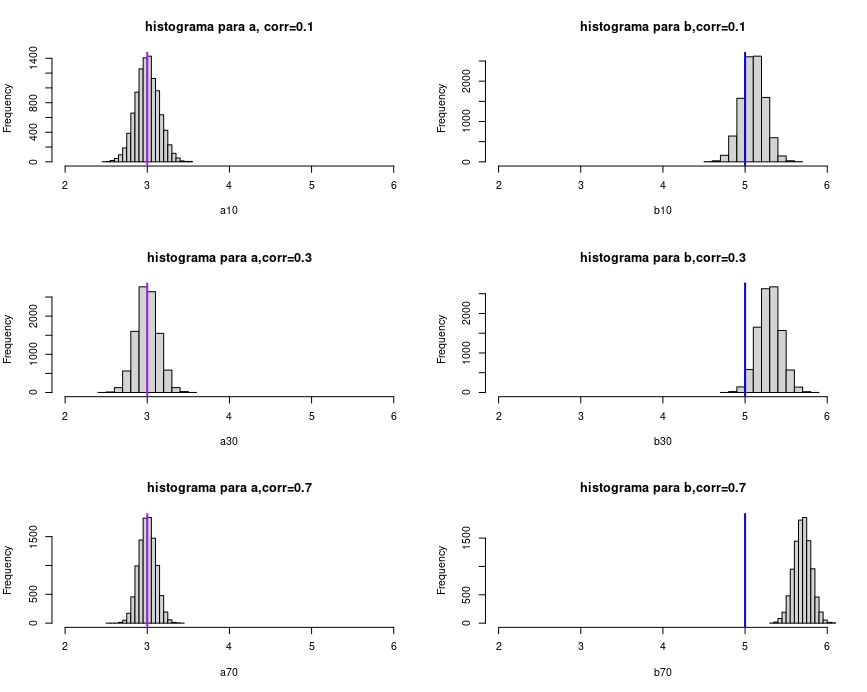

FIG 4: obtención de los coeficientes sesgados

Como puede ver en la FIG 4, cuanto mayor sea la correlación entre el error y la variable explicativa, mayor es el sesgo cometido (de tal forma que el estimador se aleja del verdadero valor poblacional)

Ejercicio

Piense ahora en su proyecto del primer cuatrimestre. Si estimó modelos de regresión ¿tiene motivos para pensar que podría haber estimado coeficientes sesgados?

Otro ejercicio resuelto Como vio en los vídeos, se menciona que-cuanto mayor relacionadas estén las variables explicativas en un modelo de regresión- más imprecisa es la estimación. Esto afectará a la desviación típica estimada del coeficiente y-por tanto- a su significatividad estadística (muchas veces, al usar el p-valor, diremos que una variable no es relevante cuando, en realidad, sí lo es). En este ejercicio de simulación, mostramos dicho resultado. Aquí analizamos el siguiente modelo:

\[ y=3+5x_1-2x_2+u \]

veremos que los estimadores resultan insesgados, pero la varianza de la distribución crece con la correlación entre las variables.

 #El efecto de variables correlacionadas en un modelo de regresión
  
  #y=3+5x1-2x2+u
  
  a10<-vector()
  b10<-vector()
  b20<-vector()
  n<-50
  for(i in 1:10000) {
    
    cmat <- c(1, .95,.95, 1)
    bvn <- rnorm_multi(n, 2, 0, 1, cmat, 
                       varnames = c("x1", "x2"))
    u<-rnorm(n,0,sd=3)
    x_1<-bvn$x1
    x_2<-bvn$x2
    y<-3+5*x_1-2*x_2+u
    M1<-lm(y~x_1+x_2)
    a10[i]<-M1$coefficients[1]
    b10[i]<-M1$coefficients[2]
    b20[i]<-M1$coefficients[3]
  }
  
  
  
  
  a11<-vector()
  b11<-vector()
  b21<-vector()
  n<-50
  for(i in 1:10000) {
    
    cmat <- c(1, 0.05,0.05, 1)
    bvn <- rnorm_multi(n, 2, 0, 1, cmat, 
                       varnames = c("x1", "x2"))
    u<-rnorm(n,0,sd=3)
    x_1<-bvn$x1
    x_2<-bvn$x2
    y<-3+5*x_1-2*x_2+u
    M1<-lm(y~x_1+x_2)
    a11[i]<-M1$coefficients[1]
    b11[i]<-M1$coefficients[2]
    b21[i]<-M1$coefficients[3]
  }
  
  
  
  
  par(mfrow=c(1,3))
  hist(a10, col=rgb(1,0,0,0.5),xlim = c(2,6), main="constante. Rojo: corr=0.95, Azul=corr(0.05)")
  hist(a11,col=rgb(0,0,1,0.5),  xlim = c(2,6), add=T)
  abline(v =3, col = "purple", lwd = 2)
  
  hist(b10, col=rgb(1,0,0,0.5),xlim = c(2,8), main="b1. Rojo: corr=0.95, Azul=corr(0.05)")
  hist(b11,col=rgb(0,0,1,0.5),  xlim = c(2,8), add=T)
  abline(v =5, col = "blue", lwd = 2)
  hist(b20, col=rgb(1,0,0,0.5),xlim = c(-6,2.5), main="b2. Rojo: corr=0.95, Azul=corr(0.05)")
  hist(b21,col=rgb(0,0,1,0.5),  xlim = c(-6,2.5), add=T)
  abline(v =-2, col = "blue", lwd = 2)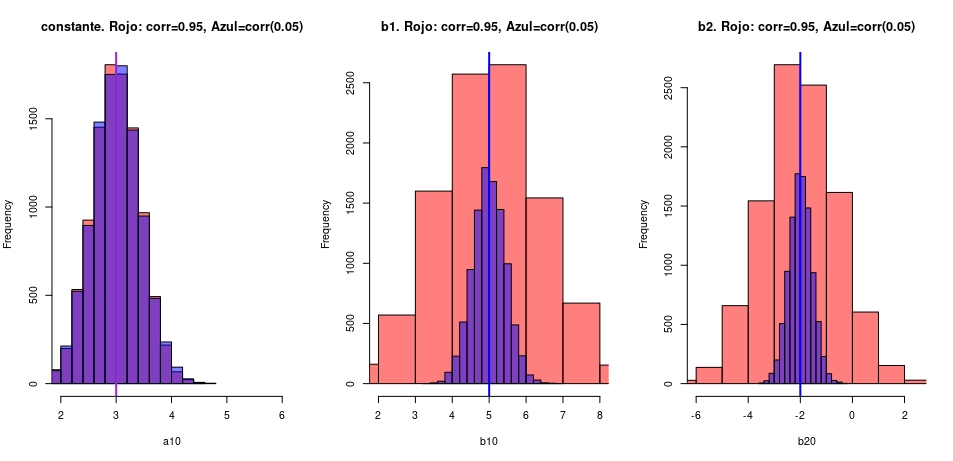

FIG 1: Resultado del ejercicio

Clase 6: la técnica del bootstrapping

Todo lo que ha aprendido en las clases anteriores tenía un objetivo: entender la idea del bootstrapping. Debemos añadir, sin embargo, otra de las utilidades de la simulación para cerrar el círculo. Con la simulación también podemos resolver problemas de probabilidad.

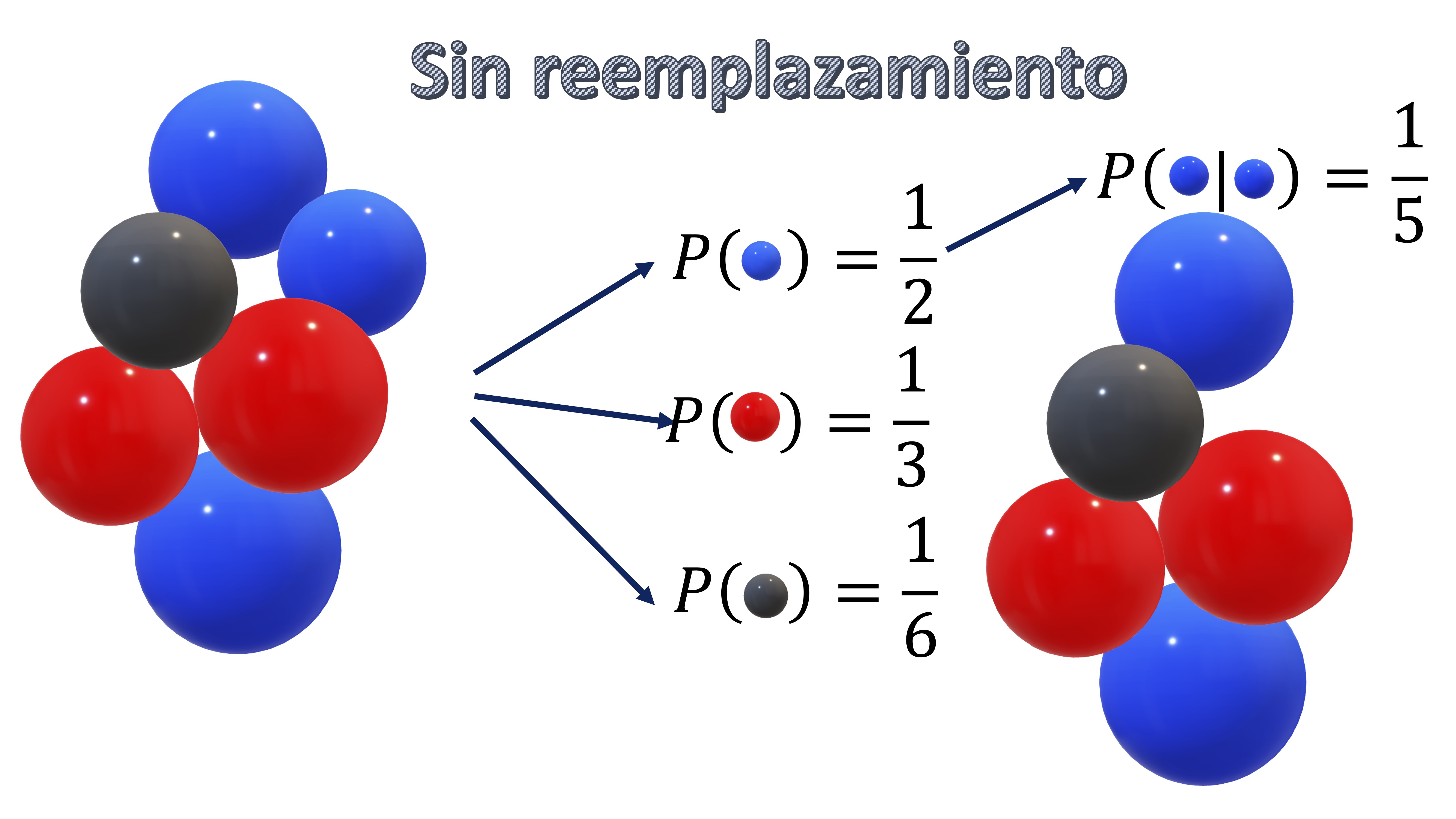
El muestreo con reemplazamiento

Esto ya lo ha hecho cuando resolvía los tediosos problemas de probabilidad con bolas de colores. En la FIG1, tenemos un ejemplo de muestreo con “reemplazamiento”. Tiene sus bolas originales, y la probabilidad de obtener una de cada color. Si quiere, por ejemplo, saber qué probabilidad tiene de sacar dos veces bola azul si una vez saca una bola la vuelve a depositar en la urna (reemplazamiento), tiene que darse cuenta de que son sucesos independientes y, por tanto \(P(azul|azul)=P(azul)\times P(azul)=\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}\).

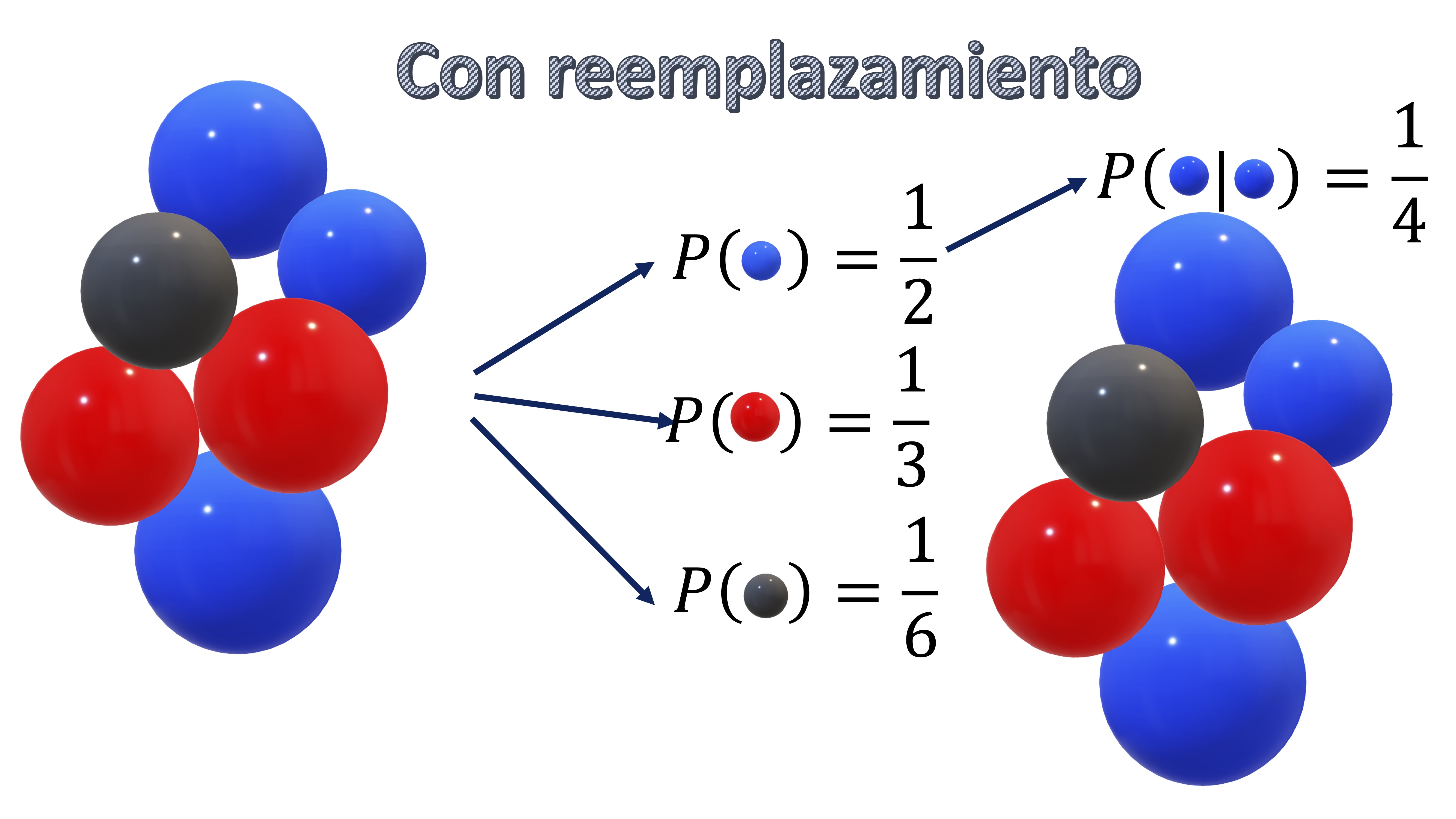
FIG 1: muestreo con reemplazamiento

Esto lo puede simular en R. Por ejemplo, cree un vector donde \(1\) sea azul, \(2\) sea rojo y \(3\) sea negro.

x=c(1,1,1,2,2,3)

Utilizando la función sample, podrá simular cualquier salida de la urna. Por ejemplo, aquí le estamos diciendo que saque dos bolas con reemplazamiento (es decir, R saca una bola, vuelve a depositarla en la urna, y saca de nuevo otra)

sample(x, 2, replace = TRUE)

Tomando el resultado frecuentista de que

\[ P(azul|azul)=\frac{veces\: que\: salen\:2\: bolas\: azules}{veces\:totales} \]

generamos un código que nos permita obtener-simulando un conjunto de casos posibles- el número de favorables. Deberá aproximarse dicho resultado a la probabilidad real que es 0.25.

for(i in 1:10000) {
  
  y<-sample(x, 2, replace = TRUE)
  if (y[1]==1 && y[2]==1){
  count<-count+1}
}

Prob=count/10000

> Prob
[1] 0.2475

Muestreo sin reemplazamiento

Lo mismo ocurrirá si hace el muestreo sin reemplazamiento. en este caso, la probabilidad de obtener azul una vez se ha obtenido azul no es independiente, puesto que el número de bolas será distinto. Entonces, tendrá que ocurrir lo que ve en la FIG2

FIG 2: muestreo sin reemplazamiento

x=c(1,1,1,2,2,3)

count<-0

for(i in 1:10000) {
  
  y<-sample(x, 2, replace = FALSE)
  if (y[1]==1 && y[2]==1){
    count<-count+1}
}


Prob=count/10000

> Prob
[1] 0.2035

Para intentar estimular la idea del bootstrapping, primer recordamos un marco “sencillo” y general relativo a la construcción de intervalos de confianza (aplicable inmediatamente a la inferencia clásica) para entender en qué punto estamos y qué hemos “refrescado” simulando:

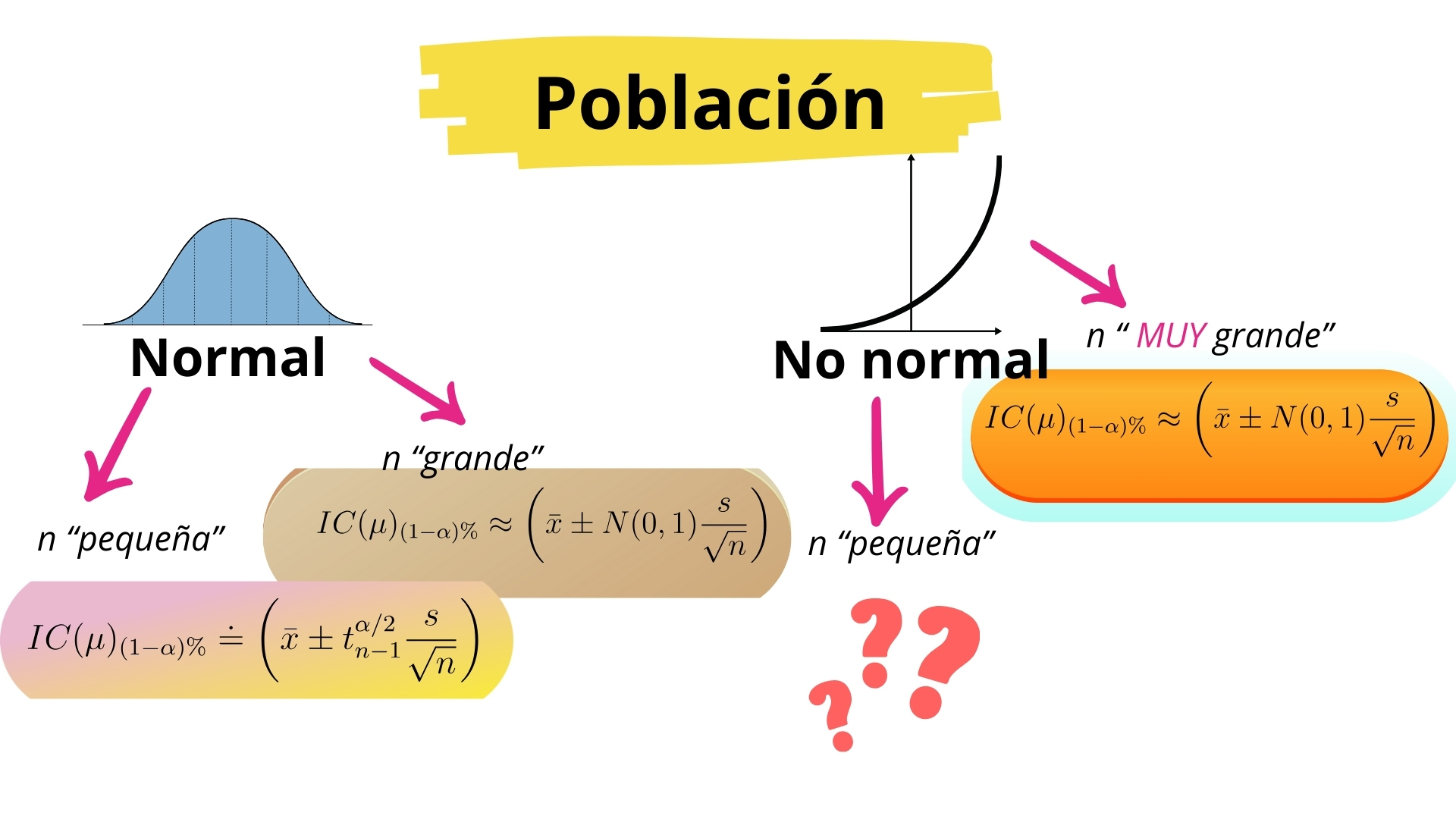FIG 3: el marco conceptual Como vimos, si tenemos motivos para pensar que los elementos de nuestra población se distribuyen de acuerdo a una normal, y si el muestreo se ha hecho conforme al muestreo aleatorio simple:

si el tamaño muestral es pequeño (\(n<50\)) podemos construir el intervalo de confianza de manera exacta usando una t de student.

Si el tamaño muestral empieza a crecer, entonces podemos construir un intervalo de confianza “aproximado” usando el TCL y la distribución normal para la obtención del valor pivote del intervalo.

Ahora bien, si tenemos motivos para sospechar que la población no se distribuye normal y, además, es asimétrica, entonces

Si la muestra es pequeña, no podemos hacer nada -por ahora-.

Si la muestra es grande, de nuevo, podemos usar el TCL. Eso sí, hemos visto que una muestra grande puede implicar un valor de \(n\) de miles de unidades.

El “bootstrap” es una técnica que nace para tratar de aproximar “distribuciones” empíricas (es decir, con la muestra disponible) de los estadísticos de interés. En un principio, se pensó que era la solución “para muestras pequeñas”. Luego, se ha ido viendo que suele ser muy útil para obtener resultados de diferente tipo (intervalos de confianza, predicciones probabilísticas, etc…) utilizando los datos disponibles para elaborar los resultados deseados. Lo iremos viendo.

Lo primero que hicimos, con la gente que había en clase es pedir que escribieran sus alturas en una tarjeta:

FIG 4: el experimento

como verá, sólo había 7 alumnos aunque, iluso de mí, preparé más tarjetas por si acaso. La idea del bootstrapping es la siguiente:

¿Cómo funciona el bootstrapping?

Asuma que nunca va a poder acceder a la población. Sólo tiene una muestra de tamaño \(n\). La que sea. Entonces, lo que va a hacer es, como si fuera un ejercicio de simulación de los anteriores, es usar la muestra “como si fuera la población”. De esta manera, tendrá que hacer extracciones de la muestra (sacar tarjetitas con la altura del alumno) con reemplazamiento (volviendo a dejar la tarjeta) y sacando otra. Asi, generara todas las muestras bootstrap que quiera de tamaño \(n\). De tal forma que los valores “más frecuentes” saldrán más veces.

Así lo hice en clase:

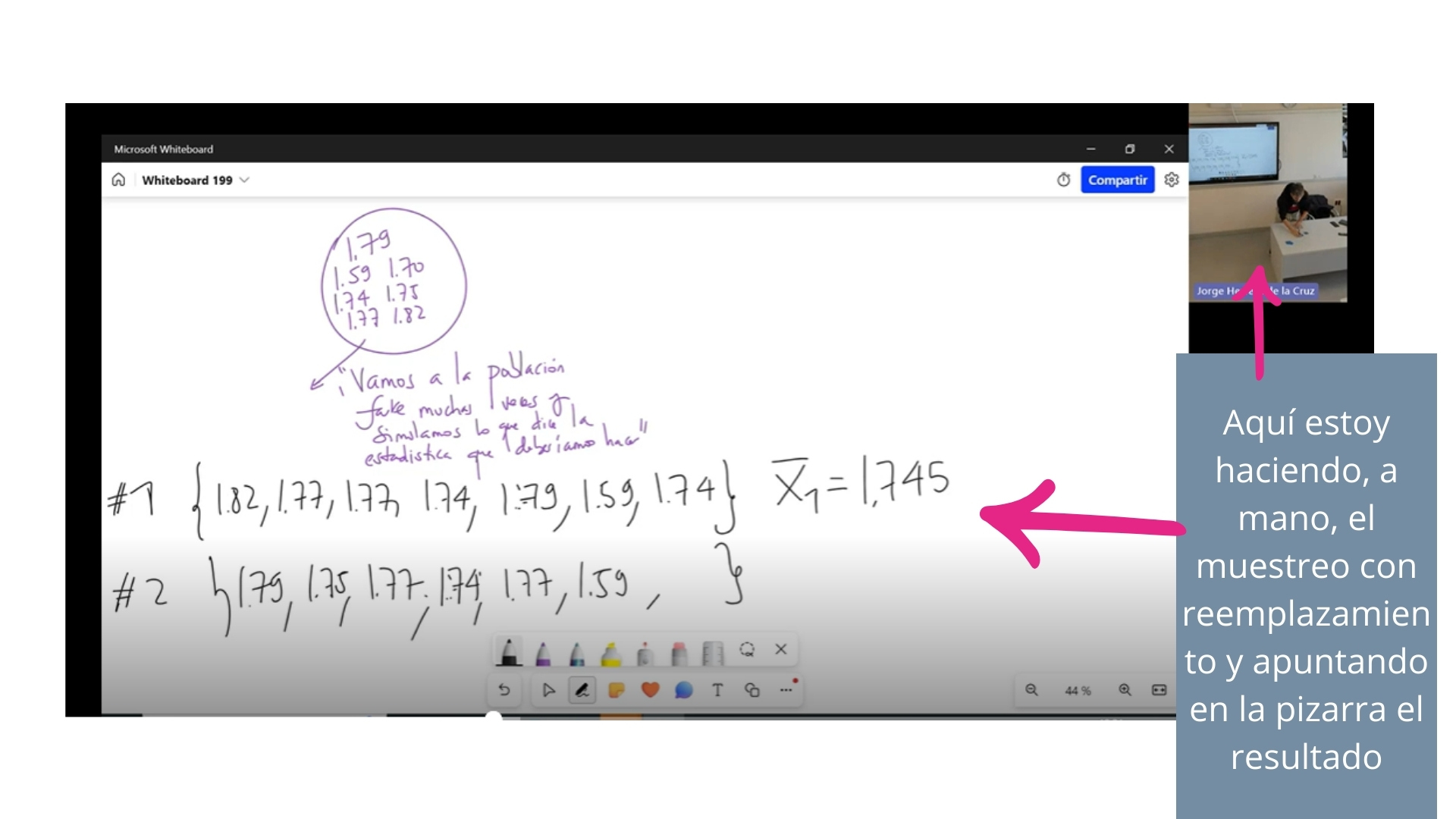
FIG 5: el experimento (II)

Como ve, la muestra consiste en los 7 elementos \(\{1.79,1.59,1.74,1.70,1.75,1.77,1.82\}\). En la primera extracción que hice se repite \(1.77\) dos veces y, por ejemplo, \(1.70\) no sale. La media de altura de esa primera muestra bootstrap es \(1.745\). Como verá, estamos haciendo algo parecido a lo visto en las clases anteriores, sólo que ahora la población no “la simulamos al azar” sino que viene dada por la muestra disponible. Ahora bien, podemos generar todas las réplicas (muestras bootstrap) que quiera mediante el ordenador. Así, por ejemplo, puede ver cómo se distribuye el estadístico “media muestral de la altura”.

#ALTURAS

X=c(1.79,1.59,1.70,1.74,1.75,1.77,1.82)
n=7
mX<-0
y<-0

for(i in 1:10000) {
 
  id<-sample(c(1:n), n, replace = TRUE)  
  y<-X[id]
    mX[i]=mean(y)
}

hist(mX)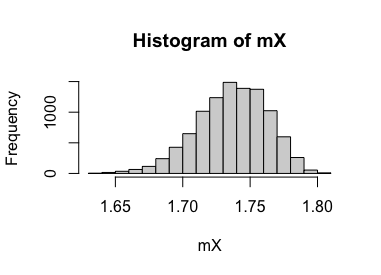

FIG 6: el experimento (iii) Fíjese que, este estadístico no es simétrico puesto que los datos que obtenemos no parecen proceder de una normal. Ahora bien, tenemos tan pocos datos que hay que tomarlo con cautela. Imagine que tiene un atípico como Pau Gasol. Entonces, en esta muestra tan pequeña va a estar sobrerrepresentado

#ALTURAS

X=c(1.79,1.59,1.70,1.74,1.75,1.77,2.20)
n=7
mX<-0
y<-0

for(i in 1:10000) {
 
  id<-sample(c(1:n), n, replace = TRUE)  
  y<-X[id]
    mX[i]=mean(y)
}

hist(mX)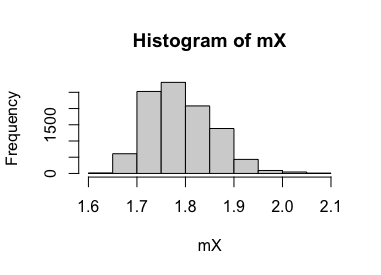

FIG 7: el experimento (iii) Ahora, como verá, la asimetría es claramente a la derecha y-quizás-estimando una distribución empírica sesgada de la altura media de la población que pretendemos representar. Pero no le podemos pedir más a 7 datos!

Otra cosa que puede hacer con bootstraping es obtener el p-valor de un contraste sin utilizar la rígida teoría estadística. Supongamos que queremos testar la hipótesis nula

[ Ho: \ H1: >1.75

]

Lo que haremos es simular estadísticos de contraste para cada muestra bootstrapp y contaremos cuántos son mayores que 0, ya que

#ALTURAS

X=c(1.79,1.59,1.70,1.74,1.75,1.77,1.82)
n=7
mX<-0
y<-0
t<-0
T<-(mean(X)-1.75)/(sd(X)/sqrt(n))
for(i in 1:10000) {
 
  id<-sample(c(1:n), n, replace = TRUE)  
  y<-X[id]
    mX[i]=mean(y)
    t[i]<-(mX[i]-1.75)/(sd(y)/sqrt(n))
   
}

 mean(t>T)
[1]0.5029

En este caso, obtenemos 0.5029. Un p-valor distinto al que obtendríamos si hacemos el test basado en normalidad de la población (con un p-valor de 0.6665)

t.test(X, mu = 1.75, alternative = "greater")

One Sample t-test

data:  X
t = -0.45227, df = 6, p-value = 0.6665
alternative hypothesis: true mean is greater than 1.75

Por otro lado, también puede construir intervalos de confianza para la media poblacional. La técnica que contamos aquí es una de las más sencillas aunque, debido a ello, está sometida a críticas que exceden el nivel del curso.

#ALTURAS

X=c(1.79,1.59,1.70,1.74,1.75,1.77,2.20)
n=7
mX<-0
y<-0

for(i in 1:10000) {
 
  id<-sample(c(1:n), n, replace = TRUE)  
  y<-X[id]
    mX[i]=mean(y)
}

quantile(mX, probs = c(0.025,0.975))

y este sería el intervalo de confianza al 95% de la altura poblacional 
    2.5%    97.5% 
1.681429 1.782857

Ejercicio para pensar ¿Cómo se construye un intervalo de confianza para la mediana?

#ALTURAS
X=c(1.79,1.59,1.70,1.74,1.75,1.77,1.82)
n=7
mX<-0
y<-0

for(i in 1:10000) {
  
  id<-sample(c(1:n), n, replace = TRUE)  
  y<-X[id]
  mX[i]=median(y)
}

quantile(mX, probs = c(0.025,0.975))

2.5%  97.5% 
 1.70  1.79

Clase 7: la técnica del bootstrapping aplicada a la regresión

La idea del bootstrapping aplicada a la regresión consiste en lo siguiente: usted tiene unos datos originales, por ejemplo, la muestra de la FIG3

FIG 3: una muestra para estimar un modelo de regresión

Ahora, usted obtiene una estimación para \(\alpha\) y para \(\beta\) y se pregunta ¿podría tener una distribución? Entonces, va a asumir que esa muestra es su población (es una asunción, no es la realidad) y, entonces, va a hacer muestreos con reemplazamiento de los pares que tiene, de tal forma que pueda estimar modelos de regresión alternativos

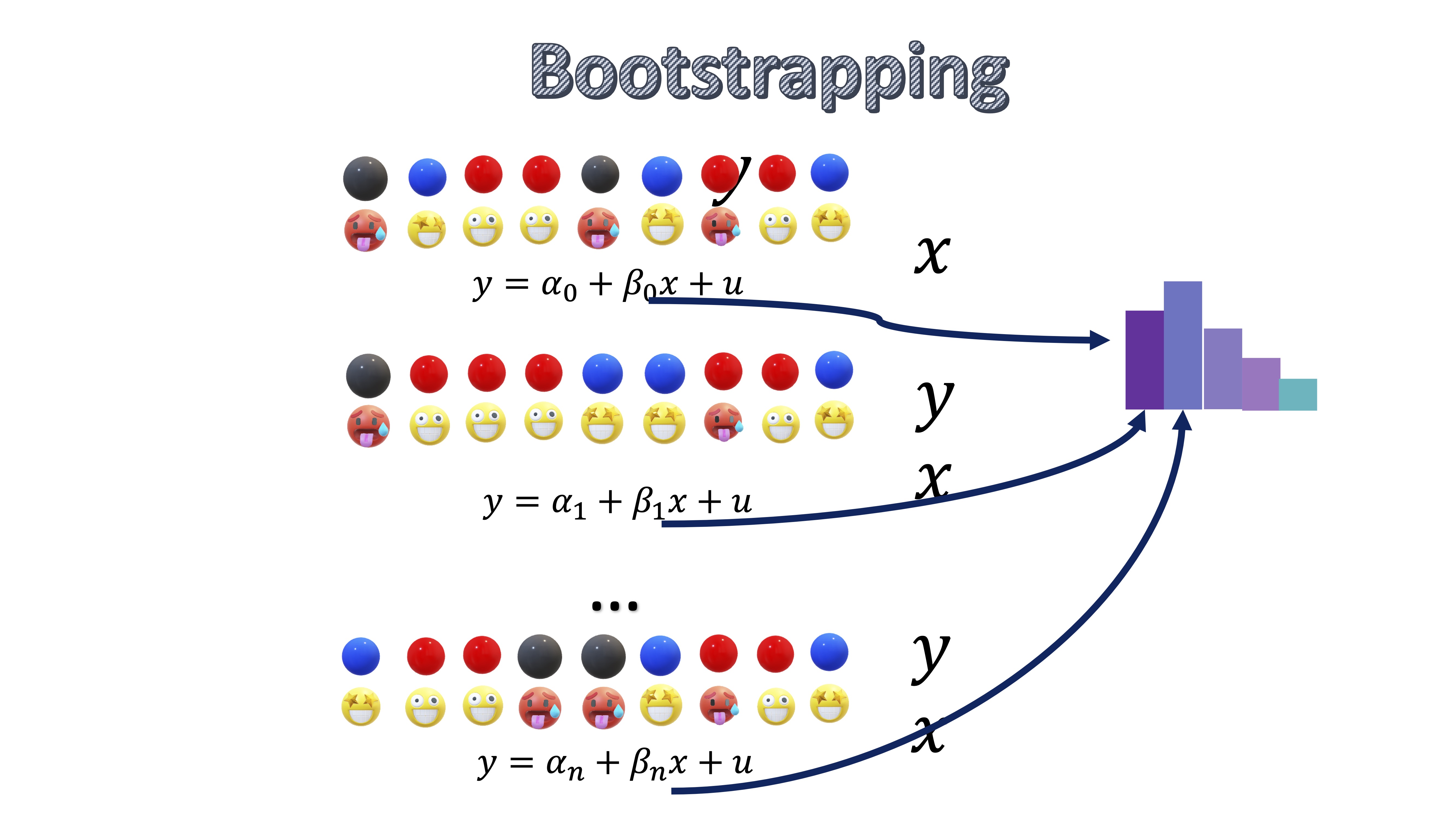
FIG 4: la idea del bootstrapping

Como ve, cada iteración que hace, es como si sorteara en la urna qué elementos de la muestra se utilizan y en qué proporción. Habrá elementos (bolas) que no saque en una iteración y otras que las saque muchas veces. Como ve, lo que está haciendo es generar muchas muestras alternativas a partir de una única muestra.

Esta técnica es útil para:

Obtener intervalos de confianza para parámetros cuando el modelo no lo permite (piense en modelos complicados, donde no se puede obtener una expresión analítica de las varianzas)

Obtener intervalos de confianza para parámetros cuando los errores no siguen una distribución normal (y la muestra es pequeña)

Obtener intervalos de confianza para predicciones

Vea cómo utilizarla. Por ejemplo, generamos un modelo de regresión lineal donde todo funciona. Entonces, el script del bootstrap es el siguiente

#declaramos los vectores donde guardaremos las estimaciones
b<-vector()
a<-vector()
#generamos la muestra aleatoria del modelo de regresión
set.seed(123)
n<-100
u<-rnorm(n,0,sd=3)
x<-runif(n)
y<-3+5*x+u
#estimamos un primer modelo base
M0<-lm(y~x)

for(i in 1:10000) {

 id<-sample(c(1:n), n, replace = TRUE)  
  X<-x[id]
  Y<-y[id]
  M1<-lm(Y~X)
  a[i]<-M1$coefficients[1]
  b[i]<-M1$coefficients[2]
  
}



par(mfrow=c(1,2))
hist(a, main="histograma para a")
abline(v =3, col = "purple", lwd = 2)
hist(b, main="histograma para b")
abline(v =5, col = "blue", lwd = 2)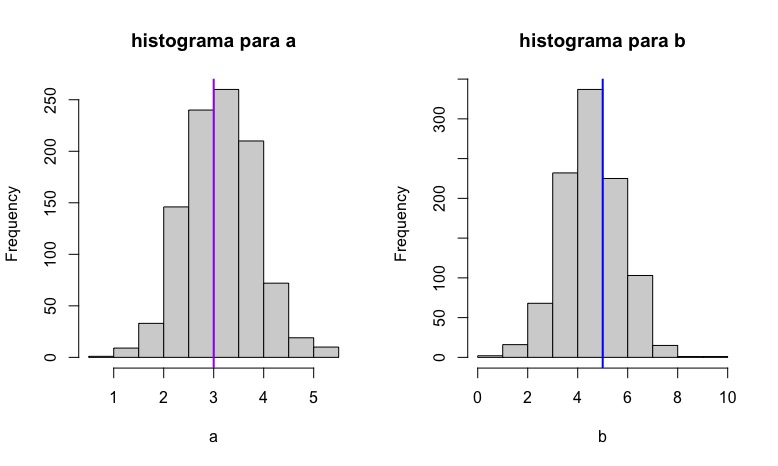

FIG 5: Primer ejemplo del bootstrap De hecho, puede comprobar cómo los intervalos de confianza que obtiene son similares. Mediante el modelo :

#esta es la regresión inicial# 
> summary(M0)

Call:
lm(formula = y ~ x)


Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   3.0196     0.5325   5.671 1.44e-07 ***
x             5.5177     0.9384   5.880 5.69e-08 ***

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.086 on 48 degrees of freedom
Multiple R-squared:  0.2106,    Adjusted R-squared:  0.1941 
F-statistic:  12.8 on 1 and 48 DF,  p-value: 0.0008027

Donde un Intervalo de confianza para el parámetro \(\beta\) se obiene como

\[ IC\left(\beta\right)_{\left(1-\alpha\right)\%}\equiv\left(5.51-1.96\times0.9384,5.51+1.96\times0.9384\right)=(3.6707,7.349) \]

Como puede ver, si calculamos el IC mediante los resultados del bootstrap, tendremos

> quantile(b, c(.025, .5, .975)) 
    2.5%      50%    97.5% 
3.690361 5.502940 7.38899

que es un intervalo similar. Ahora bien, ¿qué ocurre si los errores no se distribuyen de forma normal? En este caso, pedimos que los errores se distribuyan de manera uniforme.

b<-vector()
a<-vector()
set.seed(123)
n<-50
u<-runif(n,-3,3)
x<-runif(n)
y<-3+5*x+u
M0<-lm(y~x)

for(i in 1:10000) {
  
  id<-sample(c(1:n), n, replace = TRUE)  
  X<-x[id]
  Y<-y[id]
  M1<-lm(Y~X)
  a[i]<-M1$coefficients[1]
  b[i]<-M1$coefficients[2]
  
}

En este caso, es importante notar que la hipótesis principal para obtener intervalos de confianza de parámetros en modelos de regresión lineal, como ya se vio, es que los errores se distribuyan normal. Partiendo del modelo original de regresión, obtenido con los datos simulados (con error NO normal), calculamos el intervalo de confianza para los parámetros obtenido como si los errores fueran normales

#esta es la regresión inicial# 
> summary(M0)

Call:
lm(formula = y ~ x)


Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.8818     0.5051   5.705 7.05e-07 ***
x             5.5005     0.9183   5.990 2.60e-07 ***
---
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.086 on 48 degrees of freedom
Multiple R-squared:  0.2106,    Adjusted R-squared:  0.1941 
F-statistic:  12.8 on 1 and 48 DF,  p-value: 0.0008027

Donde un Intervalo de confianza para el parámetro \(\beta\) se obiene como

\[ IC\left(\beta\right)_{\left(1-\alpha\right)\%}\equiv\left(5.50-1.96\times0.9183,5.50+1.96\times0.9183\right)=(3.7001,7.2998) \]

mientras que el intervalo, calculado con la muestra bootstrap, será

> quantile(b, c(.025, .5, .975)) 
    2.5%      50%    97.5% 
3.598279 5.506940 7.382569

que difiere del calculado asumiendo normalidad y que, en el caso de distribuciones de errores con mayor asmetría, etc… podría dar resultados mucho más diferentes.

Ejemplo de diferentes aplicaciones del bootstrap

Objetivo Aplicar las diferentes técnicas de remuestreo con el fin de:

Entender cómo obtener un p-valor mediante la aplicación del bootstrap (y su comparación asumiendo normalidad en los errores o que se cumplen las propiedades asintóticas de los estimadores (Teorema Central del Límite))

Realizar predicción condicionada con bootstrap como alternativa al uso del “p-valor” y la inferencia automática para valorar el impacto cuantitativo de una variable de interés.

Utilizaremos los datos de enfermedades coronarias “Heart Disease” disponibles en la intranet

Utilizaremos una submuestra para individuos de más de 65 años y estimaremos el siguiente modelo

\[ Disease_i=logit(\beta_0+\beta_1 age+\beta_2sex+\beta_3chol) \]

library(readr)
heart <- read_delim("heart_MD.csv", delim = ";", 
                       escape_double = FALSE, trim_ws = TRUE)


n=dim(heart)[1]

b0<-0
b1<-0
b2<-0
b3<-0

datos<-data.frame(heart$target,heart$age,heart$sex,heart$chol)

datos2<-subset(datos,heart.age>65)

for(i in 1:1000) {
  
  id<-sample(c(1:n), n, replace = TRUE)  
  datos_bootstrap<-datos2[id,]
  mod<-glm(heart.target~heart.age+heart.sex+heart.chol,data=datos_bootstrap,family="binomial")
  b0[i]<-mod$coefficients[1]
  b1[i]<-mod$coefficients[2]
  b2[i]<-mod$coefficients[3]
  b3[i]<-mod$coefficients[4]
  
}

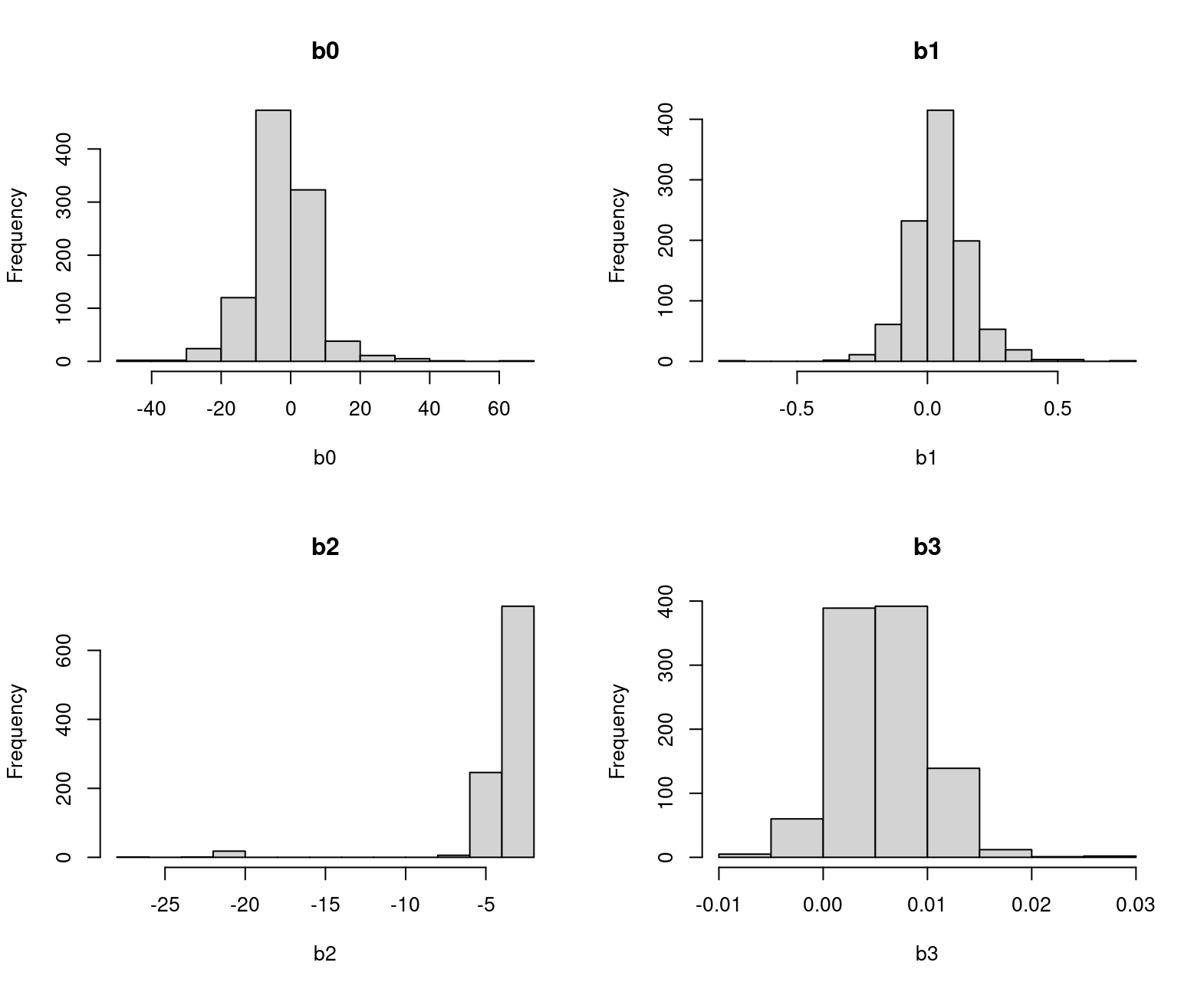FIG 6: Resultado del Bootstrap con el modelo de los datos coronarios Esta estimación sugiere que los parámetros \(b_2\) y \(b_3\) presentan asimetrías que, de cara a la inferencia habitual podría dar lugar a conclusiones muy distintas. Por ejemplo,

> mod<-glm(heart.target~heart.age+heart.sex+heart.chol,data=datos2,family="binomial")
> summary(mod)

Call:
glm(formula = heart.target ~ heart.age + heart.sex + heart.chol, 
    family = "binomial", data = datos2)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) -1.535468   6.567222  -0.234    0.815    
heart.age    0.037327   0.095104   0.392    0.695    
heart.sex   -3.452659   0.613535  -5.627 1.83e-08 ***
heart.chol   0.004988   0.005611   0.889    0.374    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 153.870  on 110  degrees of freedom
Residual deviance:  99.681  on 107  degrees of freedom
AIC: 107.68

Number of Fisher Scoring iterations: 5

asigna a la variable “sex” un p-valor cercano a cero, sugiriendo una alta capacidad explicativa/predictiva. Recuerde que este p-valor, en el modelo logit, se obtiene asumiendo que se cumplen los supuestos del TCL. Como se vio previamente, muchas veces, dadas las condiciones de la muestra, se necesitan tamaños muestrales muy altos para que el TCL opere correctamente. Por otro lado, podemos generar -mediante bootstrap- los correspondientes estadísticos de contraste y obtener el p-valor empírico. Veamos cómo:

Paso 1 Obtenemos, mediante bootstrap diferentes una muestra de diferentes estadísticos para contrastar \(H_0 : \beta_i=0\) frente a \(H_1 :\beta_i\neq 0\), para \(i=0,1,2,3\).

t0<-0
t1<-0
t2<-0
t3<-0


for(i in 1:1000) {
  
  id<-sample(c(1:n), n, replace = TRUE)  
  datos_bootstrap<-datos2[id,]
  mod<-glm(heart.target~heart.age+heart.sex+heart.chol,data=datos_bootstrap,family="binomial")
  t0[i]<-summary(mod)$coefficients[,3][1] 
  t1[i]<-summary(mod)$coefficients[,3][2] 
  t2[i]<-summary(mod)$coefficients[,3][3] 
  t3[i]<-summary(mod)$coefficients[,3][4] 
  
}

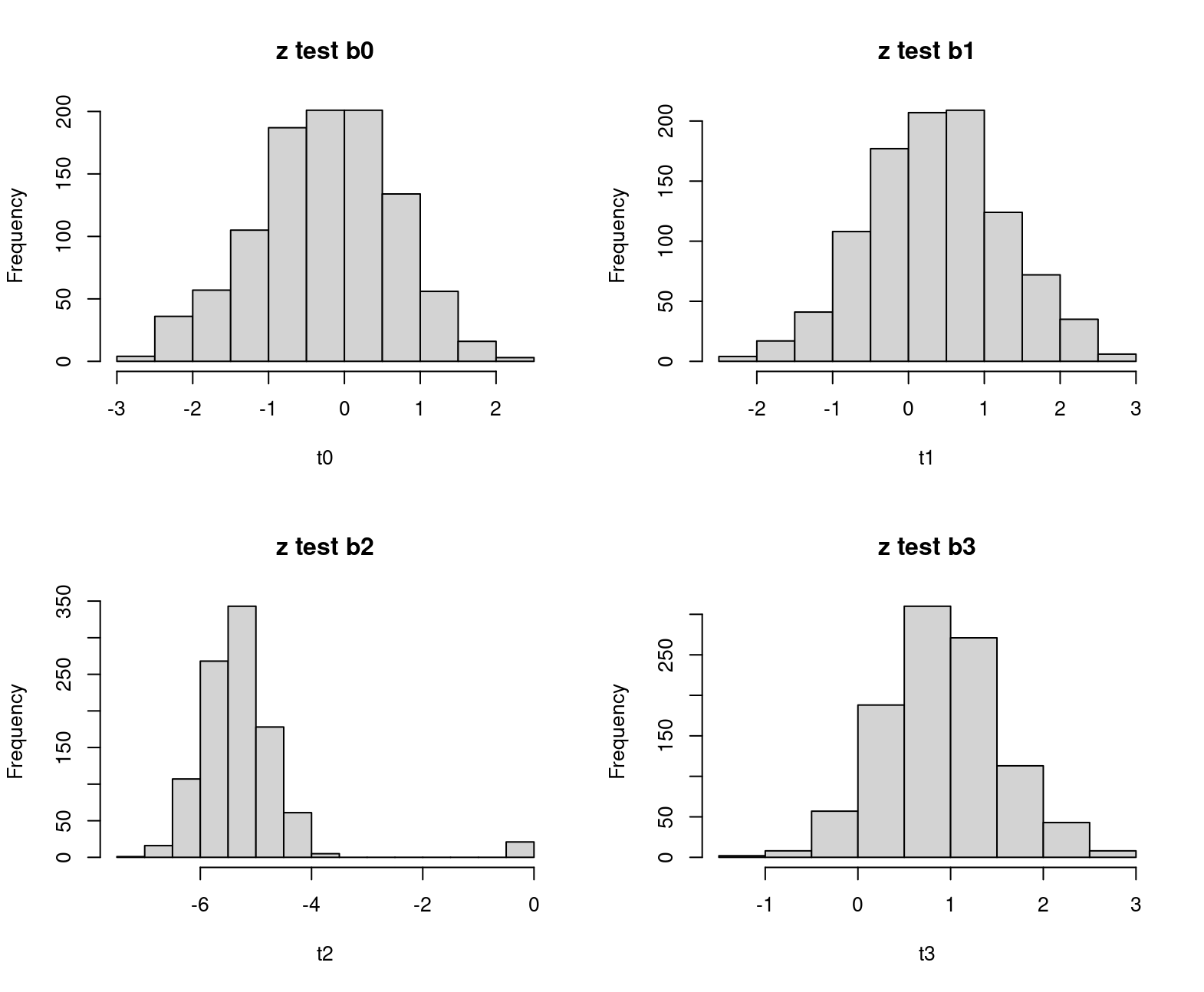FIG 7: Distribuciones de los estadísticos de contraste mediante bootstrap >- Paso 2 Dado que el p-valor es la probabilidad de encontrar un estadístico de contraste más extremo al obtenido, bajo la hipótesis nula, en nuestro caso consiste en contar cuántos de los 1000 estadísticos superan-en valor absoluto- a los obtenidos en el modelo inicial. Esto lo llamaremos el “p-valor empírico”. Cuanto más simétrica la distribución del estadístico que hemos obtenido mediante bootstrap, más se parecerán a las obtenidas en la regresión.

> mean(abs(t0)>0.234)
[1] 0.798
> mean(abs(t1)>0.392)
[1] 0.694
> mean(abs(t2)>5.627)
[1] 0.308
> mean(abs(t3)>0.889)
[1] 0.523

Paso 3 desconfíe: como verá, los p-valores de los estadísticos de contraste que tienden a ser simétricos, se parecen a los obtenidos en la regresión. Pero, por ejemplo, en el caso del p-valor asociado a la variable “sex” parece que ya no tiene tres asteriscos.

Sin embargo, como ya hemos contado a lo largo del curso, conviene preguntarle al modelo para aprender de él. Por ejemplo, utilicemos bootstrapping para simular la probabilidad de tener enfermedad coronaria para un paciente de 70 años, sex=1 y con dos valores distintos de colesterol: 150 y 300

pred1<-0
pred2<-0
data_predict<-data.frame(heart.age=70,heart.sex=1,heart.chol=300)
data_predict2<-data.frame(heart.age=70,heart.sex=1,heart.chol=150)
for(i in 1:1000) {
  
  id<-sample(c(1:n), n, replace = TRUE)  
  datos_bootstrap<-datos2[id,]
  mod<-glm(heart.target~heart.age+heart.sex+heart.chol,data=datos_bootstrap,family="binomial")
  
  pred1[i]<-predict.glm(mod,newdata=data_predict, type="response")
  pred2[i]<-predict.glm(mod,newdata=data_predict2, type="response")
  
}


c1 <- rgb(173,216,230,max = 255, alpha = 80, names = "lt.blue")
c2 <- rgb(255,192,203, max = 255, alpha = 80, names = "lt.pink")
 hgA <- hist(pred1, breaks = 30, plot = FALSE) # Save first histogram data
 hgB <- hist(pred2, breaks = 30, plot = FALSE) # Save 2nd histogram data

 plot(hgA, col = c1) # Plot 1st histogram using a transparent color
 plot(hgB, col = c2, add = TRUE) # Add 2nd histogram using different color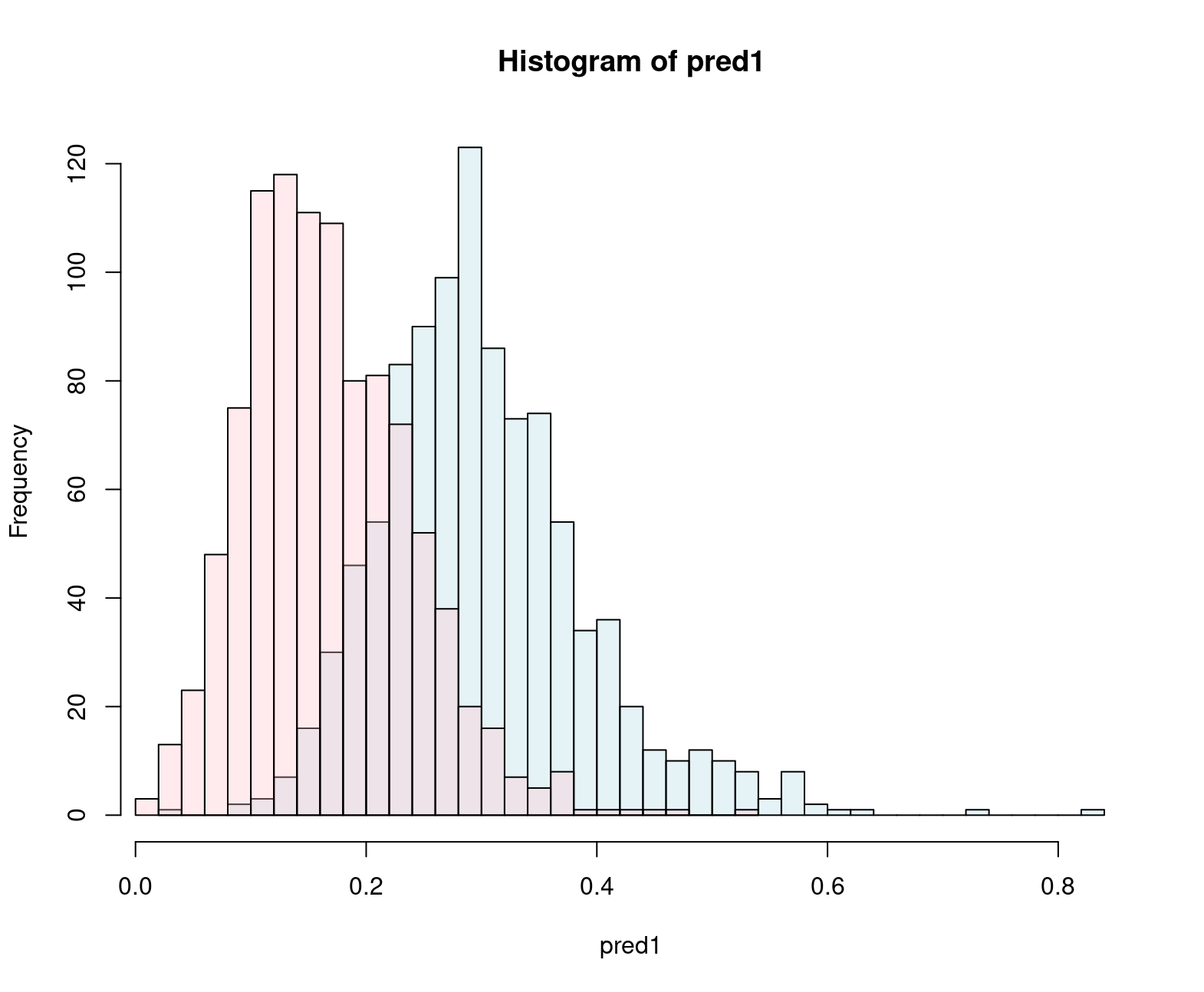

FIG 7: Predicción “bootstrap” de dos tipos de individuo Como verá, aquí puede observar varias cosas:

El posible impacto sobre la probabilidad de enfermedad coronaria para los dos niveles de colesterol (rojo=150, azul=300).

Quizás no tenga que pronunciarse sobre si es o no relevante: eso tendrá que juzgarlo un usuario del modelo (médico o experto), su tarea es proporcionarle estimaciones y una medida de la incertidumbre

En este gráfico se aprecian ambas: la posible diferencia entre los dos niveles de colesterol y la incertidumbre asociada a las predicciones.

Ejercicio: con los datos de How Couples Meet and Stay Together tiene que calcular la probabilidad de que una pareja dure más de 30 años si se llevan 10 años de edad, tienen diferente nivel de estudios, están casados y cohabitan. ¿Cómo cambia esa probabilidad si se llevan 5 o 20 años?

solución

Para resolverlo, primero hemos hecho un análisis descriptivo del que destaca 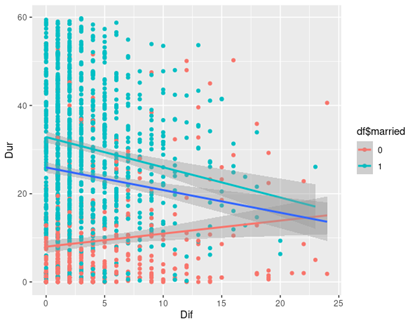FIG 8: un gráfico sobre la posible relación entre la diferencia de edad y la duración de la relación cómo el impacto de la diferencia de edad es distinto si se estña casado (impacto negativo) que si no se está (mucho más disperso e impreciso, pero con pendiente positiva).

 library(readr)
couples<- read_delim("HCMST_Ex (1).csv", 
                           delim = ";", escape_double = FALSE, locale = locale(decimal_mark = ",", 
                                                                               grouping_mark = ""), trim_ws = TRUE)


couples$same_ed<-couples$my_level==couples$partner_level
couples$age_diff<-abs(couples$myage-couples$mypartner)


n<-dim(couples)[1]
pred1<-0
pred2<-0
pred3<-0
data_predict1<-data.frame(age_diff=5,same_ed=FALSE,married=1,cohabit=1)
data_predict2<-data.frame(age_diff=10,same_ed=FALSE,married=1,cohabit=1)
data_predict3<-data.frame(age_diff=20,same_ed=FALSE,married=1,cohabit=1)

for(i in 1:10000) {
  
  id<-sample(c(1:n), n, replace = TRUE)  
  datos_bootstrap<-couples[id,]
 
  mod<-lm(dur~same_ed+age_diff*married+cohabit,data=datos_bootstrap)
  
  pred1[i]<-predict(mod,newdata=data_predict1)
  pred2[i]<-predict(mod,newdata=data_predict2)
  pred3[i]<-predict(mod,newdata=data_predict3)

}


xmin <- min(pred1, pred2,pred3)
xmax <- max(pred1, pred2,pred3)
# Create the first histogram
hist(pred1, main = "Predicción Duración relación", xlab = "Dur", ylab = "Frecuencia",
     col=rgb(0,0,1,0.5), xlim = c(xmin, xmax))
# Create the second histogram
hist(pred2, main = "dif=10 años", xlab = "Dur", ylab = "Frecuencia",
     col=rgb(1,0,0,0.5), add = TRUE, xlim = c(xmin, xmax))
hist(pred3, main = "Predicción Duración relación", xlab = "Dur", ylab = "Frecuencia",
     col=rgb(0,1,0,0.5), add = TRUE, xlim = c(xmin, xmax))
abline(v=30, col="black",lwd=2,lty="dotted")
legend("topleft", legend=c("5 años","10 años","20 años"), col=c(rgb(0,0,1,0.5),rgb(1,0,0,0.5),rgb(0,1,0,0.5)), pt.cex=2, pch=15 )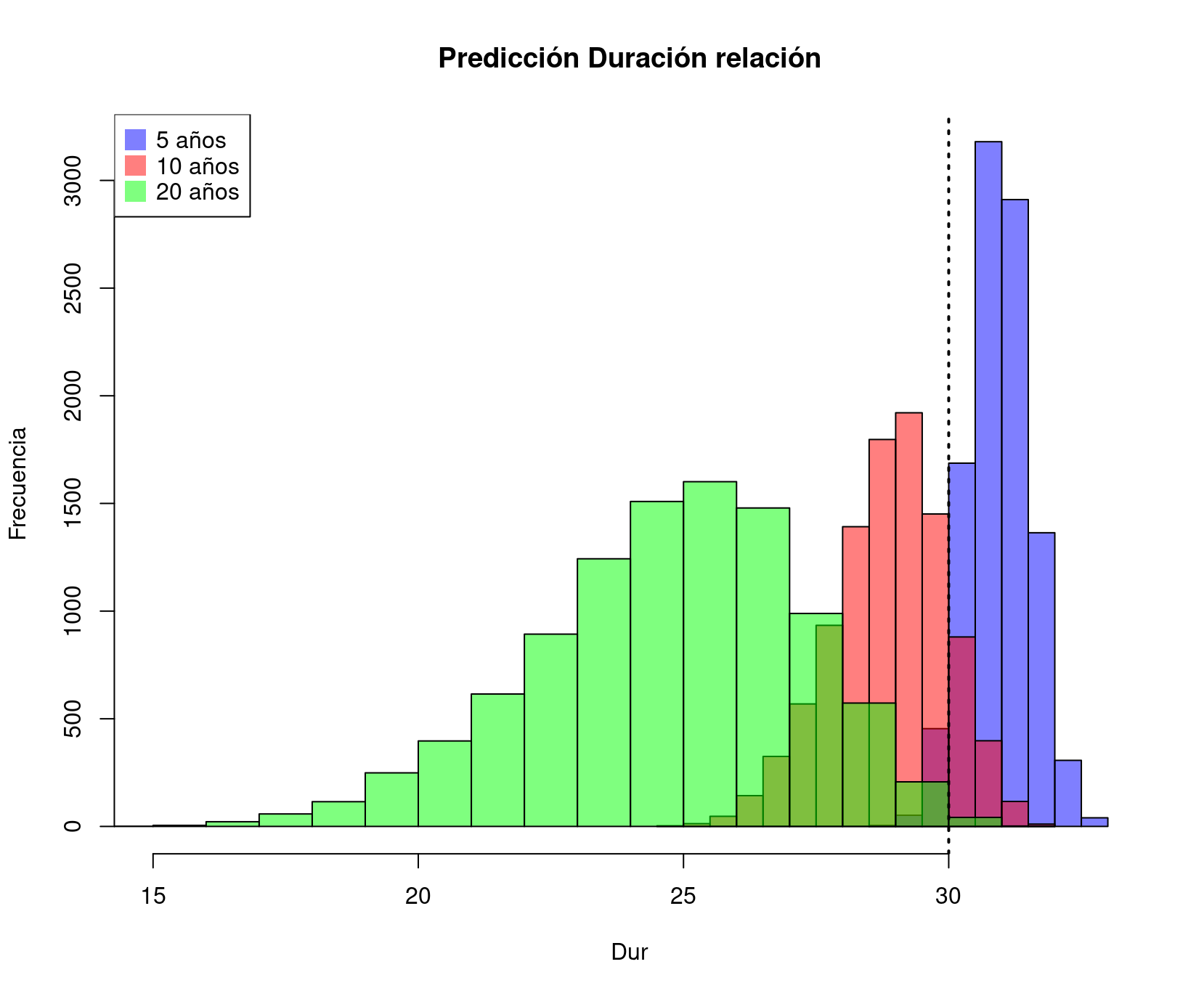

FIG 9: Predicción “bootstrap” de la duración de las distintas relaciones

¿Cómo calcular esas probabilidades?

Sólo hay que “contar” casos

> mean(pred1>30)
[1] 0.9489
> mean(pred2>30)
[1] 0.1405
> mean(pred3>30)
[1] 0.0044
>

En clase-ese templo del conocimiento al que, a estas alturas, pocos vienen, comentaremos todas las cosas que pueden verse en estos gráficos y que permiten obtenerse de estos análisis.

** Fin del Bloque**

En este bloque ha aprendido a entender una técnica de mucha utilidad en el mundo de la ciencia de datos: la simulación. Con suerte, además, habrá tenido la oportunidad de seguir discutiendo conceptos que lleva ya, años, viendo en estadística y que, quizás, no define y entiende con precisión.

FIG