BLOQUE 5: Introducción al aprendizaje automático
clase 1: así resuelven problemas de optimización los ordenadores
El aprendizaje automático que, en inglés, se conoce como machine learning pertenece a una rama de la inteligencia artificial, cuyo objetivo es desarrollar técnicas que permitan que las computadoras aprendan. Diremos que una computadora aprende cuando es capaz de conseguir un objetivo mediante el empleo de un conjunto de algoritmos y el uso de información externa, es decir, datos. En el aprendizaje automático, una computadora tratará de reproducir la realidad a partir de un entrenamiento adecuado con datos y modelos.
Pese a que las técnicas que ha visto en el semestre anterior están también absorbidas por la inteligencia artificial, se presenta en este capítulo una técnica de las más famosas y celebradas en esta área: las redes neuronales. Para entender los fundamentos de las redes neuronales, deberá recordar antes ciertos conceptos de cálculo diferencial para, posteriormente, ser capaz de entender “redes neuronales” sencillas.
Lo primero que deberemos preguntarnos, antes de tratar de entender una red neuronal, es cómo un ordenador busca el óptimo de una función. Piense que el ordenador no sigue, necesariamente, los mismos pasos que usted cuando trata de resolver dichos problemas a mano.
Recuerde que este es un curso de fundamentos y que, por tanto, aquí va a aprender los cimientos sobre los que se asientan multitud de aplicaciones de interés, no los aspectos más complicados ni novedosos.
Ejemplo 1
Piense en la función
\[ f(x)=x^2 \]
¿Cómo busca la máquina el mínimo global?
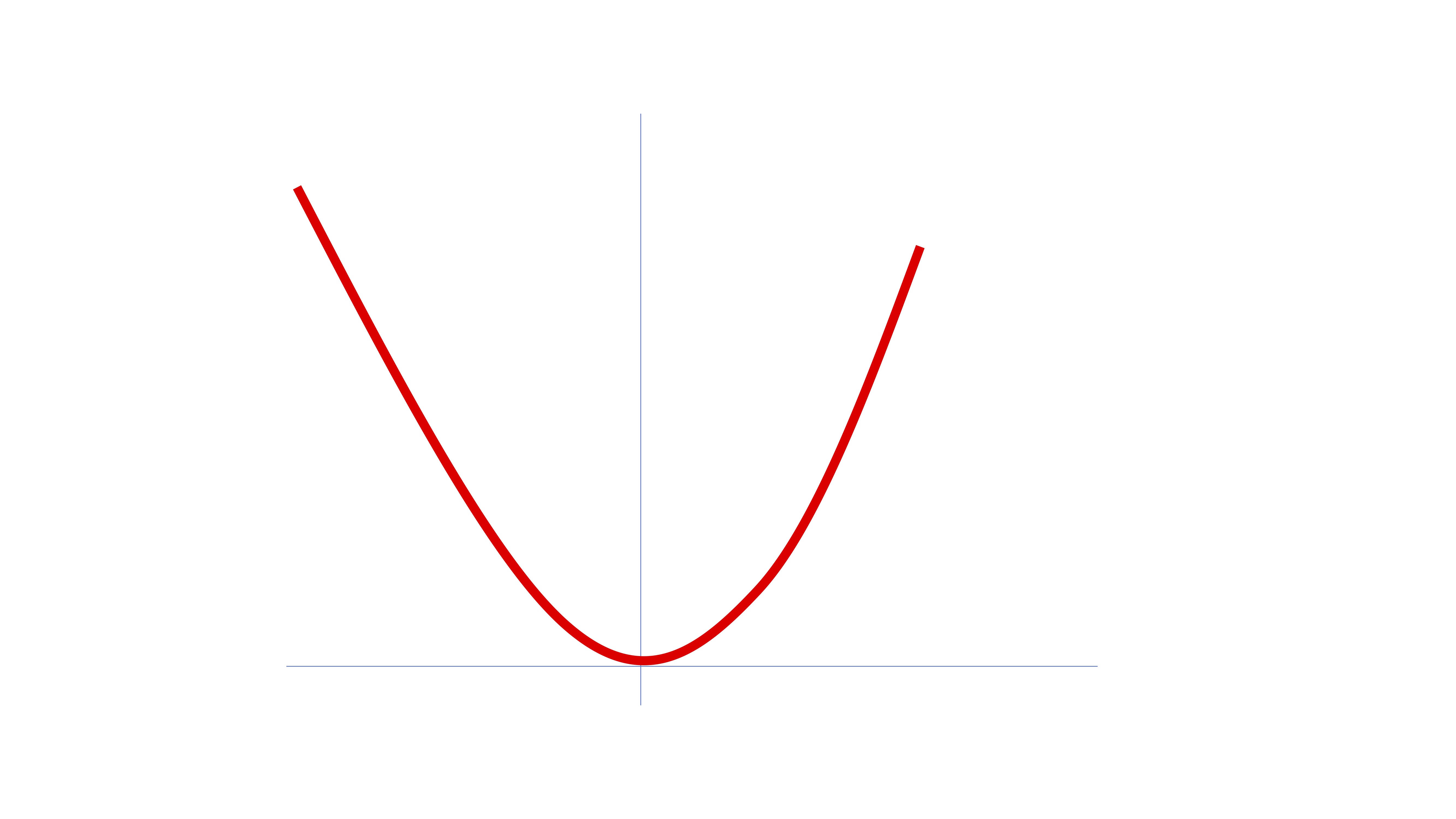
Las máquinas harán algo parecido a lo que hacen los humanos. Intentarán buscar un punto \(x\in\mathbb{R}\) donde se anule la derivada. Para ello, y a diferencia de como lo hacemos nosotros, se situarán en un punto cualquiera de la función (ver FIG 2) que llamaremos, por ejemplo, \(x_{0}\).
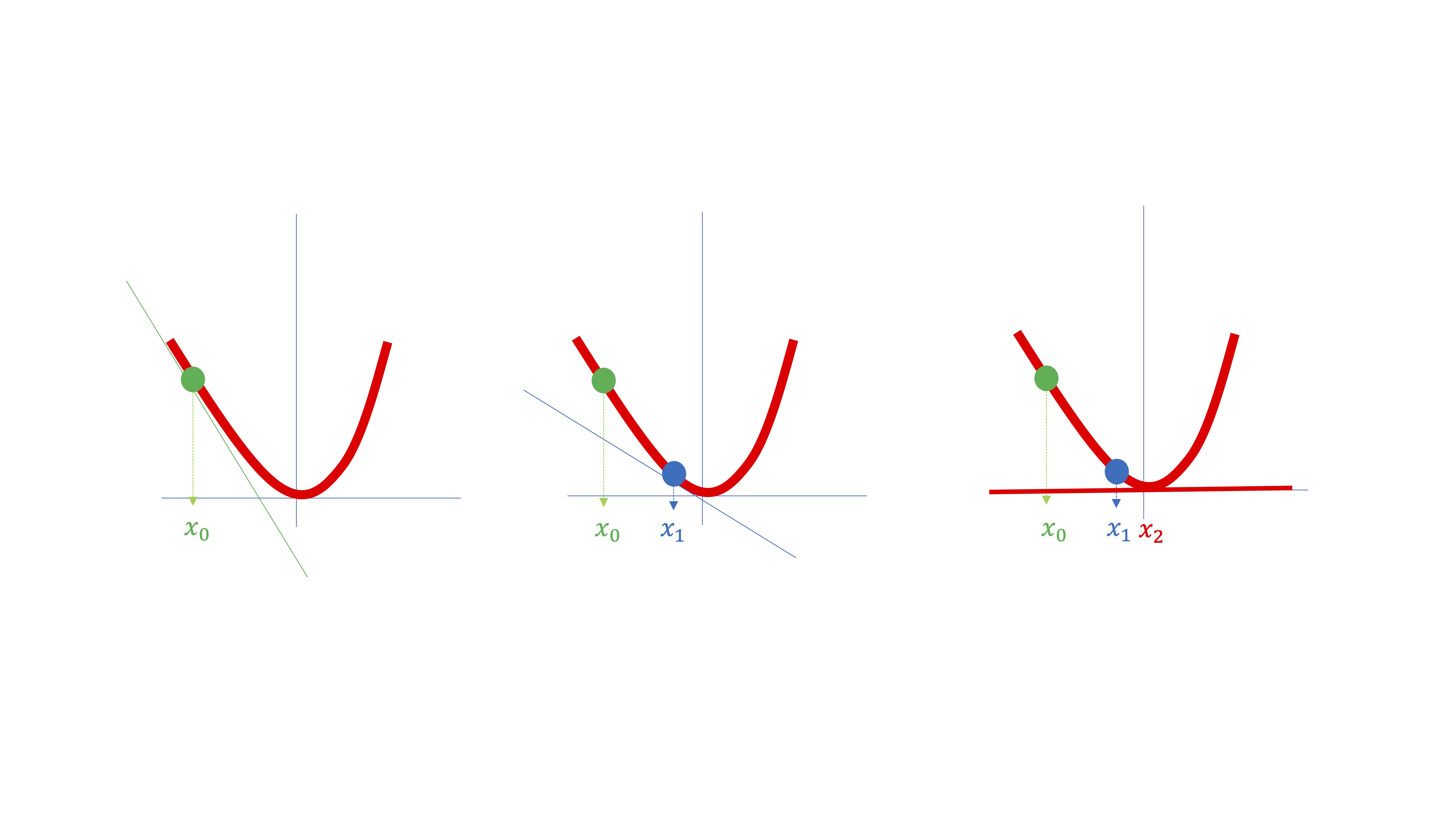
Entonces, la máquina obtendrá la derivada de la función evaluada en ese punto \(f'(x_{0})\) y tratará de buscar un nuevo punto \(x_{1}\), por ejemplo, donde la derivada sea menor, ya que pretende conseguir ese punto \(x\in\mathbb{R}\) en el que la derivada de la función se anule (es decir, en la FIG 2 sería \(x_{2}\)).
Recordemos que la derivada de una función en un punto es la pendiente de la recta tangente a dicho punto. Por eso, en la FIG 2 se han dibujado esas rectas.
El propio dibujo nos sugiere que podemos realizar los siguientes pasos (aunque, por ahora, no tenga claro exactamente por qué)
- Empiece en un punto aleatorio \(x_{0}\)
- Calcule la derivada de la función evaluada en ese punto \(f'(x_{0})\)
- Muévase al siguiente punto en sentido contrario a la derivada: \(x_{1}\rightarrow x_{0}-f'(x_{0})\)…
- …pero para que no sea muy exagerado, muévase un poquito (elija \(h\rightarrow0\)) es decir \(x_{1}\rightarrow x_{0}-hf'(x_{0})\)
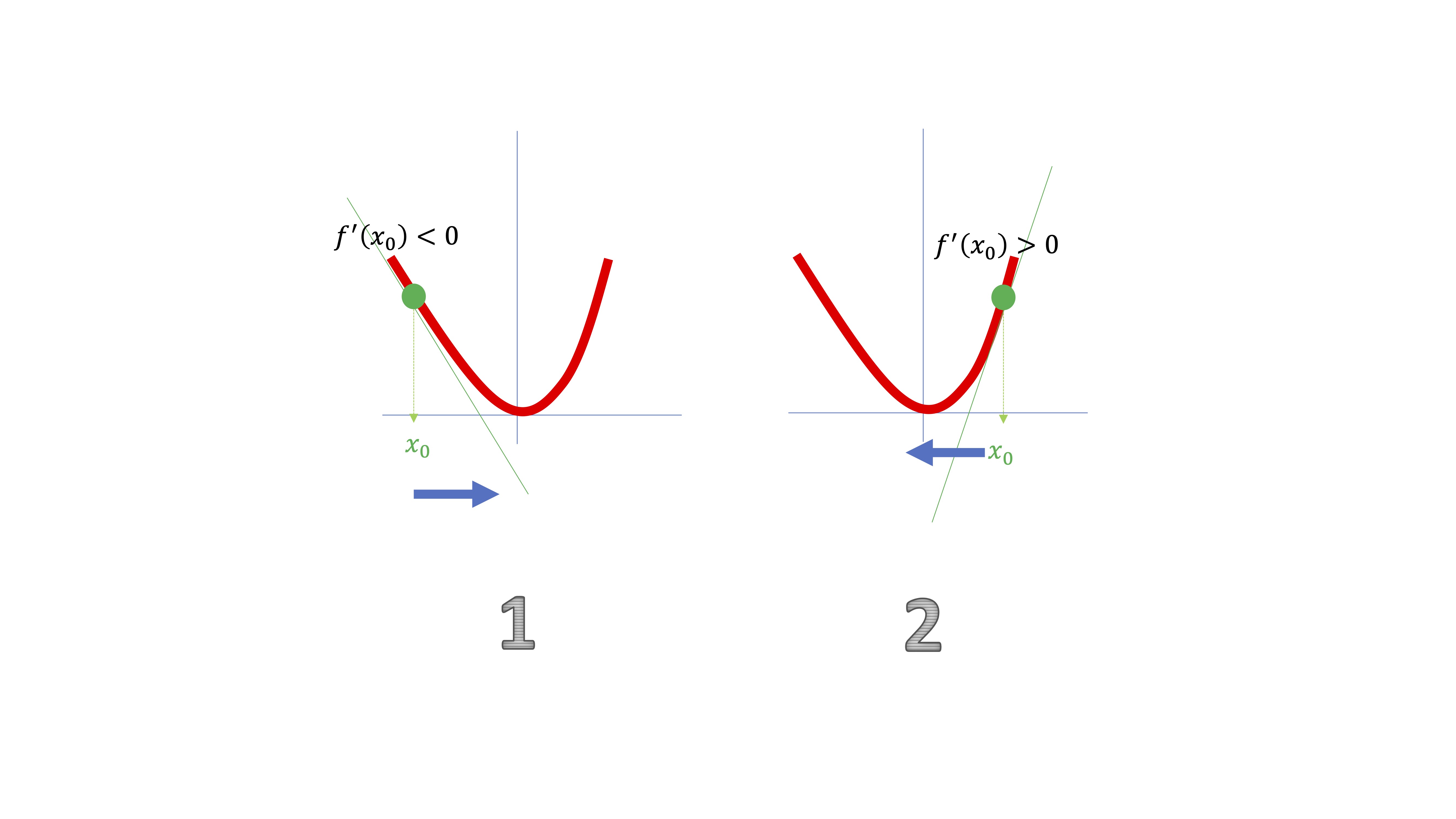
Como ve en la FIG 3, en la situación #1, la derivada le da una información muy útil: la función está decreciendo en un entorno del punto \(x_{0}\). Ahora bien, como verá, necesitará moverse “ligeramente” a la derecha, por lo que deberá ir en sentido \(-hf'(x_{0})\). En la situación #2, pasará al contrario.
Para que avance ligeramente de un punto a otro, deberá introducir un valor para \(h>0\) muy cercano a cero que se denominará “tasa de aprendizaje” de tal forma que para pasar de un punto a otro utilizará la expresión \[ x_{1}\rightarrow x_{0}-h f'(x_{0}) \]
con \(h\rightarrow 0\).
Ejercicio
Diseñe un algoritmo en R para minimizar la función \(y=x^2\). Para ello, deberá crear una función (objetivo) y su derivada. Deberá, asimismo, definir un valor de tolerancia (para tener un criterio de parada del algoritmo). Entones, a partir de un punto inicial, deberá iterar en el bucle que cree en el algoritmo mediante la regla:
\[ x_{new}\rightarrow x_{old}-h f'(x_{old}). \]
Donde \(x_{new}\) es el punto siguiente candidato a minimizar la función que se obtiene a partir de un punto previo llamado \(x_{old}\).
Además, debe definir \(h>0\) como un parámetro pequeño y deberá evaluar, a cada paso, \(\vert f(x_{new})-f(x_{old})\vert\). Cuando esa diferencia sea menor que el valor de tolerancia, entonces el algoritmo deberá pararse. ¿Dónde encuentra el mínimo? ¿Cómo influye la tolerancia y el valor \(h\) en la búsqueda de ese mínimo?
# defina una función objetivo, por ejemplo, y=x^2
fobj<- function(x) {
x[1]^2
}
# almacene la derivada de la función, en este caso, y'=2x
der<- function(x) {
2*x[1]
}
# fije un valor de tolerancia para detener el algoritmo
tol<-0.000001
#inicie en un punto (el que quiera)
y<-vector()
w<-vector()
y[1]=2 #valor inicial "aleatorio". Elija el que le apetezca.
h<-0.01 #defina el parámetro de "aprendizaje"
dist<-1+tol #defina un valor inicial para la función que evaluará la diferencia entre valores de la función objetivo
i<-1
while (dist > tol) {
y[2]<-y[1]-h*der(y[1]) #esta es la iteración basada en Taylor
dist<-abs(fobj(y[1])-fobj(y[2])) #aquí se mira si la función objetivo cambia mucho o no
y[1]<-y[2]
w[i]<-y[1] #creamos este vector para ver cómo evoluciona desde el punto inicial hasta que llega al valor de x que minimiza la función
i<-i+1
}¿Por qué funciona el método en el que \(x_{1}\rightarrow x_{0}-h f'(x_{0})\)? Un argumento heurístico
Debemos recordar que, mediante Taylor, podemos aproximar una función “complicada” (pero diferenciable) en un punto \(x_{0}\) mediante una función muy sencilla (en este caso, con una recta). Si nos movemos cerca del entorno de \(x_0\). Esa es una de las ideas básicas que ha aprendido en cálculo durante el grado.
Es decir, aproximamos en el entorno de \(x_0\) una función diferenciable \(f(x)\) como
\[ f(x)\simeq f(x_0)+hf'(x_0), \]
donde \(h=(x-x_0)\), indicando la diferencia entre el valor “nuevo” de \(x\) frente al valor “viejo” de \(x\), llamado \(x_0\).
POr lo tanto, si usamos
\[ x_{new}= x_{old}-h f'(x_{old}). \]
y aproximamos el valor de la función en \(x_{new}\) utilizando Taylor:
\[ f(x_{new})\simeq f(x_{old})+f'(x_{old}) \underbrace{(x_{new}-x_{old})}_{h} \]
es decir
\[ f(\underbrace{x_{old}-h f'(x_{old})}_{x_{new}})\simeq f(x_{old})+f'(x_{old}) \underbrace{(x_{new}-x_{old})}_{hf'(x_{old})} \]
pero como
\[ x_{new}= x_{old}-h f'(x_{old}), \]
entonces,
\[ x_{new}-x_{old}=-h f'(x_{old}), \]
Sustituyendo, tenemos que
\[ f(\underbrace{x_{old}-h f'(x_{old})}_{x_{new}})\simeq f(x_{old})-f'(x_{old})(h f'(x_{old})) \]
De tal forma que
\[ f(x_{new})- f(x_{old})=-f'(x_{old})(h f'(x_{old})) \]
es decir,
\[ f(x_{new})< f(x_{old}) \]
Siguiendo estos pasos, la función mejora (es decir, se hace menor) localmente. Hasta que llega al mínimo tras un conjunto finito de pasos. El resultado dependerá, por tanto, del valor de \(h\).
Ejercicio Pruebe en el algoritmo del ejercicio resuelto anterior cómo la elección de \(h\) muy grande podría provocar que este no converja y no encuentre el mínimo global. Pruebe, sin embargo, que la elección demasiado “pequeña” podría hacer que tarde mucho tiempo en encontrar el mínimo.
Ejercicio 2 Pruebe ahora a buscar el mínimo de la función \(f(x)=\sin(x)\). Para ello, elija distintos puntos de partida \(x=[-1,1.5,3,7,10]\) (y anote dónde se encuentra el mínimo para cada punto de inicio. ¿Qué puede decir entonces acerca del típo de óptimos que encuentra este algoritmo?
Efectivamente, este algoritmo encuentra óptimos locales. En general es muy difícil, computacionalmente, asegurarse de que estamos ante un óptimo global (aunque en sus clases de cálculo diferencial no le resultaba tan complicado, ¿no?)
¿Cómo trabajaría la computadora si la función que quiere optimizar tiene dos variables? Imagine que quiere buscar el mínimo de
\[ f\left(x_{1},x_{2}\right)=x_{1}^{2}+x_{2}^{2} \]
¿se podrían utilizar las estrategias que se han esbozado anteriormente? Habrá que adaptarlas. Para ello, recuerde cómo se visualizaban, en el plano, funciones de dos variables (que, como recordará, son funciones tridimensionales)
Visualización de una función en dos variables
Partamos de las siguientes dos funciones
\[ f_{1}\left(x_{1},x_{2}\right)=x_{1}^{2}+x_{2}^{2}, \]
\[ f_{2}\left(x_{1},x_{2}\right)=log(x_{1}^{2}+x_{2}^{2}) \]
Puede visualizarlas usando primero google (o Geogebra).
Como verá, ambas figuras vistas desde arriba (es decir, desechando el eje \(z\)) presentan un aspecto común. Eso es porque ambas funciones tienen las mismas curvas de nivel
Definamos una curva de nivel como los puntos del dominio de la función (en este caso, \((x_1,x_2)\)) que nos proporcionan un valor, \(C\), como imagen de la función. Es decir
\[ Nivel=\left\{ \left(x_{1},x_{2}\right)\in D\::\:f(x_{1},x_{2})=C\right\} \]
De esta forma, dando diferentes valores a \(C\) se pueden esbozar las curvas de nivel de esta y poder entender hacia dónde crece/decrece.
- En este caso concreto, note que la imagen de \(f_{1}\) siempre es \(Im(f_{1})\geq0\) ( ya que la función sólo puede tomar valores iguales o mayores que cero), por lo que las curvas de nivel
\[ Nivel_{1}=\left\{ \left(x_{1},x_{2}\right)\in D\::\:x_{1}^{2}+x_{2}^{2}=C,C\geq0\right\} \]
tendremos, entonces, circunferencias concéntricas de radio \(\sqrt{C}\) (que son las que ves en la FIG 4).
Piense ¿Cómo se obtienen las curvas de nivel de \(f_2\)?
Recuerde, por otro lado, que las derivadas parciales primeras de una función de \(n\) variables se almacenan en el gradiente. Es decir, el vector gradiente de la función \(f(x_{1},...,x_{n})\) es un vector en \(\mathbb{R}^{n}\) tal que
\[ \nabla f(x_{1},...,x_{n})=\left[\frac{\partial f}{\partial x_{1}},...,\frac{\partial f}{\partial x_{n}}\right] \]
Recuerde, ahora, de su curso de Cálculo Diferencial, las propiedades del gradiente:
El gradiente de una función en un punto es perpendicular a la curva de nivel en dicho punto
El gradiente de una función en un punto marca el sentido de crecimiento/decrecimiento más rápido de la función
Piense, entonces, sobre esta idea:
En la FIG 6 mostramos algunas curvas de nivel de una función y nos posamos en un punto cualquiera (con valor 32: esto es, en ese punto la función vale 32). Las flechas roja y amarilla son el gradiente de la función en ese punto, puesto que son perpendiculares a la curva de nivel. La flecha roja indica el sentido de crecimiento más rápido (la función tomará un valor mayor si alcanza la siguiente curva de nivel). La flecha amarilla marca el sentido de decrecimiento más rápido (la función alcanzará, por tanto, un menor valor si sigue dicha flecha)
De hecho, es fácil ver (FIG. 7) que -si tomamos otros posibles caminos, representados por otras flechas- creceremos o decreceremos pero, sin duda, tardaremos más, puesto que la longitud de las flechas es mayor.
El método que hemos aprendido anteriormente, entonces, funcionará de la misma forma que vimos en la clase anterior. Iremos en sentido contrario al gradiente si nuestro objetivo es minimizar la función. De esta forma, en un conjunto finito de pasos, podremos estar tan cerca del mínimo como queramos.
Es momento de aplicar la idea visa en la #clase 1 a un problema que ya ha visto en otras ocasiones: el de los mínimos cuadrados. Como recuerda, es un problema de optimización que da lugar a la estimación de los parámetros en un modelo de regresión. En este caso, tenemos observaciones para \(\left\{ y_{i},x_{i}\right\}\) y buscamos los valores de \(\hat{\beta}_{0},\hat{\beta}_{1}\) que mejor ajusten, de manera lineal, la relación entre ambas variables. Para ello, recuerde, este es el modelo poblacional
\[ y_{i}=\beta_{0}+\beta_{1}x_{i}+u_{i} \]
su objetivo es minimizar la suma de residuos al cuadrado, es decir, sea esta la función a la que debemos buscar el valor de \(\hat{\beta}_{0},\hat{\beta}_{1}\)
\[ y_{i}=\hat{\beta}_{0}+\hat{\beta}_{1}x_{i}+\hat{u}_{i}, \] el problema de minimización que pretendemos resolver consiste en
\[ \min_{\hat{\beta}_{0},\hat{\beta}_{1}}SR=\min_{\hat{\beta}_{0},\hat{\beta}_{1}}\sum_{i=1}^{n}\hat{u}_{i}^{2}=\min_{\hat{\beta}_{0},\hat{\beta}_{1}}\sum_{i=1}^{n}\left(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1}x_{i}\right)^{2} \]
Donde el gradiente de la función objetivo resulta ser
\[ \nabla SR=\left[-2\sum_{i=1}^{n}\left(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1}x_{i}\right),-2\sum_{i=1}^{n}\left(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1}x_{i}\right)x_{i}\right]^{T} \]
El método del gradiente, aplicado a una función con \(n\) variables es, en esencia, similar al anterior. Recuerde que la aproximación de Taylor de primer orden, para una función de dos variables \(f(x,y)\), en el entorno de un punto \(\left(x_{0},y_{0}\right)\) es \[ f(x,y)\approx f(x_{0},y_{0})+\frac{\partial f}{\partial x}\left(x_{0},y_{0}\right)h_{x}+\frac{\partial f}{\partial y}\left(x_{0},y_{0}\right)h_{y} \]
De nuevo, \(h_{x}=\left(x-x_{0}\right),h_{y}=\left(y-y_{0}\right).\) Asumiendo que \(h_{x},h_{y}\rightarrow0\) deberá trabajar como en el caso con una variable:
- Parte de un punto inicial \(\left(x_{0},y_{0}\right)\)
- Busca un candidato mejor a mínimo \(\left(x_{1},y_{1}\right)\rightarrow\left(x_{0},y_{0}\right)-h\left[\frac{\partial f}{\partial x}\left(x_{0},y_{0}\right),\frac{\partial f}{\partial y}\left(x_{0},y_{0}\right)\right]\)
Donde \(h>0\) es un número pequeño (y común para ambas variables). Como ve, está utilizando el gradiente de la función \((\left[\frac{\partial f}{\partial x}\left(x_{0},y_{0}\right),\frac{\partial f}{\partial y}\left(x_{0},y_{0}\right)\right])\) multiplicado por \(-h\) para poder ir en el sentido de mayor decrecimiento de esta (que es \(-\nabla f(x,y)).\)
#genere un modelo de regresión con datos
x<-rnorm(100,1,1)
y<-3+2*x+rnorm(100,0,1)
#Cree la función objetivo y el gradiente de la función objetivo
fobj2<- function(b) { sum(y-b[1]-b[2]*x)^2 } #escriba la función objetivo donde y,x son datos
der<- function(b) { c(-2*sum(y-b[1]-b[2]*x),-2*sum((y-b[1]-b[2]*x)*x))} #escriba el gradiente de la función objetivo
tol<-0.000001 #declare un parámetro de tolerancia
bold<-vector()
bnew<-vector()
bold[1]=30
bold[2]=20 #Dé valores iniciales a los parámetros
h<-0.001 #dé un valor al parámetro de aprendizaje
dist<-1+tol
i<-1
while (dist > tol) {
grad<-der(bold) #evalúe el gradiente en el punto "old"
bnew[1]<-bold[1]-h*(grad[1]) #actualice los valores
bnew[2]<-bold[2]-h*(grad[2])
dist<-abs(fobj2(bnew)-fobj2(bold)) #analice el cambio en la función objetivo
bold<-bnew
i<-i+1}Ejercicios Pruebe, de nuevo, la convergencia del método si \(h\) toma valores grandes. Razone sobre la importancia de controlar el tamaño de \(h\) para la convergencia del método. Qué ocurre si \(h=0.00000001\)? ¿Qué otros factores pueden afectar a la velocidad de convergencia?
Clase 2: Los modelos de redes neuronales (I)
Antes de entender lo básico de una red neuronal, deberemos definir una función compuesta .
Ideas sobre la composición de funciones que debe conocer
Las funciones compuestas surgen debido a las dependencias que pueden existir entre las variables de un modelo matemático. Por ejemplo, en la ecuación (0.1) diremos que la variable \(y\) depende de la variable \(x\) pero, a su vez, la variable \(x\) depende de la variable \(t:\)
\[\begin{equation} y=f(x)\;\;x=g(t) \tag{0.1} \end{equation}\]
De este modo, podríamos decir igualmente-si nos interesa especialmente dicho análisis- que la variable \(y\) depende de la variable \(t\). Para escribir esto, ya que que la relación entre \(x\) e \(y\) viene dada por \(f\) y la relación entre \(x\) y \(t\) viene dada por \(g\), diremos que \(f\) es una función compuesta por la \(g\). lo resumimos así: \(f\circ g\), o también:
\[ y=f(g(t)). \]
De hecho, otra manera de escribirlo, de acuerdo con la figura FIG 1, es mediante una función \(F\) (por ejemplo) de tal forma que:
\[ y=F(t). \]
¿Cómo se analiza el cambio de \(y\) cuando se modifica \(t\)? Gráficamente, se puede ver en la FIG 1 que: si se cambia \(t\), ese cambio afecta a la \(x\) y la \(x\) afecta a la \(y\).
Por ejemplo, tiene que \(f(x)=\ln\left(x\right)\) y \(x=g(t)=3t^{2}+2\) entonces, al componerlas, obtienes \[ y=\ln\left(3t^{2}+2\right). \] Por lo que \[ \frac{\mathrm{d}y}{\mathrm{d}t}=f'(x)\frac{\mathrm{d}x}{\mathrm{d}t} \], es decir \(\frac{\mathrm{d}y}{\mathrm{d}t}=\frac{1}{x} 6t\) pero \(x=3t^{2}+2\), por lo que \[ \frac{\mathrm{d}y}{\mathrm{d}t}=\frac{1}{3t^{2}+2}6t \]
que es la regla de derivación del logaritmo neperiano de una función compuesta, como ha estudiado en bachillerato. Ahora es el momento de analizar algunos casos para funciones de \(n\) variables.
Por ejemplo, imagine que quiere comprarse un PC. ¿De qué depende el precio del PC? Imaginemos que, por un lado, de la memoria RAM, del acabado, y del precio de un MAC (su competidor). ¿De qué dependen la memoria RAM, el acabado y el precio del MAC? Imaginemos, por ejemplo, la memoria RAM y el precio del MAC dependen de la disponibilidad de chips. Podemos representar esta función con el siguiente diagrama de la FIG2.
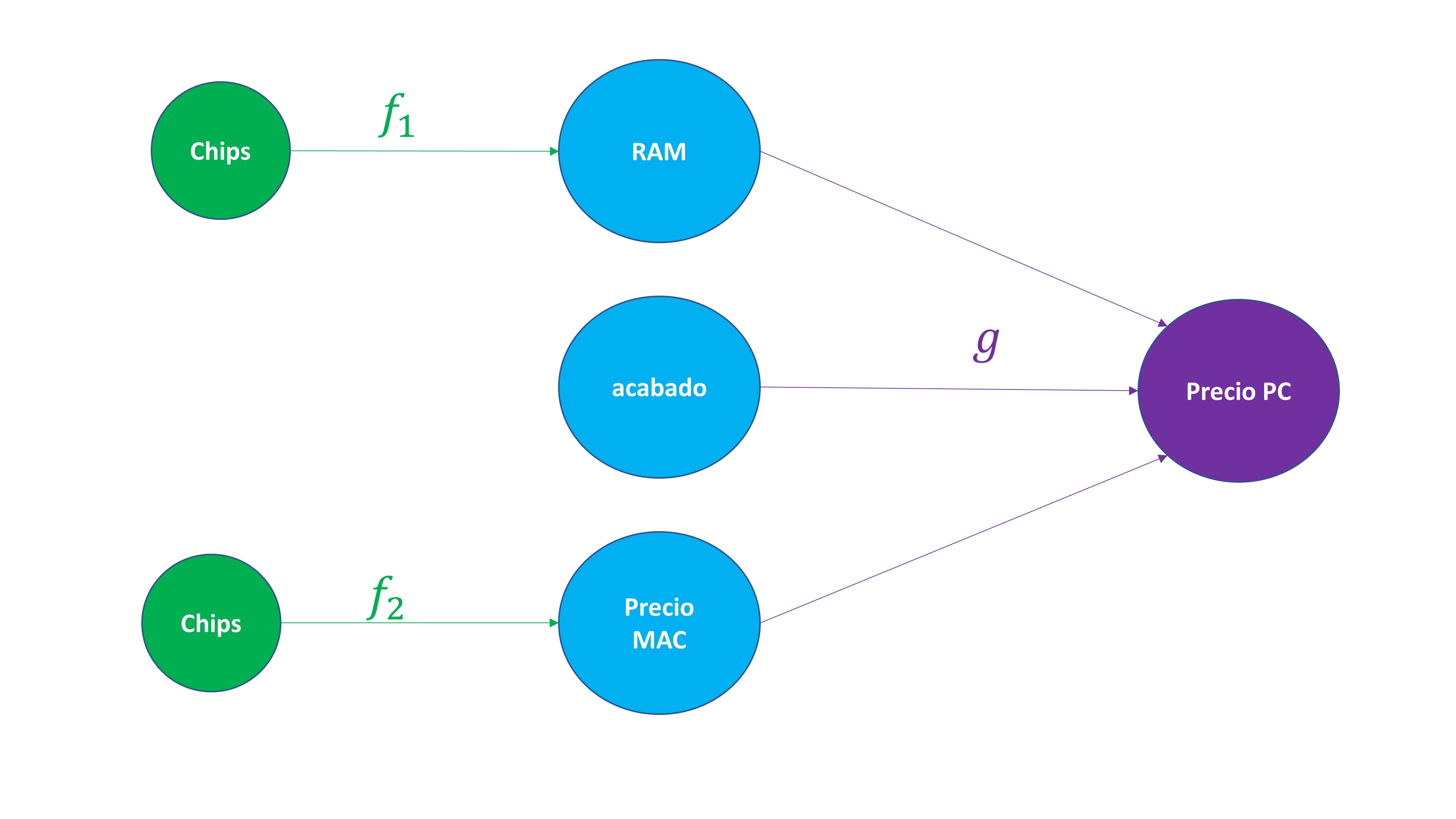
Es decir, puede observar que, por un lado:
\[ RAM=f_1(Chips). \]
\[ P.MAC=f_2(Chips). \]
\[ P.PC=g(RAM,P.MAC,Acabado). \]
Y que, mediante la composición, tendrá que
\[ P.PC=g(f_1(chips),f_2(chips),Acabado). \]
De esta forma, si usted conoce la cantidad de chips que hay disponibles, y el acabado que desea, puede obtener, a través de la composición de funciones el precio del PC.
Veremos que un modelo de red neuronal se basa, de alguna manera, en esta idea: composición de funciones. El punto de vista de los modelos de redes neuronales es algo así:
Las relaciones entre variables son complejas y altamente no lineales. Busquemos una estructura en forma de red que sistematice esas posibles relaciones y trate de capturar la complejidad y la no linealidad de una manera eficiente.
El enfoque que se va a dar a los modelos de redes neuronales se aleja del tradicional en el que se explican estos modelos como una “imitación” del funcionamiento del cerebro. Hay cantidad de textos que explican cómo estos modelos replican, en cierta forma, la manera en que las neuronas reciben la información y la propagan.
En nuestro caso, se pretenderá entender que una red neuronal es un modelo que, a través de técnicas de aprendizaje automático, trata de aprender de un conjunto de datos abordando la no linealidad en el proceso que genera estos datos.
Para ello, se presentarán diferentes esquemas que le permitirán ir entendiendo, paso a paso, la idea fundamental de los modelos de redes neuronales. Como ya se ha aprendido, la simulación puede ser una herramienta potente de aprendizaje. Se propondrán, de hecho, esquemas iniciales y sencillos con datos simulados, de tal forma que pueda ejecutarlos paso a paso para comprobar lo que se está explicando.
El esquema que se presenta en esta clase se denomina “perceptrón multicapa” (de nuevo, la palabra perceptrón hace alusión al cerebro) y consiste en un esquema como el de la FIG 1
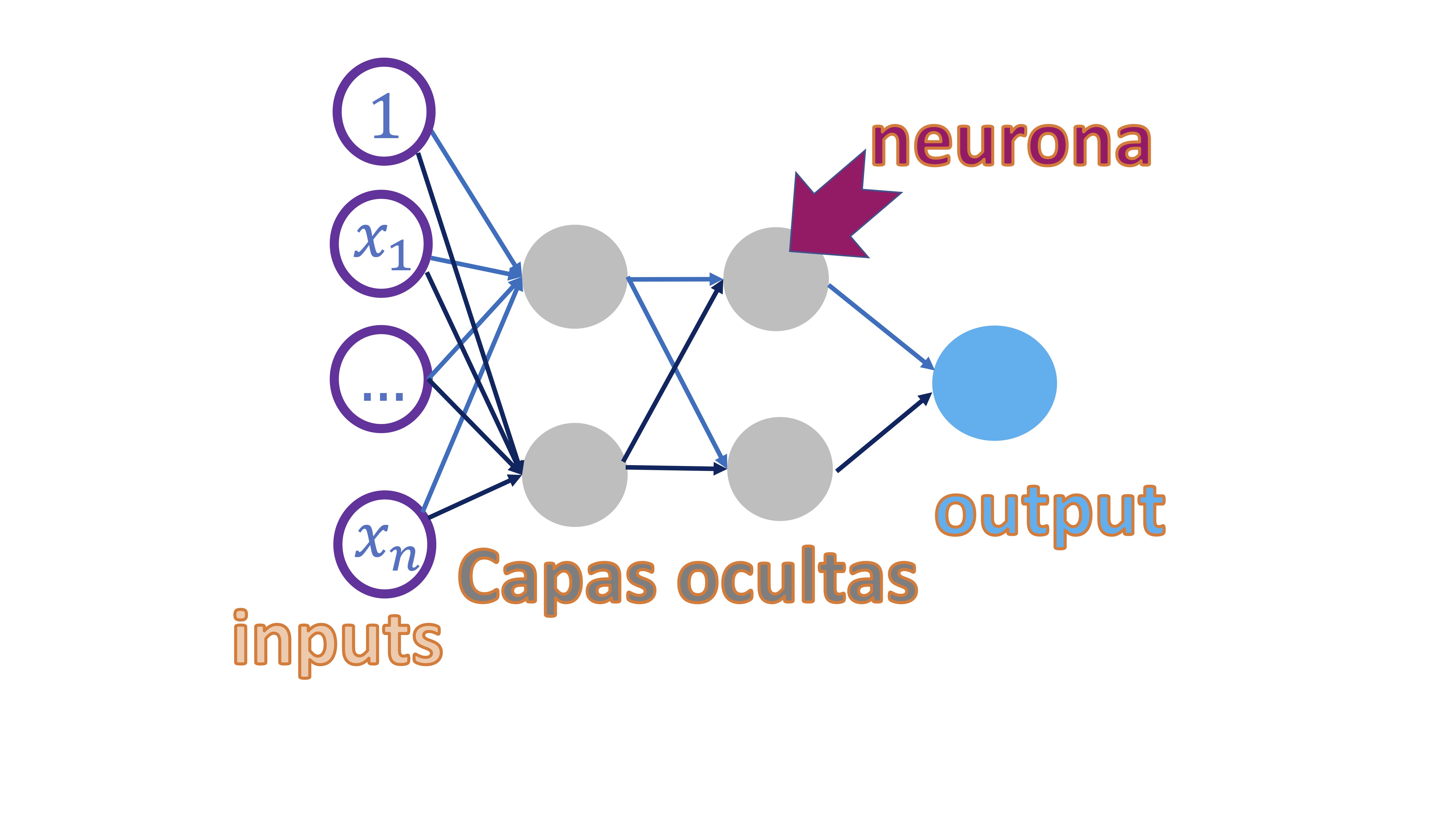
como decimos, hay multitud de esquemas de redes neuronales. Este, tomado de “towardsdatascience”, es el más completo que hemos encontrado. Nótese que lo que hemos traducido como “perceptrón multicapa” en la FIG 2 se conoce como “Deep Feed Forward”.
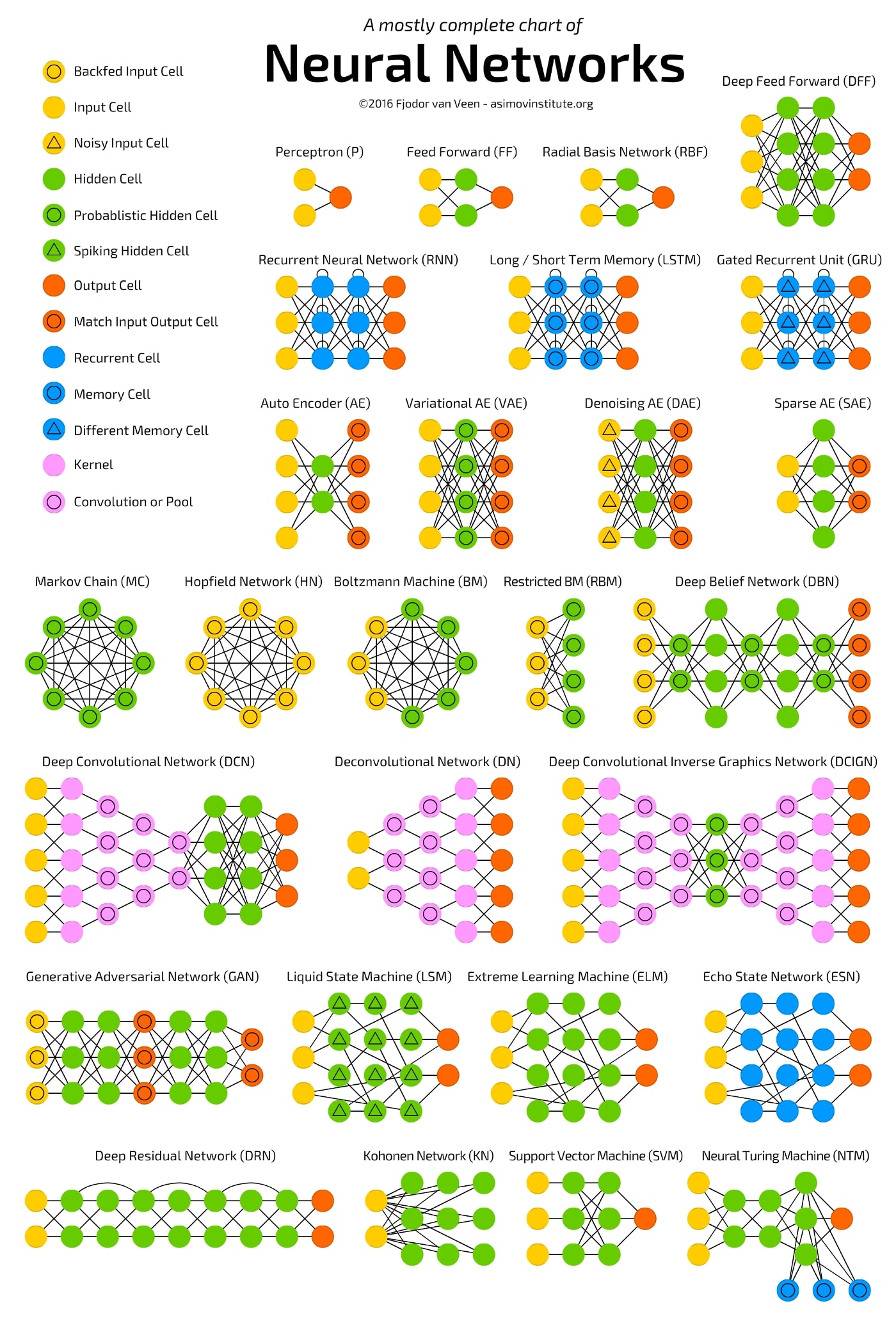
El perceptrón multicapa consiste en una red en la que el punto de partida es un conjunto de “inputs” que, en su caso, serán variables explicativas (piense en su proyecto del primer cuatrimestre). Cada observación de cada input se conecta con el siguiente elemento, que se llama neurona, y que- en este caso- se organizan por “capas” que van dotándole a la red de más complejidad. Las neuronas tendrán lo que, habitualmente, se denomina función de activación y que es lo que permite que se conecten los nodos entre sí. Veremos que, matemática, lo que estaremos construyendo es una composición de funciones y que, además, esto le permitirá ser capaz de modelar la ya comentada no linealidad entre las variables. El final de todo este proceso es conectar los inputs con el output final (que será la variable/variables que usted quiere predecir) de tal forma que, mediante la complejidad del modelo, pueda capturar relaciones que otros modelos más rígidos no serán capaces.
Ojo con el sobreajuste
Sin embargo, estos modelos son famosos por sobreajustar los datos, implicando que error o ruido se confunda con señal.
Ejemplo 1: Un modelo lineal
Lo primero que se va a hacer es visualizar un sencillo modelo lineal. Verá que, en ese caso, la propia red neuronal le ofrecerá, como resultado de salida, los mismos parámetros que proporciona la estimación mínimo cuadrática. Sin embargo, este ejemplo le permitirá entender de manera más concreta el esquema de red neuronal que se propuso antes sin entrar en mucho detalle.
-El esquema es muy sencillo. Suponga que tiene un input (además de una constante) y que, directamente, quiere ir al output sin pasar por ninguna capa oculta. Además, la función que relaciona el input con el output es lineal (lo que indicamos con una barrita naranja en el círculo azul)
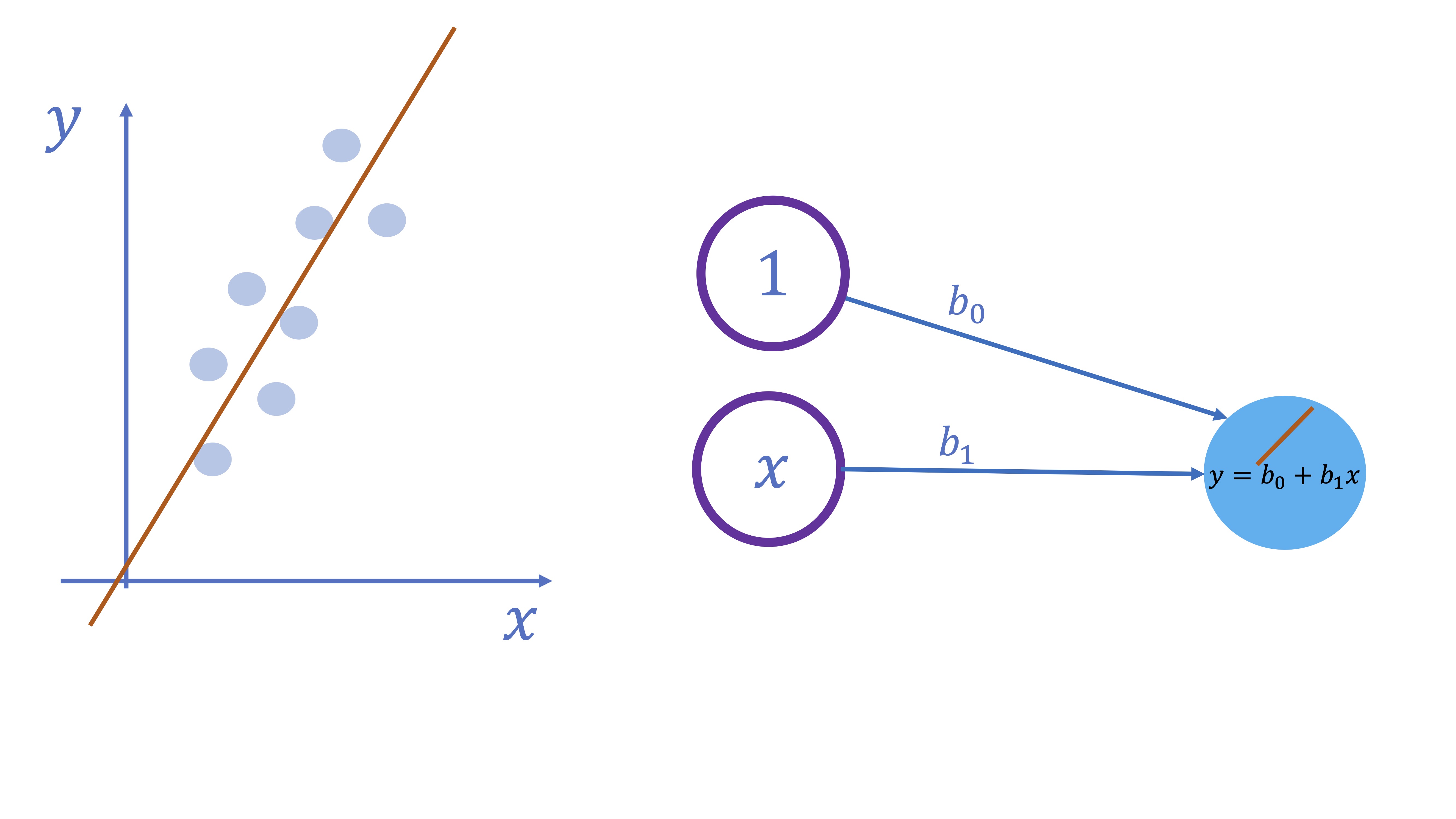
Para ver que funciona, en [R], vamos a jugar- de nuevo- a ser Dios. Para ello, proponemos un modelo poblacional (por ejemplo, \(y=2+5x+u\), con \(u\rightarrow N(0,1)\)) y obtendremos una muestra de tamaño \(n=100\) y veremos si el método es capaz de recuperar los valores de los parámetros.
#librerías/paquetes que necesita
install.packages("quantmod")
library(quantmod)
install.packages("neuralnet")
library(neuralnet)
install.packages('kimisc')
library(kimisc)
#genera un modelo del que conoce los parámetros
x1<-rnorm(100,1,1)
u<-rnorm(100,0,1)
y<-2+5*x1+u
#almacena las variables en un DF
DATOS.L<-data.frame(y,x1)
#entrena una red neuronal MP con 0 capas ocultas
red<-neuralnet(y~x1,hidden=0,data=DATOS.L,rep=30)
plot(red) lo que da lugar a lo que esperaba: al no tener capas ocultas y la función que vincula el input con el output es lineal, los parámetros son los del modelo de regresión
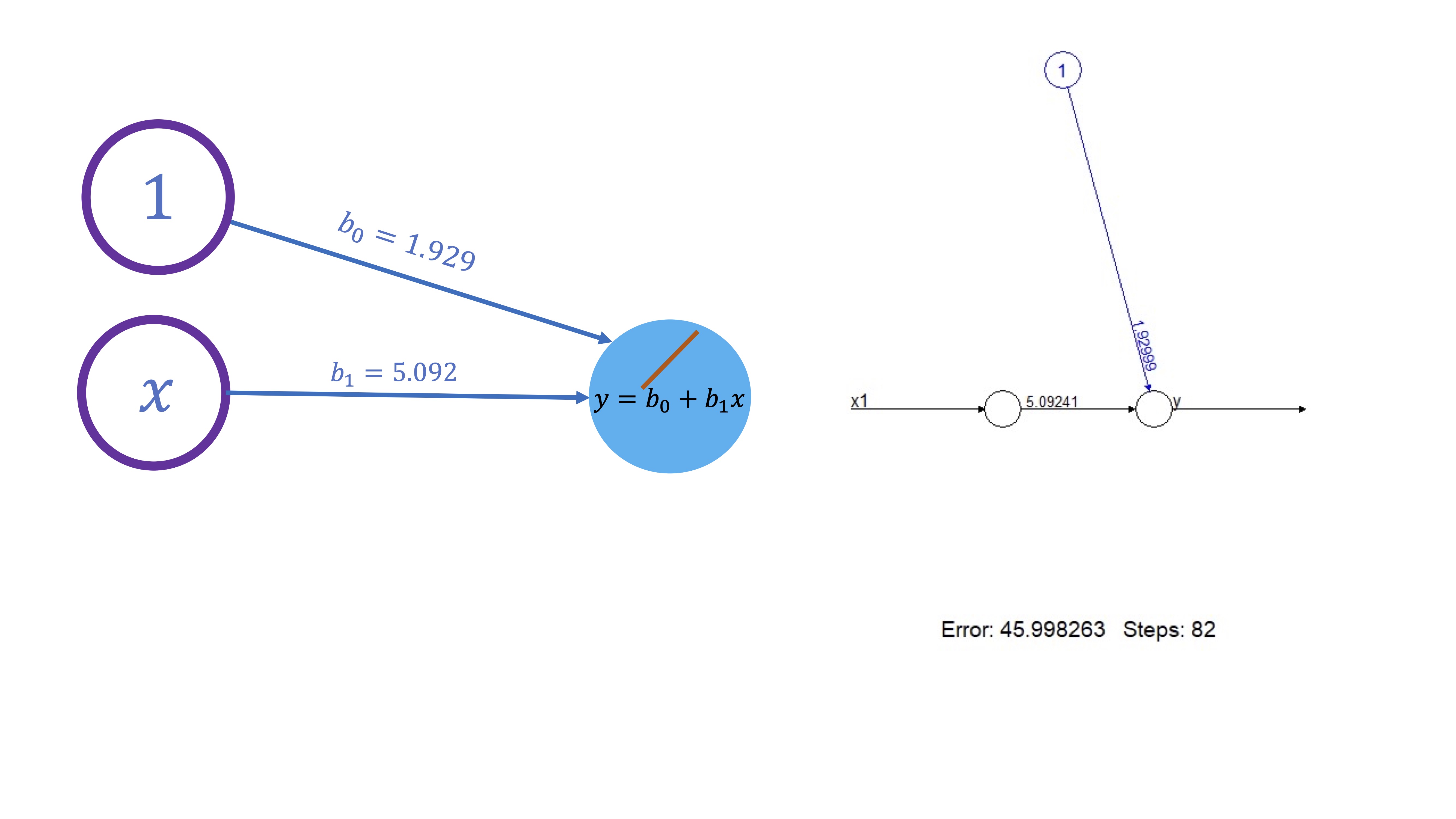
de hecho, si estima los parámetros del correspondiente modelo de regresión, obtendrá lo mismo
NOTA: cada vez que ejecuta este código, dado que la generación de los valores de las variables es aleatoria, obtendrá otros resultados. En realidad, esto se podría haber solucionado poniendo una semilla, pero se me olvidó cuando hice el dibujo :)
Este modelo es muy sencillo y, por tanto, no tiene ninguna aplicación práctica más que la de poder comprobar que todo funciona como se espera.
Ejercicio resuelto
Complique el modelo lineal de forma innecesaria (añadiendo, por ejemplo, dos neuronas) y escriba la ecuación correspondiente del modelo.
Los argumentos de entrada de la función son, por un lado, las variables (input y output), el conjunto de datos sobre el que se entrena la red, el número de neuronas en una capa (2), la función de activación (que, en este caso, es la logística).
#genera un modelo del que conoce los parámetros
set.seed(123)
x1<-rnorm(100,1,1)
u<-rnorm(100,0,1)
y<-2+5*x1+u
#almacena las variables en un DF
DATOS.L<-data.frame(y,x1)
#entrena una red neuronal MP con 1 capa ocultas
red<-neuralnet(y~x1,hidden=2,data=DATOS.L,act.fct="logistic")
plot(red) Ejercicio Escriba las ecuaciones correspondientes que se desprenden de la red anterior
Empezamos desde el output hasta el input
Output:
\[ y=-10.47+21.90 N_{1}+24.01 N_{2} \]
Neuronas
\[ \begin{cases} N_{1}=\frac{1}{1+e^{-\left(0.16+0.91\times x_1\right)}}\\ N_{2}=\frac{1}{1+e^{-\left(-3.90+0.97\times x_1\right)}} \end{cases} \]
Entonces, si queremos hacer una predicción para la variable \(y\), dado un valor de \(x_1\), por ejemplo, \(x_1=1\), deberemos deshacer el camino:
Sustituyo en las neuronas el valor de \(x_1\)
\[ \begin{cases} N_{1}=\frac{1}{1+e^{-\left(0.16+0.91\right)}} \rightarrow N_1=0.74\\ N_{2}=\frac{1}{1+e^{-\left(-3.90+0.97\right)}}\rightarrow N_2=0.05 \end{cases} \]
Una vez tenemos el valor de las neuronas, entonces, obtenemos la predicción del output
\[ y=-10.47+21.90 \times 0.74+24.01 \times 0.05\rightarrow y=6.93. \]
Una predicción similar (salvo errores de redondeo) podemos obtenerla con [R]
¿Qué ha aprendido?
Aquí puede ver cómo la inclusión de neuronas implica una composición matemática de funciones. ¿Predecirá mejor que el modelo anterior?
Esto se puede comprobar mediante validación cruzada. Vamos a simular un modelo con dos variables de entrada y una salida que-en realidad- se comporte como una regresión. Entrenaremos el modelo de red neuronal adecuado y otro “sobreparametrizado”. Los pondremos a competir mediante validación cruzada.
#genera un modelo del que conoce los parámetros
x1<-rnorm(100,1,5)
x2<-runif(100)
u<-rnorm(100,0,sqrt(3))
y<-3+2*x1-4*x2+u
Datos_NN<-data.frame(y,x1,x2)
error1<-vector() #creamos un vector que almacenará 50 errores
error2<-vector() #creamos un vector que almacenará 50 errores
for(i in 1:150){ #Iniciamos los subíndices: este es el de la iteración
random <- sample(1:nrow(Datos_NN), size = floor(.7*nrow(Datos_NN))) # Elegimos la muestra de entrenamiento al azar
train<-Datos_NN[random,]
test <-Datos_NN[-random, ] #por lo que la muestra de test es la contraria
red1<-neuralnet(y~x1+x2,hidden=0,data=train,linear.output=TRUE,stepmax=1e7) #configuración con 1 capa oculta
red2<-neuralnet(y~x1+x2,hidden=2,act.fct="logistic",data=train,linear.output=TRUE,stepmax=1e7) #configuración con 2 capas ocultas
O_mod1<-predict(red1, newdata=test)
O_mod2<-predict(red2, newdata=test)
O_real<-(test$y)
error1[i]<-mean((O_real-O_mod1)^2)
error2[i]<-mean((O_real-O_mod2)^2)
}
par(mfrow = c(2, 1))
hist(error1, main="modelo verdadero")
hist(error2,main="modelo falso")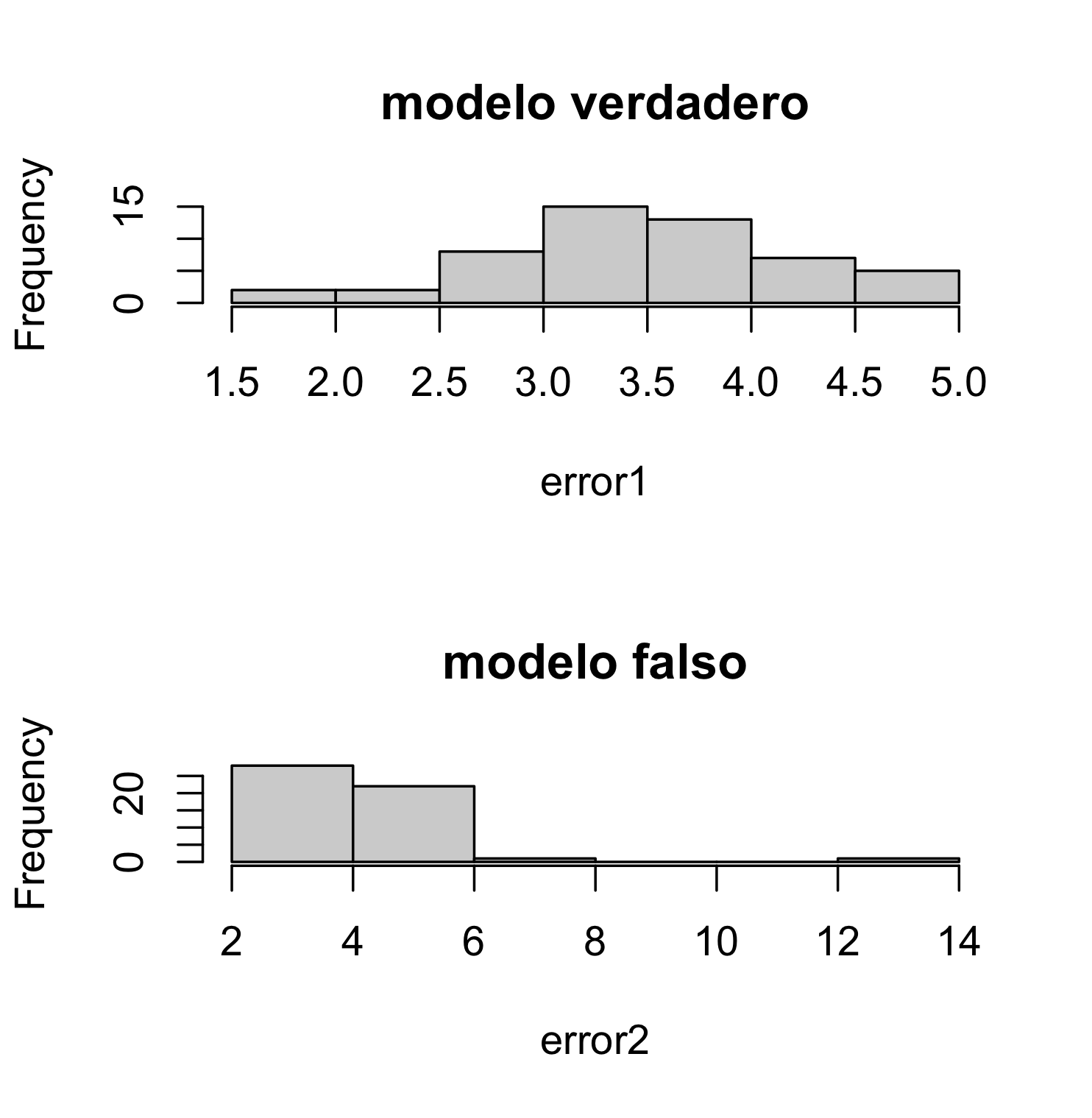
Como vemos, el modelo con más neuronas predice peor, con claridad.
Clase 3: Los modelos de redes neuronales (II)
Seguimos aprendiendo sobre redes neuronales, basándonos en lo que ya sabemos.
Ejemplo 2: un modelo logístico
De nuevo, se puede trabajar sobre un modelo no lineal sencillo y conocido previamente (como puede ser un logístico). Este, sería equivalente a un esquema como el siguiente
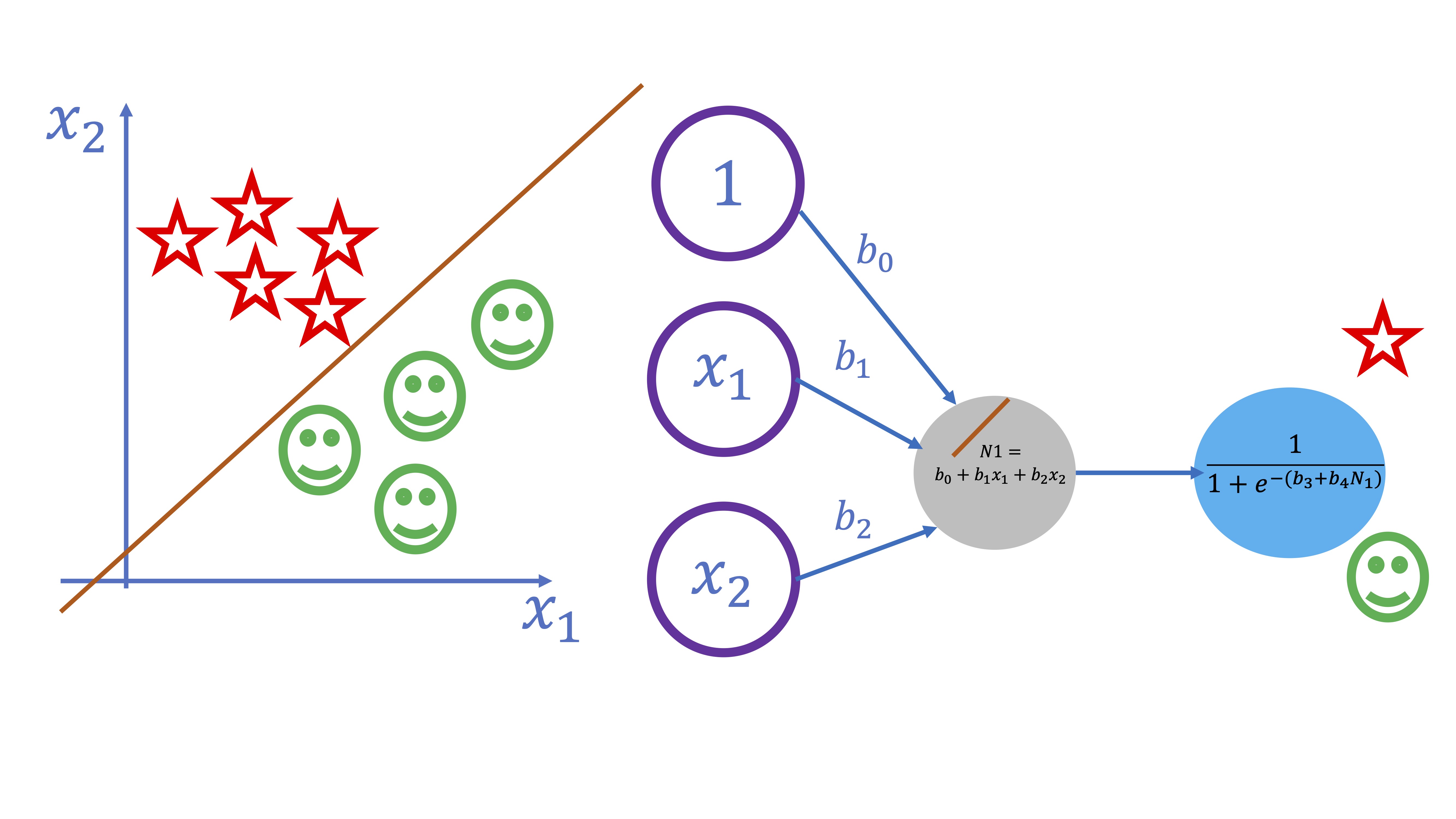
En este ejemplo se pretende separar dos clases (los smiles y las estrellas) atendiendo a los valores que toman las variables \(x_{1}\) y \(x_{2}\). Como verá la FIG 1, ambos conjuntos son fácilmente separables a través de una recta. Eso sí, como el OUTPUT es una variable cualitativa, necesitaremos que la salida del modelo sea la probabilidad de pertenecer a una u otra clase. Es por ello que la función “output” deberá ser la función logística, es decir:
\[ y=\frac{1}{1+e^{-(\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2})}} \]
Para entender con claridad esto, simulemos datos que proceden de dos variables explicativas continuas y una variable explicada dicotómica. Concretamente, siguiendo este script:
x1<-rnorm(1000,0,1) #Simulamos las variables continuas
x2<-rnorm(1000,0,1)
z = 1 + 2*x1 - 3*x2 #nos invetamos la ecuación linel que separa
pr = 1/(1+exp(-z)) #obtenemos la probabilidad a través de la logística
y = rbinom(1000,1,pr) #creamos una variable dicotómica a través de nuestros resultados
DATOS.B = data.frame(y=y,x1=x1,x2=x2) #almacenamos los datos en un "dataframe"
qplot(x1, x2, colour =y, data = DATOS.B) #lo dibujamos para ver que cuadrapuede generar algo como lo que verá en la FIG 2
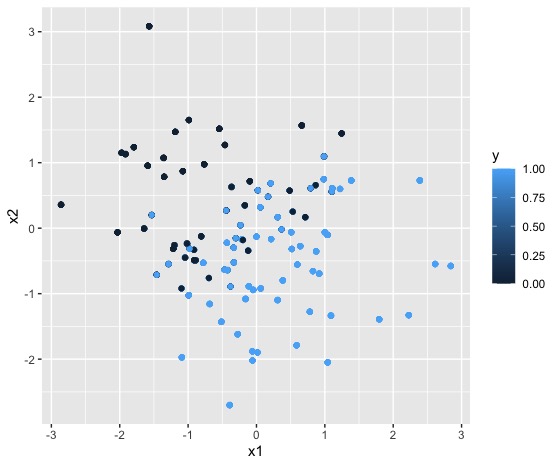si ahora entrena el modelo
obtendrá
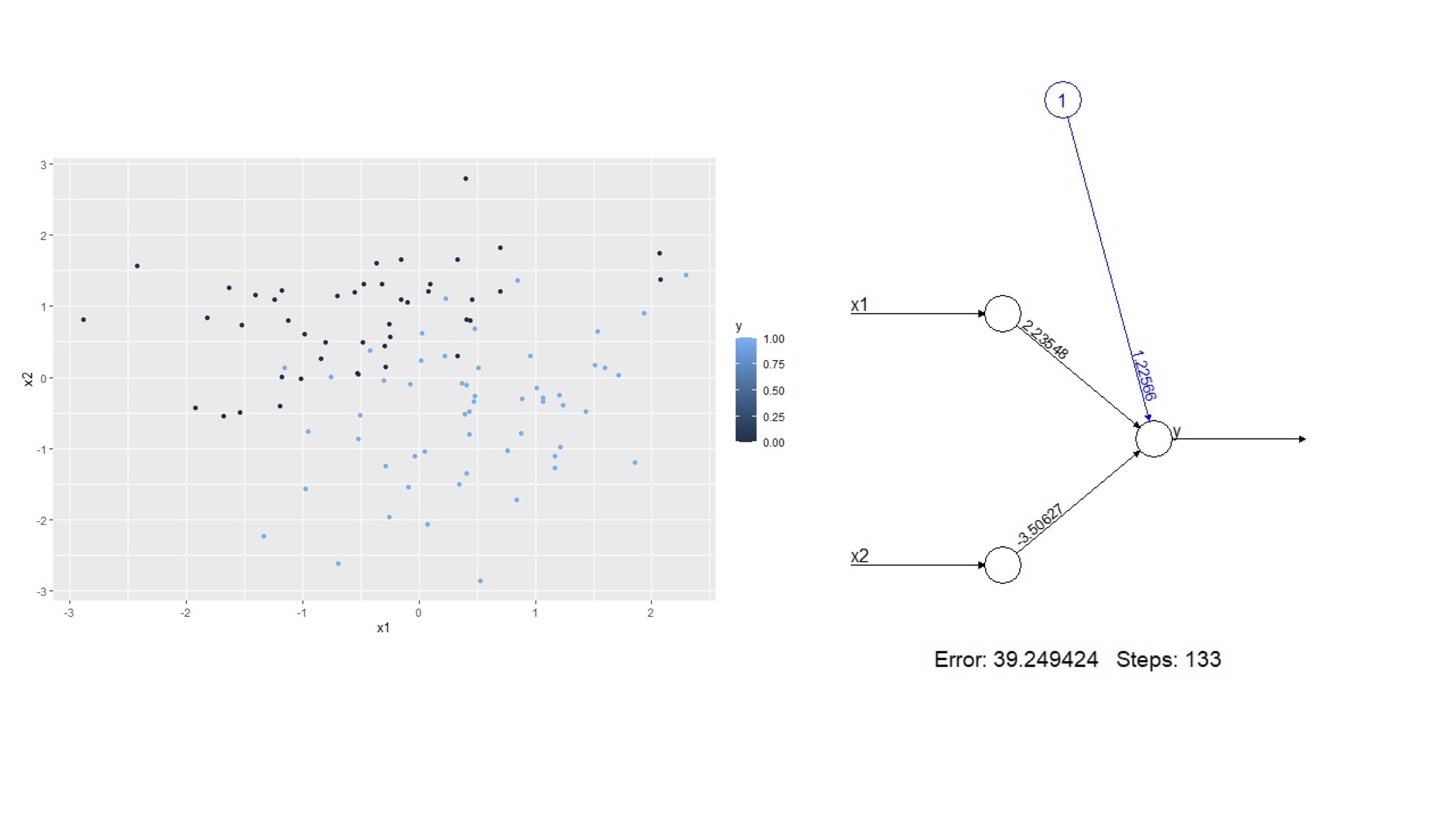
es importante notar que la función de activación sigue siendo lineal (\(\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}\)) pero la salida (es decir, la función output, es logística -lo cual se indica con un FALSE en linear. output). Observe que, si ajusta, un modelo binomial a los datos, obtendrá unos coeficientes similares a los que proporciona la red que ha entrenado
no son los mismos, puesto que ya no es un modelo lineal y cada uno de ellos tiene una rutina distinta de estimación de los parámetros. En este caso,ambos coeficientes han de ser aproximadamente iguales a los que se han impuesto aquí:
\[ \beta_{0}=1; \beta_{1}=2, \beta_{2}=-3. \]
Ejercicio para profundizar
Genere el modelo \(y_i=2-3x_i+u_i\) con \(i=1,...,500\) y \(u\rightarrow N(0,1)\) Cree una rutina de validación cruzada de tal forma que obtenga una distribución del error de predicción con los siguientes modelos:
- Una regresión lineal
- Una regresión cuadrática
- Un modelo de red neuronal con 1 neurona
- Un modelo de red neuronal con 2 neuronas
¿qué ha aprendido sobre la complejidad?
solución
#genera un modelo del que conoce los parámetros
x1<-rnorm(500,1,1)
u<-rnorm(500,0,1)
y<-2-3*x1+u
#almacena las variables en un DF
DATOS.L<-data.frame(y,x1)
error1<-vector() #creamos un vector que almacenará 50 errores
error2<-vector() #creamos un vector que almacenará 50 errores
error3<-vector() #creamos un vector que almacenará 50 errores
error4<-vector() #creamos un vector que almacenará 50 errores
for(i in 1:50){ #Iniciamos los subíndices: este es el de la iteración
random <- sample(1:nrow(DATOS.L), size = floor(.7*nrow(DATOS.L))) # Elegimos la muestra de entrenamiento al azar
train<-DATOS.L[random,]
test <-DATOS.L[-random, ] #por lo que la muestra de test es la contraria
mod1<-lm(y~x1, data=train)
mod2<-lm(y~x1+x1**2, data=train)
red1<-neuralnet(y~x1,hidden=1,data=train,linear.output=TRUE,stepmax=1e7) #configuración con 1 capa oculta
red2<-neuralnet(y~x1,hidden=2,data=train,linear.output=TRUE,stepmax=1e7) #configuración con 2 capas ocultas
O_mod1<-predict(mod1, newdata=test)
O_mod2<-predict(mod2, newdata=test)
O_red1<-predict(red1, newdata=test)
O_red2<-predict(red2, newdata=test)
O_real<-(test$y)
error1[i]<-mean((O_real-O_mod1)^2)
error2[i]<-mean((O_real-O_mod2)^2)
error3[i]<-mean((O_real-O_red1)^2)
error4[i]<-mean((O_real-O_red2)^2)
}Hasta ahora se ha trabajado con estructuras de red neuronal demasiado sencillas que, en realidad, no aportan ninguna utilidad al modelado, ya que han servido para entender las ideas básicas de una red neuronal. A continución proponemos problemas donde la red neuronal pasa a ser decisiva. Por ejemplo, en el siguiente gráfico
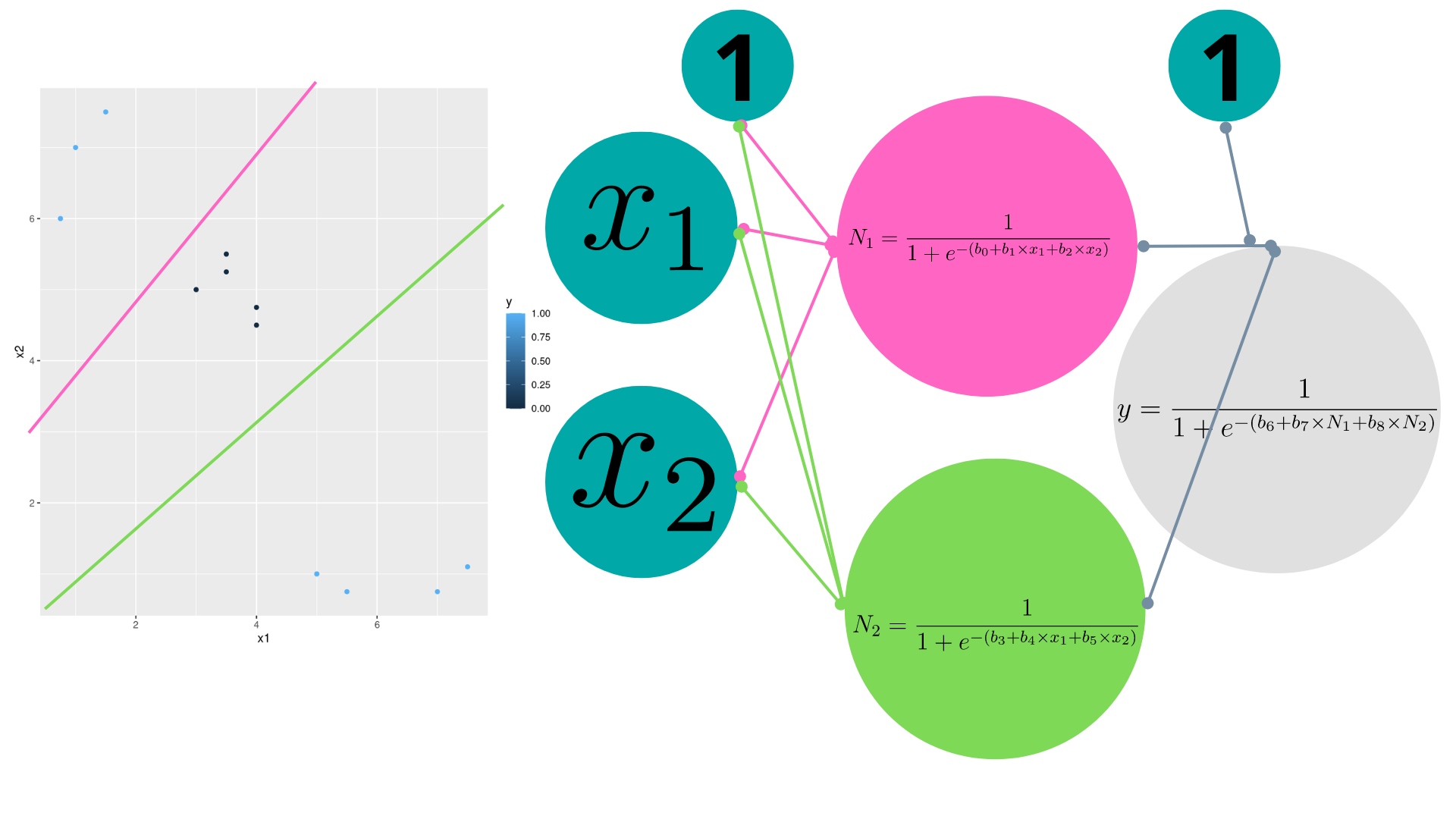
Como ve, queremos clasificar una variable con dos posibles resultados,(1,0), ante los valores que toman \(x_{1},x_{2}\). En este caso, hay cierta mezcla entre los 1 y los 0, de tal forma que un modelo logit no sería capaz de hacer una buena separación (en la clase anterior ha podido repasar cómo funciona el modelo logit). Para ello, necesitará dos neuronas que, primeramente, construyan las dos rectas que separan las regiones de interés (nótese en el dibujo cómo se remarcan en colores ambas rectas). Lo hará a través de una función de activación logística. Una vez las obtenga, deberá combinarlas y obtener una probabilidad (por lo que deberá usar ahí la función logística).
Estos son los datos con los que se ha hecho el gráfico
Sean los siguientes datos \(y=(1,1,1,0,0,0,0,0,1,1,1,1)\) \(x_1=(1,1.5,0.75,3,3.5,3.5,4,4,5,5.5,7,7.5)\) \(x_2=(7,7.5,6,5,5.5,5.25,4.75,4.5,1,0.75,0.75,1.1)\)
- Modele \(y=f(x_1,x_2)\) mediante un modelo logit y una red neuronal con 1 y 2 neuronas.
- Evalúe la capacidad de ajuste de ambos modelos mediante una matriz de confusión
La solución podemos verla utilizando este código
library(scales)
# Data
y <- c(1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1)
x1 <- c(1, 1.5, 0.75, 3, 3.5, 3.5, 4, 4, 5, 5.5, 7, 7.5)
x2 <- c(7, 7.5, 6, 5, 5.5, 5.25, 4.75, 4.5, 1, 0.75, 0.75, 1.1)
DATOS.C <- data.frame(y, x1, x2)
# Escalo las variables de entrada
scaled_data <- as.data.frame(lapply(DATOS.C[, -1], scale))
# añado la variable target
scaled_data <- data.frame(y=DATOS.C$y, scaled_data)
# Creo la red neuronal
red1 <- neuralnet(y ~ x1 + x2,
hidden = 1,
linear.output = FALSE,
data = scaled_data)
# Plot the neural network
red2<-neuralnet(y~x1+x2,hidden=2,data=scaled_data,linear.output=FALSE)
par(mfrow = c(2, 1))
plot(red1)
plot(red2)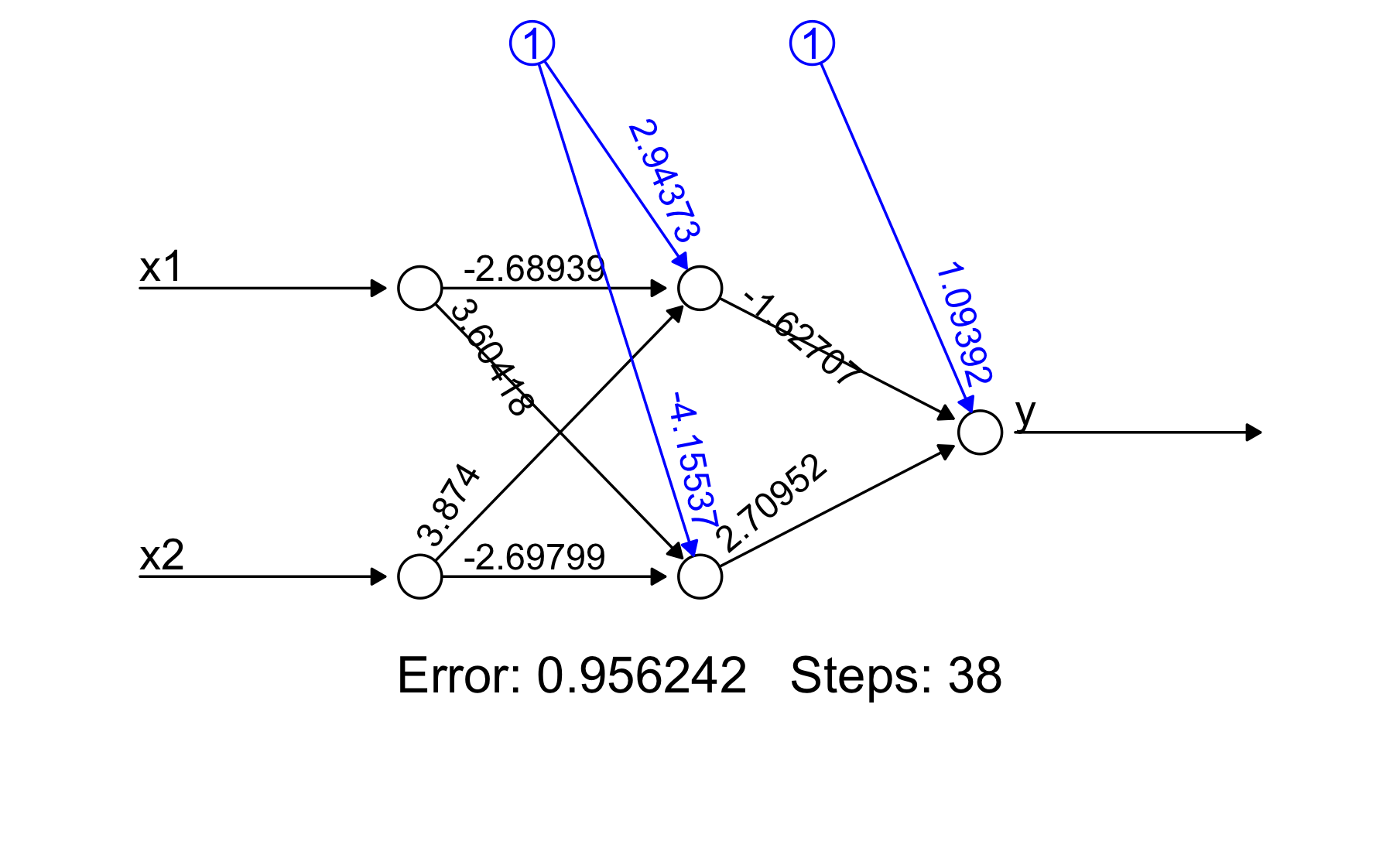
Note que este resultado puede escribirse como sigue:
- Salida: \(y=\frac{1}{1+e^{-(1.09-1.62N_{1}+2.70N_{2})}}\)
- Capa interna, neurona 1 \(N_1=\frac{1}{1+e^{-(2.94-2.68x_{1}+3.87x_{2})}}\)
- Capa interna, neurona 2 \(N_2=\frac{1}{1+e^{-(4.15+3.60x_{1}-2.69x_{2})}}\)
¿Qué modelo proporciona un mejor ajuste?
Puede utilizar una matriz de confusión para analizar ambos modelos
fit1<-predict(red1,scaled_data)
y_1_fit<-fit1>0.5
table(y_1_fit, scaled_data$y)
y_1_fit 0 1
FALSE 5 3
TRUE 0 4
fit2<-predict(red2,scaled_data)
y_2_fit<-fit2>0.5
table(y_2_fit, scaled_data$y)
y_2_fit 0 1
FALSE 5 0
TRUE 0 7Como puede ver, el segundo modelo- que hemos visto que es el adecuado- no comete ningún error de clasificación.
Podemos seguir aumentando la complejidad. Por ejemplo, en este otro caso, queremos encontrar la función que separa estos elementos que, como vemos, presentan una nueva complicación: no vale separar sólo con dos rectas, hay que buscar otra recta adicional y, posteriormente, juntarlas. Para ello, se debe añadir otra neurona:
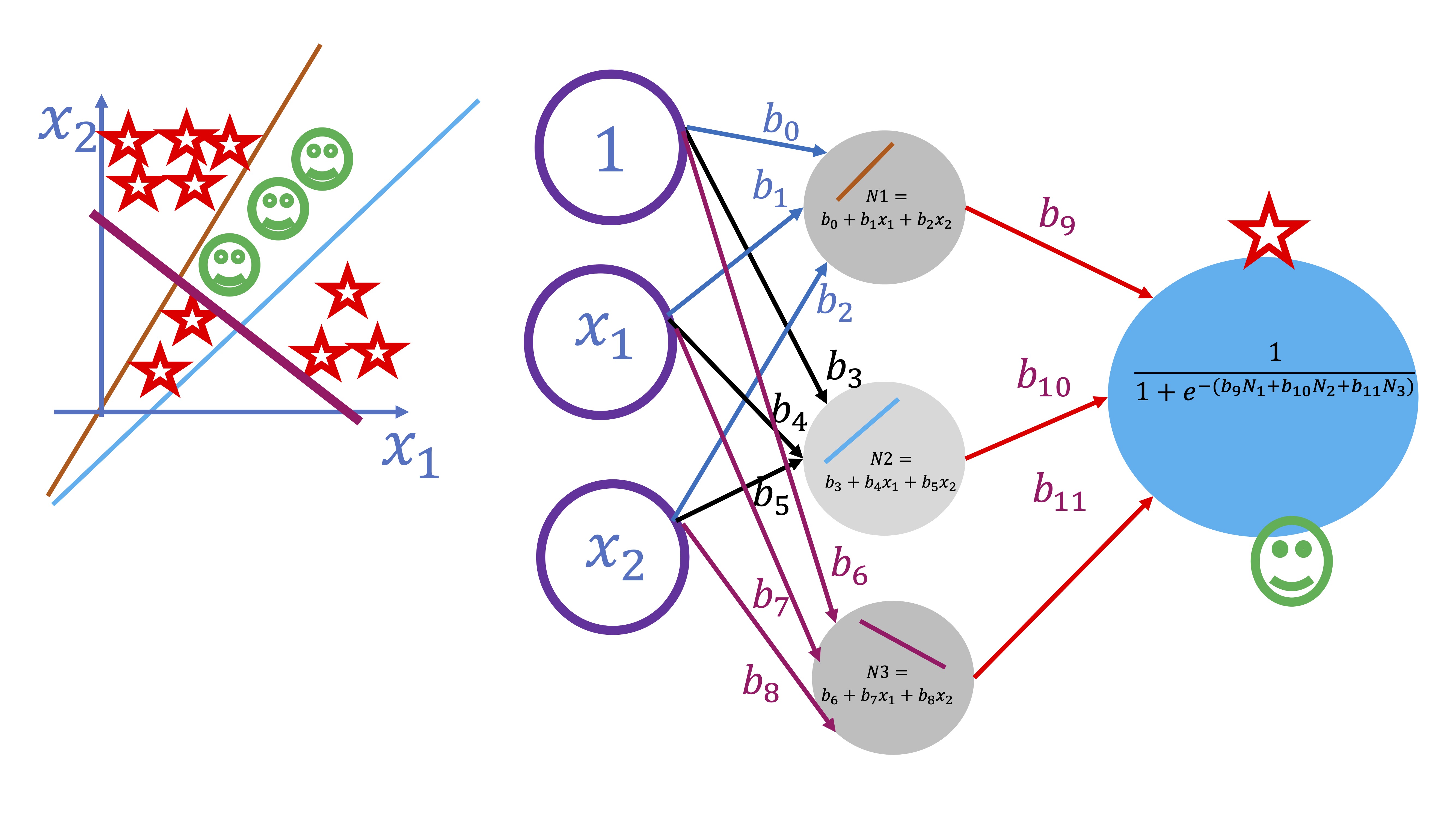
y conectarlas posteriormente, como se puede ver en la figura. Añadir neuronas, por tanto, genera una estructura más compleja que permite ir entrenando el modelo correspondiente.
Pero ¿Y si se incrementan las capas ocultas? Las capas ocultas surgen cuando se busca crear una estructura más compleja al interactuar las neuronas de la primera capa. Como se ve en la FIG 5, en este caso, al cortarse ciertas rectas, se generan subconjuntos donde cambia la clase de la variable \(y\). Esas interacciones se modelan creando una capa nueva.
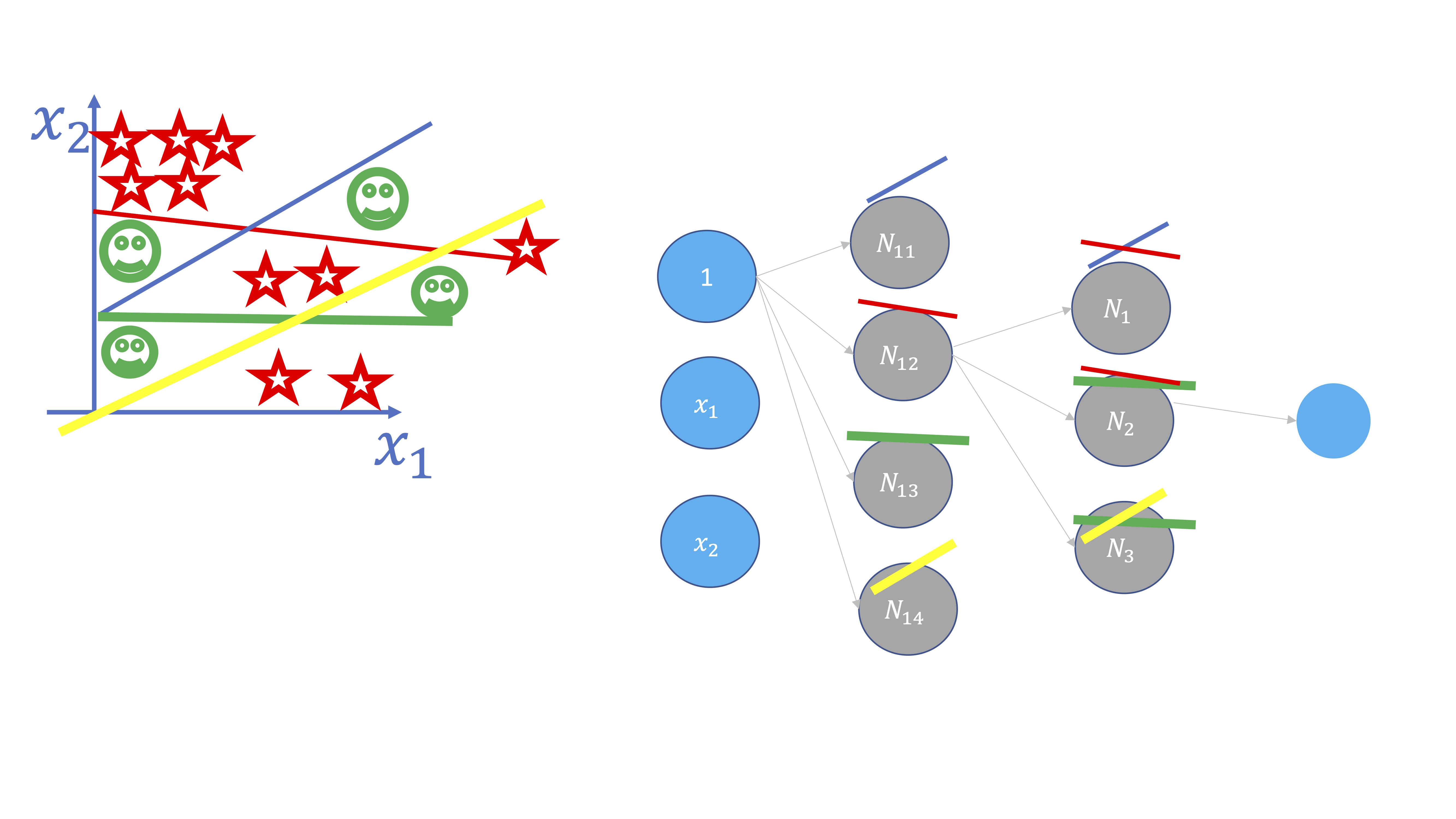
Por lo tanto:
- Se añaden neuronas cuando se quieren crear ‘barreras’ separadoras en el modelo
- Se crean capas ocultas cuando las “barreras” trazadas interactúan entre ellas (se cortan)
Ejercicio propuesto
Utilice estos datos para analizar qué configuración de redes neuronales podría ajustar mejor
x1<-c(1,1.5,0.75,3,3.5,3.5,4,4,5,5.5,7,7.5,2,3,2.75,1.5,4,4,4.15,4,6,6.5,6,7,2,2,3,3,4,4,6,6.25,5.75,6)
x2<-c(7,7.5,6,5,5.5,5.25,4.75,4.5,1,0.75,0.75,1.1,2,2.5,2,2.25,2,2.1,2.2,2.3,5.5,5.5,5.5,5.5,5.5,4,4.5,5.5,5.25,4,3,3,3,3)
y=c(1,1,1,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1,0,0,1,1,0,1,0,0,0,0)
DATOS<-data.frame(y,x1,x2)
scaled_data <- as.data.frame(lapply(DATOS[, -1], scale))
# añado la variable target
scaled_data <- data.frame(y=DATOS$y, scaled_data)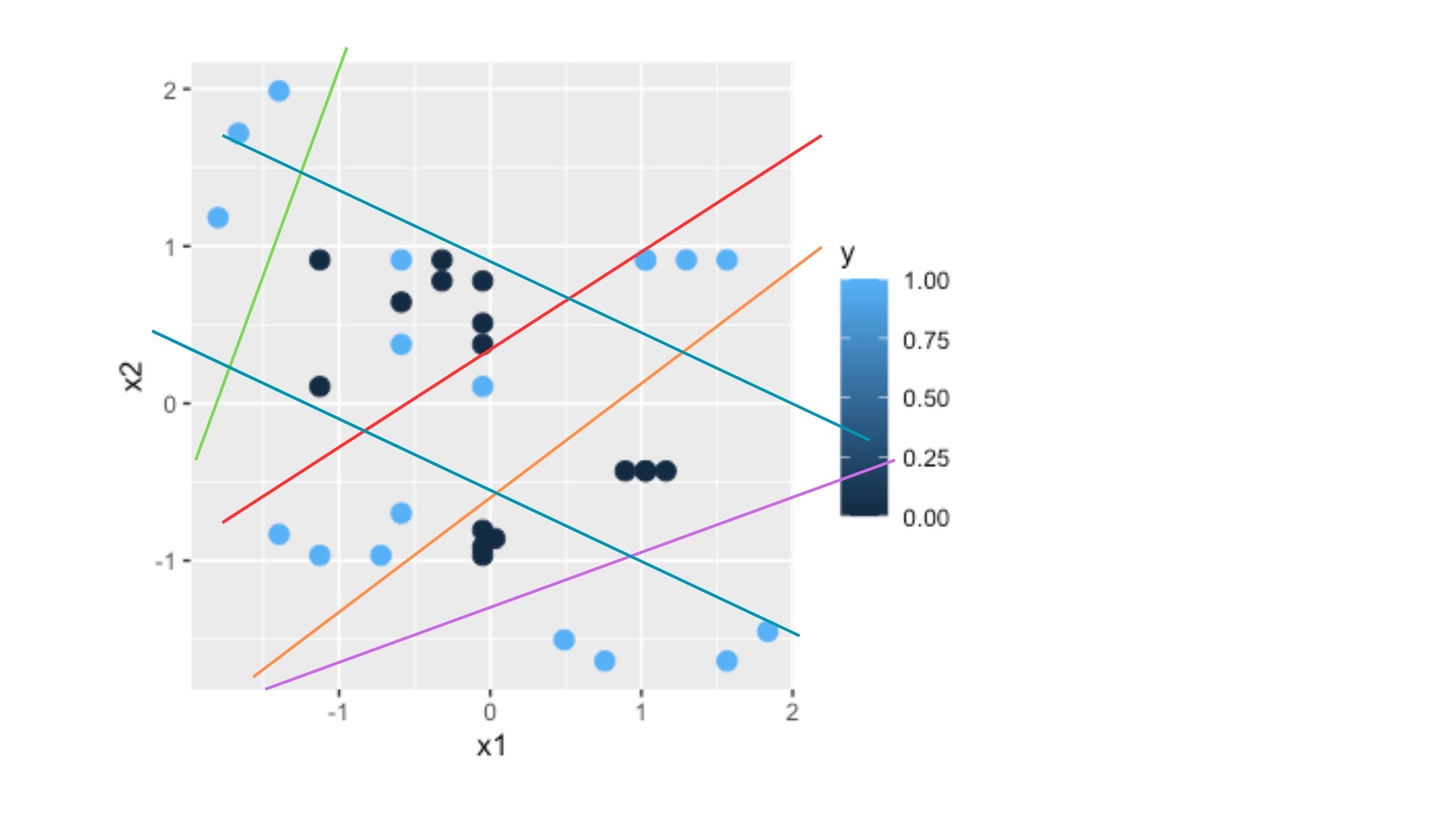
El siguiente script le permitirá ver cómo la complejidad en la relación entre las variables \(x_1,x_2\) con la variable \(y\) nos obliga a introducir 3 capas ocultas (mediante el comando hidden). En el primer ejemplo (red1) se usan sólo 2 neuronas y podrá ver en la tabla CM cómo la red neuronal clasifica incorrectamente bastantes observaciones. Al aumentar tanto las neuronas como las capas, (red2), puede ver que la clasificación es “casi” perfecta.
qplot(x1,x2,colour=y, data=scaled_data)+geom_point(size=3)
red1<-neuralnet(y~x1+x2,rep=6,hidden=c(2),data=scaled_data, linear.output = FALSE)
y1<-predict(red1, newdata=scaled_data)
y1_n<-y1>0.5
CM<- table(y1_n, y)
# y
#y1_n 0 1
# FALSE 16 4
# TRUE 0 14
set.seed(1234)
red2<-neuralnet(y~x1+x2,hidden=c(4,3),data=scaled_data, linear.output = FALSE)
y1_2<-predict(red2, newdata=scaled_data)
y2_n<-y1_2>0.50
CM<- table(y2_n, y)
# y
#y2_n 0 1
# FALSE 16 2
# TRUE 0 16
set.seed(1234)
red3<-neuralnet(y~x1+x2,hidden=c(4,3,3),data=scaled_data, linear.output = FALSE)
y1_3<-predict(red3, newdata=scaled_data)
y3_n<-y1_3>0.50
CM<- table(y3_n, y)
# y
# y3_n. 0 1
# FALSE 15 0
# TRUE 1 18
plot(red3)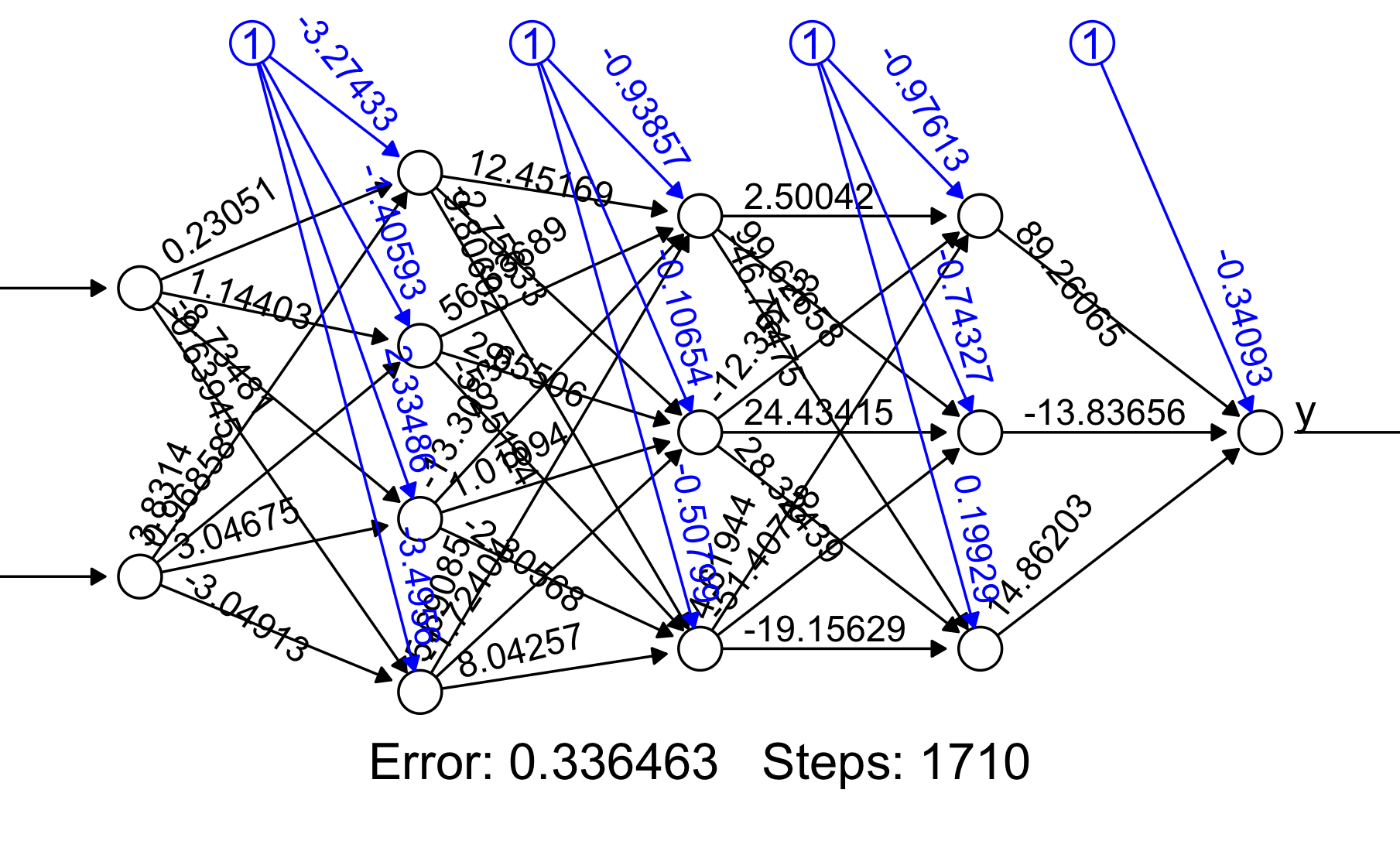
Sin embargo, esto nos puede llevar a un claro problema: el sobreajuste/sobreentrenamiento. Con redes neuronales es fácil ser capaz de alcanzar altos niveles de ajuste de los modelos a los datos, sin embargo, por dicho motivo, es fácil estar asumiendo ruido del modelo como si fuera señal y, por lo tanto, incurrir en errores importantes de predicción fuera de la muestra.
Ahí tiene el gráfico de la red 3 y, en el script puede ver su nivel de ajuste: clasifica mal 1 observación ¿a qué precio?
Clase 4: Entrenamiento de modelos de redes neuronales(I)
Para entender cómo se entrenan los modelos de redes neuronales y, por tanto, se obtienen las estimaciones para cada uno de los parámetros de la red, podemos ver el modelo de red neuronal como una composición de funciones. Por ejemplo, en la FIG 1, podemos ver el esquema de dependencias que da lugar a la composición de funciones
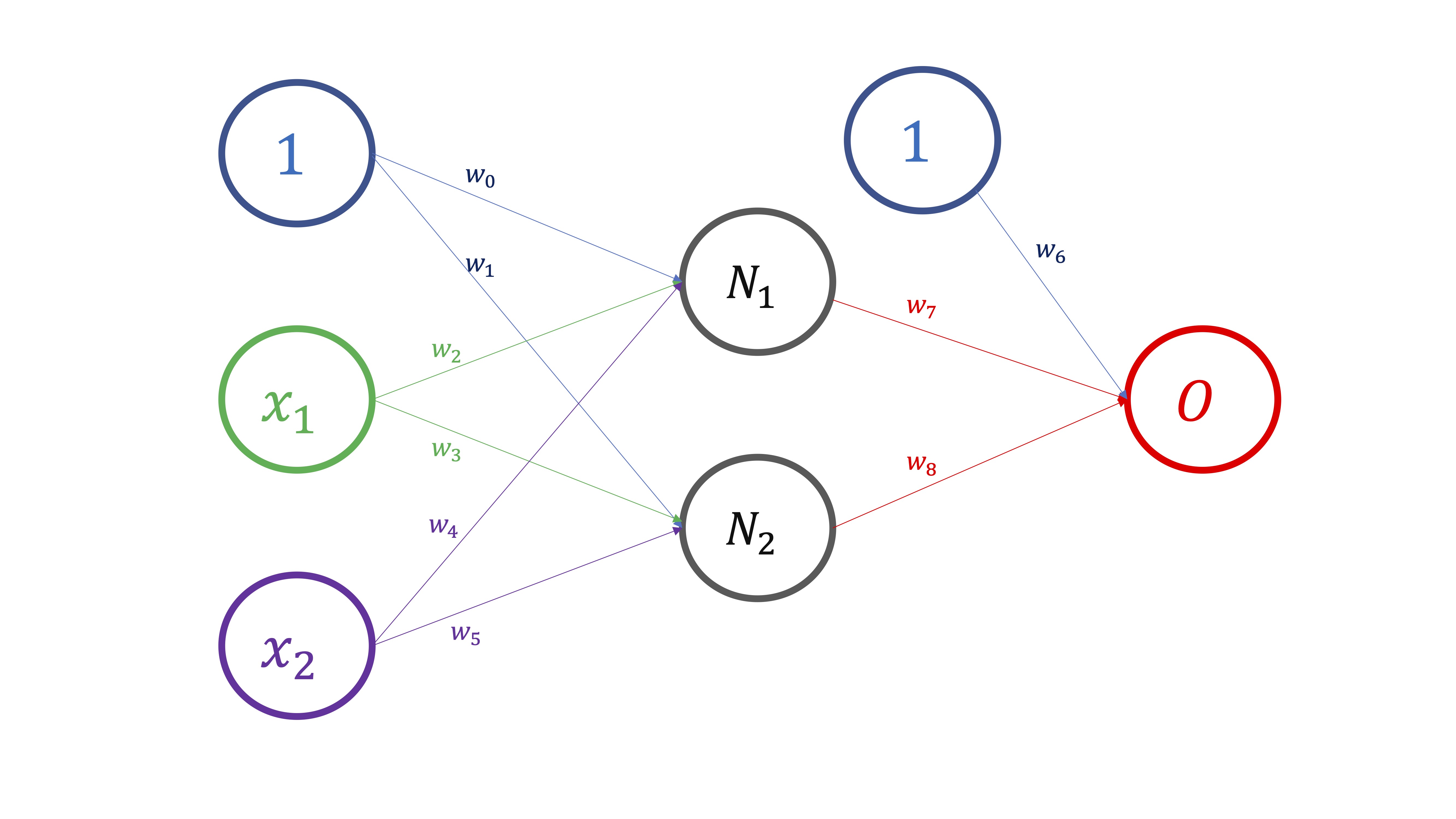Para empezar, dados unos valores para \((x_1,x_2)\), necesitamos conocer los valores de los pesos \(w_0,w_1,...,w_5\) y así obtener \(N_1,N_2\). Ahí tenemos, por tanto, que
\[
(w_0,w_2,w_4;1,x_1,x_2)\mapsto N_1
\]
\[
(w_1,w_3,w_5;1,x_1,x_2)\mapsto N_2
\]
Una vez obtenemos estas dos neuronas, \((N_1,N_2)\), obtenemos el “output”, de tal forma que
\[ (w_6,w_7,w_8;1,N_1,N_2)\mapsto O \]
y, entonces, comparamos el output que nos da el modelo, \(O\), con las verdaderas observaciones \(O_{real}\) de tal forma que
\[ Error=(O_{real}-O)^2 \]
Ahora, si hacemos esto para las \(T\) observaciones de que dispongamos en la muestra, obtendremos como medida del error, el error cuadrático medio,esto es,
\[ ECM=\frac{\sum(O_{real}-O)_{i}^{2}}{T}. \]
Para ello,note:
- Que la variable \(O\) es continua (por eso nos interesa utilizar el error cuadrático medio)
- Si la variable \(O\) fuese discreta (binaria o con valores múltiples) el criterio que nos interesaría optimizar sería algún error de clasificación (falsos positivos, falsos negativos, etc…)
- En las funciones de activación se suele requerir que sean diferenciables. De ahí a que, casi siempre, se utilizan las mismas, como ya verá.
El algoritmo para obtener esos pesos se conoce como retropropagación y, básicamente, funciona así:
- Dé pesos iniciales aleatorios (en este caso, \(w_{0}=0.1,w_{1}=0.1,...,w_{8}=0.6\))
- PROPAGACIÓN HACIA DELANTE Compute (a través de la composición de funciones) la predicción del output (FIG2).
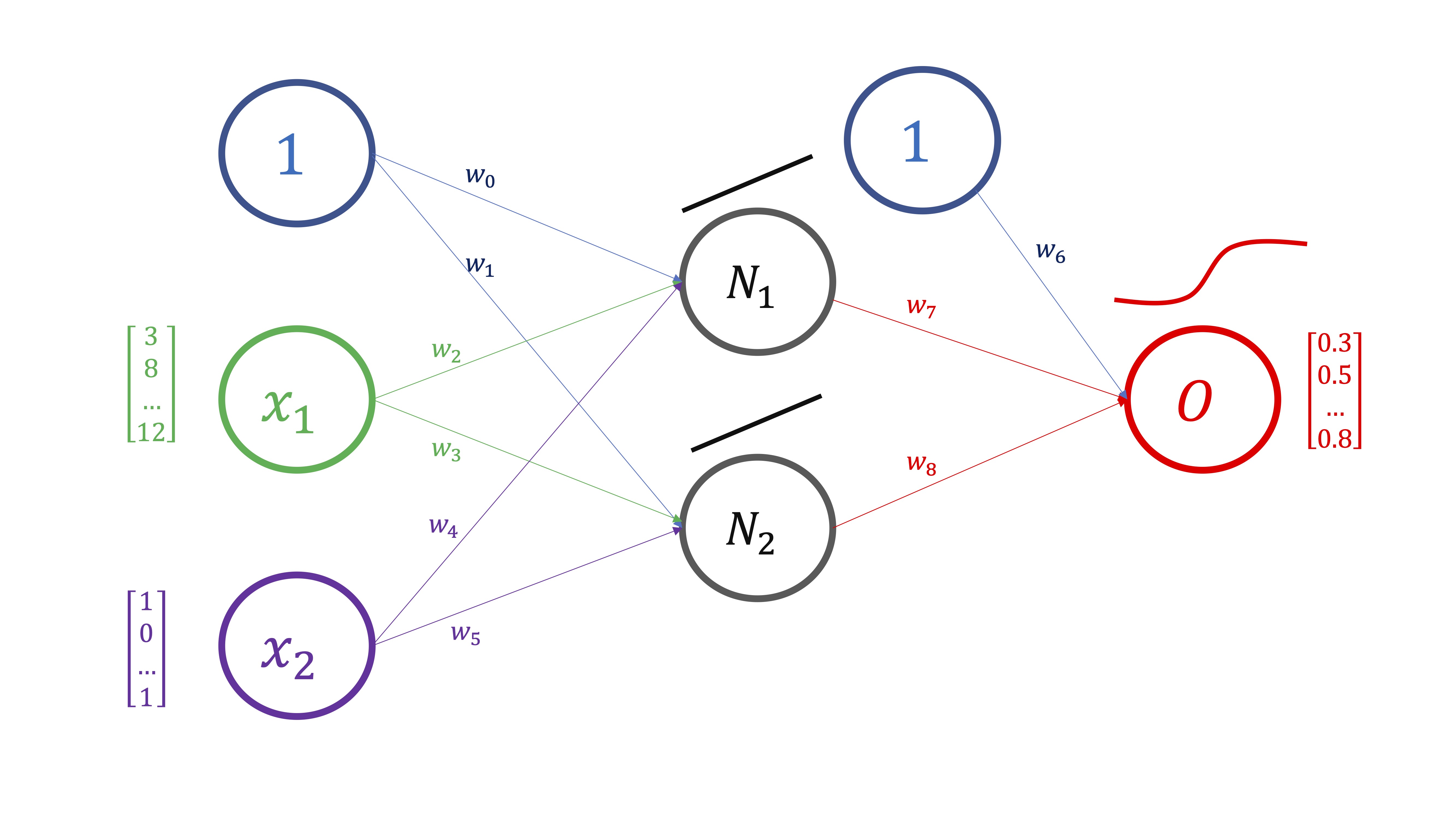
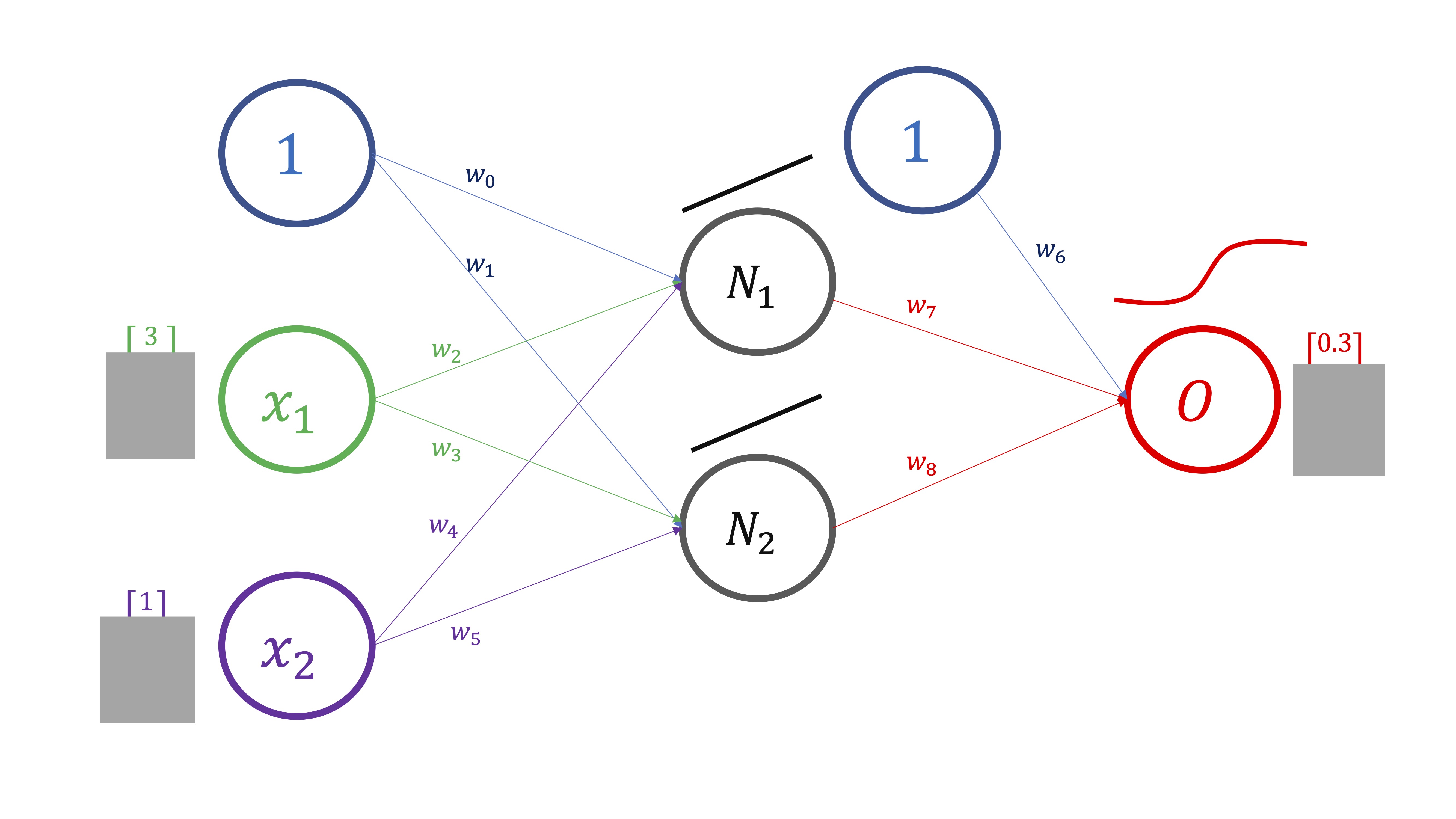
En este caso (FIG3), lo haremos para un sólo valor de los inputs y del output, pero en realidad se hace para todo el vector de datos:
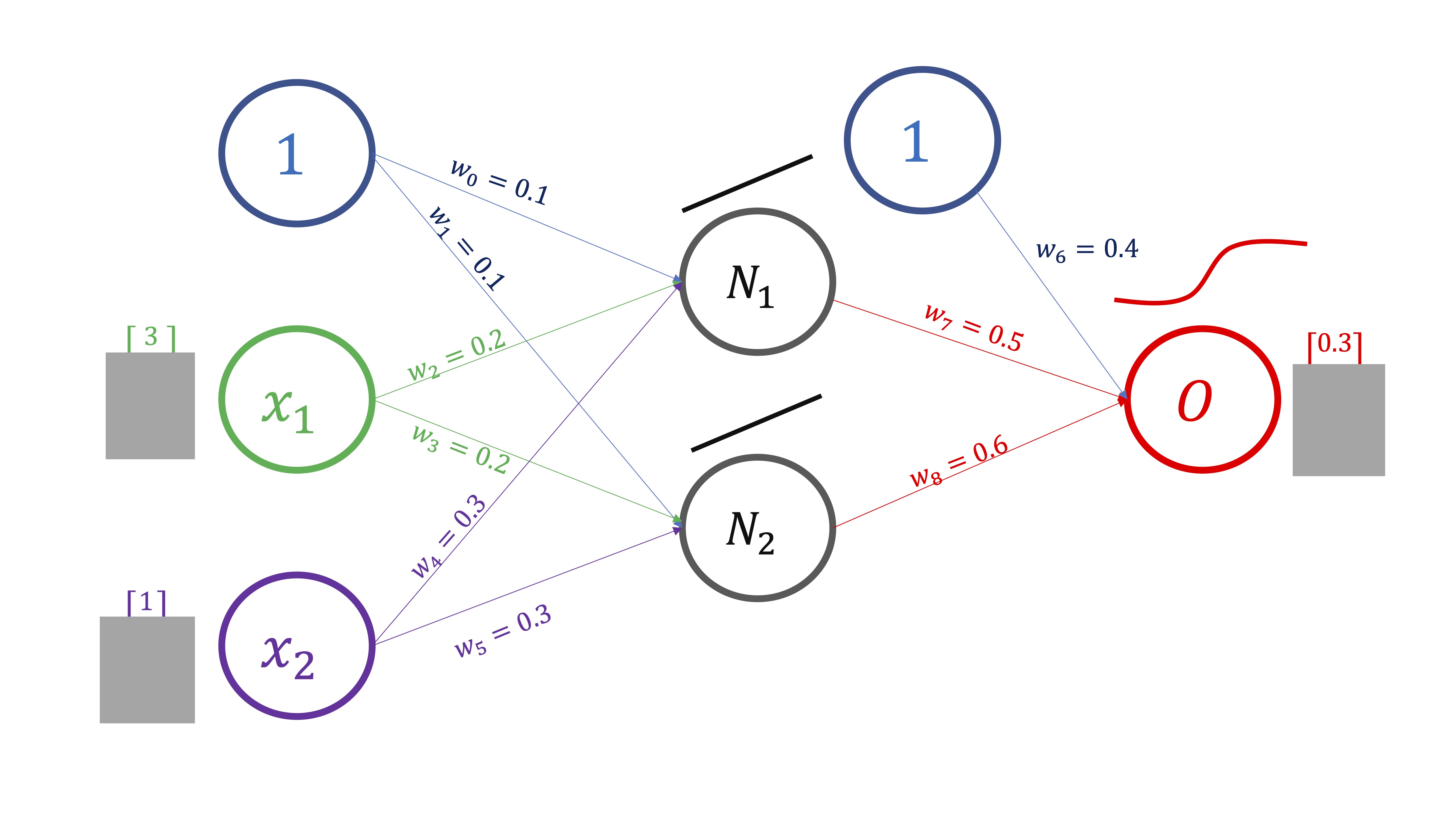
\[ \begin{cases} N_{1}=w_{0}+w_{2}x_{1}+w_{4}x_{2} & \Rightarrow N_{1}=0.1+0.2\times3+0.3\times1=1\\ N_{2}=w_{1}+w_{3}x_{1}+w_{5}x_{2} & \Rightarrow N_{2}=0.1+0.2\times3+0.3\times1=1\\ \hat{O}=\frac{1}{1+e^{-\left(w_{6}+w_{7}N_{1}+w_{8}N_{2}\right)}} & \Rightarrow\hat{O}=\frac{1}{1+e^{-\left(0.4+0.5\times1+0.6\times1\right)}}=0.81 \end{cases} \]
Ya tiene una predicción hecha por el modelo para \(O_{real}\) . Puede calcular el error que comete. Este modelo predice \(O=0.81\) pero, en realidad, \(O_{real}=0.3\)
- Evalúe el error cuadrático medio (\(ECM=\frac{\sum_{i=1}^{^{T}}\left(O_{i}-\hat{O_{i}}\right)^{2}}{T})\) que, en este caso, para simplificar \(N=1\) y obtiene \(ECM=\left(0.3-0.81\right)^{2}=0.26\). El objetivo ahora es minimizar este error. Para ello, deberá buscar nuevos pesos que mejoren el \(ECM.\) Es decir, quiere
\[ \min_{w_{0},w_{1},....,w_{8}}ECM \]
Este problema de minimización, que es complejo- pues involucra a una función compuesta de otras funciones (y que aquí se ha simplificado para que pueda entenderlo)- se debe hacer de manera iterativa utilizando, por ejemplo, el método del gradiente. Es decir, supongamos que quiere mejorar la estimación de \(w_{7}\), tendrá que seguir la regla ya aprendida en clases anteriores:
\[ w_{7}^{new}=w_{7}^{old}-h\frac{\partial ECM}{\partial w_{7}} \]
de tal forma que \(h\rightarrow0\)
Fíjese:
\[ \begin{cases} N_{1}=w_{0}+w_{2}x_{1}+w_{4}x_{2}\\ N_{2}=w_{1}+w_{3}x_{1}+w_{5}x_{2}\\ O=\frac{1}{1+e^{-\left(w_{6}+w_{7}N_{1}+w_{8}N_{2}\right)}}\\ ECM=\frac{\sum_{i=1}^{^{T}}\left(O_{real,i}-O_{i}\right)^{2}}{T} & \Rightarrow ECM=\frac{\sum_{i=1}^{^{T}}\left(O_{real,i}-\frac{1}{1+e^{-\left(w_{6}+w_{7}N_{1}+w_{8}N_{2}\right)}}\right)^{2}}{T} \end{cases} \]
De tal forma, que si necesita calcular
\[ \frac{\partial ECM}{\partial w_{7}} \]
deberá utilizar la regla de la cadena:
\[ \frac{\partial ECM}{\partial w_{7}}=2\left(O_{real}-O\right)^{2}\left(\frac{e^{-\left(w_{6}+w_{7}N_{1}+w_{8}N_{2}\right)}N_{1}}{\left(1+e^{-\left(w_{6}+w_{7}N_{1}+w_{8}N_{2}\right)}\right)^{2}}\right) \] y, sustituyendo, \[ \frac{\partial ECM}{\partial w_{7}}=2\times0.26\left(\frac{0.22\times1}{0.81^{2}}\right)=0.17 \]
por lo que \[ w_{7}^{new}=0.5-h\times0.17 \]
El nuevo valor del parámetro, como verá, dependerá del valor de \(h\) el cual, ya vimos, afecta al proceso de convergencia (y, por tanto, de obtención del resultado del método de optimización).
- RETROPROPAGACIÓN Una vez tiene actualizados todos los parámetros utilizando este procedimiento (llamado Backward) deberá volver a obtener los nuevos valores de \(O\), es decir, predicciones nuevas de la variable output y optimizar, de nuevo, el error. Esto es lo que se conoce como “retropropagación”.
El algoritmo consiste en dar de manera iterativa los pasos de “propagación hacia delante (forward)” y de “retropropagación (backpropagation)” hasta que se considere que el \(ECM\) ha alcanzado un mínimo (generalmente, local).
Entrenamiento de modelos de redes neuronales(II)
El objetivo ahora es tratar de buscar un mecanismo para decidir los valores que tendrán los hiperparámetros de nuestra red neuronal. Llamaremos hiperparámetros a aquellos que debemos definir nosotros. A un nivel básico, el número de capas ocultas y el de neuronas por capa. Aunque, dependiendo de la función que utilice para entrenar sus modelos, puede requerir fijar más parámetros (por ejemplo, el valor de \(h\) en el algoritmo de “retropropagación”, o el número máximo de iteraciones, etc…).
La mejor manera de evitar el temido sobreajuste, será mediante un mecanismo de validación cruzada. sin embargo, la contrapartida estriba en el coste computacional que tienen los modelos de redes neuronales. Veamos un ejemplo con los datos anteriores.
x1<-c(1,1.5,0.75,3,3.5,3.5,4,4,5,5.5,7,7.5,2,3,2.75,1.5,4,4,4.15,4,6,6.5,6,7,2,2,3,3,4,4,6,6.25,5.75,6)
x2<-c(7,7.5,6,5,5.5,5.25,4.75,4.5,1,0.75,0.75,1.1,2,2.5,2,2.25,2,2.1,2.2,2.3,5.5,5.5,5.5,5.5,5.5,4,4.5,5.5,5.25,4,3,3,3,3)
y=c(1,1,1,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1,0,0,1,1,0,1,0,0,0,0)
DATOS.D<-data.frame(y,x1,x2)
qplot(x1,x2,colour=y, data=DATOS.D)+geom_point(size=3)será interesante, hacer un juicio basado en información visual. Trate de ver, mediante gráficos, la relación que tienen las variables que considera más relevantes
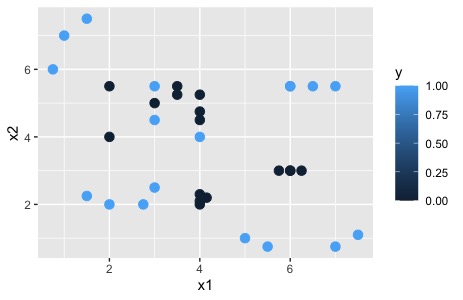En este caso, puede ver que hay cierta confusión en la relación entre \(x1,x2\) y \(O\), sugiriendo que necesitará más de una capa oculta para modelar la no-linealidad de dicha relación.
Puede ser sensato analizar el mejor modelo basado en una, dos y-como máximo- 3 capas ocultas y un conjunto de neuronas que, como mínimo serán 3 (dos variables input y una constante). El máximo es desconocido, pero podemos probar con el conjunto \({3,5,7}\), como mucho.
error<-mat.or.vec(50, 9) #creamos un vector que almacenará 50 errores y 9 configuraciones distintas
neurons<-c(3,5,7) #creamos un vector que contiene los diferentes valores del número de neuronas
for(i in 1:50){ #Iniciamos los subíndices: este es el de la iteración
for (j in 1:3){ #este es el subíndice del número de neuronas
random <- sample(1:nrow(DATOS.D), size = floor(.7*nrow(DATOS.D))) # Elegimos la muestra de entrenamiento al azar
train<-DATOS.D[random,]
test <-DATOS.D[-random, ] #por lo que la muestra de test es la contraria
red1<-neuralnet(y~x1+x2,hidden=c(neurons[j]),data=train, linear.output = FALSE) #configuración con 1 capa oculta
red2<-neuralnet(y~x1+x2,hidden=c(neurons[j],neurons[j]),data=train, linear.output = FALSE) #configuración con 2 capas ocultas
red3<-neuralnet(y~x1+x2,hidden=c(neurons[j],neurons[j],neurons[j]),data=train, linear.output = FALSE) #configuración con 3 capas ocultas
O_red1<-predict(red1, newdata=test,type="response")
O_red2<-predict(red2, newdata=test,type="response")
O_red3<-predict(red3, newdata=test,type="response")
O_red1_n<-as.numeric(O_red1>0.5)
O_red2_n<-as.numeric(O_red2>0.5)
O_red3_n<-as.numeric(O_red3>0.5)
O_real<-(test$y)
X<-data.frame(O_red1_n,O_red2_n,O_red3_n,O_real)
xt1<-table(factor(X[,1],levels=0:1),factor(X[,4],levels=0:1))
xt2<-table(factor(X[,2],levels=0:1),factor(X[,4],levels=0:1))
xt3<-table(factor(X[,3],levels=0:1),factor(X[,4],levels=0:1))
error[i,j]<-(xt1[1,2]+xt1[2,1])/length(O_red1_n) #medimos los errores de clasificación
error[i,j+3]<-(xt2[1,2]+xt2[2,1])/length(O_red2_n)
error[i,j+6]<-(xt3[1,2]+xt3[2,1])/length(O_red3_n)
}}La matriz “error” nos proporciona, por columnas:
2 neuronas 1 capa oculta
5 neuronas 1 capa oculta
7 neuronas 1 capa oculta
2 neuronas 2 capas ocultas
5 neuronas 2 capas ocultas
7 neuronas 2 capas ocultas
2 neuronas 3 capas ocultas
5 neuronas 3 capas ocultas
7 neuronas 3 capas ocultas
Para cada una de estas configuraciones, tenemos mediciones del error. Puede comprobar que la columna 6 es la que tiene un menor error promedio (es decir, utilizando 7 neuronas y 2 capas ocultas).
Ejercicio Trabaje con su conjunto de datos, entrenando un modelo de red neuronal. Juegue a combinar los modelos que ha utilizado hasta ahora incluyendo el de red neuronal (la combinación más sencilla: promedio de ambos modelos)
En la práctica
Respecto a la decisión de cuantas capas ocultas deberíamos tomar, se suele recomendar:
0 - Sólo es capaz de aproximar problemas “linealmente separables”. Piense en los ejemplos iniciales de la CLASE 2 y la CLASE 3
1 - Puede aproximar funciones más generales (piense en los ejemplos de la CLASE 3 donde las observaciones estaban “más mezcladas”).
2 -Puede aproximar funciones arbitrarias y con mucha heterogeneidad (el último ejemplo de la clase 3, donde necesitamos meter otra capa oculta adicional para tratar de capturar la alta no linealidad en la relación entre los inputs/output)
Respecto al número de neuronas:
El uso de pocas neuronas, tenderá al “infraajuste”. El uso de demasiadas neuronas, nos llevará al sobreajuste. En general, el n´mero de variables y el tamaño de la base de datos condicionarán la selección tanto del número de neuronas como del número de capas ocultas.
Hay algunas reglas que deberían usarse como “orientativas”. A partir de estas, podría generar un conjunto de validaciones cruzadas con configuraciones similares, para determinar cuál es la más adecuada.
Número de neuronas totales de la red
- Criterio 1. Debería estar entre el tamaño de la capa de entrada (es decir, el número de variables inputs) y el de la capa de salida.
- Criterio 2. Debería ser 2/3 del tamaño de la capa (# variables) de entrada más el tamaño de la capa de salida (# variables)
- Criterio 3. Menos del doble del tamaño de la capa de entrada.
Número de capas ocultas
Empiece siempre con una. Si los resultados son pobres, entonces, introduzca una capa adicional.
- Sugerimos que empiece con estas recomendaciones a la luz de su problema y, posteriormente, usando validación cruzada, determine- en un entorno a esta propuesta- qué funciona mejor.
En la siguiente parte del curso, entrenaremos modelos de redes neuronales y discutiremos sobre ellos. No olvide que estas notas (con sus erratas y errores) no están mal. Pero, de vez en cuando, puede coger un objeto que inventaron los humanos para dejar sin árboles el planeta, pero que queda muy mono:
