BLOQUE 2: TÉCNICAS DE APRENDIZAJE SUPERVISADO
Clase 1. La validación de modelos
Un paso importante en el proceso de análisis de datos es buscar alguna manera imparcial de analizar el desempeño de un modelo. En general, no es sensato utilizar magnitudes que analizan el grado de ajuste de un modelo (\(R^2\), ECM, etc…) ya que cuanto mayor sea el conjunto de variables utilizado en un modelo, mayor será el grado de ajuste (y menor su ECM): es decir, podemos estar cayendo en sobreajustar un modelo: asumiendo error como si fuera señal, que suele decirse. Sin embargo, ello no quiere decir que el modelo sea más útil para realizar una predicción.
Técnica 1: Entrenamiento+Test
Una técnica sencilla para analizar cómo se desenvuelve un modelo es la partición entre entrenamiento y test. Generalmente, se elige una proporción alta para el entrenamiento (en torno al 70%) y el resto se dedica a test:
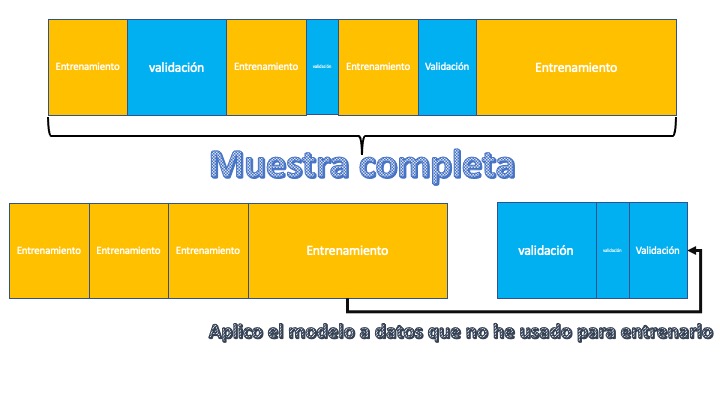
Esta elección se realiza de manera aleatoria de tal forma que la partición realizada nos permita analizar, de manera adecuada, la población de estudio tanto en el entrenamiento de modelos como en su testado. El modo de trabajo es sencillo:
- Elija la muestra de entrenamiento y validación, así como la variable que quiere predecir (\(y_T,y_V\)) y los predictores (los almacenamos en una matriz: \(\bf{X_T,X_v}\))
- Utilice la muestra de entrenamiento para estimar los modelos que considere (haciendo, por ejemplo, un análisis descriptivo previo sólo a ese conjunto de datos), de tal forma que tiene, por ejemplo, \(N\) modelos: \(y_T=f_1(\bf{X_T})\),\(y_T=f_2(\bf{X_T})\),…,\(y_T=f_N(\bf{X_T})\), donde \(f_1,f_2,...,f_N\) son los modelos.
- con el modelo que ha entrenado, seleccione la muestra de test y se lo aplica. De esta forma tendrá, por ejemplo con el modelo \(j\), \(\hat{y}=f_j(\bf{X_V})\) las predicciones que realiza dicho modelo con los datos de validación de \(\bf{X}\). De esta forma, podrá comparar la predicción del modelo (\(\hat{y}\)) con las observaciones que tiene almacenadas del conjunto de validación (\(y_V\)).
- Puede calcular, entonces, alguna medida de error promedio que le interese o, lo que es más interesante, analizar la distribución empírica de los errores de predicción para distintos modelos alternativos.
- Esta técnica podría utilizarla como un complemento a la inferencia estadística tradicional. Si considera que una variable es significativa (o relevante), entonces mediante este análisis, debería proporcionarle un error predictivo menor, al incluirla en el modelo, que en el caso en que esta variable no esté.
- Esta técnica le puede ayudar a elegir modelos (si tiene varios modelos candidatos y quiere quedarse con uno de ellos, puede elegir el que menor error le proporcione en la validación)
- Sin embargo, esta técnica está muy condicionada por la elección del entrenamiento y la validación.
#Ejemplo hecho en clase con los datos de "heart.csv"
S<-dim(heart)[1] #obtengo cuántas filas tiene la base
id<-seq(1,0.7*S,1) #genero un indicador que extraerá esas filas
train<-heart[id,] #obtengo la muestra de entrenamiento
test<-heart[-id,] #obtengo la muestra de test
Mtrain<-glm(target~chol+age+trestbps,family=binomial, data=train)# Entreno el modelo 1 con la muestra de train
prediction<-predict.glm(Mtrain, test,type="response") #predigo con el modelo 1 y la muestra de validación
disease_pred1<-prediction>0.5
table(disease_pred1, test$target) #realizo una matriz de confusión para analizar los distintos errores y aciertosTécnica 2: Validación Cruzada aleatoria
Una manera de mejorar el último aspecto de la técnica anterior, consistirá en tener más información sobre el error de predicción. Para ello, se puede hacer un muestreo tanto de los datos que se destinarán a entrenamiento como aquellos que se utilizarán para validación. La idea de la validación cruzada es hacer “un montón de veces” la partición entre entrenamiento y validación utilizando para ello extracciones aleatorias (sin reemplazamiento) de las muestras. Visualmente, consiste en el esquema de la FIG2:
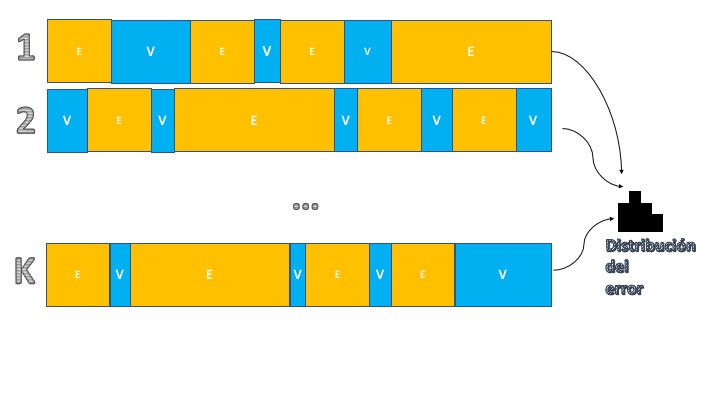
Como se puede ver, consiste en replicar la estructura anterior pero ahora se hará \(K\) veces, particionando la muestra entre entrenamiento y validación. Ello nos permitirá tener \(K\) observaciones de la medida de error que le interese y, por tanto, tener una distribución dicha medida del error de predicción. Esto es ventajoso, pues nos permite comparar entre modelos de una manera más objetiva, puesto que las particiones aleatorias permiten ver cómo funciona el modelo en submuestras distintas. Para entender el algoritmo de validación cruzada, tiene aquí un ejemplo en el que se quiere discutir qué modelo es mejor en el caso de las enfermedades cardiacas:
- M1. Regresión logística sólo con colesterol
- M2. Regresión logística con colesterol y edad
- M3. Regresión logística con colesterol, edad y azúcar y la interacción entre colesterol y edad y azúcar y edad
- M4. Regresión logística con colesterol, edad, azúcar y tensión en reposo y la interacción entre colesterol y edad y azúcar y edad y tensión y edad.
N<-1000 #Decido el número de simulaciones que quiero hacer
error1f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 1
error2f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 2
error3f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 1
error4f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 1
for(i in 1:N){ #Inicio el bucle
sample <- sample.int(n = nrow(heart),size = floor(.7*nrow(heart)), replace = F) #me da el sorteo de filas aleatorias
train <- heart[sample, ] #Obtengo la muestra de entrenamiento
test <- heart[-sample, ] #y la muestra de validación
Mtrain1<-glm(target~chol,family="binomial", data=train)# Entreno el modelo 1 con la muestra de train
Mtrain2<-glm(target~chol+age+as.factor(fbs),data=train,family="binomial")
Mtrain3<-glm(target~chol*age+as.factor(fbs)*chol*age,data=train,family="binomial")
Mtrain4<-glm(target~chol*age+as.factor(fbs)*chol*age+trestbps*chol,data=train,family="binomial")
prediction_1<-predict.glm(Mtrain1, test,type="response") #predigo con el modelo 1 y la muestra de validación
prediction_2<-predict.glm(Mtrain2, test,type="response") #predigo con el modelo 2 y la muestra de validación
prediction_3<-predict.glm(Mtrain3, test,type="response") #predigo con el modelo 3 y la muestra de validación
prediction_4<-predict.glm(Mtrain4, test,type="response") #predigo con el modelo 4 y la muestra de validación
disease_pred1<-prediction_1>0.5
disease_pred2<-prediction_2>0.5
disease_pred3<-prediction_3>0.5
disease_pred4<-prediction_4>0.5
error1<-table(disease_pred1, test$target) #obtenemos el error de predicción 1 para cada elemento de validación
error2<-table(disease_pred2, test$target)#obtenemos el error de predicción 2 para cada elemento de validación
error3<-table(disease_pred3, test$target) #obtenemos el error de predicción 3 para cada elemento de validación
error4<-table(disease_pred4, test$target) #obtenemos el error de predicción 4 para cada elemento de validación
#de la matriz de confusión almacenamos un error de interés: FALSOS POSITIVOS
error1f[i]<-error1[2,1]
error2f[i]<-error2[2,1]
error3f[i]<-error3[2,1]
error4f[i]<-error4[2,1]
}
E1 <- data.frame( errors = error1f )
E2 <- data.frame( errors = error2f )
E3 <- data.frame( errors = error3f )
E4 <- data.frame( errors = error4f )
CombinedData <- data.frame(E1,E2,E3,E4)
boxplot(CombinedData,names=c("chol","chol+age+fbs","interact 1","interact 2"))Ejercicio Analice los errores cometidos
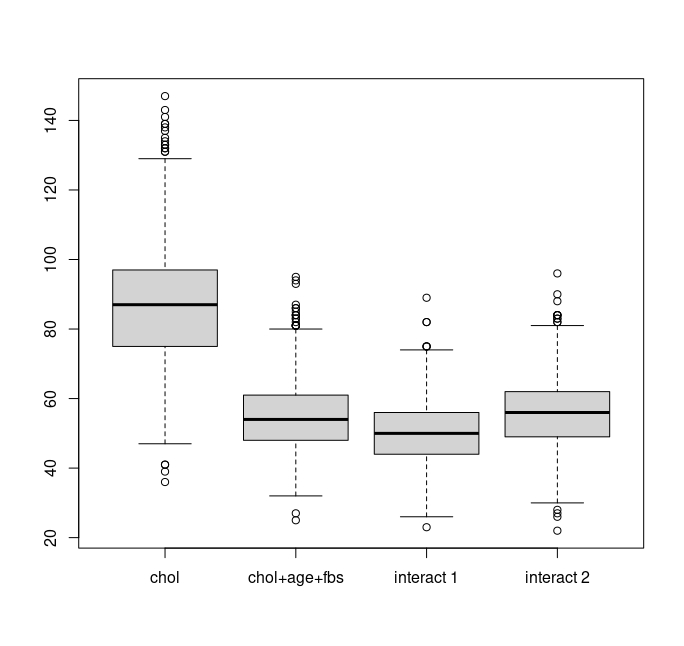
Podemos ver que el modelo 1 es el que más falsos positivos proporciona. El modelo 3, en este caso, parece batir al resto: los errores más grandes (atípicos) son superados por los atípicos del modelo 2 y del 4 y, además, es el que tiene más probabilidad de cometer errores muy pequeños.
Cómo combinar modelos (opcional, veremos más ideas en el segundo cuatrimestre)
Una idea extendida en estadística es que, en general, no hay “un mejor” modelo. Casi siempre funcionará mejor, si su objetivo es predecir, tener un conjunto de posibles modelos para los cuales, la predicción final, será una combinación de ellos. ¿Cómo combinar los modelos? Hay mucha literatura al respecto pero:
- Puede elegir usted basado en algún criterio de experto. Ojo, porque eso tendrá que argumentarlo bien
- Puede hacer una media/mediana de la predicción.
- Puede tratar de estimar pesos en función de algún criterio.
Ejercicio Con los datos de los SIMPSON busque cómo, realizando validación cruzada, combinar modelos a los que se les penalice realizar predicciones que se alejen +/- 0.5 puntos.
FINAL_SIMPSON$D<-ifelse(FINAL_SIMPSON$id<200,1,0) #generamos una variable Dummy para indicar los primeros 200 episodios
N<-100 #Decido el número de simulaciones que quiero hacer
error1f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 1
error2f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 2
w1<-rep(0,N) #Creo un vector para almacenar pesos del modelo 1
w2<-rep(0,N) #Creo un vector para almacenar pesos del modelo 2
for(i in 1:N){ #Inicio el bucle
sample <- sample.int(n = nrow(Resto_SIMPSON),size = floor(.7*nrow(Resto_SIMPSON)), replace = F) #me da el sorteo de filas aleatorias
train <- Resto_SIMPSON[sample, ] #Obtengo la muestra de entrenamiento
test <- Resto_SIMPSON[-sample, ] #y la muestra de validación
Mtrain1<-lm(imdb_rating~sumH, data=train)# Entreno el modelo 1 con la muestra de train
Mtrain2<-lm(imdb_rating~sumH*D, data=train) # Entreno el modelo 2 con la muestra de train
prediction_1<-predict(Mtrain1, test) #predigo con el modelo 1 y la muestra de validación
prediction_2<-predict(Mtrain2, test) #predigo con el modelo 2 y la muestra de validación
error1<-test$imdb_rating-prediction_1 #obtenemos el error de predicción 1 para cada elemento de validación
error2<-test$imdb_rating-prediction_2 #obtenemos el error de predicción 2 para cada elemento de validación
m1_pos<-sum(abs(error1)<0.5) # número de predicciones que no se equivocan en más/menos 0.5
m2_pos<-sum(abs(error2)<0.5) # número de predicciones que no se equivocan en más/menos 0.5
w1[i]<-m1_pos/(m1_pos+m2_pos)
w2[i]<-m2_pos/(m1_pos+m2_pos)
}
#obtengo los pesos finales
W1<-mean(w1)
W2<-mean(w2)
W1_f<-W1/(W1+W2)
W2_f<-W2/(W1+W2)Reflexión sobre la elección de medidas de error
A veces es más arriesgado cometer un falso negativo, es decir, predecir que alguien tiene un bajo riesgo cuando en realidad tienen un alto riesgo, ya que esto impedirá que reciban atención/cuidado/citas. Pero en otros casos, los falsos positivos presentan un riesgo más alto. Por ejemplo, en enfermedades de la próstata, los falsos positivos en una prueba de detección significan que el paciente recibirá una prueba más invasiva y arriesgada (y costosa) que luego mostrará que son verdaderos negativos. Sin embargo, la enfermedad de la próstata suele progresar muy lentamente, por lo que en realidad sería más seguro para los pacientes en general tener más falsos negativos (es decir, dejar pasar a algunos pacientes que en realidad tienen la enfermedad de la próstata) que someter a pruebas invasivas (y costosas) a más pacientes. Cuando algo avanza muy lentamente, hay oportunidades para detectarlo más tarde cuando esté un poco peor y sea más fácil de detectar. Sin embargo, el cáncer de ovario avanza muy, muy rápido; si obtienes un falso negativo en una prueba de detección, existe una alta probabilidad de que el paciente muera porque se propaga tan rápidamente que es probable que no se realice otra prueba de ningún tipo antes de que sea demasiado tarde para detenerlo, por lo que es mucho mejor tener pruebas de detección con más falsos positivos.
En otras palabras, a veces la reducción global del riesgo favorece las pruebas/predicciones con más falsos negativos, y otras veces favorece las pruebas/predicciones con más falsos positivos. Pero en general, en el ámbito de la atención médica, más del 90 por ciento del tiempo es más seguro sobreestimar el riesgo para que el paciente tenga más probabilidades de recibir atención/cuidado que subestimar el riesgo, por lo que los profesionales de la salud a menudo ajustan los modelos para aumentar el riesgo en lugar de reducirlo.
Esto se puede aplicar a cualquier contexto (pero da la impresión de que en términos de salud lo entendemos enseguida). Piense, por ejemplo, en una campaña de Marketing de la conocida “venta cruzada”. Usted está en su compañía telefónica y quieren ofrecerle otro servicio. ¿Qué será peor, un falso positivo o un falso negativo?
Piense en términos de: coste de publicidad, coste de centralita para ofrecer el producto, etc…
Clase 2. Los árboles de clasificación
Vamos ahora a presentar una técnica que permite predecir, de la misma manera que hemos hecho hasta ahora, una variable objetivo (por ejemplo, la puntuación de los episodios de los Simpson, el tener una enfermedad o no, etc…) utilizando un conjunto de variables explicativas. Vamos a entender, primeramente, la filosofía.
variable objetivo cualitativa: árbol de clasificación
Imagine que tiene una base de datos donde cuenta con dos variables explicativas (\(X_{1},X_{2})\) y pretende explicar la variable \(Y\) que, en este caso, sólo presenta dos posibles valores \(Y=\{S\acute{I},NO\}.\) Piense, por ejemplo, en que \(Y\) se corresponde con la devolución (o no) de un crédito y \(X_{1},X_{2}\) son variables continuas que miden dos características de cada individuo. Entonces, podemos visualizar la información disponible en este gráfico:
Si observa detenidamente, es fácil encontrar cierta manera, usando rectángulos, de clasificar en bloques los síes y los noes:
Ahora bien, si quiere representar la regla que le permita saber, de un vistazo, si conceder o no el crédito, puede hacer un diagrama de árbol. Consiste en poner la misma información que tiene en la FIG2 de una manera más sistemática, de tal forma que le sea fácil de seguir:
Sin embargo, en la vida real los datos, en general, tendrán una estructura caótica, nada obvia en muchos casos y, por lo tanto, deberemos dejar a los ordenadores que construyan estos árboles. Veamos los pasos que seguirá un algoritmo que genera árboles de clasificación.
Los datos, ahora, serán ligeramente diferentes, para que el ejercicio tenga “más gracia”
PASO 1: Elegir un punto de corte
Lo primero que hace su computadora es “rastrear” entre las \(n\) variables explicativas disponibles. Por ejemplo, empieza por \(X_{1}\) , la discretiza (es decir, la convierte en una variable discreta tomando un tamaño predefinido para el corte, por ejemplo \(X_{1}=\{0,0.1,0.2,0.3,....,12\}\) y se va parando en cada uno de esos valores. Entonces, hace unas cuentas que vamos a ir desarrollando. Para que se vea bien la idea, vamos a suponer que, en su trabajo de rastreo, se para en \(X_{1}=3:\)
PASO 2: Plantearse cómo de bueno es ese punto de corte
Necesitamos alguna medida que nos permita analizar si el punto de corte debe ser \(X_{1}=3\) o debemos seguir buscando. Una idea, que parece bastante clara, es contabilizar qué tal discrimina, el corte en \(X_{1}=3\), los síes y los noes. La mejor discriminación sería, obviamente, que a la izquierda (es decir, \(X_{1}<3)\) hubiera sólo síes y a la derecha (\(X_{1}>3)\) hubiera sólo noes. Eso no es así (salvo en contadas ocasiones relacionadas con el problema de predicción perfecta del que hablamos en clases pasadas) y, por tanto, debemos asumir que hay cierta heterogeneidad en los grupos. A esa heterogeneidad la llamaremos caos o entropía. Cuanto más caos o entropía haya en un grupo, peor lo estará haciendo el método. Por ejemplo, en el grupo que se forma si \(X_{1}<3\) vemos que, claramente, los síes ganan a los noes. Ese grupo es poco caótico o, dirá, tendrá una entropía baja. Esto quiere decir que, si \(X_{1}<3\), nos podemos apostar el cuello a que la mejor predicción es SÍ ya que, seguramente, no nos equivocaremos. Pero ¿se atrevería a jugarse todo su dinero para predecir qué ocurrirá con el individuo si \(X_{1}>3?\) Seguramente, no. Y eso es, naturalmente, porque el grupo está más desorganizado o caótico. No sabría, entonces, si apostar al SÍ o al NO.
Entran las matemáticas: ESTO ES VOLUNTARIO, NO SE LE VA A PREGUNTAR POR ELLO DE FORMA RIGUROSA
Es el momento de plantearse cómo cuantificar el grado de caos o, como hemos dicho, entropía presenta cada grupo. Hay varias expresiones pero nosotros vamos a elegir una clásica:
\[ E\left(p_{1},p_{2},...,p_{n}\right)=\sum_{i=1}^{n}-p_{i}\log_{2}(p_{i}) \]
donde \(n\) es el número de posibles valores de la variable dependiente (en nuestro caso, 2) y \(p_{i}\) representa la frecuencia relativa de cada una de las categorías en el grupo (es decir, la probabilidad que tienen de pertenecer al grupo). Por ejemplo, en este caso, en el grupo generado por \(X_{1}<3\), tendremos:
\[ {\color{green}P(S\acute{I})=\frac{10}{12}=\frac{5}{6}},{\color{red}P(NO)=\frac{2}{12}=\frac{1}{6}} \]
de tal forma que la entropía será: \[ E_{1}=-\frac{5}{6}\log_{2}\frac{5}{6}-\frac{1}{6}\log_{2}\frac{1}{6}=0.35 \]
Por otro lado, en el grupo generado por \(X_{1}>3\), tendremos:
\[ {\color{green}P(S\acute{I})=\frac{15}{28}},{\color{red}P(NO)=\frac{13}{28}} \]
de tal forma que la entropía será: \[ E_{2}=-\frac{15}{28}\log_{2}\frac{15}{28}-\frac{13}{28}\log_{2}\frac{13}{28}=0.64 \]
Finalmente, necesitamos una medida global de caos para la participación que ha realizado el algoritmo. Para ello, obtendremos una media ponderada de la entropía \[ E=\frac{12}{40}(0.35)+\frac{28}{40}(0.64)=0.55 \]
PASO 3: decidir sobre el resultado
¿Qué tal es ese 0.55 que hemos obtenido? Pues no lo sabemos. Deberemos compararlo con otro corte. Lo que hará su ordenador es obtener las entropías asociadas a cada corte y quedarse con la que dé un valor menor. Por ejemplo, si corta en \(X_{1}=6,\) como en la figura:
de nuevo, haciendo los números, tendrá, si \(X_{1}<6\)
\[ {\color{green}P(S\acute{I})=\frac{13}{22}},{\color{red}P(NO)=\frac{9}{22}} \]
de tal forma que la entropía será: \[ E_{1}=-\frac{13}{22}\log_{2}\frac{13}{22}-\frac{9}{22}\log_{2}\frac{9}{22}=0.60 \]
Por otro lado, en el grupo generado por \(X_{1}>6\), tendremos:
\[ {\color{green}P(S\acute{I})=\frac{12}{18}=\frac{2}{3}},{\color{red}P(NO)=\frac{6}{18}=\frac{1}{3}} \]
de tal forma que la entropía será: \[ E_{2}=-\frac{2}{3}\log_{2}\frac{2}{3}-\frac{1}{3}\log_{2}\frac{1}{3}=0.55 \]
Finalmente, necesitamos una medida global de caos. Para ello, obtendremos una media ponderada:
\[ E=\frac{22}{40}(0.60)+\frac{18}{40}(0.55)=0.57 \]
que, como ve, es ligeramente peor que el anterior.
Resumiendo:
el ordenador, entonces, lo que hará es tomar nota de las diferentes entropías asociadas a cada una de las particiones en torno a \(X_{1}\). Elegirá, por tanto, el corte que menor entropía produzca. A continuación, hará lo mismo con \(X_{2}\). El árbol entonces, se empezará por la variable cuyo corte genere menor entropía global es decir, entre las entropías para cada corte de \(X_{1}\)y \(X_{2}\) elegirá el corte de la variable que menor entropía tenga. A partir de ese corte, irá eligiendo cortes sucesivos en ambas variables, de manera alternativa.
Con \(N\) variables, sucede lo mismo: del conjunto \(\{X_{1},...,X_{N}\}\) de variables, elegirá aquella que -al hacer una primera partición- devuelva una menor entropía. A partir de ahí, hará lo mismo: realizará cortes en todas las variables e irá quedándose el resultado que menor entropía proporcione en cada iteración. ¿Hasta cuándo? Necesitaremos un criterio de parada. Ese criterio lo veremos en la siguiente clase.
EJERCICIO
Busque una librería de [R] que entrene árboles de clasificación, y trate de- siguiendo la documentación- ser capaz de entrenar un árbol para predecir si un individuo tendrá problemas cardiacos dado su nivel de colesterol y edad
propuesta de solución Aquí elegimos la librería rpart pero puede elegir cualquier otra de las disponibles.
tree.v2 <-rpart(target~chol+age,data=heart, method="class",cp=0.02)
summary(tree.v2)
rpart.plot(tree.v2)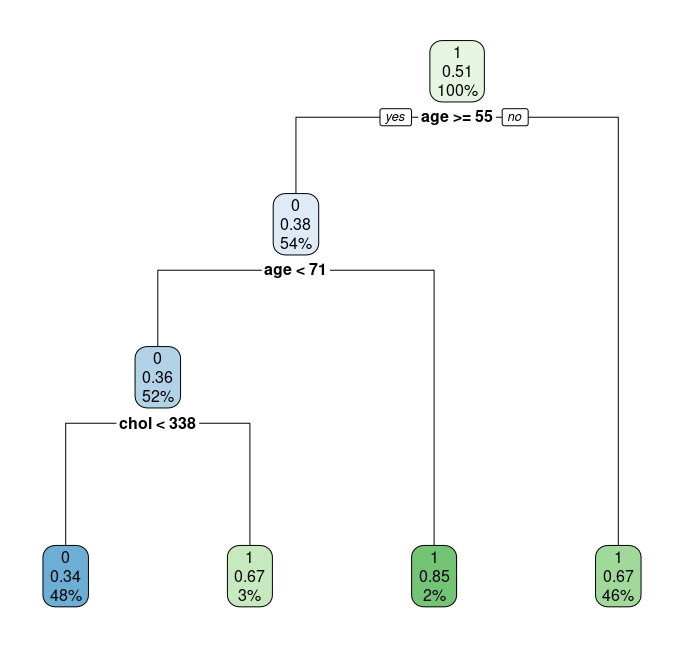
Explicamos lo que significa con detalle:
- El primer nodo tiene el 100% de la muestra (que tiene un 51% de eventos iguales a 1). Si nos quedáramos en ese nodo y no siguiéramos, deberíamos predecir que una persona, elegida al azar de la población de este estudio, tiene un 51% de probabilidades de tener un problema cardiaco.
- Si vamos al siguiente nodo: si una persona tiene menos de 55 años, entonces será clasificado como paciente con riesgo de problema cardiaco (esto es, el 67% de los individuos menores de 55 años tienen un problema cardiaco en la muestra). Si tiene más de 55 años, entonces:
- si es mayor o igual a 71 años, de nuevo se clasifica con riesgo de problema cardiaco (el 85% de los individuos mayores de 71 años lo tienen en la muestra)
(esto lo puede ver, por ejemplo, con:
- Ahora bien, si el individuo es mayor de 71 años y su colesterol es inferior a 338, entonces no se clasifica como individuo de riesgo (al revés, si su colesterol es superior a 338).
Ahora bien, la idea de este sencillo árbol es introducirnos a cómo se trabaja con ellos. Como ve, gráficamente es una herramienta atractiva de trabajo. Además, los cortes en cada una de las ramas genera “interacciones” entre variables. Lo cual ya vemos que es de interés en los problemas de la vida real, dada la complejidad de las posibles relaciones entre variables.
Clase 3. Los árboles de clasificación (elección del árbol)
Es el momento de indagar más sobre la construcción de los árboles. En general, diremos que los árboles tienden a sobreajustar la muestra. De hecho, son muy sensibles a la propia muestra, cambiando (bastante) el resultado si se añaden o eliminan observaciones. La razón es sencilla: el procedimiento que hemos contado anteriormente nos puede llevar a hacer árboles que clasifiquen perfectamente la muestra (para ello, sólo se necesita añadir ramas y más ramas). Sin embargo, esto será perjudicial cuando intentemos utilizar el propio árbol para predecir. Es por ello que parece sensato, de nuevo, utilizar validación cruzada para la elección de un árbol óptimo.
Sin embargo, lo normal es que en la propia validación cruzada se decida sobre un conjunto de árboles posibles:
- basados en subconjuntos de variables distintas
- basados en diferentes tamaños del propio árbol
Nos enfocamos en la idea segunda. Tenemos que pensar que cada rama que se añade, esta supone un “coste” puesto que hace el árbol más complejo.
Lo normal es que se utilice una medida de coste:
\[ CP(T)=R(T)+\alpha T \] con \(\alpha>0\). \(R(T)\) es una medida de error de clasificación para el árbol con T ramas. Por otro lado, se penaliza el número de ramas (T) mediante un parámetro \(\alpha\). La librería rpart no permite que el usuario proponga un valor, sino que lo estima internamente.
AL acto de elegir el número de ramas que irán en el árbol se le denomina podado o pruning.
Por ejemplo, aquí puede ver el resultado para el árbol de la FIG6 de la clase anterior
> summary(tree.v2)
Call:
rpart(formula = target ~ chol + age, data = heart, method = "class",
cp = 0.02)
n= 1025
CP nsplit rel error xerror xstd
1 0.2665 0 1.000 1.000 0.0321
2 0.0281 1 0.733 0.733 0.0307
3 0.0220 2 0.705 0.723 0.0306
4 0.0200 3 0.683 0.709 0.0305Si se fija en la función que ha generado este árbol, en “control” se puso que CP debía llegar a 0.02, como mucho. Al llegar ahí se para. Se ha fijado 0.02 para que el árbol no fuera muy “grande”. Verá que si no pone nada, el árbol sale más grande (R tiene la orden interna de usar 0.01) como parámetro por defecto. En este caso, cuando se detiene el algoritmo lo hace en “nsplit=3”, esto es, hace tres particiones (age>=55, age<71,chol>338)
De esta forma, usted puede jugar con dichos parámetros de control en la validación cruzada. A continuación le mostramos una posible idea:
- Como puntos importantes, creamos un vector con diferentes parámetros de control (es decir, valores umbral para podar el árbol)
- Para ello, tenemos que tener dos bucles: uno para almacenar errores y otro para probar distintos parámetros de control
- Por otro lado, elegimos una medida de error (en este caso, ele elemento 1,2 de la matriz de confusión-como se ve en la última línea de código- es decir, predecir que el individuo tiene anemia y que, en realidad, no la tenga )
error<-mat.or.vec(50, 4) #creamos un vector que almacenará 50 errores
cpv<-c(0.001,0.01,0.02,0.1) #creamos un vector que contiene los diferentes valores del parámetro de control
for(i in 1:50){ #Iniciamos los subíndices: este es el de la iteración
for (j in 1:4){ #este es el subíndice del parámetro de control
random <- sample(1:nrow(heart), size = floor(.7*nrow(heart))) # Elegimos la muestra de entrenamiento al azar
train<-heart[random,]
test <-heart[-random, ] #por lo que la muestra de test es la contraria
tree.v1 <-rpart(target~age+chol+trestbps+fbs,data=train,control = rpart.control(cp = cpv[j],minsplit=10), method="class") #permitimos que el parámetro de control cp, varíe y minsplit es el número mínimo de observaciones en un nodo
tree.pred <- predict(tree.v1, newdata = test, type = "class") #predecimos con la muestra «test»
xt1<-table(tree.pred, test$target) #obtenemos la tabla de confusión...
error[i,j]<-xt1[2,1]/length(tree.pred) #...y de la tabla seleccionamos la(s) magnitud(es) que nos interesen
}}Atendiendo al gráfico de la FIG1, se puede intuir que el árbol con cp=0.001 sería el que proporciona un menor error de FALSOS POSITIVOS.
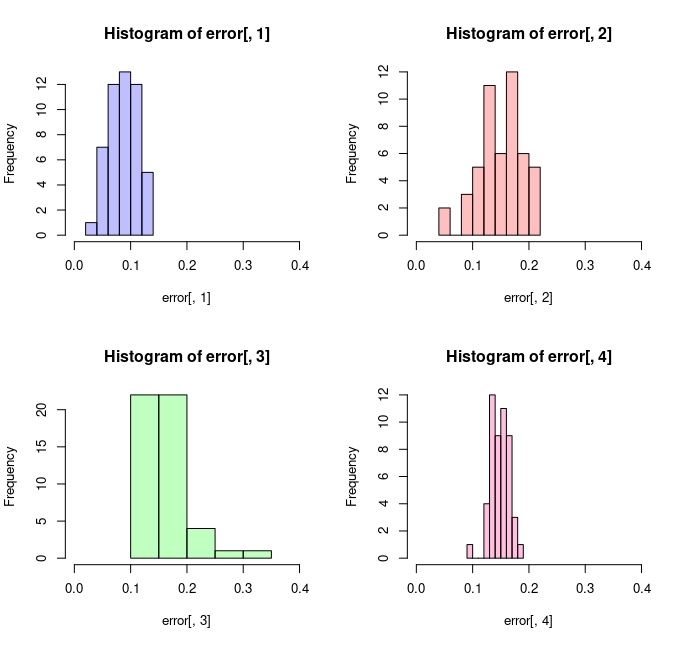
Puede generar estos errores usando este script
p1 <- hist(error[,1])
p2 <- hist(error[,2])
p3 <- hist(error[,3])
p4 <- hist(error[,4])
par(mfrow=c(2,2))
plot( p1, col=rgb(0,0,1,1/4), xlim=c(0,0.4))
plot( p2, col=rgb(1,0,0,1/4), xlim=c(0,0.4))
plot( p3, col=rgb(0,1,0,1/4), xlim=c(0,0.4))
plot( p4, col=rgb(1,0,1/2,1/4), xlim=c(0,0.4)) Ahora bien, un problema que presentan los árboles es su inestabilidad. Pruebe a entrenar los mismos árboles de estos ejercicios eliminando una parte de la muestra. Puede que los resultados, y el propio árbol, sean muy distintos.
Otro problema puede ser la “interpretabilidad” del resultado. Por ejemplo, el árbol “ganador” con cp=0.001 sería este
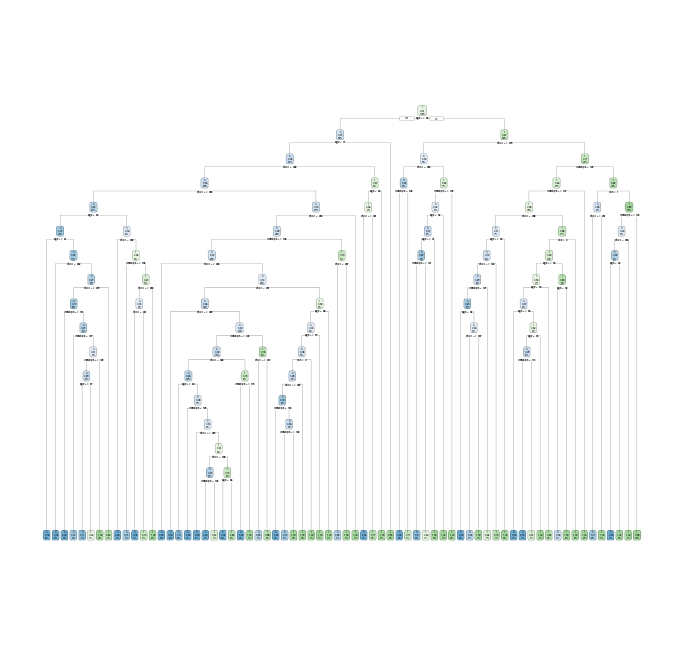¿qué puede decir del efecto del colesterol sobre la enfermedad cardiaca?
Al final del bloque, en un apéndice, discutiremos algo más sobre ello. La clave: buscar la interpretabilidad
Los árboles de regresión
Por otra parte, si la variable que quiere predecir es continua (o discreta, pero no cualitativa) podrá ajustar un árbol de regresión. La idea de su mecanismo es similar a lo que acaba de ver. Supongamos que tenemos dos variables candidatas (por ejemplo, \(x_1\),\(x_2\)) para explicar una tercera (\(y\)). Podemos visualizar los datos disponibles en la FIG 3
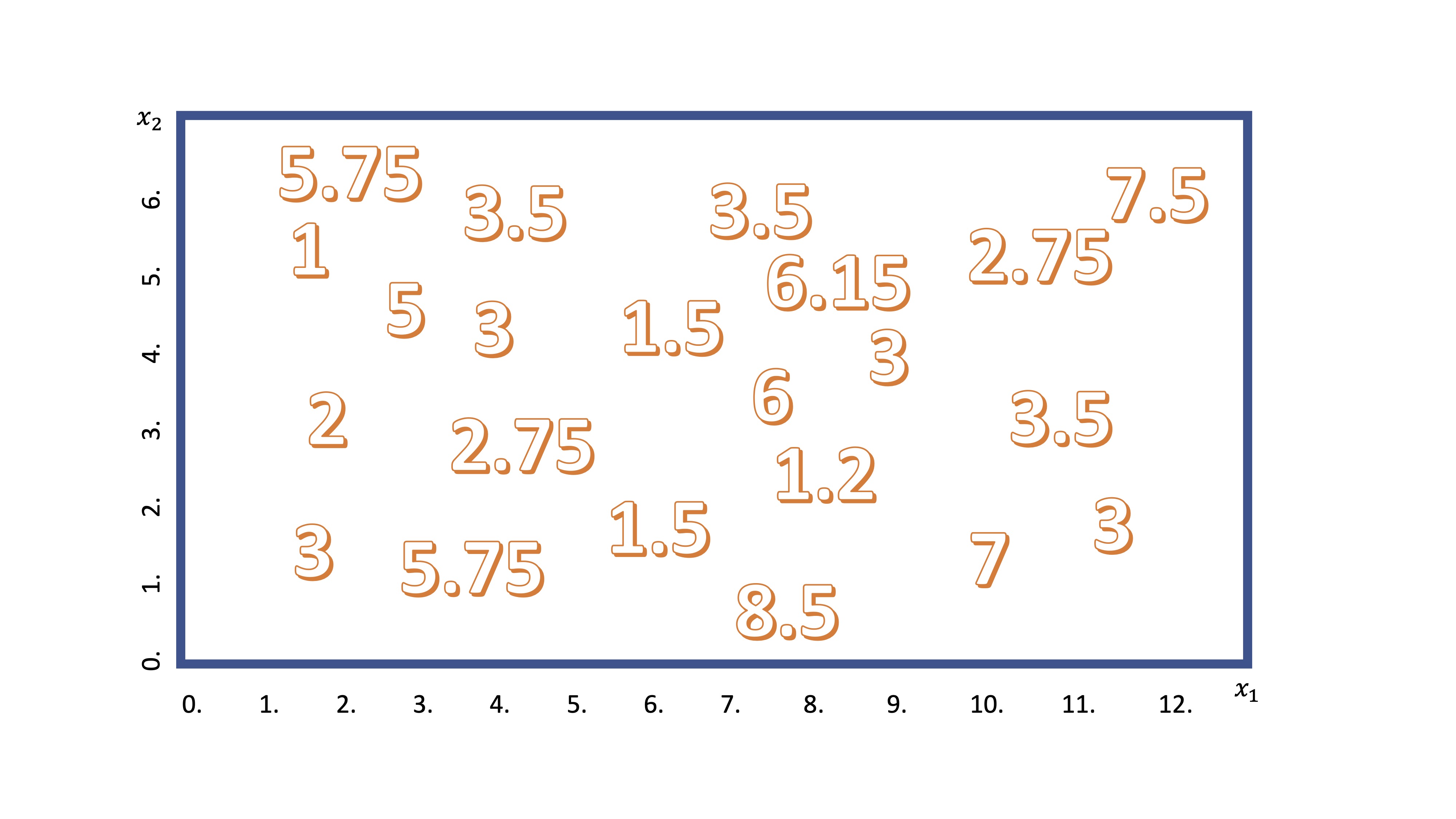
Ahora, como ya sabe, el algoritmo empezará a realizar un corte en una de las variables. De manera secuencial, discretizará la variable \(x_1\), en porciones pequeñas (por ejemplo, \(x_1=[0,0.5,1,1.5,2,....,12])\) y realizará cortes para ver cuál es mejor. Imagine que se para en el corte \(x_1=5\), entonces, tendrá algo así:
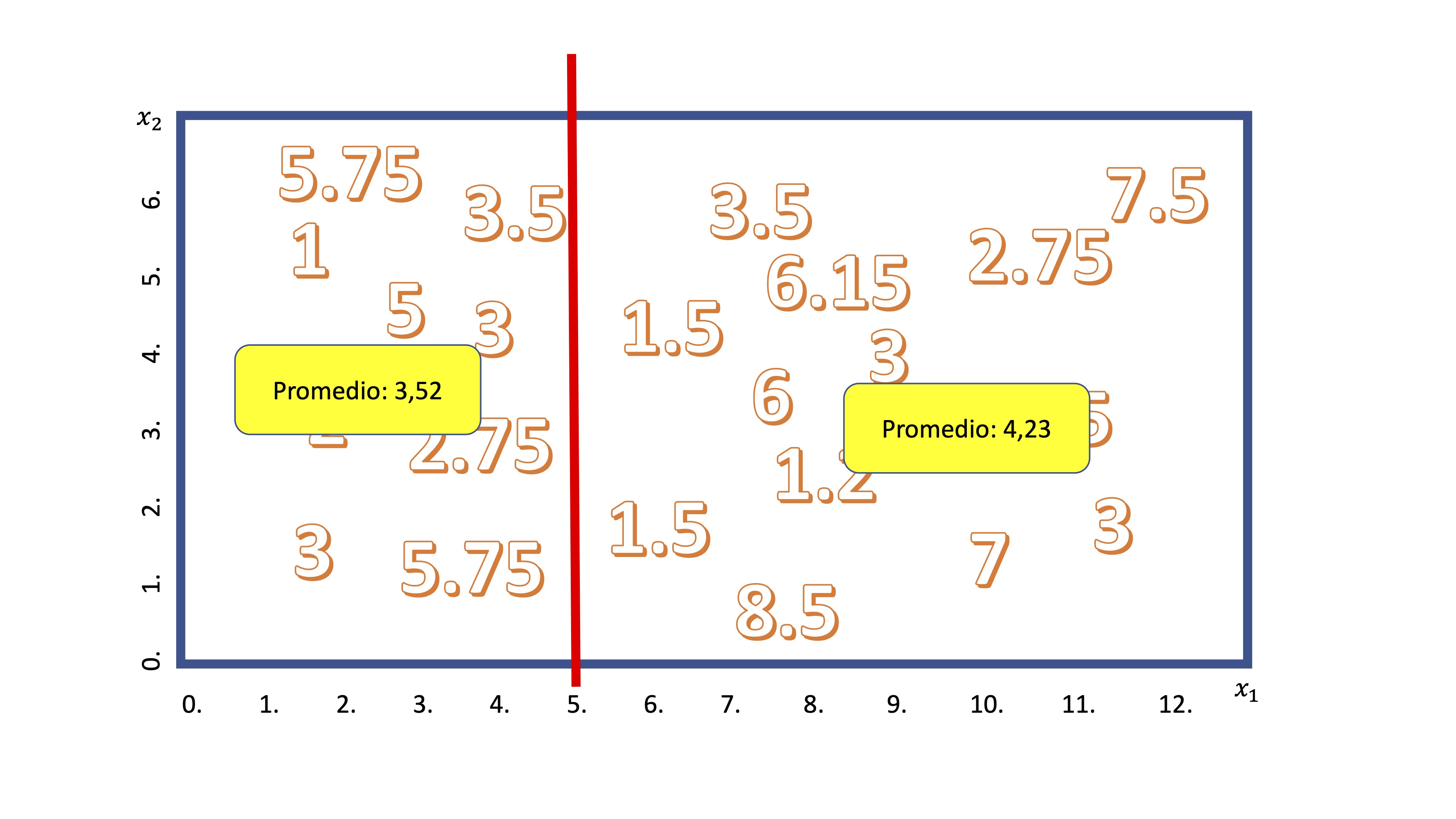Como ahora el promedio de la variable \(y\) tiene sentido, el algoritmo calcula - para cada grupo- la media condicionada al corte. En este caso, diremos que si \(x_1<5\), entonces el valor esperado para \(y\) es 3.52 y, en caso contrario es 4.23.
Ahora debemos preguntarnos si el corte es “bueno”. Para ello, el algoritmo calcula el Error cuadrático Medio. Para el grupo \(x_1<5\) será \(ECM_1=\frac{(5.75-3,52)^2+(3.5-3.52)^2+....+(5.75-3,52)^2}{9}\) y lo mismo para el otro grupo \(ECM_2=\frac{(3.5-4,23)^2+(6.15-4.23)^2+....+(3-4,23)^2}{13}\). La suma de ambos será el error cuadrático de la partición. Buscará aquella partición que minimice esta suma. Luego, alternatá entre todas las variables explicativas y elegirá empezar a cortar el árbol por aquella que minimice dicha suma. De la misma manera, irá alternando entre las variables de acuerdo con algún criterio de parada, de nuevo, relacionado con el parámetro de control (que regula cuántas ramas tendrá el árbol).
El siguiente esquema le permite ajustar un árbol de regresión. Tendrá que poner en “method” la palabra anova que significa “análisis de varianza”. Esto infica a la librería rpart que ha de entrenar un árbol con variable explicada continua.
rating<-SIMPSONS_FINAL$rating_imdb
BART<-SIMPSONS_FINAL$Bart
HOMER<-SIMPSONS_FINAL$Homer
arbol_simpsons<- rpart(formula = rating ~BART+HOMER, method = "anova", control=list(cp = 0.01, xval = 10))
rpart.plot(arbol_simpsons)Obtendrá algo así,
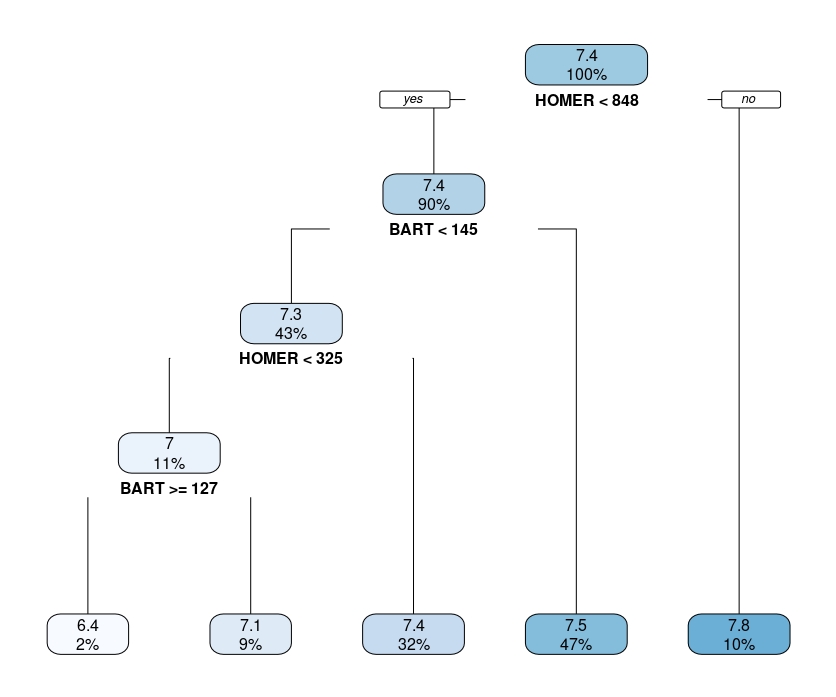
que, recuerde, deberá interpretar como el promedio condicional. Por ejemplo, el último nodo de la derecha quiere decir que cuando Homer tiene más de 848 líneas de guión los episodios tienen, de media un 7.8. Y eso pasa en el 10% de la muestra.
Clase 4. Análisis discriminante lineal
Seguimos con la propuesta de tratar de encontrar modelos que nos permitan ser capaces de predecir una variable dicotómica (\(y=\{0,1\}\)) a través de un conjunto de variables predictoras: \(x_1,x_2,...,x_k\). Es una técnica sencilla, puesto que en su denominación incluye la palabra “lineal” y, por tanto, nos lleva a buscar “rectas, planos, etc…” que mejor separan los “0” y los “1” de la variable \(y\), condicionada por el valor de las variables \(x_1,....,x_k\). Antes de presentar la técnica, vamos a hablar de ciertas ideas de interés que, además, nos servirán más adelante.
Primeramente, ¿Cómo reducimos información en dos o más variables? Esto está muy relacionado con la idea de “proyección”. Aunque, para entenderlo, vamos a empezar sin hacer una proyección: pero la idea es muy similar.
Imaginemos que tenemos varios individuos y hemos medido dos variables ¿Cómo transformamos la información de cada individuo, que-en este caso- está en dos dimensiones a una nueva información que esté en una dimensión? Esto ya lo ha hecho, por ejemplo, cuando calcula un promedio. Imagine que las variables 1 y 2 están medidas en las mismas unidades y que, por tanto, tiene sentido obtener un promedio (por ejemplo, son los saldos de dos cuentas corrientes de cada individuo en miles de euros). El promedio de dos variables \(x,y\) consiste en \(\frac{x+y}{2}\), es decir
\[ nueva\:variable_{i}=0.5x_{i}+0.5y{}_{i}\:\:i=1,..,6 \]
| Id | \(x\) | \(y\) | nueva variable |
|---|---|---|---|
| 1 | 4.5 | 3 | 3.75 |
| 2 | 1 | -1 | 0 |
| 3 | -1 | -2 | -1.5 |
| 4 | -3 | -1.5 | -2.25 |
| 5 | -1.5 | 1.5 | 0 |
| 6 | 0 | 0 | 0 |
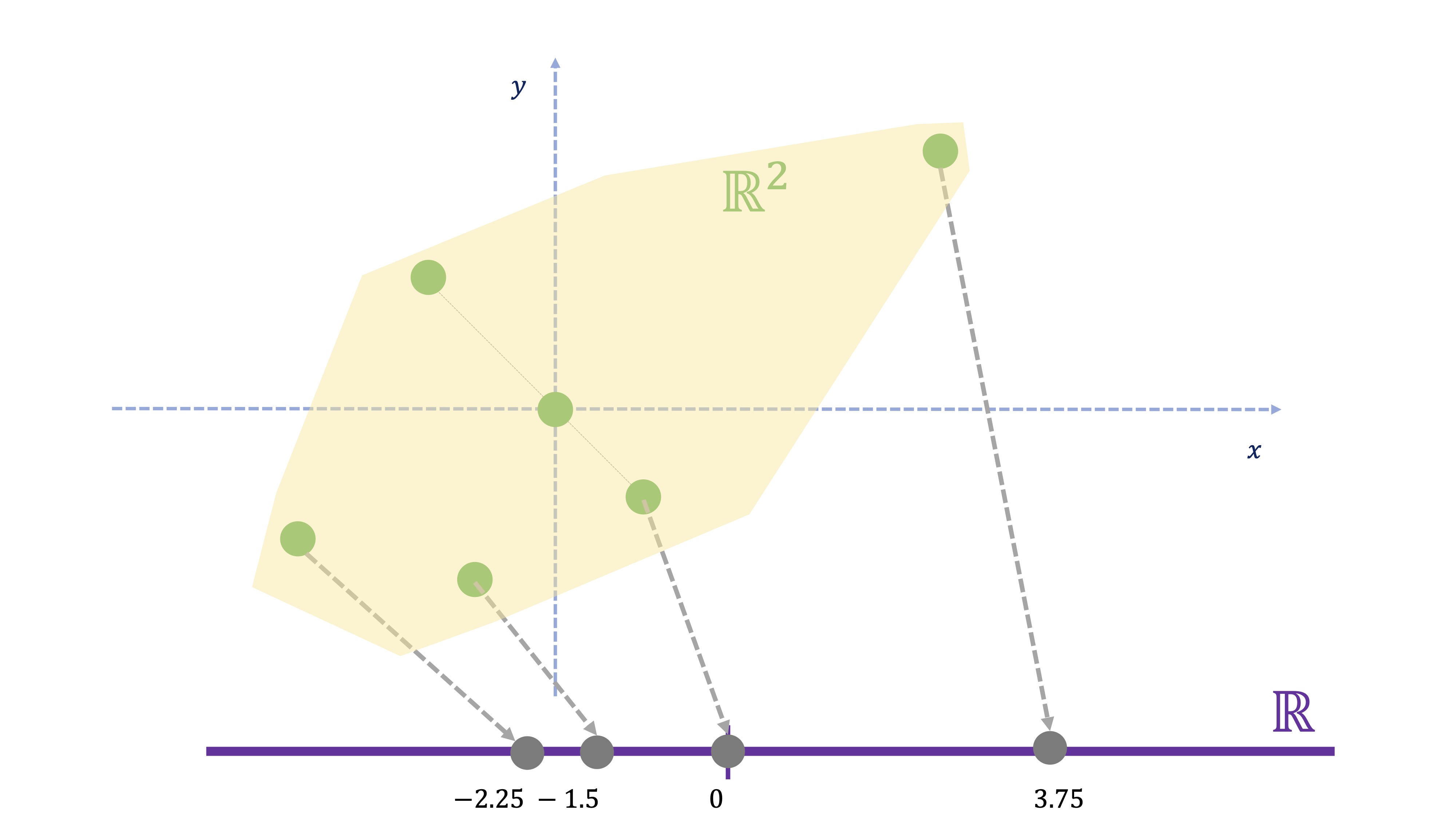
Si se da cuenta (FIG 1), la nueva variable se representa sólo sobre un eje, ya que hemos resumido la información de las dos variables de cada individuo al promedio. Es decir: hemos reducido un punto en \(\mathbb{R}^{2}\) (por ejemplo \((4.5,3)\) a otro punto en \(\mathbb{R}\) (es decir, el par \((4.5,3)\) se convierte en \(3.75\) . Ahora bien:
- ¿Y si las variables están relacionadas pero medidas en unidades distintas (años, euros, etc…)? El promedio no tiene sentido
- ¿Cómo se proyecta en realidad?
Vayamos al caso que nos preocupa. Empecemos con una medición, por ejemplo. Disponemos del saldo en cuenta de un conjunto de individuos. Pero disponemos, además, de si en el pasado estos individuos devolvieron o no un crédito. Nos preguntamos si, dada una cantidad de saldo, otros individuos que no pertenezcan a la muestra devolverán (\(y=1\)) o no (\(y=0\)) el préstamo.
| Id | \(x\) | \(y\) |
|---|---|---|
| 1 | 4.5 | 1 |
| 2 | 6.5 | 1 |
| 3 | 5 | 1 |
| 4 | 3 | 1 |
| 5 | 2 | 0 |
| 6 | 1 | 1 |
| 7 | 1.5 | 0 |
| 8 | -1 | 0 |
| 9 | -2 | 0 |
| 10 | -5.5 | 0 |
Gráficamente, podemos ver cómo se organizan la devolución o no del crédito de en la FIG2
Como vemos, para valores de \(x>3\) está claro que podemos clasificar al individuo como un probable cliente que devolverá el crédito. Si \(x<0\), deberíamos pensar que es improbable que devuelva el crédito. Pero ¿qué ocurre para \(x\in(0,3)\)? Ahí puede ver cierta confusión, puesto que algunos individuos, en ese intervalo, han devuelto el crédito y otros, no. ¿Seremos capaces de predecir con mayor precisión? La técnica de análisis lineal discriminante nace con ese objetivo. Para verlo más claramente, añadiremos una nueva variable a nuestro análisis: \(x_2\), que es la edad del individuo.
| Id | \(x_1\) | \(x_2\) | \(y\) |
|---|---|---|---|
| 1 | 4.5 | 30 | 1 |
| 2 | 6.5 | 35 | 1 |
| 3 | 5 | 30 | 1 |
| 4 | 3 | 40 | 1 |
| 5 | 2 | 55 | 0 |
| 6 | 1 | 30 | 1 |
| 7 | 1.5 | 60 | 0 |
| 8 | -1 | 65 | 0 |
| 9 | -2 | 70 | 0 |
| 10 | -5.5 | 75 | 0 |
y nos encontramos con algo así (FIG3)
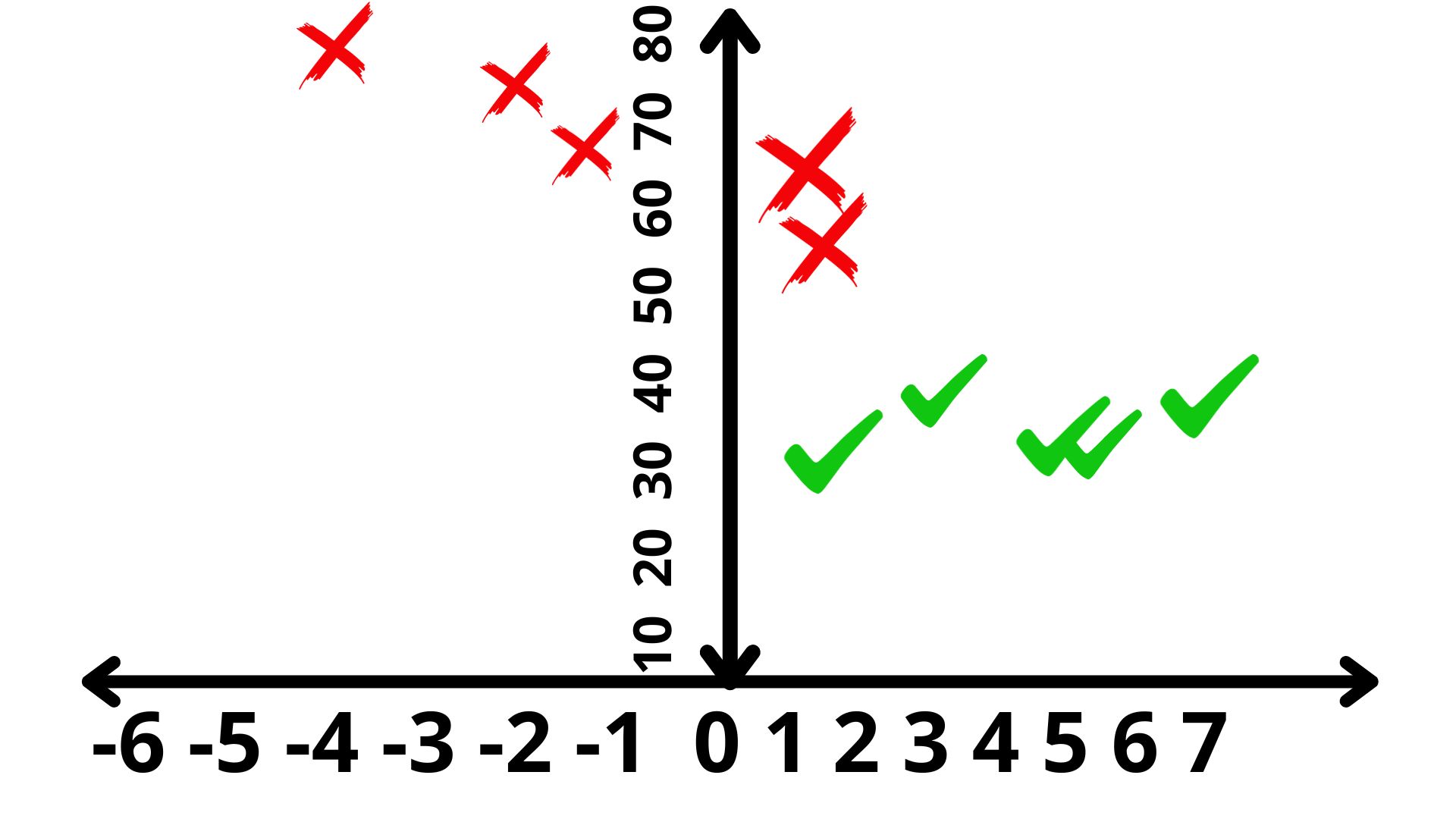
Parece que detectamos algún patrón: gente mayor de 50 años y con saldo pequeño (o negativo) no devolverá el crédito. De hecho, mentalmente, podemos trazar una recta que va a tener mucho interés a continuación. Veamos en la FIG 4:
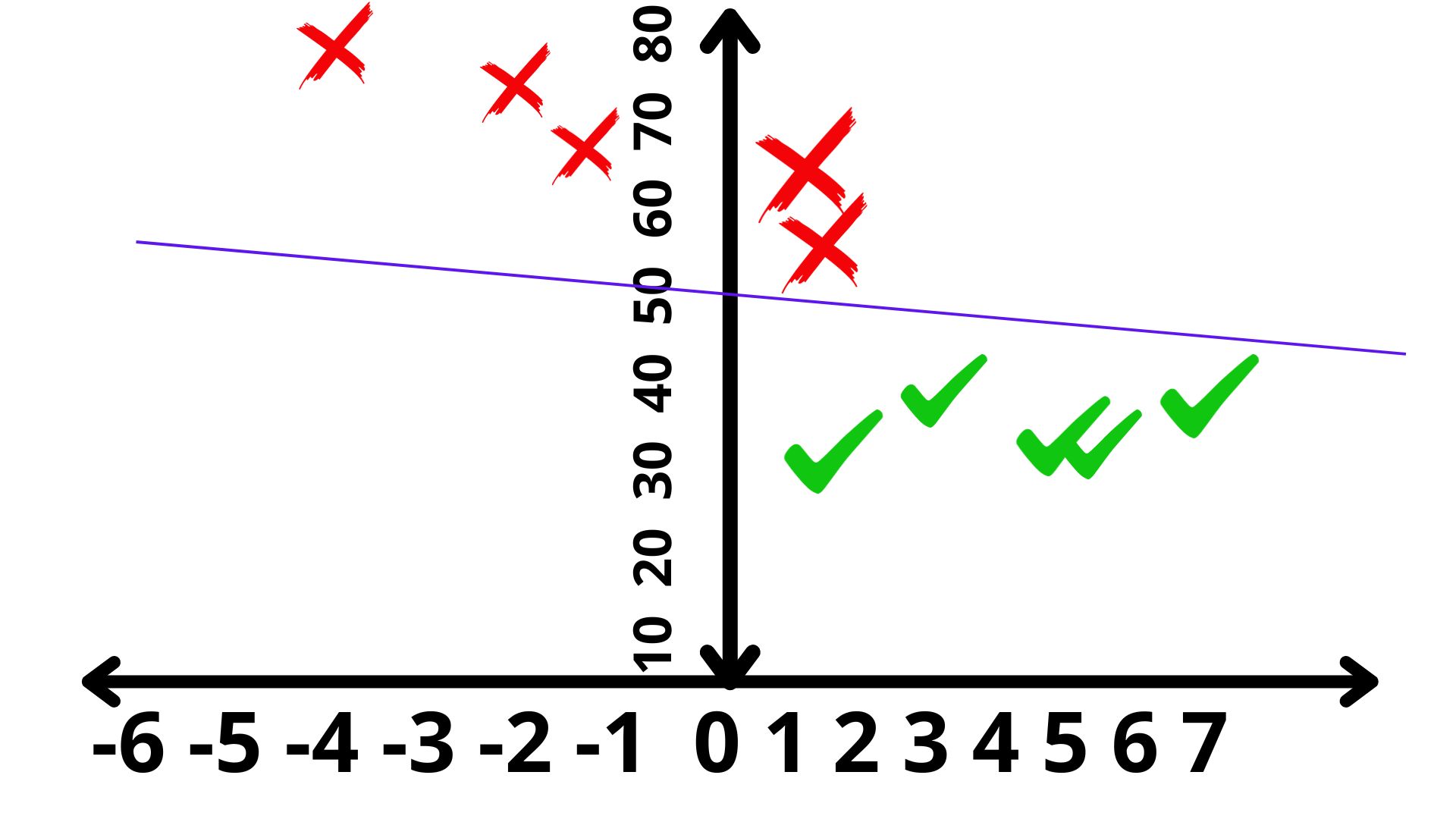Esta primera recta trata de separar entre los que pagan y los que no. Usando la idea de reducir la información en 2 dimensiones a una dimensión-como hicimos antes, podemos proyectar los datos sobre la recta (la proyección, en este caso consiste en trazar una línea desde el punto a la recta tal formen un ángulo recto)
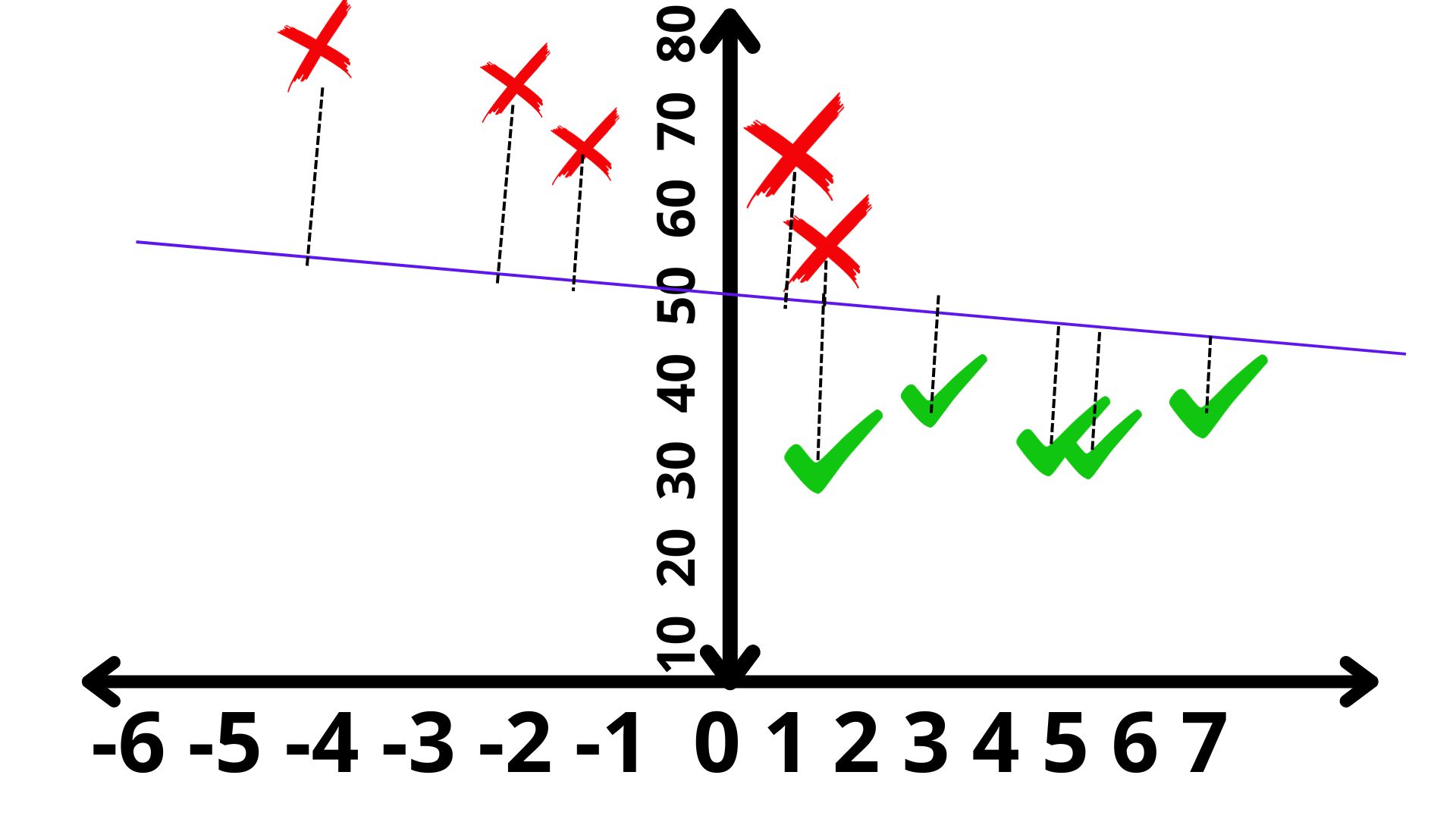Ahora dibujamos sobre nuestra recta las proyecciones de cada uno de los casos y pensamos qué tal discrimina a través de la proyección de los puntos sobre dicha recta (FIG6)
.jpg)
No sé, quizás vuelva a encontrarse una parte algo confusa, ¿no?
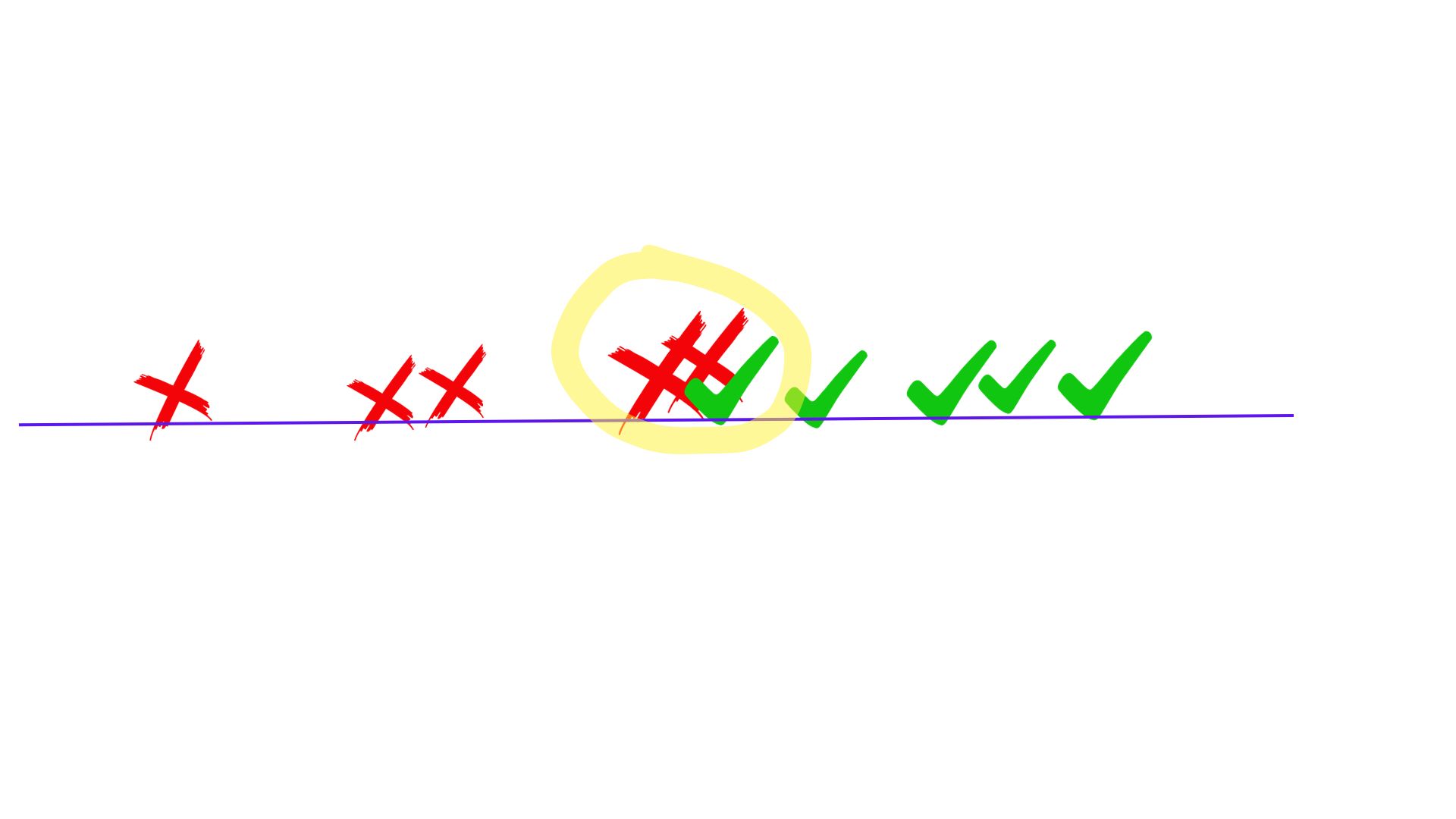
Sin saber muy bien qué unidades tiene el eje donde representamos los puntos, volvemos a ver que “hacia la derecha” es más probable que el crédito se devuelva. Hacia la izquierda, no. Pero ¿qué pasa en el centro? Nos preguntamos, entonces, ¿hay alguna otra forma de buscar una proyección mejor? Veamos esta (FIG7)
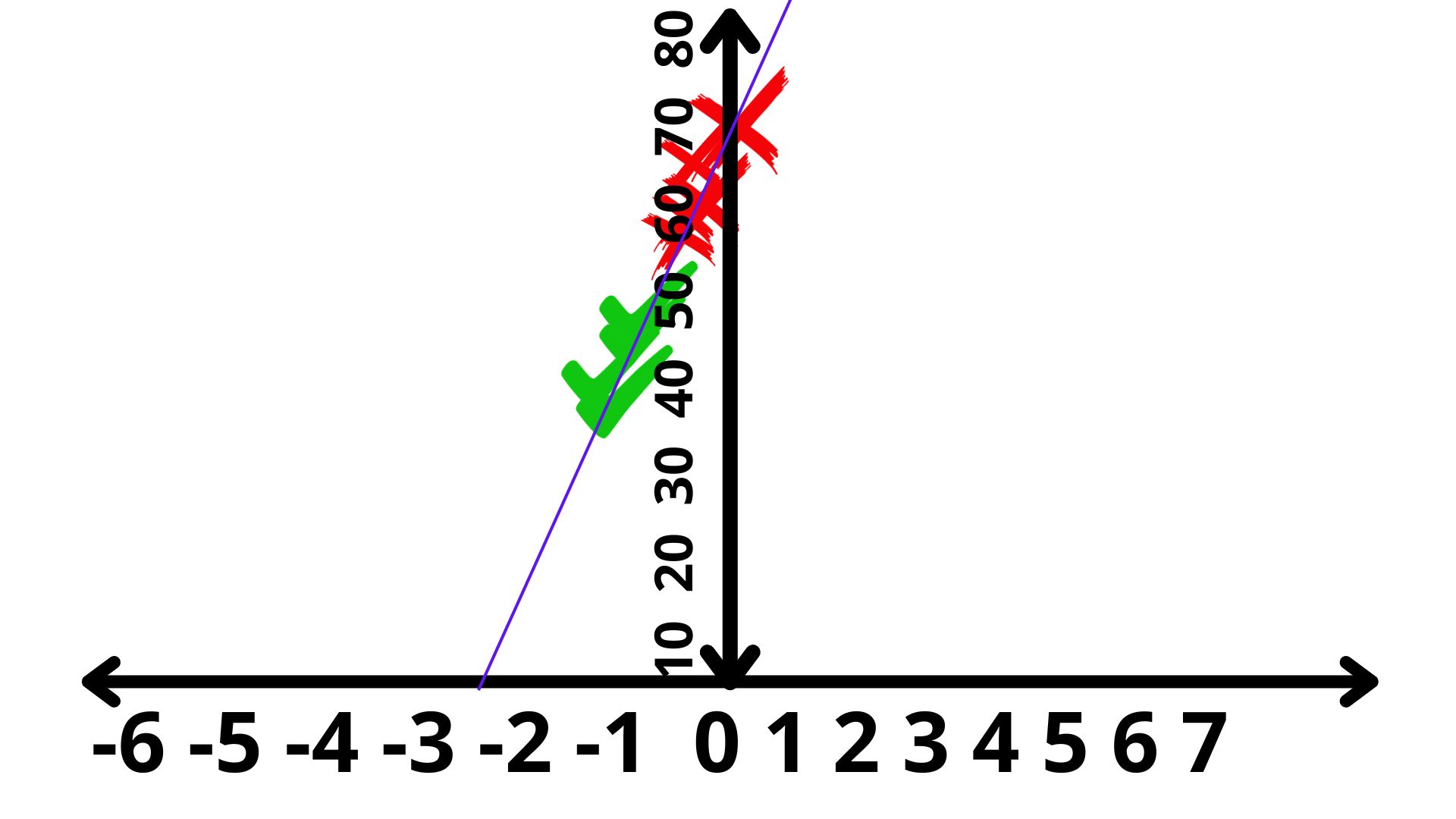Si la rotamos, podemos ver mejor cómo esta recta cumple con su cometido: nos agrupa la gente que paga, por un lado, y la que no paga por otro:
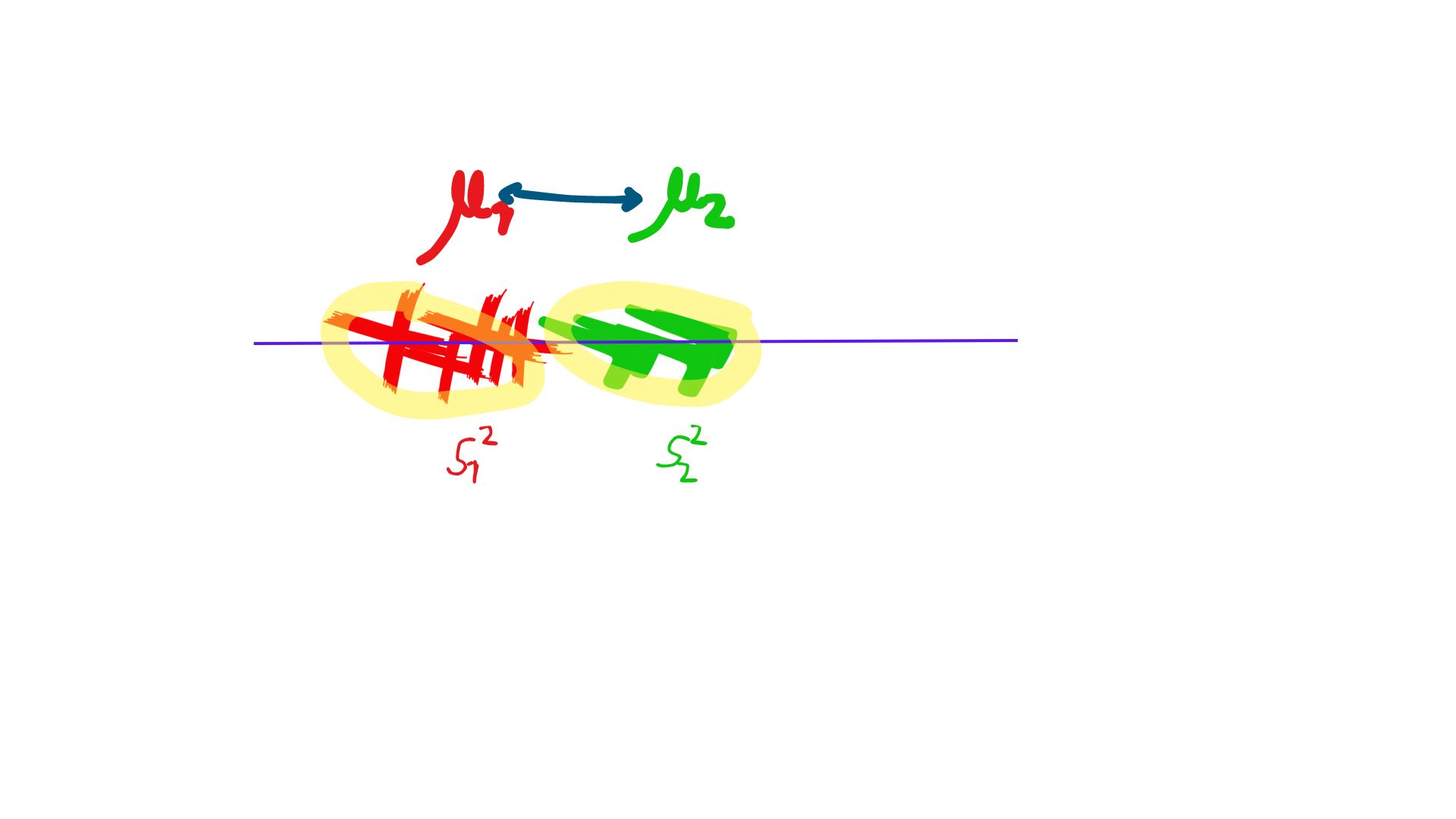Para ello, ha buscado lo siguiente:
- una función que maximice las distancias entre las medias de ambos grupos
- Pero que, a la vez, minimice las varianzas de los grupos: esto es, que las observaciones estén concentradas a las medias de estos.
Pregunta: ¿Es la única función que cumple con esas ideas? BUSQUE MÁS
Matemáticamente, este problema de optimización es interesante y muy elegante. Sin embargo, nos lo vamos a saltar siempre y cuando haya entendido la idea. Veamos cómo [R] nos busca la función
x1<-c(4.5,6.5,5,3,2,1,1.5,-1,-2,-5.5)
x2<-c(30,35,30,40,55,30,60,65,70,75)
y<-c(1,1,1,1,0,1,0,0,0,0)
DATOS = data.frame(y=y,x1=x1,x2=x2) #almacenamos los datos en un "dataframe"
qplot(x1, x2, colour =y, data = DATOS) #lo dibujamos para ver que cuadra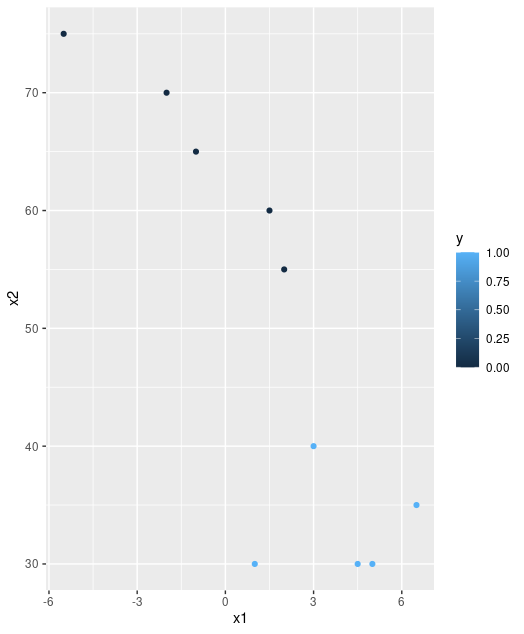
library(MASS)
library(klaR)
linear <- lda(y~x1+x2, DATOS)
linear
Group means:
x1 x2
0 -1 65
1 4 33
Coefficients of linear discriminants:
LD1
x1 -0.1893061
x2 -0.1966936Donde, en este caso, nos proporciona información relevante: El grupo de gente que no paga tiene un valor promedio de deuda de -1 y una edad promedio de 65 años. La gente que paga tiene un valor promedio en la cuenta corriente de 4 y 33 años. Por otro lado, nos permite obtener el valor del “discriminante” de tal forma que, si este es mayor que cero, entonces se clasificará al individuo como un 1 y viceversa
De hecho,la función que obtenemos es
\[ discriminante_i=-0.18\times (cuenta_i-1.5)-0.19\times (edad_i-49) \]
donde la variable cuenta y edad están escritas en desviaciones a sus medias. Si el discriminante es mayor que cero, entonces se clasificará la observación con un 1. En caso contrario, como un 0. Así lo calcula [R]
library(MASS)
library(klaR)
p<-predict(linear,DATOS)
$x
LD1
1 3.169261
2 1.807180
3 3.074608
4 1.486284
5 -1.274815
6 3.831832
7 -2.163630
8 -2.673833
9 -3.467995
10 -3.788892y tiene una interesante representación gráfica para ver la calidad de la discriminación
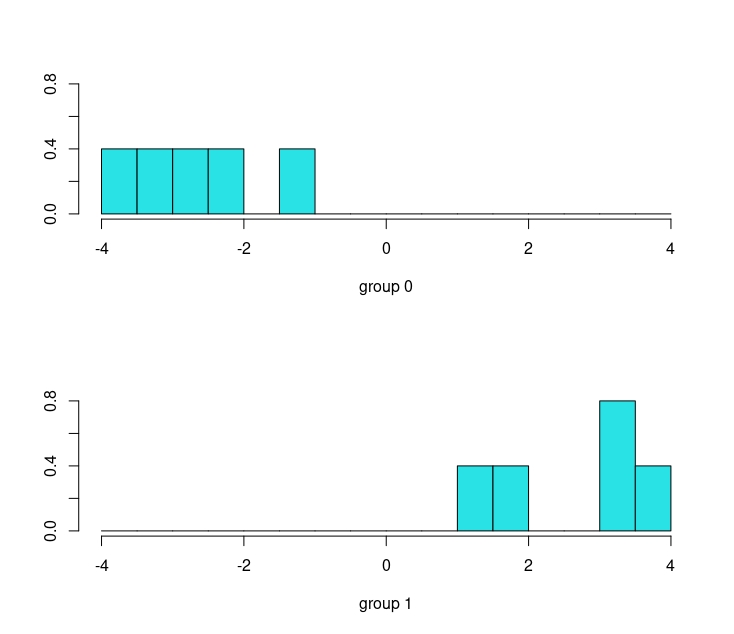
OJO
Para que el método funcione, previamente la función “lda” escala/estandariza las variables. Veamos, paso a paso, cómo obtener las predicciones.
De esta forma, la función que nos permite obtener el discriminante es
\[ discriminante_i=-0.18\times (cuenta_i-1.5)-0.19\times (edad_i-49) \]
Como el primer individuo tiene un saldo de 4.5 y una edad de 30 años
\[ discriminante_1=-0.1893\times 3-0.1966(-19)= 3.17, \]
que, como vimos anteriormente, es el valor del discriminante del primer sujeto. Otro resultado de interés que proporciona el LDA es la probabilidad de pertenencia a cada grupo, llamada posterior (la calcula vía el Teorema de Bayes, pero omitiremos los detalles)
> p
$class
[1] 1 1 1 1 0 1 0 0 0 0
Levels: 0 1
$posterior
0 1
1 4.360264e-08 1.000000e+00
2 6.351331e-05 9.999365e-01
3 7.233372e-08 9.999999e-01
4 3.531911e-04 9.996468e-01
5 9.989065e-01 1.093493e-03
6 1.261003e-09 1.000000e+00
7 9.999906e-01 9.441650e-06
8 9.999994e-01 6.167722e-07
9 1.000000e+00 8.824984e-09
10 1.000000e+00 1.586511e-09En este ejemplo sencillo, además, podemos obtener una visualización de la recta que separa ambos grupos (no se parece a las que hemos hecho antes a mano alzada, pero está cumple con criterios óptimos)
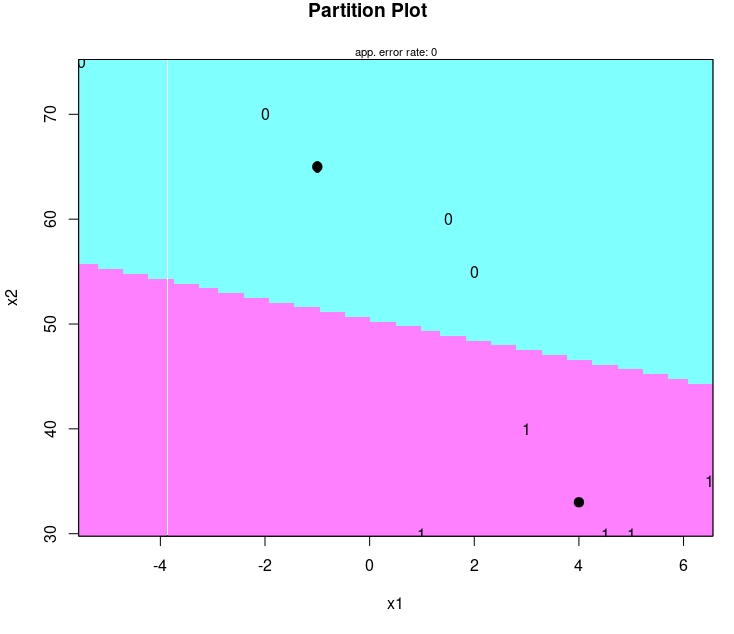Fíjate que la recta que divide ambos casos puedes obtenerla de aquí:
\[ discriminante_i=-0.18\times (cuenta_i-1.5)-0.19\times (edad_i-49) \]
el punto donde discrimina
\[ 0=-0.18\times (cuenta_i-1.5)-0.19\times (edad_i-49) \]
es decir
\[ 0=-0.18\times cuenta_i-0.19\times Edad_i+9.58 \]
Finalmente
\[ 9.58=0.18\times cuenta_i+ 0.19\times Edad_i \] Si despejas, como en la FIG 11,
\[ \frac{9.58-0.18\times cuenta_i}{0.19}= Edad_i \]
te sale, aproximadamente,la recta que delimita los semiplanos azul y rosa.
###Ejercicio resuelto {-} ¿Cómo funciona con los datos de “Heart”?
Empezaremos tratando de predecir la variable “target” usando la edad y el colesterol
linear <- lda(target~age+chol, heart)
p<-predict(linear,heart)
Prior probabilities of groups:
0 1
0.4868293 0.5131707
Group means:
age chol
0 56.56914 251.2926
1 52.40875 240.9791
Coefficients of linear discriminants:
LD1
age -0.105136938
chol -0.004418475Como vemos, no parece ser un buen predictor:
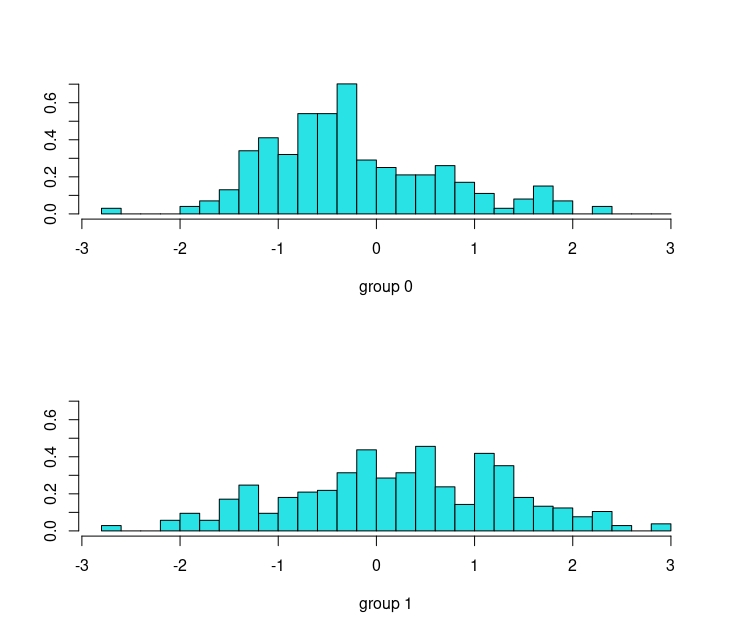De hecho,haciendo el mismo dibujo que antes, vemos que no parece muy exitoso:
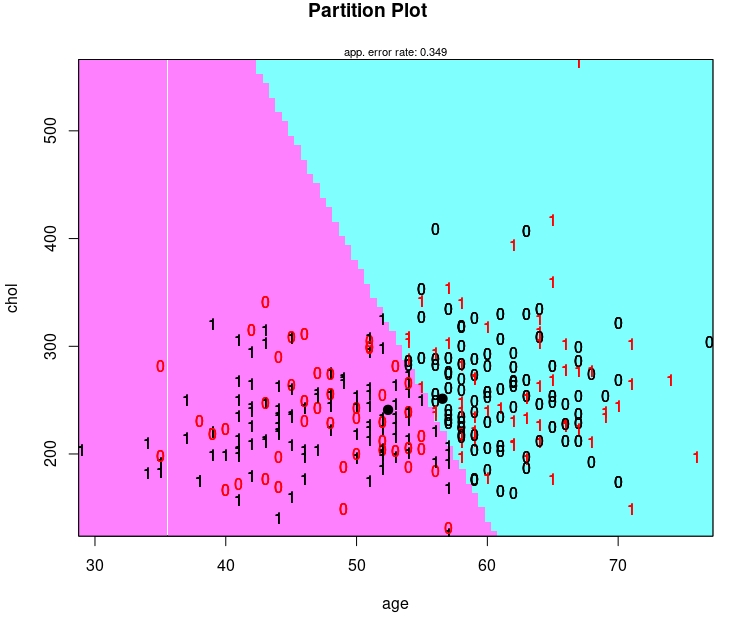
- Escribe la ecuación del discriminante lineal. ¿Qué variable tiene más impacto en la discriminación a juzgar por los coeficientes?
- Veamos ahora qué ocurre si introducimos dos variables más: las pulsaciones (thalach) y la tensión en resposo (restbps) ¿Mejora la habilidad de separar entre grupos?
- Haz una comparación con el modelo de regresión logística y el de árbol de clasificación ¿Quién lo hace mejor? Puedes usar validación cruzada y alguna medida de error que te parezca sensata.
Clase 5. “K” vecinos (KNN)
El algoritmo de los “k-vecinos”, también conocido como KNN, es un clasificador de aprendizaje supervisado no paramétrico que utiliza la idea de “proximidad” para realizar clasificaciones o predicciones en subconjuntos de datos “parecidos”: dime con quién andas y te diré quién eres. Ahora, explico cada idea de las que acabo de lanzar.
- Clasificador: nos va a ayudar a predecir la clase más probable de un ítem dados los valores de otro conjunto de predictores (esto ya lo hace un logit, lo hace un árbol, lo hace LDA. Luego, no diga que no aprende cosas en “Minería”)
- Aprendizaje supervisado: hasta ahora sólo hemos aprendido técnicas de aprendizaje supervisado. Es decir, usted conoce el valor del target y trata de entrenar algoritmos que lo puedan predecir. ¿Por qué se llama supervisado? Pues porque al saber el valor del target, puede también conocer qué error comete en el entrenamiento y en la validación. Puede, entonces, “supervisar” el funcionamiento de cada algoritmo. ¿Qué será el no supervisado? En la clase que viene lo sabrá.
- No paramétrico: Se basa en no tener que asumir ninguna hipótesis acerca de una función que relaciona las variables predictoras con el “target”. Por ejemplo, un logit es un método paramétrico porque, a partir de la función logística (que hace de unión entre el target y las predictoras), usted estima valores a los parámetros asociados a dicha función. Un árbol, como verá es no paramétrico. ¿LDA? Piense un momento: sí es paramétrico.
Sigamos…
Aunque puede utilizarse tanto para problemas de regresión como de clasificación, KNN se usa típicamente como un algoritmo de clasificación.
Ejemplo: Tenemos datos de una variable objetivo que toma valores \(\{0,1\}\) y dos variables continuas, \(x_1, x_2\).
Surge la siguiente pregunta:
- Llega una nueva observación, el punto \(A(3.2,3.9)\) : ¿cómo la predigo? ¿Como un 0, como un 1? mire la FIG 2 y piense en diferentes posibilidades.
La propuesta de KNN es fijarse en “K” vecinos más cercanos y quedarse con la clase “más popular”. Es decir, suponga que elige compararse con \(K=5\) vecinos. Deberá buscar las 5 observaciones que están más cerca y, entonces, contar cuántas pertenecen a cada clase. La nueva observación,A, recibirá, entonces, la etiqueta mayoritaria: un 0.
De aquí nos surgen otras dos preguntas:
- P.1: ¿Cómo se miden los puntos que están más cerca de otro?
- P.2: ¿Cuánto debe valer “K”?
Para la primera pregunta hay una solución rápida: use una medida de distancia. Dese cuenta de que aquí tiene que elegir una medida de distancia entre puntos en \(n\) dimensiones (donde \(n\) es el número de variables predictoras que tiene). Una manera de medir dicha distancia es mediante la norma euclídea, que es una generalización del Teorema de Pitágoras:
Por ejemplo, si tenemos dos puntos \(A(5,3)\) y \(B(1,4)\), la distancia entre ambos puntos (Distancia/Norma Euclídea) se puede calcular como:
\(d(A,B)=\sqrt{(5-1)^2+(3-4)^2}=\sqrt{17}\)
Dibuje los puntos y dese cuenta de que está calculando la hipotenusa de un triángulo rectángulo.
No importa el número de coordenadas que tenga el punto. Si quiero calcular la distancia entre el punto \(A(1,2,3,7,-2)\) y el punto \(B(0,1,1,2,5)\), deberé aplicar
\(d(A,B)=\sqrt{(1-0)^2+(2-1)^2+(3-1)^2+(7-2)^2+(-2-5)^2}\)
El funcionamiento de KNN se puede explicar según el siguiente algoritmo:
- Paso 1: Seleccionar el número K de vecinos.
- Paso 2: Calcular la distancia euclidea de los K vecinos.
- Paso 3: Tomar los K vecinos más cercanos según la distancia euclídea calculada.
- Paso 4: Entre estos K vecinos, contar el número de puntos de datos en cada categoría.
- Paso 5: Asignar los nuevos puntos de datos a esa categoría para la cual el número de vecinos es máximo.
IMPORTANTE
Si las variables están medidas en diferentes unidades (lo cual es habitual) es recomendable estandarizar (reescalar) dichas variables. Una variable \(x\) con media \(\bar{x}\) y desviación típica \(\sigma_{x}\) se puede transformar a una variable con media cero y desviación típica 1 mediante la operación \(\frac{(x-\bar{x})}{\sigma_{x}}\).
Al estandarizar las variables, estamos haciendo un cambio de escala. Por ejemplo, si la media de la altura de la clase es 1.75 y la desviación típica es 0.25, un individuo que mide 2 metros, estandarizado, valdrá:
\[ \frac{2-1.75}{0.25}= 1 \]
Ese 1 quiere decir que este individuo está “una desviación” típica por encima de la media. Es decir, la unidad de medida de variables estandarizadas son “desviaciones típicas” y nos permiten comparar variables bien distintas. Por ejemplo, si tenemos euros y años, podemos encontrarnos con esta situación
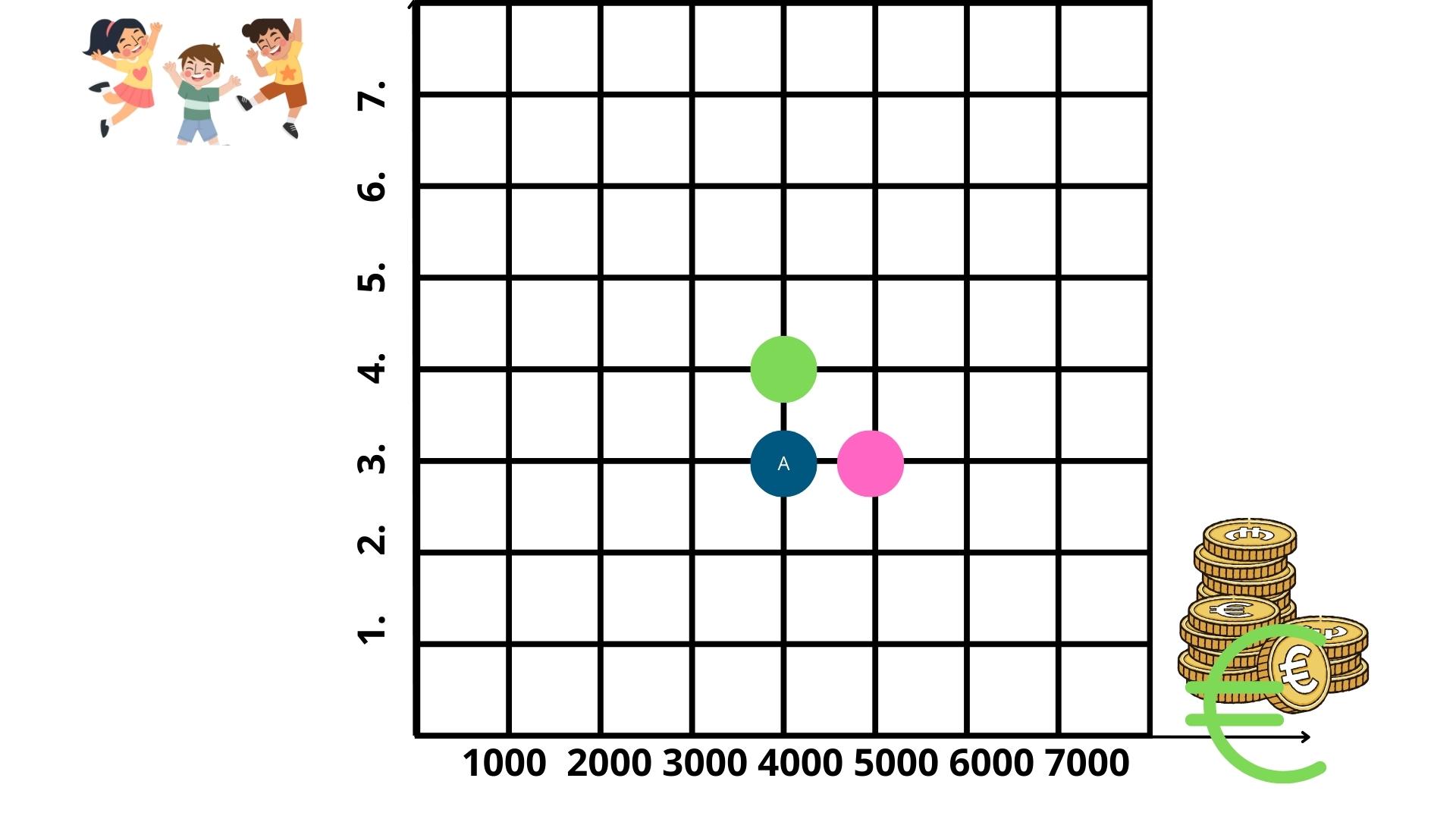
El punto rosa y el verde están a la misma distancia del punto A. Sin embargo:
\(d(A,rosa)=\sqrt{(4000-5000)^2+(3-3)^2}=1000\)
\(d(A,verde)=\sqrt{(4000-4000)^2+(3-4)^2}=1\)
La medida de distancia saldrá distorsionada, y nos dirá que el punto rosa está mil veces más lejos del punto A que el punto verde, lo cual es falso. Entonces, si no estandarizamos las variables (cuantitativas continuas o discretas), es muy probable que -si estas son muy grandes- dominen en el cálculo de la distancia.
Estandarizar las variables
Sin embargo, eso no quiere decir que esté convirtiendo a la variable en Normal (error común), simplemente la está cambiando de escala.
Respecto a P.2, la elección de \(K\) se puede realizar mediante validación cruzada. Elija, cómo no, una medida de error y busque el valor de \(K\) que minimiza dicha medida. Eso sí, recuerde que para estandarizar, deberá utilizar la media y la desviación típica del set de entrenamiento. No estandarice con la media y la desviación típica del set de “test”, puesto que estaría haciéndose trampas. Usted sólo conocerá los estadísticos descriptivos de la muestra de “entrenamiento”, y deberá aplicarlos a la muestra “test”.
Ejercicio utilice la librería “Class” y la función “knn” para entrenar los datos de enfermedades cardiacas. Utilice como variables predictoras el colesterol, la edad, las pulsaciones, el ritmo cardiaco, si el individuo tiene diabetes y el resultado de la prueba de electrocardiograma. Realice un conjunto de predicciones para ver cómo clasifica el algoritmo para distintos valores de k.
install.packages("class")
library(class)
error<-mat.or.vec(50, 10) #creamos un vector que almacenará 50 errores para 10 posibles valores de K
kv<-c(1,2,3,4,5,6,7,8,9,10) #creamos un vector que contiene los diferentes valores del parámetro K
for(i in 1:50){ #Iniciamos los subíndices: este es el de la iteración
for (j in 1:10){ #este es el que seleccionará secuencialmente el parámetro K
random <- sample(1:nrow(heart), size = floor(.7*nrow(heart))) # Elegimos la muestra de entrenamiento al azar
train<-heart[random,]
test <-heart[-random, ]
Predictoras.Train<-data.frame(train$age,train$chol,train$thalach,train$trestbps) #creamos el conjunto de variables "predictoras" continuas (que necesitarán ser estandarizadas)
Predictoras_scaled.Train<-scale(Predictoras.Train) #estandarizamos el conjunto de variables predictoras
Predictoras_scaled.Train_F<-data.frame(Predictoras_scaled.Train,train$restecg,train$fbs) #añadimos las variables predictoras discretas a las ya estandarizadas (las discretas no se estandarizan)
target<-train$target #guardamos la variable "target"
New_data<-data.frame(test$age,test$chol,test$thalach,test$trestbps) #creamos el conjnto de variables predictoras continuas (del test) que deberán ser estandarizadas
scaled.New_data <- scale(New_data, attr(Predictoras_scaled.Train, "scaled:center"), attr(Predictoras_scaled.Train, "scaled:scale")) # estandarizamos las variables del test con las medias y desviaciones típicas del "train" para no "autoengañarnos"
scaled.New_data_F <- data.frame(scaled.New_data,test$restecg,test$fbs) #añadimos las variables discretas al conjunto de test
knn.pred<-knn(train = Predictoras_scaled.Train_F, test = scaled.New_data_F, cl = target,k=kv[j]) #aplicamos knn al conjunto test
xt1<-table(knn.pred, test$target) #obtenemos la tabla de confusión...
error[i,j]<-(xt1[1,2]+xt1[2,1])/length(knn.pred) #...y de la tabla seleccionamos la(s) magnitud(es) que nos interesen de error o de acierto.
}}Apéndice: tratar de explorar e interpretar nuestros modelos
La ganadora del considerado “Premio Nobel” en Inteligencia Artificial, Cynthia Rudin (https://en.wikipedia.org/wiki/Cynthia_Rudin) escribió un interesante artículo académico muy provocador titulado:
LA POLÉMICA
Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead
puede ver el artículo-en abierto- aquí: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC9122117/
En este, citamos directamente esta parte del principio, que motivará nuestra discusión:
- There has been an increasing trend in healthcare and criminal justice to leverage machine learning (ML) for high-stakes prediction applications that deeply impact human lives. Many of the ML models are black boxes that do not explain their predictions in a way that humans can understand. The lack of transparency and accountability of predictive models can have (and has already had) severe consequences; there have been cases of people incorrectly denied parole [1], poor bail decisions leading to the release of dangerous criminals, ML-based pollution models stating that highly polluted air was safe to breathe [2], and generally poor use of limited valuable resources in criminal justice, medicine, energy reliability, finance, and in other domains [3].
- Rather than trying to create models that are inherently interpretable, there has been a recent explosion of work on “Explainable ML,” where a second (posthoc) model is created to explain the first black box model. This is problematic. Explanations are often not reliable, and can be misleading, as we discuss below. If we instead use models that are inherently interpretable, they provide their own explanations, which are faithful to what the model actually computes.
Aterrizando, de forma modesta, a esta asignatura, lo que nos viene a decir es que deberíamos tener cuidado con los algoritmos/modelos que utilicemos y de los que no entendamos cómo están prediciendo. Ya no sólo es cuestión de hacer un trabajo ético, sino por supervivencia: su cliente es lo primero que querrá entender “¿cómo funciona el algoritmo?¿Cómo decide?”
Por otro lado, hay un esfuerzo- criticado por Cynthia Rudin en este texto- por tratar de entender qué hace un algoritmo no interpretable. Esto nos lleva a hacer un ejercicio de “aproximación” de un modelo complicado por otro más sencillo.
Por ejemplo, la librería IML de R (Interpretable Machine Learning) https://rdrr.io/cran/iml/src/R/iml.R, trata de buscar alternativas para explicar modelos poco inteligibles.
Nosotros tomaremos un punto intermedio. Como consejos:
- Haga siempre un buen análisis exploratorio. Ahí es donde aprenderá de sus datos y podrá tomar decisiones. No deje que sea la máquina la que tome esas decisiones por usted de manera “oscura”.
- Empiece con el modelo/modelos más sencillos e interpretables. No desdeñe ninguna de las regresiones y trate de explotar sus posibilidades (por ejemplo, interacciones, formas sencillas no lineales, etc…)
- No utilice criterios de selección de variables automáticos. Haga una cuidadosa validación del modelo bajo distintos criterios
- Piense en escenarios y analice las predicciones del modelo para dicho escenario. Eso le ayudará a entender qué está ocurriendo.
Ejemplo con los datos “Heart”
La base de datos “Heart”, con la que ha trabajado este semestre, es un buen ejemplo con la que trabajar. Está llena de paradojas y, además, le obliga a tratar de precisar y discutir varios aspectos:
- ¿Qué pregunta trata de responder? Esto le será siempre útil. Imagine que nos piden que busquemos un modelo predictivo de enfermedad cardiaca: así de simple. Generalmente, esa pregunta es demasiado ambiciosa y sería recomendable iterar con el cliente para ir “poco a poco”. Nuestro inicio es seleccionar como posibles variables predictoras las que se obtendrían de análisis y exploraciones baratas (descartando, por ejemplo, un TAC). Ya seguiremos adelante si el cliente puede invertir en hacer esas pruebas o si nos interesa, particularmente, el efecto predictivo de estas frente a lo que ya sabemos.
0.1 Primer intento
Lo más natural es tratar de empezar con un modelo que sea manejable y que entienda bien lo que obtiene de él. Por ejemplo, en el caso de los datos “Heart”, puede tratar de analizar cómo evoluciona la probabilidad de enfermedad cardiaca ante cambios en las pulsaciones (thalach) y la edad. Dejaremos de lado el colesterol, que ya le hemos dado mucha paliza con él. Una primera idea, será usar el modelo que ya había construido a lo largo del curso (donde la edad era un posible factor confusor y se trató como una variable de interacción) y generar distintos escenarios.
¿Cómo NO hacerlo? Una tentación podría ser dejar fijos unos valores (por ejemplo, el promedio del resto de variables) y mover las pulsaciones y la edad. Sin embargo, imagine que deja fijo un colesterol de 100, no azúcar en sangre y un pulso de 70. ¿Es creíble que esos valores los tenga un individuo de 70 años? No. Si deja fija esas variables, podría estar capturando un efecto poco preciso, sesgado o no creíble.
¿Cómo hacerlo? Vuelva al primer día. Haga un análisis descriptivo de los valores que toman las otras variables por edades, por ejemplo. Utilice esos valores para generar los escenarios.
Por ejemplo, con estas líneas de código puede analizar los estadísticos descriptivos desglosados por edades
age_q<- as.factor(ifelse(heart$age<40, '40',
ifelse(heart$age>=40 & heart$age<50, '40-50',
ifelse(heart$age>=50 & heart$age<65, '50-65', '65 and more'))))
heart<-data.frame(heart,age_q)
library(doBy)
tab1<-summaryBy(target ~ age_q, data = heart,
FUN = list(mean, max, min, median, sd))
tab2<-summaryBy(chol ~ age_q, data = heart,
FUN = list(mean, max, min, median, sd))
tab3<-summaryBy(trestbps ~ age_q, data = heart,
FUN = list(mean, max, min, median, sd))
tab4<-summaryBy(thalach ~ age_q, data = heart,
FUN = list(mean, max, min, median, sd))
tab5<-summaryBy(fbs ~ age_q, data = heart,
FUN = list(mean, max, min, median, sd))
#así puede ver "en sucio" los resultados
tab1
age_q target.mean target.max target.min target.median target.sd
1 40 1.736842 2 1 2 0.4442617
2 40-50 1.662447 2 1 2 0.4738759
3 50-65 1.438449 2 1 1 0.4966159
4 65 and more 1.485507 2 1 1 0.5016107
tab2
age_q chol.mean chol.max chol.min chol.median chol.sd
1 40 213.4211 321 175 204 36.99853
2 40-50 235.0549 341 141 235 44.78595
3 50-65 250.5278 409 126 244 49.37121
4 65 and more 258.7971 564 149 251 66.67222
> tab3
age_q trestbps.mean trestbps.max trestbps.min trestbps.median trestbps.sd
1 40 126.0702 140 94 126 11.31980
2 40-50 123.9536 152 101 122 12.42307
3 50-65 133.7926 200 94 130 17.94029
4 65 and more 137.6812 180 100 140 20.30964y utilizar estos descriptivos para generar los escenarios
library(mgcv)
library(ggplot2)
library(mgcViz)
library(pheatmap)
library(readr)
heart<-read_csv("heart_FINAL.csv")
heart$sex <- as.factor(heart$sex)
heart$fbs <- as.factor(heart$fbs)
heart$restecg <- as.factor(heart$restecg)
heart$target<- as.factor(heart$target)
#entrenamos el modelo logit con interacciones
log2_explain<-glm( target ~chol*age+as.factor(fbs)*chol*age+trestbps*chol+as.factor(restecg)*age*chol+thalach*age*chol+as.factor(sex), data =heart, family = binomial)
#generamos los distintos escenarios
Esc1<-data.frame(age=rep(40,8),chol=rep(213,8), fbs=as.factor(c(0,0,0,0,0,0,0,0)),restecg=as.factor(c(1,1,1,1,1,1,1,1)),thalach=c(100,110,125,140,150,160,170,190),sex=as.factor(c(1,1,1,1,1,1,1,1)),trestbps=rep(126,8))
P40_thal<-predict.glm(log2_explain,Esc1,"response")
Esc2<-data.frame(age=rep(50,8),chol=rep(235,8), fbs=as.factor(c(0,0,0,0,0,0,0,0)),restecg=as.factor(c(1,1,1,1,1,1,1,1)),thalach=c(100,110,125,140,150,160,170,190),sex=as.factor(c(1,1,1,1,1,1,1,1)),trestbps=rep(123,8))
P50_thal<-predict.glm(log2_explain,Esc2,"response")
Esc3<-data.frame(age=rep(60,8),chol=rep(250,8), fbs=as.factor(c(1,1,1,1,1,1,1,1)),restecg=as.factor(c(1,1,1,1,1,1,1,1)),thalach=c(100,110,125,140,150,160,170,190),sex=as.factor(c(1,1,1,1,1,1,1,1)),trestbps=rep(133,8))
P60_thal<-predict.glm(log2_explain,Esc3,"response")
Esc4<-data.frame(age=rep(70,8),chol=rep(258,8), fbs=as.factor(c(1,1,1,1,1,1,1,1)),restecg=as.factor(c(1,1,1,1,1,1,1,1)),thalach=c(100,110,125,140,150,160,170,190),sex=as.factor(c(1,1,1,1,1,1,1,1)),trestbps=rep(137,8))
P70_thal<-predict.glm(log2_explain,Esc4,"response")
data_frame_predict<-data.frame(P40_thal,P50_thal,P60_thal,P70_thal)
DM<-data.matrix(data_frame_predict)
# y estas son las probabilidades previstas para cada nivel de thalalch:
#DM
#P40_thal P50_thal P60_thal P70_thal
#1 0.02995026 0.04625253 0.09577739 0.2688194
#2 0.06177880 0.07957910 0.13023107 0.2850484
#3 0.17018034 0.17068578 0.20105399 0.3104623
#4 0.38977126 0.32883255 0.29723019 0.3370739
#5 0.57666803 0.46623476 0.37416476 0.3554205
#6 0.74392960 0.60895848 0.45803414 0.3742020
#7 0.86103079 0.73519451 0.54435120 0.3933703
#8 0.96573105 0.89821493 0.70477389 0.4326524Con estas líneas, ha creado diversos escenarios. Por ejemplo, P40_thal son individuos de 40 años. Se introducen diversos niveles de thalach (que es la variable que queremos que fluctúe) y se fijan unos niveles promedio del resto de variables según el análisis descriptivo muestral para dichos individuos. Y así, sucesivamente. Luego, usamos el modelo para predecir cada segmento de edad y mostramos en una tabla, mediante un mapa de calor, los resultados obtenidos.
pheatmap(DM, display_numbers =T,cluster_rows=FALSE,cluster_cols=FALSE,fontsize_number=25,fontsize_col=20,fontsize_row=20,labels_row=c("100","110","125","140","150","160","170","190"),labels_col=c("40","50","60","70"),legend=FALSE,dendrogram=FALSE)Esto, nos lleva al siguiente gráfico:
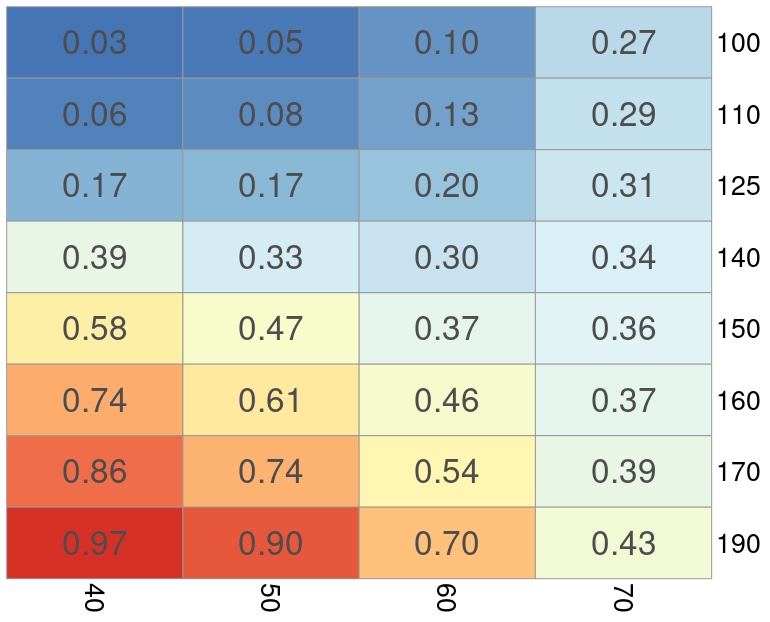Donde puede analizar el impacto que tiene, por grupo de edad, un incremento en las pulsaciones sobre la probabilidad de tener enfermedad cardiaca- condicionado por valores probables del resto de variables de cada grupo de edad.
Como verá:
- Las pulsaciones tienen un efecto más fuerte en individuos jóvenes que viejos
- Esto indicaría que para individuos de más de 70 años (i) o las pulsaciones no son un factor de riesgo relevante, (ii) o hay otros factores más relevantes que no lo son para individuos más jóvenes (iii) que la submuestra de mayores será menos útil para analizar el efecto de esta variable sobre la probabilidad de enfermedad cardiaca.
Estas discusiones pueden ser, simplemente, hipótesis, que tendrá que contrastar con su cliente. Pero es importante que piense sobre ello y muestre habilidad de discusión al respecto: en esto consiste ser científico/a de datos. Si empieza por aquí, ya podrá ponerse el preciado “Data Scientist” en LinkedIn.
Ejercicio Haga esto mismo, por ejemplo, con algún otro modelo más “caja negra”. Mire a ver qué ocurre con análisis discriminante lineal, o K vecinos. No es difícil de implementar con el código que ya tiene y le ayudará mucho.
0.2 El paquete IML
La “interpretabilidad” de los modelos de Machine Learning, como hemos dicho, está dando mucho de qué hablar y se está escribiendo sobre ello. Al texto de la premiada Cynthia Rudin, responde Christoph Molnar. Un brillante estadístico que ha trabajado en interpretabilidad. En esencia, dice:
- Pick interpretation approaches based on your goals:
- Debug and improve the model: I’m currently participating in an ML competition and I’m using SHAP and permutation feature importance for finding modeling errors such as target leakage or improving the model with, for example, better-engineered features.
-Justify the predictions in high-stakes scenarios: ML is used in lots of places where maybe it shouldn’t be used at all, like risk assessment of criminal recidivism (e.g. COMPAS). Such high-stakes scenarios require a way to challenge the model outputs, which in turn requires understanding how the decision was made.
-Extract insights from the model about the world: Many researchers already rely on machine learning + interpretability in their work
Y dice que, en resumen, piense primero en la(s) pregunta(s) que quiere responder y, por tanto, qué modelo le vendrá mejor.
El caso es que Christoph tiene un libro (versión en abierto: https://christophm.github.io/interpretable-ml-book/) muy interesante y bien escrito sobre interpretabilidad y una librería en R, que permite analizar cómo predice cualquier algoritmo de Machine Learning. Aunque hay que ir con cuidado, esos análisis son meras “aproximaciones” y podrían estar muy errados. Por lo tanto, volvamos al principio: use siempre algoritmos que sepa explicar a su cliente. Si no funcionan y cometen errores no admisibles, trate de ver si algoritmos más complicados, mejoran la habilidad predictiva. Entonces, use estas metodologías para tratar de aproximar cuáles son sus mecanismos predictivos.
0.2.1 La función “Efectos locales acumulados: ALE”
Funciona de la siguiente manera. Imagine, de nuevo, que quiere analizar el efecto de thalach sobre la probabilidad de problema cardiaco. La función ALE hará una discretización de la variable “thalach” más fina de la que hemos hecho aquí (aprovecha la potencia computacional), por ejemplo, de 100 a 200 de 1 en 1. Entonces, para un valor 101 de thalach, busca todas las observaciones en la muestra con 101 de thalach (que tendrán diferentes valores del resto de variables como colesterol o edad) y realiza la predicción de probabilidad de enfermedad cardiaca para un valor 100 de thalach y para uno de 102. Entonces, al final calcula la diferencia entre ambas probabilidades, y puede estudiar cuál es el impacto de una variación marginal en el nivel de thalach sobre la probabilidad de contraer enfermedad, para cualquier valor de este.
Se implementa de la siguiente manera:
library(iml)
heart$sex <- as.factor(heart$sex)
heart$fbs <- as.factor(heart$fbs)
heart$restecg <- as.factor(heart$restecg)
heart$target<- as.factor(heart$target)
log2<-glm( target ~chol*age+as.factor(fbs)*chol*age+trestbps*chol+as.factor(restecg)*age*chol+thalach*age*chol+as.factor(sex), data =train, family = binomial)
X <- heart[which(names(heart) != "target")]
predictor <- Predictor$new(log2, data = X,
y = heart$target, type = "response")
ale <- FeatureEffect$new(predictor, feature = "thalach",method="ale")
ale$plot()y obtendrá:
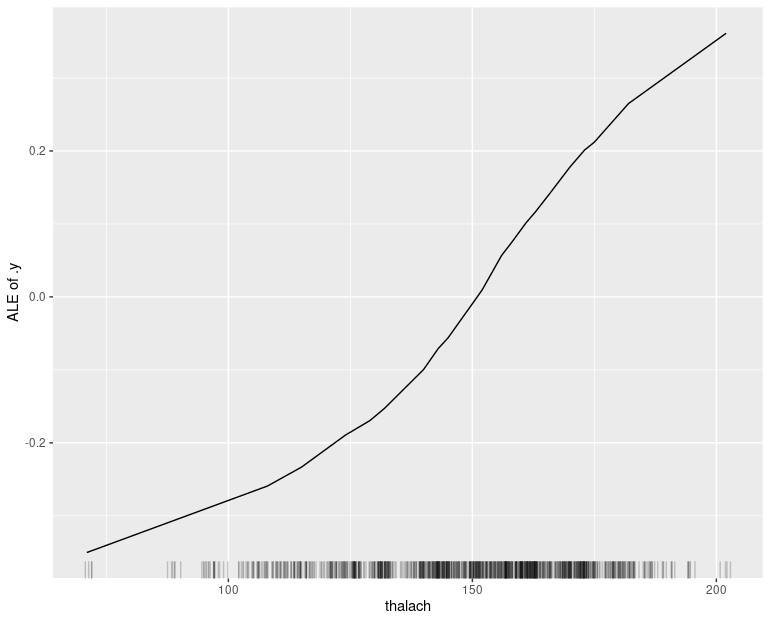Donde observamos un efecto en el que, hasta un nivel de 150 la probabilidad de enfermedad coronaria decrece (cada vez menos) y, a partir de 150, la probabilidad empieza a crecer. Fíjese que, en torno a thalach de 170 la probabilidad puede crecer 0.2 puntos (lo cual, no es desdeñable).
Además, puede tratar de analizar la interacción entre dos variables de interés. En este caso, la edad y thalach:
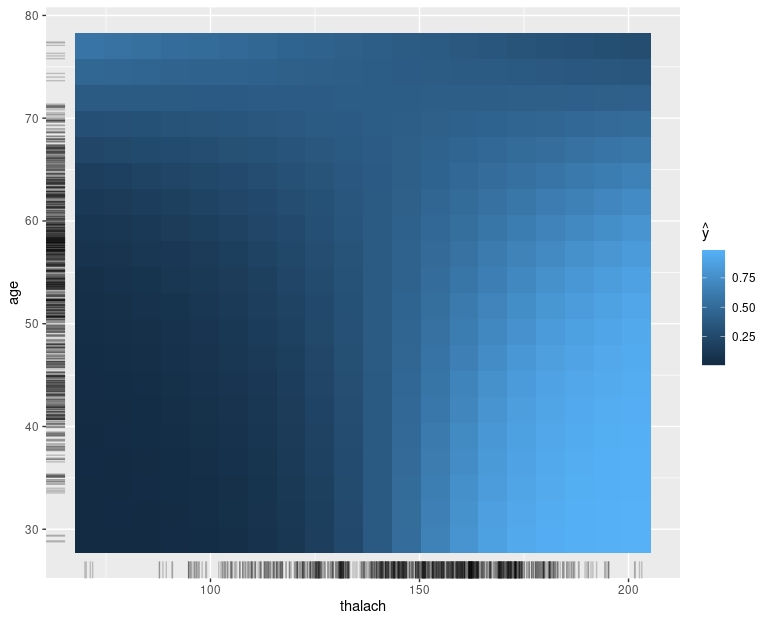Volvemos a encontrar algo parecido, fíjese en los colores claros: son probabilidades altas: se corresponden con valores altos de thalach e individuos jóvenes. ¡Eso ya lo vimos en nuestro análisis más casero!
Como verá, esto es una pequeña introducción. Seguiremos luchando por entender bien los modelos/algoritmos con los que trabajamos. Hágalo en su proyecto. Es importante.