Clase 2: regresión espuria y cointegración
Ejemplo aplicado
Vamos a entender todo este marco conceptual utilizando simulación. Mediante esta, crearemos series temporales que nos permitirán analizar los posibles casos en los que nos encontraremos.
Caso 1 Las series son estacionarias en media.
Simular una serie estacionaria en media, la más sencilla de todas, es inmediato. Vamos a generar dos series \(y_{1,t},y_{2,t}\) que se distribuyen normal y que sean independientes e idénticamente distribucídas. Esto quiere decir que conociendo el pasado de la serie es imposible predecir su futuro.
- Paso 1: generamos las series
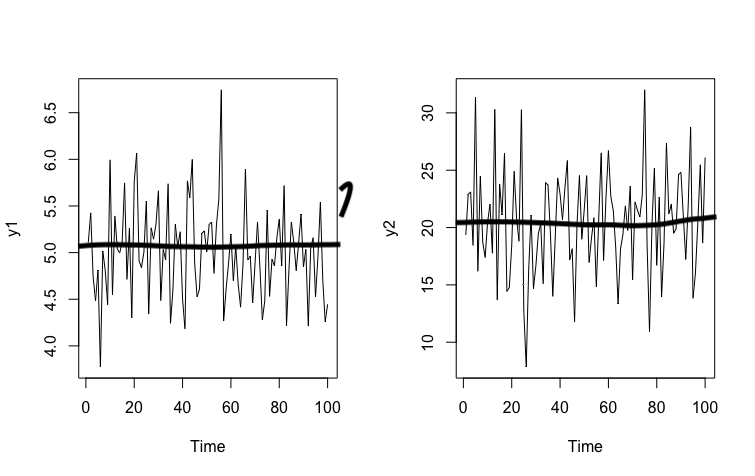
- Paso 2: ¿Cómo sabemos que son i.i.d, esto es, que conociendo el presente no podemos predecir el futuro?
Una herramienta muy buena para ver esto se llama “función de autocorrelación”, esto es, “acf”
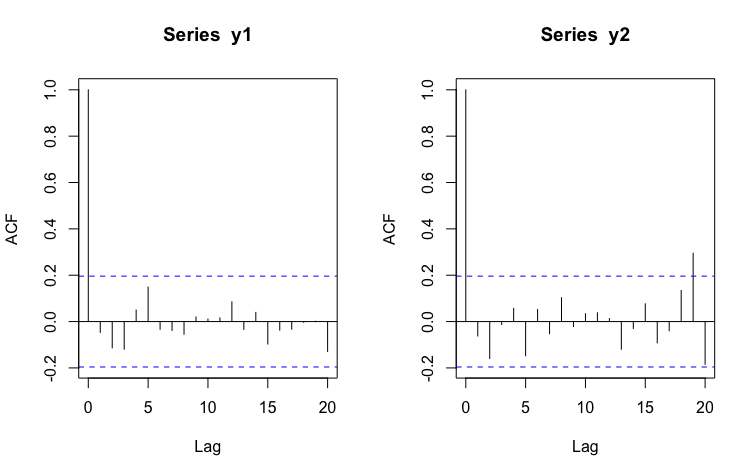
Cada “Lag” de la ACF te proporciona la información del grado de correlación de la serie en el momento \(t\) frente a momentos pasados \(t-1\), \(t-2\), etc… Si esos valores son pequeños (como ocurre aquí, al estar entre las bandas azules) entonces, diremos que el pasado de la serie no ayuda a predecir el futuro.
La mejor predicción que puede hacer de las series son sus promedios
Ahora bien, ¿y si intentamos relacionarlas? POr ejemplo, mediante una regresión,
\[ y_{1,t}=\alpha+\beta y_{2,t}+u_{t} \]
Esperaríamos que \(\beta=0\) y que \(\mathbb{R}^2=0\). Veamos:
summary(lm(y1~y2))
Residuals:
Min 1Q Median 3Q Max
-1.08929 -0.30956 0.04058 0.24701 1.19527
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.70759 0.22455 20.965 <2e-16 ***
y2 0.01381 0.01098 1.258 0.212
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.471 on 98 degrees of freedom
Multiple R-squared: 0.01588, Adjusted R-squared: 0.005839
F-statistic: 1.581 on 1 and 98 DF, p-value: 0.2115Efectivamente, no parece haber problema. Pero ¿Qué ocurre si las series son no estacionarias?
Vamos a hacer el mismo juego de simulación y veamos,
Ejemplo aplicado con series no estacionarias
Caso 2 Las series son NO estacionarias en media.
Para simular una serie no estacionaria en media, deberemos hacer una suma acumulada de procesos aleatorios que se distribuyen normal con media cero y varianza constante.
- Paso 1: generamos las series
a1<-rnorm(100,0,1)
x1<-cumsum(a1)
a2<-rnorm(100,0,2)
x2<-cumsum(a2)
par(mfrow = c(1, 2))
ts.plot(x1)
ts.plot(x2)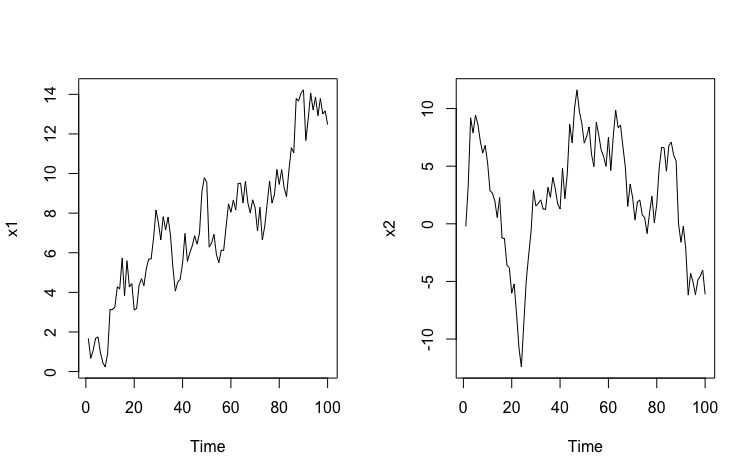
- Paso 2: Veamos que, además, estas series se caracterizan porque el pasado “lejano” ayuda a predecir el presente:
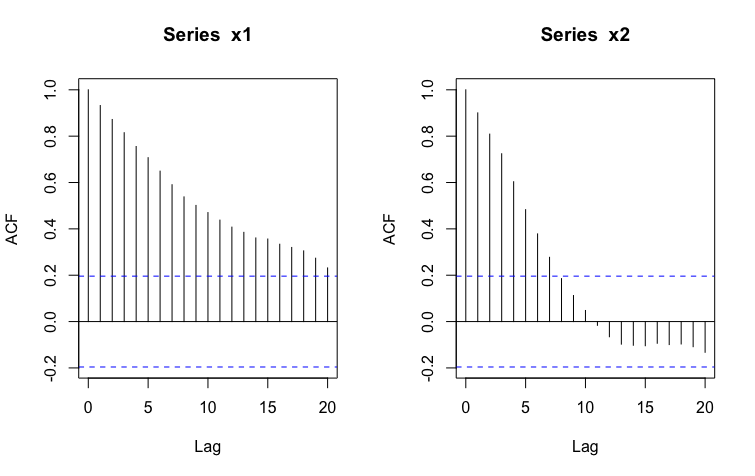
Veamos que esto puede ser un “problema” si pretendemos relacionarlas. Esa “fuerza” del pasado hará que confundamos la verdadera relación entre las series que es, en realidad, nula (ya que se han generado independientemente)
Ahora bien, ¿y si intentamos relacionarlas? POr ejemplo, mediante una regresión,
\[ x_{1,t}=\alpha+\beta x_{2,t}+u_{t} \]
Esperaríamos que \(\beta=0\) y que \(\mathbb{R}^2=0\). Veamos:
summary(lm(x1~x2))
Residuals:
Min 1Q Median 3Q Max
-5.5275 -2.1584 -0.3856 2.2910 6.7661
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.54814 0.37211 9.535 1.24e-15 ***
x2 0.16453 0.02805 5.866 6.05e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.869 on 98 degrees of freedom
Multiple R-squared: 0.2599, Adjusted R-squared: 0.2523
F-statistic: 34.41 on 1 and 98 DF, p-value: 6.051e-08Efectivamente, tanto el \(\beta \neq 0\) y que \(\mathbb{R}^2 \neq 0\).
¿Entonces? Esto es una regresión espuria ¿Cómo podemos detectarla?
Para ello, se definió la “cointegración”
COINTEGRACIÓN
Un conjunto de series temporales (en este caso, dos: \(x_t\), \(y_t\)) cointegran (es decir, tienen una relación estable y verdadera a largo plazo) si
- \(x_t\), \(y_t\) son paseos aleatorios (series no estacionarias)
- en la regresión:
\[ y_{t}=\alpha+\beta x_{t}+u_{t} \]
los residuos \(\hat u_t\) son estacionarios
Nota que en caso contrario se dirá que NO COINTEGRAN y que, por tanto, la relación es espuria. Por otro lado, no se dice nada de las series que ya son estacionarias. La cointegración se estudia sólo cuando las series con las que trabajamos son no estacionarias
En este caso, podemos analizar los residuos del modelo y obtendremos
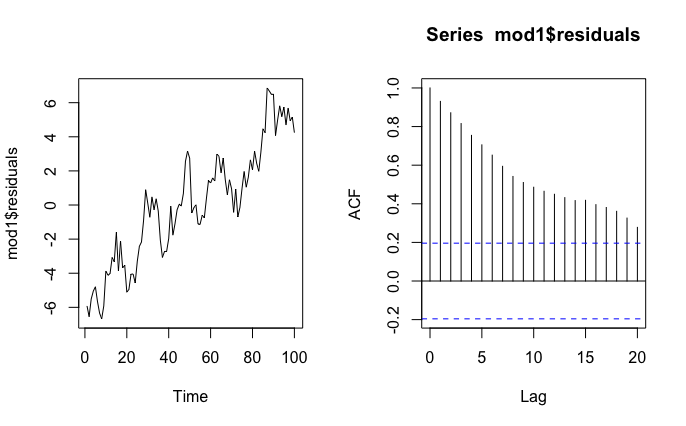
** SI NO COINTEGRAN** >- Sabemos que el problema viene de que “las series no estacionarias” pueden dar la falsa apariencia de que están altamente relacionadas entre sí. Entonces, ¿qué ocurre con la relación entre ambas si elimina la tendencia?
Uno puede probar a eleminiar la tendencia de las series mediante el uso de primeras diferencias (es muy raro necesitar más de una diferencia). Entonces, debería estimar el modelo
[
y_t=+x_t+u_t
]
donde
[
y_t=y_t-y_{t-1}
]
[
x_t=x_t-x_{t-1}
]
indican las variaciones de los datos entre el periodo \(t\) y \(t-1\).
Caso 3 Las series son NO estacionarias en media pero sí cointegran
Simulemos ahora un modelo de series no estacionarias en media pero que sí están relacionadas
- Paso 1: generamos las series no independientes
a1<-rnorm(100,0,1)
x1<-cumsum(a1)
a2<-rnorm(100,0,15)
y<-8+5*x1+a2
par(mfrow = c(1, 2))
ts.plot(x1)
ts.plot(y)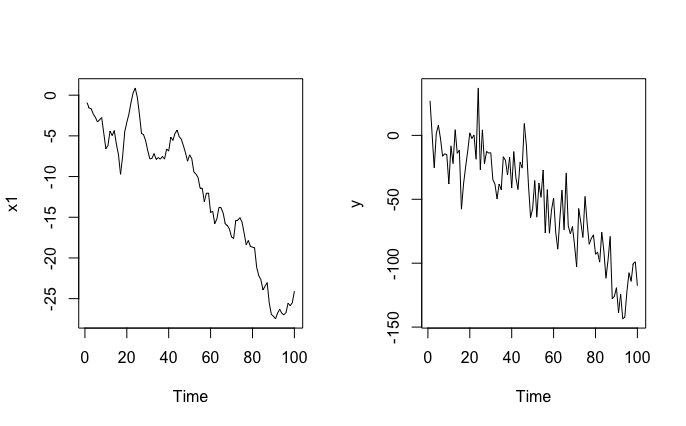
Ahora bien, ¿y si intentamos relacionarlas? Por ejemplo, mediante una regresión,
\[ y_t=\alpha+\beta x_{1,t}+u_{t} \]
Esperaríamos que \(\beta\neq 0\) y que \(\mathbb{R}^2\neq 0\). Veamos:
summary(lm(y~x1))
Residuals:
Min 1Q Median 3Q Max
-30.373 -9.309 0.063 10.899 34.701
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.4035 2.6478 1.663 0.0995 .
x1 4.7248 0.1849 25.560 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 15.03 on 98 degrees of freedom
Multiple R-squared: 0.8696, Adjusted R-squared: 0.8682
F-statistic: 653.3 on 1 and 98 DF, p-value: < 2.2e-16Efectivamente, tanto el \(\beta \neq 0\) y que \(\mathbb{R}^2 \neq 0\).
¿Cómo nos aseguramos de que esta refresión no sea espuria?
De nuevo, como ya ha visto, debe analizar los residuos de la regresión y comprobar si son o no estacionarios.
Analicemos los residuos
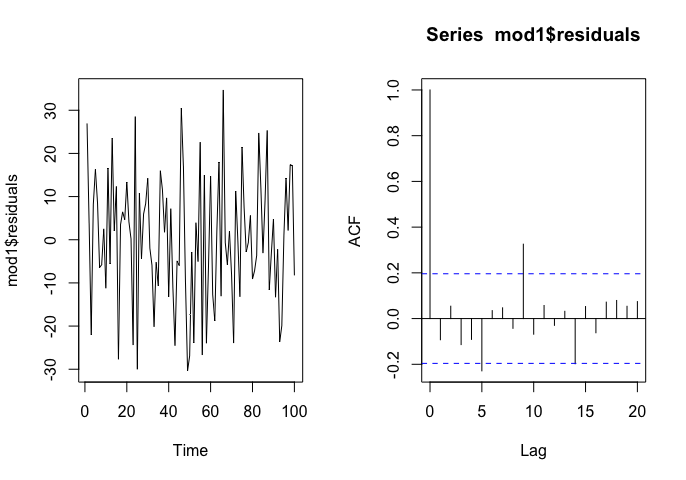
En este caso, la regresión no es espuria y podemos fiarnos de ella. Sin embargo, lo normal es encontrar series que-probablemente tengan relación- pero que no cointegren. Entonces, lo más normal es trabajar con estas sin tendencia, si consideramos que puede haber relación entre ellas.
Si cointegran, la literatura aconseja especificar un modelo más complejo llamado “modelo de corrección de errores” que excede el objetivo de este curso.
En resumen:
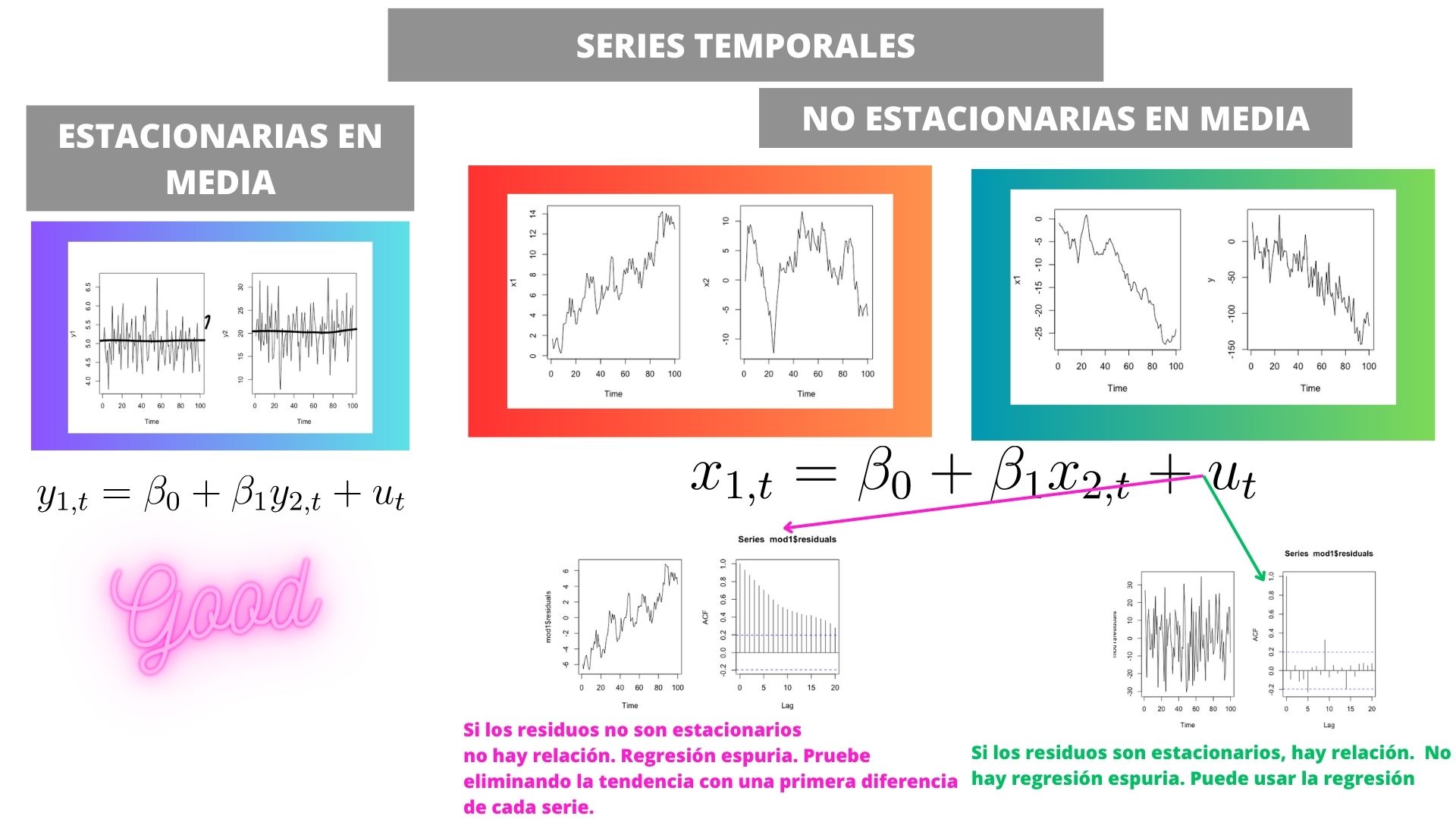
Clase 2: Aplicación de lo aprendido sobre cointegración/regresión espuria
Lo que pudo observar en la clase anterior fue algo que descubrieron Engle y Granger, premios Nobel, a mediados del siglo pasado. Las series temporales con comportamiento no estacionario (paseo aleatorio) al relacionarse entre ellas suelen:
- Mostrar una correlación elevada
- En la regresión todo parece “muy significativo”
Pero, a todas luces, no tienen sentido. Se llaman: regresiones espurias donde “espurio” significa falso. El problema es que, al tener un comportamiento tendencial similar, es la tendencia común la que explica esa relación entre ellas. Es decir, el número de turistas y de nacimientos dependen de variables comunes no especificadas: bonanza económica, estación del año, etc…
Como ya hemos visto, una forma de ver que, efectivamente, no hay mucha relación entre ambas, es generar la diferencia de ambas series (para eliminar la tendencia) y estimar una regresión en “primeras diferencias”, esto es:
\[ \Delta Turistas_{t}=\alpha+\beta \Delta Matrimonios_{t}+u_{t} \]
library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)
datos <- read_excel("datos_INE.xlsx")
matrimonios.t=ts(datos[,2],frequency=12,start=c(2015,10))
turistas.t=ts(datos[,3],frequency=12,start=c(2015,10))
d_matrimonios<-diff(matrimonios.t)
d_turistas<-diff(turistas.t)
mod2<-lm(d_turistas~d_matrimonios)
lm(formula = d_turistas ~ d_matrimonios)
Residuals:
Min 1Q Median 3Q Max
-3956740 -1018875 265210 1243441 4308444
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -69500.0 230677.2 -0.301 0.764
d_matrimonios -200.7 259.5 -0.773 0.442
Residual standard error: 1984000 on 72 degrees of freedom
Multiple R-squared: 0.008238, Adjusted R-squared: -0.005537
F-statistic: 0.598 on 1 and 72 DF, p-value: 0.4419Ahora, las conclusiones son bien distintas.
De esto se dieron cuenta Engle y Granger y elaboraron la teoría de la cointegración. Es un tema muy extenso y aquí vamos a resumir de una forma “ligera” para poder trabajar de manera sensata con series temporales sin tener- para ello- que cubrir mucha teoría.
library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)
datos <- read_excel("datos_INE.xlsx")
matrimonios.t=ts(datos[,2],frequency=12,start=c(2015,10))
turistas.t=ts(datos[,3],frequency=12,start=c(2015,10))
mod1<-lm(turistas.t~matrimonios.t)
ts.plot(mod1$residuals)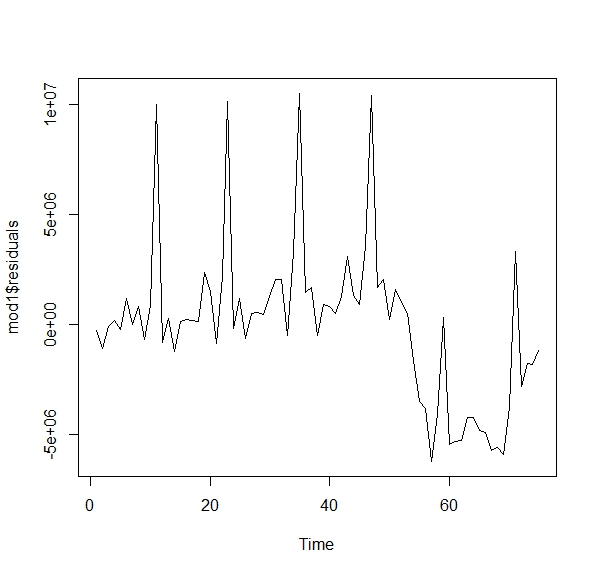
Como ve, no parecen aleatorios. Si fueran aleatorios, sería difícil entender la pauta que marcan. Una forma de ver esto es con lo que se llama la función de autocorrelación. Esta consiste en analizar la relación que tiene un residuo en tiempo \(t\) con su pasado \(t-1,t-2,...\). Si fuera aleatorio (ruido blanco) no debería existir tal relación
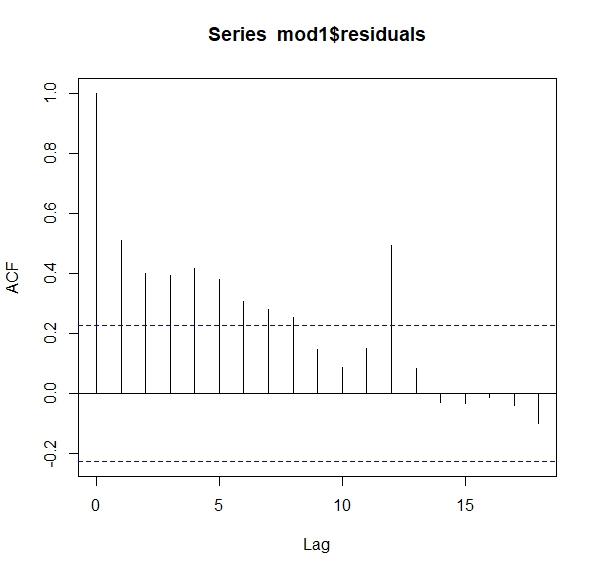Ahora tenemos otro modelo, donde queremos predecir la inflación utilizando un índice de incertidumbre económica. Sospechamos que la incertidumbre puede afectar a la inflación y queremos estimar el modelo:
\[ IPC_{t}=\alpha+\beta Incertidumbre_{t}+u_{t} \]
¿qué puede decir?
install.packages("astsa")
library(astsa)
library(xts)
inflacion<-read_excel("TS_INF_UNC.xlsx")
df_ts <- ts(xts(inflacion[,2:3],order.by = inflacion$Date), frequency = 12, start = c(2002,1))
mod1<-lm(IPC~UNC, data=df_ts)
ts.plot(mod1$residuals)Es fácil ver que las series no son estacionarias en media y que, además, los residuos de la regresión que se ha especificado, no son ruido blanco. Decimos, entonces, que las series no cointegran. Sin embargo, en este caso:
- Conceptualmente, nos parece de interés ver el impacto de la incertidumbre en la inflación
- Puede haber más maneras de relacionar ambas variables, como hemos visto antes
Si no cointegran podemos probar qué tal funciona la relación en primeras diferencias:
d_IPC= diff(df_ts[,"IPC"])
d_UNC=diff(df_ts[,"UNC"])
mod2<-lm(d_IPC~d_UNC)
Residuals:
Min 1Q Median 3Q Max
-1.99030 -0.27859 0.01035 0.31242 2.97564
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.1636630 0.0364853 4.486 1.11e-05 ***
d_UNC 0.0003424 0.0007208 0.475 0.635
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5815 on 252 degrees of freedom
Multiple R-squared: 0.0008949, Adjusted R-squared: -0.00307
F-statistic: 0.2257 on 1 and 252 DF, p-value: 0.6351¿qué opina sobre la posible relación entre ambas variables?
COINTEGRACIÓN
Lo que aquí presentamos es algo “muy básico” que le permitirá entender la idea, aunque es un tema muy extenso y lleno de complejidad estadística. Sin embargo, lo visto aquí le permitirá plantearse cualquier respuesta que pueda dar, precipitada, sobre la relación de series temporales con tendencia.
Los indicadores adelantados
Imagine que sigue pensando que pensar que el índice de incertidumbre puede ayudar a predecir la inflación. Quizás, estimando este modelo:
\[ \Delta IPC_{t}=\alpha+\beta \Delta UNC_{t}+u_{t} \]
No encuentra una gran relación. Pero eso no quiere decir que no deba seguir indagando. Uno de los motivos es que, es muy común que en series con alta frecuencia (por ejemplo, mensuales) haya algunas series que tarden un tiempo (algún mes) en hacer efecto sobre otra. A esto lo llamamos “indicador adelantado”. Es decir, cuando uno observa qué pasa con un “indicador adelantado” puede tratar de inferir qué ocurrirá con la otra serie en el futuro.
Un ejemplo sencillo de por qué un indicador adelantado es útil es pensar en el modelo anterior: si quiere predecir la inlación del mes siguiente, utilizando el índice de incertidumbre, deberá tener una predicción de la incertidumbre para el mes siguiente. Estamos en las mismas.
Si tiene un indicador adelantado, no necesitará jugar a adivinar lo que valdrán las variables predictoras. Un ejemplo de un modelo de indicador adelantado, será:
\[ \Delta IPC_{t}=\alpha+\beta \Delta UNC_{t-1}+u_{t} \]
ya que, cuando quiera predecir la inflación en el periodo \(t+1\),
\[ \Delta IPC_{t+1}=\alpha+\beta \Delta UNC_{t}+u_{t+1} \]
Sólo neceistará introducir el dato actual de \(\Delta UNC\), que es un dato que ya sabe no tiene que predecirlo. Por cierto, la predicción la escribimos como
\[ \mathbb{E} (\Delta IPC_{t+1}|\Delta UNC_{t})=\alpha+\beta \Delta UNC_{t} \]
es decir, ¿qué espero de la inflación mañana, en \(t+1\), con la información de la incertidumbre que tengo hoy, en \(t\) ? Como ve, el error tiene esperanza cero (espero, en promedio, no equivocarme, aunque sé que lo haré con cierta probabilidad).
Otras versiones de modelos con indicadores adelantados serán:
\[ \Delta IPC_{t}=\alpha+\beta_1 \Delta UNC_{t-1}+\beta_2\Delta UNC_{t-2}+...+\beta_k\Delta UNC_{t-k}+u_{t} \]
¿Cómo decidir \(k\)? Como nuestro objetivo es predecir lo mejor posible, lo lógico es buscar alguna manera de analizar la habilidad predictiva del modelo para diferentes \(k\). Efectivamente, como ya estará pensando, tanto gráficos como la técnica de “validación cruzada” es una buen son buenas maneras de ello.
Idea 1
Una manera gráfica de analizar la posible capacidad que tiene la incertidumbre sobre la inflación es mediante gráficos de nube de puntos de los retardos de la variaable incertidumbre (en primeras diferencias) frente a la inflación:
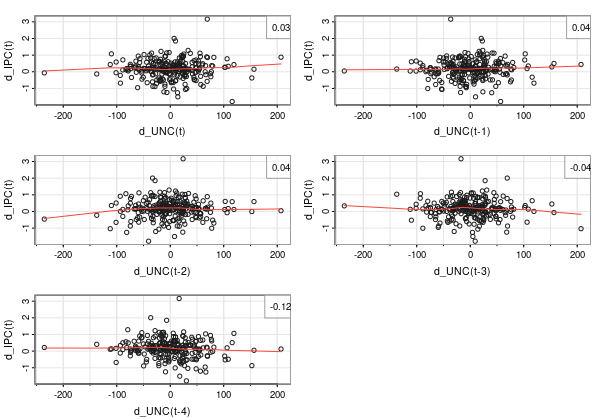
- ¿Cree que la relación es relevante?
No lo parece, aunque vamos a seguir indagando en más posibilidades. Muchas veces, hay componentes de las series temporales, como la estacionalidad, que pueden enmascarar la verdadera relación. Luego lo comprobaremos.
Idea 2: Validación cruzada en series temporales
En series temporales también se puede realizar validación cruzada. La particularidad de estos datos (el orden ha de ser cronológico) hace que no se pueda realizar como con datos de individuos (donde se puede realizar un conjunto de remuestreos aleatorios y seleccionar un amplio número de submuestras con las que entrenar el modelo). En este caso, además, se une el hecho habitual de que las series temporales no son excesivamente amplias.
Lo normal para hacer validación cruzada consiste en elegir una muestra de datos de entrenamiento (desde el principio o desde una observación adecuada para nuestros objetivos), entrenar el conjunto de modelos correspondientes para esa muestra y, posteriormente, realizar predicciones al horizonte correspondiente y validarlas con los datos no utilizados en el entrenamiento.
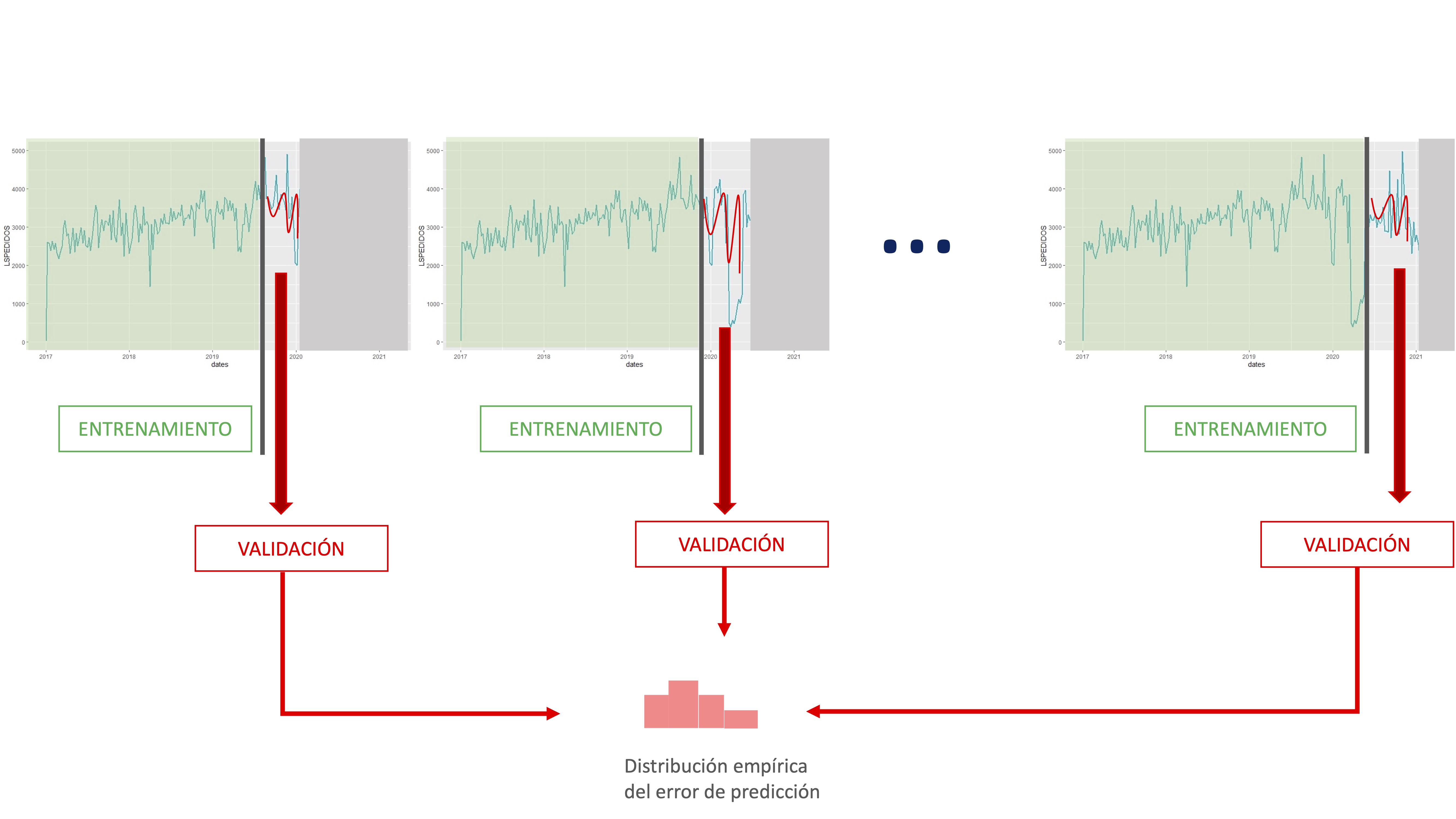
De esta manera, vamos obteniendo información asociada a la habilidad predictiva de cada modelo mediante el almacenamiento de sus errores de predicción. Presentamos, a continuación, un esquema numérico para la realización de la validación cruzada. El ejemplo lo vamos a realizar con la serie de inflación, tratando de ver qué especificación de “indicador adelantado” es mejor. Para ello, en el modelo
\[ \Delta IPC_{t}=\alpha+\beta_1 \Delta UNC_{t-1}+\beta_2\Delta UNC_{t-2}+...+\beta_k\Delta UNC_{t-k}+u_{t} \]
Entrenaremos cuatro versiones \(k=1\), \(k=2\), \(k=3\) y \(k=4\). Nos parece razonable pensar que, como mucho, la incertidumbre pasada que afecte a la inflación será la de 4 periodos (meses) atrás.
library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)
install.packages("dynlm")
library(dynlm)
inflacion<- read_excel("TS_INF_UNC.xlsx")
df_ts <- ts(xts(inflacion[,2:3],order.by = inflacion$Date), frequency = 12, start = c(2002,1))
d_IPC= diff(df_ts[,"IPC"])
d_UNC=diff(df_ts[,"UNC"])
#Elijo cuantos datos quiero tener para empezar
T <- 100
#obtengo el total de datos de la muestra
n<-length(d_IPC)
#genero dos vectores vacíos para almacenar errores
error1<-vector()
error2<-vector()
error3<-vector()
error4<-vector()
#Creo un bucle que va a ir elaborando predicciones a horizonte 1
for(i in 1:(n-T-1)) {
#extrae la muestra con la que entrenará
IPCshort <- d_IPC[1:(T+i)]
d_UNCshort <- d_UNC[1:(T+i)]
#extrae el dato real con el que comparar
IPCnext <- d_IPC[(T+i+1)]
#convierte en series temporales las variables que se van a utilizar
IPCshort = ts(IPCshort, frequency = 12, start=c(2002,02))
d_UNCshort = ts(d_UNCshort, frequency = 12, start=c(2002,02))
#Entrena los modelos de indicador adelantado con "hasta cuatro meses de adelanto"
fit1 <- dynlm(IPCshort~L(d_UNCshort,1))
fit2 <- dynlm(IPCshort~L(d_UNCshort,1)+L(d_UNCshort,2))
fit3 <- dynlm(IPCshort~L(d_UNCshort,1)+L(d_UNCshort,2)+L(d_UNCshort,3))
fit4 <- dynlm(IPCshort~L(d_UNCshort,1)+L(d_UNCshort,2)+L(d_UNCshort,3)+L(d_UNCshort,4))
#obtengo las predicciones (a mano) de cada modelo.
forecast1<-fit1$coefficients[1]+ fit1$coefficients[2]*tail(d_UNCshort,n=1)
forecast2<-fit2$coefficients[1]+ fit2$coefficients[2]*tail(d_UNCshort,n=1)+fit2$coefficients[3]*tail(d_UNCshort,n=2)[1]
forecast3<-fit3$coefficients[1]+ fit3$coefficients[2]*tail(d_UNCshort,n=1)+fit3$coefficients[3]*tail(d_UNCshort,n=2)[1]+fit3$coefficients[4]*tail(d_UNCshort,n=3)[1]
forecast4<-fit4$coefficients[1]+ fit4$coefficients[2]*tail(d_UNCshort,n=1)+fit4$coefficients[3]*tail(d_UNCshort,n=2)[1]+fit4$coefficients[4]*tail(d_UNCshort,n=3)[1]+fit4$coefficients[5]*tail(d_UNCshort,n=4)[1]
#obtengo los errores de predicción (porcentuales en valor absoluto )
error1[i]<-abs((IPCnext-forecast1)/IPCnext)
error2[i]<-abs((IPCnext-forecast2)/IPCnext)
error3[i]<-abs((IPCnext-forecast3)/IPCnext)
error4[i]<-abs((IPCnext-forecast4)/IPCnext)
}
hgm1 <- hist(error1, breaks = 20, plot = FALSE)
hgm2 <- hist(error2, breaks = 20, plot = FALSE)
hgm3 <- hist(error3, breaks = 20, plot = FALSE)
hgm4 <- hist(error4, breaks = 20, plot = FALSE)
c1 <- rgb(173,216,230,max = 255, alpha = 80)
c2 <- rgb(180,150,30,max = 255, alpha = 80)
c3 <- rgb(0,50,50,max = 255, alpha = 80)
c4 <- rgb(50,25,230,max = 255, alpha = 80)
plot(hgm1, col = c1,main="Errores de los modelos", xlab="errores")
plot(hgm2, col = c2, add = TRUE)
plot(hgm3, col = c3, add = TRUE)
plot(hgm4, col = c4, add = TRUE) ¿Con qué modelo quedarse?
En general, no hay un criterio claro que nos permita decantarnos por un único modelo. Puede darse el caso, como en este ejemplo si hace los gráficos de error de predicción, de que los candidatos predigan de forma similar (donde podría ser interesante promediar las predicciones de cada uno de los modelos elegidos) o que haya interesantes diferencias entre ellos. En general, parece sensato buscar alguna forma de combinar los modelos. Una propuesta para combinarlos puede ser desde hacer una media aritmética de las predicciones o, por ejemplo, una media ponderada en función de cuál prediga mejor.
- En este caso, si hace los gráficos, comprobará que todos tienen un comportamiento similar. Entonces, le convendrá quedarse con el más sencillo. Lo siguiente que deberá juzgar es la distribución del error del modelo 1
finite1<-is.finite(error1)
error1<-error1[finite1]
#modelo sólo con indicador adelantado
summary(error1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.01784 0.59126 0.86404 1.62145 1.35779 34.51434
- Note que el error es en tanto por uno, por lo que el 25% mejor de los escenarios simulados cometen un error cercano al 60%. El error mediano es un 86% y el 25 % peor de los modelos comete un 135% de error.
- El error medio parece poco representativo, puesto que dado el error máximo en la muestra, este está sesgado hacia la derecha.
¿Puede mejorar estos resultados?