Review 1

Measures of central tendency and measures of dispersion

Mean, median, mode

Median: The median is the middle value of the ordered sample values. It is the number which is half-way into the list of reported values

Mode: The mode is the value with highest frequency in the sample.

Mean:

\[\overline{x} = \frac{1}{n}\sum x_i\]

Easier way to calculate the mean

Sample: 0, 0, 1, 3, 3, 4, 4, 4, 5, 8.

x f fx
0 2 0
1 1 1
3 2 6
4 3 12
5 1 5
8 1 8
\(\sum x = 21\) \(\sum f=10\) \(\sum fx=32\)

\[\overline{x} = \frac{\sum fx}{\sum f} = \frac{32}{10} = 3.2\]

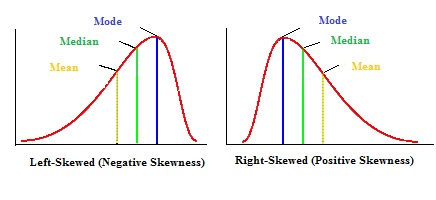
Skweness

It is important to understand how the skewness of a distribution influences the relationship between the mean, median and mode. The figure below is from here.

Standard deviation

\[sd = \sqrt{\frac{f(x - \overline{x})^2}{n-1} }\]

\(x\) f fx \(x - \overline{x}\) \((x - \overline{x})^2\) \(f(x - \overline{x})^2\)
… … … … … …
. \(\sum f\) \(\sum fx\) \(\sum above = A\)

Calculate the standard deviation: \[sd = \sqrt{\frac{A}{n-1} }\]

Variance

\[variance = sd^2\]

Z-scores

\[z=\frac{x_i-\overline{x}}{sd}\]

where \(s\) is the sample standard deviation

Recall that, for the z-distribution:

  • Mean = 0
  • SD = 1

Confidence intervals

Standard error: \[se = \frac{sd}{\sqrt{n}}\]

CIs: \[\text{Lower bound} = \bar x - z_{(\frac{\alpha}{2})}se\]

\[\text{Upper bound} = \bar x + z_{(\frac{\alpha}{2})}se\]

  • For 95% CI: \(z_{(\frac{\alpha}{2})}= z_{0.025} \approx 2\)
  • For 99% CI: \(z_{(\frac{\alpha}{2})}= z_{0.005} \approx 3\)

Hypothesis testing: one-sample t-test

\[t = \frac {\bar x-\mu_0}{se}\]

    1. We reject the null hypothesis only when the calculated \(t\) is higher than the critical value (\(c_\alpha\)).
    1. We reject the null hypothesis only when \(p \leq \alpha\)
    1. We reject the null hypothesis if the mean difference CI does not include 0.

Practice questions

  1. Suppose \(\overline{x} = 10\) for a negatively skewed distribution. What could be the median and mode of this distribution?
  1. median = 11 and mode = 12
  2. median = 12 and mode = 11
  1. Suppose you created a z-score distribution from a given sample. What is the mean of this distribution?
  1. 1
  2. 0
  3. There is not enough information to calculate the mean.
  1. The p-value equals:
  1. \(\alpha\)
  2. The significance level
  3. 0.05
  1. What is the percentile of a z-score \(z= 1.18\)
  1. 45%
  2. 17%
  3. 88%
  1. Using the z-table, find the values of z:
  1. That is just above 97.5% of all values in the distribution.
  2. That is just above 99.5% of all values in the distribution.
  1. Using the t-table, find the value of t for:
  1. Two-tail, \(\alpha=0.05\) (n=31)
  2. One-tail, \(\alpha=0.05\) (n=31)
  3. Two-tail, \(\alpha=0.01\) (n=31)
  4. One-tail, \(\alpha=0.01\) (n=31)
  1. Compared to a 95% confidence interval, a 99% confidence interval:
  1. Is more precise
  2. Is more accurate
  1. If \(p = 0.03\)
  1. We reject the null when \(\alpha = 0.05\)
  2. We reject the null when \(\alpha = 0.01\)
  3. We never reject the null
  1. As the absolute value of \(t_{calculated}\) increases, we are:
  1. More likely to reject the null
  2. Less likely to reject the null
  1. Given a 95% mean difference CI = (-0.12;1.2), do we reject the null that the population mean = 15 (assuming \(\alpha = 0.05)\)?
  1. Yes
  2. No
  1. As sample size increases a 95% CI becomes:
  1. Narrower, more precise
  2. Less accurate