Topic 2 Measures of central tendency and dispersion

2.1 Central tendency

• Mean
• Median
• Mode

Example

We asked 10 people to report the number of books they each read last month.

They reported the following:

5, 3, 4, 3, 0, 1, 4, 4, 8, 0.

Some notation

Before we calculate the mode we need to know the following notation (this will also be useful for calculating the mean, variance, standard deviation…)

• $x$: refers to each value taken by a given variable in the sample. In this example, the variable “number of books” takes the values: 0, 1, 3, 4, 5 and 8.
• $f$: refers to the frequency of each of the $x$ values (the number of times individuals reported this value)

Easy way to calculte: write the following table:

Values in order: 0, 0, 1, 3, 3, 4, 4, 4, 5, 8.

x	f	fx
0	2	0
1	1	1
3	2	6
4	3	12
5	1	5
8	1	8
$\sum x = 21$	$\sum f=10$	$\sum fx=32$

2.1.1 Mean

The mean is the unweighted average of the values in the sample.

$$\overline{x} = \frac{1}{n}\sum x_i$$ Note tha $x_i$ refers to each observation reported in the sample (it is not the same as $x$).

This can take a long time to calculate by hand.

Easier way to calculate the mean (see Prof. Hassad’s notes):

$$\overline{x} = \frac{\sum fx}{\sum f} = \frac{32}{10} = 3.2$$

2.1.2 Median

Step 1: list all values in ascending order.

0, 0, 1, 3, 3, 4, 4, 4, 5, 8.

Step 2: Do I have an odd or even total number of reported values?

Even total: There are two middle values. The median is the average between those two values.

In the number of books example, the median is: $$Median = \frac{3+4}{2} = 3.5$$

Odd total: There is only one middle value. The median is this middle value.

2.1.3 Mode

The mode is the value with highest frequency (highest f).

How about the following:

x	f
0	2
1	3
3	3
4	3
5	1
8	1

All of those are the mode.

Intuition: How many winners are there if runners tie in first place in a given competition?

How about the following?

x	f
0	1
1	1
3	1
4	1
5	1
8	1

Here there is no mode.

Normal distribution:

Mean = Median = Mode

Mode, Mean, and Meadian are useful to discribe the shape of a distribution.

But they are not enough! We need new tools.

2.2 Measures of dispersion

• Variance
• Standard deviation
• Range
• Skewness

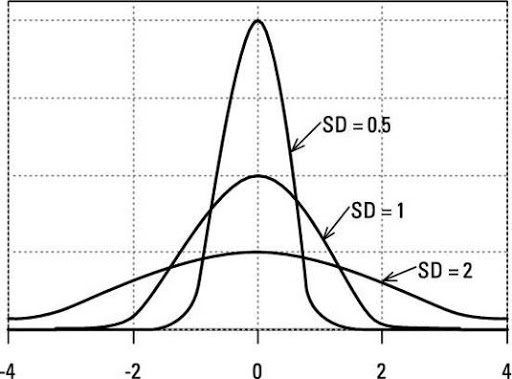
2.2.1 Standard deviation

Use the same table and expand it:

Note that $\overline{x}$ is the mean you just calculated.

$x$	f	fx	$x - \overline{x}$	$(x - \overline{x})^2$	$f(x - \overline{x})^2$
…	…	…	…	…	…
.	$\sum f$	$\sum fx$			$\sum above = A$

Calculate the standard deviation:

Or, more formally:

$$sd = \sqrt{\frac{f(x - \overline{x})^2}{n-1} }$$

$$sd = \sqrt{\frac{A}{n-1} }$$

Note that the standard deviation of a standard normal distribution is 1.

2.2.2 Variance:

$$variance = sd^2$$

Note that the variance of a standard normal distribution is 1.

2.2.3 Range

Range = Max-Min

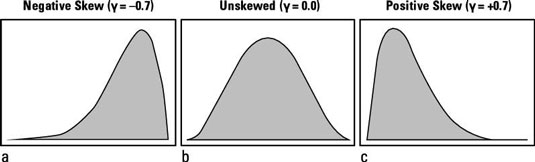
2.2.4 Skewness

• If skewness is more than 1 or less than -1, then we have a highly skewed distribution.
• If skewness is between -1 and -1/2 or between 1 and 1/2, then we have a moderatly skewed distribution.
• If skewness is between -1/2 and 1/2, then we have an approximatly symmetric distribution (or a negligible degree of skewness).

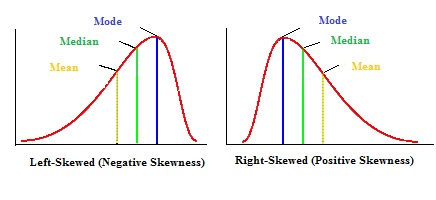
2.2.5 Example of calculations

The following are data for the variable: number of movies watched in the past month.

1; 5; 5; 4; 5; 4; 0; 15; 1; 0; 0; 1.

Calculate: mean, media, mode, variance, standard deviation and range.

$x$	f	fx	$x - \overline{x}$	$(x - \overline{x})^2$	$f(x - \overline{x})^2$
0	3	0	-3.4	11.56	34.68
1	3	3	-2.4	5.76	17.28
4	2	8	0.6	0.36	0.72
5	3	15	1.6	2.56	7.68
15	1	15	11.6	134.56	134.56
.	$\sum f = 12$	$\sum fx = 41$			$\sum above = 194.92$

$$\overline{x} = \frac{\sum fx}{\sum f} = \frac{41}{12} = 3.4$$

Mode = 0 , 1 , 5

Median = (4 + 1) / 2 = 2.5

$$sd = \sqrt{\frac{194.92}{11} } = \sqrt{17.72} = 4.2$$ $$sd^2 = 17.72$$

$$Range = 15 - 0 = -15$$