7 Two Factor Classification with Categorical and Continuous Interactions
In this Chapter we will use the same dataset and will only consider non-missing values of Age, Gender, and Diabetic status.
We will follow much the same process of EDA with categorical features and making connections between the p-value of the chi square test and feature importance in logistic regression.
In addition, we will also have a more in-depth discussion around re-leveling logistic regression analysis and the impact it has on model interpret-ability.
This time we will have 3 primary model examples to compare:
- Logistic regression with rand_class feature
- Logistic regression with binned age and Gender features
- Logistic regression with Age interacted with Gender
A_DATA <- readRDS('C:/Users/jkyle/Documents/GitHub/Jeff_Data_Wrangling/Week_2/DATA/A_DATA.RDS')
library('tidyverse')
#> -- Attaching packages --------------------------------------- tidyverse 1.3.1 --
#> v ggplot2 3.3.3 v purrr 0.3.4
#> v tibble 3.1.2 v dplyr 1.0.6
#> v tidyr 1.1.3 v stringr 1.4.0
#> v readr 1.4.0 v forcats 0.5.1
#> -- Conflicts ------------------------------------------ tidyverse_conflicts() --
#> x dplyr::filter() masks stats::filter()
#> x dplyr::lag() masks stats::lag()
A_DATA <- A_DATA %>%
select(SEQN, Age, Gender, DIABETES) %>%
mutate(DIABETES_factor = as.factor(DIABETES)) %>%
na.omit()
A_DATA %>%
glimpse()
#> Rows: 95,547
#> Columns: 5
#> $ SEQN <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,~
#> $ Age <dbl> 2, 77, 10, 1, 49, 19, 59, 13, 11, 43, 15, 37, 70, 81, ~
#> $ Gender <chr> "Female", "Male", "Female", "Male", "Male", "Female", ~
#> $ DIABETES <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, ~
#> $ DIABETES_factor <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, ~\(~\)
\(~\)
7.1 Bin Age
Additionally, we will create deciles for the Age range:
A_DATA <- A_DATA %>%
mutate(age_bucket = as.factor(ntile(Age,10)))
A_DATA %>%
head()
#> # A tibble: 6 x 6
#> SEQN Age Gender DIABETES DIABETES_factor age_bucket
#> <dbl> <dbl> <chr> <dbl> <fct> <fct>
#> 1 1 2 Female 0 0 1
#> 2 2 77 Male 0 0 10
#> 3 3 10 Female 0 0 3
#> 4 4 1 Male 0 0 1
#> 5 5 49 Male 0 0 8
#> 6 6 19 Female 0 0 5Here’s a nice summary table of the various Age buckets we created:
Age_bucket_Table <- A_DATA %>%
select(Age, age_bucket) %>%
group_by(age_bucket) %>%
summarise(min_age = min(Age),
mean_age = round(mean(Age),2),
median_age = median(Age),
max_age = max(Age),
.groups = 'keep') %>%
ungroup() %>%
mutate(age_range = paste0(min_age, ' <= Age <= ', max_age )) %>%
select(-min_age, -max_age) %>%
arrange(age_bucket)
Age_bucket_Table %>%
print(n=10)
#> # A tibble: 10 x 4
#> age_bucket mean_age median_age age_range
#> <fct> <dbl> <dbl> <chr>
#> 1 1 2.22 2 1 <= Age <= 4
#> 2 2 6.52 7 4 <= Age <= 9
#> 3 3 11.2 11 9 <= Age <= 13
#> 4 4 15.6 16 13 <= Age <= 18
#> 5 5 21.2 21 18 <= Age <= 26
#> 6 6 31.0 31 26 <= Age <= 36
#> 7 7 41.4 41 36 <= Age <= 47
#> 8 8 52.4 52 47 <= Age <= 59
#> 9 9 63.9 64 59 <= Age <= 70
#> 10 10 77.3 78 70 <= Age <= 85\(~\)
\(~\)
7.2 Add noise feature
Additionally, we add a variable rand_class to the data-set. rand_class will be sampled from the options of Rand_A or Rand_B. We will then randomly sort the data, and for every 5th row we will assign Rand_C to rand_class:
set.seed(85763099)
A_DATA$rand_class <- sample(c('Rand_A','Rand_B'),
size = nrow(A_DATA),
replace = TRUE)
A_DATA$rand_sort <- runif(nrow(A_DATA))
A_DATA <- A_DATA %>%
arrange(rand_sort) %>%
mutate(rn = row_number()) %>%
mutate(rn_mod_5 = rn %% 5 ) %>%
mutate(rand_class = if_else( rn_mod_5 == 0,
"Rand_C",
rand_class)) %>%
select(-rn, -rn_mod_5, -rand_sort) %>%
mutate(rand_class = as.factor(rand_class))A_DATA %>%
head()
#> # A tibble: 6 x 7
#> SEQN Age Gender DIABETES DIABETES_factor age_bucket rand_class
#> <dbl> <dbl> <chr> <dbl> <fct> <fct> <fct>
#> 1 55074 1 Female 0 0 1 Rand_A
#> 2 14467 20 Female 0 0 5 Rand_B
#> 3 70222 60 Male 0 0 9 Rand_A
#> 4 4265 4 Male 0 0 1 Rand_A
#> 5 37574 38 Male 0 0 7 Rand_C
#> 6 38302 32 Female 0 0 6 Rand_A\(~\)
\(~\)
7.3 dplyr statistics
For categorical data we are typically reviewing counts between various groups:
A_DATA %>%
group_by(DIABETES, Gender) %>%
tally() %>%
pivot_wider(names_from = Gender, values_from = n)
#> # A tibble: 2 x 3
#> # Groups: DIABETES [2]
#> DIABETES Female Male
#> <dbl> <int> <int>
#> 1 0 45188 43552
#> 2 1 3371 3436A_DATA %>%
group_by(DIABETES, rand_class) %>%
tally() %>%
pivot_wider(names_from = rand_class, values_from = n)
#> # A tibble: 2 x 4
#> # Groups: DIABETES [2]
#> DIABETES Rand_A Rand_B Rand_C
#> <dbl> <int> <int> <int>
#> 1 0 35506 35503 17731
#> 2 1 2712 2717 1378\(~\)
\(~\)
7.4 chisq.test
Suppose that \(n\) observations in a random sample from a population are classified into \(k\) mutually exclusive classes with respective observed numbers \(O_i\) (for \(i = 1, 2, \ldots, k\)).
The null hypothesis in the chi-square test assumes \(p_i\) is the probability that an observation falls into the \(i\)-th class.
Therefore, for all \(i\), we have an expected frequencies: \[E_{i} = n \cdot p_{i}\]
Note since the \(p_i\) are probabilities we have that:
\[\sum_{i=1}^k p_i = 1 \] Since there are \(n\) observations we have:
\[ n = n \sum_{i=1}^k p_i = \sum_{i=1}^k n \cdot p_i = \sum_{i=1}^k E_{i} \]
However, we have observed values:
\[ \sum_{i=1}^k O_i = n \]
Therefore, under the null hypothesis of the chi-square we have that:
\[ \sum_{i=1}^k E_{i} = n \sum_{i=1}^kp_i = \sum_{i=1}^kO_i \] For the chi-squared test statistic We define :
\[ \chi^2 \sim \sum_{i=1}^k\frac{(O_i - E_i)^2}{E_i} = n \cdot \sum_{i=1}^k \frac{ \left( \frac{O_i}{n} - p_i \right)^2 }{p_i}\]
where \(\chi^2\) is the chi-square distribution with:
- \(k-1\) degrees of freedom
- \(O_{i}\) = the number of observations of type \(i\).
- \(E_{i} = n \cdot p_{i}\) = the expected (theoretical) frequency of type \(i\), asserted by the null hypothesis that the fraction of type \(i\) in the population is \(p_{i}\)
\(~\)
\(~\)
7.5 Gender
In this section we will compare t-tests on Gender between groups of DIABETES.
First we can create a table of Gender and DIABETES:
tbl_DM2_Gender <- table(A_DATA$DIABETES, A_DATA$Gender)
tbl_DM2_Gender
#>
#> Female Male
#> 0 45188 43552
#> 1 3371 3436Notice this gives the same result as our dplyr query.
Let’s compare the mean ages between the Diabetic and non-Diabetic populations:
chisq.tbl_DM2_Gender <- chisq.test(tbl_DM2_Gender)Here’s a look at the output
chisq.tbl_DM2_Gender
#>
#> Pearson's Chi-squared test with Yates' continuity correction
#>
#> data: tbl_DM2_Gender
#> X-squared = 4.8966, df = 1, p-value = 0.02691let’s review the structure
str(chisq.tbl_DM2_Gender,1)
#> List of 9
#> $ statistic: Named num 4.9
#> ..- attr(*, "names")= chr "X-squared"
#> $ parameter: Named int 1
#> ..- attr(*, "names")= chr "df"
#> $ p.value : num 0.0269
#> $ method : chr "Pearson's Chi-squared test with Yates' continuity correction"
#> $ data.name: chr "tbl_DM2_Gender"
#> $ observed : 'table' int [1:2, 1:2] 45188 3371 43552 3436
#> ..- attr(*, "dimnames")=List of 2
#> $ expected : num [1:2, 1:2] 45100 3459 43640 3348
#> ..- attr(*, "dimnames")=List of 2
#> $ residuals: 'table' num [1:2, 1:2] 0.417 -1.504 -0.423 1.529
#> ..- attr(*, "dimnames")=List of 2
#> $ stdres : 'table' num [1:2, 1:2] 2.23 -2.23 -2.23 2.23
#> ..- attr(*, "dimnames")=List of 2
#> - attr(*, "class")= chr "htest"For instance here are the observed:
chisq.tbl_DM2_Gender$observed
#>
#> Female Male
#> 0 45188 43552
#> 1 3371 3436Note this is the same as tbl_DM2_Gender
tbl_DM2_Gender == chisq.tbl_DM2_Gender$observed
#>
#> Female Male
#> 0 TRUE TRUE
#> 1 TRUE TRUEThe expected distribution should be:
chisq.tbl_DM2_Gender$expected
#>
#> Female Male
#> 0 45099.539 43640.461
#> 1 3459.461 3347.539The residulas are Person residuals and are defined as (observed - expected) / sqrt(expected):
chisq.tbl_DM2_Gender$residuals
#>
#> Female Male
#> 0 0.4165484 -0.4234546
#> 1 -1.5039980 1.52893377.5.1 p-value review
Review the p-value of the chi-square test between two groups.
The null hypothesis is that each person’s gender is independent of the person’s diabetic status.
If the p-value is
- greater than .05 then we accept the null-hypothesis
- less than .05 then we reject the null-hypothesis
7.5.2 broom
We can tidy-up the results if we utilize the broom package. Recall that broom::tidy tells R to look in the broom package for the tidy function. The tidy function in the broom library converts many base R outputs to tibbles.
tibble_chisq.tbl_DM2_Gender <- broom::tidy(chisq.tbl_DM2_Gender) %>%
mutate(dist_1 = "Non_DM2.Gender") %>%
mutate(dist_2 = "DM2.Gender")the broom::tidy transforms the list return of chisq.test output into a tibble we can also add variable to help us remember where the data came from.
tibble_chisq.tbl_DM2_Gender %>%
glimpse()
#> Rows: 1
#> Columns: 6
#> $ statistic <dbl> 4.896648
#> $ p.value <dbl> 0.02690888
#> $ parameter <int> 1
#> $ method <chr> "Pearson's Chi-squared test with Yates' continuity correctio~
#> $ dist_1 <chr> "Non_DM2.Gender"
#> $ dist_2 <chr> "DM2.Gender"Our current p-value is tibble_chisq.tbl_DM2_Gender$p.value = 0.0269089, since the p-value is less than .05 we reject the null-hypothesis, Gender is not independent of the person’s diabetic status.
7.6 Associated \(\chi^2\) Plots
7.6.1 Balloon Plot
This balloon plot shows the frequency table, now the area of the circle is proportional to the frequency counts.
gplots::balloonplot(tbl_DM2_Gender,
main ="Balloon Plot for Gender by Diabetes \n Area is proportional to Freq.")
7.6.2 vcd::mosaic
With the vcd::mosaic function you get another “area graph” this time with the groups highlighted by color:
library(vcd)
#> Loading required package: grid
mosaic(A_DATA$DIABETES ~ A_DATA$Gender,
gp = shading_max,
main = "Mosaic plot of Gender by Diabetic Status")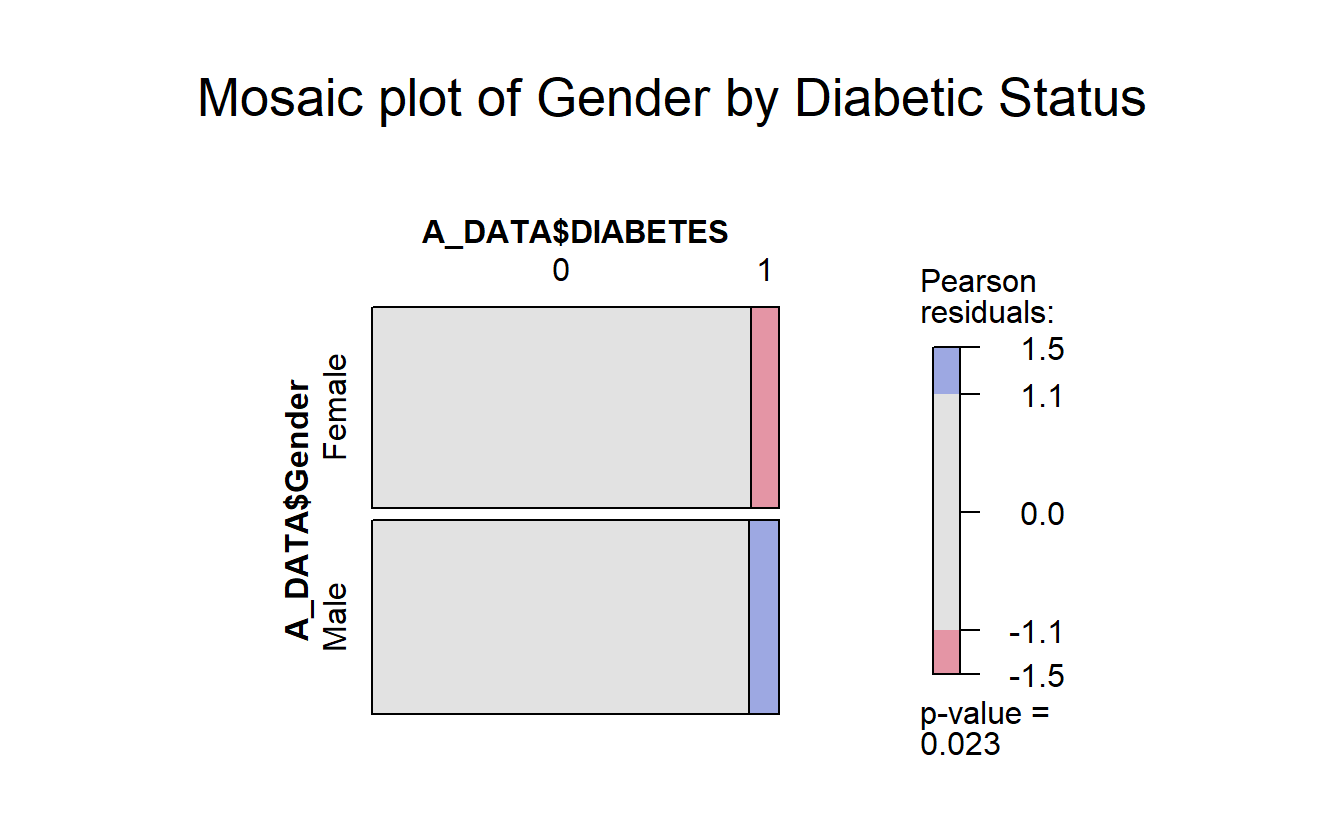
In the vcd::mosaic plot:
- Blue indicates that the observed value is higher than the expected value if the data were random.
- Red color specifies that the observed value is lower than the expected value if the data were random.
For example, from this mosaic plot, it can be seen that the number of Diabetic males is higher than expected.
7.6.3 corrplot::corrplot
corrplot::corrplot(chisq.tbl_DM2_Gender$residuals,
is.cor = FALSE)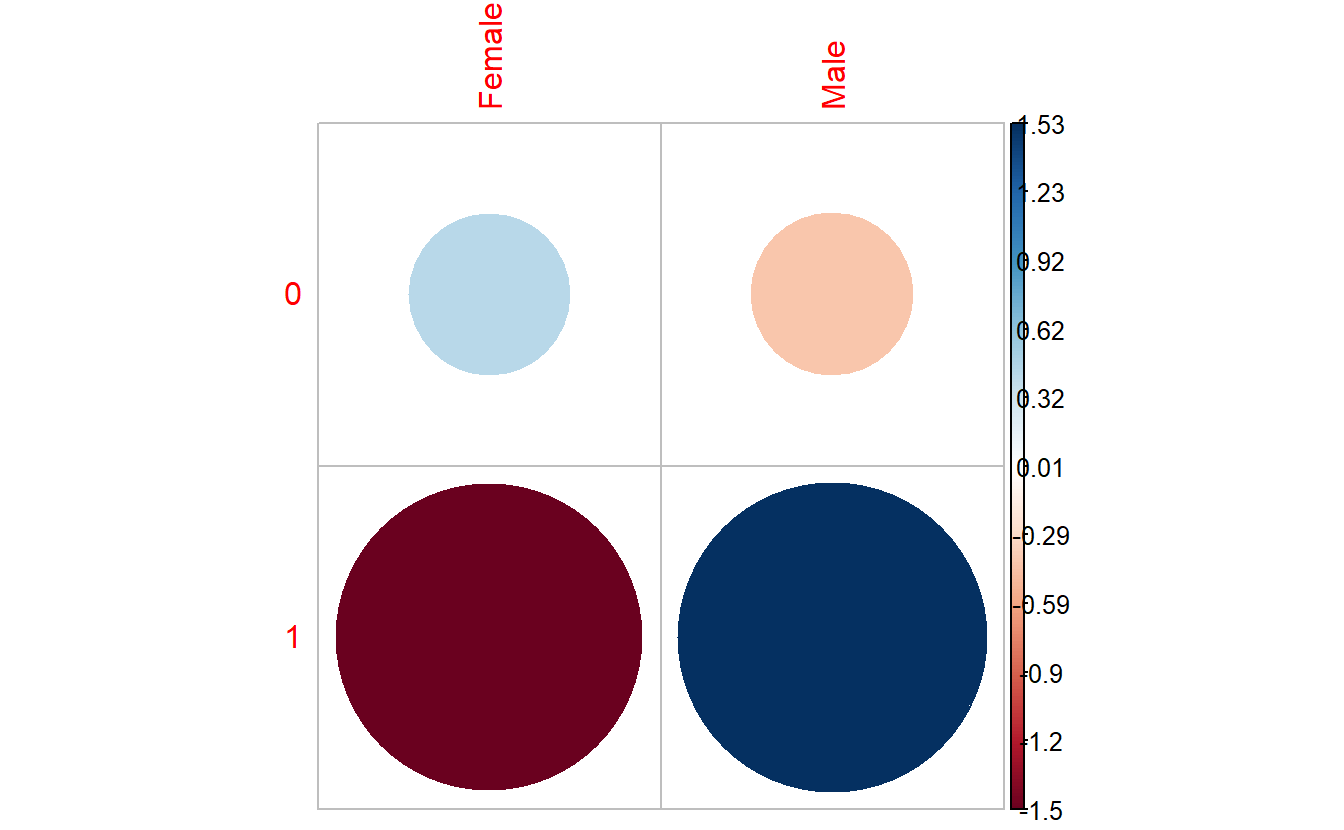
In the corrplot::corrplot plot:
Positive residuals are in blue. Positive values specify an attraction (positive association) between the corresponding row and column variables. In the image above, we can see there are an association between
DIABETESand being a Male.Negative residuals are in red. This implies a repulsion (negative association) between the corresponding row and column variables. For example the
DIABETICs are negatively associated (or “not associated”) with the Females.
\(~\)
\(~\)
7.7 rand_class chisq.test
As we did with Gender above, we can extract lists of rand_classs for each type of DIABETES:
tbl_DM2_rand_class <- table(A_DATA$DIABETES, A_DATA$rand_class)
tbl_DM2_rand_class
#>
#> Rand_A Rand_B Rand_C
#> 0 35506 35503 17731
#> 1 2712 2717 1378Let’s compute chisq.test for rand_class and the Diabetic and non-Diabetic populations:
chisq.test.tbl_DM2_rand_class <- chisq.test(tbl_DM2_rand_class)
chisq.test.tbl_DM2_rand_class
#>
#> Pearson's Chi-squared test
#>
#> data: tbl_DM2_rand_class
#> X-squared = 0.27803, df = 2, p-value = 0.8702tibble_chisq.test.tbl_DM2_rand_class <- broom::tidy(chisq.test.tbl_DM2_rand_class) %>%
mutate(dist_1 = "Non_DM2.rand_class") %>%
mutate(dist_2 = "DM2.rand_class")
tibble_chisq.test.tbl_DM2_rand_class %>%
glimpse()
#> Rows: 1
#> Columns: 6
#> $ statistic <dbl> 0.278026
#> $ p.value <dbl> 0.8702167
#> $ parameter <int> 2
#> $ method <chr> "Pearson's Chi-squared test"
#> $ dist_1 <chr> "Non_DM2.rand_class"
#> $ dist_2 <chr> "DM2.rand_class"7.7.1 plots
gplots::balloonplot(tbl_DM2_rand_class,
main ="Balloon Plot for rand_class by Diabetes \n Area is proportional to Freq.")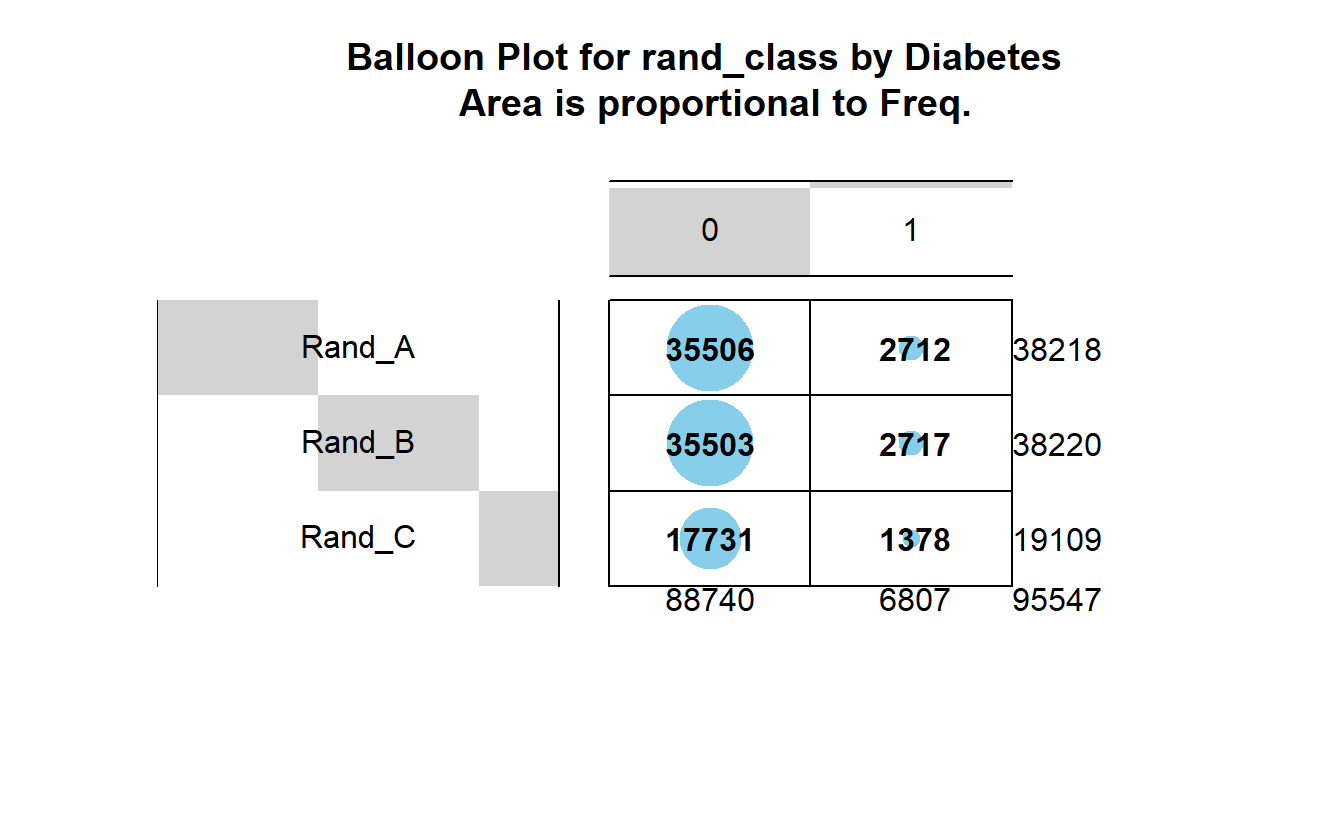
mosaic(A_DATA$DIABETES ~ A_DATA$rand_class,
gp = shading_max,
main = "Mosaic plot of rand_class by Diabetic status")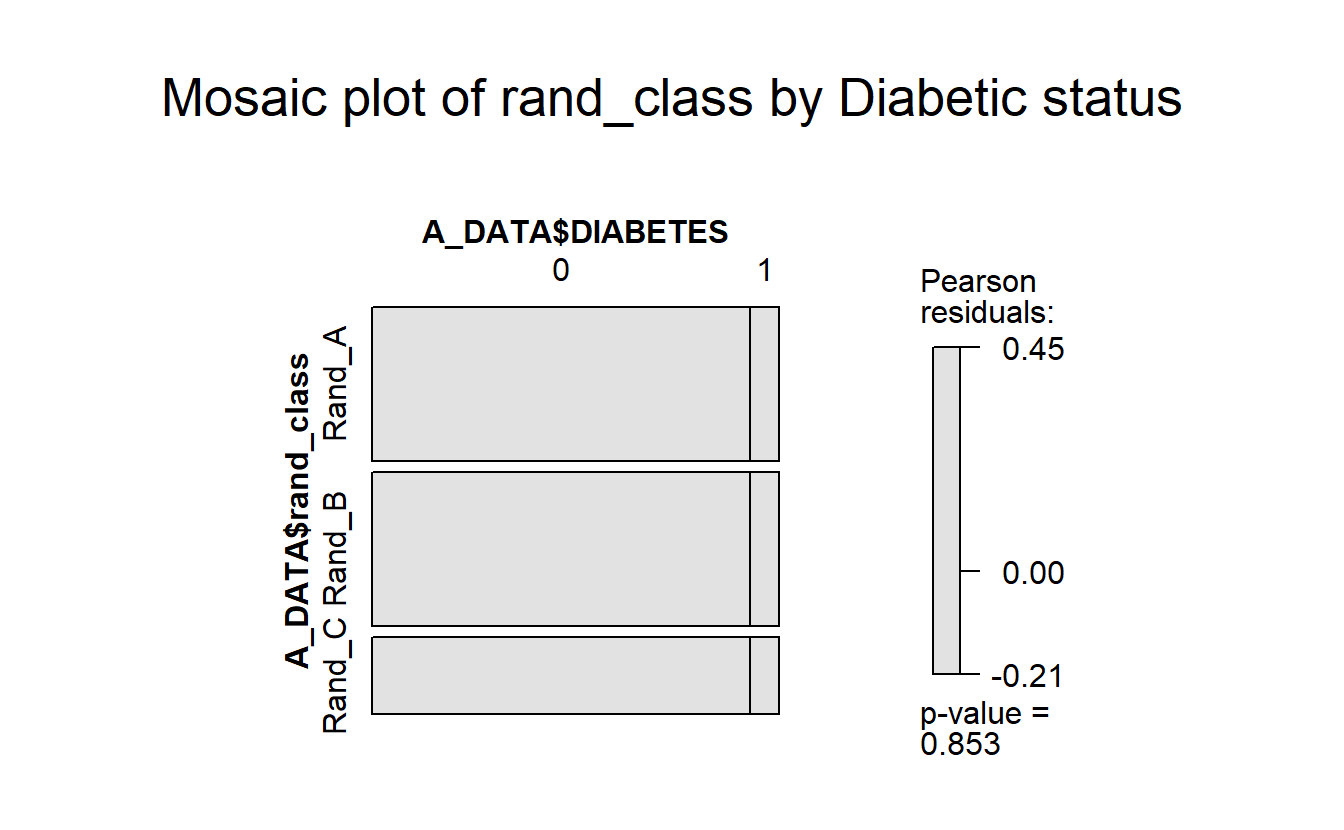
Again, notice the lack of color and the p-value of 0.8702167
corrplot::corrplot(chisq.test.tbl_DM2_rand_class$residuals,
is.cor = FALSE)
We can see there are an association between DIABETES and being in Rand_C, however, it’s not a strong enough to give us a statistically significant chi-square p-value.
bind_rows(tibble_chisq.tbl_DM2_Gender,
tibble_chisq.test.tbl_DM2_rand_class) %>%
select(statistic, p.value, dist_1, dist_2)
#> # A tibble: 2 x 4
#> statistic p.value dist_1 dist_2
#> <dbl> <dbl> <chr> <chr>
#> 1 4.90 0.0269 Non_DM2.Gender DM2.Gender
#> 2 0.278 0.870 Non_DM2.rand_class DM2.rand_classWe see that the p.value is near 0 for Gender but close to 1 for rand_class, our interpretation is that Gender has a statistically significant impact on Diabetic status whereas rand_class does not.
\(~\)
\(~\)
7.8 Non-Missing Data
A_DATA.no_miss <- A_DATA %>%
select(SEQN, DIABETES, DIABETES_factor, Age, age_bucket, Gender, rand_class) %>%
mutate(DIABETES_factor = fct_relevel(DIABETES_factor, c('0','1') ) ) %>%
na.omit()7.8.1 ANOVA
aov(DIABETES ~ age_bucket,
data = A_DATA.no_miss) %>%
summary()
#> Df Sum Sq Mean Sq F value Pr(>F)
#> age_bucket 9 786 87.35 1507 <2e-16 ***
#> Residuals 95537 5536 0.06
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1aov(DIABETES ~ Gender,
data = A_DATA.no_miss) %>%
summary()
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Gender 1 0 0.3277 4.953 0.0261 *
#> Residuals 95545 6322 0.0662
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1aov(DIABETES ~ rand_class,
data = A_DATA.no_miss) %>%
summary()
#> Df Sum Sq Mean Sq F value Pr(>F)
#> rand_class 2 0 0.00920 0.139 0.87
#> Residuals 95544 6322 0.06617aov(DIABETES ~ rand_class + age_bucket + Gender,
data = A_DATA.no_miss) %>%
summary()
#> Df Sum Sq Mean Sq F value Pr(>F)
#> rand_class 2 0 0.01 0.159 0.85321
#> age_bucket 9 786 87.35 1507.513 < 2e-16 ***
#> Gender 1 1 0.54 9.270 0.00233 **
#> Residuals 95534 5535 0.06
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1\(~\)
\(~\)
7.8.2 split data
sample.SEQN <- sample(A_DATA.no_miss$SEQN,
size = nrow(A_DATA.no_miss)*.6,
replace = FALSE)A_DATA.train <- A_DATA.no_miss %>%
filter(SEQN %in% sample.SEQN)
A_DATA.test <- A_DATA.no_miss %>%
filter(!(SEQN %in% sample.SEQN))\(~\)
\(~\)
7.9 Train Logistic Regression Models
7.9.1 RAND
RAND <- glm(DIABETES_factor ~ rand_class,
data= A_DATA.train,
family = "binomial")7.9.1.1 RAND Model Output
library('broom')
RAND
#>
#> Call: glm(formula = DIABETES_factor ~ rand_class, family = "binomial",
#> data = A_DATA.train)
#>
#> Coefficients:
#> (Intercept) rand_classRand_B rand_classRand_C
#> -2.60585 0.02914 0.06257
#>
#> Degrees of Freedom: 57327 Total (i.e. Null); 57325 Residual
#> Null Deviance: 29180
#> Residual Deviance: 29180 AIC: 29190
summary(RAND)
#>
#> Call:
#> glm(formula = DIABETES_factor ~ rand_class, family = "binomial",
#> data = A_DATA.train)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -0.3890 -0.3828 -0.3828 -0.3775 2.3139
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -2.60585 0.02615 -99.639 <2e-16 ***
#> rand_classRand_B 0.02914 0.03672 0.794 0.427
#> rand_classRand_C 0.06257 0.04431 1.412 0.158
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 29185 on 57327 degrees of freedom
#> Residual deviance: 29183 on 57325 degrees of freedom
#> AIC: 29189
#>
#> Number of Fisher Scoring iterations: 57.9.1.1.1 RAND training errors table
RAND %>%
broom::glance()
#> # A tibble: 1 x 8
#> null.deviance df.null logLik AIC BIC deviance df.residual nobs
#> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <int> <int>
#> 1 29185. 57327 -14591. 29189. 29216. 29183. 57325 573287.9.1.1.2 RAND coefficent table
RAND.CoEff <- RAND %>%
broom::tidy() %>%
mutate(odds_ratio = if_else(term == '(Intercept)',
as.numeric(NA),
round(exp(estimate),4))) %>%
mutate(model = "RAND")
RAND.CoEff %>%
knitr::kable()| term | estimate | std.error | statistic | p.value | odds_ratio | model |
|---|---|---|---|---|---|---|
| (Intercept) | -2.6058458 | 0.0261529 | -99.6390572 | 0.0000000 | NA | RAND |
| rand_classRand_B | 0.0291425 | 0.0367176 | 0.7936917 | 0.4273749 | 1.0296 | RAND |
| rand_classRand_C | 0.0625733 | 0.0443109 | 1.4121414 | 0.1579083 | 1.0646 | RAND |
Notice that when we filter for significant features we find only the intercept:
RAND %>%
broom::tidy() %>%
filter(p.value <= .05) %>%
mutate(odds_ratio = if_else(term == '(Intercept)',
as.numeric(NA),
round(exp(estimate),4)))
#> # A tibble: 1 x 6
#> term estimate std.error statistic p.value odds_ratio
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) -2.61 0.0262 -99.6 0 NA\(~\)
\(~\)
7.9.2 DISCREATE
A_DATA.train %>%
group_by(DIABETES_factor, Gender, rand_class, age_bucket) %>%
summarise(Pop_N = n_distinct(SEQN)) %>%
ggplot(aes(x = age_bucket , y = rand_class , size = Pop_N, color=DIABETES_factor)) +
geom_point() +
facet_grid(DIABETES_factor ~ rand_class + Gender)
#> `summarise()` has grouped output by 'DIABETES_factor', 'Gender', 'rand_class'. You can override using the `.groups` argument.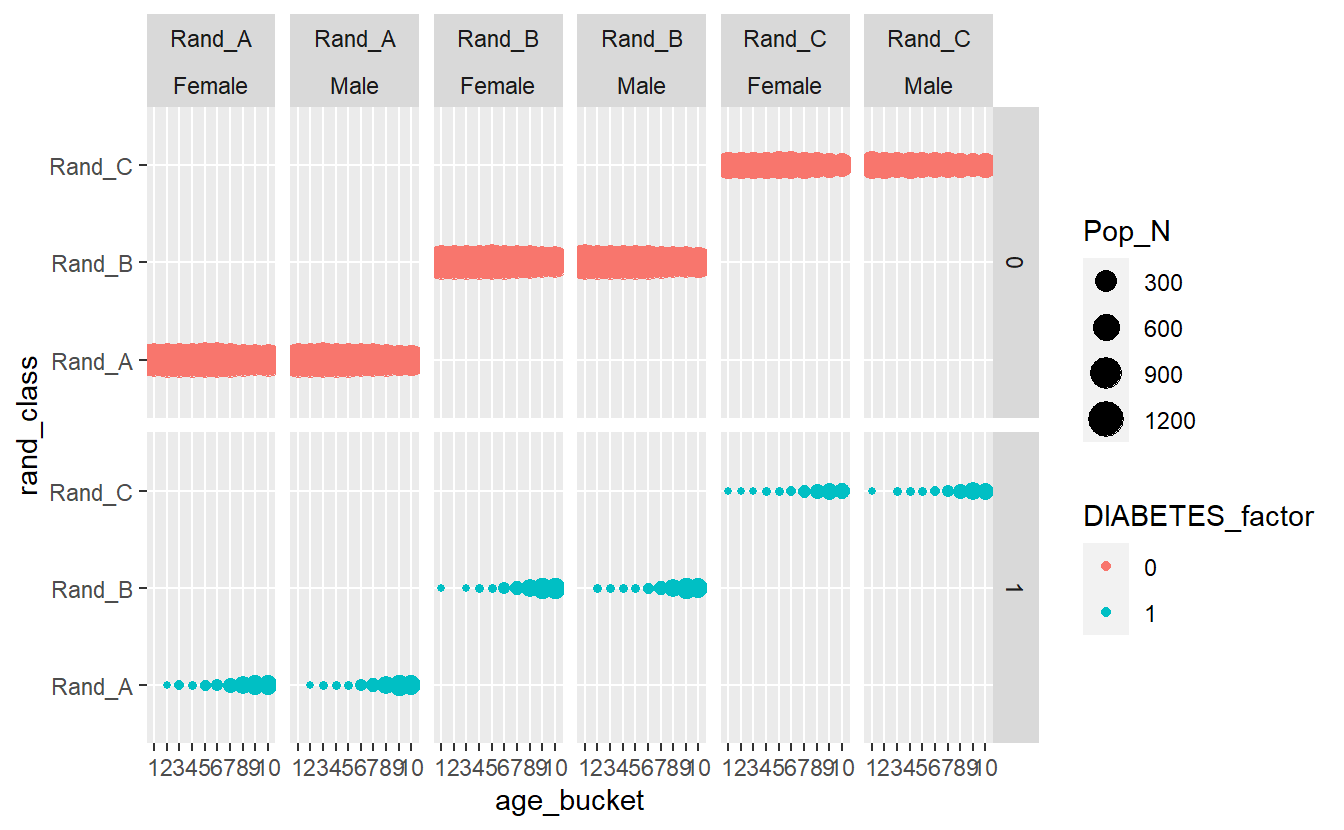
Interactive_DISCREATE <- A_DATA.train %>%
group_by(DIABETES_factor, Gender, rand_class, age_bucket) %>%
summarise(Pop_N = n_distinct(SEQN)) %>%
ggplot(aes(x = age_bucket , y = rand_class , size = Pop_N, color=DIABETES_factor)) +
geom_point() +
facet_wrap(~Gender)
#> `summarise()` has grouped output by 'DIABETES_factor', 'Gender', 'rand_class'. You can override using the `.groups` argument.
Interactive_DISCREATE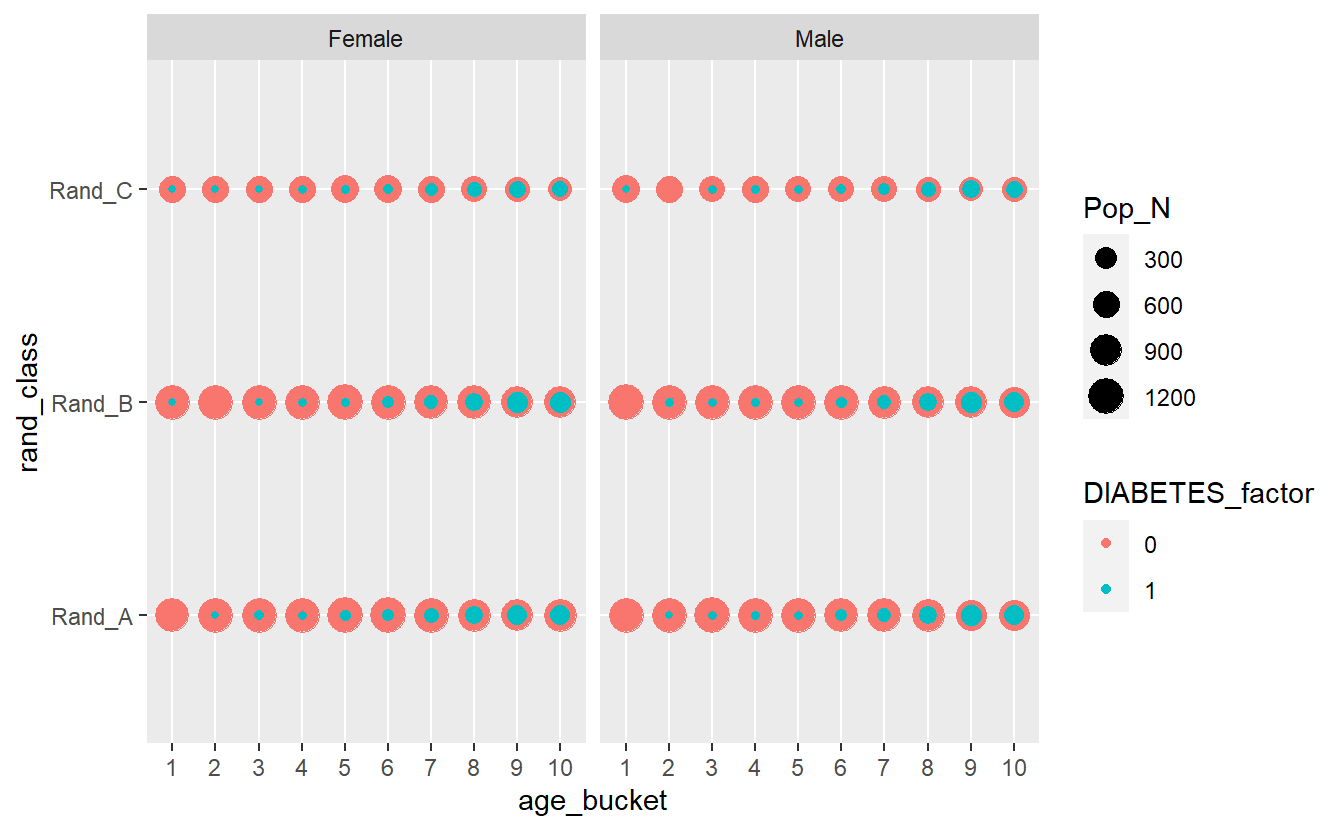
plotly::ggplotly(Interactive_DISCREATE)Most evident from the above graphs is the effect the age_bucket has on the number of diabetics, we can see that as the age buckets increase from 1 to 10 the size of the population bubble also increases.
We can run an anova test on these features:
aov(DIABETES ~ rand_class + age_bucket + Gender,
data = A_DATA.no_miss) %>%
summary()
#> Df Sum Sq Mean Sq F value Pr(>F)
#> rand_class 2 0 0.01 0.159 0.85321
#> age_bucket 9 786 87.35 1507.513 < 2e-16 ***
#> Gender 1 1 0.54 9.270 0.00233 **
#> Residuals 95534 5535 0.06
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Again, our findings here indicated that Gender and age_bucket will have an effect on Diabetes but that rand_class will not.
DISCREATE <- glm( DIABETES_factor ~ age_bucket + Gender,
data= A_DATA.train,
family = "binomial")7.9.2.1 DISCREATE Model Output
Let’s take a moment to review the coefficient table for this DISCRETE model:
DISCREATE.coeff <- DISCREATE %>%
tidy() %>%
mutate(odds_ratio = if_else(term == '(Intercept)',
as.numeric(NA),
round(exp(estimate),4))) %>%
mutate(model = "DISCREATE")
DISCREATE.coeff %>%
knitr::kable()| term | estimate | std.error | statistic | p.value | odds_ratio | model |
|---|---|---|---|---|---|---|
| (Intercept) | -7.6146924 | 0.5762706 | -13.213745 | 0.0000000 | NA | DISCREATE |
| age_bucket2 | 0.9839005 | 0.6759473 | 1.455588 | 0.1455066 | 2.6749 | DISCREATE |
| age_bucket3 | 1.9455128 | 0.6160562 | 3.158012 | 0.0015885 | 6.9972 | DISCREATE |
| age_bucket4 | 2.2471417 | 0.6063191 | 3.706203 | 0.0002104 | 9.4607 | DISCREATE |
| age_bucket5 | 2.5584518 | 0.5979523 | 4.278689 | 0.0000188 | 12.9158 | DISCREATE |
| age_bucket6 | 3.7950325 | 0.5827046 | 6.512790 | 0.0000000 | 44.4797 | DISCREATE |
| age_bucket7 | 4.8899177 | 0.5784673 | 8.453231 | 0.0000000 | 132.9426 | DISCREATE |
| age_bucket8 | 5.7858758 | 0.5771984 | 10.024068 | 0.0000000 | 325.6671 | DISCREATE |
| age_bucket9 | 6.3964667 | 0.5767926 | 11.089718 | 0.0000000 | 599.7223 | DISCREATE |
| age_bucket10 | 6.2919605 | 0.5768601 | 10.907256 | 0.0000000 | 540.2114 | DISCREATE |
| GenderMale | 0.1115659 | 0.0349007 | 3.196670 | 0.0013902 | 1.1180 | DISCREATE |
As we expected, as you get older your risk of diabetes, increases.
#> Warning: Unknown or uninitialised column: `age_rang`.However, these odds ratios may not be as helpful as we would like them to be for interpretation. For instance, right now we can say that when a patient is in the highest age bucket (70 <= Age <= 85) then the odds of having a diabetes increases by 540.2114 times compared to patients in the lowest age bucket ; so having this as the basis of comparison is not as helpful as it could be.
7.9.2.2 re-leveling factors in the DISCREATE model
Sometimes it is helpful to re-leveling factors in R; within the context of logistic regression we will be able to reset our comparison group so that we have a more even basis of comparison - let’s re-level right on the 36 <= Age <= 47 age bucket:
discrete_releveled <- A_DATA.train %>%
mutate(age_bucket = fct_relevel(age_bucket,'7'))now we can fit a new logistic regression
DISCREATE_r <- glm( DIABETES_factor ~ age_bucket + Gender,
data= discrete_releveled,
family = "binomial")DISCREATE_r.coeff <- DISCREATE_r %>%
broom::tidy() %>%
mutate(odds_ratio = if_else(term == '(Intercept)',
as.numeric(NA),
round(exp(estimate),4))) %>%
mutate(model = "Refactored DISCREATE")DISCREATE_r.coeff <- Age_bucket_Table %>%
mutate(term = paste0('age_bucket',age_bucket)) %>%
left_join(DISCREATE_r.coeff) %>%
mutate(model = "Refactored DISCREATE")
#> Joining, by = "term"DISCREATE_r.coeff %>%
knitr::kable()| age_bucket | mean_age | median_age | age_range | term | estimate | std.error | statistic | p.value | odds_ratio | model |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.22 | 2 | 1 <= Age <= 4 | age_bucket1 | -4.8899177 | 0.5784673 | -8.453231 | 0 | 0.0075 | Refactored DISCREATE |
| 2 | 6.52 | 7 | 4 <= Age <= 9 | age_bucket2 | -3.9060171 | 0.3578624 | -10.914857 | 0 | 0.0201 | Refactored DISCREATE |
| 3 | 11.18 | 11 | 9 <= Age <= 13 | age_bucket3 | -2.9444049 | 0.2251338 | -13.078466 | 0 | 0.0526 | Refactored DISCREATE |
| 4 | 15.64 | 16 | 13 <= Age <= 18 | age_bucket4 | -2.6427760 | 0.1969373 | -13.419378 | 0 | 0.0712 | Refactored DISCREATE |
| 5 | 21.24 | 21 | 18 <= Age <= 26 | age_bucket5 | -2.3314659 | 0.1694240 | -13.761130 | 0 | 0.0972 | Refactored DISCREATE |
| 6 | 31.02 | 31 | 26 <= Age <= 36 | age_bucket6 | -1.0948852 | 0.1034459 | -10.584136 | 0 | 0.3346 | Refactored DISCREATE |
| 7 | 41.43 | 41 | 36 <= Age <= 47 | age_bucket7 | NA | NA | NA | NA | NA | Refactored DISCREATE |
| 8 | 52.36 | 52 | 47 <= Age <= 59 | age_bucket8 | 0.8959581 | 0.0656958 | 13.637991 | 0 | 2.4497 | Refactored DISCREATE |
| 9 | 63.91 | 64 | 59 <= Age <= 70 | age_bucket9 | 1.5065490 | 0.0620357 | 24.285211 | 0 | 4.5111 | Refactored DISCREATE |
| 10 | 77.32 | 78 | 70 <= Age <= 85 | age_bucket10 | 1.4020428 | 0.0626430 | 22.381484 | 0 | 4.0635 | Refactored DISCREATE |
Notice that age_bucket7 is missing from the above coefficient table and now we have age_bucket1 this is because we re-factored to level 7, so now all of the odds ratios are computed relative to the age group 36 <= Age <= 47.
When the odds ratio is 1, this means the coefficient in the logistic regression model is ln(1) = 0; meaning changes in the feature has no impact on the outcome.
If a patient is in the highest age bucket, then the odds of having an diabetes increases by 4.0635 times compared to patients aged 36 <= Age <= 47.
In addition to looking for large coefficients or odds ratios we can also review for odds ratios which are between 1 and 0 - these features will have the opposite effect; in that having them reduces the odds of the outcome compared to the baseline group.
So for this example, patient’s in the lowest age bracket decreases their likelihood of having diabetes by 99.25% compared to patients aged 36 <= Age <= 47.
\(~\)
\(~\)
7.9.3 INTERACTION
We can get interaction terms by using * notion:
INTERACTION <- glm(DIABETES_factor ~ Age + Age*Gender ,
data= A_DATA.train,
family = "binomial") 7.9.3.1 INTERACTION Coefficent Table
INTERACTION
#>
#> Call: glm(formula = DIABETES_factor ~ Age + Age * Gender, family = "binomial",
#> data = A_DATA.train)
#>
#> Coefficients:
#> (Intercept) Age GenderMale Age:GenderMale
#> -5.141922 0.054206 -0.126711 0.004352
#>
#> Degrees of Freedom: 57327 Total (i.e. Null); 57324 Residual
#> Null Deviance: 29180
#> Residual Deviance: 23070 AIC: 23080
INTERACTION.CoEff <- INTERACTION %>%
broom::tidy() %>%
mutate(odds_ratio = if_else(term == '(Intercept)',
as.numeric(NA),
round(exp(estimate),4))) %>%
mutate(model= "Interaction")
INTERACTION.CoEff %>%
knitr::kable()| term | estimate | std.error | statistic | p.value | odds_ratio | model |
|---|---|---|---|---|---|---|
| (Intercept) | -5.1419222 | 0.0741063 | -69.385736 | 0.0000000 | NA | Interaction |
| Age | 0.0542061 | 0.0011938 | 45.406599 | 0.0000000 | 1.0557 | Interaction |
| GenderMale | -0.1267111 | 0.1067307 | -1.187204 | 0.2351471 | 0.8810 | Interaction |
| Age:GenderMale | 0.0043521 | 0.0017159 | 2.536280 | 0.0112037 | 1.0044 | Interaction |
\(~\)
\(~\)
7.10 Compare Models
7.10.1 Coefficent Compairson
CoEff_Compare <- bind_rows(RAND.CoEff,
INTERACTION.CoEff,
DISCREATE.coeff,
DISCREATE_r.coeff)
CoEff_Compare %>%
glimpse()
#> Rows: 28
#> Columns: 11
#> $ term <chr> "(Intercept)", "rand_classRand_B", "rand_classRand_C", "(In~
#> $ estimate <dbl> -2.605845822, 0.029142453, 0.062573281, -5.141922164, 0.054~
#> $ std.error <dbl> 0.026152855, 0.036717600, 0.044310917, 0.074106329, 0.00119~
#> $ statistic <dbl> -99.6390572, 0.7936917, 1.4121414, -69.3857359, 45.4065992,~
#> $ p.value <dbl> 0.000000e+00, 4.273749e-01, 1.579083e-01, 0.000000e+00, 0.0~
#> $ odds_ratio <dbl> NA, 1.0296, 1.0646, NA, 1.0557, 0.8810, 1.0044, NA, 2.6749,~
#> $ model <chr> "RAND", "RAND", "RAND", "Interaction", "Interaction", "Inte~
#> $ age_bucket <fct> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,~
#> $ mean_age <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,~
#> $ median_age <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,~
#> $ age_range <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,~CoEff_Compare %>%
mutate(Feature = reorder(term, estimate)) %>%
ggplot(aes(y=Feature, x=estimate, color=model)) +
geom_point() +
geom_errorbarh(aes(xmax = estimate + std.error, xmin = estimate - std.error, height = .2)) +
ggtitle(expression("Comparing model estimates of " ~ beta[i]))
#> Warning: Removed 1 rows containing missing values (geom_point).
#> Warning: Removed 1 rows containing missing values (geom_errorbarh).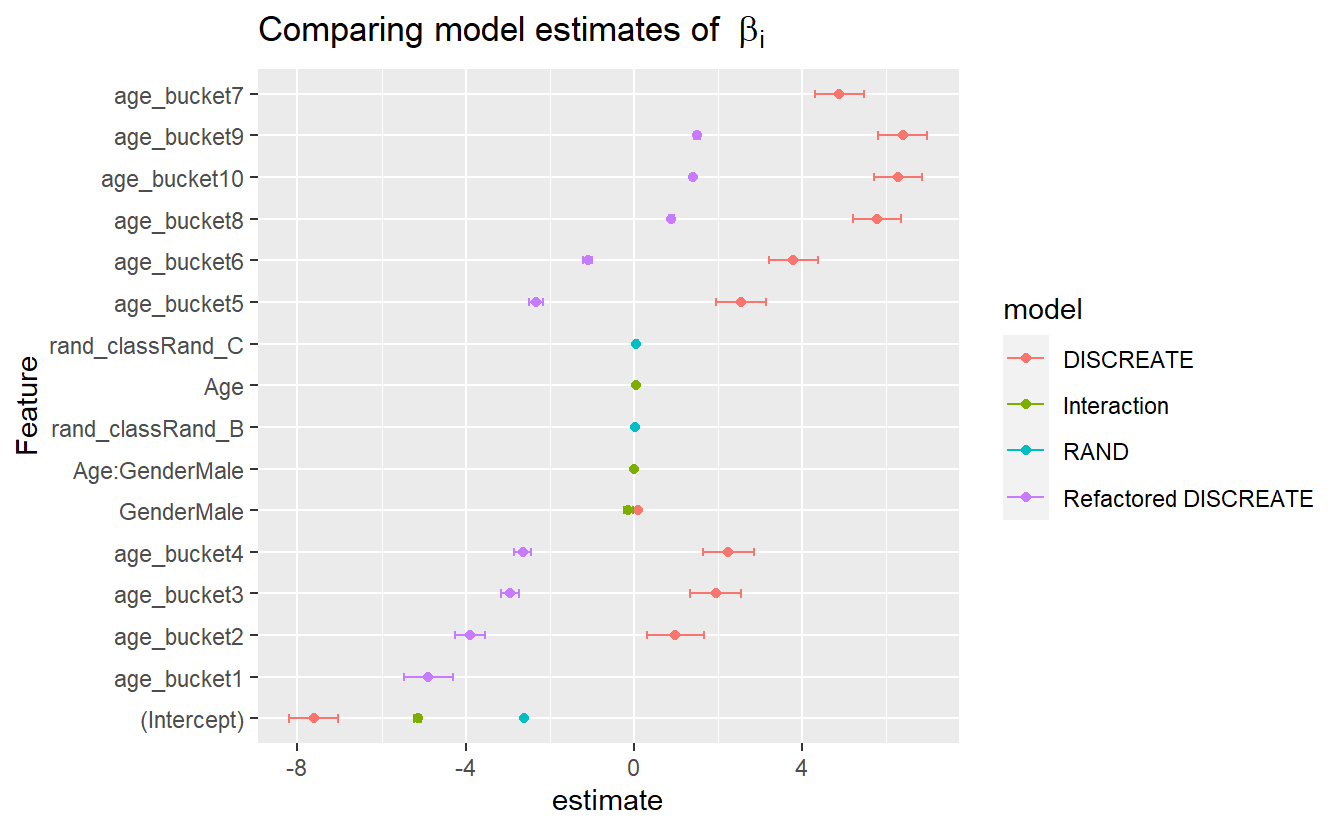
CoEff_Compare %>%
mutate(Feature = reorder(term, odds_ratio)) %>%
ggplot(aes(y=Feature, x=odds_ratio, color=model)) +
geom_point() +
geom_errorbarh(aes(xmax = exp(estimate + std.error), xmin = exp(estimate - std.error), height = .2)) +
ggtitle(expression("Comparing model estimates of Odds Ratios" ~ exp(beta[i])))
#> Warning: Removed 4 rows containing missing values (geom_point).
#> Warning: Removed 1 rows containing missing values (geom_errorbarh).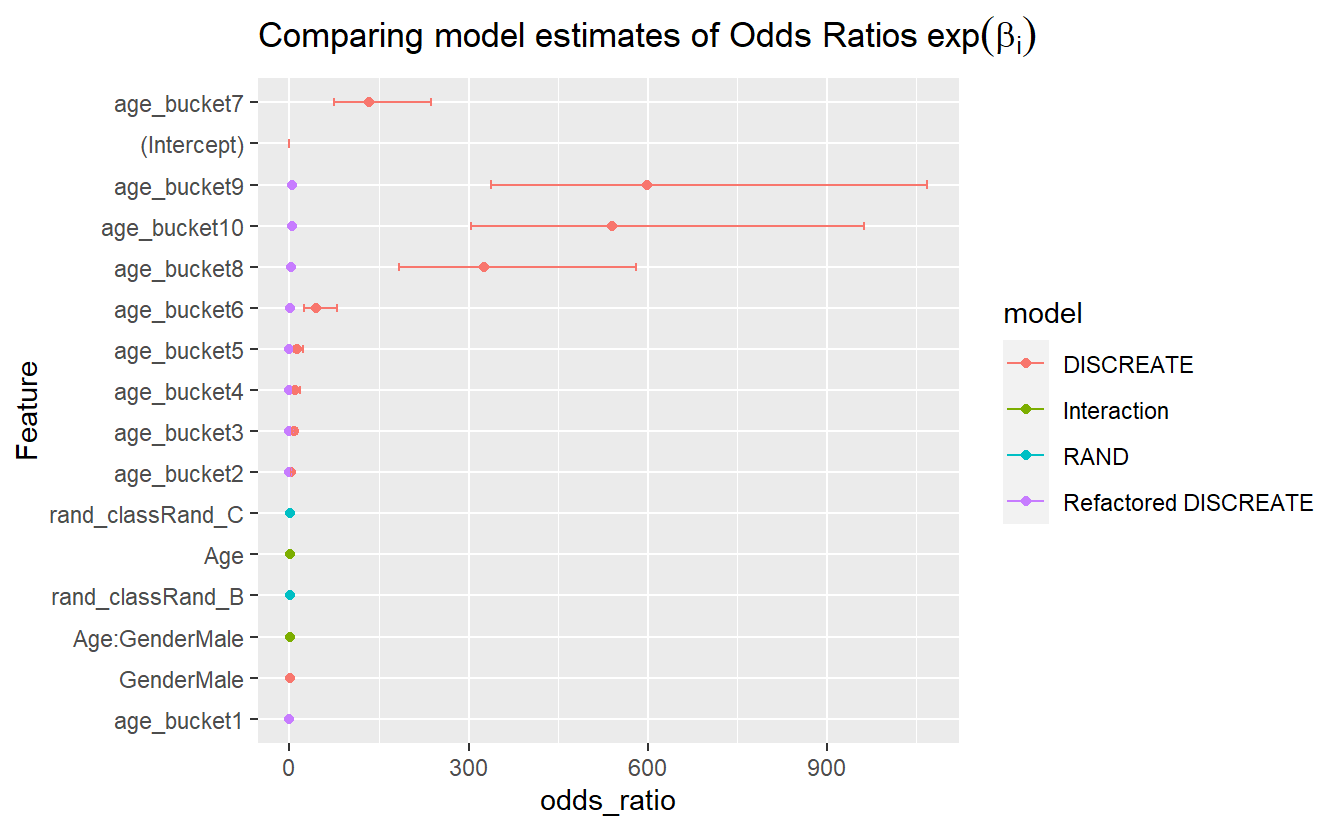
CoEff_Compare %>%
mutate(Feature = reorder(term, p.value)) %>%
ggplot(aes( y = Feature, x = p.value , fill=model)) +
geom_bar(stat = 'identity', position = 'dodge') +
labs(title = "Comparing model Coefficent p-values")
#> Warning: Removed 1 rows containing missing values (geom_bar).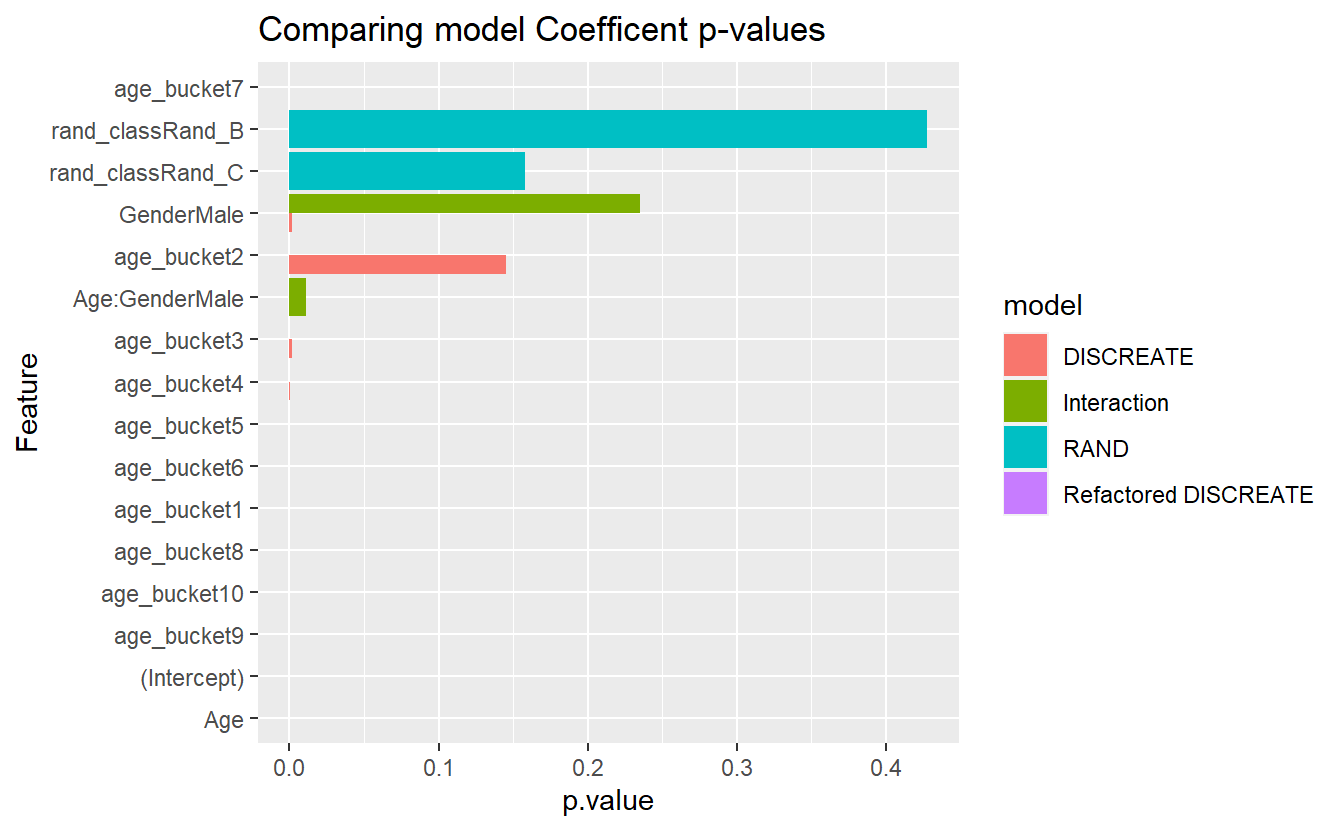
7.10.2 Model Training Errors
model_train_errors <- bind_rows(
RAND %>% glance() %>% mutate(model = 'RAND'),
DISCREATE %>% glance() %>% mutate(model = 'DISCREATE'),
INTERACTION %>% glance() %>% mutate(model = 'INTERACTION')
)
model_train_errors %>%
select(model, AIC, BIC, logLik, colnames(model_train_errors)) %>%
arrange(AIC)
#> # A tibble: 3 x 9
#> model AIC BIC logLik null.deviance df.null deviance df.residual nobs
#> <chr> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <int> <int>
#> 1 DISCRE~ 22229. 22328. -11104. 29185. 57327 22207. 57317 57328
#> 2 INTERA~ 23079. 23115. -11536. 29185. 57327 23071. 57324 57328
#> 3 RAND 29189. 29216. -14591. 29185. 57327 29183. 57325 57328\(~\)
\(~\)
7.11 Logit Model Score Helper Function
We have three models (RAND, DISCRETE, & INTERACTION), and in each of the models we need to:
- score the training dataset
- find a threshold
- score the test data, and use threshold to make define predicted classes
If we review the str of the RAND model:
str(RAND,1)
#> List of 30
#> $ coefficients : Named num [1:3] -2.6058 0.0291 0.0626
#> ..- attr(*, "names")= chr [1:3] "(Intercept)" "rand_classRand_B" "rand_classRand_C"
#> $ residuals : Named num [1:57328] -1.07 -1.07 -1.07 -1.08 -1.07 ...
#> ..- attr(*, "names")= chr [1:57328] "1" "2" "3" "4" ...
#> $ fitted.values : Named num [1:57328] 0.0688 0.0688 0.0688 0.0729 0.0688 ...
#> ..- attr(*, "names")= chr [1:57328] "1" "2" "3" "4" ...
#> $ effects : Named num [1:57328] 158.042 0.22 1.412 -0.28 -0.269 ...
#> ..- attr(*, "names")= chr [1:57328] "(Intercept)" "rand_classRand_B" "rand_classRand_C" "" ...
#> $ R : num [1:3, 1:3] -61.2 0 0 -24.6 30 ...
#> ..- attr(*, "dimnames")=List of 2
#> $ rank : int 3
#> $ qr :List of 5
#> ..- attr(*, "class")= chr "qr"
#> $ family :List of 12
#> ..- attr(*, "class")= chr "family"
#> $ linear.predictors: Named num [1:57328] -2.61 -2.61 -2.61 -2.54 -2.61 ...
#> ..- attr(*, "names")= chr [1:57328] "1" "2" "3" "4" ...
#> $ deviance : num 29183
#> $ aic : num 29189
#> $ null.deviance : num 29185
#> $ iter : int 5
#> $ weights : Named num [1:57328] 0.064 0.064 0.064 0.0676 0.064 ...
#> ..- attr(*, "names")= chr [1:57328] "1" "2" "3" "4" ...
#> $ prior.weights : Named num [1:57328] 1 1 1 1 1 1 1 1 1 1 ...
#> ..- attr(*, "names")= chr [1:57328] "1" "2" "3" "4" ...
#> $ df.residual : int 57325
#> $ df.null : int 57327
#> $ y : Named num [1:57328] 0 0 0 0 0 0 0 0 0 0 ...
#> ..- attr(*, "names")= chr [1:57328] "1" "2" "3" "4" ...
#> $ converged : logi TRUE
#> $ boundary : logi FALSE
#> $ model :'data.frame': 57328 obs. of 2 variables:
#> ..- attr(*, "terms")=Classes 'terms', 'formula' language DIABETES_factor ~ rand_class
#> .. .. ..- attr(*, "variables")= language list(DIABETES_factor, rand_class)
#> .. .. ..- attr(*, "factors")= int [1:2, 1] 0 1
#> .. .. .. ..- attr(*, "dimnames")=List of 2
#> .. .. ..- attr(*, "term.labels")= chr "rand_class"
#> .. .. ..- attr(*, "order")= int 1
#> .. .. ..- attr(*, "intercept")= int 1
#> .. .. ..- attr(*, "response")= int 1
#> .. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
#> .. .. ..- attr(*, "predvars")= language list(DIABETES_factor, rand_class)
#> .. .. ..- attr(*, "dataClasses")= Named chr [1:2] "factor" "factor"
#> .. .. .. ..- attr(*, "names")= chr [1:2] "DIABETES_factor" "rand_class"
#> $ call : language glm(formula = DIABETES_factor ~ rand_class, family = "binomial", data = A_DATA.train)
#> $ formula :Class 'formula' language DIABETES_factor ~ rand_class
#> .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
#> $ terms :Classes 'terms', 'formula' language DIABETES_factor ~ rand_class
#> .. ..- attr(*, "variables")= language list(DIABETES_factor, rand_class)
#> .. ..- attr(*, "factors")= int [1:2, 1] 0 1
#> .. .. ..- attr(*, "dimnames")=List of 2
#> .. ..- attr(*, "term.labels")= chr "rand_class"
#> .. ..- attr(*, "order")= int 1
#> .. ..- attr(*, "intercept")= int 1
#> .. ..- attr(*, "response")= int 1
#> .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
#> .. ..- attr(*, "predvars")= language list(DIABETES_factor, rand_class)
#> .. ..- attr(*, "dataClasses")= Named chr [1:2] "factor" "factor"
#> .. .. ..- attr(*, "names")= chr [1:2] "DIABETES_factor" "rand_class"
#> $ data : tibble [57,328 x 7] (S3: tbl_df/tbl/data.frame)
#> ..- attr(*, "na.action")= 'omit' Named int [1:5769] 19 30 46 48 51 63 99 119 160 173 ...
#> .. ..- attr(*, "names")= chr [1:5769] "19" "30" "46" "48" ...
#> $ offset : NULL
#> $ control :List of 3
#> $ method : chr "glm.fit"
#> $ contrasts :List of 1
#> $ xlevels :List of 1
#> - attr(*, "class")= chr [1:2] "glm" "lm"we notice that there is a $data this is the training data stored in the model object RAND
arsenal::comparedf(A_DATA.train, RAND$data)
#> Compare Object
#>
#> Function Call:
#> arsenal::comparedf(x = A_DATA.train, y = RAND$data)
#>
#> Shared: 7 non-by variables and 57328 observations.
#> Not shared: 0 variables and 0 observations.
#>
#> Differences found in 0/7 variables compared.
#> 0 variables compared have non-identical attributes.Rather than performing the same operation 3x in a row we will use that fact the training data exists within the glm model output below to functionalize our scoring procedure from the last chapter, we encourage you to review sections 6.14.2 and 6.14.3; notice the changes made from there to the function below.
We create a function logit_model_scorer as follows:
logit_model_scorer <- function(my_model, my_data){
# extracts models name
my_model_name <- deparse(substitute(my_model))
# store model name into a new column called model
data.s <- my_data %>%
mutate(model = my_model_name)
# store the training data someplace
train_data.s <- my_model$data
# score the training data
train_data.s$probs <- predict(my_model,
train_data.s,
'response')
# threshold query
threshold_value_query <- train_data.s %>%
group_by(DIABETES_factor) %>%
summarise(mean_prob = mean(probs, na.rm=TRUE)) %>%
ungroup() %>%
filter(DIABETES_factor == 1)
# threshold value
threshold_value <- threshold_value_query$mean_prob
# score test data
data.s$probs <- predict(my_model,
data.s,
'response')
# use threshold to make prediction
data.s <- data.s %>%
mutate(pred = if_else(probs > threshold_value, 1,0)) %>%
mutate(pred_factor = as.factor(pred)) %>%
mutate(pred_factor = relevel(pred_factor, ref='0'))
# return scored data
return(data.s)
}In the function above, data.s is the “new data” we wish to make a prediction on and train_data.s is the training data stored within in the model object.
We then follow the steps outlined in the previous chapter to:
Compute a threshold value as the mean probability of the DIABETIC class on the training set.
Use the threshold to make a predicted class on the “new data.”
What does my_model_name <- deparse(substitute(my_model)) do?
Here is the R help for substitute & deparse:
substitute - returns the parse tree for the (unevaluated) expression expr, substituting any variables bound in env.
deparse - Turn unevaluated expressions into character strings.
Let’s explore what happens when we pass our stored model RAND:
substitute(RAND)
#> RANDis telling R to parse the expression into an unevaluated expression, RAND; (Note lack of quotes) then
deparse(substitute(RAND))
#> [1] "RAND"turns the unevaluated expressions into character string the character sting "RAND" (Note existance of quote) that we need for the input in the mutate step for the model = my_model_name.
Similarly,
substitute(INTERACTION)
#> INTERACTION
deparse(substitute(INTERACTION))
#> [1] "INTERACTION"7.11.1 Test Function
It’s always good practice to try and test your function:
logit_model_scorer(RAND , A_DATA.test) %>%
glimpse()
#> Rows: 38,219
#> Columns: 11
#> $ SEQN <dbl> 14467, 19500, 58411, 19525, 86101, 49428, 11398, 84044~
#> $ DIABETES <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ~
#> $ DIABETES_factor <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ~
#> $ Age <dbl> 20, 22, 79, 55, 14, 36, 26, 58, 8, 75, 38, 80, 40, 60,~
#> $ age_bucket <fct> 5, 5, 10, 8, 4, 6, 5, 8, 2, 10, 7, 10, 7, 9, 3, 3, 7, ~
#> $ Gender <chr> "Female", "Male", "Male", "Female", "Female", "Male", ~
#> $ rand_class <fct> Rand_B, Rand_B, Rand_B, Rand_A, Rand_A, Rand_A, Rand_C~
#> $ model <chr> "RAND", "RAND", "RAND", "RAND", "RAND", "RAND", "RAND"~
#> $ probs <dbl> 0.07065288, 0.07065288, 0.07065288, 0.06876314, 0.0687~
#> $ pred <dbl> 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, ~
#> $ pred_factor <fct> 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, ~We see that our function worked it has successfully run our protocol.
7.11.2 Make Predictions
We can deploy our function as follows:
A_DATA.test.scored.compare <- bind_rows(
logit_model_scorer(RAND , A_DATA.test) ,
logit_model_scorer(DISCREATE, A_DATA.test),
logit_model_scorer(INTERACTION , A_DATA.test)
)A_DATA.test.scored.compare %>%
glimpse()
#> Rows: 114,657
#> Columns: 11
#> $ SEQN <dbl> 14467, 19500, 58411, 19525, 86101, 49428, 11398, 84044~
#> $ DIABETES <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ~
#> $ DIABETES_factor <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ~
#> $ Age <dbl> 20, 22, 79, 55, 14, 36, 26, 58, 8, 75, 38, 80, 40, 60,~
#> $ age_bucket <fct> 5, 5, 10, 8, 4, 6, 5, 8, 2, 10, 7, 10, 7, 9, 3, 3, 7, ~
#> $ Gender <chr> "Female", "Male", "Male", "Female", "Female", "Male", ~
#> $ rand_class <fct> Rand_B, Rand_B, Rand_B, Rand_A, Rand_A, Rand_A, Rand_C~
#> $ model <chr> "RAND", "RAND", "RAND", "RAND", "RAND", "RAND", "RAND"~
#> $ probs <dbl> 0.07065288, 0.07065288, 0.07065288, 0.06876314, 0.0687~
#> $ pred <dbl> 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, ~
#> $ pred_factor <fct> 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, ~\(~\)
\(~\)
7.12 Evaluate models
7.12.1 ROC Curve
library('yardstick')
#> For binary classification, the first factor level is assumed to be the event.
#> Use the argument `event_level = "second"` to alter this as needed.
#>
#> Attaching package: 'yardstick'
#> The following object is masked from 'package:readr':
#>
#> spec
levels(A_DATA.test.scored.compare$DIABETES_factor)
#> [1] "0" "1"Currently our event-level is the second option, 1!
AUC.DM2_Gender <- A_DATA.test.scored.compare %>%
group_by(model) %>%
roc_auc(truth = DIABETES_factor, probs, event_level = "second") %>%
select(model, .estimate) %>%
rename(AUC_estimate = .estimate) %>%
mutate(model_AUC = paste0(model, " AUC : ", round(AUC_estimate,4)))
AUC.DM2_Gender
#> # A tibble: 3 x 3
#> model AUC_estimate model_AUC
#> <chr> <dbl> <chr>
#> 1 DISCREATE 0.846 DISCREATE AUC : 0.8464
#> 2 INTERACTION 0.846 INTERACTION AUC : 0.8457
#> 3 RAND 0.495 RAND AUC : 0.4946
A_DATA.test.scored.compare %>%
left_join(AUC.DM2_Gender) %>%
group_by(model_AUC) %>%
roc_curve(truth= DIABETES_factor, probs, event_level = "second") %>%
autoplot() +
labs(title = "ROC Curve " ,
subtitle = 'test set scored on logistic regression')
#> Joining, by = "model"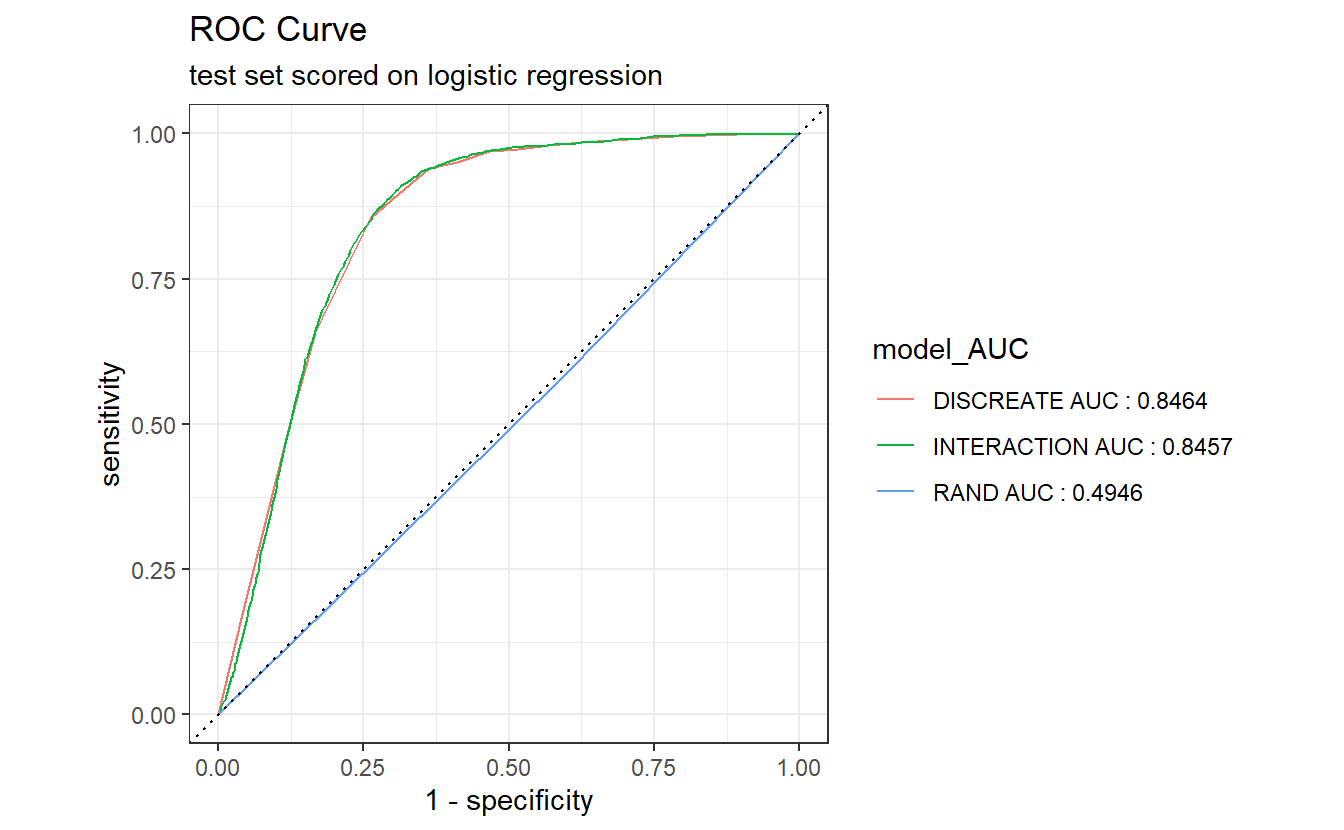
\(~\)
\(~\)
7.12.2 Precision-Recall Curve
PR_AUC <- A_DATA.test.scored.compare %>%
group_by(model) %>%
pr_auc(DIABETES_factor, probs, event_level='second') %>%
select(model, .estimate) %>%
rename(PR_AUC_estimate = .estimate) %>%
mutate(model_PR_AUC = paste0(model, " PR_AUC : ", round(PR_AUC_estimate,4)))
A_DATA.test.scored.compare %>%
left_join(PR_AUC) %>%
arrange(PR_AUC_estimate) %>%
group_by(model_PR_AUC) %>%
pr_curve(DIABETES_factor, probs, event_level='second') %>%
autoplot() +
labs(title = "PR Curve " ,
subtitle = 'test set scored on logistic regression')
#> Joining, by = "model"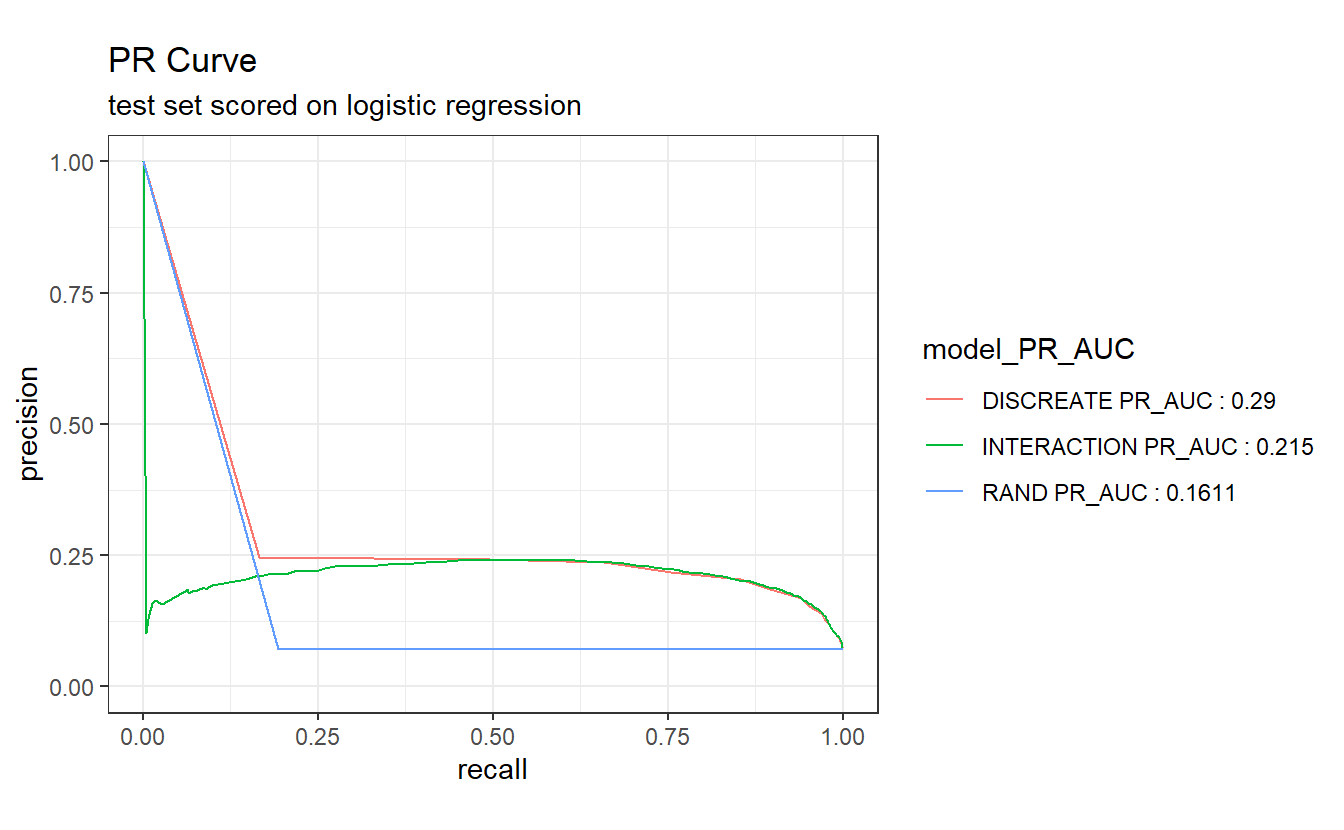
\(~\)
\(~\)
7.12.3 Gain Curves
The gain curve below for instance showcases that we can review the top 25% of probabilities within the DISCREATE and INTERACTION models and we will find roughtly 75% of the diabetic population.
A_DATA.test.scored.compare %>%
group_by(model) %>%
gain_curve(truth = DIABETES_factor, probs, event_level = "second") %>%
autoplot()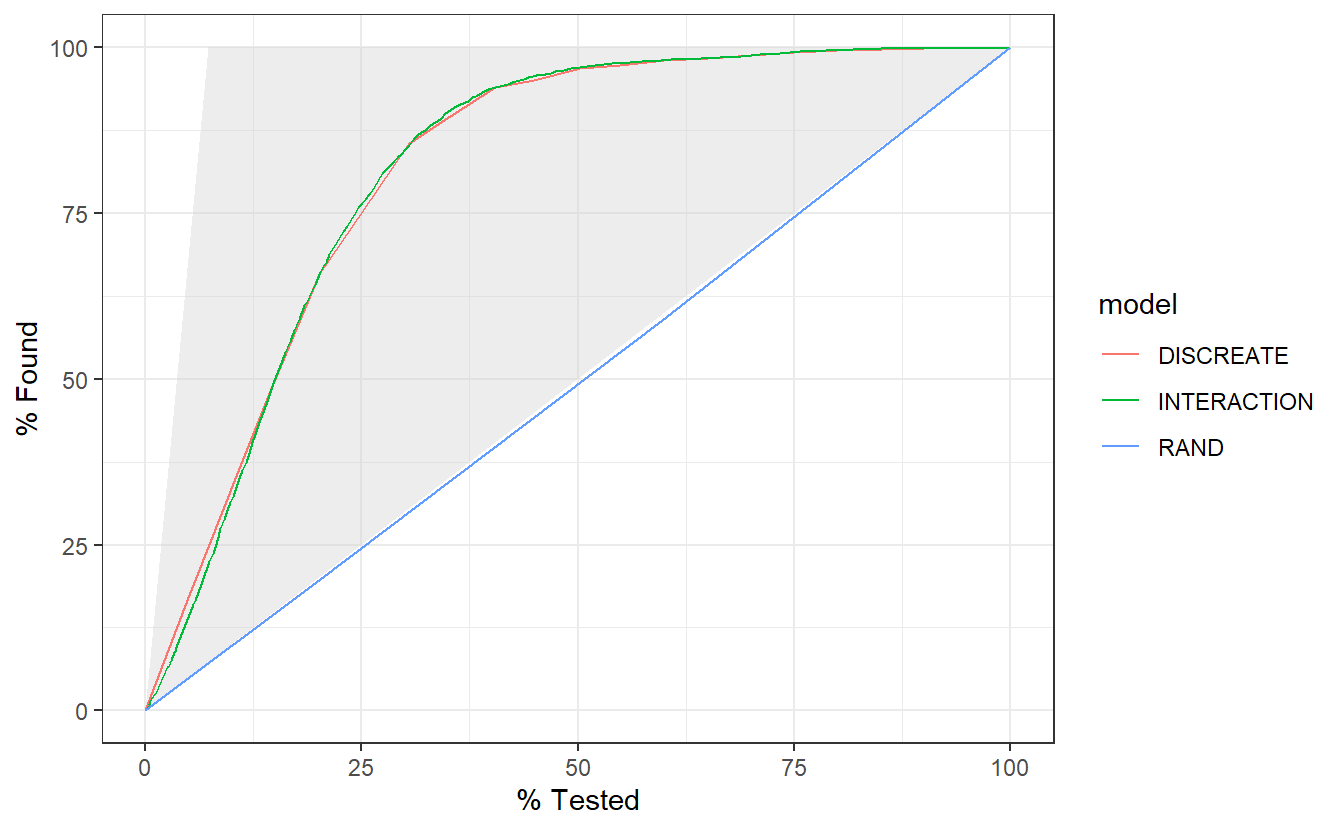
\(~\)
\(~\)
7.12.4 Lift Curves
DISCRETElift curve is nearly monotonically decreasing from 3.5 to about 3.0 in the the top 25% of probabilities in the model.INTERACTIONlift curve appears “the mode is much less than the mean in that normal distribution,” theDISCREATEmodel only seems to benefit for the top 12.5% of high probabilityDISCRETEscores, after that graphs are nearly identical.RADappears to perform sightly worse than selecting members at random.
A_DATA.test.scored.compare %>%
group_by(model) %>%
lift_curve(truth = DIABETES_factor, probs, event_level = "second") %>%
autoplot()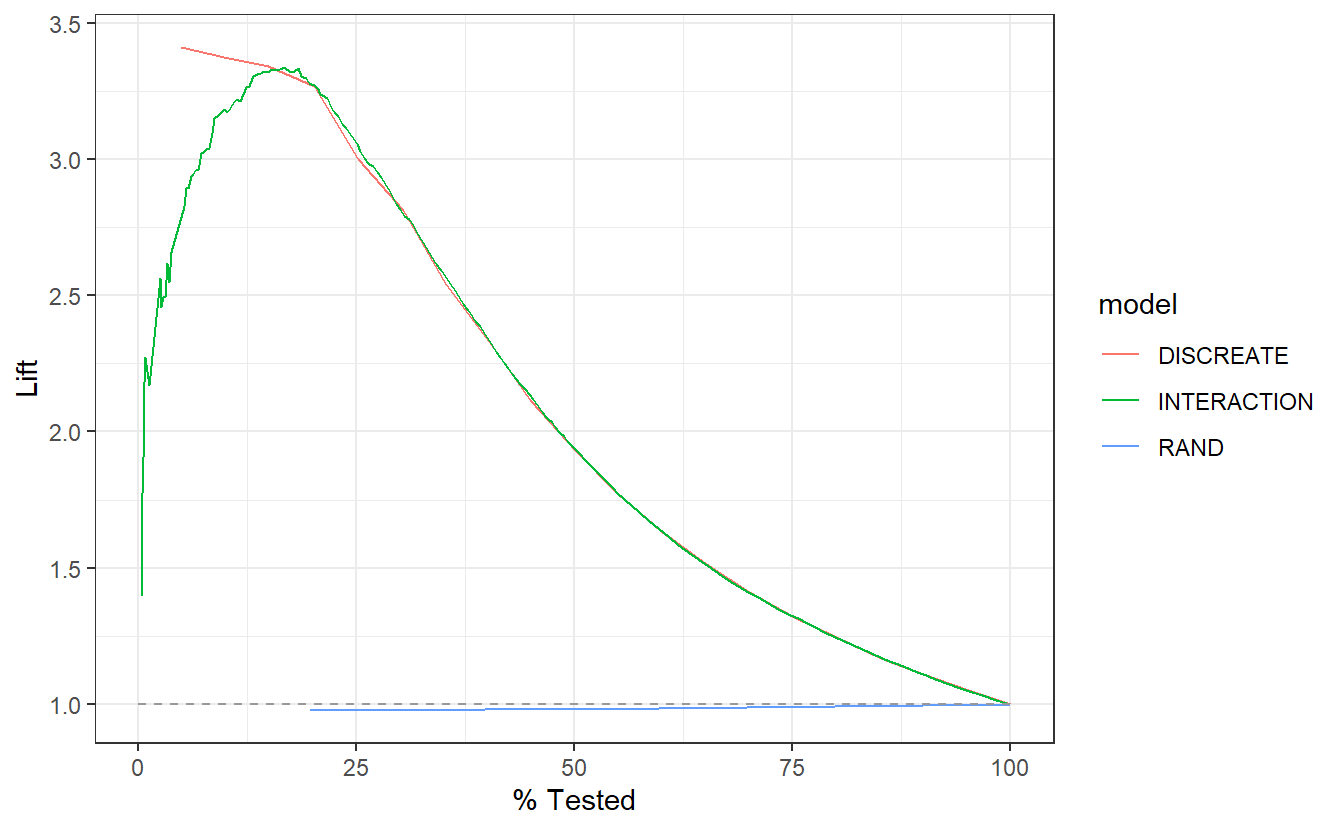
7.12.5 Confusion Matrix
CM <- A_DATA.test.scored.compare %>%
group_by(model) %>%
conf_mat(DIABETES_factor, pred_factor)
CM %>%
glimpse()
#> Rows: 3
#> Columns: 2
#> $ model <chr> "DISCREATE", "INTERACTION", "RAND"
#> $ conf_mat <list> [29566, 5879, 947, 1827, NULL], [31354, 4091, 1478, 1296, NUL~Here are the three confusion matrices:
CM$conf_mat
#> [[1]]
#> Truth
#> Prediction 0 1
#> 0 29566 947
#> 1 5879 1827
#>
#> [[2]]
#> Truth
#> Prediction 0 1
#> 0 31354 1478
#> 1 4091 1296
#>
#> [[3]]
#> Truth
#> Prediction 0 1
#> 0 14244 1142
#> 1 21201 1632Let’s get heat maps for the 3 confusion matrices, below the map function at work again; recall a typical call to map looks like map(.x, .f, ...) here:
.x- A list or atomic vector (CM$conf_mat- list of confusion matrices).f- A function (autoplot)...- Additional arguments passed on to the mapped function- In this case
type = "heatmap"are the additional arguments passed into the function.f = autoplot
- In this case
Notice also, this is not inside a mutate function as we are not adding any variables to our data-frame. We will discuss other functions from purrr in the next chapter.
map(CM$conf_mat, autoplot, type = "heatmap")
#> [[1]]
#>
#> [[2]]
#>
#> [[3]]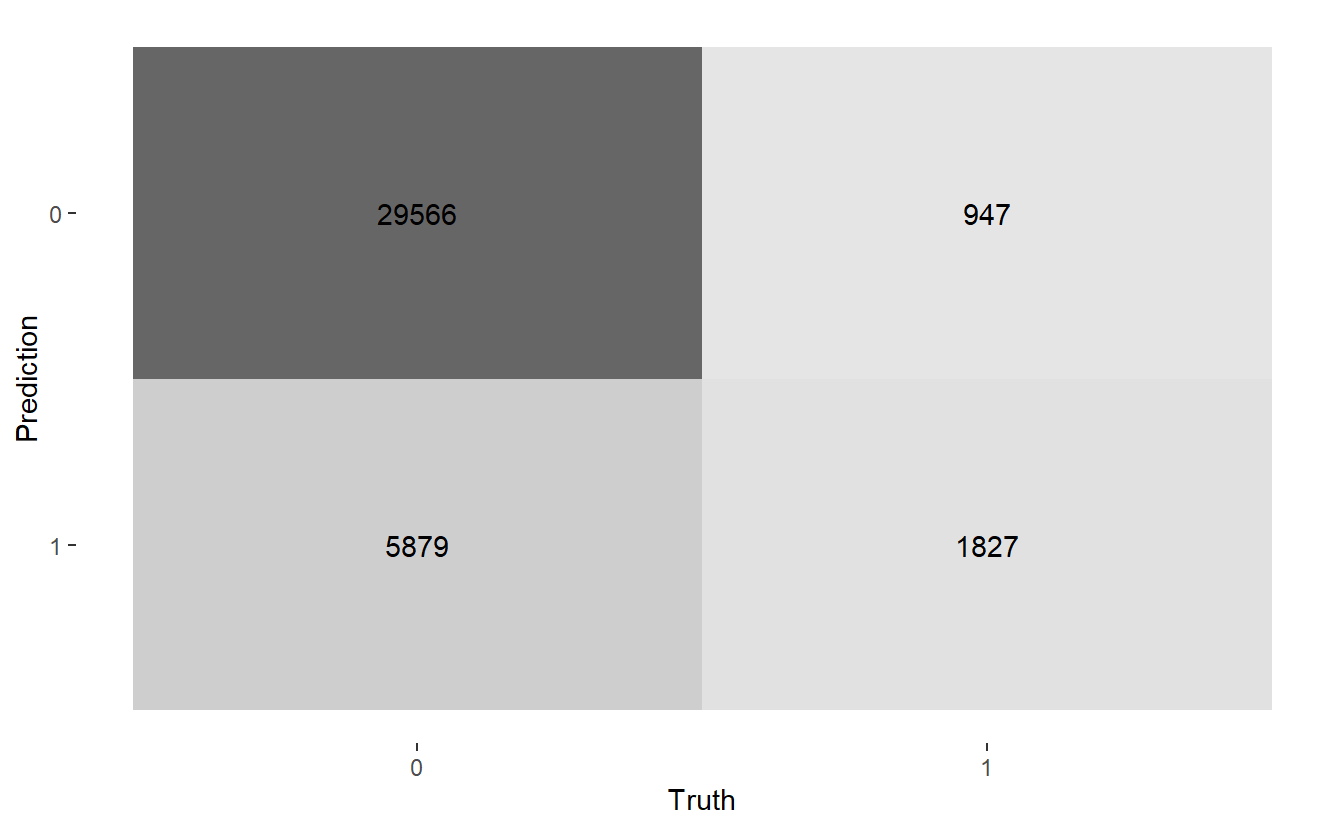
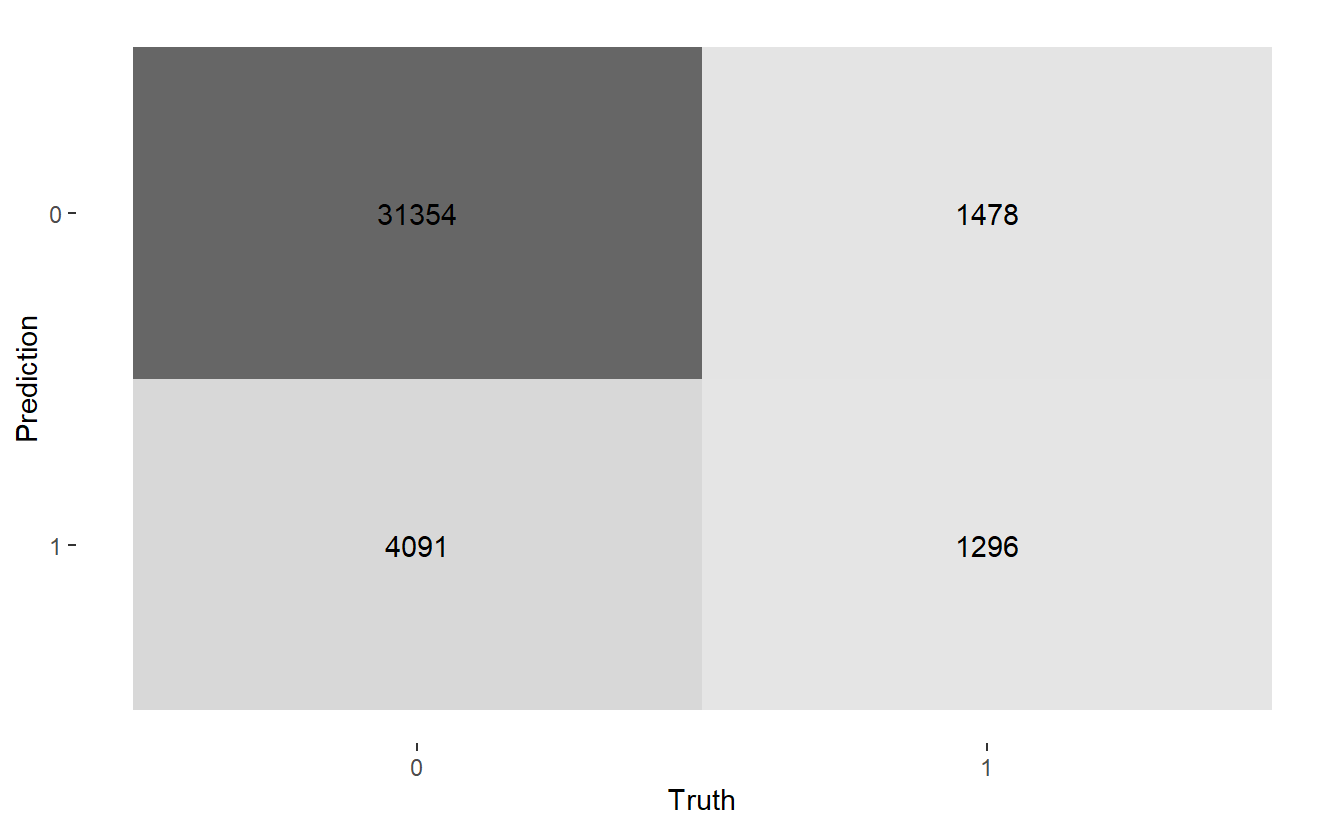
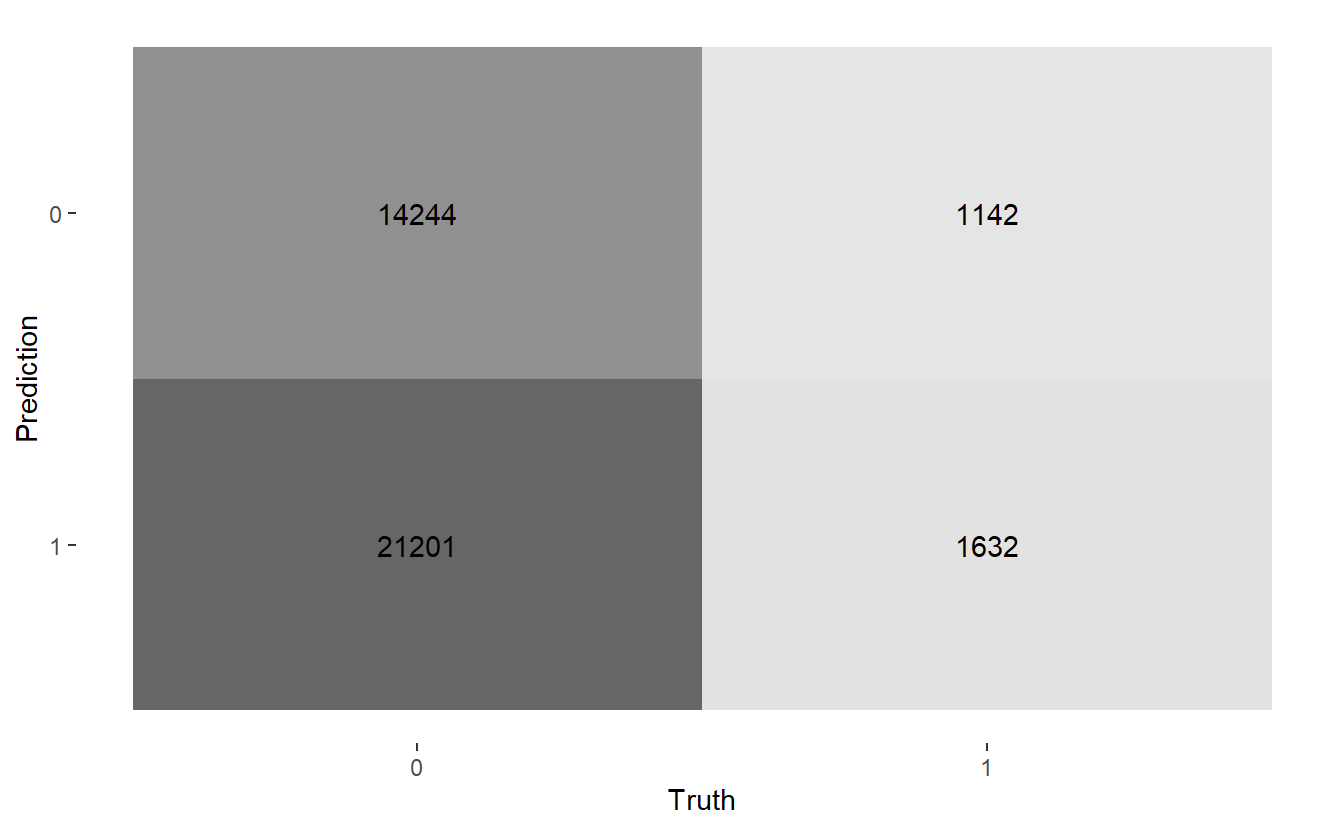
Above we see we get three graphs, one for each of the three confusion matrices.
7.12.6 Model Evaluation Metrics
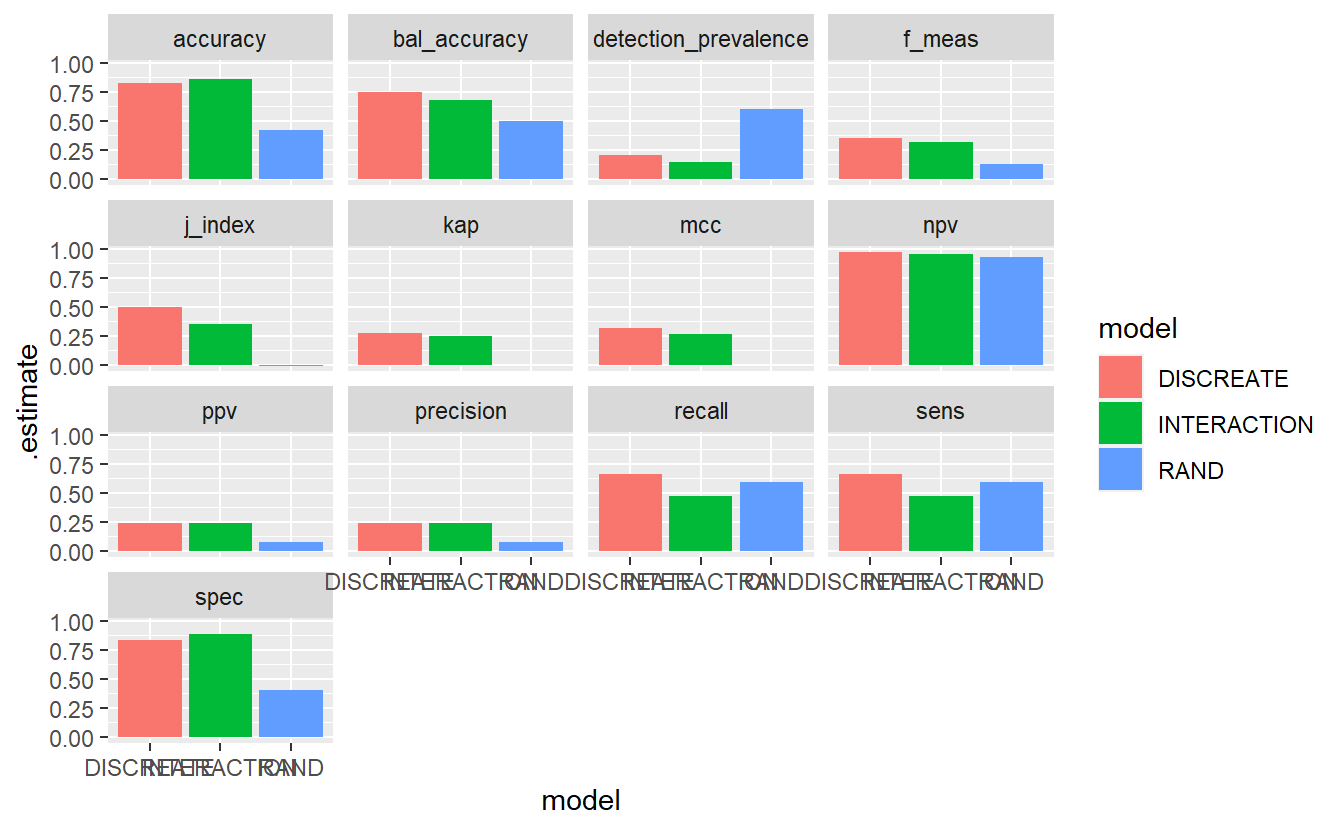
A_DATA.test.scored.compare %>%
group_by(model) %>%
conf_mat(truth = DIABETES_factor, pred_factor) %>%
mutate(sum_conf_mat = map(conf_mat,summary, event_level = "second")) %>%
unnest(sum_conf_mat) %>%
select(model, .metric, .estimate) %>%
ggplot(aes(x = model, y = .estimate, fill = model)) +
geom_bar(stat='identity', position = 'dodge') +
facet_wrap(.metric ~ . )