Hypothesis testing
Data Analytics Module
Lecturer: Hans van der Zwan
Handout 05
Topic: t tests and chi square tests
Literature
Rumsey D. J. (2010). Statistical Essentials for Dummies. Hoboken: Wiley Publishing.
Ismay C. & Kim A. Y. (2019). ModernDive. Statistical Inference for Data Science. https://moderndive.com.
Recommended literature
Preparation class
See module description
7 Hypothesis testing
In quantitative research testing of hypotheses is a commonly used technique to operationalize a research (sub)question. It is a technique to find out whether support for a formulated hypothesis (the HA-hypothesis) can be found in the data.
7.1 Examples of the use of hypotheses testing in research
Example 1 (fictitious example)
Research topic: effect on income of receiving a master degree at THUAS.
Studies from universities in the US show an increase in net income of on average 1,200 euros per year after obtaining a master’s degree.
The question to answer is: is the income development after graduation from a master program at THUAS comparable with the income development after graduation for a master program at a university in the USA? Based on former studies it is expected that the increase of the net income is higher than in the USA. To operationalize the question the hypothesis can be stated that the mean difference in net income before and after graduation from a master program at THUAS is more than 1,200 euro. To test this hypothesis data has to be collected from graduates from a master degree at THUAS, especially differences in net income after and before obtaining the degree. From this data a test statistic has to been calculated, in this case the sample mean of the differences. Based on the value of this statistic the conclusion has to be drawn. To conclude that support for the hypothesis has been found, it is nog enough that the sample mean is more than 1,200 euro, it should be significant more.
Some examples of conclusions from scientific papers.
Example 2
Students taking statistics courses in psychology at the University of Washington reported studying more hours for tests (M = 121, SD = 14.2) than did UW college students in general, t(33) = 2.10, p = .034.
Example 3
The group using mental images recalled significantly more words (M = 25, SD = 4.71) than the group that did not use mental images (M = 19, SD = 4.22), t(18) = -3.00, p = .001.
Example 4 Comparison of final GPAs for athletes (M = 3.39, SD = .31) and non-athletes (M = 3.47, SD = .31) revealed no significant differences between the groups; t(167) = -1.56, ns.
Example 5
Self-efficacy and grade-point average were significantly correlated, r = .54, p < .05.
What all these tests have in common is that a hypothesis about a population is tested based on a sample and a conclusion is drawn based on a calculated p-value.
7.2 Hypotheses testing about proportions: binomial and proportion tests
See handout06.
Tests on proportions can be used in case we have to do with a categorical variable with two categories.
7.3 Hypotheses testing about an average value
Besides hypotheses about a proportion, hypotheses about a mean value are most common. For instance, to check whether a bottling process is under control, a test can be performed to check whether the mean content of a produced batch of bottles with wine is not less than 750 ml:
H0: μ = 750
HA: μ < 750
\(\alpha\) = .05 (the chosen significance level)
To test this hypotheses a sample from the production has been drawn. Sample statistics: n = 30, sample mean M = 745 ml, sample standard deviation SD = 15 ml.
If H0 is true, the sample mean will not differ much from 750. What ‘much’ means depends on the sample size and on the variation in the data (which can be measured by the standard deviation):
- the higher the sample size, the closer the sample mean will be to the population mean;
- the less variation in the data, the closer the sample mean will be to the population mean.
From mathematics the distribution of the possible sample means is known1; based on this knowledge the P-value from this test result can be calculated.
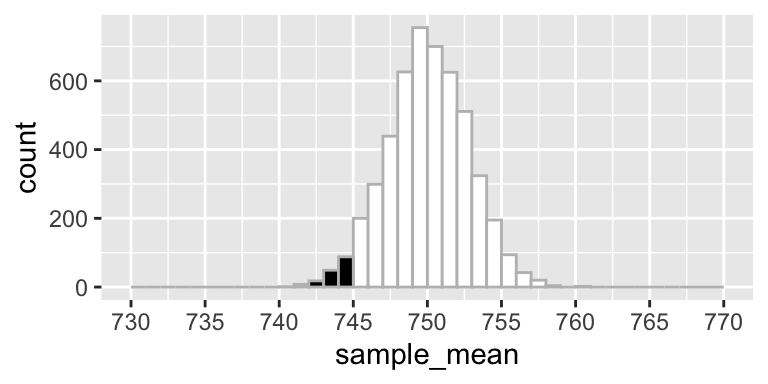
Figure 1. Distribution of the sample means (n = 30) assuming population mean = 750 (the H0 value) and population standard deviation = 15 (estimation based on the sample data). The black area corresponds with the probability of drawing a sample with sample mean less than 745 from this population.
In this example the P-value equals 0.039.2 Because this is lower than .05 (the common significance level), the H0-hypothesis is rejected. The distribution in Figure 1 looks like a normal distribution, but actually we have to do with a t-distribution. A t-distribution can be seen as an adjusted normal distribution; the adjustment is necessary because the population standard deviation is unknown and estimated. The uncertainty that comes with this estimate, is neutralized by making use of a t-distribution with 29 (n-1) so called degrees of freedom (df).
EXERCISE 7.1
7.4 One sided and two sided tests
The tests so far discussed were all one-sided test, i.e. the HA-hypothesis has a “<” (les than) or a “>” (greater than) sign. There are situations in which the direction of the hypothesis is not clear, but the aim of the test is to investigate whether a mean (or a proportion or a median or …) differs from a certain given value. Or the question can be whether the mean of two groups differs or not. In these cases a two-sided test can be used.
Example: filling processes
In case of a filling process the average content should have a certain value. E.g. packs of sugar are filled and ought to have a content of 1000 grams. There will always be some variation in the contants of a batch of packs of sugar, but on average the content must be 1000 grams. To check whether the process is under control, a sample from the batch can be drawn and the hypotheses to test are:
H0: mean content = 1000
HA: mean content <> 1000
The H0 is rejected if the sample mean is significant less than 1000 but also when this mean is significant more than 1000 grams.
If the sample mean equals 1010 gram, than as far away from the expected value, which equals 1000 grams, is more than 1010 or less than 990 gram.
Suppose the sample statistics are: n = 10, sample mean = 1010 and sample standard deviation = 20 grams. The test used is a two-sided t-test; based on the sample results (N = 10, M = 1010, SD = 15) the H0-hypothesis will not be rejected, t(9) = 2.108, P = 0.064.
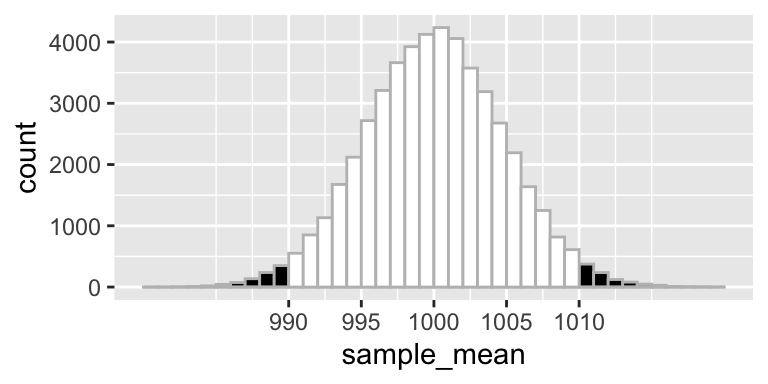
Figure 2. Distribution of sample means (n = 10) from a population with mean = 1000 and standard deviation = 15. The black area represents the P-value of a two sided test, in case the sample mean equals 1010.
7.5 Overview of commonly used tests
7.5.1 One sample tests
7.5.1.1 One sample binomial test for a proportion
To perform a test about a population proportion \(\pi\) against a standard (norm), a binomial test can be used.
The HA- hypothesis can be:
HA: \(\pi\) < \(\pi_0\) (lower-tail test)
HA: \(\pi\) > \(\pi_0\) (lower-tail test)
HA: \(\pi\) <> \(\pi_0\) (two-sided test)
In all cases, the P-values are calculated assuming \(\pi\) = \(\pi_0\).
7.5.1.2 One sample t-test for the mean
To perform a test about a population mean μ against a standard (norm), a t-test can be used if the sample size is large enough.3 Based on the sample mean M and the sample standard deviation SD, a t-value is calculated by calculating the standardized value of the mean:
t = \(\frac{M - \mu_0}{\frac{SD}{\sqrt(n)}}\). This t-value is a metric for the place of the sample mean M in the distribution of possible sample means, assuming H0 is true.
The HA- hypothesis can be:
HA: \(\mu\) < \(\mu_0\) (lower-tail test)
HA: \(\mu\) > \(\mu_0\) (upper-tail test)
HA: \(\mu\) <> \(\mu_0\) (two-sided test)
In all cases, the P-values are calculated assuming \(\mu\) = \(\mu_0\).
7.5.1.3 Chi-square goodness of fit test
The chi-square goodness of fit test is applicable in case of one categorical variable. It is used to determine whether sample data are consistent with a hypothesized distribution. For a chi-square goodness of fit test, the hypotheses take the following form.
H0: The data are consistent with a specified distribution.
HA: The data are not consistent with a specified distribution.
Typically, the null hypothesis (H0) specifies the proportion of observations at each level of the categorical variable. The alternative hypothesis (HA) states that at least one of the specified proportions is not true.
To perform the test, use vassarstats.net; the chi square goodness-of-fit test can be found under ‘Frequency Data’.
Exercise 7.1 to 7.5
7.5.2 Two sample tests
7.5.2.1 Two independent samples proportion test
A two sample proportion test is used to test assumptions about the difference between two proportions in case of not to small sample sizes (rule of thumb: n >= 30 for both samples).
The test statistic used is a z-value; see Rumsey (2010) for formula.
The HA- hypothesis can be:
HA: \(\pi\)I < \(\pi\)II (lower-tail test)
HA: \(\pi\)I > \(\pi\)II (upper-tail test)
HA: \(\pi\)I <> \(\pi\)II (two-sided test)
In all cases, the P-values are calculated assuming \(\pi\)I = \(\pi\)II.
7.5.2.2 Two independent samples t-test for difference between
A two sample proportion test is used to test assumptions about the difference between two proportions in case of not to small sample sizes (rule of thumb: n >= 15 for both samples).
The test statistic used is a t-value; see Rumsey (2010) for formula.
The HA- hypothesis can be:
HA: \(\mu\)I < \(\mu\)II (lower-tail test)
HA: \(\mu\)I > \(\mu\)II (upper-tail test)
HA: \(\mu\)I <> \(\mu\)II (two-sided test)
In all cases, the P-values are calculated assuming \(\mu\)I = \(\mu\)II.
7.5.2.3 Paired t-test for the difference between two means
Pairwise tests concern the comparison of the same group of individuals, or matched pairs, being measured twice, before and after an ‘intervention’.
If the scale of the variable used is numeric, a paired t-test for the difference between two means may be a good choice to test whether an intervention works or not.
7.5.2.4 Wilcoxon rank sum test
The Wilcoxon rank sum test is an alternative for the independent two sample t-test, which is especially applicable in case of only a small number of observations.
7.5.2.5 Wilcoxon rank sign test
The Wilcoxon rank sign test is an alternative for the paired sample t-test, which is especially applicable in case of only a small number of observations.
7.5.2.6 Chi square test
To test whether two categorical variables are significantly associated the chi square test is commonly used. There are some assumptions that must be met to allow the use of this test.
7.5.2.7 Fisher exact test
To test whether there is a significant association between two categorical variables and the assumptions of the chi square test are not met, the Fisher exact test is an alternative.
7.6 Hypotheses testing summarized
In a statistical testing procedure, a test statistic is chosen depending on what is being tested. A random sample is drawn and the value of the test statistic in this sample is calculated. If, assuming H0 is true, this value is far from what is expected, H0 is rejected, otherwise it isn’t. The possible values of this test statistic are divided in a critical (“reject the H0-hypothesis region”) region and a “don’t reject the H0-hypothesis” region. The border value between the two regions is called critical value. If the sample statistic falls in the critical region the H0-hypothesis is rejected. A common way to decide whether the sample statistic falls in the critical region is to calculate the P-value, this is the probability to find a value as found in the sample or even more extreme, assuming H0 is true. Most statistical software package used to perform a significance test, will report the critical value, the sample value and the P-value. It’s up to the researcher to draw the conclusion depending on the significance level (\(\alpha\)-risk) used. If the P-value is less than \(\alpha\), H0 is rejected.
Above the principles of hypothesis testing are discussed. Lots of tests have been developed for all kind of situations. There are tests about a population parameter, tests that compare two or more groups, tests concerning numerical variables and tests concerning categorical variables. One of the issues in a statistical research is to decide which test is appropriate. What all tests have in common is the use of a test statistic, the division of all possible values of the test statistic in an acceptance and a critical region and the calculation of the P-value. What a researcher has to do:
- decide which test is appropriate
- perform the test, using statistical software
- interpret the output, especially compare the P-value with the α-level used: if P-value < α, H0 is rejected, otherwise not
- writing it up according conventions used in the paper (APA).
7.7 Confidence Intervals
Calculation of Confidence Intervals is closely related to the topic of Hypotheses Testing. In stead of reporting the result of a hypothesis test on a certain parameter (e.g. an average value, a proportion, the difference between two averages or two proportions), the researcher reports a confidence interval (CI) that contains the value of this parameter with 95% (or another percentage) certainty. The advantage is, that in general a CI is more informative. A significance test, informs the reader whether the value of a parameter is significant more than (or less or different from) a certain value. Especially with large datasets, even small differences can be statistical significant, even when the difference doesn’t have practical implications. Reporting a CI gives the possibility to judge whether a measured difference is ‘practical significant’ or not. Such a judgement is based on domain knowledge, not on statistics.
Example Assume a researcher wants to test whether the air quality in the first half year of 2020 increased. The researcher uses the average PM10 level measured in The Netherlands in the first half year of 2020 to measure air quality and tests whether the average is less than 20 \(\mu\)g/m\(^3\). The collected data are hourly measured levels: N = 200,000, M = 19.95, SD = 10.
Based on this results, the measured value is significantly less than 20, p = .025. The 95% CI (two-sided) is [19.91, 19.99].4
In many cases a statistical application reports a CI in the output. For instance if a regression analysis is performed in Excel, the output contains a CI for the coefficient of the X-variables in the model and for the intercept as well. This CI can be helpfull to judge the effect of a marginal change in one of the X-varibles (ceteris paribus) on the Y-variable.
On this website a simulation is used to illustrate sampling theory, especially the most important theorem of statistics, The Central Limit Theorem, can be illustrated with this animation.↩
P-values for common tests can be calculated with this web app.↩
Which sample size is large enough depends on the form of the distribution in the population; most textbooks say n = 30 is large enough, in most situations it is assumed that even n = 20 is large enough to use a t-test; if it may be assumed that the population distribution is symmetric even n = 10 may be large enough.↩
For a one sided test it is more common to calculate a one sided CI; in this case a right sided 95% CI is [<–; 19.987].↩