Association Analysis

Data Analytics Module
Lecturer: Hans van der Zwan
Handout 04
Topic: association analysis

Literature
Rumsey D. J. (2010). Statistical Essentials for Dummies. Hoboken: Wiley Publishing.
Ismay C. & Kim A. Y. (2019). ModernDive. Statistical Inference for Data Science. https://moderndive.com.

Recommended literature

Preparation class
See module description

4 Association analysis

In many cases data analysis is about analyzing association between variables: measuring the strength of a relationship, testing whether the relationship is significant (or can be attributed to chance because the relationship is measured using a random sample), describing the relationship with a mathematical equation.
The objective of this kind of analysis can be predicting or estimating an output based on one or more inputs or just to examine the relationships between different variables and the structure of the data. In this lesson, the emphasis is on the former.

When it is about predicting and estimating there are one response (dependent) variable (the Y-variable) and one or more explanatory (independent) variables (X variables). Problems with a categorical response variable are referred to as classification problems, while those involving a numeric response as regression problems.

4.1 Relationships between two categorical variables

Common ways to examine relationships between two categorical variables:

• Graphical: clustered bar chart; stacked bar chart
  
• Descriptive statistics: cross tables
• Metric to measure the strength of the relation:
  • phi coefficent, in case of two binary variables
  • Cramer’s V
    see: http://groups.chass.utoronto.ca/pol242/Labs/LM-3A/LM-3A_content.htm and use http://vassarstats.net menu ‘frequency data’ for calculations
• Hypotheses testing:
  • tests on difference between proportions
    
  • chi-square tests a test to test whether two categorical variables are independent

Example: PPD LONDON, association between OLD/NEW and LEASEHOLD/FREEHOLD
Research sub question: is there a dependency between the variables TYPE and LEASEHOLD/FREEHOLD for properties in London?
The question is answered based on the properties sold in January 2019.

Table 1
Houses sold in London in January 2019,
divided by TYPE and FREEHOLD/LEASEHOLD

TYPE	F	L
DETACHED	35	2
FLAT	7	775
SEMI-DETACHED	121	4
TERRACED	420	22

Note. As can be seen in this table the distribution over the Freehold and Leashold categories differ for the different types. The question is, whether the association between the two variables is significant.
The strength of the relationship can be measured by Cramer’s V, this metric has a value of 0.949 in this case. This means there is a very strong relationship between TYPE and FREEHOLD/LEASEHOLD; if the type is known good predictions can be made for the FREEHOLD/LEASEHOLD category.

Example: crime incidents in 2017 in Washington, D.C.
The file Crime_Incidents_in_2017.csv (source: http://us-city.census.okfn.org/) contains information about crimes in Washington D.C. in 2017.
To analyse whether there is a relationship between the variables METHOD, a categorical variable with free unique values (GUN, KNIFE and OTHERS), and SHIFT a categorical variable with three unique values (DAY, EVENING, MIDNIGHT) a contingency table has been created.

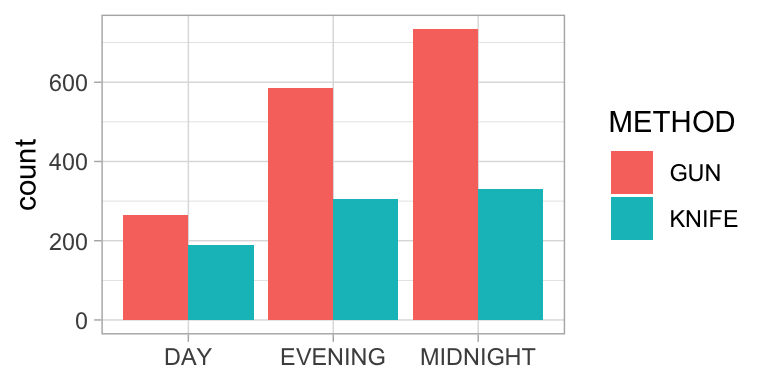
Figure 1. Crimes in Washington D.C. in 2017.

Table 2
Crimes in Washington D.C. in 2017

In this example Cramer’s V equals 0.08. The relationship between the two variables is very weak, although it is significant, chisquare(2) = 15.290, p < .001.

4.2 Relationship between categorical and numeric variable

Common ways to examine relationships between two categorical variables:

• Graphical: side-by-side boxplots, side-by-side histograms, multiple density curves
  
• Tabulation: five number summary/ descriptive statistis per category in one table
  
• Hypotheses testing:
  • t test on difference between means
    
  • Wilcoxon ranksumtest (also called Mann Whitney U-test) (also applicable in the case of small samples)

Example: comparison airpollution between Amsterdam and Rotterdam
A comparison of the difference between airpollution caused by PM10 in Amsterdam, location Einsteinweg and Rotterdam, location Statenweg. The comparison is based on the figures from 2018 as reported on the RIVM website.

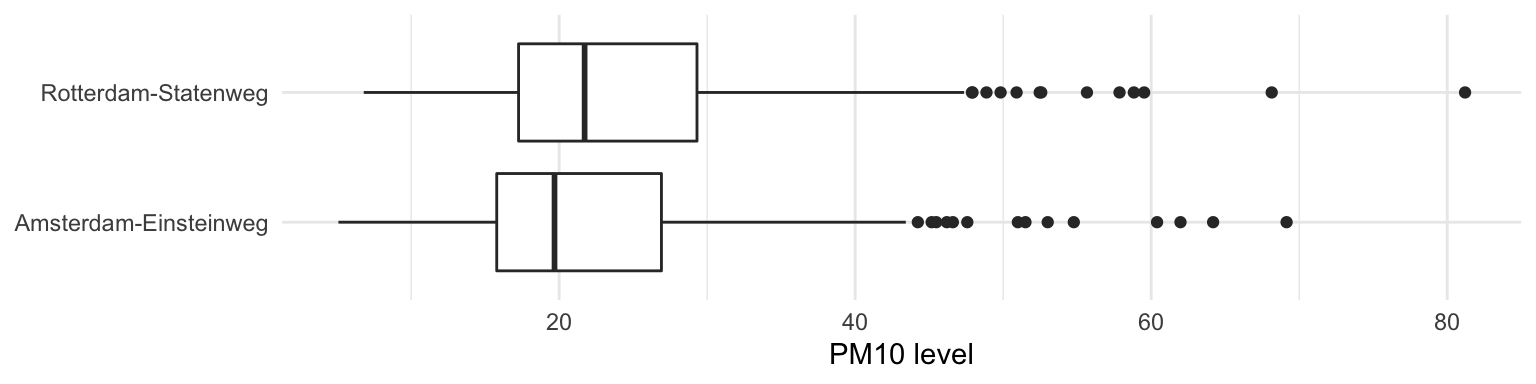Figure 2. Daily average PM10 levels in 2018 on a location in Amsterdam and a location in Rotterdam. Overall the air quality in Rotterdam is worse than in Amsterdam.

Table 3
Summary statistics daily PM10 levels

A paired t-test is used to investigate whether the daily average values in Amsterdam-Einsteinweg differ from these in Rotteram-Statenweg. Based on this test it can be concluded that the difference between the daily values in Amsterdam (M = 22.5, SD = 10.0) and Rotterdam (M = 24.3, SD = 10.5) is significant, t(362) = -8.847, p < .001.

EXERCISE 4.1

4.3 Relationship between two numerical variables

Common ways to examine relationships between two numerical variables:

• Graphs per variable in order to verify whether there are any outliers (boxplots / histograms).
  
• Table: summary statistics per variable; verify whether there are missing data.
  
• Graphical: scatterplot to graph the relationship between the two variables. Verify whether the graph supports that there exists a linear relationship and examine whether there are outliers.
  
• Measure of linear association: correlation coefficient.
  Notice: statistical association is not the same as a causal relation!!
  
• Describing the relationship using a mathematical model: linear regression analysis.

EXERCISE 4.2

4.3.1 Correlation coefficient

The correlation coefficient r is a measure for the strength of a linear relationship between two variables. More about how to interpret a correlation coefficient can be found on this website .

4.3.1.1 Significant correlation

Even when there is no correlation between two variables the correlation coefficient calculated based on a sample will not be 0. That’s why it is quite common to use a significance test to test whether the r value differs significantly from 0. More about this test can be found here.

4.3.2 Least square regression

Video.
In Excel, the equation of the OLS (Ordinary Least Squares) regression line can be found in different ways:
- Plotting the regression line and its equation in the scatterplot.
- Using menu choice: data/data analysis/regression.
- Using formulas to calculate the intercept (formula: intercept) and the slope (formula: slope) of the regression line.

4.3.2.1 MS Excel regression output

Figure 3 shows the MS Excel regression output for the Dutch car examples (see abve).

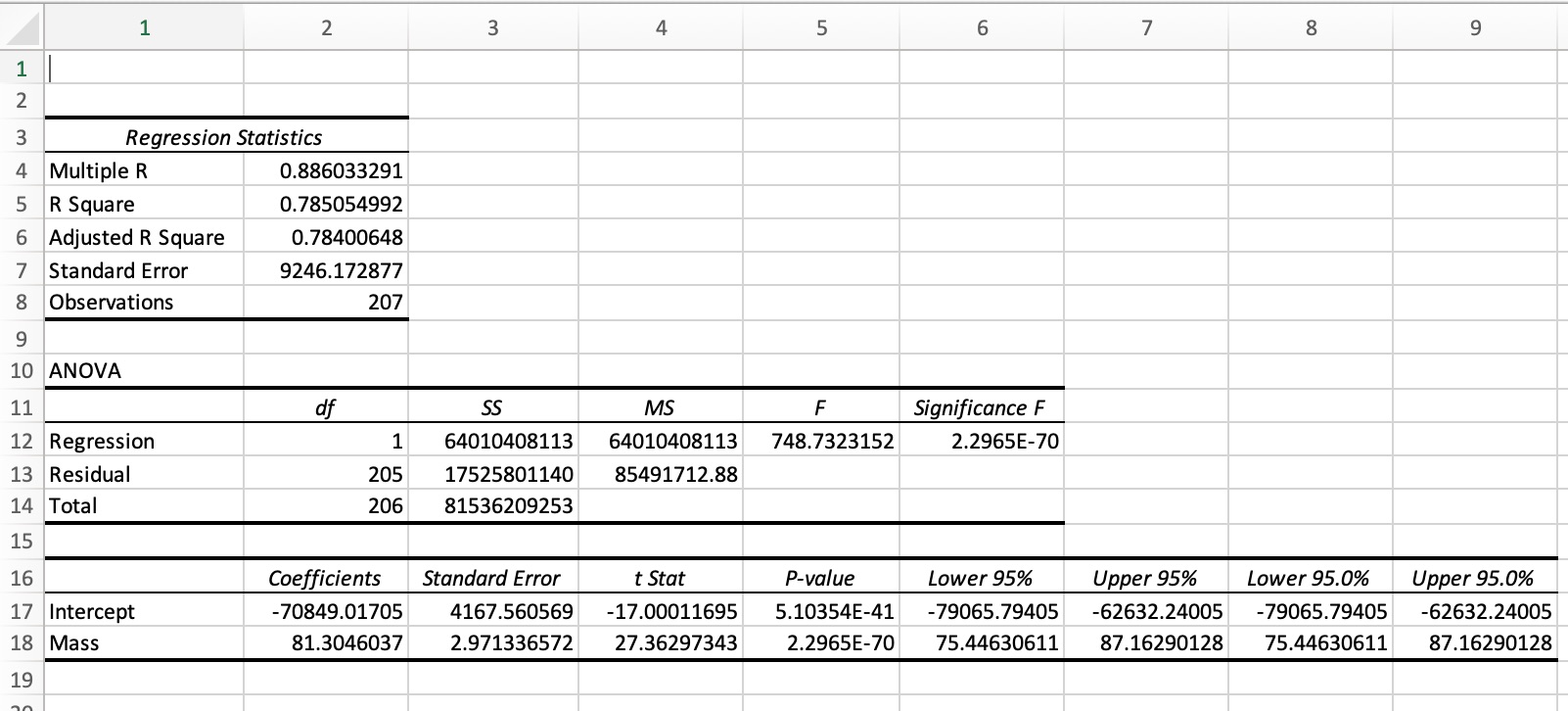
Figure 3. Regression output created with MS Excel, menu: data/Data Analysis/Regression.

The regression model in the example output in figure 3 can be described by the equation:
CATALOG PRICE = -70,849 + 81.30 x MASS, where
MASS is the mass of the car in kg, and
CATALOG PRICE is the catalog price in euro.

Call:
lm(formula = Catalog_price ~ Mass, data = rdw)

Residuals:
   Min     1Q Median     3Q    Max 
-47701  -4551   -765   4342  50948 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -70849.017   4167.561  -17.00   <2e-16 ***
Mass            81.305      2.971   27.36   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9246 on 205 degrees of freedom
Multiple R-squared:  0.7851,    Adjusted R-squared:  0.784 
F-statistic: 748.7 on 1 and 205 DF,  p-value: < 2.2e-16

Figure 4. Regression output RDW example, using R.

4.3.2.2 Assessing the regression model

After generating a regression model it is important to assess the model. This is done to judge whether the model fits the data and, in case of comparing models, which model fits the data best.

Coefficient of determination R²
In case of simple linear regression, i.e. with just one X-variable, the R2 value is the correlation coefficient squared. In a multiple regression setting it’s more complicated.

In general, the following equation holds: R² = \(1 - \frac{variation\ of\ Y-values\ around\ the\ regression\ line}{variation\ of\ the\ Yvalues\ around\ the\ mean\ Yvalue}\) = \(1 - \frac{\sum(Y-\hat{Y})^{2}}{\sum(Y-\bar{Y})^{2}}\)

The denominator in this expression, \(\Sigma(Y - \bar{Y})^{2}\), measures the total variation in the Y-values around the mean Y-value. The numerator, \(\Sigma(Y - \hat{Y})^{2}\), measures the variation of the Y-values around the model Y-value (the \(\hat{Y}\)-values). The latter is the variation in the Y-values that is not explained by the regression model.
So the fraction measures the part of the variation in the Y-values around the mean that is not explained by the regression model.
So R² measures the proportion of the variation in the Y-values that is explained by the regression model. In all cases: 0 <= R² <= 1.

Interval estimate for the regression coefficient In the Excel regression output the coefficient of the MASS variable is estimated to be 81.3. This is an estimate based on the sample data. If another sample from the same population would be used, the estimate for this coefficient would be different. In other words, the ‘real’ coefficient can be a little bit more or a little bit less than 81.3. The output also shows a so called 95%-interval estimate for the coefficient with borders 75.4 and 87.2. This means that we can be 95% sure that the coefficient lies between these two values. In the context of this example: the effect of an increase of MASS with 1 kg is an increase of the average PRICE between 75.4 and 87.2 euro.

P-values of the coefficient(s)
Another way to assess the coefficient is based on the reported P-value of the MASS variable. This P-value of the coefficients is used to determine whether an X-variable is significant in the model. Most common interpretation: a P-value less than .05 indicates that the X-variable is significant. The test for which this P-value is calculated is:
H₀: \(\beta\) = 0
H_A: \(\beta\) <> 0, where \(\beta\) is the coefficient of the X-variable in question.
Not rejecting H₀ means the coefficient of the X-variable doesn’t differ significantly from 0, in other words Y doesn’t depend significantly on X.

The standard error of the estimate s_e
The standard error of the estimate is a metric for the spread around the regression line.
The value can be used to estimate the so-called margin of error if the model is used to predict a Y-value given the X-value(s). As a rule of thumb, the margin of error that should be taken in account when predicting a Y-value is 2xs_e.
So the smaller the s_e value the better the model can predict a Y-value.
To evaluate the value of s_e, it is compared with \(\bar{Y}\), commonly by dividing s_e by \(\bar{Y}\).

4.3.3 Assessing the model in the RDW example

R² = .785, which means that 78.5% of the variation in catalog prices is explained by the variation in masses.
The regression coeeficient of the MASS variable (81.3) differs significantly from 0, p < .001. MASS is a significant variable.
s_e = 9246; if the model is used to estimate the catalog price, based on the mass of a car, a margin of error of 18,492 (2 x s_e) should be taken in account. In other words, this model is not a very good model to predict catalog prices.

EXERCISE 4.3 and 4.4