Data Analysis: summary statistics

Data Analytics Module
Lecturer: Hans van der Zwan
Handout 02
Topic: summary statistics

Literature
Rumsey D. J. (2010). Statistical Essentials for Dummies. Hoboken: Wiley Publishing.

Recommended literature

Preparation class
Watch: https://www.youtube.com/watch?v=9NUjHBNWe9M (15 min), introduction to MS Excel pivot tables; especially important if you are not used to working with pivot tables
Watch: https://www.youtube.com/watch?v=rAN6DBctgJ0&t=4s (5 min), measures for central tendency (SLC)
Watch: https://www.youtube.com/watch?v=dq_D30kyR1A (17 min), meaning of the standard deviation (Nystrom)

2 Summary statistics

Graphs show the form of the distribution of the data and are a very usefull tool in exploring a dataset. Besides graphs, statistics that summarize the (distribution of the) data, are used to transform data into information. The five-number summary, which forms the basis for a boxplot, is a good example of summarizing data.
The most important statistics are statistics which measure central tendency and spread. Which summary statistics are appropriate depends on the type of a variable (categorical or numerical) and the context of the data to be studied.

2.1 Central tendency metrics

Metrics for central tendency: (arithmetric) mean and median. For grouped data, also the mode can be used to measure the central tendency. With individual cases the mode is in most cases not a good metric for central tendency, because an individual observation can have the highest frequency without being in the center of the distribution.

2.2 Measuring spread

Most common metrics to measure variation in the data: range, interquartile range (IQR), variance and standard deviation.

2.3 Other statistics used to summarize the data

There are many other statistics that can be used to describe a data set. Some examples:

• the number of observations in the data set; actually this is almost always the first statistic reported;
  
• the proportion of the data that has a certain property; e.g. the proportion of voters supporting the proposal in the last tweet of president Trump;
  
• 5% trimmed mean: the mean of the data after removing the 5% lowest and the 5% highest values;
  
• variation coefficent (VC): \(\frac{SD}{MEAN}\);
  
• skewness coefficient.

2.4 Aggregating and summarizing data

In many cases data are summarized per group. E.g. houseprices in the Netherlands can be summarized per province or per municipality, healthcare costs can be summarized per age group etc.

Example: table with summary statistics of houses sold in London in January 2019

Table 1

Summary statistics houses sold in London in January 2019

london <- read.xlsx("Datafiles/HP_LONDON_JAN19.xlsx") %>%
  mutate(TYPE = factor(TYPE, levels = c("F", "D", "S", "T"),
                          labels = c("FLAT", "DETACHED", "SEMI-DETACHED", "TERRACED")))

summary_stats <- london %>% 
  group_by(TYPE) %>% 
  summarize(COUNT = n(),
            AVERAGE = round(mean(PRICE), -2),
            MEDIAN = round(median(PRICE), -2),
            SD = round(sd(PRICE), -2),
            PERC_ABOVE_1mln = round(100*(sum(PRICE > 1000000) / COUNT),1))

flextable(summary_stats) %>% 
  width(width = 1.5) %>% 
  colformat_num(col_keys = c("AVERAGE", "SD", "MEDIAN", "SD"), digits = 0, big.mark = ",") %>% 
  colformat_num(col_keys = "PERC_ABOVE_1mln", digits = 1) 

TYPE	COUNT	AVERAGE	MEDIAN	SD	PERC_ABOVE_1mln
FLAT	782	592,700	445,000	612,700	9.1
DETACHED	37	1,498,800	1,250,000	873,100	62.2
SEMI-DETACHED	125	982,200	805,000	642,400	32.8
TERRACED	442	876,100	630,000	919,700	23.5

Note. Average, median and standard deviation (SD) are in GB Pounds. The last column gives the percentages of properties sold with a selling price above 1 mln GPB. Underlying data are retrieved from http://landregistry.data.gov.uk/app/ppd/.

2.5 Summarizing data using MS Excel

MS Excel comes with a lot of statistical functions which can be used to create a data summary. For an overview of statistical functions in Excel, see here.

Another possibility to create an overview of the most common summary statistics, is using the analyses toolpak. On the internet, one can find many instruction manuals how to use this add-in, see for instance here.

To create Table 1, some more complicated formulas have been used. See Figure 1.

Figure 1

Screenshot with part of the formulas used in Excel to create Table 1

Note. To produce this table, use has been made of named areas in the worksheet with the data. ID refers to the array with the ID’s of the transactions, PRICE to the array with the prices paid, etc.

EXERCISE 2.1

2.6 Standardizing variables

In many cases it is useful to transform values to another unit of measurement. E.g. if in a data set there is a temperature variable (TEMP) measured in degrees Fahrenheit and for one reason or another the unit should be degrees Celsius, the following variable transformation can be used: TEMP_CELCIUS = (TEMP – 32) x 5/9.

A common transformation used is standardizing; the values of a variable (X-variable) are transformed into a new variable (Z-variable) which is the location of the observation relative to the mean, expressed in standard deviations: \(z = \frac{x\;-\;mean}{standard\;deviation}\) .

The z-value gives information about the place of a certain observation in the distribution.

2.7 Collecting data: open data sources

• Statistics Netherlands (CBS): https://opendata.cbs.nl/#/CBS/en/
• World Bank: https://data.worldbank.org/
  
• EU Open data portal: https://data.europa.eu/euodp/en/home
  
• Open data US government: https://www.data.gov/
  
• Data banks accessible via THUAS University website
  • Lexis Nexis
  • Company.info

Open data sources offer data in a variety of different formats. A common used format is the csv (comma seperated values) format. Be aware that sometimes the semi-colon instead of the comma is used as a seperator in such a file.

EXERCISE 2.2

2.8 Some MS Excel tips and tricks

• using $-signs to copy formulas with cells fixed
• naming cells
  
• advanced filter
  
• pivot tables
  
• common statistical functions

2.9 Example research case: comparison of the air quality in the four major Dutch cities

In May 2019 the municipality administration of Amsterdam announced that from 2030 on cars that run on diesel or petrol are not allowed in the city [https://www.cnet.com/roadshow/news/amsterdam-ban-gas-diesel-cars-motorcycles-2030/]. This because of the effect of these vehicles on the air quality in the city.
Although there were a lot of negative reactions on this intention, it is well known that bad air quality has a negative influence on people’s health, see for instance this WHO publication. The question can be asked if the other major cities in The Netherlands should consider measures similar to these of Amsterdam.
The above considerations lead to the research question:
Are the four largest cities in the Netherlands different in terms of air quality?
To answer this question, it has been subdivided into a couple of sub questions:
(Q1) How can air quality be measured?
(Q2) What are standards for healthy air quality?
(Q3) How does air quality relate to human health?
(Q4) Which patterns can be identified in the air quality in the four major cities over the year?
(Q5) Which patterns can be identified in the air quality in the four major cities during a day?
(Q6) Are there significant differences between the quality of the air in Amsterdam, Rotterdam, Utrecht and The Hague.

Assume that, based on the answer on Q1 and Q2, the PM10 level has been used as metric for air quality in this research. To answer the field research questions (Q4, Q5 and Q6) use has been made of secundary data which is collected by the Netherlands National Institute for Public Health and the Environment (RIVM) and published on luchtmeetnet.nl. This research is based on the published figures from 2018.

2.9.1 PM10 data 2018 for Amsterdam, Rotterdam and The Hague

PM10 levels as measured at six locations in Amsterdam city centre, two locations in The Hague city centre, two locations in Utrecht and four locations in Rotterdam city centre, are used.

• table with locations
  
• map with position of these locations

2.9.1.1 Data collecting and cleaning

At all locations the PM10 level is measured every hour. The data set contains negative values. These are due to problems with the measurement instruments and are replaced by NA (not available). A graphical data analysis has been performed to detect outliers. Outliers are examined and it has been discussed how to deal with these values.

2.9.2 Operationalization (1): pattern over the year

Identifying yearly patrons in the data has been done by:

• graphical analysis of time series
  • summarize the data per day using the average PM10 level per day per city
  • plot a time series graph of these averages for the different cities
  • optional: plot other graphs that give insight in the yearly pattern
• summary statistics per day for the different days of the week
• summary statistics per week
  
• summary statistics per month

2.9.3 Operationalization (2): daily pattern identification

Identify daily patterns in the data has been done by:

• graphical analysis of hourly data (how to do that with hourly data from different locations from a whole year?)
  
• summary statistics per city for the different hours per day

2.9.4 Operationalization (3): comparing the major cities

Comparing the air quality in the different cities has been done by:

• graphical analysis
  • boxplots per city
• interpreting the different graphs
  
• comparing the data per city with the standards set by the WHO
• binomial test whether the number of days with an unhealthy level is higher in Amsterdam than in the other two cities
  
• t test whether the average of the daily averages is higher in Amsterdam than in the other two cities

2.9.5 Results data analysis

2.9.5.1 Data per city

• table with number of valid measurements per station and per city
• table with problems in the data set; for instance days with only a small couple of valid measurements
  
• graph with time series of daily averages per city
  
• table with summary statistics per weekday and comment
• tables with summary statistics per week and month and comments
• graphs to analyze daily patterns in the data (e.g. boxplot)
  
• table with summary statistics per hour

2.9.5.2 Comparing air quality in the four major Dutch cities

• graphical analysis: boxplots (and histograms)
  
• comments
• comparing the cities with the WHO standards; table with number of days for the different healthy levels defined by the WHO
  
• results binomial tests en t-tests

2.9.6 Conclusion

• present the conclusions from the research (no new findings in this part)

EXERCISE 2.3

2.10 Tables in a scientific report

The basics concerning tables in a scientific report according to APA style can be found here APA guidelines for tables.
As for figures, tables should speak for themselves.
Also notice the sparing use of lines, no vertical lines and only a couple of horizontal lines above and below the column headings and below the last row.

Table 2

Example Table in APA format: Summary Statistics Prices Properties Sold in London

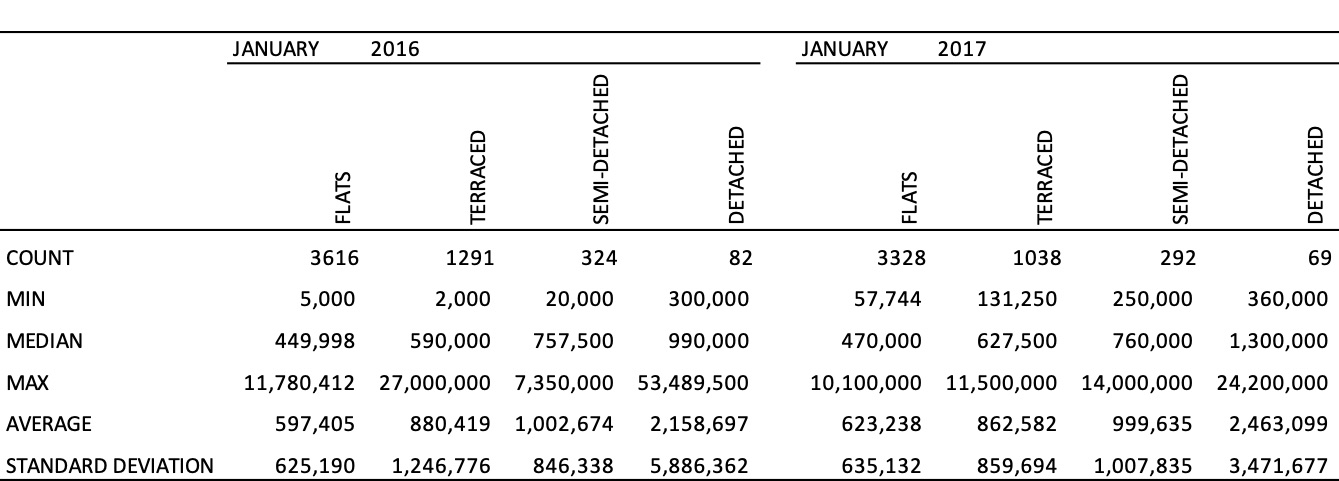
Note. Amounts are in GBP