library(tidyverse)
library(rpart)
library(randomForest)
library(xgboost)
library(neuralnet)10 Comparação entre Modelos de Classificação Multiclasses
Suponha um problema de classificação que, em vez de cada instância (observação) pertencer a uma de duas possíveis classes, ela pertence a uma entre \(k\) possíveis classes. Neste caso, não teremos como medida de comparação a entropia cruzada e não mais a AUC uma vez que não teremos mais a curva ROC.
10.1 Entropia Cruzada
Para o caso do problema com mais de duas classes a expressão da entropia cruzada precisa ser generalizada.
\[ EC = - \dfrac{1}{N} \sum_{i=1}^N \sum_{k=1}^K y_{k,i}\ln(\hat{y}_{k,i}) \]
sendo, \(N\) o número de instâncias (observações), \(K\) o número de classes, \(y_{k,i}\) a variável indicadora da classe \(k\), isto é, \(y_{k,i} = 1\) se a isntância \(i\) pertence a classe \(k\) e 0 caso contrário, e \(\hat{y}_{k,i}\) o valor de saída para a classe \(k\).
10.2 Matriz de Confusão
No caso dos problemas multi-classes a classe prevista será definida pela classe com maior probabilidade associada. Uma vez definida a previsão das classes é possível costruir a matriz de confusão, semelhante ao caso binário, mas agora com o número de linhas e de colunas iguais ao número de classes possíveis.
No caso da classificação multiclasses a Acurácia mantém a mesma interpretação, a taxa de acerto e é definida pela razão entre a soma dos valores na diagonal principal e a soma de todos as entradas da matriz de confusão.
Já as demais medidas de qualidade, como sensibilidade, especificidade, precisão, etc, serão dadas por classe, como por exemplo, a snesibilidade da classe A é a taxa de acerto da classe entre os indivíduos da classe A
\[ Sensibilidade = \dfrac{VP_A}{VP_A + FN_A} \]
Sendo,
\(VP_A\) = total de previsões realizadas para a classe A que de fato eram da classe A.
\(FN_A\) = total das previsões realizadas para as classes diferentes da classe A que eram da classe A
10.3 Vamos praticar
10.3.1 Carregar os pacotes necessários
10.3.2 Carregar as bases de treino e teste
base_treino_final = readRDS(file="salvos//base_treino_final.rds")
base_teste_final = readRDS(file="salvos//base_teste_final.rds")10.3.3 Carregar os modelos já ajustados
Nas últimas semanas ajustamos diferentes modelos de classificação binária. Agora é a hora de carregar todos eles para comparar o desempenho e discutir se algum deles apresenta desempenho melhor que outros.
TREE_CLASS_3 = readRDS(file = "salvos//TREE_CLASS_3.rds")
RF_CLASS_3 = readRDS(file = "salvos//RF_CLASS_3.rds")
XGB_CLASS_3 = readRDS(file = "salvos//XGB_CLASS_3.rds")
NN0_CLASS_3 = readRDS(file = "salvos//NN0_CLASS_3.rds")
NN1_CLASS_3 = readRDS(file = "salvos//NN1_CLASS_3.rds")
NN2_CLASS_3 = readRDS(file = "salvos//NN2_CLASS_3.rds")
NN3_CLASS_3 = readRDS(file = "salvos//NN3_CLASS_3.rds")10.3.4 Previsões
X_treino = base_treino_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
NU_MATRICULAS,
INSE,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO,
PORTE_ESCOLA)
Y_treino = base_treino_final$TAXA_PART_CATX_teste = base_teste_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
NU_MATRICULAS,
INSE,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO,
PORTE_ESCOLA)
base_teste_final = base_teste_final |>
mutate(TAXA_PART_CAT = ifelse(NU_TAXA_PARTICIPACAO >= 86, "alta", ifelse(NU_TAXA_PARTICIPACAO <= 67, "baixa","media")))
Y_teste = base_teste_final$TAXA_PART_CAT10.3.4.1 Árvore de Classificação
y_TREE_treino = predict(TREE_CLASS_3,newdata = X_treino)
head(y_TREE_treino) alta baixa media
1 0.63261218 0.06270032 0.3046875
2 0.63261218 0.06270032 0.3046875
3 0.07839355 0.60592774 0.3156787
4 0.07839355 0.60592774 0.3156787
5 0.63261218 0.06270032 0.3046875
6 0.07839355 0.60592774 0.3156787y_TREE_teste = predict(TREE_CLASS_3,newdata = X_teste)
head(y_TREE_teste) alta baixa media
1 0.63261218 0.06270032 0.3046875
2 0.63261218 0.06270032 0.3046875
3 0.63261218 0.06270032 0.3046875
4 0.07839355 0.60592774 0.3156787
5 0.07839355 0.60592774 0.3156787
6 0.07839355 0.60592774 0.315678710.3.4.2 Floresta Aleatória
y_RF_treino = predict(RF_CLASS_3,newdata = X_treino,type = "prob")
head(y_RF_treino) alta baixa media
1 0.930 0.004 0.066
2 0.856 0.012 0.132
3 0.782 0.072 0.146
4 0.736 0.078 0.186
5 0.230 0.040 0.730
6 0.006 0.880 0.114y_RF_teste = predict(RF_CLASS_3,newdata = X_teste,type="prob")
head(y_RF_teste) alta baixa media
1 0.660 0.046 0.294
2 0.516 0.076 0.408
3 0.474 0.096 0.430
4 0.152 0.348 0.500
5 0.342 0.262 0.396
6 0.124 0.452 0.42410.3.4.3 XGBoost
O XGBoost precisa receber as variáveis categóricas transformadas para indicadoras.
MX_treino = model.matrix(~. , data = X_treino)[,-1]
MX_teste = model.matrix(~. , data = X_teste)[,-1]pred = predict(XGB_CLASS_3,newdata = MX_treino)
y_XGB_treino = matrix(pred,byrow = TRUE,ncol=3,dimnames = list(NULL,c("baixa","media","alta")))
head(y_XGB_treino) baixa media alta
[1,] 0.005048582 0.1204156 0.87453580
[2,] 0.018599473 0.3436234 0.63777715
[3,] 0.140126988 0.2988443 0.56102866
[4,] 0.215170622 0.5532405 0.23158883
[5,] 0.032674577 0.3711857 0.59613973
[6,] 0.721569836 0.2627570 0.01567309pred = predict(XGB_CLASS_3,newdata = MX_teste)
y_XGB_teste = matrix(pred,byrow = TRUE,ncol=3,dimnames = list(NULL,c("baixa","media","alta")))
head(y_XGB_teste) baixa media alta
[1,] 0.02384563 0.3434063 0.63274813
[2,] 0.01764193 0.5015282 0.48082986
[3,] 0.02082709 0.6092329 0.36993998
[4,] 0.30541852 0.5243214 0.17026012
[5,] 0.27399266 0.4279339 0.29807341
[6,] 0.46973675 0.4761013 0.0541619210.3.4.4 Rede Neural
Para o modelo de redes neurais foi feita a padronização dos dados. O correto aqui é realizar a mesma padronização realizada para o dados que treinaram o modelo.
X1_treino = base_treino_final |> select(NU_MATRICULAS,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO)
X1_treino_s = scale(X1_treino)
mx = X1_treino_s |> attr("scaled:center")
sx = X1_treino_s |> attr("scaled:scale")X1_teste = base_teste_final |> select(NU_MATRICULAS,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO)X1_teste_s = X1_teste |> mutate(
NU_MATRICULAS = (X1_teste$NU_MATRICULAS - mx["NU_MATRICULAS"])/sx["NU_MATRICULAS"],
PC_FORMACAO_DOCENTE = (X1_teste$PC_FORMACAO_DOCENTE - mx["PC_FORMACAO_DOCENTE"])/sx["PC_FORMACAO_DOCENTE"],
NU_TAXA_PERMANENCIA = (X1_teste$NU_TAXA_PERMANENCIA - mx["NU_TAXA_PERMANENCIA"])/sx["NU_TAXA_PERMANENCIA"],
NU_TAXA_REPROVACAO = (X1_teste$NU_TAXA_REPROVACAO - mx["NU_TAXA_REPROVACAO"])/sx["NU_TAXA_REPROVACAO"],
NU_TAXA_ABANDONO = (X1_teste$NU_TAXA_ABANDONO - mx["NU_TAXA_ABANDONO"])/sx["NU_TAXA_ABANDONO"]
)X2_treino = base_treino_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
INSE,
PORTE_ESCOLA)
X2_treino_m = model.matrix(~. , data = X2_treino)[,-1]
MX_treino_s = cbind(X1_treino_s,X2_treino_m)X2_teste = base_teste_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
INSE,
PORTE_ESCOLA)
X2_teste_m = model.matrix(~. , data = X2_teste)[,-1]
MX_teste_s = cbind(X1_teste_s,X2_teste_m)Enfim a previsão, tanto na base de treino quanto na base de teste.
y_NN0_treino = predict(NN0_CLASS_3,newdata=MX_treino_s)
head(y_NN0_treino) [,1] [,2] [,3]
1 0.956771423 0.002425004 0.2255450
2 0.837507316 0.011344961 0.3405840
3 0.723440732 0.065761862 0.2843134
4 0.223944728 0.173650159 0.3867122
5 0.621914019 0.033264578 0.3859799
6 0.003912993 0.766464562 0.3282611colnames(y_NN0_treino) = levels(base_treino_final$TAXA_PART_CAT)
head(y_NN0_treino) alta baixa media
1 0.956771423 0.002425004 0.2255450
2 0.837507316 0.011344961 0.3405840
3 0.723440732 0.065761862 0.2843134
4 0.223944728 0.173650159 0.3867122
5 0.621914019 0.033264578 0.3859799
6 0.003912993 0.766464562 0.3282611y_NN0_teste = predict(NN0_CLASS_3,newdata=MX_teste_s)
colnames(y_NN0_teste) = levels(base_treino_final$TAXA_PART_CAT)
head(y_NN0_teste) alta baixa media
1 0.80251969 0.01453386 0.3874969
2 0.84516245 0.01125859 0.3698904
3 0.78783656 0.01026242 0.3828752
4 0.09773163 0.33752107 0.5098336
5 0.23307637 0.15295055 0.5018133
6 0.08059259 0.32792840 0.3371242y_NN1_treino = predict(NN1_CLASS_3,newdata=MX_treino_s)
colnames(y_NN1_treino) = levels(base_treino_final$TAXA_PART_CAT)
head(y_NN1_treino) alta baixa media
1 0.88388787 0.01174733 0.2983204
2 0.84142286 0.01671020 0.3007979
3 0.74011396 0.03051298 0.3050969
4 0.33915449 0.14659327 0.3171107
5 0.73877622 0.03071704 0.3051450
6 0.02044493 0.80372381 0.3402189y_NN1_teste = predict(NN1_CLASS_3,newdata=MX_teste_s)
colnames(y_NN1_teste) = levels(base_treino_final$TAXA_PART_CAT)
head(y_NN1_teste) alta baixa media
1 0.8287538 0.01827561 0.3014315
2 0.8430510 0.01651197 0.3007136
3 0.8343501 0.01757905 0.3011563
4 0.1303621 0.36753920 0.3258930
5 0.3587847 0.13620675 0.3164988
6 0.1244773 0.37980778 0.3262736y_NN2_treino = predict(NN2_CLASS_3,newdata=MX_treino_s)
colnames(y_NN2_treino) = levels(base_treino_final$TAXA_PART_CAT)
head(y_NN2_treino) alta baixa media
1 0.74168166 0.02710792 0.4000357
2 0.71141592 0.03079297 0.4036914
3 0.86865225 0.02676680 0.1944077
4 0.27745514 0.13606359 0.4490239
5 0.65576716 0.03815278 0.4098970
6 0.01079596 0.77154854 0.5375764y_NN2_teste = predict(NN2_CLASS_3,newdata=MX_teste_s)
colnames(y_NN2_teste) = levels(base_treino_final$TAXA_PART_CAT)
head(y_NN2_teste) alta baixa media
1 0.7067632 0.03137784 0.4042332
2 0.7119746 0.03072308 0.4036260
3 0.7149829 0.03034804 0.4032727
4 0.1322562 0.25867963 0.4719211
5 0.3254870 0.11455261 0.4433923
6 0.1196749 0.27800304 0.4747650y_NN3_treino = predict(NN3_CLASS_3,newdata=MX_treino_s)
colnames(y_NN3_treino) = levels(base_treino_final$TAXA_PART_CAT)
head(y_NN3_treino) alta baixa media
1 0.92378194 0.003092837 0.08252503
2 0.79143785 0.013899242 0.20951674
3 0.74577796 0.018556382 0.23929315
4 0.26952737 0.180579219 0.59147693
5 0.45556697 0.090175736 0.51154218
6 0.01605072 0.810773224 0.21088358y_NN3_teste = predict(NN3_CLASS_3,newdata=MX_teste_s)
colnames(y_NN3_teste) = levels(base_treino_final$TAXA_PART_CAT)
head(y_NN3_teste) alta baixa media
1 0.6324236 0.03840782 0.3602109
2 0.7885891 0.01422857 0.2125496
3 0.6676586 0.03163077 0.3279939
4 0.1151312 0.29124633 0.5346144
5 0.3092354 0.16533330 0.6052929
6 0.1936382 0.48637930 0.363080310.3.5 Comparação entre medidas de qualidade do ajuste na base de treino
10.3.6 Entropia Cruzada
Para calcular o valor da entropria cruzada em cada previsão será necessário criar antes uma função para realizar o seu cálculo. Vamos relembrar e implementar em seguida.
\[ EC = - \dfrac{1}{N} \sum_{i=1}^N \sum_{k=1}^K y_{k,i}\ln(\hat{y}_{k,i}) \]
EC_multi = function(real,Mprev){
m = ncol(Mprev)
n = nrow(Mprev)
Mreal = matrix(0,ncol=m,nrow = n)
colnames(Mreal) = colnames(Mprev)
for(i in 1:n){
Mreal[i,as.character(real[i])] = 1
}
return(-mean(Mreal*log(Mprev + 0.00001)))
}(EC_TREE_treino = EC_multi(real = Y_treino , Mprev = y_TREE_treino))[1] 0.286676(EC_RF_treino = EC_multi(real = Y_treino , Mprev = y_RF_treino))[1] 0.06860227(EC_XGB_treino = EC_multi(real = Y_treino , Mprev = y_XGB_treino))[1] 0.1959319(EC_NN0_treino = EC_multi(real = Y_treino , Mprev = y_NN0_treino))[1] 0.2590338(EC_NN1_treino = EC_multi(real = Y_treino , Mprev = y_NN1_treino))[1] 0.2631472(EC_NN2_treino = EC_multi(real = Y_treino , Mprev = y_NN2_treino))[1] 0.2557237(EC_NN3_treino = EC_multi(real = Y_treino , Mprev = y_NN3_treino))[1] 0.2463854Perceberam novamente um NaN? Saberiam explicar?
Vejamos agora os resultados na base de teste.
(EC_TREE_teste = EC_multi(real = Y_teste , Mprev = y_TREE_teste))[1] 0.2844465(EC_RF_teste = EC_multi(real = Y_teste , Mprev = y_RF_teste))[1] 0.2453527(EC_XGB_teste = EC_multi(real = Y_teste , Mprev = y_XGB_teste))[1] 0.2417251(EC_NN0_teste = EC_multi(real = Y_teste , Mprev = y_NN0_teste))[1] 0.2600952(EC_NN1_teste = EC_multi(real = Y_teste , Mprev = y_NN1_teste))[1] 0.2625964(EC_NN2_teste = EC_multi(real = Y_teste , Mprev = y_NN2_teste))[1] 0.2591537(EC_NN3_teste = EC_multi(real = Y_teste , Mprev = y_NN3_teste))[1] 0.2503591EC_matriz = matrix(data = c(EC_TREE_treino, EC_RF_treino, EC_XGB_treino, EC_NN0_treino, EC_NN1_treino, EC_NN2_treino, EC_NN3_treino, EC_TREE_teste, EC_RF_teste, EC_XGB_teste, EC_NN0_teste, EC_NN1_teste, EC_NN2_teste, EC_NN3_teste),nrow = 2,ncol = 7,byrow = TRUE)
colnames(EC_matriz) = c("TREE","RF","XGB","NN0","NN1","NN2","NN3")
rownames(EC_matriz) = c("treino","teste")
EC_matriz TREE RF XGB NN0 NN1 NN2 NN3
treino 0.2866760 0.06860227 0.1959319 0.2590338 0.2631472 0.2557237 0.2463854
teste 0.2844465 0.24535269 0.2417251 0.2600952 0.2625964 0.2591537 0.2503591barplot(
height = EC_matriz,beside = TRUE,
main = "EC para Classificação Multiclasse",
col = c("gold","gold",
"orange2","orange2",
"red","red",
"violet","violet",
"purple","purple",
"skyblue","skyblue",
"darkblue","darkblue",
"springgreen","springgreen",
"darkgreen","darkgreen"))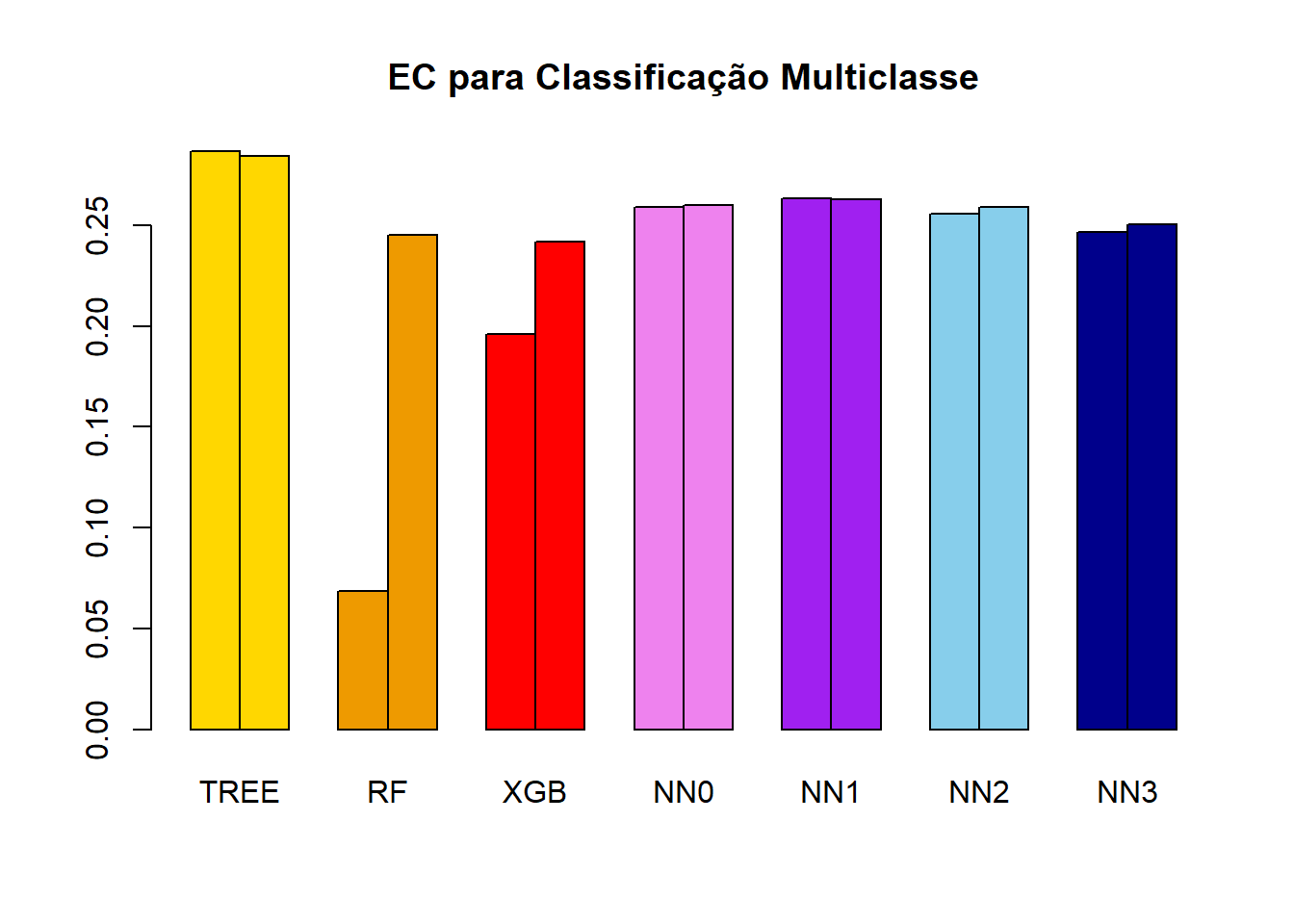
10.3.7 Matriz de Confusão
As previsões para as classes podem ser definidas a partir da regra: a classe prevista será aquela com maior probabilidade. Vejamos como ficaria para o método do XGBoost.
y_XGB_classe_treino = ifelse(y_XGB_treino[,"alta"]>y_XGB_treino[,"baixa"] & y_XGB_treino[,"alta"]>y_XGB_treino[,"media"],"alta",ifelse(y_XGB_treino[,"baixa"]>y_XGB_treino[,"media"],"baixa","media"))
y_XGB_classe_treino = factor(y_XGB_classe_treino)
head(y_XGB_classe_treino)[1] alta alta alta media alta baixa
Levels: alta baixa mediay_XGB_classe_teste = ifelse(y_XGB_teste[,"alta"]>y_XGB_teste[,"baixa"] & y_XGB_teste[,"alta"]>y_XGB_teste[,"media"],"alta",ifelse(y_XGB_teste[,"baixa"]>y_XGB_teste[,"media"],"baixa","media"))
y_XGB_classe_teste = factor(y_XGB_classe_teste)
head(y_XGB_classe_teste)[1] alta media media media media media
Levels: alta baixa mediaUma vez definidas as previsões para as classes é possível usar a matriz de confusão para se encontrar as medidas de qualidade do ajuste da classifciação, como acurácia, falso negativo, falso positivo, etc, para cada categoria.
library(caret)
MC_treino = confusionMatrix(as.factor(Y_treino),as.factor(y_XGB_classe_treino))
MC_treinoConfusion Matrix and Statistics
Reference
Prediction alta baixa media
alta 3470 155 356
baixa 145 3488 330
media 861 1030 1865
Overall Statistics
Accuracy : 0.7541
95% CI : (0.7462, 0.7619)
No Information Rate : 0.3994
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.63
Mcnemar's Test P-Value : < 2.2e-16
Statistics by Class:
Class: alta Class: baixa Class: media
Sensitivity 0.7752 0.7464 0.7311
Specificity 0.9293 0.9324 0.7933
Pos Pred Value 0.8716 0.8801 0.4965
Neg Pred Value 0.8697 0.8468 0.9136
Prevalence 0.3826 0.3994 0.2180
Detection Rate 0.2966 0.2981 0.1594
Detection Prevalence 0.3403 0.3387 0.3210
Balanced Accuracy 0.8523 0.8394 0.7622MC_teste = confusionMatrix(as.factor(Y_teste),as.factor(y_XGB_classe_teste))
MC_testeConfusion Matrix and Statistics
Reference
Prediction alta baixa media
alta 1055 67 199
baixa 47 1087 180
media 409 441 413
Overall Statistics
Accuracy : 0.6555
95% CI : (0.6403, 0.6704)
No Information Rate : 0.4092
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.4818
Mcnemar's Test P-Value : < 2.2e-16
Statistics by Class:
Class: alta Class: baixa Class: media
Sensitivity 0.6982 0.6815 0.5215
Specificity 0.8886 0.9014 0.7263
Pos Pred Value 0.7986 0.8272 0.3270
Neg Pred Value 0.8231 0.8034 0.8562
Prevalence 0.3876 0.4092 0.2032
Detection Rate 0.2707 0.2789 0.1060
Detection Prevalence 0.3389 0.3371 0.3240
Balanced Accuracy 0.7934 0.7915 0.6239