
5 Floresta Aleatória
Random Forest, ou Floresta Aleatória, método desenvolvido por (Breiman 2001), utiliza um conjunto de Árvores de Decisão para realizar tarefas de classificação ou regressão. Os métodos, como a Floresta Aleatória, que dá-se pela combinação de outros métodos são denominados como ensemble. O conceito fundamental das Florestas Aleatórias é a sabedoria das multidões: um número grande de modelos não correlacionados, no caso as árvores, operando em conjunto irão performar melhor do que cada modelo individual.
Antes de apresentar o método veja um experimento feito com 50 pessoas, para ilustrar a ideia da sabedoria das multidões. Cada pessoa viu uma foto de uma garrafa de 300ml, transparente, com grãos de feijão nela. Mais ou menos até a metade da garrafa. Em seguida cada participante deu um palpite sobre o número grãos de feijão na garrafa.
A quantidade exata de grãos de feijão na garrafa era 524, valor marcado com a linha em preto no gráfico apresentado na @ref(fig:palpites). As linhas pontilhadas em preto representam um intervalo de raio 100, ou seja, estão nos números 424 e 624. Cada palpite de um participante é um ponto vermelho. Veja que a maioria dos palpites estão fora do intervalo pontilhado, que mostra que a maioria dos participantes não deram um bom palpite. O normal é errar mesmo. Mas quando calculamos o valor médio dos palpites, linha pontilhada em vermelho, temos um palpite muito melhor do que os palpites individuais.
A ideia da Floresta Aleatória é essa: em vez de construir uma única árvore para realizar previsões serão construídas muitas árvores, diferentes entre si. A previsão final será a média da previsão de todas as árvores.
Seguem algumas vantagens da Floresta Aleatória em relação à uma única árovre de decisão:
Alta precisão: A Random Forest geralmente produz resultados mais precisos em comparação com um único modelo de árvore de decisão, especialmente quando o conjunto de dados é grande e complexo.
Resistência ao overfitting: Ao combinar previsões de várias árvores, a Foresta Aleatória reduz o risco de overfitting, ou seja, de criar um modelo excessivamente ajustado aos dados de treinamento e com baixa capacidade de generalização para novos dados.
Melhor desempenho com bases contendo outliers: uma vez que cada árvore da floresta é gerada por uma amostra bootstrap das observações (linhas), a observações com outliers nem sempre serão selecionadas, e com isso estes valores atípicos não geram uma grande influência no resultado final.
Melhor absorção da informação contida em cada covariável: como as partições das árvores da floresta consideram um seleção das covariáveis (colunas), algumas partições não levam em consideração a covariável mais importante e com isso outras variáveis conseguem exercer influência no resultado final.
5.1 Bagging
A Floresta Aleatória é um modelo com bagging. Um modelo com bagging é uma abordagem de aprendizado de máquina ensemble que combina múltiplos modelos individuais em um único modelo mais robusto e preciso. O termo “bagging” é uma abreviação de “bootstrap aggregating”, que se refere às duas principais etapas do processo.
O processo começa gerando várias amostras de treinamento com reposição a partir do conjunto de dados original. Isso significa que cada amostra é obtida aleatoriamente, permitindo que uma mesma amostra apareça múltiplas vezes e outras possam não ser selecionadas. O objetivo é criar várias versões do conjunto de treinamento, cada uma com pequenas variações nos dados de entrada.

Em seguida, um modelo individual é treinado em cada uma das amostras de treinamento geradas no passo anterior. No caso da Floresta Aleatória, este modelo individual é a Árvore de Decisão.
Ao fazer uma previsão usando o modelo com bagging, as previsões de cada modelo individual são combinadas para obter uma única previsão final. O bagging ajuda a reduzir o overfitting, pois as variações introduzidas nas amostras de treinamento aumentam a diversidade dos modelos individuais.
Segundo (James et al. 2013), o bagging é particularmente útil para árvores de decisão. Para aplicar o bagging no Modelo de Árvores de Decisão simplesmente contrói-se \(B\) árvores de decisão usando os \(B\) conjuntos de treinamento gerados pelo bootstrap. Essas árvores são cultivadas profundamente, ou seja, deixamos elas crescere o quanto quiserem. Portanto, cada árvore individual tem alta variância, mas baixo viés.
5.2 Partições
Neste momento já ficou claro porque a Floresta se chama Aleatória. Mas o bagging não é a única parte aleatória da floresta. Na costrução de uma árvore da Floresta Aleatória, cada vez que uma divisão em um nó da árvore será realizado, um sorteio de \(m\) covariáveis, entre todas as \(p\) covariáveis da base, é realizado. As covariáveis selecionadas serão as únicas candidatas à realizar a partição no nó.Uma nova amostra de \(m\) covariáveis é selecionada em cada divisão da árvore e, tipicamente, escolhe-se \(m \approx \sqrt{p}\).
A decisão de não usar todas as covariáveis como candidatas para uma partição em um nó reduz a correlação entre as árvores da floresta. Como a saída de uma Floresta aleatória é feita, em geral, pela média das saídas de cada árvore, a redução da correlação entre as árvores reduz a variância da saída do método, tornando mais confiável.
Uma outra vantagem neste processo é que ao considerar apenas um subconjunto das covariáveis, em muitos nós a partição é realizada sem que a covariáveis mais importante seja uma candidata. Isto permite que outras covariáveis tenham mais chances de serem escolhidas.
5.3 Regressão x Classificação
Até o momento só foi falado sobre árvores de decisão, de forma geral, sem diferenciar o caso de regressão do de classificação. A única diferença entre os dois casos é que para regressão a Floresta Aleatória é uma floresta de árvores de regressão, enquanto que para classificação, é uma floresta de árvores de classificação.
A previsão também é semelhante, a resposta que a Floresta Aleatória retorna é a média simples das respostas de todas as árvores. Ou seja, a nova observação, para a qual queremos fazer uma previsão, é colocada como dado de entrada em todas as árvores da floresta e cada árvore retorna um valor de previsão. A previsão da floresta aleatória será a média das previsões das árvores.
5.4 Algoritmo
Considere uma base de dados supervisionada, onde \(Y\) é a variável resposta (qualitativa ou quantitativa) e \(X_j\), \(j=1, 2, \ldots, p\) são as \(p\) covariáveis. Para cada observação \(i\), \(i=1, 2, \ldots, n\), isto é, para cada linha \(i\) da base, temos \(Y_i\) o valor da variável resposta para a observação \(i\) e \(X_{i,j}\) o valor ca covariável \(j\) para a observação \(i\). Posto isso, segue o algorítimo para o Método de Floresta Aleatória.
Escolhe-se o valor do hiperparâmtro \(B\), que é o número de árvores na floresta.
Faça \(b=1\) .
Selecione uma amostra de tamanho \(n\) do banco de treino a partir do método bootstrap, com reposição (bagging).
A amostra selecionada será a base de dados de entrada de uma nova árvore, vamos chamá-la de \(X\).
Faça um sorteio aleatório simples, sem reposição, de \(\sqrt{p}\) covariáveis entre as \(p\) covariáveis de \(X\). Vamos chamar de \(J\) o conjunto dos índices das covariáveis sorteadas.
Defina a covariável \(j \in J\) e o valor \(s \in \mathrm{R}\) tais que minimizam a soma dos índices Gini, para o caso de um problema de classificação, ou o \(RSS\), para o caso de um problema de regressão, nas regiões \(R_1 = \{X|X_j < s\}\) e \(R_2 = \{X|X_j \ge s\}\).
Verifique se em \(R_1\) um dos critérios de parada foi atingido. Se sim, este nó é uma folha e vá para o passo 8. Se não, faça \(X = R_1\) e volte para o passo 4.
Verifique se em \(R_2\) um dos critérios de parada foi atingido. Se sim, este nó é uma folha e vá para o passo 8. Se não, faça \(X = R_2\) e volte para o passo 4.
Faça \(b = b + 1\). Se \(b \le B\), volte para o passo 2. Caso contrário, FIM.
5.5 Como realizar previsões
Uma vez a floresta construída, ela pode ser usada para prever a variável resposta de novas observações. Para isso a nova observação passa a ser dado de entrada para todas as árvores da floresta. Cada uma das \(B\) árvores fornece uma previsão para a nova observação, vamos chamar de \(\hat{y}^b\) a previsão feita pela árvore \(b\) para a entrada \(y\). A previsão da floresta será:
\[ \hat{y} = \dfrac{\sum_{b=1}^B \hat{y}^b}{B} \]
5.6 Vamos praticar
Vamos repetir a prática dos dois últimos capítulos, mas agora com a Floresta Aleatória.
# Carregar pacotes e base de treino
library(tidyverse)
library(rpart)
base_treino = readRDS(file="salvos//base_treino_final.rds")Para criar modelos de Floresta Aleatória será usado o pacote randomForest (Liaw and Wiener 2002).
#install.packages("randomForest")
library(randomForest)Como o processo de criação das árvores trabalha com sorteios, é importante fixar a semente para garantir a reprodutibilidade do código.
set.seed(123456789)Regressão
Vejamos os resultados das regressões já feitas para a árvore de regressão agora com o método da Floresta Aleatória. A função a ser usada é a randomForest, do pacote de mesmo nome. No primeiro argumento desta função, x, deve ser colocadas as covariáveis. No argumento y é informado a variável alvo.
Não é preciso informar se o modelo é de classificação ou regressão. A função identifica o tipo da variável y e automaticamente escolhe regressão se ela for numérica ou classificação se ela for fator.
X = base_treino |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
NU_MATRICULAS,
INSE,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO,
PORTE_ESCOLA)
Y = base_treino$NU_MEDIA_MTRF_REG <- randomForest(x = X, y = Y, ntree=500)As variáveis importantes para esse modelo são guardadas no próprio objeto gerado pela função randomForest.
importancia = RF_REG$importance
sort(importancia[,1],decreasing = TRUE) INSE TP_DEPENDENCIA_ADM_ESCOLA SG_UF_ESCOLA
18135538.5 11270949.6 5544725.6
NU_TAXA_ABANDONO PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA
5316415.8 3352157.5 2902835.6
NU_MATRICULAS NU_TAXA_REPROVACAO PORTE_ESCOLA
2713152.3 2626921.8 747547.7
TP_LOCALIZACAO_ESCOLA
105558.5 A previsão pode ser feita pela mesma função predict.
y_ = predict(RF_REG)
y = base_treino$NU_MEDIA_MT
(RSS = sum((y - y_)^2))[1] 13793526(EMQ = mean((y-y_)^2))[1] 1178.934(R2 = 1 - sum((y-y_)^2)/sum((y-mean(y))^2))[1] 0.7500438Classificação Binária
A principal difereça será que neste caso teremos que criar a variável alvo, que não está na base.
TAXA_PART_BAIXA = ifelse(base_treino$TAXA_PART_CAT == "baixa",1,0)
Y = factor(TAXA_PART_BAIXA)
RF_CLASS_2 <- randomForest(x = X, y = Y, ntree=500)As variáveis mais importantes do modelo são.
importancia = RF_CLASS_2$importance
sort(importancia[,1],decreasing = TRUE) NU_TAXA_ABANDONO SG_UF_ESCOLA TP_DEPENDENCIA_ADM_ESCOLA
837.59164 835.02445 763.24067
NU_MATRICULAS PC_FORMACAO_DOCENTE NU_TAXA_REPROVACAO
565.03250 559.24304 550.37407
NU_TAXA_PERMANENCIA INSE PORTE_ESCOLA
536.64724 358.35479 117.67270
TP_LOCALIZACAO_ESCOLA
26.39092 Para realizar previsões usaremos a função predicr com o argumento type="prob".
y_ = predict(RF_CLASS_2,type="prob")
class(y_)[1] "matrix" "array" "votes" dim(y_)[1] 11700 2head(y_) 0 1
1 0.9848485 0.01515152
2 0.9668246 0.03317536
3 0.6216216 0.37837838
4 0.7551020 0.24489796
5 0.8548387 0.14516129
6 0.2512563 0.74874372Para gerar a curva ROC, o pacote pROC (Robin et al. 2011) .
library(pROC)
ROC = roc(response = Y,predictor = y_[,"1"])
plot.roc(ROC,
print.auc = TRUE,
print.thres = TRUE)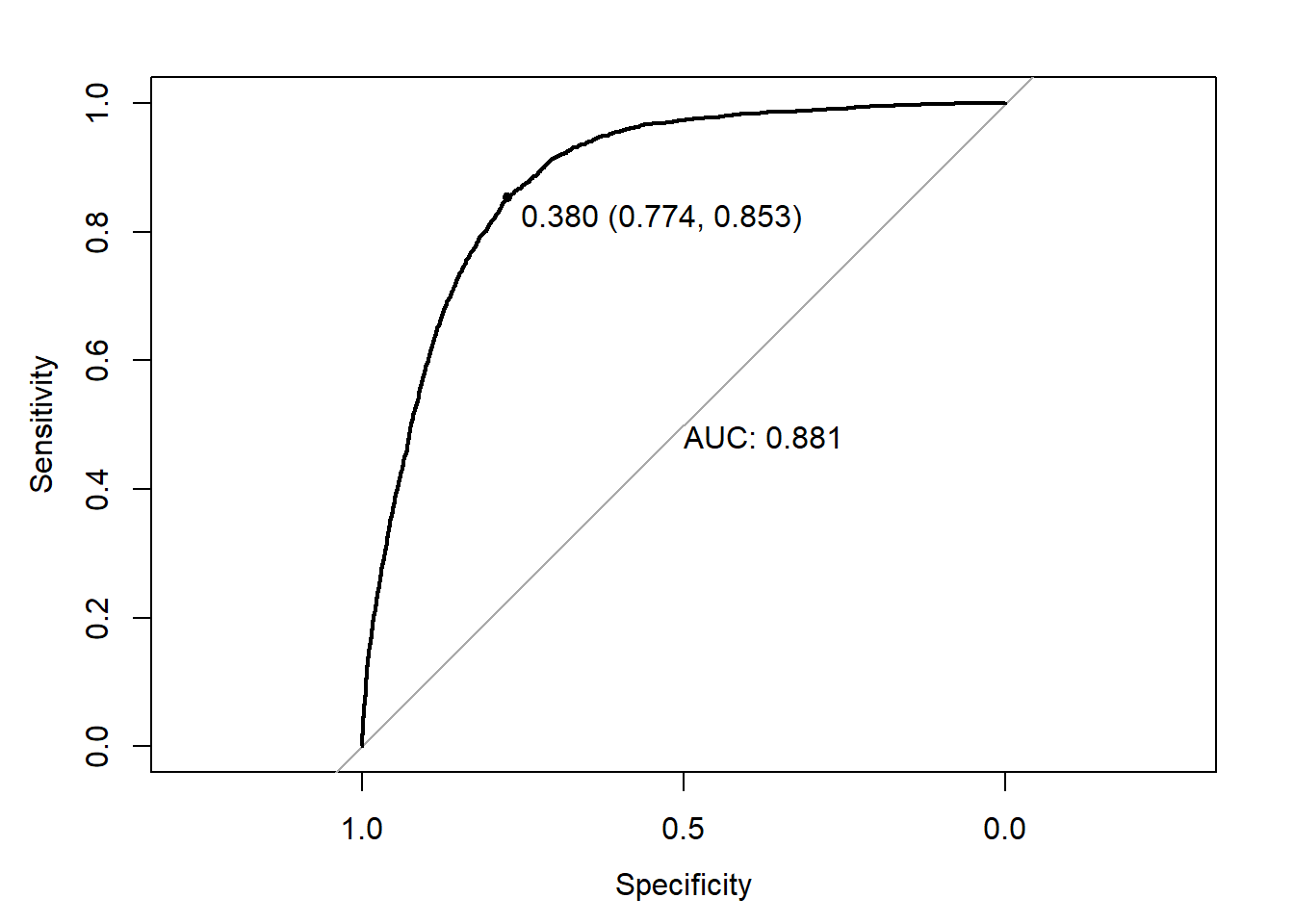
y_classe = ifelse(y_[,"1"]>0.380,1,0)
library(caret)
confusionMatrix(Y,as.factor(y_classe))Confusion Matrix and Statistics
Reference
Prediction 0 1
0 5989 1748
1 582 3381
Accuracy : 0.8009
95% CI : (0.7935, 0.8081)
No Information Rate : 0.5616
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.5852
Mcnemar's Test P-Value : < 2.2e-16
Sensitivity : 0.9114
Specificity : 0.6592
Pos Pred Value : 0.7741
Neg Pred Value : 0.8531
Prevalence : 0.5616
Detection Rate : 0.5119
Detection Prevalence : 0.6613
Balanced Accuracy : 0.7853
'Positive' Class : 0
Classificação Multiclasses
Vejamos agora o desempenho do método de Floresta Aleatória para o problema de classificação com 3 classes.
Y = base_treino$TAXA_PART_CATRF_CLASS_3 <- randomForest(x = X, y = Y, ntree=500)As variáveis importantes para o problema de classificação com três classes são:
importancia = RF_CLASS_3$importance
sort(importancia[,1],decreasing = TRUE) SG_UF_ESCOLA NU_TAXA_ABANDONO PC_FORMACAO_DOCENTE
1096.8254 1012.2523 996.0189
NU_TAXA_PERMANENCIA NU_TAXA_REPROVACAO NU_MATRICULAS
954.8354 945.2357 940.6938
TP_DEPENDENCIA_ADM_ESCOLA INSE PORTE_ESCOLA
874.5123 491.5692 197.0325
TP_LOCALIZACAO_ESCOLA
40.8423 A previsão é novamente realizada pela função predict.
y_ = predict(RF_CLASS_3, type = "prob")
head(y_) alta baixa media
1 0.81005587 0.01117318 0.1787709
2 0.63076923 0.03076923 0.3384615
3 0.42702703 0.18378378 0.3891892
4 0.22424242 0.23636364 0.5393939
5 0.60962567 0.10695187 0.2834225
6 0.01630435 0.67391304 0.3097826A classe prevista será aquela com maior probabilidade de ocorrer.
y_classe = ifelse(y_[,"alta"]>y_[,"baixa"] & y_[,"alta"]>y_[,"media"],"alta", ifelse(y_[,"baixa"]>y_[,"media"],"baixa","media"))
y_classe = factor(y_classe)
levels(y_classe)[1] "alta" "baixa" "media"confusionMatrix(data = y_classe, reference = Y)Confusion Matrix and Statistics
Reference
Prediction alta baixa media
alta 3175 168 1153
baixa 151 3116 1243
media 655 679 1360
Overall Statistics
Accuracy : 0.6539
95% CI : (0.6452, 0.6626)
No Information Rate : 0.3403
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.4794
Mcnemar's Test P-Value : < 2.2e-16
Statistics by Class:
Class: alta Class: baixa Class: media
Sensitivity 0.7975 0.7863 0.3621
Specificity 0.8289 0.8198 0.8321
Pos Pred Value 0.7062 0.6909 0.5048
Neg Pred Value 0.8881 0.8822 0.7340
Prevalence 0.3403 0.3387 0.3210
Detection Rate 0.2714 0.2663 0.1162
Detection Prevalence 0.3843 0.3855 0.2303
Balanced Accuracy 0.8132 0.8030 0.5971saveRDS(RF_REG,file="salvos//RF_REG.rds")
saveRDS(RF_CLASS_2,file="salvos//RF_CLASS_2.rds")
saveRDS(RF_CLASS_3,file="salvos//RF_CLASS_3.rds")