library(tidyverse)
library(rpart)
library(randomForest)
library(xgboost)
library(neuralnet)8 Comparação entre Modelos de Regressão
Netse capítulo serão abordadas formas de mensurar a qualidade do ajuste de modelos de regressão, assim como formas de investigar a existência ou não de sobreajuste.
8.1 Medida de qualidade do ajuste
Para os problemas de regressão a variável resposta \(Y\) é uma variável quantitativa. Suponha que um modelo de regressão \(k\) realizou a previsões \(\hat{y}_i^k\) para a \(i\)-ésima observação da variável \(Y\). Suponha \(y_i\) o real valor observado para a \(i\)-ésima observação da variável \(Y\).
| i | Valor observado | Previsão para o Modelo 1 | Previsão para o Modelo 2 | Previsão para o Modelo 3 |
|---|---|---|---|---|
| 1 | \(y_1\) | \(\hat y_1^1\) | \(\hat y_1^2\) | \(\hat y_1^3\) |
| 2 | \(y_2\) | \(\hat y_2^1\) | \(\hat y_2^2\) | \(\hat y_2^3\) |
| 3 | \(y_3\) | \(\hat y_3^1\) | \(\hat y_3^2\) | \(\hat y_3^3\) |
| … | … | … | … | … |
| N | \(y_N\) | \(\hat y_N^1\) | \(\hat y_N^2\) | \(\hat y_N^3\) |
No contexto deste curso os modelos apresentados na tabela acima podem ser modelos lineares, de árvores de regressão, floresta aleatória, gradiente bossting e redes neurais. Além disso, é possível fazer uma tabela como a apresentada acima para os dados da base de treino e para os dados na base de teste.
Para comparar o desempenho dos diferentes modelos de regressão são usadas medidas baseadas na diferença entre valor real observado \(y_i\) e valor estimado estimado \(\hat{y}_i\), chamada de resíduo. Uma vez conhecidos os resíduos é possível usar o SSE (soma dos erros ao quadrado) ou MSE (média dos erros ao quadrado) para comparar a qualidade do ajuste dos diferentes modelos.
\[ SSE^k = \sum_{i=1}^N (\hat{y}_i^k - y_i)^2 \qquad \qquad MSE^k = \dfrac{1}{N} \sum_{i=1}^N (\hat{y}_i^k - y_i)^2 = \dfrac{SSE}{N} \]
Suponha o MSE como medida de comparação. Esta medida pode ser calculada para os valores da base de treino e também da base de teste. Assim é possível construir a seguinte tabela.
| Modelo | MSE na base de treino | MSE na base de teste |
|---|---|---|
| 1 | \(MSE^1_{treino}\) | \(MSE^1_{teste}\) |
| 2 | \(MSE^2_{treino}\) | \(MSE^2_{teste}\) |
| 3 | \(MSE^3_{treino}\) | \(MSE^3_{teste}\) |
O modelo com menor MSE na base de teste será aquele que melhor conseguiu capturar a informação dos dados. Observar o valor do MSE na base de treino também pode trazer informações importantes, como por exemplo, se um modelo apresenta sobreajuste. Quando um modelo apresenta MSE na base de treino bem menor que o MSE na base de teste, principalmente quando comparado com os outros modelos, percebemos a ocorrência do sobreajuste (overfiting).
Essa comparação pode ficar bem mais visual se usarmos gráficos de barras, como veremos na parte prática desta aula.
8.2 Vamos Praticar
8.2.1 Carregar os pacotes necessários
8.2.2 Carregar base de treino e teste
Para comparar o desempenho dos modelos ajustados tanto na base de treino quanto na base de teste vamos carregar as duas bases criadas.
base_treino_final = readRDS(file="salvos//base_treino_final.rds")
glimpse(base_treino_final)Rows: 11,700
Columns: 21
$ SG_UF_ESCOLA <fct> RO, RO, RO, RO, RO, RO, RO, RO, RO, RO, RO, …
$ CO_ESCOLA_EDUCACENSO <chr> "11000058", "11000244", "11000260", "1100031…
$ NO_ESCOLA_EDUCACENSO <chr> "CENTRO DE ENSINO CLASSE A", "COLEGIO DOM BO…
$ TP_DEPENDENCIA_ADM_ESCOLA <fct> Privada, Privada, Estadual, Estadual, Privad…
$ TP_LOCALIZACAO_ESCOLA <fct> Urbana, Urbana, Urbana, Urbana, Urbana, Rura…
$ NU_MATRICULAS <dbl> 137, 55, 97, 44, 34, 41, 24, 33, 28, 72, 61,…
$ NU_PARTICIPANTES_NEC_ESP <dbl> 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2,…
$ NU_PARTICIPANTES <dbl> 130, 49, 96, 38, 29, 22, 21, 24, 19, 57, 55,…
$ NU_TAXA_PARTICIPACAO <dbl> 94.89, 89.09, 98.97, 86.36, 85.29, 53.66, 87…
$ NU_MEDIA_CN <dbl> 591.64, 508.74, 505.77, 484.43, 480.60, 443.…
$ NU_MEDIA_CH <dbl> 652.34, 586.45, 582.16, 540.06, 591.92, 483.…
$ NU_MEDIA_LP <dbl> 604.53, 531.35, 527.39, 489.87, 532.11, 452.…
$ NU_MEDIA_MT <dbl> 627.66, 529.87, 492.85, 456.92, 486.22, 429.…
$ NU_MEDIA_RED <dbl> 732.00, 591.84, 580.83, 543.68, 602.07, 415.…
$ INSE <fct> Grupo 6, Grupo 5, Grupo 5, Grupo 4, Grupo 4,…
$ PC_FORMACAO_DOCENTE <dbl> 67.5, 56.0, 53.6, 73.9, 46.2, 34.6, 63.3, 48…
$ NU_TAXA_PERMANENCIA <dbl> 78.46, 81.63, 85.42, 63.16, 58.62, 72.73, 76…
$ NU_TAXA_REPROVACAO <dbl> 3.9, 10.5, 10.8, 22.2, 9.9, 6.5, 35.1, 11.4,…
$ NU_TAXA_ABANDONO <dbl> 0.0, 0.8, 0.0, 3.9, 1.4, 18.0, 0.0, 7.0, 13.…
$ PORTE_ESCOLA <fct> Maior que 90 alunos, De 31 a 60 alunos, Maio…
$ TAXA_PART_CAT <fct> alta, alta, alta, alta, media, baixa, alta, …base_teste = readRDS(file="salvos//base_teste.rds")
glimpse(base_teste)Rows: 3,898
Columns: 27
$ NU_ANO <fct> 2015, 2015, 2015, 2015, 2015, 2015, 2015, 20…
$ CO_UF_ESCOLA <fct> 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, …
$ SG_UF_ESCOLA <fct> RO, RO, RO, RO, RO, RO, RO, RO, RO, RO, RO, …
$ CO_MUNICIPIO_ESCOLA <fct> 1100205, 1100205, 1100205, 1100205, 1100205,…
$ NO_MUNICIPIO_ESCOLA <fct> Porto Velho, Porto Velho, Porto Velho, Porto…
$ CO_ESCOLA_EDUCACENSO <chr> "11000171", "11000198", "11000252", "1100038…
$ NO_ESCOLA_EDUCACENSO <chr> "CENTRO EDUCACIONAL MOJUCA", "CENTRO EDUCACI…
$ TP_DEPENDENCIA_ADM_ESCOLA <fct> Privada, Privada, Privada, Estadual, Estadua…
$ TP_LOCALIZACAO_ESCOLA <fct> Urbana, Urbana, Urbana, Urbana, Urbana, Urba…
$ NU_MATRICULAS <dbl> 20, 39, 26, 75, 28, 35, 67, 24, 81, 259, 39,…
$ NU_PARTICIPANTES_NEC_ESP <dbl> 1, 0, 0, 1, 0, 0, 0, 0, 0, 2, 0, 0, 0, 2, 0,…
$ NU_PARTICIPANTES <dbl> 17, 37, 23, 59, 25, 27, 62, 24, 45, 211, 29,…
$ NU_TAXA_PARTICIPACAO <dbl> 85.00, 94.87, 88.46, 78.67, 89.29, 77.14, 92…
$ NU_MEDIA_CN <dbl> 458.46, 529.05, 523.38, 450.47, 478.66, 442.…
$ NU_MEDIA_CH <dbl> 533.51, 583.87, 591.66, 517.74, 547.20, 517.…
$ NU_MEDIA_LP <dbl> 472.62, 547.11, 563.45, 469.17, 503.59, 467.…
$ NU_MEDIA_MT <dbl> 459.72, 507.22, 528.93, 417.62, 455.35, 418.…
$ NU_MEDIA_RED <dbl> 507.82, 652.43, 583.48, 518.64, 552.00, 528.…
$ NU_MEDIA_OBJ <lgl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, …
$ NU_MEDIA_TOT <lgl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, …
$ INSE <fct> Grupo 4, Grupo 5, Grupo 5, Grupo 3, Grupo 4,…
$ PC_FORMACAO_DOCENTE <dbl> 58.3, 67.7, 72.7, 62.9, 75.5, 60.3, 61.7, 52…
$ NU_TAXA_PERMANENCIA <dbl> 70.59, 40.54, 52.17, 64.41, 44.00, 37.04, 70…
$ NU_TAXA_APROVACAO <dbl> 94.6, 90.1, 84.5, 54.9, 59.9, 85.4, 55.6, 92…
$ NU_TAXA_REPROVACAO <dbl> 5.4, 9.9, 13.1, 44.8, 39.0, 5.0, 24.0, 7.4, …
$ NU_TAXA_ABANDONO <dbl> 0.0, 0.0, 2.4, 0.3, 1.1, 9.6, 20.4, 0.0, 12.…
$ PORTE_ESCOLA <fct> De 1 a 30 alunos, De 31 a 60 alunos, De 1 a …8.2.3 Limpeza da base de teste
Veja que a base de teste ainda é a base bruta após o sorteio de treino e teste. Para que os modelos ajustados com a base de treino possam realizar previsões nas escolas que estão na base de teste é preciso replicar todo tratamento feito na base de treino agora na base de teste.
Primeiro vamos lembrar das variáveis que foram excluídas da base de treino bruta. Estas devem também serem excluídas da base de teste bruta.
Na análise de dados faltantes feita na base de treino em um primeiro momento excluímos as variáveis NU_MEDIA_OBJ e NU_MEDIA_TOT. Faremos o mesmo então com a base de teste.
base_teste = base_teste |> select(-c(NU_MEDIA_OBJ, NU_MEDIA_TOT))Na análise de covariância (quase) zero foi excluída a variável NU_ANO.
base_teste = base_teste |> select(-NU_ANO)Na análise de multicolinearidade foram excluídas a variável NU_TAXA_APROVACAO.
base_teste = base_teste |> select(-NU_TAXA_APROVACAO)Vejamos agora se existe algum dado faltante na base de teste. Caso tenha dado faltante nas variáveis quantitativas, será imputado a ele o valor médio da variável em questão na base de treino. Caso tenha dado faltante nas variáveis qualitativas, será imputado a ele a moda da variável em questão na base de treino.
library(naniar)
base_teste |> gg_miss_var()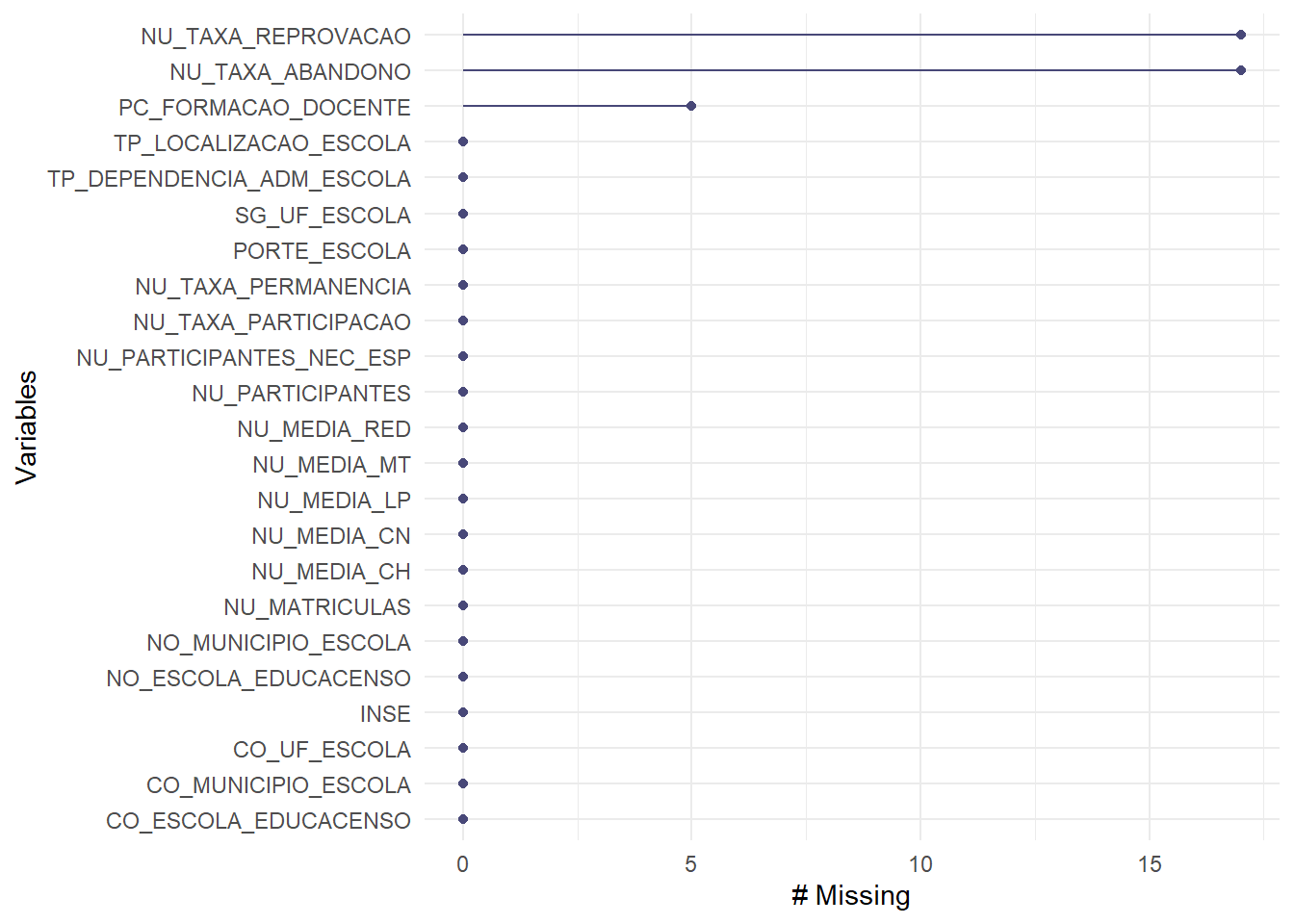
Temos dados faltantes nas variáveis NU_TAXA_REPROVACAO, NU_TAXA_ABANDONO e PC_FORMACAO_DOCENTE.
base_teste = base_teste |> mutate(
NU_TAXA_REPROVACAO =
replace_na(NU_TAXA_REPROVACAO,mean(base_treino_final$NU_TAXA_REPROVACAO)),
NU_TAXA_ABANDONO =
replace_na(NU_TAXA_ABANDONO, mean(base_treino_final$NU_TAXA_ABANDONO)),
PC_FORMACAO_DOCENTE =
replace_na(PC_FORMACAO_DOCENTE,mean(base_treino_final$PC_FORMACAO_DOCENTE))
)Verificando se ainda há dados faltantes.
base_teste |> miss_var_summary()# A tibble: 23 × 3
variable n_miss pct_miss
<chr> <int> <dbl>
1 CO_UF_ESCOLA 0 0
2 SG_UF_ESCOLA 0 0
3 CO_MUNICIPIO_ESCOLA 0 0
4 NO_MUNICIPIO_ESCOLA 0 0
5 CO_ESCOLA_EDUCACENSO 0 0
6 NO_ESCOLA_EDUCACENSO 0 0
7 TP_DEPENDENCIA_ADM_ESCOLA 0 0
8 TP_LOCALIZACAO_ESCOLA 0 0
9 NU_MATRICULAS 0 0
10 NU_PARTICIPANTES_NEC_ESP 0 0
# ℹ 13 more rowsVamos salvar essa base de teste modificada como base_teste_final.
base_teste_final = base_teste
saveRDS(base_teste_final,file="salvos//base_teste_final.rds")8.2.4 Carregar os modelos já ajustados
Nas últimas semanas ajustamos diferentes modelos de regressão. Agora é a hora de carregar todos eles para comparar o desempenho e discutir se algum deles se destaca em relação aos outros.
ML_REG = readRDS(file = "salvos//ML_final.rds")
TREE_REG = readRDS(file = "salvos//TREE_REG.rds")
RF_REG = readRDS(file = "salvos//RF_REG.rds")
XGB_REG = readRDS(file = "salvos//XGB_REG.rds")
NN0_REG = readRDS(file = "salvos//NN0_REG.rds")
NN1_REG = readRDS(file = "salvos//NN1_REG.rds")
NN2_REG = readRDS(file = "salvos//NN2_REG.rds")
NN3_REG = readRDS(file = "salvos//NN3_REG.rds")
NN22_REG = readRDS(file = "salvos//NN22_REG.rds")8.2.4.1 Previsões
Já fizemos o cálculo da previsão na base de treino. Vamos repetir esse processo e depois buscar a previsão para os valores na base de teste. Neste momento a maior atenção deve ser ao formato que cada modelo recebe os dados de entrada.
Para melhor organizar essa etapa vamos criar um data frame X somente com as covariáveis e vamos chamar de Y a variável de interesse, que neste caso será a nota média de matemática de cada escola. Veja que teremos um X e um Y para cada base, treino e teste.
X_treino = base_treino_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
NU_MATRICULAS,
INSE,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO,
PORTE_ESCOLA)
Y_treino = base_treino_final |> select(NU_MEDIA_MT)X_teste = base_teste_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
NU_MATRICULAS,
INSE,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO,
PORTE_ESCOLA)
Y_teste = base_teste_final |> select(NU_MEDIA_MT)8.2.4.1.1 Modelo Linear
y_ML_treino = predict(ML_REG,newdata = X_treino)
head(y_ML_treino) 1 2 3 4 5 6
628.3762 548.1647 515.3022 461.0753 498.5366 419.8621 y_ML_teste = predict(ML_REG,newdata = X_teste)
head(y_ML_teste) 1 2 3 4 5 6
501.7871 542.9200 537.2661 433.8930 447.1222 451.7591 8.2.4.1.2 Árvore de Classificação
y_TREE_treino = predict(TREE_REG,newdata = X_treino)
head(y_TREE_treino) 1 2 3 4 5 6
617.5129 535.1318 535.1318 433.0279 499.8683 433.0279 y_TREE_teste = predict(TREE_REG,newdata = X_teste)
head(y_TREE_teste) 1 2 3 4 5 6
499.8683 535.1318 535.1318 433.0279 433.0279 433.0279 8.2.4.1.3 Floresta Aleatória
y_RF_treino = predict(RF_REG,newdata = X_treino)
head(y_RF_treino) 1 2 3 4 5 6
613.8665 534.6305 499.4215 452.4827 489.2183 430.5997 y_RF_teste = predict(RF_REG,newdata = X_teste)
head(y_RF_teste) 1 2 3 4 5 6
490.2183 538.7752 523.3529 436.4407 456.2225 445.1411 8.2.4.1.4 XGBoost
O XGBoost precisa receber as variáveis categóricas transformadas para indicadoras.
MX_treino = model.matrix(~. , data = X_treino)[,-1]
MX_teste = model.matrix(~. , data = X_teste)[,-1]y_XGB_treino = predict(XGB_REG,newdata = MX_treino)
head(y_XGB_treino)[1] 638.7858 545.4161 509.9700 455.8942 483.9985 432.8139y_XGB_teste = predict(XGB_REG,newdata = MX_teste)
head(y_XGB_teste)[1] 496.2523 534.3057 528.1185 441.2662 459.1462 447.70698.2.4.1.5 Rede Neural
Para o modelo de redes neurais foi feita a padronização dos dados. O correto aqui é realizar a mesma padronização realizada para o dados que treinaram o modelo.
X1_treino = base_treino_final |> select(NU_MATRICULAS,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO)
X1_treino_s = scale(X1_treino)
mx = X1_treino_s |> attr("scaled:center")
mx NU_MATRICULAS PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA NU_TAXA_REPROVACAO
85.920855 60.438816 75.977907 8.822432
NU_TAXA_ABANDONO
3.776296 sx = X1_treino_s |> attr("scaled:scale")
sx NU_MATRICULAS PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA NU_TAXA_REPROVACAO
84.370154 17.233894 19.766292 7.923032
NU_TAXA_ABANDONO
5.504834 X1_teste = base_teste_final |> select(NU_MATRICULAS,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO)
head(X1_teste)# A tibble: 6 × 5
NU_MATRICULAS PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA NU_TAXA_REPROVACAO
<dbl> <dbl> <dbl> <dbl>
1 20 58.3 70.6 5.4
2 39 67.7 40.5 9.9
3 26 72.7 52.2 13.1
4 75 62.9 64.4 44.8
5 28 75.5 44 39
6 35 60.3 37.0 5
# ℹ 1 more variable: NU_TAXA_ABANDONO <dbl>X1_teste_s = X1_teste |> mutate(
NU_MATRICULAS = (X1_teste$NU_MATRICULAS - mx["NU_MATRICULAS"])/sx["NU_MATRICULAS"],
PC_FORMACAO_DOCENTE = (X1_teste$PC_FORMACAO_DOCENTE - mx["PC_FORMACAO_DOCENTE"])/sx["PC_FORMACAO_DOCENTE"],
NU_TAXA_PERMANENCIA = (X1_teste$NU_TAXA_PERMANENCIA - mx["NU_TAXA_PERMANENCIA"])/sx["NU_TAXA_PERMANENCIA"],
NU_TAXA_REPROVACAO = (X1_teste$NU_TAXA_REPROVACAO - mx["NU_TAXA_REPROVACAO"])/sx["NU_TAXA_REPROVACAO"],
NU_TAXA_ABANDONO = (X1_teste$NU_TAXA_ABANDONO - mx["NU_TAXA_ABANDONO"])/sx["NU_TAXA_ABANDONO"]
)
head(X1_teste_s) # A tibble: 6 × 5
NU_MATRICULAS PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA NU_TAXA_REPROVACAO
<dbl> <dbl> <dbl> <dbl>
1 -0.781 -0.124 -0.273 -0.432
2 -0.556 0.421 -1.79 0.136
3 -0.710 0.711 -1.20 0.540
4 -0.129 0.143 -0.585 4.54
5 -0.687 0.874 -1.62 3.81
6 -0.604 -0.00805 -1.97 -0.482
# ℹ 1 more variable: NU_TAXA_ABANDONO <dbl>X2_treino = base_treino_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
INSE,
PORTE_ESCOLA)
X2_treino_m = model.matrix(~. , data = X2_treino)[,-1]
MX_treino_s = cbind(X1_treino_s,X2_treino_m)X2_teste = base_teste_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
INSE,
PORTE_ESCOLA)
X2_teste_m = model.matrix(~. , data = X2_teste)[,-1]
MX_teste_s = cbind(X1_teste_s,X2_teste_m)Enfim a previsão..
y_NN0_treino = predict(NN0_REG,newdata=MX_treino_s)
head(y_NN0_treino) [,1]
1 628.3670
2 548.1393
3 515.2709
4 461.0268
5 498.4976
6 420.4111Lembre-se que para os demais modelos foi realizada uma padronização na variável resposta Y, que deverá ser desfeita para voltarmos a unidade original.
y_NN1_treino = predict(NN1_REG,newdata=MX_treino_s)
head(y_NN1_treino) [,1]
1 1.94814539
2 0.62507659
3 0.08218911
4 -0.51602712
5 -0.05089251
6 -0.93733401m = scale(Y_treino) |> attr("scaled:center")
s = scale(Y_treino) |> attr("scaled:scale")
y_NN1_treino = y_NN1_treino*s + m
head(y_NN1_treino) [,1]
1 626.2148
2 535.3463
3 498.0607
4 456.9751
5 488.9206
6 428.0396y_NN2_treino = predict(NN2_REG,newdata=MX_treino_s)
y_NN2_treino = y_NN2_treino*s + m
head(y_NN2_treino) [,1]
1 613.4767
2 535.9381
3 498.2472
4 455.9046
5 494.6937
6 431.4598y_NN3_treino = predict(NN3_REG,newdata=MX_treino_s)
y_NN3_treino = y_NN3_treino*s + m
head(y_NN3_treino) [,1]
1 621.5019
2 531.9791
3 495.9750
4 453.5376
5 486.9010
6 430.6552y_NN22_treino = predict(NN22_REG,newdata=MX_treino_s)
y_NN22_treino = y_NN22_treino*s + m
head(y_NN22_treino) [,1]
1 622.5476
2 540.6319
3 471.8973
4 452.5491
5 501.2423
6 424.6354O mesmo será feito na base de teste. Inclusive a transformação da predição será feita com os mesmos valores de m e s.
y_NN0_teste = predict(NN0_REG,newdata=MX_teste_s)
head(y_NN0_teste) [,1]
1 501.7275
2 542.8963
3 537.2330
4 433.8547
5 447.0721
6 451.6995y_NN1_teste = predict(NN1_REG,newdata=MX_teste_s)
y_NN1_teste = y_NN1_teste*s + m
head(y_NN1_teste) [,1]
1 494.4606
2 531.5471
3 520.1586
4 443.0709
5 452.1852
6 448.0886y_NN2_teste = predict(NN2_REG,newdata=MX_teste_s)
y_NN2_teste = y_NN2_teste*s + m
head(y_NN2_teste) [,1]
1 497.5827
2 537.8663
3 528.8802
4 442.8848
5 453.0234
6 449.9291y_NN3_teste = predict(NN3_REG,newdata=MX_teste_s)
y_NN3_teste = y_NN3_teste*s + m
head(y_NN3_teste) [,1]
1 490.3149
2 539.5645
3 528.5035
4 446.4767
5 452.5586
6 446.2040y_NN22_teste = predict(NN22_REG,newdata=MX_teste_s)
y_NN22_teste = y_NN22_teste*s + m
head(y_NN22_teste) [,1]
1 506.2587
2 537.0642
3 522.9174
4 447.6476
5 454.5991
6 441.41728.2.4.2 Comparação entre medidas de qualidade do ajuste na base de treino
O valor que queremos prever para a base de treino é:
y_treino = Y_treino$NU_MEDIA_MT(MSE_treino_ML = mean((y_ML_treino - y_treino)^2))[1] 1327.195(MSE_treino_TREE = mean((y_TREE_treino - y_treino)^2))[1] 1614.55(MSE_treino_RF = mean((y_RF_treino - y_treino)^2))[1] 302.6464(MSE_treino_XGB = mean((y_XGB_treino - y_treino)^2))[1] 836.2317(MSE_treino_NN0 = mean((y_NN0_treino - y_treino)^2))[1] 1327.183(MSE_treino_NN1 = mean((y_NN1_treino - y_treino)^2))[1] 1243.765(MSE_treino_NN2 = mean((y_NN2_treino - y_treino)^2))[1] 1166.974(MSE_treino_NN3 = mean((y_NN3_treino - y_treino)^2))[1] 1139.287(MSE_treino_NN22 = mean((y_NN22_treino - y_treino)^2))[1] 1176.839(R2_treino_ML =
1 - sum((y_ML_treino - y_treino)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_treino)^2))[1] 0.7186097(R2_treino_TREE =
1 - sum((y_TREE_treino - y_treino)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_treino)^2))[1] 0.6576849(R2_treino_RF =
1 - sum((y_RF_treino - y_treino)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_treino)^2))[1] 0.9358332(R2_treino_XGB =
1 - sum((y_XGB_treino - y_treino)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_treino)^2))[1] 0.8227031(R2_treino_NN0 =
1 - sum((y_NN0_treino - y_treino)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_treino)^2))[1] 0.7186122(R2_treino_NN1 =
1 - sum((y_NN1_treino - y_treino)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_treino)^2))[1] 0.7362983(R2_treino_NN2 =
1 - sum((y_NN2_treino - y_treino)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_treino)^2))[1] 0.7525794(R2_treino_NN3 =
1 - sum((y_NN3_treino - y_treino)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_treino)^2))[1] 0.7584496(R2_treino_NN22 =
1 - sum((y_NN22_treino - y_treino)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_treino)^2))[1] 0.7504879barplot(
height = c(MSE_treino_ML,
MSE_treino_TREE,
MSE_treino_RF,
MSE_treino_XGB,
MSE_treino_NN0,
MSE_treino_NN1,
MSE_treino_NN2,
MSE_treino_NN3,
MSE_treino_NN22),
names.arg = c("ML","TREE","RF","XGB","NN0","NN1","NN2","NN3","NN22"),
main = "MSE na base de treino",
col = c("gold","orange2","red","violet","purple","skyblue","darkblue","springgreen","darkgreen"))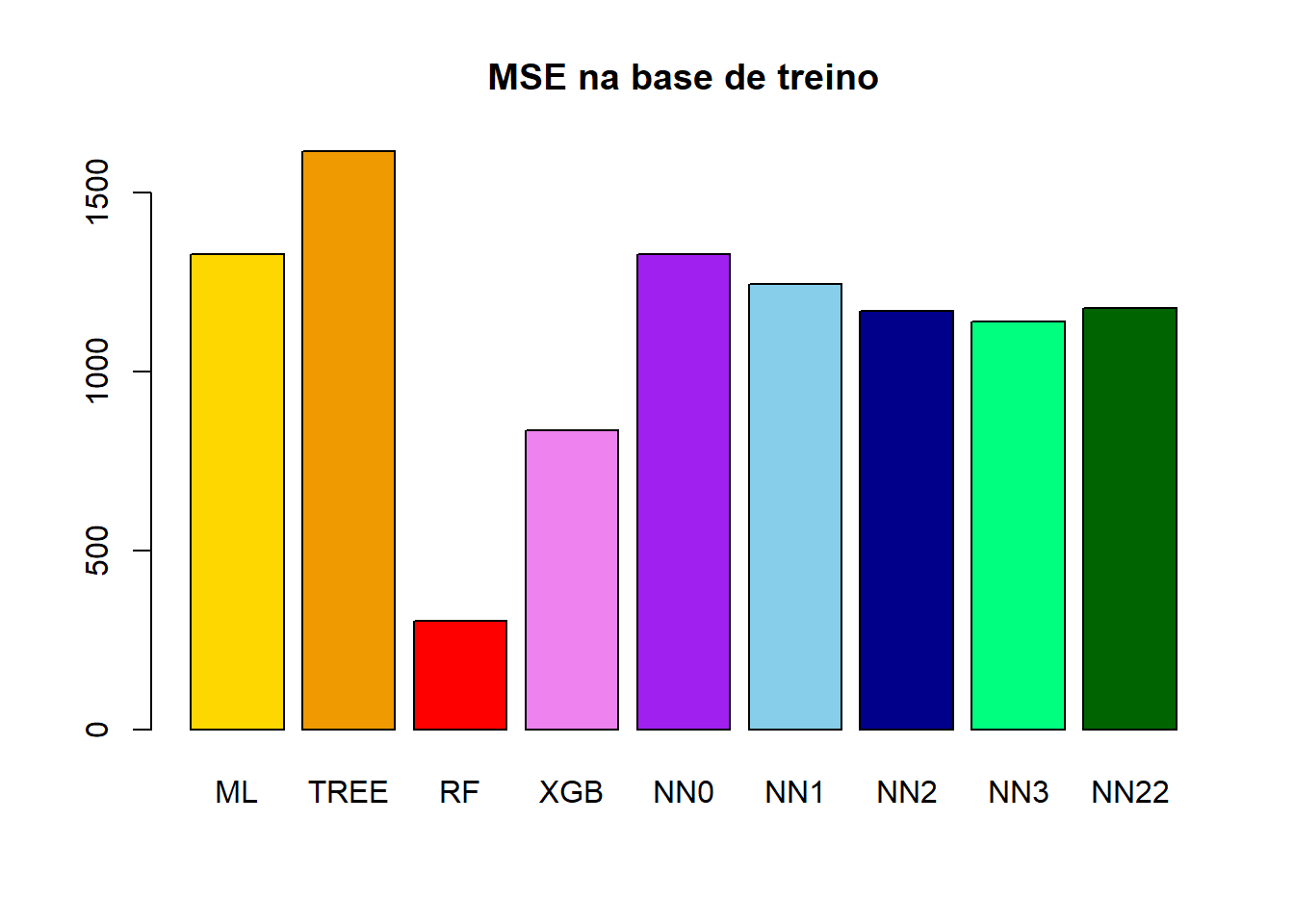
barplot(
height = c(R2_treino_ML,
R2_treino_TREE,
R2_treino_RF,
R2_treino_XGB,
R2_treino_NN0,
R2_treino_NN1,
R2_treino_NN2,
R2_treino_NN3,
R2_treino_NN22),
names.arg = c("ML","TREE","RF","XGB","NN0","NN1","NN2","NN3","NN22"),
main = "R2 na base de treino",ylim = c(0,1),
col = c("gold","orange2","red","violet","purple","skyblue","darkblue","springgreen","darkgreen"))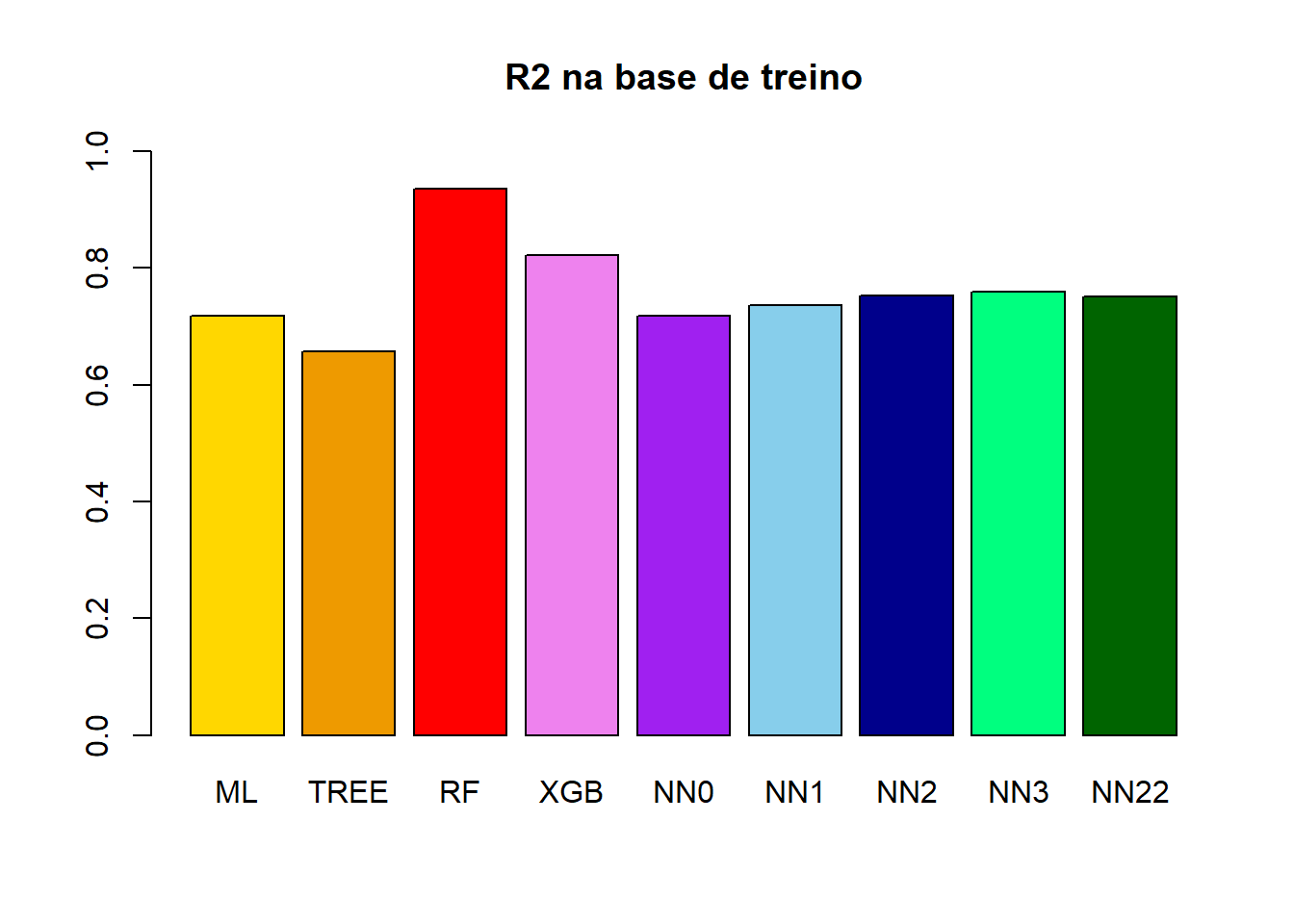
8.2.4.3 Comparação entre medidas de qualidade do ajuste na base de teste
O valor que queremos prever para a base de teste é:
y_teste = Y_teste$NU_MEDIA_MT(MSE_teste_ML = mean((y_ML_teste - y_teste)^2))[1] 1703.434(MSE_teste_TREE = mean((y_TREE_teste - y_teste)^2))[1] 1672.391(MSE_teste_RF = mean((y_RF_teste - y_teste)^2))[1] 1199.286(MSE_teste_XGB = mean((y_XGB_teste - y_teste)^2))[1] 1206.674(MSE_teste_NN0 = mean((y_NN0_teste - y_teste)^2))[1] 1703.268(MSE_teste_NN1 = mean((y_NN1_teste - y_teste)^2))[1] 1323.418(MSE_teste_NN2 = mean((y_NN2_teste - y_teste)^2))[1] 1250.795(MSE_teste_NN3 = mean((y_NN3_teste - y_teste)^2))[1] 1230.689(MSE_teste_NN22 = mean((y_NN22_teste - y_teste)^2))[1] 1301.802(R2_teste_ML =
1 - sum((y_ML_teste - y_teste)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_teste)^2))[1] 0.6537608(R2_teste_TREE =
1 - sum((y_TREE_teste - y_teste)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_teste)^2))[1] 0.6600706(R2_teste_RF =
1 - sum((y_RF_teste - y_teste)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_teste)^2))[1] 0.7562337(R2_teste_XGB =
1 - sum((y_XGB_teste - y_teste)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_teste)^2))[1] 0.754732(R2_teste_NN0 =
1 - sum((y_NN0_teste - y_teste)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_teste)^2))[1] 0.6537944(R2_teste_NN1 =
1 - sum((y_NN1_teste - y_teste)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_teste)^2))[1] 0.7310026(R2_teste_NN2 =
1 - sum((y_NN2_teste - y_teste)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_teste)^2))[1] 0.7457639(R2_teste_NN3 =
1 - sum((y_NN3_teste - y_teste)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_teste)^2))[1] 0.7498506(R2_teste_NN22 =
1 - sum((y_NN22_teste - y_teste)^2)/sum((mean(Y_treino$NU_MEDIA_MT) - y_teste)^2))[1] 0.7353963(MSE_teste_ML = mean((y_ML_teste - y_teste)^2))[1] 1703.434(MSE_teste_TREE = mean((y_TREE_teste - y_teste)^2))[1] 1672.391(MSE_teste_RF = mean((y_RF_teste - y_teste)^2))[1] 1199.286(MSE_teste_XGB = mean((y_XGB_teste - y_teste)^2))[1] 1206.674(MSE_teste_NN0 = mean((y_NN0_teste - y_teste)^2))[1] 1703.268(MSE_teste_NN1 = mean((y_NN1_teste - y_teste)^2))[1] 1323.418(MSE_teste_NN2 = mean((y_NN2_teste - y_teste)^2))[1] 1250.795(MSE_teste_NN3 = mean((y_NN3_teste - y_teste)^2))[1] 1230.689(MSE_teste_NN22 = mean((y_NN22_teste - y_teste)^2))[1] 1301.802barplot(
height = c(MSE_teste_ML,
MSE_teste_TREE,
MSE_teste_RF,
MSE_teste_XGB,
MSE_teste_NN0,
MSE_teste_NN1,
MSE_teste_NN2,
MSE_teste_NN3,
MSE_teste_NN22),
names.arg = c("ML","TREE","RF","XGB","NN0","NN1","NN2","NN3","NN22"),
main = "MSE na base de teste",
col = c("gold","orange2","red","violet","purple","skyblue","darkblue","springgreen","darkgreen"))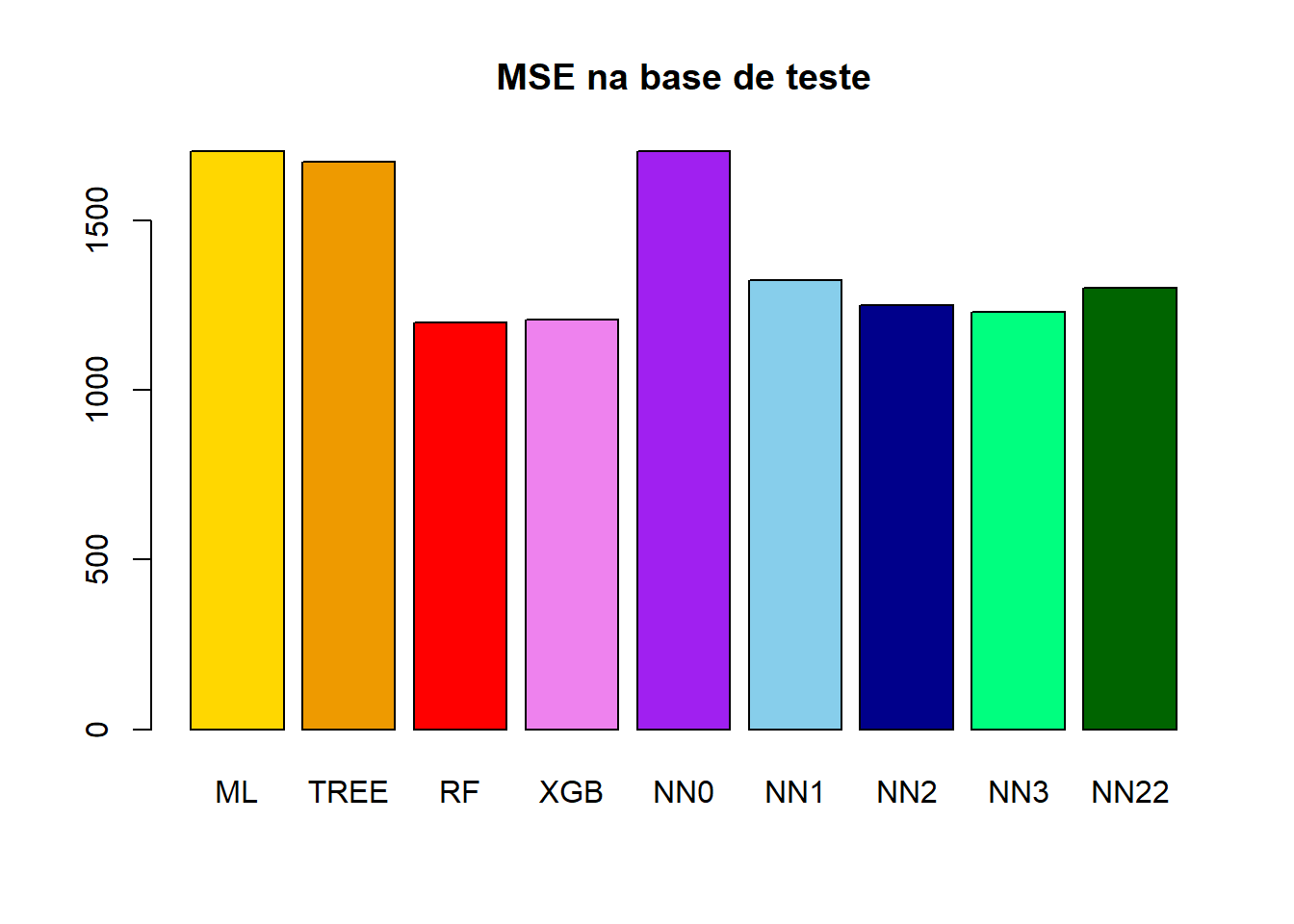
(R2_teste_ML =
1 - sum((y_ML_teste - y_teste)^2)/sum((mean(Y_teste$NU_MEDIA_MT) - y_teste)^2))[1] 0.6537342(R2_teste_TREE =
1 - sum((y_TREE_teste - y_teste)^2)/sum((mean(Y_teste$NU_MEDIA_MT) - y_teste)^2))[1] 0.6600445(R2_teste_RF =
1 - sum((y_RF_teste - y_teste)^2)/sum((mean(Y_teste$NU_MEDIA_MT) - y_teste)^2))[1] 0.756215(R2_teste_XGB =
1 - sum((y_XGB_teste - y_teste)^2)/sum((mean(Y_teste$NU_MEDIA_MT) - y_teste)^2))[1] 0.7547132(R2_teste_NN0 =
1 - sum((y_NN0_teste - y_teste)^2)/sum((mean(Y_teste$NU_MEDIA_MT) - y_teste)^2))[1] 0.6537678(R2_teste_NN1 =
1 - sum((y_NN1_teste - y_teste)^2)/sum((mean(Y_teste$NU_MEDIA_MT) - y_teste)^2))[1] 0.730982(R2_teste_NN2 =
1 - sum((y_NN2_teste - y_teste)^2)/sum((mean(Y_teste$NU_MEDIA_MT) - y_teste)^2))[1] 0.7457443(R2_teste_NN3 =
1 - sum((y_NN3_teste - y_teste)^2)/sum((mean(Y_teste$NU_MEDIA_MT) - y_teste)^2))[1] 0.7498314(R2_teste_NN22 =
1 - sum((y_NN22_teste - y_teste)^2)/sum((mean(Y_teste$NU_MEDIA_MT) - y_teste)^2))[1] 0.735376barplot(
height = c(R2_teste_ML,
R2_teste_TREE,
R2_teste_RF,
R2_teste_XGB,
R2_teste_NN0,
R2_teste_NN1,
R2_teste_NN2,
R2_teste_NN3,
R2_teste_NN22),
names.arg = c("ML","TREE","RF","XGB","NN0","NN1","NN2","NN3","NN22"),
main = "R2 na base de teste",ylim = c(0,1),,
col = c("gold","orange2","red","violet","purple","skyblue","darkblue","springgreen","darkgreen"))
8.2.4.4 Treino e Teste juntos
MSE = matrix(data = c(MSE_treino_ML,MSE_teste_ML,
MSE_treino_TREE,MSE_teste_TREE,
MSE_treino_RF,MSE_teste_RF,
MSE_treino_XGB,MSE_teste_XGB,
MSE_treino_NN0,MSE_teste_NN0,
MSE_treino_NN1,MSE_teste_NN1,
MSE_treino_NN2,MSE_teste_NN2,
MSE_treino_NN3,MSE_teste_NN3,
MSE_treino_NN22,MSE_teste_NN22),
nrow = 9,ncol = 2,byrow = T)
colnames(MSE) = c("treino","teste")
rownames(MSE) = c("ML","TREE","RF","XGB","NN0","NN1","NN2","NN3","NN22")
MSE treino teste
ML 1327.1948 1703.434
TREE 1614.5501 1672.391
RF 302.6464 1199.286
XGB 836.2317 1206.674
NN0 1327.1826 1703.268
NN1 1243.7653 1323.418
NN2 1166.9744 1250.795
NN3 1139.2873 1230.689
NN22 1176.8390 1301.802barplot(height = t(MSE),main = "Comparação do MSE",
col=c(rep("gold",2),
rep("orange2",2),
rep("red",2),
rep("violet",2),
rep("purple",2),
rep("skyblue",2),
rep("darkblue",2),
rep("springgreen",2),
rep("darkgreen",2)),
beside = T)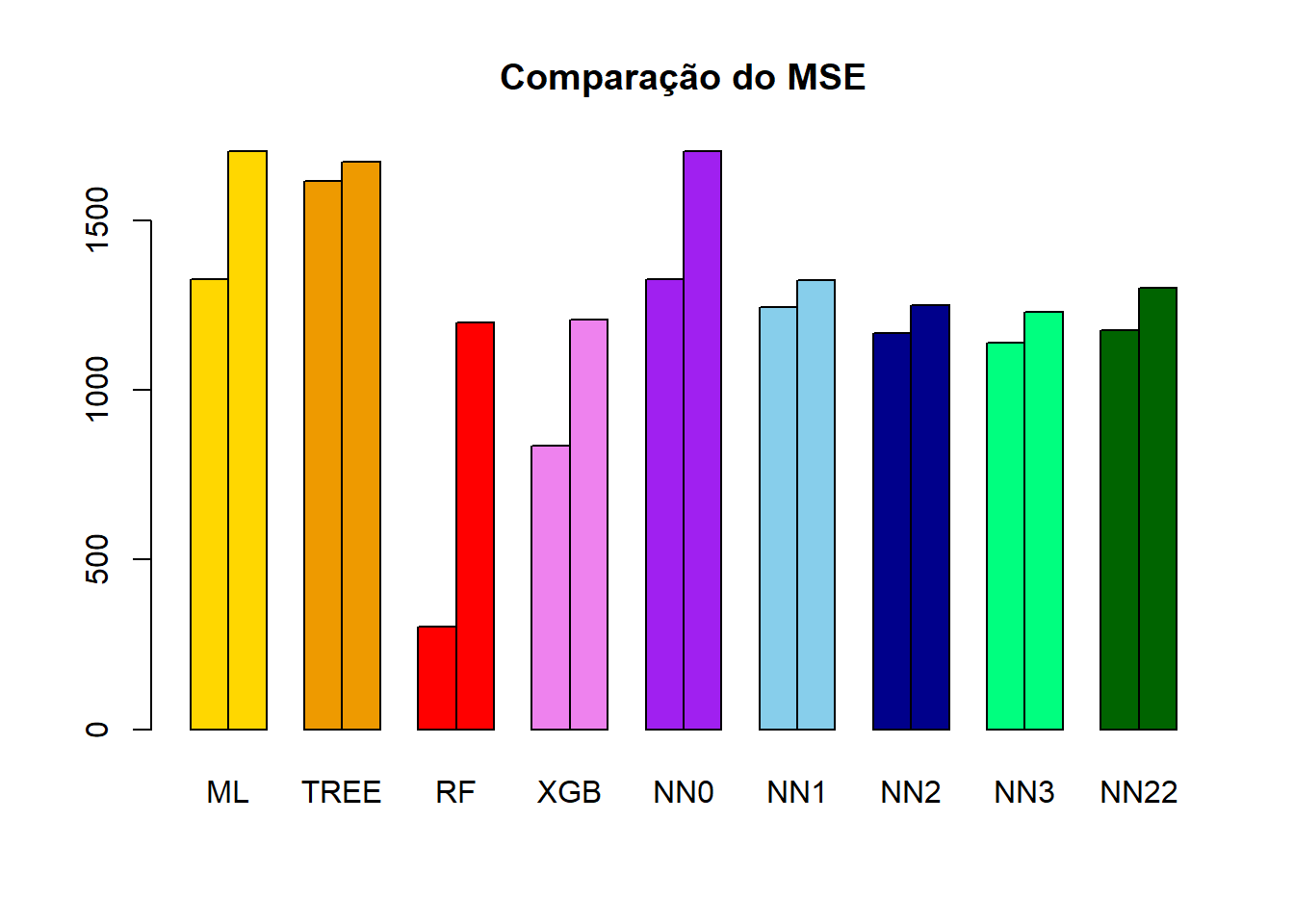
R2 = matrix(data = c(R2_treino_ML,R2_teste_ML,
R2_treino_TREE,R2_teste_TREE,
R2_treino_RF,R2_teste_RF,
R2_treino_XGB,R2_teste_XGB,
R2_treino_NN0,R2_teste_NN0,
R2_treino_NN1,R2_teste_NN1,
R2_treino_NN2,R2_teste_NN2,
R2_treino_NN3,R2_teste_NN3,
R2_treino_NN22,R2_teste_NN22),
nrow = 9,ncol = 2,byrow = T)
colnames(R2) = c("treino","teste")
rownames(R2) = c("ML","TREE","RF","XGB","NN0","NN1","NN2","NN3","NN22")
R2 treino teste
ML 0.7186097 0.6537342
TREE 0.6576849 0.6600445
RF 0.9358332 0.7562150
XGB 0.8227031 0.7547132
NN0 0.7186122 0.6537678
NN1 0.7362983 0.7309820
NN2 0.7525794 0.7457443
NN3 0.7584496 0.7498314
NN22 0.7504879 0.7353760barplot(height = t(R2),main = "Comparação do R2",ylim=c(0,1),
col=c(rep("gold",2),
rep("orange2",2),
rep("red",2),
rep("violet",2),
rep("purple",2),
rep("skyblue",2),
rep("darkblue",2),
rep("springgreen",2),
rep("darkgreen",2)),
beside = T)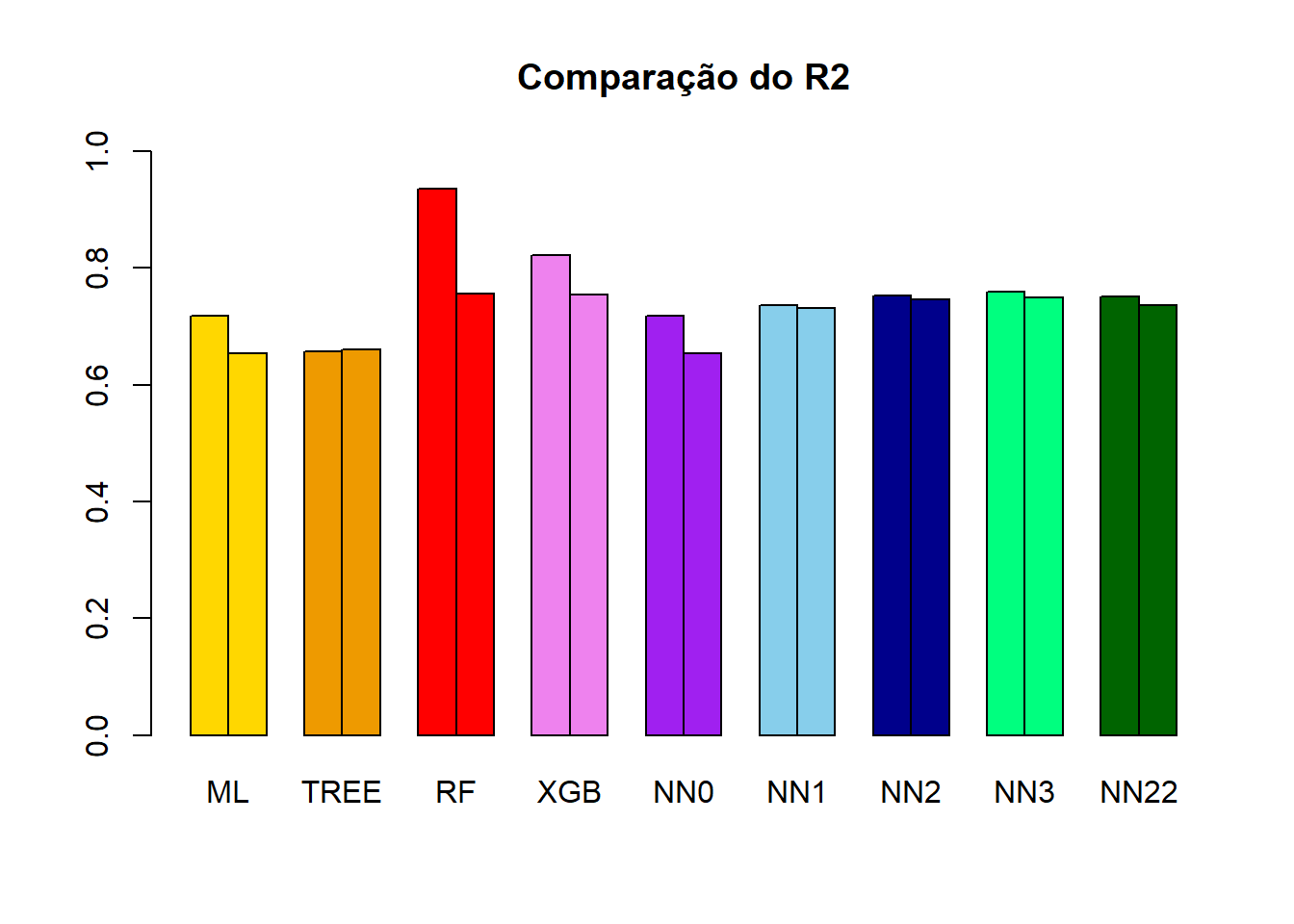
8.3 Validação Cruzada
Repara que a comparação dos modelos só pode ser realizada de verdade após a análise dos seus desempenhos na em valores que não foram aqueles usados para treino. Mas na prática, os dados de teste são aqueles que não conhecemos a variável resposta, não podemos usar ele, por exemplo, para escolher o melhor modelo.
A validação cruzada (k-fold cross-validation) é um processo de análise do ajuste do modelo que pode ser feito na base de treino, antes de verificar o seu desempenho na base de teste. Este processo é muito útil para se encontrar valores para comparar modelos e escolher os hiperparâmetros, por exemplo.
Para realizar a validação cruzada a base de treino é dividida aleatoriamente em \(k\) pedaços de (aproximadamente) mesmo tamanho. Uma vez a base de treino dividida, o modelo é ajustado utilizando como treino \(k-1\) pedaços e checando o desempenho no pedaço que ficou de fora, chamado de base de validação. Esse processo é feito \(k\) vezes e calculados as medidas de desempenho. Ao final do processo, em vez de um valor do MSE na base de treino, teremos \(k\) valores do MSE na base de treinamento e \(k\) valores do MSE na base de validação.
Divide a base de treino em \(k\) partes;
Faz \(i=1\);
Considere a parte \(i\) como base de validação e o restante da base de dados como base de treino.
Ajuste cada modelo para a base de treino.
Calcule o MSE na base de validação para cada modelo ajustado na base de treino.
Faz \(i = i + 1\) e se \(i \le k\), volte para o passo 3.
Realizar a validação cruzada para se chegar ao melhor modelo de regressão é uma avaliação bem mais ampla do que simplesmente testar o modelo no treino e no teste. Por exemplo, realizando \(K\) ajustes do mesmo modelo na base de treino deixando sempre um pedaço para validação diminui a chance do sorteio da base de treino ter sido favorável para um ou outro modelo.
No final, em vez de comparar o valor do MSE na base de treino e teste, serão comparados estatísticas para os \(K\) valores do MSE na base de treino e validação. Esses valores nos levarão à escolha do melhor modelo.
| TREINO | VALIDÇÃO | |||||||
| Modelo | Mínimo | Mediana | Média | Máximo | Mínimo | Mediana | Média | Máximo |
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
8.3.1 Vamos Praticar
A particção da base de treino em \(k\) pedaços pode ser feita pelo pacote caret.
library(caret)
set.seed(1234567890)
K = 10
n=nrow(base_treino_final)
indices_folds = createFolds(1:n,k=K)
class(indices_folds)[1] "list"length(indices_folds)[1] 10head(indices_folds$Fold01)[1] 7 8 11 25 27 41head(indices_folds$Fold02)[1] 12 19 20 22 43 44O grande custo da validação cruzada é que em vez de ajustarmos o modelo \(1\times\) na base de treino, isso será feito \(k\times\). No caso deste exemplo, será feito \(10\times\).
Para simplificar a explicação vamos usar a validação cruzada para comparar: Modelos Lineares, Árvore de Regressão, Floresta Aleatória com 100 e com 500 florestas e XBGoost com 100 e com 500 árvores.
Cada um desses modelos será ajustado à uma base de treino, isso será feito \(10\times\) e vamos guardar para comparação os valores do MSE e R2.
MSE_treino = matrix(data=NA,nrow = K,ncol = 6)
colnames(MSE_treino) = c("ML","TREE","RF100","RF500","XGB100","XGB500")
R2_treino = matrix(data=NA,nrow = K,ncol = 6)
colnames(R2_treino) = c("ML","TREE","RF100","RF500","XGB100","XGB500")
MSE_valida = matrix(data=NA,nrow = K,ncol = 6)
colnames(MSE_valida) = c("ML","TREE","RF100","RF500","XGB100","XGB500")
R2_valida = matrix(data=NA,nrow = K,ncol = 6)
colnames(R2_valida) = c("ML","TREE","RF100","RF500","XGB100","XGB500")
for(f in 1:K){
valida_X = X_treino |> dplyr::slice(indices_folds[[f]])
valida_Y = Y_treino |> dplyr::slice(indices_folds[[f]])
valida_MX = model.matrix(~., data = valida_X)[,-1]
treino_X = X_treino |> dplyr::slice(-indices_folds[[f]])
treino_Y = Y_treino |> dplyr::slice(-indices_folds[[f]])
treino_MX = model.matrix(~., data = treino_X)[,-1]
y_valida = valida_Y$NU_MEDIA_MT
y_treino = treino_Y$NU_MEDIA_MT
y_barra = mean(treino_Y$NU_MEDIA_MT)
ML = lm(NU_MEDIA_MT ~ ., data = cbind(treino_X,treino_Y))
TREE = rpart(NU_MEDIA_MT ~ ., data = cbind(treino_X,treino_Y))
RF_100 = randomForest(x = treino_X,y = treino_Y$NU_MEDIA_MT,ntree = 100)
RF_500 = randomForest(x = treino_X,y = treino_Y$NU_MEDIA_MT,ntree = 500)
XGB_100 = xgboost(data = treino_MX,label = treino_Y$NU_MEDIA_MT,objective = "reg:squarederror",nrounds = 100)
XGB_500 = xgboost(data = treino_MX,label = treino_Y$NU_MEDIA_MT,objective = "reg:squarederror",nrounds = 500)
y_ = predict(ML,newdata = valida_X)
MSE_valida[f,1] = mean((y_valida - y_)^2)
R2_valida[f,1] = 1 - sum((y_valida - y_)^2)/sum((y_valida - y_barra)^2)
y_ = predict(ML,newdata = treino_X)
MSE_treino[f,1] = mean((y_treino - y_)^2)
R2_treino[f,1] = 1 - sum((y_treino - y_)^2)/sum((y_treino - y_barra)^2)
y_ = predict(TREE,newdata = valida_X)
MSE_valida[f,2] = mean((y_valida - y_)^2)
R2_valida[f,2] = 1 - sum((y_valida - y_)^2)/sum((y_valida - y_barra)^2)
y_ = predict(TREE,newdata = treino_X)
MSE_treino[f,2] = mean((y_treino - y_)^2)
R2_treino[f,2] = 1 - sum((y_treino - y_)^2)/sum((y_treino - y_barra)^2)
y_ = predict(RF_100,newdata = valida_X)
MSE_valida[f,3] = mean((y_valida - y_)^2)
R2_valida[f,3] = 1 - sum((y_valida - y_)^2)/sum((y_valida - y_barra)^2)
y_ = predict(RF_100,newdata = treino_X)
MSE_treino[f,3] = mean((y_treino - y_)^2)
R2_treino[f,3] = 1 - sum((y_treino - y_)^2)/sum((y_treino - y_barra)^2)
y_ = predict(RF_500,newdata = valida_X)
MSE_valida[f,4] = mean((y_valida - y_)^2)
R2_valida[f,4] = 1 - sum((y_valida - y_)^2)/sum((y_valida - y_barra)^2)
y_ = predict(RF_500,newdata = treino_X)
MSE_treino[f,4] = mean((y_treino - y_)^2)
R2_treino[f,4] = 1 - sum((y_treino - y_)^2)/sum((y_treino - y_barra)^2)
y_ = predict(XGB_100,newdata = valida_MX)
MSE_valida[f,5] = mean((y_valida - y_)^2)
R2_valida[f,5] = 1 - sum((y_valida - y_)^2)/sum((y_valida - y_barra)^2)
y_ = predict(XGB_100,newdata = treino_MX)
MSE_treino[f,5] = mean((y_treino - y_)^2)
R2_treino[f,5] = 1 - sum((y_treino - y_)^2)/sum((y_treino - y_barra)^2)
y_ = predict(XGB_500,newdata = valida_MX)
MSE_valida[f,6] = mean((y_valida - y_)^2)
R2_valida[f,6] = 1 - sum((y_valida - y_)^2)/sum((y_valida - y_barra)^2)
y_ = predict(XGB_500,newdata = treino_MX)
MSE_treino[f,6] = mean((y_treino - y_)^2)
R2_treino[f,6] = 1 - sum((y_treino - y_)^2)/sum((y_treino - y_barra)^2)
}Vamos primeiro analisar os valores do MSE.
apply(MSE_treino, MARGIN = 2,FUN = summary) ML TREE RF100 RF500 XGB100 XGB500
Min. 1310.781 1554.956 301.2666 297.1038 473.4504 52.33753
1st Qu. 1316.412 1604.517 307.1190 300.8684 482.3588 54.25217
Median 1326.418 1617.501 308.6415 302.0648 493.3078 56.86551
Mean 1326.658 1609.073 308.6019 302.4587 494.7160 56.71456
3rd Qu. 1338.245 1622.215 309.8591 303.3128 506.1428 58.89384
Max. 1341.761 1627.318 315.9873 309.4387 514.4858 61.65152Os valores acima indicam um resumo do MSE na base de treinamento nas 10 iterações da validação cruzada. Já os valores abaixo são um resumo do MSE na base de validação, isto é, aquela que não foi usada para treinamento.
apply(MSE_valida, MARGIN = 2,FUN = summary) ML TREE RF100 RF500 XGB100 XGB500
Min. 1201.381 1500.111 1057.676 1043.379 1085.452 1207.388
1st Qu. 1232.581 1547.207 1090.423 1088.432 1211.290 1341.058
Median 1338.114 1589.068 1199.495 1190.343 1259.056 1393.772
Mean 1337.200 1623.869 1185.809 1178.062 1261.669 1407.753
3rd Qu. 1431.681 1708.022 1247.535 1241.155 1313.372 1491.201
Max. 1480.709 1804.901 1392.717 1367.552 1457.733 1657.656Escolhida a mediana como medida de comparação, vejamos no gráfico em barras abaixo a comparação dos MSE para métodos avaliados pela validação cruzada.
M = rbind(apply(MSE_treino, MARGIN = 2,FUN = median),
apply(MSE_valida, MARGIN = 2,FUN = median))
rownames(M) = c("treino","valida")
M ML TREE RF100 RF500 XGB100 XGB500
treino 1326.418 1617.501 308.6415 302.0648 493.3078 56.86551
valida 1338.114 1589.068 1199.4948 1190.3431 1259.0559 1393.77194barplot(M,beside = T,col=c(rep("gold",2),
rep("orange2",2),
rep("red",2),
rep("violet",2),
rep("purple",2),
rep("skyblue",2)),main="mediana do MSE na validação cruzada")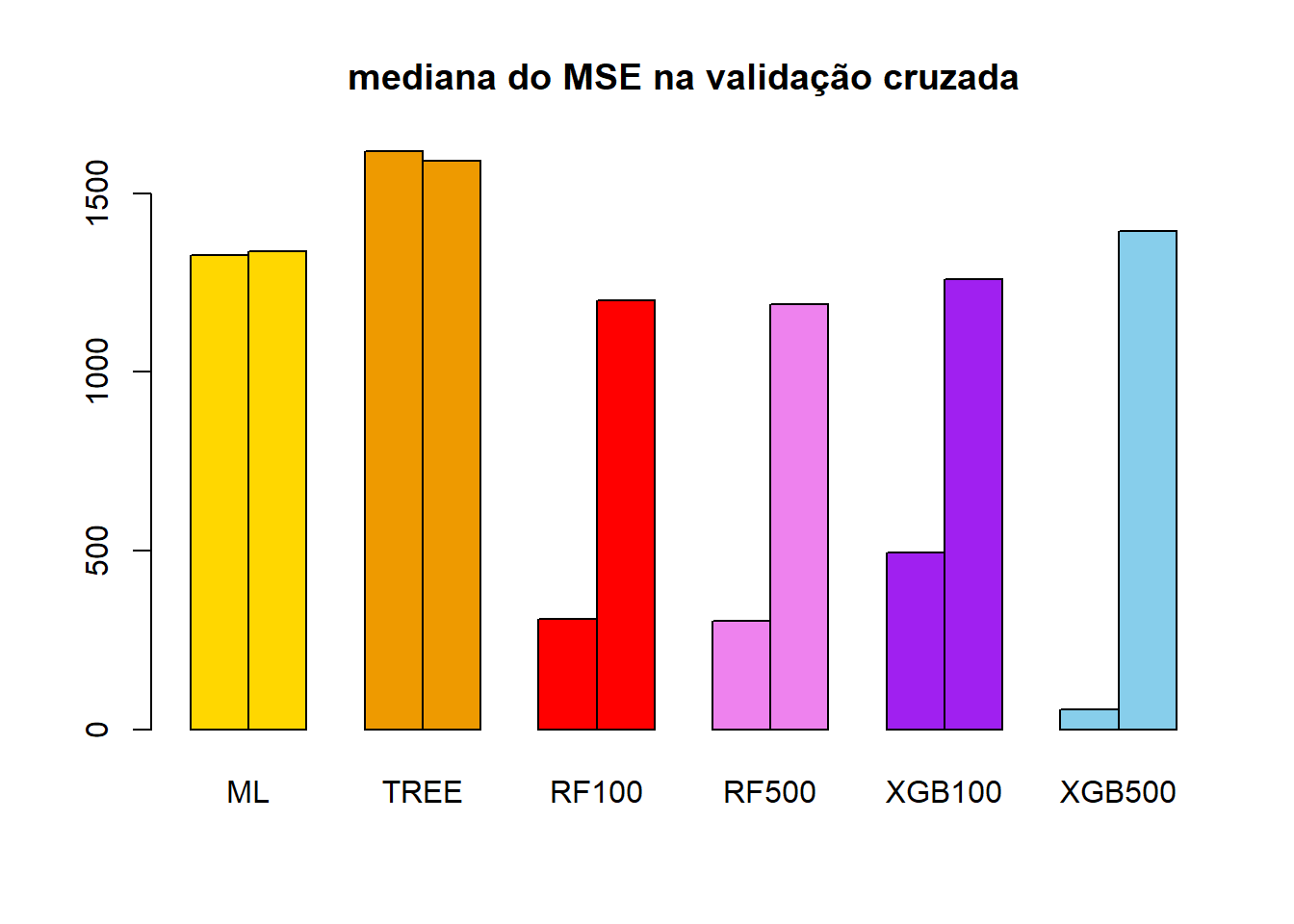
Quais informações conseguimos tirar desse gráfico?
Vamos repetir a mesma análise, agora usando como comparação o R2 e a mediana do R2.
M = rbind(apply(R2_treino, MARGIN = 2,FUN = median),
apply(R2_valida, MARGIN = 2,FUN = median))
rownames(M) = c("treino","valida")
M ML TREE RF100 RF500 XGB100 XGB500
treino 0.7188798 0.6580523 0.9345031 0.9358949 0.8952813 0.9880126
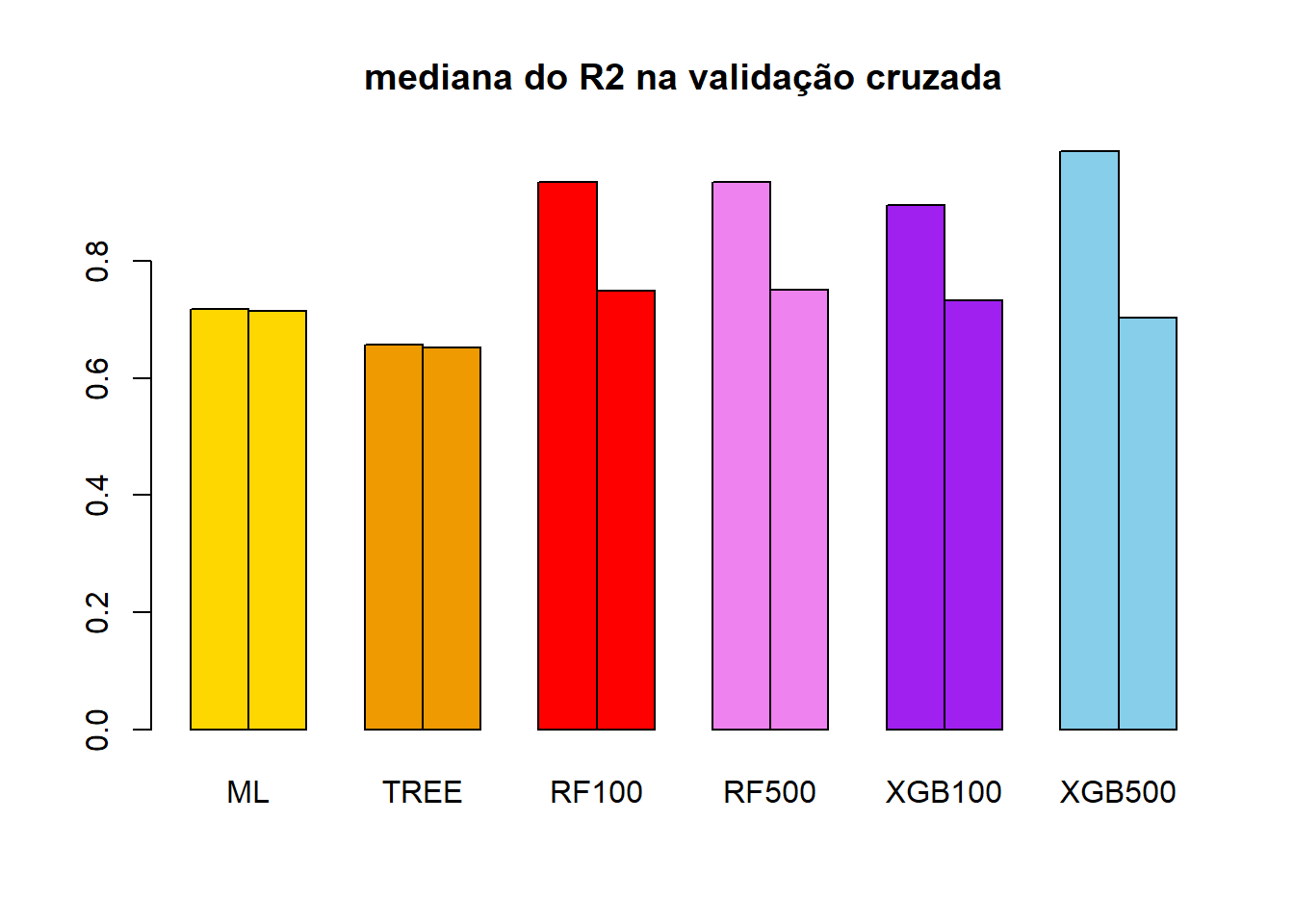
valida 0.7151772 0.6527090 0.7498031 0.7517171 0.7334596 0.7038714barplot(M,beside = T,col=c(rep("gold",2),
rep("orange2",2),
rep("red",2),
rep("violet",2),
rep("purple",2),
rep("skyblue",2)),main="mediana do R2 na validação cruzada")