library(tidyverse)
library(rpart)
library(randomForest)
library(xgboost)
library(neuralnet)9 Comparação entre Modelos de Classificação Binária
Neste capítulo serão abordadas formas de mensurar a qualidade do ajuste de modelos de classificação, assim como formas de investigar a existência ou não de sobreajuste.
Para os problemas de classificação binária, isto é, duas classes, a variável resposta \(Y\) é uma variável qualitativa que pode assumir dois valores apenas. Vamos usar um destes valores como referência e supor, sem perda de generalidade, que \(Y=1\) caso a classe seja a de referência e \(Y=0\) caso contrário. Na maioria dos casos, o que os modelos de classificação retornam é a probabilidade de ser observada a classe de referência, no caso, \(P(Y=1)\). Suponha que um modelo de regressão \(k\) realizou a previsões \(\hat{y}_i^k\) (valores entre 0 e 1) para a \(i\)-ésima observação da variável \(Y\). Suponha \(y_i\) (0 ou 1) o real valor observado para a \(i\)-ésima observação da variável \(Y\).
| i | Valor observado | Previsão para o Modelo 1 | Previsão para o Modelo 2 | Previsão para o Modelo 3 |
|---|---|---|---|---|
| 1 | \(y_1\) | \(\hat y_1^1\) | \(\hat y_1^2\) | \(\hat y_1^3\) |
| 2 | \(y_2\) | \(\hat y_2^1\) | \(\hat y_2^2\) | \(\hat y_2^3\) |
| 3 | \(y_3\) | \(\hat y_3^1\) | \(\hat y_3^2\) | \(\hat y_3^3\) |
| … | … | … | … | … |
| N | \(y_N\) | \(\hat y_N^1\) | \(\hat y_N^2\) | \(\hat y_N^3\) |
No contexto deste curso os modelos apresentados na tabela acima podem ser modelos logísticos, de árvores de classificação, floresta aleatória, gradiente bossting e redes neurais. Além disso, é possível fazer uma tabela como a apresentada acima para os dados da base de treino e para os dados na base de teste.
Para comparar o desempenho dos diferentes modelos de classificação são comparados os valores de \(y_i\) e \(\hat{y}_i\). Essa comparação pode ser feita a partir de algumas medidas diferentes, vejamos duas delas.
9.1 Entropia Cruzada
Uma vez conhecidas as previsões para a variável resposta, considerando que essas previsões serão uma probabilidade da observação pertencer a classe de referência, é possível calcular a EC (entropia cruzada) e usar essa medida como comparação de qualidade do ajuste.
\[ EC = - \dfrac{1}{N} \sum_{i=1}^N \left( y_i\ln(\hat{y}_i) + (1-y_i)\ln(1-\hat{y}_i) \right) \]
Veja que quando \(\hat{y}_i\) está próximo da classe real a parcela \(i\) do somatório é bem pequena e quando \(\hat{y}_i\) está próxima da classificação errada, a parcela \(i\) do somatório é bem grande. Quanto menor a EC, melhor o ajuste do modelo.
9.2 AUC
Já vimos que a curva ROC orienta na escolha do valor de corte para a definição da classificação final. Mas tembém podemos usar o valor da área embaixo da curva ROC, AUC, do inglês area under curve, para comparar os modelos de classificação a partir das probabilidades previstas. Vejamos como interpretar o valor de AUC.
| AUC | Resumo |
|---|---|
| mínimo | 0 |
| máximo | 1 |
| \(\le\) 0,5 | ajuste inadequado |
| AUC\(_1\) \(>\) AUC\(_2\) | Modelo 1 com melhor ajuste que Modelo 2 |
9.3 Matriz de Confusão
Os modelos de classificação retornam como previsão para a \(i\)-ésima observação um valor \(\hat{y}_i^k \in (0,1)\) e a partir da curva ROC, como já foi feito, é possível definir o critério de corte ótimo e se definir uma previsão para a classe. Suponha o seguinte critério para a escolha da classe prevista:
\[ \hat{c}_i = \left\{ \begin{array}{ll} 0 & \hbox{, se } \hat{y}_i < q\\ 1 & \hbox{, se } \hat{y}_i \ge q\\ \end{array} \right. \]
Para entender melhor a capacidade de previsão do modelo de classificação queremos encontrar as medidas de Acurácia, Precisão, Sensibilidade, entre outras. Estas medidas serão definidas a partir da matriz de confusão, que é formada pela contagem de classes reais e classes previstas.
| Real 0 | Real 1 | |
|---|---|---|
| Previsto 0 | VN | FN |
| Previsto 1 | FP | VP |
VN = verdadeiro negativo = número de observações iguais a 0 que foram previstas como 0.
FN = falso negativo = número de observações iguais a 1 que foram previstas como 0.
FP = falso positivo = número de observações iguais a 0 que foram previstas como 1.
VP = verdadeiro positivo = número de observações iguais a 1 que foram previstas como 1.
Quanto maior o número de observações na diagonal principal da matriz de confusão melhor. A partir desta tabela podemos calcular algumas medidas de desempenho para os modelos de classificação.
9.3.1 Acurácia
A acurácia é a taxa de acerto do classificador. Ela é a proporção de predições corretas dentre todas as predições.
\[ Acurácia = \dfrac{V P + V N}{V P + V N + FP + FN} \]
9.3.2 Sensibilidade (ou Recall)
A sensibilidade é a taxa de acerto dos casos positivos. Ela é a proporção de casos positivos que foram corretamente classificados como positivos.
\[ Sensibilidade = \dfrac{VP}{VP + FN} \]
9.3.3 Especificidade
A especificidade é a taxa de acerto dos casos negativos. Ela é a proporção dos casos negativos que foram corretamente classificados como negativos.
\[ Especificidade = \dfrac{VN}{VN + FP} \]
9.3.4 Precisão
A precisão é a taxa de acerto dentre as previsões positivas. Ela é a proporção dos acertos entre os casos classificados como positivos.
\[ Precisão = \dfrac{VP}{VP + FP} \]
9.3.5 F1-Score
É uma combinação da Precisão e do Recall que na prática é a média harmônica entre a Precisão e o Recall.
\[ F1-score = 2 \dfrac{Precisão \times Recall}{Precisão + Recall} \]
9.4 Vamos Praticar
9.4.1 Carregar os pacotes necessários
9.4.2 Carregar as bases de treino e teste
base_treino_final = readRDS(file="salvos//base_treino_final.rds")
base_teste_final = readRDS(file="salvos//base_teste_final.rds")9.4.3 Carregar os modelos já ajustados
Nas últimas semanas ajustamos diferentes modelos de classificação binária. Agora é a hora de carregar todos eles para comparar o desempenho e discutir se algum deles apresenta desempenho melhor que outros.
MLOG_final = readRDS(file = "salvos//MLOG_final.rds")
TREE_CLASS_2 = readRDS(file = "salvos//TREE_CLASS_2.rds")
RF_CLASS_2 = readRDS(file = "salvos//RF_CLASS_2.rds")
XGB_CLASS_2 = readRDS(file = "salvos//XGB_CLASS_2.rds")
NN0_CLASS_2 = readRDS(file = "salvos//NN0_CLASS_2.rds")
NN1_CLASS_2 = readRDS(file = "salvos//NN1_CLASS_2.rds")
NN2_CLASS_2 = readRDS(file = "salvos//NN2_CLASS_2.rds")
NN3_CLASS_2 = readRDS(file = "salvos//NN3_CLASS_2.rds")
NN22_CLASS_2 = readRDS(file = "salvos//NN22_CLASS_2.rds")9.4.4 Previsões
X_treino = base_treino_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
NU_MATRICULAS,
INSE,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO,
PORTE_ESCOLA)
Y_treino = ifelse(base_treino_final$TAXA_PART_CAT == "baixa",1,0)X_teste = base_teste_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
NU_MATRICULAS,
INSE,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO,
PORTE_ESCOLA)
base_teste_final = base_teste_final |>
mutate(TAXA_PART_CAT = ifelse(NU_TAXA_PARTICIPACAO >= 86, "alta", ifelse(NU_TAXA_PARTICIPACAO <= 67, "baixa","media")))
Y_teste = ifelse(base_teste_final$TAXA_PART_CAT == "baixa",1,0)9.4.4.1 Modelo Logístico
y_ML_treino = predict(MLOG_final,newdata = X_treino,type="response")
head(y_ML_treino) 1 2 3 4 5 6
0.002428464 0.011330761 0.065490097 0.172645701 0.033146956 0.782181552 y_ML_teste = predict(MLOG_final,newdata = X_teste,type="response")
head(y_ML_teste) 1 2 3 4 5 6
0.01438536 0.01124651 0.01020236 0.33639313 0.15157798 0.32580802 9.4.4.2 Árvore de Classificação
y_TREE_treino = predict(TREE_CLASS_2,newdata = X_treino)
head(y_TREE_treino) 0 1
1 0.9372997 0.06270032
2 0.9372997 0.06270032
3 0.7088036 0.29119639
4 0.6322751 0.36772487
5 0.9372997 0.06270032
6 0.4346350 0.56536503y_TREE_teste = predict(TREE_CLASS_2,newdata = X_teste)
head(y_TREE_teste) 0 1
1 0.9372997 0.06270032
2 0.9372997 0.06270032
3 0.9372997 0.06270032
4 0.7088036 0.29119639
5 0.7088036 0.29119639
6 0.4346350 0.565365039.4.4.3 Floresta Aleatória
y_RF_treino = predict(RF_CLASS_2,newdata = X_treino,type = "prob")
head(y_RF_treino) 0 1
1 0.994 0.006
2 0.986 0.014
3 0.860 0.140
4 0.902 0.098
5 0.946 0.054
6 0.102 0.898y_RF_teste = predict(RF_CLASS_2,newdata = X_teste,type="prob")
head(y_RF_teste) 0 1
1 0.900 0.100
2 0.908 0.092
3 0.834 0.166
4 0.598 0.402
5 0.660 0.340
6 0.508 0.4929.4.4.4 XGBoost
O XGBoost precisa receber as variáveis categóricas transformadas para indicadoras.
MX_treino = model.matrix(~. , data = X_treino)[,-1]
MX_teste = model.matrix(~. , data = X_teste)[,-1]y_XGB_treino = predict(XGB_CLASS_2,newdata = MX_treino)
head(y_XGB_treino)[1] 0.007230997 0.013061869 0.146902934 0.118033834 0.017095475 0.666431665y_XGB_teste = predict(XGB_CLASS_2,newdata = MX_teste)
head(y_XGB_teste)[1] 0.01891010 0.01582978 0.02245860 0.19928807 0.23836160 0.328431379.4.4.5 Rede Neural
Para o modelo de redes neurais foi feita a padronização dos dados. O correto aqui é realizar a mesma padronização realizada para o dados que treinaram o modelo.
X1_treino = base_treino_final |> select(NU_MATRICULAS,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO)
X1_treino_s = scale(X1_treino)
mx = X1_treino_s |> attr("scaled:center")
mx NU_MATRICULAS PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA NU_TAXA_REPROVACAO
85.920855 60.438816 75.977907 8.822432
NU_TAXA_ABANDONO
3.776296 sx = X1_treino_s |> attr("scaled:scale")
sx NU_MATRICULAS PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA NU_TAXA_REPROVACAO
84.370154 17.233894 19.766292 7.923032
NU_TAXA_ABANDONO
5.504834 X1_teste = base_teste_final |> select(NU_MATRICULAS,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO)
head(X1_teste)# A tibble: 6 × 5
NU_MATRICULAS PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA NU_TAXA_REPROVACAO
<dbl> <dbl> <dbl> <dbl>
1 20 58.3 70.6 5.4
2 39 67.7 40.5 9.9
3 26 72.7 52.2 13.1
4 75 62.9 64.4 44.8
5 28 75.5 44 39
6 35 60.3 37.0 5
# ℹ 1 more variable: NU_TAXA_ABANDONO <dbl>X1_teste_s = X1_teste |> mutate(
NU_MATRICULAS = (X1_teste$NU_MATRICULAS - mx["NU_MATRICULAS"])/sx["NU_MATRICULAS"],
PC_FORMACAO_DOCENTE = (X1_teste$PC_FORMACAO_DOCENTE - mx["PC_FORMACAO_DOCENTE"])/sx["PC_FORMACAO_DOCENTE"],
NU_TAXA_PERMANENCIA = (X1_teste$NU_TAXA_PERMANENCIA - mx["NU_TAXA_PERMANENCIA"])/sx["NU_TAXA_PERMANENCIA"],
NU_TAXA_REPROVACAO = (X1_teste$NU_TAXA_REPROVACAO - mx["NU_TAXA_REPROVACAO"])/sx["NU_TAXA_REPROVACAO"],
NU_TAXA_ABANDONO = (X1_teste$NU_TAXA_ABANDONO - mx["NU_TAXA_ABANDONO"])/sx["NU_TAXA_ABANDONO"]
)
head(X1_teste_s) # A tibble: 6 × 5
NU_MATRICULAS PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA NU_TAXA_REPROVACAO
<dbl> <dbl> <dbl> <dbl>
1 -0.781 -0.124 -0.273 -0.432
2 -0.556 0.421 -1.79 0.136
3 -0.710 0.711 -1.20 0.540
4 -0.129 0.143 -0.585 4.54
5 -0.687 0.874 -1.62 3.81
6 -0.604 -0.00805 -1.97 -0.482
# ℹ 1 more variable: NU_TAXA_ABANDONO <dbl>X2_treino = base_treino_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
INSE,
PORTE_ESCOLA)
X2_treino_m = model.matrix(~. , data = X2_treino)[,-1]
MX_treino_s = cbind(X1_treino_s,X2_treino_m)X2_teste = base_teste_final |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
INSE,
PORTE_ESCOLA)
X2_teste_m = model.matrix(~. , data = X2_teste)[,-1]
MX_teste_s = cbind(X1_teste_s,X2_teste_m)Enfim a previsão, tanto na base de treino quanto na base de teste.
y_NN0_treino = predict(NN0_CLASS_2,newdata=MX_treino_s)
head(y_NN0_treino) [,1]
1 0.002424837
2 0.011344338
3 0.065759765
4 0.173649856
5 0.033263183
6 0.766444782y_NN0_teste = predict(NN0_CLASS_2,newdata=MX_teste_s)
head(y_NN0_teste) [,1]
1 0.01453383
2 0.01125802
3 0.01026230
4 0.33751930
5 0.15295638
6 0.32792829y_NN1_treino = predict(NN1_CLASS_2,newdata=MX_treino_s)
head(y_NN1_treino) [,1]
1 0.007163705
2 0.013669674
3 0.043863887
4 0.145737811
5 0.029133836
6 0.785170249y_NN1_teste = predict(NN1_CLASS_2,newdata=MX_teste_s)
head(y_NN1_teste) [,1]
1 0.01544233
2 0.01342776
3 0.01328182
4 0.32477753
5 0.12622925
6 0.34620011y_NN2_treino = predict(NN2_CLASS_2,newdata=MX_treino_s)
head(y_NN2_treino) [,1]
1 0.002424837
2 0.011344338
3 0.065759765
4 0.173649856
5 0.033263183
6 0.766444782y_NN2_teste = predict(NN2_CLASS_2,newdata=MX_teste_s)
head(y_NN2_teste) [,1]
1 0.01453383
2 0.01125802
3 0.01026230
4 0.33751930
5 0.15295638
6 0.32792829y_NN3_treino = predict(NN3_CLASS_2,newdata=MX_treino_s)
head(y_NN3_treino) [,1]
1 0.005415985
2 0.006186957
3 0.056062551
4 0.077361390
5 0.034108793
6 0.888221636y_NN3_teste = predict(NN3_CLASS_2,newdata=MX_teste_s)
head(y_NN3_teste) [,1]
1 0.02584897
2 0.02030041
3 0.01965881
4 0.11745880
5 0.03375867
6 0.21294344y_NN22_treino = predict(NN22_CLASS_2,newdata=MX_treino_s)
head(y_NN22_treino) [,1]
1 1.437083e-12
2 7.390803e-02
3 1.033849e-01
4 1.309764e-01
5 9.242767e-02
6 8.158498e-01y_NN22_teste = predict(NN22_CLASS_2,newdata=MX_teste_s)
head(y_NN22_teste) [,1]
1 0.07275307
2 0.07286053
3 0.07118568
4 0.29437377
5 0.10116988
6 0.336411739.4.5 Entropia Cruzada
Para calcular o valor da entropria cruzada em cada previsão será necessário criar antes uma função para realizar o seu cálculo. Vamos relembrar e implementar em seguida.
\[ EC = - \dfrac{1}{N} \sum_{i=1}^N \left( y_i\ln(\hat{y}_i) + (1-y_i)\ln(1-\hat{y}_i) \right) \]
EC = function(real,prev){
-mean(real*log(prev+0.00001) + (1-real)*log(1-prev+0.00001))
}(EC_ML_treino = EC(real = Y_treino , prev = y_ML_treino))[1] 0.4110532(EC_TREE_treino = EC(real = Y_treino , prev = y_TREE_treino))[1] 1.067868(EC_RF_treino = EC(real = Y_treino , prev = y_RF_treino))[1] 1.682152(EC_XGB_treino = EC(real = Y_treino , prev = y_XGB_treino))[1] 0.3219969(EC_NN0_treino = EC(real = Y_treino , prev = y_NN0_treino))[1] 0.4110255(EC_NN1_treino = EC(real = Y_treino , prev = y_NN1_treino))[1] 0.4098638(EC_NN2_treino = EC(real = Y_treino , prev = y_NN2_treino))[1] 0.4110255(EC_NN3_treino = EC(real = Y_treino , prev = y_NN3_treino))[1] 0.3883218(EC_NN22_treino = EC(real = Y_treino , prev = y_NN22_treino))[1] 0.3915759Vejamos agora os resultados na base de teste.
(EC_ML_teste = EC(real = Y_teste , prev = y_ML_teste))[1] 0.4004441(EC_TREE_teste = EC(real = Y_teste , prev = y_TREE_teste))[1] 1.066823(EC_RF_teste = EC(real = Y_teste , prev = y_RF_teste))[1] 1.273173(EC_XGB_teste = EC(real = Y_teste , prev = y_XGB_teste))[1] 0.3811436(EC_NN0_teste = EC(real = Y_teste , prev = y_NN0_teste))[1] 0.4006069(EC_NN1_teste = EC(real = Y_teste , prev = y_NN1_teste))[1] 0.4006383(EC_NN2_teste = EC(real = Y_teste , prev = y_NN2_teste))[1] 0.4006069(EC_NN3_teste = EC(real = Y_teste , prev = y_NN3_teste))[1] 0.3962538(EC_NN22_teste = EC(real = Y_teste , prev = y_NN22_teste))[1] 0.4145789EC_matriz = matrix(data = c(EC_ML_treino, EC_TREE_treino, EC_RF_treino, EC_XGB_treino, EC_NN0_treino, EC_NN1_treino, EC_NN22_treino, EC_NN3_treino, EC_NN22_treino, EC_ML_teste, EC_TREE_teste, EC_RF_teste, EC_XGB_teste, EC_NN0_teste, EC_NN1_teste, EC_NN22_teste, EC_NN3_teste, EC_NN22_teste),nrow = 2,ncol = 9,byrow = TRUE)
colnames(EC_matriz) = c("ML","TREE","RF","XGB","NN0","NN1","NN2","NN3","NN22")
rownames(EC_matriz) = c("treino","teste")
EC_matriz ML TREE RF XGB NN0 NN1 NN2
treino 0.4110532 1.067868 1.682152 0.3219969 0.4110255 0.4098638 0.3915759
teste 0.4004441 1.066823 1.273173 0.3811436 0.4006069 0.4006383 0.4145789
NN3 NN22
treino 0.3883218 0.3915759
teste 0.3962538 0.4145789barplot(
height = EC_matriz,beside = TRUE,
main = "EC para Classificação Binária",
col = c("gold","gold",
"orange2","orange2",
"red","red",
"violet","violet",
"purple","purple",
"skyblue","skyblue",
"darkblue","darkblue",
"springgreen","springgreen",
"darkgreen","darkgreen"))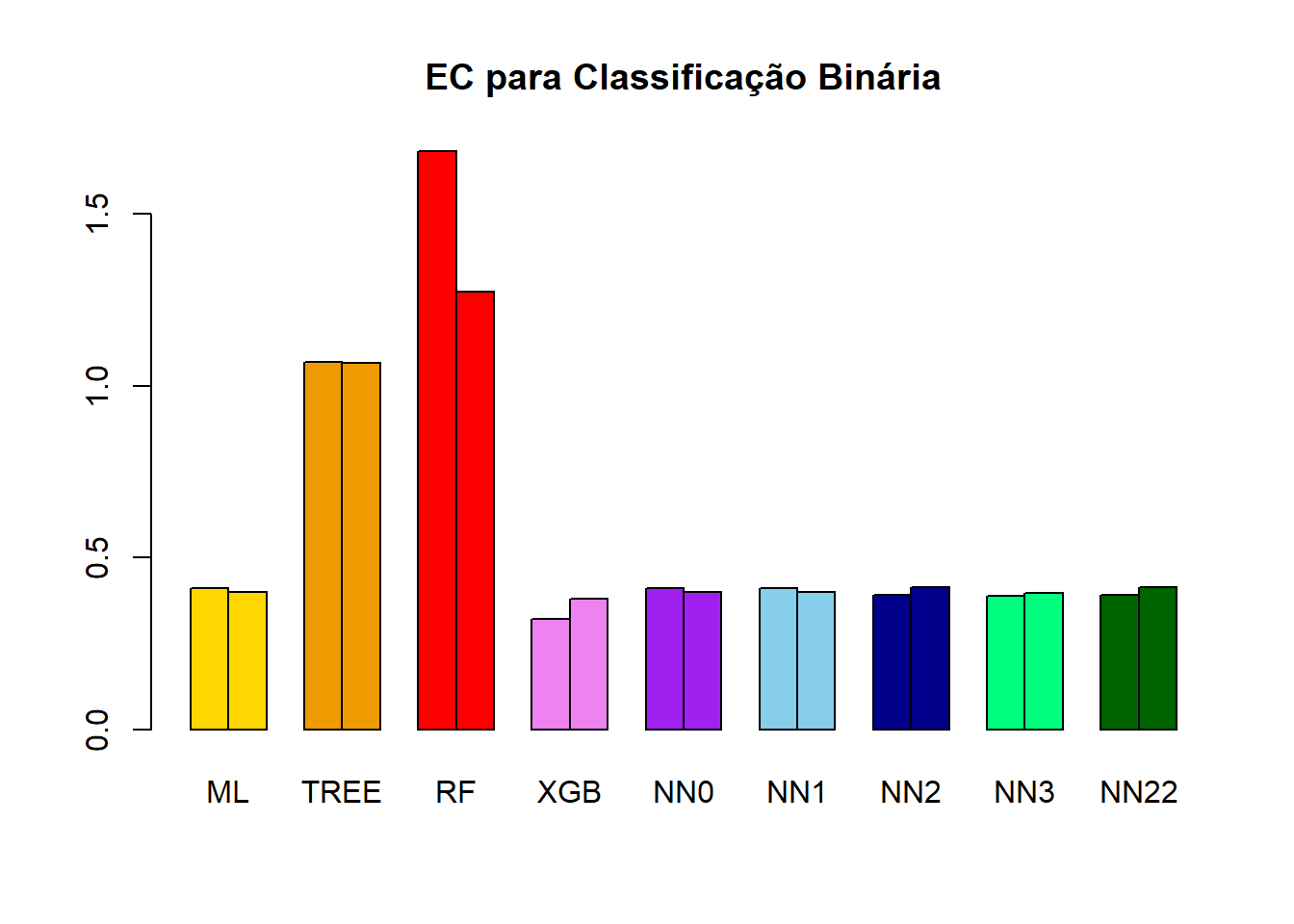
9.4.6 AUC
Para calcular o valor do AUC vamos usar o pacore pROC.
library(pROC)ROC = roc(response = Y_treino,predictor = y_ML_treino)
(AUC_ML_treino = ROC$auc)Area under the curve: 0.8769ROC = roc(response = Y_teste,predictor = y_ML_teste)
(AUC_ML_teste = ROC$auc)Area under the curve: 0.8842ROC = roc(response = Y_treino,predictor = y_TREE_treino[,2])
(AUC_TREE_treino = ROC$auc)Area under the curve: 0.8428ROC = roc(response = Y_teste,predictor = y_TREE_teste[,2])
(AUC_TREE_teste = ROC$auc)Area under the curve: 0.8509ROC = roc(response = Y_treino,predictor = y_RF_treino[,2])
(AUC_RF_treino = ROC$auc)Area under the curve: 1ROC = roc(response = Y_teste,predictor = y_RF_teste[,2])
(AUC_RF_teste = ROC$auc)Area under the curve: 0.8876ROC = roc(response = Y_treino,predictor = y_XGB_treino)
(AUC_XGB_treino = ROC$auc)Area under the curve: 0.9338ROC = roc(response = Y_teste,predictor = y_XGB_teste)
(AUC_XGB_teste = ROC$auc)Area under the curve: 0.8943ROC = roc(response = Y_treino,predictor = y_NN0_treino[,1])
(AUC_NN0_treino = ROC$auc)Area under the curve: 0.8769ROC = roc(response = Y_teste,predictor = y_NN0_teste[,1])
(AUC_NN0_teste = ROC$auc)Area under the curve: 0.8841ROC = roc(response = Y_treino,predictor = y_NN1_treino[,1])
(AUC_NN1_treino = ROC$auc)Area under the curve: 0.8767ROC = roc(response = Y_teste,predictor = y_NN1_teste[,1])
(AUC_NN1_teste = ROC$auc)Area under the curve: 0.883ROC = roc(response = Y_treino,predictor = y_NN2_treino[,1])
(AUC_NN2_treino = ROC$auc)Area under the curve: 0.8769ROC = roc(response = Y_teste,predictor = y_NN2_teste[,1])
(AUC_NN2_teste = ROC$auc)Area under the curve: 0.8841ROC = roc(response = Y_treino,predictor = y_NN3_treino[,1])
(AUC_NN3_treino = ROC$auc)Area under the curve: 0.8914ROC = roc(response = Y_teste,predictor = y_NN3_teste[,1])
(AUC_NN3_teste = ROC$auc)Area under the curve: 0.8854ROC = roc(response = Y_treino,predictor = y_NN22_treino[,1])
(AUC_NN22_treino = ROC$auc)Area under the curve: 0.8885ROC = roc(response = Y_teste,predictor = y_NN22_teste[,1])
(AUC_NN22_teste = ROC$auc)Area under the curve: 0.8844AUC_matriz = matrix(data = c(
AUC_ML_treino, AUC_TREE_treino, AUC_RF_treino, AUC_XGB_treino, AUC_NN0_treino, AUC_NN1_treino, AUC_NN22_treino, AUC_NN3_treino, AUC_NN22_treino,
AUC_ML_teste, AUC_TREE_teste, AUC_RF_teste, AUC_XGB_teste, AUC_NN0_teste, AUC_NN1_teste, AUC_NN22_teste, AUC_NN3_teste, AUC_NN22_teste),nrow = 2,ncol = 9,byrow = TRUE)
colnames(AUC_matriz) = c("ML","TREE","RF","XGB","NN0","NN1","NN2","NN3","NN22")
rownames(AUC_matriz) = c("treino","teste")
AUC_matriz ML TREE RF XGB NN0 NN1 NN2
treino 0.8768924 0.8428384 1.0000000 0.9338499 0.8769069 0.8767021 0.8884991
teste 0.8841787 0.8509468 0.8875862 0.8942521 0.8841033 0.8829897 0.8844458
NN3 NN22
treino 0.8914055 0.8884991
teste 0.8854268 0.8844458barplot(
height = AUC_matriz,beside = TRUE,
main = "AUC para Classificação Binária",
col = c("gold","gold",
"orange2","orange2",
"red","red",
"violet","violet",
"purple","purple",
"skyblue","skyblue",
"darkblue","darkblue",
"springgreen","springgreen",
"darkgreen","darkgreen"))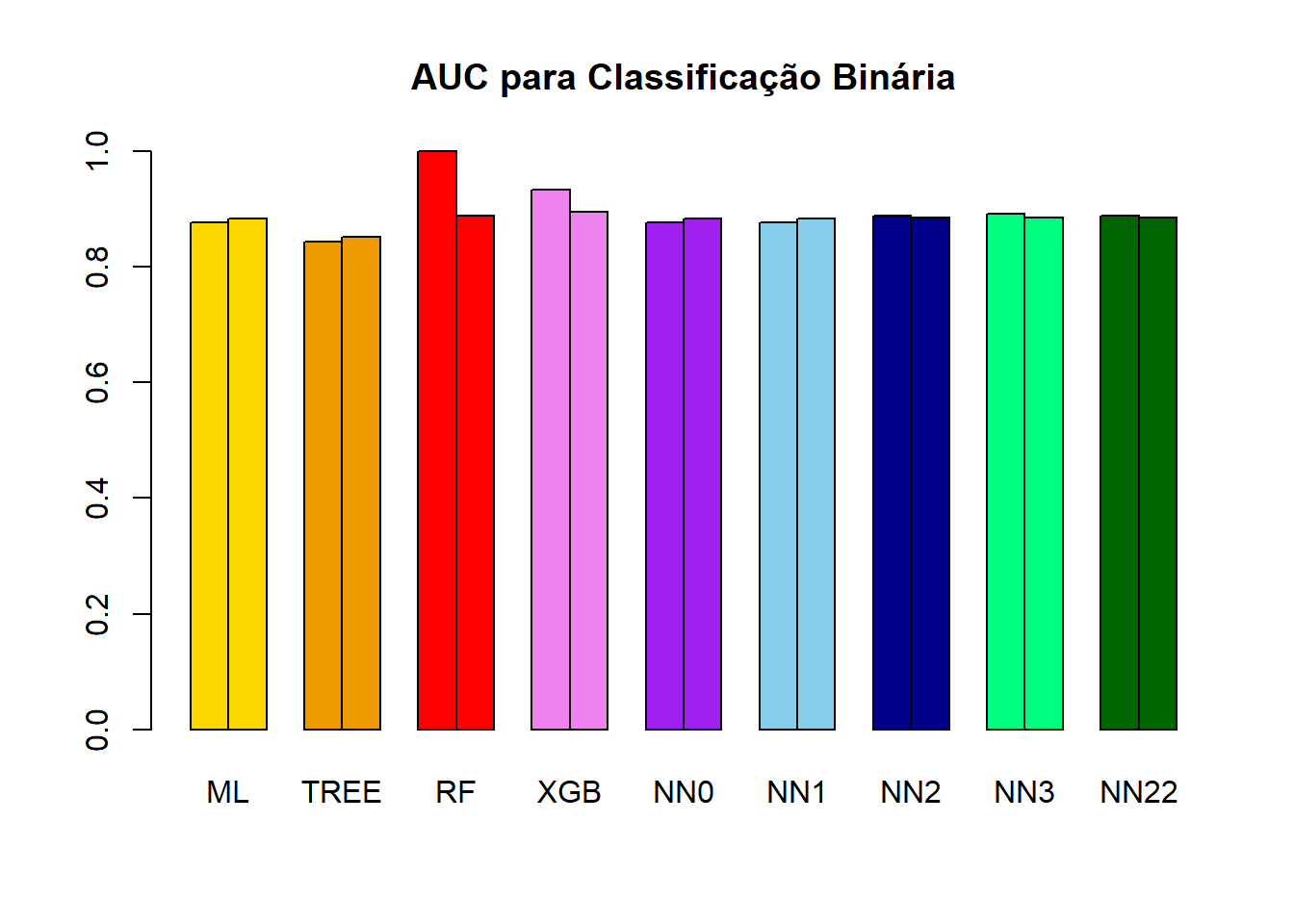
9.4.7 Matriz de Confusão
Uma vez definido o modelo a ser adotado, por exemplo, poderia ser o XGBoost, é possível usar a curva ROC na base de treino para definir o valor de corte e então realizar a previsão das classes, tanto para a base de treino quanto para a base de teste.
ROC = roc(response = Y_treino,predictor = y_XGB_treino)
plot.roc(ROC,
print.auc = TRUE,
print.thres = TRUE)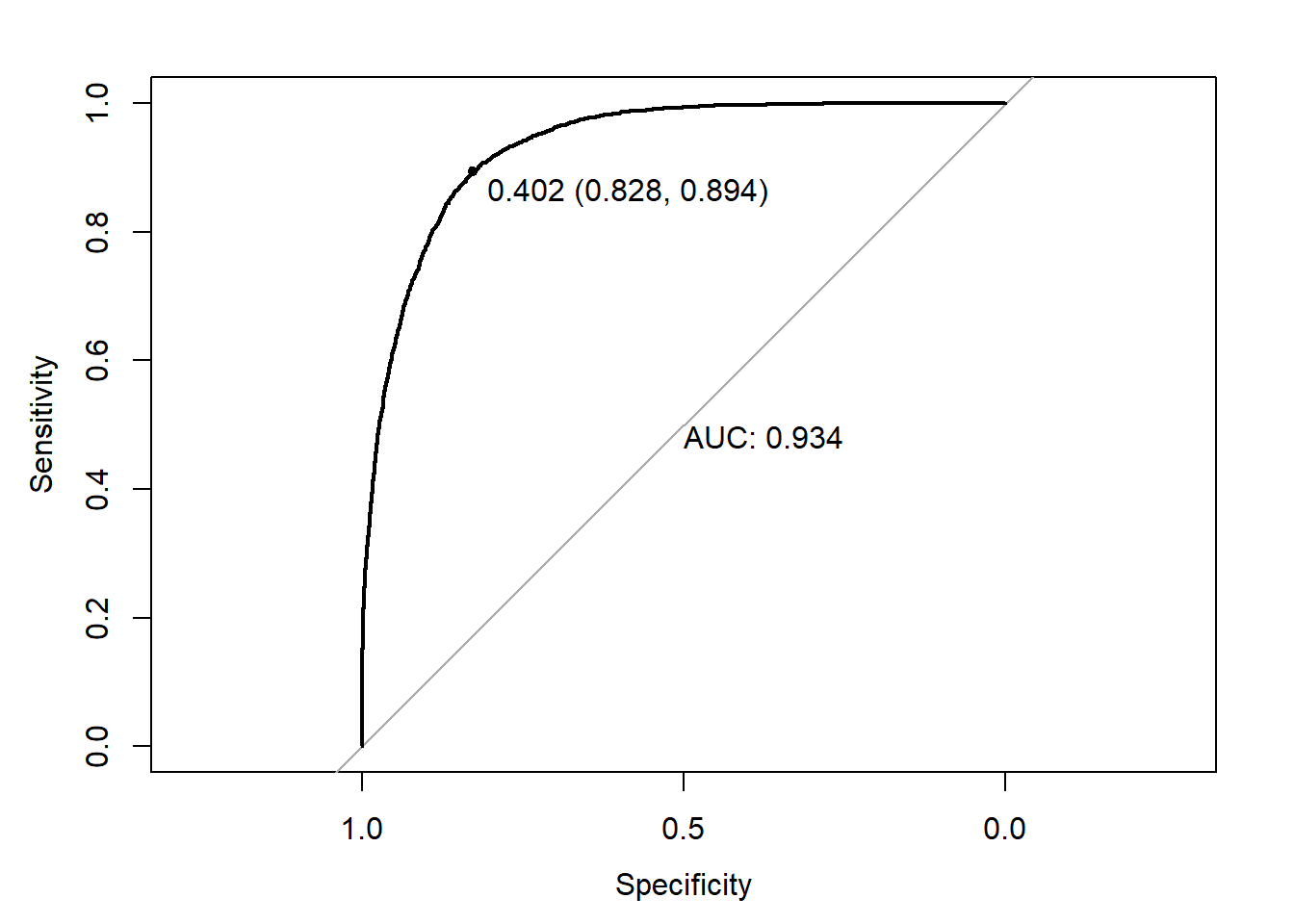
y_classe_treino = ifelse(y_XGB_treino>0.402,1,0)
y_classe_teste = ifelse(y_XGB_teste>0.402,1,0)Uma vez definidas as previsões para as classes é possível usar a matriz de confusão para se encontrar as medidas de qualidade do ajuste da classifciação, como acurácia, falso negativo, falso positivo, etc, tanto para a base de treino quanto para a base de teste.
library(caret)
MC_treino = confusionMatrix(as.factor(Y_treino),as.factor(y_classe_treino))
MC_treinoConfusion Matrix and Statistics
Reference
Prediction 0 1
0 6403 1334
1 420 3543
Accuracy : 0.8501
95% CI : (0.8435, 0.8565)
No Information Rate : 0.5832
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.6832
Mcnemar's Test P-Value : < 2.2e-16
Sensitivity : 0.9384
Specificity : 0.7265
Pos Pred Value : 0.8276
Neg Pred Value : 0.8940
Prevalence : 0.5832
Detection Rate : 0.5473
Detection Prevalence : 0.6613
Balanced Accuracy : 0.8325
'Positive' Class : 0
MC_teste = confusionMatrix(as.factor(Y_teste),as.factor(y_classe_teste))
MC_testeConfusion Matrix and Statistics
Reference
Prediction 0 1
0 2074 510
1 198 1116
Accuracy : 0.8184
95% CI : (0.8059, 0.8304)
No Information Rate : 0.5829
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.616
Mcnemar's Test P-Value : < 2.2e-16
Sensitivity : 0.9129
Specificity : 0.6863
Pos Pred Value : 0.8026
Neg Pred Value : 0.8493
Prevalence : 0.5829
Detection Rate : 0.5321
Detection Prevalence : 0.6629
Balanced Accuracy : 0.7996
'Positive' Class : 0