7 Redes Neurais
As Redes Neurais Artificiais são modelos computacionais inspirados no funcionamento do sistema nervoso de seres vivos. O sistema nervoso dos seres vivos são compostos, principalmente, por neurônios biológicos ou células nervosas. Os neurônios têm como papel principal a recepção e transmissão de sinais, permitindo assim que haja respostas aos estímulos recebidos. As redes neurais busca replicar esta estrutura de forma computacional.
7.1 Redes Neurais Biológicas vs Artificiais.
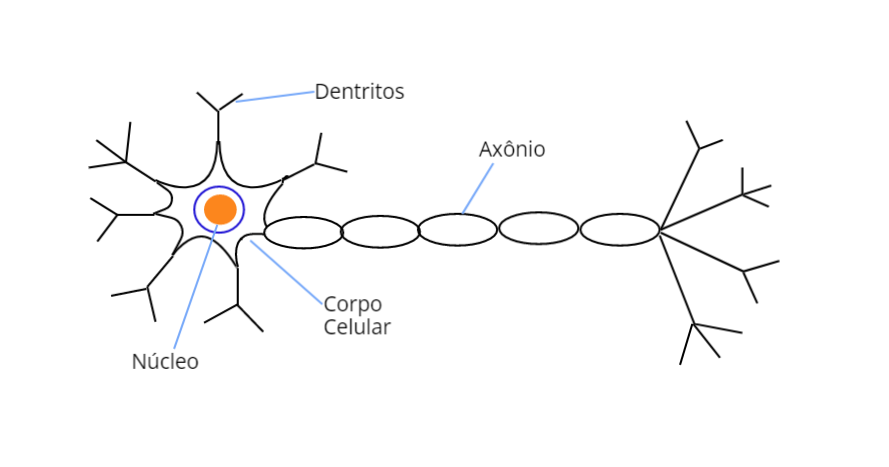
A Figura Figure 7.1 a seguir apresenta a estrutura de um neurônio biológico, com destaque para suas três partes principais, os dendritos, responsáveis pela captação contínua dos estímulos vindos dos diversos outros neurônios ou do próprio meio, o corpo celular, responsável por processar toda a informação vinda dos dendritos e o axônio, que tem a responsabilidade de conduzir os sinais para outros neurônios.
Já a Figura Figure 7.2 mostra a estrutura de um neurônio artificial proposto por (mcculloch1943logical?). Assim como no caso biológico, o modelo de neurônio artificial coleta os sinais de entrada, processa esses sinais e conduz outros sinais em sua saída.
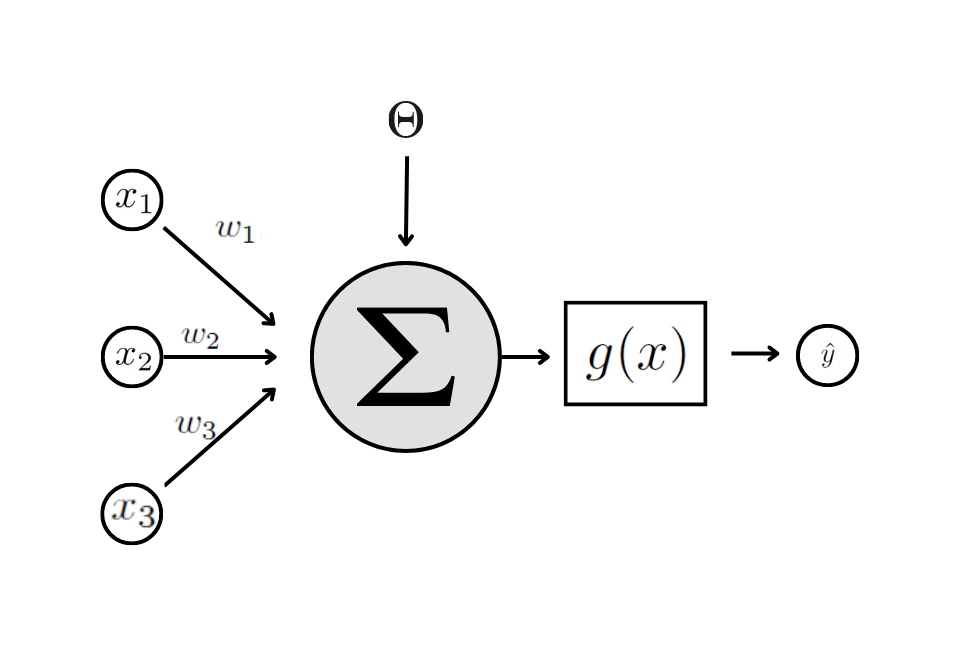
Na Figura Figure 7.2 é possível destacar os principais elementos de um neurônio artificial:
Sinais de Entrada: \(x_{1i}, x_{2i},…, x_{Mi}\). Vetor de covariáveis referentes às características de interesse.
Pesos sinápticos: \(w_1, w_2, …, w_M\). Valores que irão ponderar cada uma das variáveis de entrada da rede (parâmetros desconhecidos a serem estimados).
Combinador Linear: \(\Sigma\). Agregador dos sinais de entrada ponderados por seus respectivos pesos.
Limiar de ativação: \(\theta\). Variável que especifica qual será o limite para que o valor produzido pelo combinador linear possa gerar um valor de disparo.
Função de Ativação: \(g(.)\). Função responsável por receber os sinais de entrada após terem passado pelo combinador linear e aplica uma transformação não linear, que é enviada para a próxima camada da rede neural.
7.2 Algumas Arquiteturas
Uma rede neural é um grafo orientado de forma que cada vértice é um neurônio artificial. Quando nos referimos à arquitetura de uma rede neural estamos nos referindo sobre a disposição dos neurônios nesta combinação. Já a topologia de uma rede se refere às diferentes composições estruturais possíveis dentro da sua arquitetura, como por exemplo, as diferentes quantidades de neurônios.
A seguir a descrição de algumas arquiteturas bem usuais: Redes Neurais Artificiais, Redes Neurais Recorrentes e Redes neurais Convolucionais.
7.2.1 Redes Neurais Artificiais
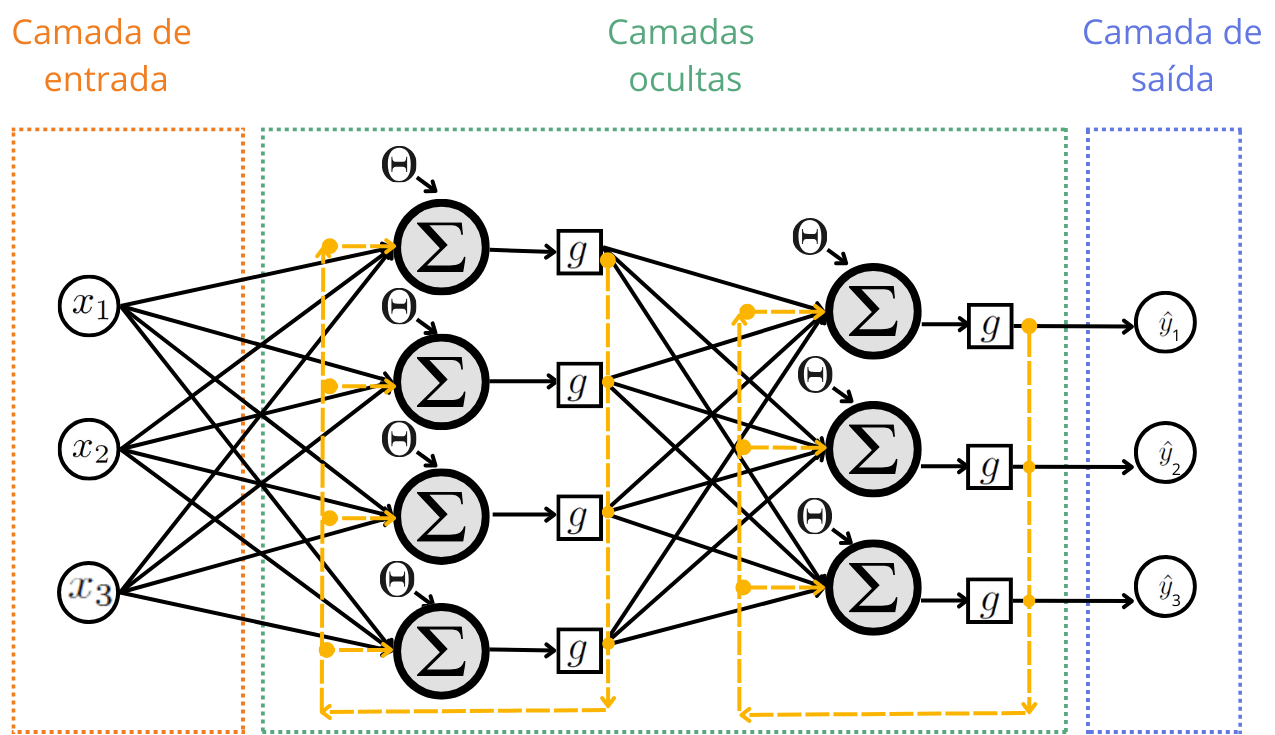
Uma Rede Neural Artificial, conhecida pela sigla ANN (do inglês Artificial Neural Networks) possui uma camada de entrada, uma ou mais camadas ocultas e uma camada de saída. Os neurônios são ligados por arestas orientadas sempre da esquerda para a direita. Veja a Figura ?fig-RNA .
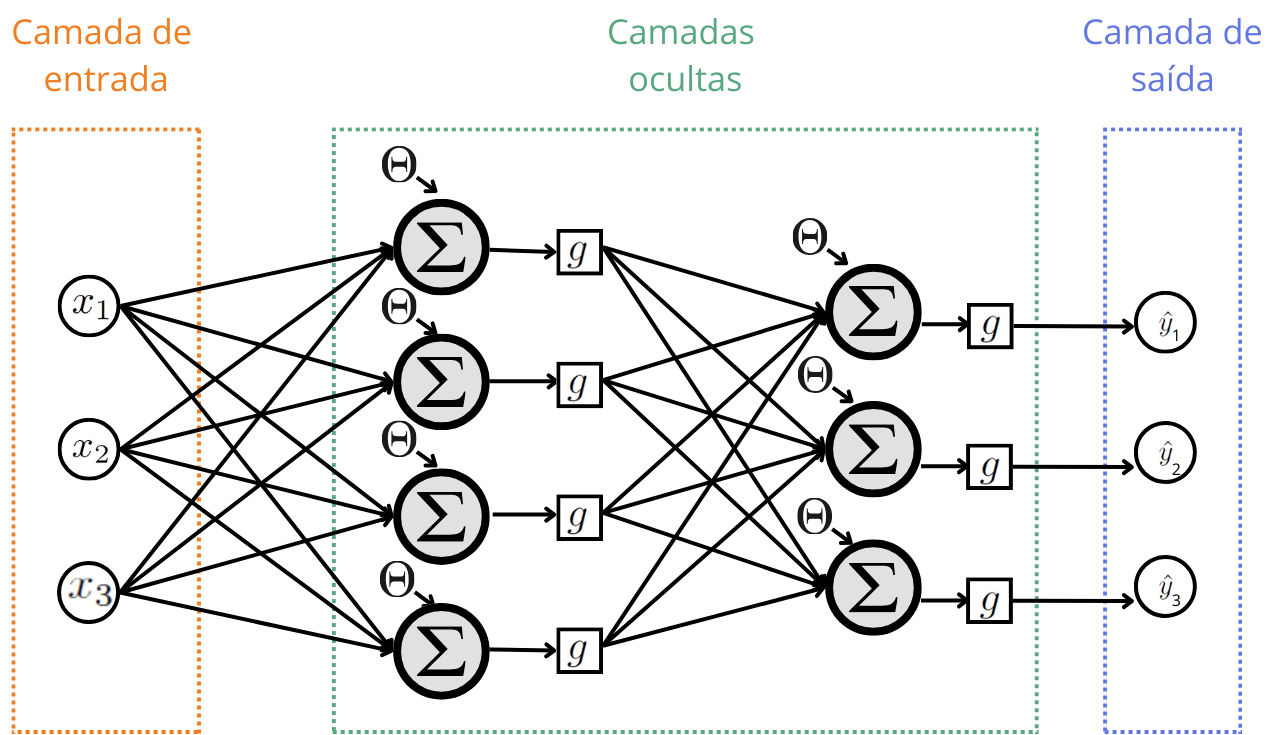
A camada de entrada recebe os valores das covariáveis, que será a fonte de alimentação para treino e previsão. Esses dados passam por uma ou várias camadas ocultas que transformam a entrada em dados processados para a camada de saída. Por fim, a camada de saída fornece a previsão para o modelo de regressão ou classificação.
7.2.2 Redes Neurais Recorrentes
A Rede Neural Recorrente, conhecida pela sigla RNN (do inglês Recurrent Neural Networks) é um tipo de rede neural usado para lidar com dados sequenciais. A sua arquitetura faz com que a entrada nos neurônios sejam não apenas a saída da camada anterior, mas também a saída da camada em questão.
Isso ocorre devido a orientação das arestas que ligam os neurônios, que nesta arquitetura nem sempre são da esquerda para a direita.
7.2.3 Redes Neurais Convolucionais
As Redes Neurais Convolucionais (CNNs - Convolutional Neural Network) são uma classe especializada de redes neurais profundas projetadas para processar dados em grade, como imagens. São amplamente utilizadas em tarefas de reconhecimento de padrões e classificação de imagens.
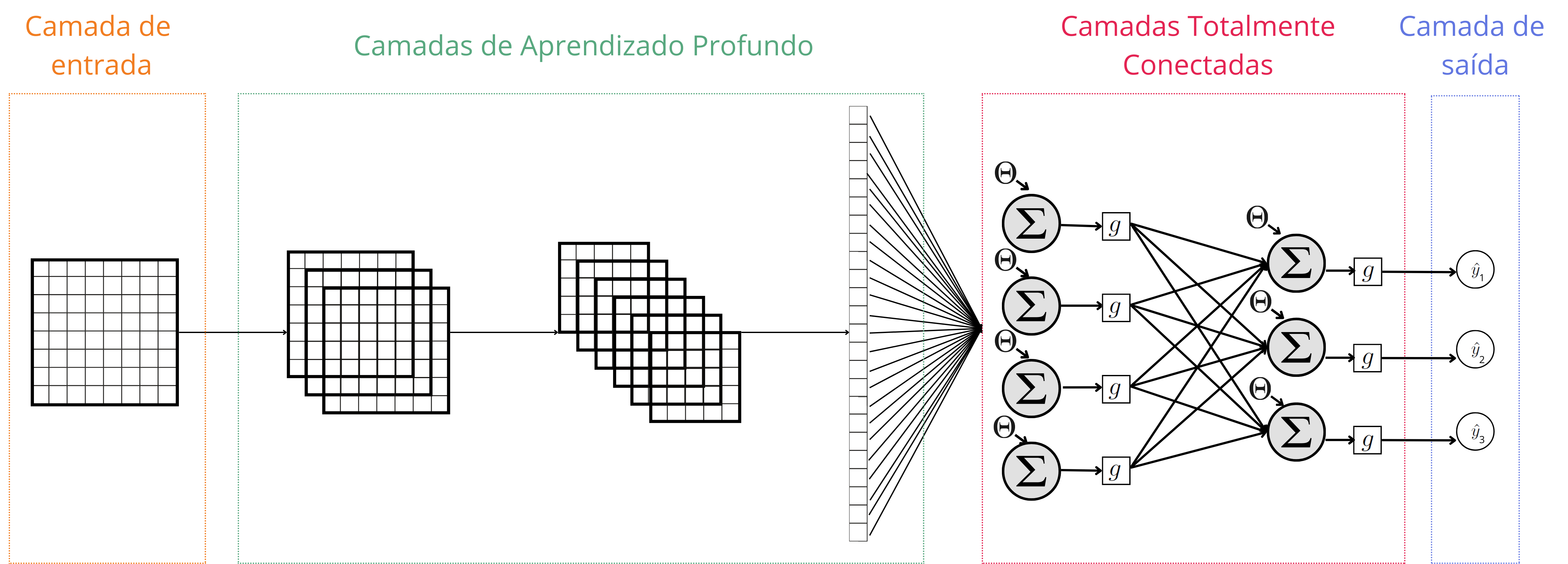
As Redes Neurais Convolucionais consistem em várias camadas que desempenham funções específicas para processar dados de entrada. As camadas principais incluem:
Camada de Entrada: Recebe os dados brutos de entrada, geralmente representando uma imagem ou outra forma de dado em grade.
Camadas de Aprendizado Profundo. Estas camadas podem ser divididas em:
camadas com operações de convolução, para reduzir a dimensão da grade e detectar padrões e características na entrada;
camadas de ativação, que aplica funções de ativação, como ReLU, para introduzir não-linearidades na rede e permitir a aprendizagem de relações mais complexas;
camadas de pooling, que reduzem a dimensionalidade espacial da representação, realizando operações de agrupamento para preservar as características mais importantes e reduzir o custo computacional; e
camada de flattening (camada de achatamento), que modificam os dados em grade para dados em forma de um vetor.
Camadas Totalmente Conectadas: Após os dados de entrada serem transformados em um vetor unidimensional, este vetor passa a ser a camada de entrada para uma ANN, que fará mais processamentos para realizar a classificação final ou a regressão. Essas camadas consolidam as características aprendidas para fazer previsões.
Camada de Saída: Fornece a saída final da rede. Por exemplo, para problemas com imagem a saída pode ser a classe da imagem (classificação) ou a posição de um objeto na imagem (regressão).
7.3 Perceptron
Neste curso vamos aprender mais detalhes sobre as Redes Neurais Artificiais (ANN). Uma ANN é uma estrutura organizada que utiliza perceptrons em camadas para aprender representações complexas de dados e realizar tarefas de aprendizado de máquina. Um perceptron é o bloco de construção elementar de uma ANN, como veremos em seguida.
Para entender o funcionamento das redes neurais mais complexa precisamos começar com o modelo mais simples. O Perceptron de Camada Única é um modelo de rede neural, proposto por (rosenblatt1958perceptron?), onde sua estrutura é composta por apenas um neurônio artificial. Esta rede pode ser usada tanto para problemas de classificação quanto para problemas de regressão.
A Figura (perceptron1?) apresenta a arquitetura do Perceptron de Camada Única. Nesta rede a camada de entrada recebe as \(M\) covariáveis, que são as entradas do único neurônio, já na camada de saida. As covariáveis são combinadas linearmente com os pesos sinápticos e o limiar de ativação. Essa combinação linear é o argumento de entrada da função de ativação, que retorna a saída do modelo, \(\hat{y}\).

Com essa arquitetura bem simples ainda é possível escrever uma equação que determina os valores previstos pela rede em termos dos valores da camada de entrada:
\[ \hat{y}_i \ = \ g \left( \ \sum\limits_{j=1}^{M} \ \hat{w}_j x_{i,j} \ + \ \hat{\Theta} \right) \]
7.4 Função de Ativação
A função de ativação \(g\) tem o papel de restringir o valor da saída, além de capturar a não linearidade dos dados. Para o caso das ANN, as funções mais usadas são a função logística e a tangente hiperbólica.
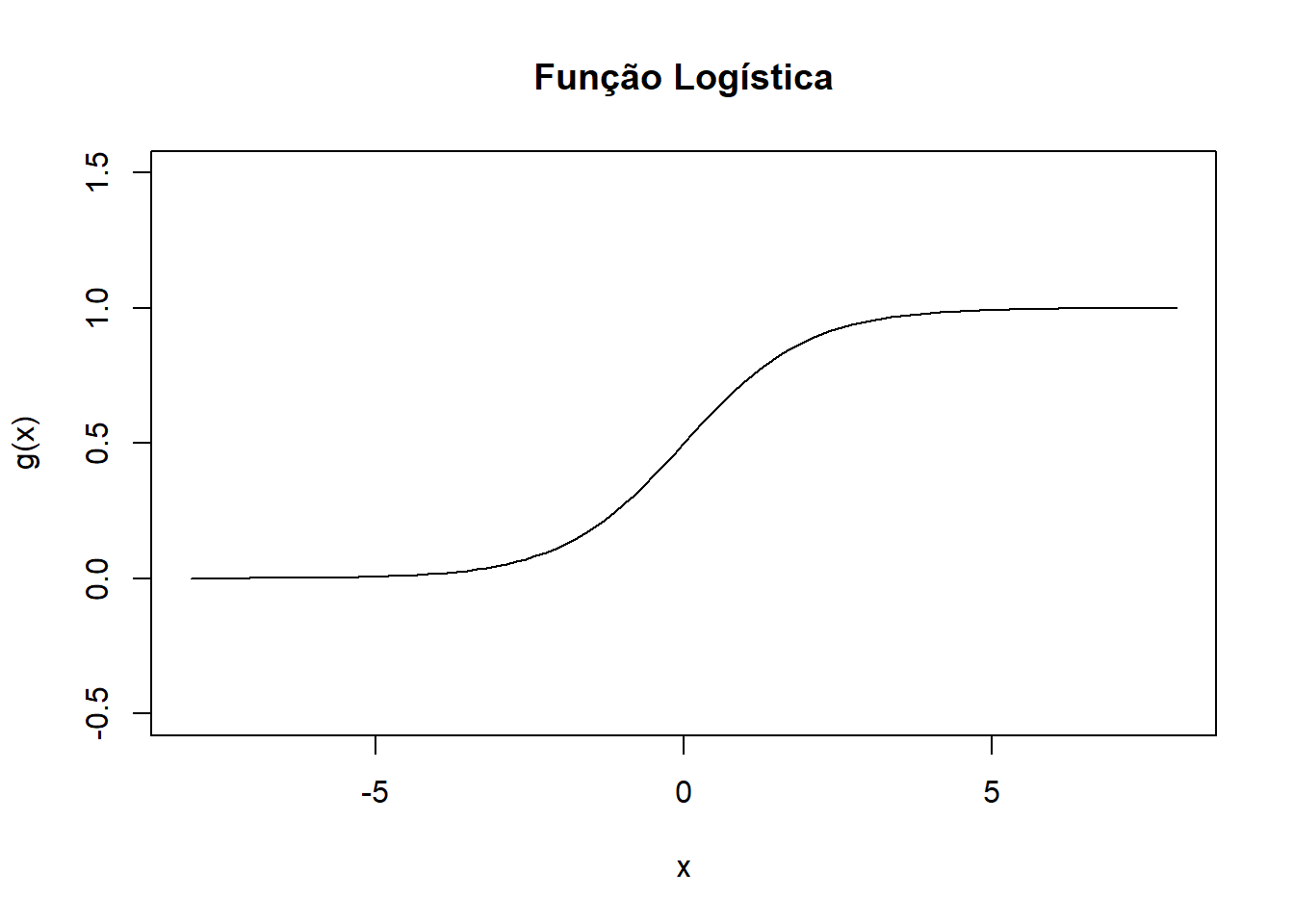
7.4.1 Função Logística (Gaussiana)
\[ g(x) = \dfrac{1}{1 + e^{-x}} \]
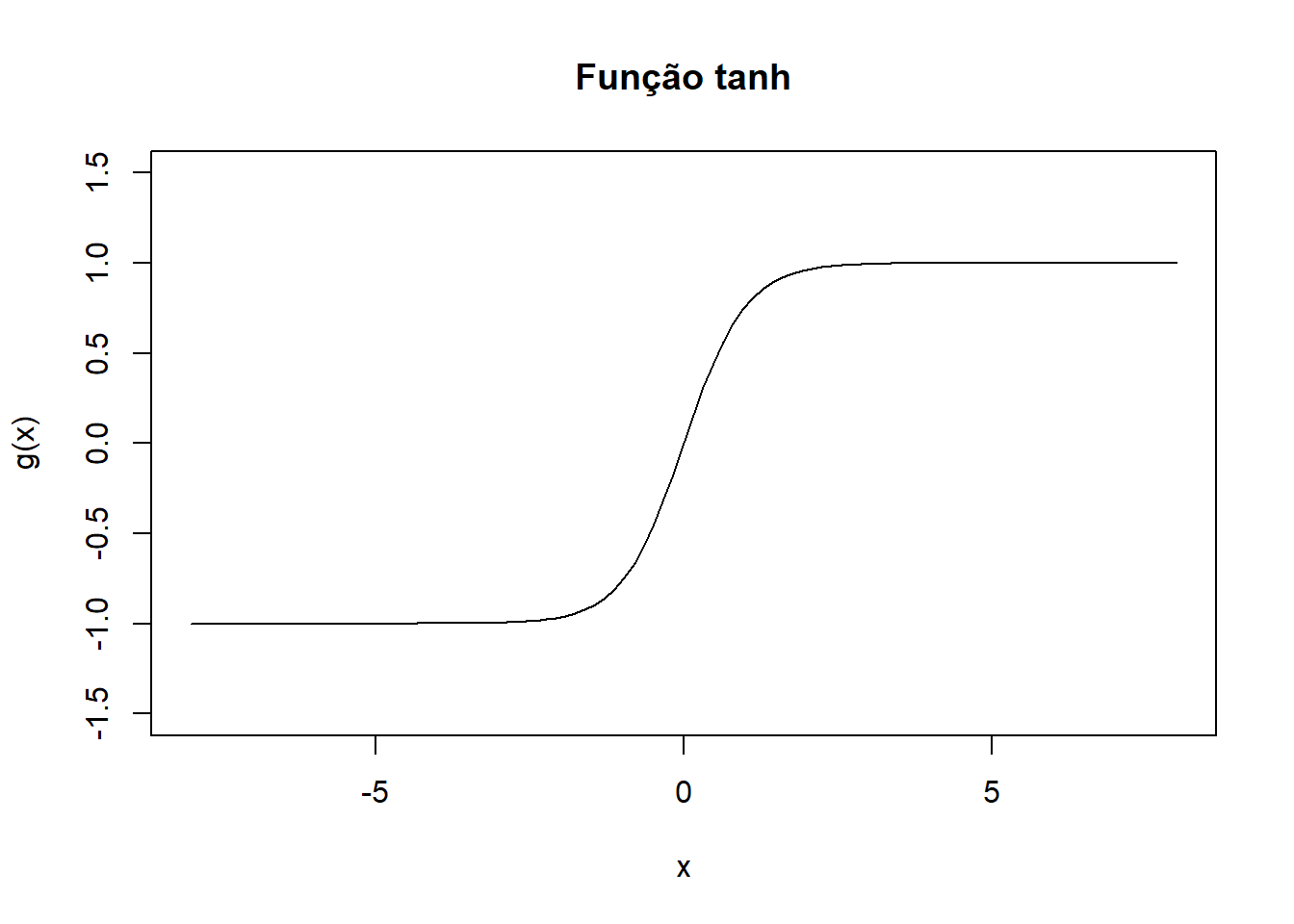
7.4.2 Função Tangente Hiperbólica
\[ g(x) = \tanh(x) = \dfrac{\sinh(x)}{\cosh(x)} = \dfrac{\dfrac{e^x - e^{-x}}{2}}{\dfrac{e^x + e^{-x}}{2}} = \dfrac{e^x - e^{-x}}{e^x + e^{-x}} = \dfrac{e^{2x} - 1}{e^{2x} + 1} \]
7.5 Padronização
Quando aplicamos as redes neurais para resolver problemas de regressão ou classificação é de grande importância realizar a padronização tanto das covariáveis quanto da variável resposta, quanto esta for contínua (regressão).
7.5.1 Transformação na variável resposta
Vale destacar que as funções de ativação, por terem o papel de restringir o valor da saída, apresentam imagem em um intervalo da reta. Para os exemplos citados vimos funções de ativação com imagem no intervalo \([0,1]\) e \([-1,1]\). Por esse motivo o modelo trabalha com variáveis respostas dentro destes intervalos. Caso a variável resposta do problema não esteja contida no intervalo definido pela imagem da função de ativação, é necessário realizar uma transformação nesta variável antes de ajustar o modelo.
Por exemplo, a transformação a seguir leva o conjunto de valores observados de \(Y\), \(y_1, y_2, \ldots, y_N\), para o intervalo \([0,1]\)
\[ \tilde{y}_i = \dfrac{y_i - \min\{y_i\}}{\max\{y_i\} - \min\{y_i\}} \]
enquanto a transformação
\[ \tilde{y}_i = 2\dfrac{y_i - \min\{y_i\}}{\max\{y_i\} - \min\{y_i\}} -1 \]
leva o conjunto de valores observados de \(Y\) para o intervalo \([-1,1]\).
Se o modelo for usado para realizar previsões, essa transformação deve ser desfeita para que os valores previstos estejam em sua escala correta. Isso será melhor discutido e trabalhado ao longo do curso.
7.5.2 Transformação nas covariáveis
Também é de extrema importância a padronização dos valores de entrada. Podemos realizar a mesma padronização feita com os valores de saída para cada covariável \(X_j\), isto é,
\[ \tilde{x}_{i,j} = \dfrac{x_{i,j} - \min\{x_{j}\}}{\max\{x_{j}\} - \min\{x_{j}\}} \]
sendo \(\min\{x_{j}\} = \min_{i=1\ldots n}\{x_{i,j}\}\) e \(\max\{x_{j}\} = \max_{i=1\ldots n}\{x_{i,j}\}\). Ou podemos realizar a subtração do valor médio e divisão pela desvio padrão.
\[ \tilde{x}_{i,j} = \dfrac{x_{i,j} - \bar{x}_j}{s_{x_j}}. \]
7.6 Perceptron Multiplas Camadas
O perceptron multicamadas é a combinação de vários perceptrons de camada única organizados em diversas camadas. A ideia principal é partir de uma rede perceptron de um único neurônio, e em vez de “imputar” os valores de cováveis neste neurônio vão entrar saídas de outras rede perceptron de camada única.
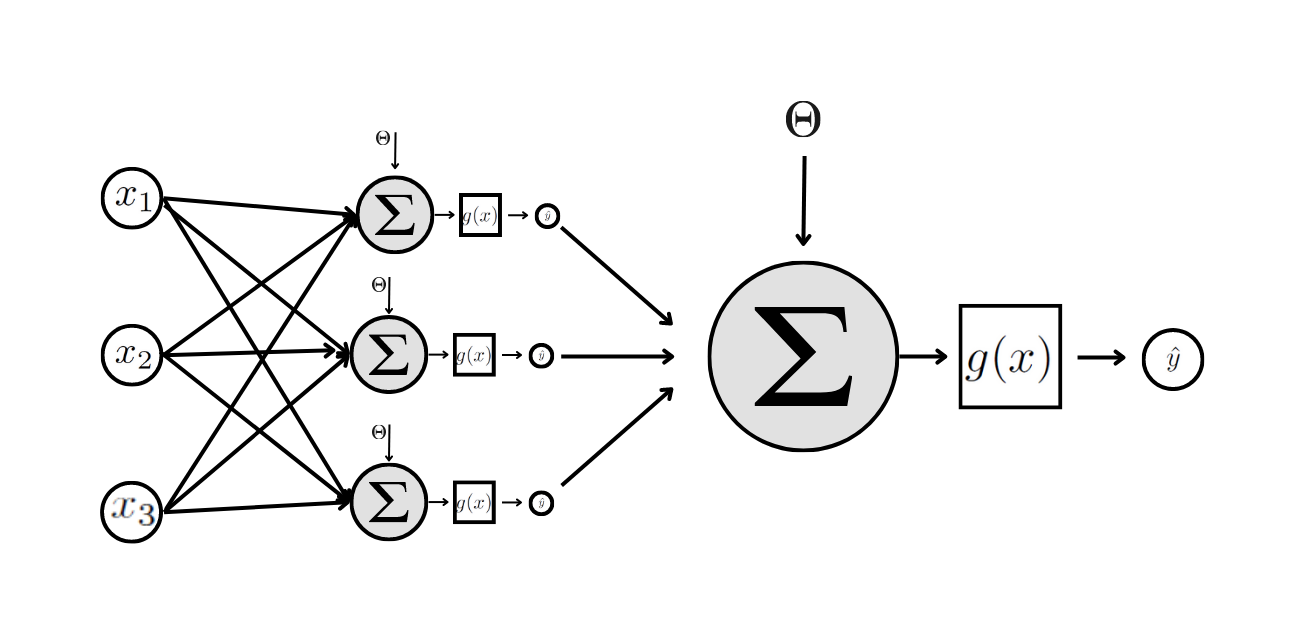
Um exemplo de uma rede Perceptron com multiplas camadas está apresentada na Figura (perceptron-2?). Esta rede possui uma camada de entrada, uma camada oculta com 3 neurônios e uma camada de saída. Esta rede possui 16 parâmetros desconhecidos, que são os pesos sinápticos mais os limiares aditivos.
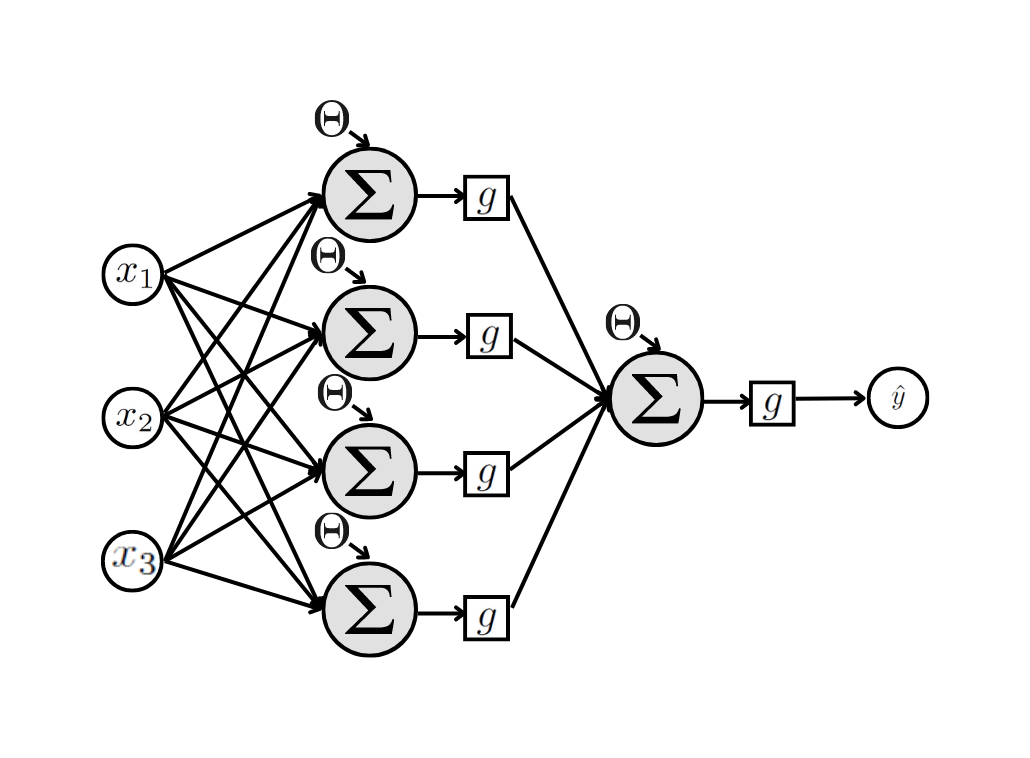
A camada oculta pode ter quantos neurônios a gente quiser, e puder estimar seus valores. Para o exemplo, a Figura (perceptron-multi-4-1?) apresenta uma rede com uma camada oculta com 4 neurônios, que resulta em 21 parâmetros desconhecidos.
 Também podemos incluir quantas novas camadas quisermos, e pudermos estimar. Para o exemplo da Figura (perceptron-multi-4-3?) a rede possui 2 camadas ocultas, a primeira com 4 neurônios e a segunda com 3. Para esta rede temos 31 parâmetros desconhecidos.
Também podemos incluir quantas novas camadas quisermos, e pudermos estimar. Para o exemplo da Figura (perceptron-multi-4-3?) a rede possui 2 camadas ocultas, a primeira com 4 neurônios e a segunda com 3. Para esta rede temos 31 parâmetros desconhecidos.
O número de parâmetros desconhecidos da rede depende do tamanho e da arquitetura da rede. Quanto mais camadas ocultas, mais parâmetros teremos e mais complexo o modelo é. É a complexidade das redes que capturam melhor padrões não lineares dos dados.
Cada neurônio da rede possui uma função de ativação, que para a rede perceptron será a função logística ou a função tnah.
7.6.1 Único neurônio na camada de saída
Estas são as redes que vimos até agora, com uma única saída. A saída \(\hat{Y}\) pode ser a estimativa para uma variável resposta contínua \(Y\), dado algum problema de regressão, ou a estimativa para uma variável resposta indicadora \(Y\), dado algum problema de classificação. Veja que neste último caso consideramos \(Y= 1\) ou \(Y=0\) para indicar se a instância pertence ou não à classe de interesse. Sendo assim, cada instância pertence a uma de duas classes possíveis.

No exemplo de rede apresentado na Figura (exemplo-4-1-saida?) são 3 covariáveis de entrada, uma camada oculta (hide) com 4 neurônios e uma camada de saída com 1 neurônio. Cada seta na figura representa um peso sináptico \(w\) ou um limiar de ativação \(\theta\). O número de parâmetros desconhecidos neste exemplo é: \((3 + 1) \times 5 = 20\).
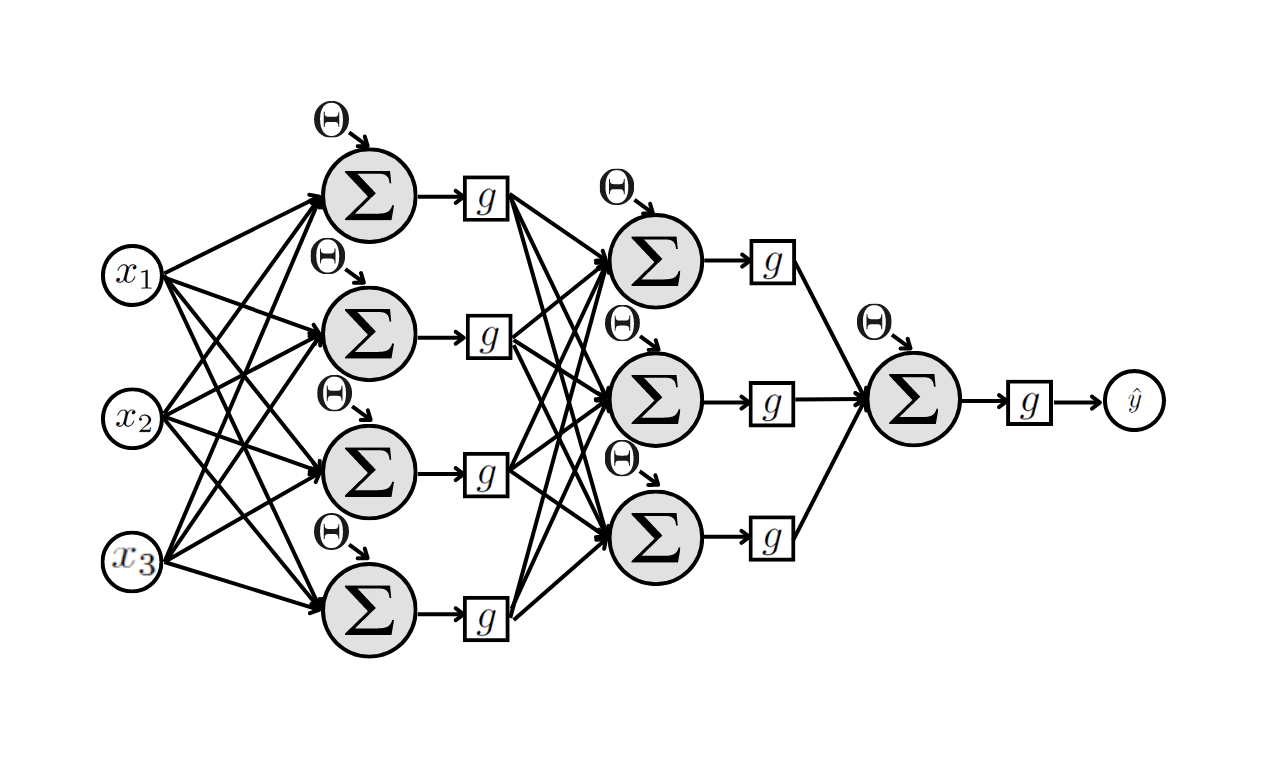
Já a rede apresentada Figura (exemplo-4-3-1-saida?) possui duas camadas ocultas, a primeira com 4 neurônios e a segunda com 3. A camada de saída contém um único neurônio. Esta rede contém \[ (3 + 1) \times 8 + (4 + 1) \times 3 + (3+1) \times 1 = 16 + 15 + 4 = 35 \] parâmetros desconhecidos.
7.6.2 Multiplos neurônio na camada de saída
Esta será a arquitetura usada para os problemas de classificação multiclasses.
Suponha um problema de classificação que, em vez de cada instância (observação) pertencer a uma de duas possíveis classes, ela pertence a uma entre \(k\) possíveis classes.
Este problema também pode ser resolvido com uma rede neural Perseptron. A rede que vai atender a esse tipo de problema será muito parecida com aquelas vistas até o momento, a diferença é que as redes para esse tipo de problema são definidas com mais de um neurônio de saída.
Se a variável resposta do problema de classificação puder assumir 1 entre \(k\) possíveis classes, o número de neurônios na camada de saída será \(k-1\). Dessa forma em vez de uma saída teremos \(k-1\) saídas, que indicam a probabilidade da instância pertencer a cada uma das \(k-1\) classes. Neste caso, a probabilidade da instância pertencer a classe que não está sendo representada por um neurônio é o complemntar da soma da probabilidade de pertencer às demais classes.

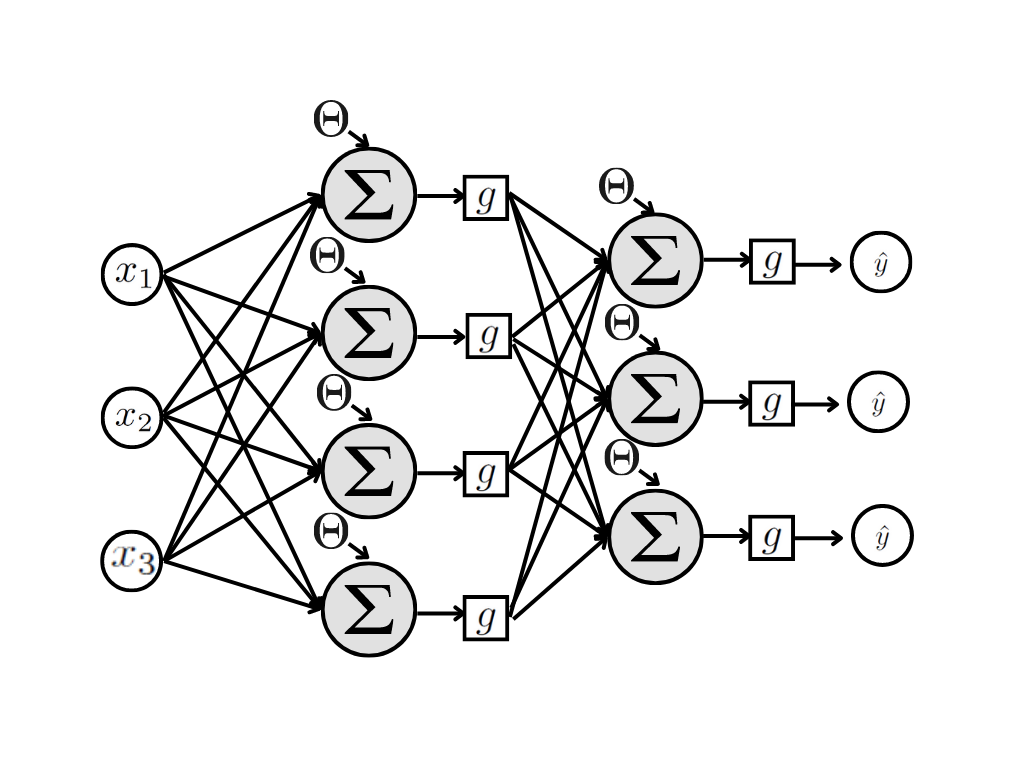
A Figura acima apresenta uma rede com 3 covariáveis de entrada, 1 camada oculta com 4 neurônios e uma camada de saída com 3 neurônios. Isso indica que esta rede foi construída para um problema de classificação com 4 classes. A saída retorna um número entre 0 e 1 e este número indica a probabilidade da instância pertencer a classe correspondente. Importante: para uma isntância qualquer a soma das saídas tem que ser menor ou igual a 1, e a probabilidade de pertencer a classe não representada será o complementar desta soma.
7.7 Vamos praticar
Primeiro, como sempre, devemos carregar os pacotes necessários para manipulação da base de dados e a base já tratada.
# Carregar pacotes e base de treino
library(tidyverse)
base_treino = readRDS(file="salvos//base_treino_final.rds")Antes de ajustar um problema de redes neurais é preciso realizar o escalonamento nas covariáveis quantitativas. Para isso vamos criar duas bases de covariáveis, primeiro uma contendo as variáveis quantitativas.
X1 = base_treino |> select(NU_MATRICULAS,
PC_FORMACAO_DOCENTE,
NU_TAXA_PERMANENCIA,
NU_TAXA_REPROVACAO,
NU_TAXA_ABANDONO)As variávais da base \(X1\) serão escalonadas antes do ajuste do modelo de redes neurais. Isto pode ser feito manualmente ou com a função scale.
X1s = scale(X1)
class(X1s)[1] "matrix" "array" Veja que o retorno da função scale é um objeto do tipo "matrix" e não mais um data.frame.
Agora faremos uma segunda base de covariáveis com aquelas categóricas.
X2 = base_treino |> select(SG_UF_ESCOLA,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA,
INSE,
PORTE_ESCOLA)Para a função neuralnet que será rodada em breve, as variáveis categóricas precisam ser transformadas em binárias e, novamente, a função model.matrix será usada para esse fim.
X2m = model.matrix(~. , data = X2)[,-1]
class(X2m)[1] "matrix" "array" head(X2m) SG_UF_ESCOLAAL SG_UF_ESCOLAAM SG_UF_ESCOLAAP SG_UF_ESCOLABA SG_UF_ESCOLACE
1 0 0 0 0 0
2 0 0 0 0 0
3 0 0 0 0 0
4 0 0 0 0 0
5 0 0 0 0 0
6 0 0 0 0 0
SG_UF_ESCOLADF SG_UF_ESCOLAES SG_UF_ESCOLAGO SG_UF_ESCOLAMA SG_UF_ESCOLAMG
1 0 0 0 0 0
2 0 0 0 0 0
3 0 0 0 0 0
4 0 0 0 0 0
5 0 0 0 0 0
6 0 0 0 0 0
SG_UF_ESCOLAMS SG_UF_ESCOLAMT SG_UF_ESCOLAPA SG_UF_ESCOLAPB SG_UF_ESCOLAPE
1 0 0 0 0 0
2 0 0 0 0 0
3 0 0 0 0 0
4 0 0 0 0 0
5 0 0 0 0 0
6 0 0 0 0 0
SG_UF_ESCOLAPI SG_UF_ESCOLAPR SG_UF_ESCOLARJ SG_UF_ESCOLARN SG_UF_ESCOLARO
1 0 0 0 0 1
2 0 0 0 0 1
3 0 0 0 0 1
4 0 0 0 0 1
5 0 0 0 0 1
6 0 0 0 0 1
SG_UF_ESCOLARR SG_UF_ESCOLARS SG_UF_ESCOLASC SG_UF_ESCOLASE SG_UF_ESCOLASP
1 0 0 0 0 0
2 0 0 0 0 0
3 0 0 0 0 0
4 0 0 0 0 0
5 0 0 0 0 0
6 0 0 0 0 0
SG_UF_ESCOLATO TP_DEPENDENCIA_ADM_ESCOLAEstadual
1 0 0
2 0 0
3 0 1
4 0 1
5 0 0
6 0 1
TP_DEPENDENCIA_ADM_ESCOLAMunicipal TP_DEPENDENCIA_ADM_ESCOLAPrivada
1 0 1
2 0 1
3 0 0
4 0 0
5 0 1
6 0 0
TP_LOCALIZACAO_ESCOLARural INSEGrupo 2 INSEGrupo 3 INSEGrupo 4 INSEGrupo 5
1 0 0 0 0 0
2 0 0 0 0 1
3 0 0 0 0 1
4 0 0 0 1 0
5 0 0 0 1 0
6 1 0 1 0 0
INSEGrupo 6 PORTE_ESCOLADe 31 a 60 alunos PORTE_ESCOLADe 61 a 90 alunos
1 1 0 0
2 0 1 0
3 0 0 0
4 0 1 0
5 0 1 0
6 0 1 0
PORTE_ESCOLAMaior que 90 alunos
1 1
2 0
3 1
4 0
5 0
6 0COmo as duas bases X1s e X2m são objetos do tipo matriz, paras finalizar o tratamento das covariáveis vamos juntá-las em uma única matriz com o comando cbind.
MX = cbind(X1s,X2m)
head(MX) NU_MATRICULAS PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA NU_TAXA_REPROVACAO
1 0.6054172 0.4097266 0.1255720 -0.6212814
2 -0.3664904 -0.2575631 0.2859461 0.2117330
3 0.1313159 -0.3968236 0.4776866 0.2495973
4 -0.4968683 0.7810878 -0.6484730 1.6884404
5 -0.6153936 -0.8262100 -0.8781570 0.1360045
6 -0.5324259 -1.4993022 -0.1643154 -0.2931242
NU_TAXA_ABANDONO SG_UF_ESCOLAAL SG_UF_ESCOLAAM SG_UF_ESCOLAAP SG_UF_ESCOLABA
1 -0.68599631 0 0 0 0
2 -0.54066948 0 0 0 0
3 -0.68599631 0 0 0 0
4 0.02247195 0 0 0 0
5 -0.43167437 0 0 0 0
6 2.58385717 0 0 0 0
SG_UF_ESCOLACE SG_UF_ESCOLADF SG_UF_ESCOLAES SG_UF_ESCOLAGO SG_UF_ESCOLAMA
1 0 0 0 0 0
2 0 0 0 0 0
3 0 0 0 0 0
4 0 0 0 0 0
5 0 0 0 0 0
6 0 0 0 0 0
SG_UF_ESCOLAMG SG_UF_ESCOLAMS SG_UF_ESCOLAMT SG_UF_ESCOLAPA SG_UF_ESCOLAPB
1 0 0 0 0 0
2 0 0 0 0 0
3 0 0 0 0 0
4 0 0 0 0 0
5 0 0 0 0 0
6 0 0 0 0 0
SG_UF_ESCOLAPE SG_UF_ESCOLAPI SG_UF_ESCOLAPR SG_UF_ESCOLARJ SG_UF_ESCOLARN
1 0 0 0 0 0
2 0 0 0 0 0
3 0 0 0 0 0
4 0 0 0 0 0
5 0 0 0 0 0
6 0 0 0 0 0
SG_UF_ESCOLARO SG_UF_ESCOLARR SG_UF_ESCOLARS SG_UF_ESCOLASC SG_UF_ESCOLASE
1 1 0 0 0 0
2 1 0 0 0 0
3 1 0 0 0 0
4 1 0 0 0 0
5 1 0 0 0 0
6 1 0 0 0 0
SG_UF_ESCOLASP SG_UF_ESCOLATO TP_DEPENDENCIA_ADM_ESCOLAEstadual
1 0 0 0
2 0 0 0
3 0 0 1
4 0 0 1
5 0 0 0
6 0 0 1
TP_DEPENDENCIA_ADM_ESCOLAMunicipal TP_DEPENDENCIA_ADM_ESCOLAPrivada
1 0 1
2 0 1
3 0 0
4 0 0
5 0 1
6 0 0
TP_LOCALIZACAO_ESCOLARural INSEGrupo 2 INSEGrupo 3 INSEGrupo 4 INSEGrupo 5
1 0 0 0 0 0
2 0 0 0 0 1
3 0 0 0 0 1
4 0 0 0 1 0
5 0 0 0 1 0
6 1 0 1 0 0
INSEGrupo 6 PORTE_ESCOLADe 31 a 60 alunos PORTE_ESCOLADe 61 a 90 alunos
1 1 0 0
2 0 1 0
3 0 0 0
4 0 1 0
5 0 1 0
6 0 1 0
PORTE_ESCOLAMaior que 90 alunos
1 1
2 0
3 1
4 0
5 0
6 0Temos um último problema a resolver. A função que vai ajusar o modelo de redes neurais não aceita variáveis cujos nomes contém espaço. E veja que isso ocorre com a matriz MX:
colnames(MX) [1] "NU_MATRICULAS" "PC_FORMACAO_DOCENTE"
[3] "NU_TAXA_PERMANENCIA" "NU_TAXA_REPROVACAO"
[5] "NU_TAXA_ABANDONO" "SG_UF_ESCOLAAL"
[7] "SG_UF_ESCOLAAM" "SG_UF_ESCOLAAP"
[9] "SG_UF_ESCOLABA" "SG_UF_ESCOLACE"
[11] "SG_UF_ESCOLADF" "SG_UF_ESCOLAES"
[13] "SG_UF_ESCOLAGO" "SG_UF_ESCOLAMA"
[15] "SG_UF_ESCOLAMG" "SG_UF_ESCOLAMS"
[17] "SG_UF_ESCOLAMT" "SG_UF_ESCOLAPA"
[19] "SG_UF_ESCOLAPB" "SG_UF_ESCOLAPE"
[21] "SG_UF_ESCOLAPI" "SG_UF_ESCOLAPR"
[23] "SG_UF_ESCOLARJ" "SG_UF_ESCOLARN"
[25] "SG_UF_ESCOLARO" "SG_UF_ESCOLARR"
[27] "SG_UF_ESCOLARS" "SG_UF_ESCOLASC"
[29] "SG_UF_ESCOLASE" "SG_UF_ESCOLASP"
[31] "SG_UF_ESCOLATO" "TP_DEPENDENCIA_ADM_ESCOLAEstadual"
[33] "TP_DEPENDENCIA_ADM_ESCOLAMunicipal" "TP_DEPENDENCIA_ADM_ESCOLAPrivada"
[35] "TP_LOCALIZACAO_ESCOLARural" "INSEGrupo 2"
[37] "INSEGrupo 3" "INSEGrupo 4"
[39] "INSEGrupo 5" "INSEGrupo 6"
[41] "PORTE_ESCOLADe 31 a 60 alunos" "PORTE_ESCOLADe 61 a 90 alunos"
[43] "PORTE_ESCOLAMaior que 90 alunos" Para relver isso podemos simplesmente renomear as colunas da matriz da forma que a gente quiser. Mas para facilitar o entendimento de cada coluna vamos fazer de outra forma: excluir os espaços.
colnames(MX) = gsub(" ","",colnames(MX))
colnames(MX) [1] "NU_MATRICULAS" "PC_FORMACAO_DOCENTE"
[3] "NU_TAXA_PERMANENCIA" "NU_TAXA_REPROVACAO"
[5] "NU_TAXA_ABANDONO" "SG_UF_ESCOLAAL"
[7] "SG_UF_ESCOLAAM" "SG_UF_ESCOLAAP"
[9] "SG_UF_ESCOLABA" "SG_UF_ESCOLACE"
[11] "SG_UF_ESCOLADF" "SG_UF_ESCOLAES"
[13] "SG_UF_ESCOLAGO" "SG_UF_ESCOLAMA"
[15] "SG_UF_ESCOLAMG" "SG_UF_ESCOLAMS"
[17] "SG_UF_ESCOLAMT" "SG_UF_ESCOLAPA"
[19] "SG_UF_ESCOLAPB" "SG_UF_ESCOLAPE"
[21] "SG_UF_ESCOLAPI" "SG_UF_ESCOLAPR"
[23] "SG_UF_ESCOLARJ" "SG_UF_ESCOLARN"
[25] "SG_UF_ESCOLARO" "SG_UF_ESCOLARR"
[27] "SG_UF_ESCOLARS" "SG_UF_ESCOLASC"
[29] "SG_UF_ESCOLASE" "SG_UF_ESCOLASP"
[31] "SG_UF_ESCOLATO" "TP_DEPENDENCIA_ADM_ESCOLAEstadual"
[33] "TP_DEPENDENCIA_ADM_ESCOLAMunicipal" "TP_DEPENDENCIA_ADM_ESCOLAPrivada"
[35] "TP_LOCALIZACAO_ESCOLARural" "INSEGrupo2"
[37] "INSEGrupo3" "INSEGrupo4"
[39] "INSEGrupo5" "INSEGrupo6"
[41] "PORTE_ESCOLADe31a60alunos" "PORTE_ESCOLADe61a90alunos"
[43] "PORTE_ESCOLAMaiorque90alunos" 7.7.1 Regressão
Serão replicados os mesmos exemplos dos métodos anteriores. Primeiro será ajustado um modelo para prever a nota em matemática das escolas e por isso vamos guardar no objeto Y os valores de para a variável resposta em questão.
Y = base_treino |> select(NU_MEDIA_MT)Para criar modelos Perceptron de Multiplas camadas será usado o pacote neuralnet (Fritsch, Guenther, and Wright 2019).
#install.packages("neuralnet")
library(neuralnet)É preciso fixar a semente para garantir a reprodutibilidade do código.
set.seed(1234567890)A função neuralnet, mesmo nome do pacote, é chamada para treinar a rede neural. No argumento de entrada data devemos colocar uma matrix cujas colunas são todas as variáveis, covariáveis e variável alvo.
O comando a seguir irá ajustar uma rede neural com nenhuma camada oculta, ou seja, um perceptron camada única. Isso é definido pelo comando hidden = 0.
NN0_REG = neuralnet(
formula = NU_MEDIA_MT ~ . ,
data = cbind(MX,Y),
hidden = 0)
class(NN0_REG)Para realizar previsões com um objeto do tipo nn, que é a saída da função neuralnet, novamente usaremos a função predict.
y_ = predict(NN0_REG,newdata=MX)
head(y_) [,1]
1 628.3670
2 548.1393
3 515.2709
4 461.0268
5 498.4976
6 420.4111As medidas de qualidade do ajuste serão calculadas como antes.
y = Y$NU_MEDIA_MT
(RSS = sum((y - y_)^2))[1] 15528037(EMQ = mean((y-y_)^2))[1] 1327.183(R2 = 1 - sum((y-y_)^2)/sum((y-mean(y))^2))[1] 0.7186122Esse processo será repetido para diferentes quantidades de camadas e de neurônios por camadas. Devido ao alto tempo de ajuste dos modelos a semente será fixada sempre antes de rodar a função neuralnet. Assim, se o código for interrompido em algum momento não será preciso fazer tudo desde o início para garantir os mesmos resultados, basta reiniciar de onde houve a interrupção.
O comando a seguir irá ajustar uma rede neural com uma camada oculta contendo um único neurônio. Isto é definido por hidden = 1.
set.seed(1234567890)
NN1_REG_Y = neuralnet(
formula = NU_MEDIA_MT ~ .,
data = cbind(MX,Y),
hidden = 1) y_ = predict(NN1_REG_Y, newdata=MX)
head(y_) [,1]
1 492.4159
2 492.4159
3 492.4159
4 492.4159
5 492.4159
6 492.4159summary(y_) V1
Min. :492.4
1st Qu.:492.4
Median :492.4
Mean :492.4
3rd Qu.:492.4
Max. :492.4 y=Y$NU_MEDIA_MT
(RSS = sum((y - y_)^2))[1] 55183767(EMQ = mean((y-y_)^2))[1] 4716.561(R2 = 1 - sum((y-y_)^2)/sum((y-mean(y))^2))[1] 0Perceba que a resposta do modelo foi toda igual e que R2 deu zero. Isso significa que o modelo é tão bom (ou tão ruim) quanto estimar pela média. Mas por que isso ocorreu com um modelo tão complexo quanto o de redes neurais? Porque não escalonamos a variável resposta. Veja a diferença no ajuste do modelo quando isso é feito.
set.seed(1234567890)
NN1_REG_sY = neuralnet(
formula = NU_MEDIA_MT ~ .,
data = cbind(MX,scale(Y)),
hidden = 1,stepmax = 1e+7) y_ = predict(NN1_REG_sY, newdata=MX)
head(y_) [,1]
1 1.94814539
2 0.62507659
3 0.08218911
4 -0.51602712
5 -0.05089251
6 -0.93733401m = scale(Y) |> attr("scaled:center")
s = scale(Y) |> attr("scaled:scale")
y_ = y_*s + m
summary(y_) V1
Min. :412.9
1st Qu.:447.4
Median :470.4
Mean :492.4
3rd Qu.:532.6
Max. :732.1 (RSS = sum((y - y_)^2))[1] 14552054(EMQ = mean((y-y_)^2))[1] 1243.765(R2 = 1 - sum((y-y_)^2)/sum((y-mean(y))^2))[1] 0.7362983Vamos então adotar os modelos de redes neurais com \(Y\) escalonado.
NN1_REG = NN1_REG_sYset.seed(1234567890)
NN2_REG = neuralnet(
formula = NU_MEDIA_MT ~ .,
data = cbind(MX,scale(Y)),
hidden = 2,
stepmax = 1e+7) A previsão dos valores para os dados de treinamento podem ser obtidos com o comando net.result.
y_ = predict(NN2_REG,newdata=MX)
y_ = y_*s + m
head(y_) [,1]
1 613.4767
2 535.9381
3 498.2472
4 455.9046
5 494.6937
6 431.4598(RSS = sum((y - y_)^2))[1] 13653600(EMQ = mean((y-y_)^2))[1] 1166.974(R2 = 1 - sum((y-y_)^2)/sum((y-mean(y))^2))[1] 0.7525794set.seed(1234567890)
NN3_REG = neuralnet(
formula = NU_MEDIA_MT ~ .,
data = cbind(MX,scale(Y)),
hidden = 3,
stepmax = 1e+06) y_ = predict(NN3_REG,newdata=MX)
y_ = y_*s + m
head(y_) [,1]
1 621.5019
2 531.9791
3 495.9750
4 453.5376
5 486.9010
6 430.6552(RSS = sum((y - y_)^2))[1] 13329662(EMQ = mean((y-y_)^2))[1] 1139.287(R2 = 1 - sum((y-y_)^2)/sum((y-mean(y))^2))[1] 0.7584496set.seed(1234567890)
NN22_REG = neuralnet(
formula = NU_MEDIA_MT ~ . ,
data = cbind(MX,scale(Y)),
hidden = c(2,2),
stepmax = 1e+06) y_ = predict(NN22_REG,newdata=MX)
y_ = y_*s + m
head(y_) [,1]
1 622.5476
2 540.6319
3 471.8973
4 452.5491
5 501.2423
6 424.6354(RSS = sum((y - y_)^2))[1] 13769016(EMQ = mean((y-y_)^2))[1] 1176.839(R2 = 1 - sum((y-y_)^2)/sum((y-mean(y))^2))[1] 0.75048797.7.2 Classificação - 2 classes
Vejamos agora como usar a rede neural Perseptron Multiplas Camadas para realizar classificação com duas classes.
TAXA_PART_BAIXA =
ifelse(base_treino$TAXA_PART_CAT == "baixa",1,0)
head(TAXA_PART_BAIXA)[1] 0 0 0 0 0 1Novamente será usada a função nerualnet, mas agora é devemos informar que linear.output = FALSE e também a medida de erro adequada, err.fct = "ce".
set.seed(1234567890)
NN0_CLASS_2 = neuralnet(
formula = TAXA_PART_BAIXA ~ .,
data = cbind(MX,TAXA_PART_BAIXA),
hidden = 0,
linear.output = FALSE,
err.fct = "ce") Novamente a função predict será usado para pegar as previsões nos dados de treino, e para o caso de classifciação o retorno será um número entre 0 e 1.
y_ = predict(NN0_CLASS_2,newdata=MX)
head(y_) [,1]
1 0.002424837
2 0.011344338
3 0.065759765
4 0.173649856
5 0.033263183
6 0.766444782library(pROC)
y = TAXA_PART_BAIXA
ROC = roc(response = y,predictor = y_)
plot.roc(ROC,
print.auc = TRUE,
print.thres = TRUE)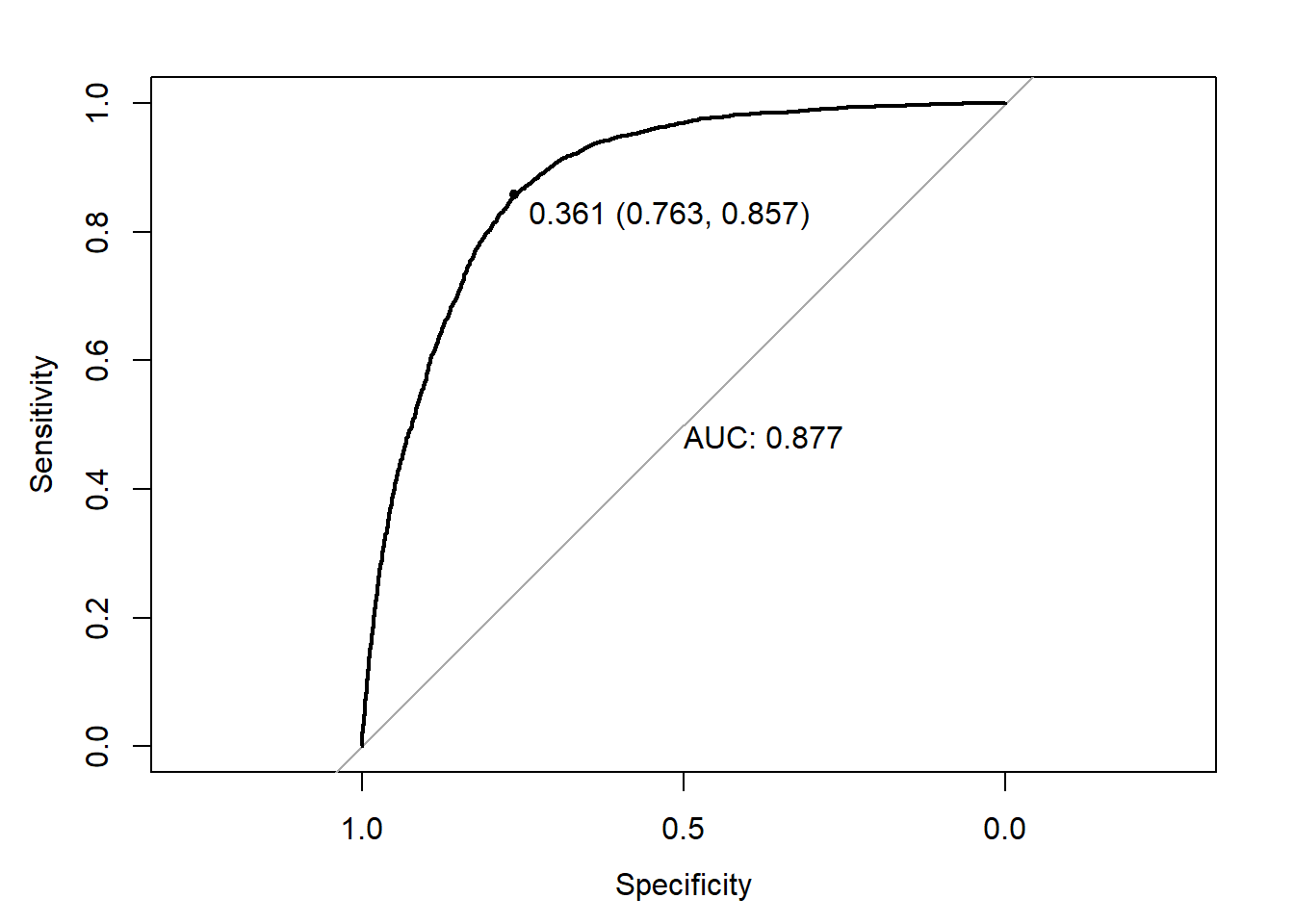
y_classe = ifelse(y_>0.361,1,0)
library(caret)
confusionMatrix(as.factor(y),as.factor(y_classe))Confusion Matrix and Statistics
Reference
Prediction 0 1
0 5899 1838
1 566 3397
Accuracy : 0.7945
95% CI : (0.7871, 0.8018)
No Information Rate : 0.5526
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.5746
Mcnemar's Test P-Value : < 2.2e-16
Sensitivity : 0.9125
Specificity : 0.6489
Pos Pred Value : 0.7624
Neg Pred Value : 0.8572
Prevalence : 0.5526
Detection Rate : 0.5042
Detection Prevalence : 0.6613
Balanced Accuracy : 0.7807
'Positive' Class : 0
O processo será repetido para diferentes quantidades de camadas e diferentes quantidades de neurônios por camadas.
set.seed(1234567890)
NN1_CLASS_2 = neuralnet(
formula = TAXA_PART_BAIXA ~ .,
data = cbind(MX,TAXA_PART_BAIXA),
hidden = 1,
linear.output = FALSE,
err.fct = "ce") y_ = predict(NN1_CLASS_2,newdata=MX)
ROC = roc(response = y,predictor = y_)
plot.roc(ROC,
print.auc = TRUE,
print.thres = TRUE)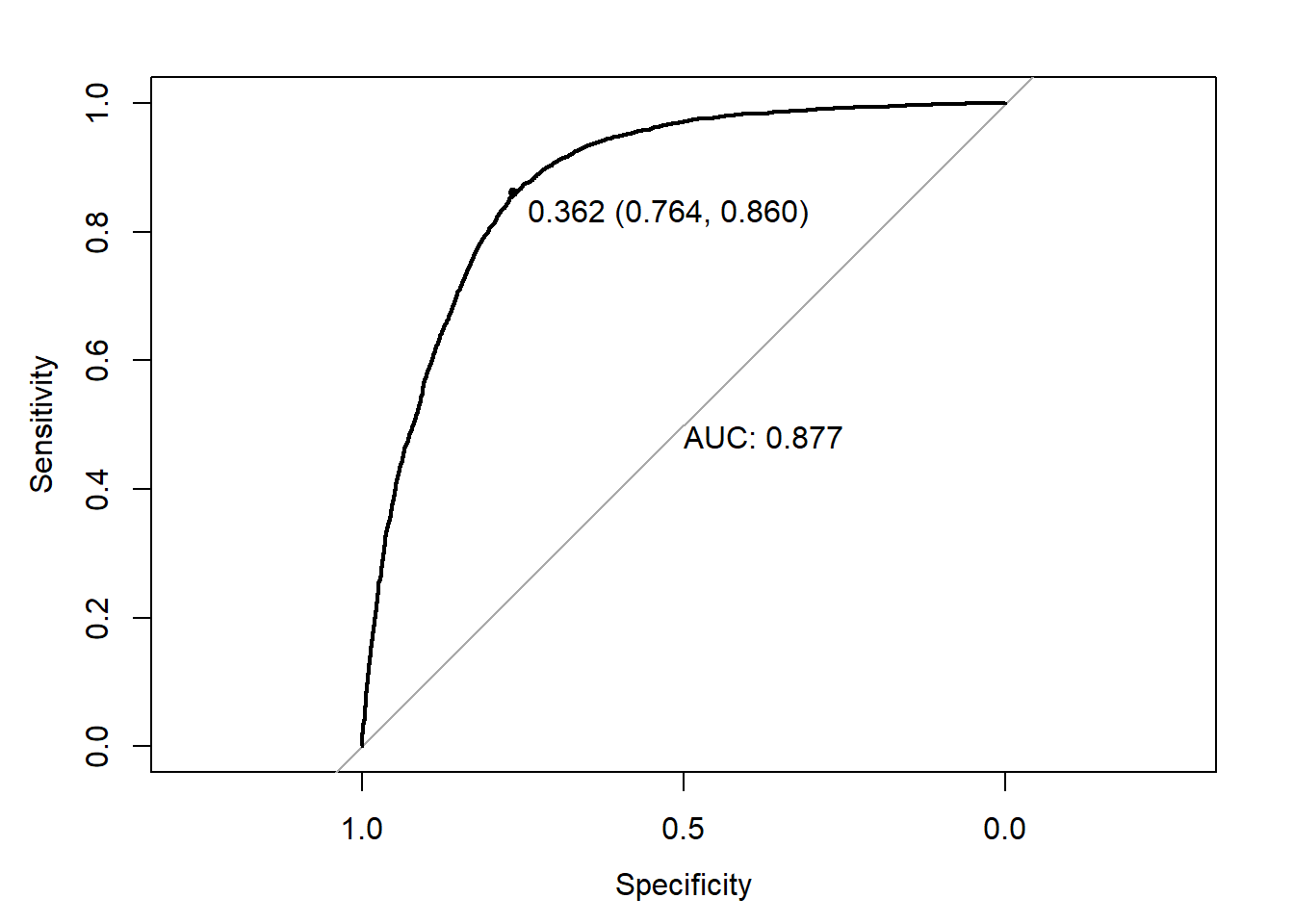
y_classe = ifelse(y_>0.362,1,0)
confusionMatrix(as.factor(y),as.factor(y_classe))Confusion Matrix and Statistics
Reference
Prediction 0 1
0 5911 1826
1 556 3407
Accuracy : 0.7964
95% CI : (0.789, 0.8037)
No Information Rate : 0.5527
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.5785
Mcnemar's Test P-Value : < 2.2e-16
Sensitivity : 0.9140
Specificity : 0.6511
Pos Pred Value : 0.7640
Neg Pred Value : 0.8597
Prevalence : 0.5527
Detection Rate : 0.5052
Detection Prevalence : 0.6613
Balanced Accuracy : 0.7825
'Positive' Class : 0
Agora segue o exemplo para a arquitetura com 1 camada oculta contendo 2 e 3 neurônios, respectivamente.
set.seed(1234567890)
NN2_CLASS_2 = neuralnet(
formula = TAXA_PART_BAIXA ~ .,
data = cbind(MX,TAXA_PART_BAIXA),
hidden = 2,
linear.output = FALSE,
err.fct = "ce")y_ = predict(NN2_CLASS_2,newdata=MX)
ROC = roc(response = y,predictor = y_)
plot.roc(ROC,
print.auc = TRUE,
print.thres = TRUE)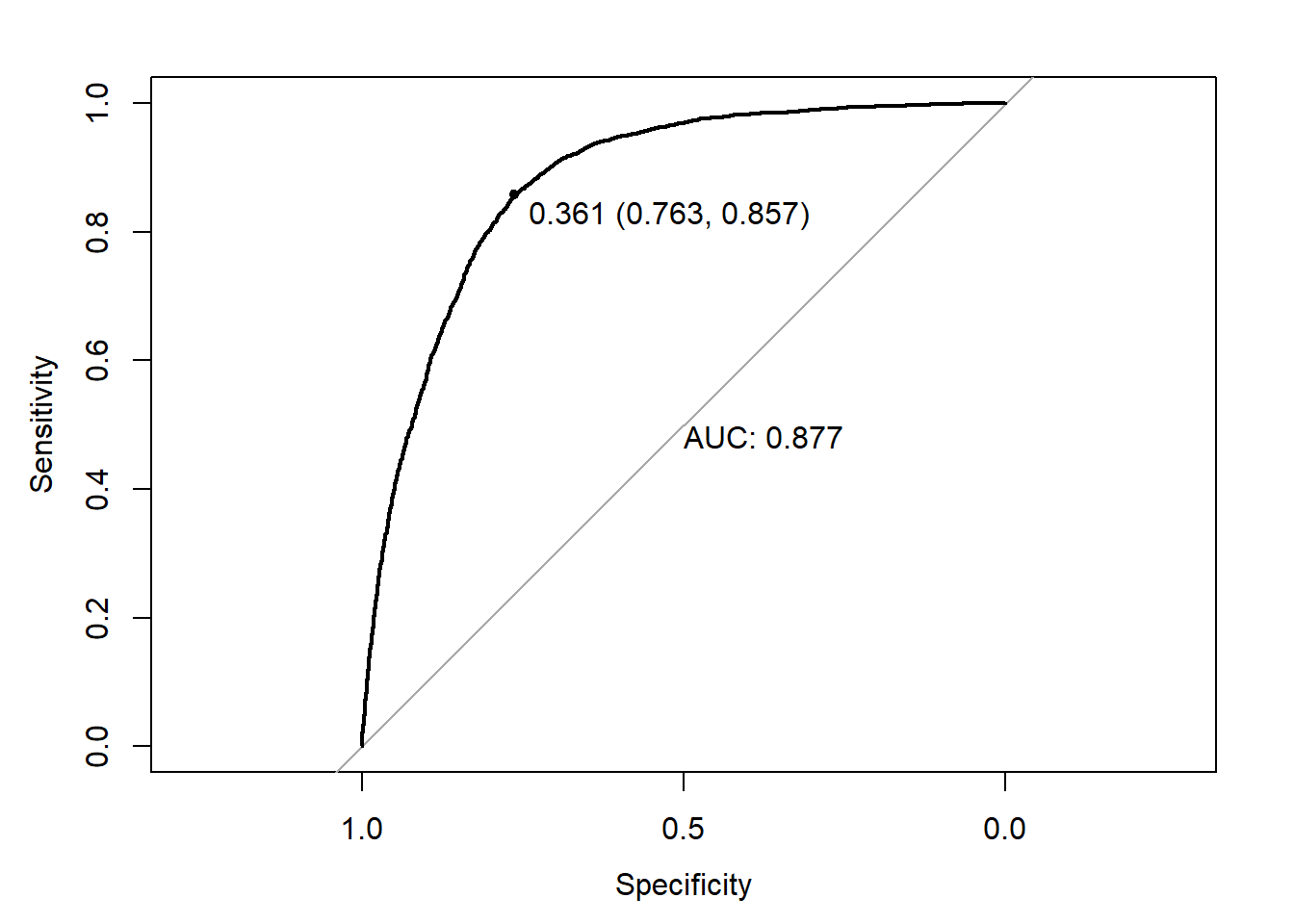
y_classe = ifelse(y_>0.361,1,0)
confusionMatrix(as.factor(y),as.factor(y_classe))Confusion Matrix and Statistics
Reference
Prediction 0 1
0 5899 1838
1 566 3397
Accuracy : 0.7945
95% CI : (0.7871, 0.8018)
No Information Rate : 0.5526
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.5746
Mcnemar's Test P-Value : < 2.2e-16
Sensitivity : 0.9125
Specificity : 0.6489
Pos Pred Value : 0.7624
Neg Pred Value : 0.8572
Prevalence : 0.5526
Detection Rate : 0.5042
Detection Prevalence : 0.6613
Balanced Accuracy : 0.7807
'Positive' Class : 0
set.seed(1234567890)
NN3_CLASS_2 = neuralnet(
formula = TAXA_PART_BAIXA ~ .,
data = cbind(MX,TAXA_PART_BAIXA),
hidden = 3,
linear.output = FALSE,
err.fct = "ce")y_ = predict(NN3_CLASS_2,newdata=MX)
ROC = roc(response = y,predictor = y_)
plot.roc(ROC,
print.auc = TRUE,
print.thres = TRUE)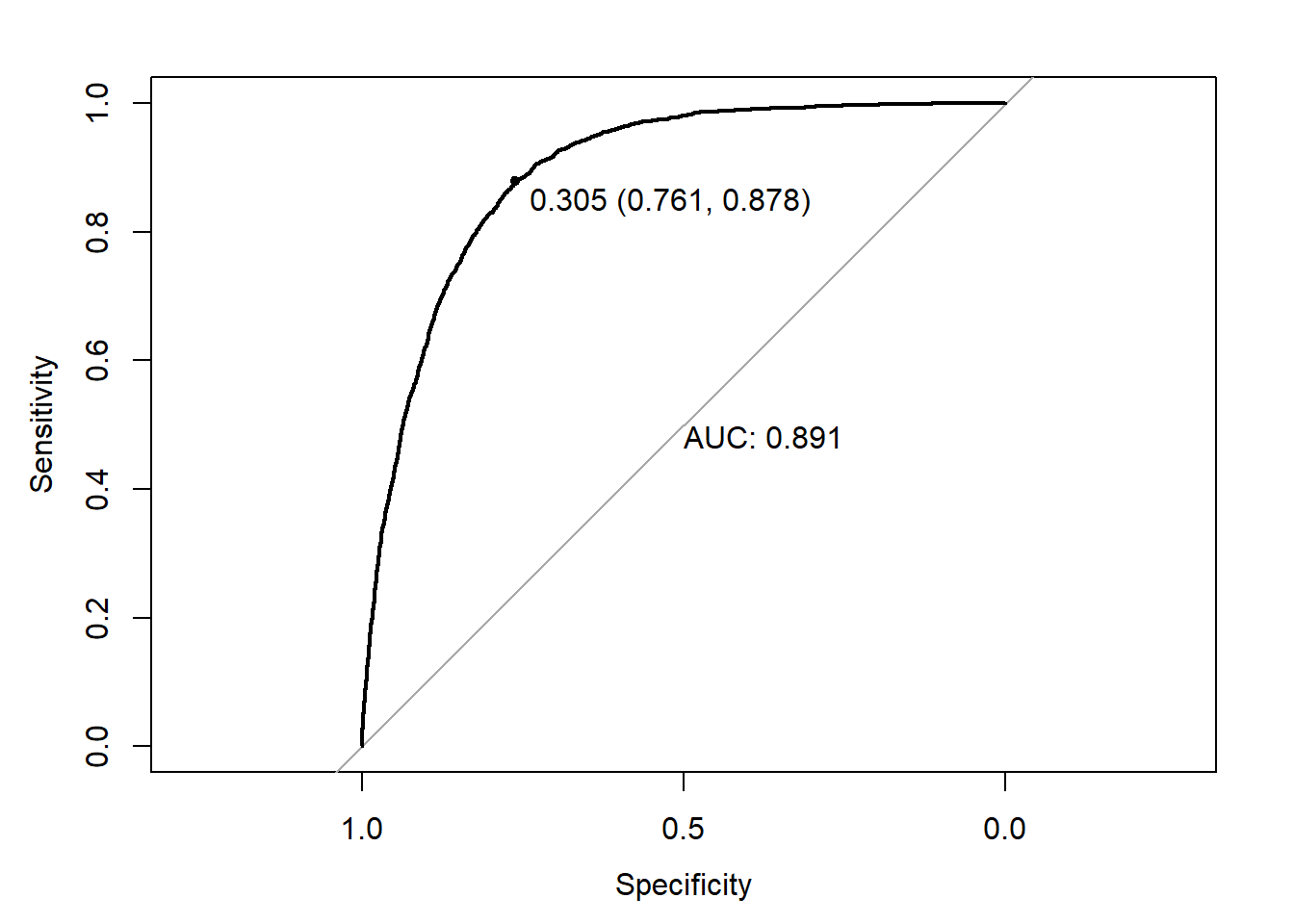
y_classe = ifelse(y_>0.305,1,0)
confusionMatrix(as.factor(y),as.factor(y_classe))Confusion Matrix and Statistics
Reference
Prediction 0 1
0 5888 1849
1 482 3481
Accuracy : 0.8008
95% CI : (0.7934, 0.808)
No Information Rate : 0.5444
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.5898
Mcnemar's Test P-Value : < 2.2e-16
Sensitivity : 0.9243
Specificity : 0.6531
Pos Pred Value : 0.7610
Neg Pred Value : 0.8784
Prevalence : 0.5444
Detection Rate : 0.5032
Detection Prevalence : 0.6613
Balanced Accuracy : 0.7887
'Positive' Class : 0
set.seed(1234567890)
NN22_CLASS_2 = neuralnet(
formula = TAXA_PART_BAIXA ~ .,
data = cbind(MX,TAXA_PART_BAIXA),
hidden = c(2,2),
linear.output = FALSE,
err.fct = "ce")y_ = predict(NN22_CLASS_2,newdata=MX)
ROC = roc(response = y,predictor = y_)
plot.roc(ROC,
print.auc = TRUE,
print.thres = TRUE)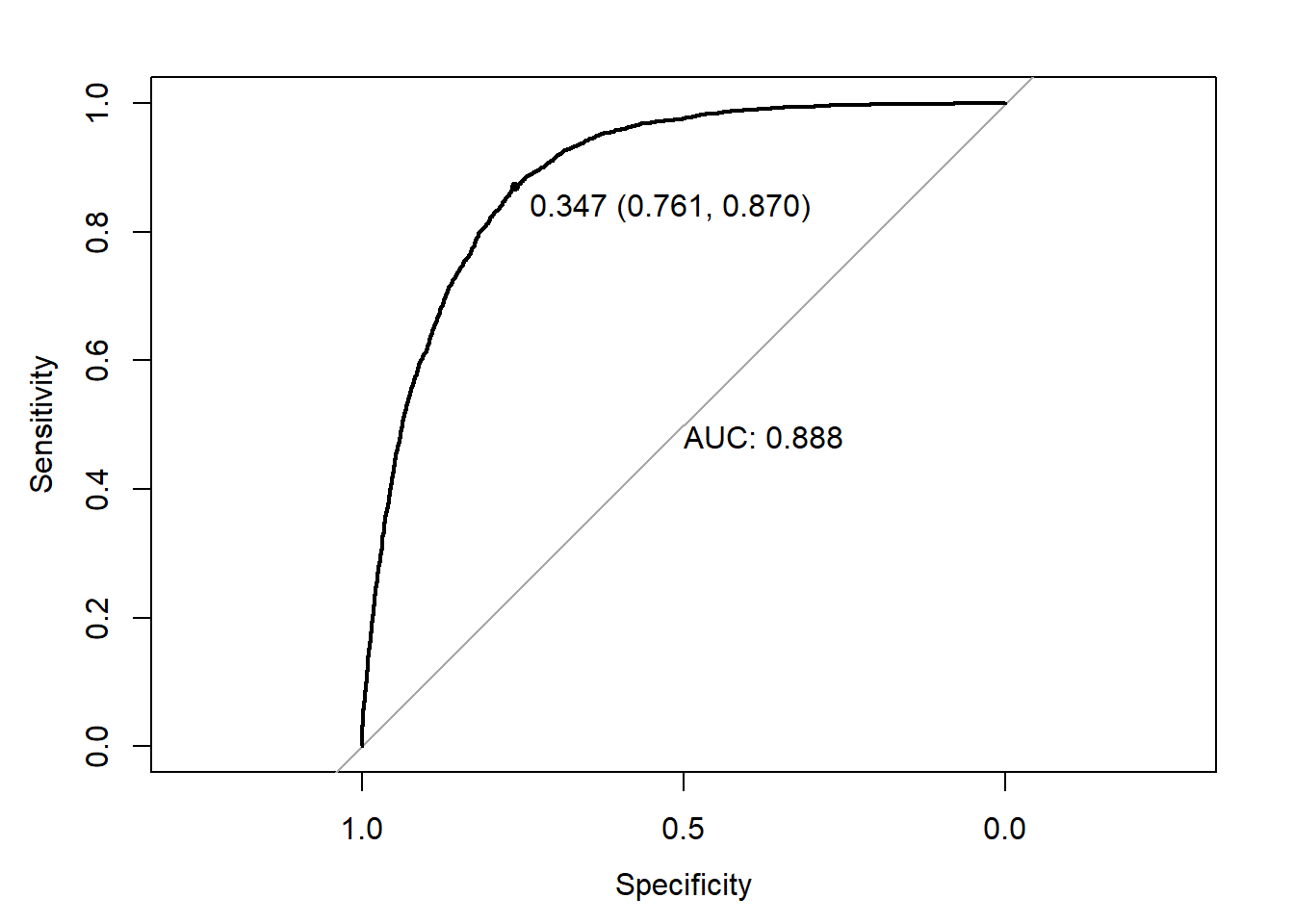
y_classe = ifelse(y_>0.347,1,0)
confusionMatrix(as.factor(y),as.factor(y_classe))Confusion Matrix and Statistics
Reference
Prediction 0 1
0 5893 1844
1 518 3445
Accuracy : 0.7981
95% CI : (0.7907, 0.8054)
No Information Rate : 0.5479
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.5834
Mcnemar's Test P-Value : < 2.2e-16
Sensitivity : 0.9192
Specificity : 0.6514
Pos Pred Value : 0.7617
Neg Pred Value : 0.8693
Prevalence : 0.5479
Detection Rate : 0.5037
Detection Prevalence : 0.6613
Balanced Accuracy : 0.7853
'Positive' Class : 0
7.7.3 Classifciação - 3 classes
Y = base_treino |> select(TAXA_PART_CAT)
MY = model.matrix(~ . , Y)[,-1]
head(MY) TAXA_PART_CATbaixa TAXA_PART_CATmedia
1 0 0
2 0 0
3 0 0
4 0 0
5 0 1
6 1 0Para indicar que o problema é de treinar uma rede neural que deve prever uma entre três classes, o argumento formula deve conter a estrutura apresentada no código a seguir.
set.seed(1234567890)
NN0_CLASS_3 = neuralnet(
formula = TAXA_PART_CAT ~ . ,
data = cbind(MX,Y),
hidden = 0,
linear.output = FALSE,
err.fct = "ce") A previsão será a probabilidade das duas classes indicadas no argumento formula, classe baixa e classe média. A probabilidade da classe alta será obtida através das probabilidades previstas para as outras duas classes.
y_ = predict(NN0_CLASS_3,newdata=MX)
head(y_) [,1] [,2] [,3]
1 0.956771423 0.002425004 0.2255450
2 0.837507316 0.011344961 0.3405840
3 0.723440732 0.065761862 0.2843134
4 0.223944728 0.173650159 0.3867122
5 0.621914019 0.033264578 0.3859799
6 0.003912993 0.766464562 0.3282611A saída para o modelo com 3 classes de previsão será uma matriz com 3 colunas. A ordem das colunas é dada pela ordem dos levels da variável resposta categórica. Vamos nomear as colunas dessa forma para facilitar as análises.
colnames(y_) = levels(Y$TAXA_PART_CAT)
head(y_) alta baixa media
1 0.956771423 0.002425004 0.2255450
2 0.837507316 0.011344961 0.3405840
3 0.723440732 0.065761862 0.2843134
4 0.223944728 0.173650159 0.3867122
5 0.621914019 0.033264578 0.3859799
6 0.003912993 0.766464562 0.3282611A classe prevista pelo modelo será aquela de maior probabilidade entre as três.
y_classe = apply(X = y_,MARGIN = 1,FUN = which.max)
head(y_classe)1 2 3 4 5 6
1 1 1 3 1 2 y_classe = factor(y_classe,
levels = c(1,2,3),
labels = colnames(y_))
head(y_classe) 1 2 3 4 5 6
alta alta alta media alta baixa
Levels: alta baixa mediaVejamos o resutado do modelo de classificação a partir da matriz de confusão.
y = base_treino$TAXA_PART_CAT
confusionMatrix(data = y_classe,reference = y)Confusion Matrix and Statistics
Reference
Prediction alta baixa media
alta 3318 233 1405
baixa 299 3367 1539
media 364 363 812
Overall Statistics
Accuracy : 0.6408
95% CI : (0.632, 0.6495)
No Information Rate : 0.3403
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.4581
Mcnemar's Test P-Value : < 2.2e-16
Statistics by Class:
Class: alta Class: baixa Class: media
Sensitivity 0.8335 0.8496 0.2162
Specificity 0.7878 0.7624 0.9085
Pos Pred Value 0.6695 0.6469 0.5276
Neg Pred Value 0.9017 0.9082 0.7103
Prevalence 0.3403 0.3387 0.3210
Detection Rate 0.2836 0.2878 0.0694
Detection Prevalence 0.4236 0.4449 0.1315
Balanced Accuracy 0.8106 0.8060 0.5623Agora mais um modelo de previsão para o problema com 3 classes. Neste modelo haverá 1 camada com 1 neurônio.
set.seed(1234567890)
NN1_CLASS_3 = neuralnet(
formula = TAXA_PART_CAT ~ . ,
data = cbind(MX,Y),
hidden = 1,
linear.output = FALSE,
err.fct = "ce") y_ = predict(NN1_CLASS_3,newdata = MX)
colnames(y_) = levels(Y$TAXA_PART_CAT)
head(y_) alta baixa media
1 0.88388787 0.01174733 0.2983204
2 0.84142286 0.01671020 0.3007979
3 0.74011396 0.03051298 0.3050969
4 0.33915449 0.14659327 0.3171107
5 0.73877622 0.03071704 0.3051450
6 0.02044493 0.80372381 0.3402189y_classe = apply(X = y_,MARGIN = 1,FUN = which.max)
y_classe = factor(y_classe,
levels = c(1,2,3),
labels = levels(Y$TAXA_PART_CAT))
head(y_classe) 1 2 3 4 5 6
alta alta alta alta alta baixa
Levels: alta baixa mediaconfusionMatrix(data = y_classe,reference = y)Confusion Matrix and Statistics
Reference
Prediction alta baixa media
alta 3429 257 1580
baixa 273 3452 1691
media 279 254 485
Overall Statistics
Accuracy : 0.6296
95% CI : (0.6207, 0.6383)
No Information Rate : 0.3403
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.4406
Mcnemar's Test P-Value : < 2.2e-16
Statistics by Class:
Class: alta Class: baixa Class: media
Sensitivity 0.8613 0.8711 0.12913
Specificity 0.7620 0.7462 0.93291
Pos Pred Value 0.6512 0.6374 0.47642
Neg Pred Value 0.9142 0.9187 0.69378
Prevalence 0.3403 0.3387 0.32103
Detection Rate 0.2931 0.2950 0.04145
Detection Prevalence 0.4501 0.4629 0.08701
Balanced Accuracy 0.8117 0.8086 0.53102O processo será repetido para outras quantidades de camadas e de neurônios por camada.
set.seed(1234567890)
NN2_CLASS_3 = neuralnet(
formula = TAXA_PART_CATbaixa + TAXA_PART_CATmedia ~ . ,
data = cbind(MX,MY),
hidden = 2,
linear.output = FALSE) y_ = predict(NN2_CLASS_3, newdata=MX)
head(y_) [,1] [,2] [,3]
1 0.74168166 0.02710792 0.4000357
2 0.71141592 0.03079297 0.4036914
3 0.86865225 0.02676680 0.1944077
4 0.27745514 0.13606359 0.4490239
5 0.65576716 0.03815278 0.4098970
6 0.01079596 0.77154854 0.5375764y_classe = apply(X = y_,MARGIN = 1,FUN = which.max)
head(y_classe)1 2 3 4 5 6
1 1 1 3 1 2 y_classe = factor(y_classe,
levels = c(1,2,3),
labels = levels(Y$TAXA_PART_CAT))
head(y_classe) 1 2 3 4 5 6
alta alta alta media alta baixa
Levels: alta baixa mediasummary(y_classe) alta baixa media
4560 5298 1842 confusionMatrix(data = y_classe,reference = y)Confusion Matrix and Statistics
Reference
Prediction alta baixa media
alta 3181 175 1204
baixa 308 3397 1593
media 492 391 959
Overall Statistics
Accuracy : 0.6442
95% CI : (0.6354, 0.6529)
No Information Rate : 0.3403
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.4637
Mcnemar's Test P-Value : < 2.2e-16
Statistics by Class:
Class: alta Class: baixa Class: media
Sensitivity 0.7990 0.8572 0.25532
Specificity 0.8213 0.7543 0.88885
Pos Pred Value 0.6976 0.6412 0.52063
Neg Pred Value 0.8880 0.9116 0.71627
Prevalence 0.3403 0.3387 0.32103
Detection Rate 0.2719 0.2903 0.08197
Detection Prevalence 0.3897 0.4528 0.15744
Balanced Accuracy 0.8102 0.8057 0.57209set.seed(1234567890)
NN3_CLASS_3 = neuralnet(
formula = TAXA_PART_CATbaixa + TAXA_PART_CATmedia ~ . ,
data = cbind(MX,MY),
hidden = 3,
linear.output = FALSE) y_ = predict(NN3_CLASS_3, newdata=MX)
colnames(y_) = levels(Y$TAXA_PART_CAT)
head(y_) alta baixa media
1 0.92378194 0.003092837 0.08252503
2 0.79143785 0.013899242 0.20951674
3 0.74577796 0.018556382 0.23929315
4 0.26952737 0.180579219 0.59147693
5 0.45556697 0.090175736 0.51154218
6 0.01605072 0.810773224 0.21088358y_classe = apply(X = y_,MARGIN = 1,FUN = which.max)
y_classe = factor(y_classe,
levels = c(1,2,3),
labels = levels(Y$TAXA_PART_CAT))
head(y_classe) 1 2 3 4 5 6
alta alta alta media media baixa
Levels: alta baixa mediay = base_treino$TAXA_PART_CAT
confusionMatrix(data = y_classe,reference = y)Confusion Matrix and Statistics
Reference
Prediction alta baixa media
alta 3017 180 1066
baixa 234 3241 1362
media 730 542 1328
Overall Statistics
Accuracy : 0.6484
95% CI : (0.6396, 0.657)
No Information Rate : 0.3403
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.471
Mcnemar's Test P-Value : < 2.2e-16
Statistics by Class:
Class: alta Class: baixa Class: media
Sensitivity 0.7578 0.8178 0.3536
Specificity 0.8386 0.7937 0.8399
Pos Pred Value 0.7077 0.6700 0.5108
Neg Pred Value 0.8704 0.8948 0.7332
Prevalence 0.3403 0.3387 0.3210
Detection Rate 0.2579 0.2770 0.1135
Detection Prevalence 0.3644 0.4134 0.2222
Balanced Accuracy 0.7982 0.8058 0.5967Ao final, lembre-se de salvar os objetos gerados com tanto custo computacional.
saveRDS(NN0_REG,file="salvos//NN0_REG.rds")
saveRDS(NN1_REG,file="salvos//NN1_REG.rds")
saveRDS(NN2_REG,file="salvos//NN2_REG.rds")
saveRDS(NN3_REG,file="salvos//NN3_REG.rds")
saveRDS(NN22_REG,file="salvos//NN22_REG.rds")saveRDS(NN0_CLASS_2,file="salvos//NN0_CLASS_2.rds")
saveRDS(NN1_CLASS_2,file="salvos//NN1_CLASS_2.rds")
saveRDS(NN2_CLASS_2,file="salvos//NN2_CLASS_2.rds")
saveRDS(NN3_CLASS_2,file="salvos//NN3_CLASS_2.rds")saveRDS(NN0_CLASS_3,file="salvos//NN0_CLASS_3.rds")
saveRDS(NN1_CLASS_3,file="salvos//NN1_CLASS_3.rds")
saveRDS(NN2_CLASS_3,file="salvos//NN2_CLASS_3.rds")
saveRDS(NN3_CLASS_2,file="salvos//NN3_CLASS_2.rds")