4 Árvores de Decisão
Esse capítulo tem como objetivo apresentar o Modelo de Árvore de Decisão, tanto para Regressão quanto para Classificação.
Um modelo de Árvore de Decisão é um algoritmo de Aprendizado de Máquina supervisionado usado para resolver problemas de Classificação ou de Regressão. Ele é chamado de “Árvore de Decisão” porque o algoritmo cria uma estrutura de dados de árvore binária, que é construída a partir de decisões tomadas a partir dos dados de treinamento.
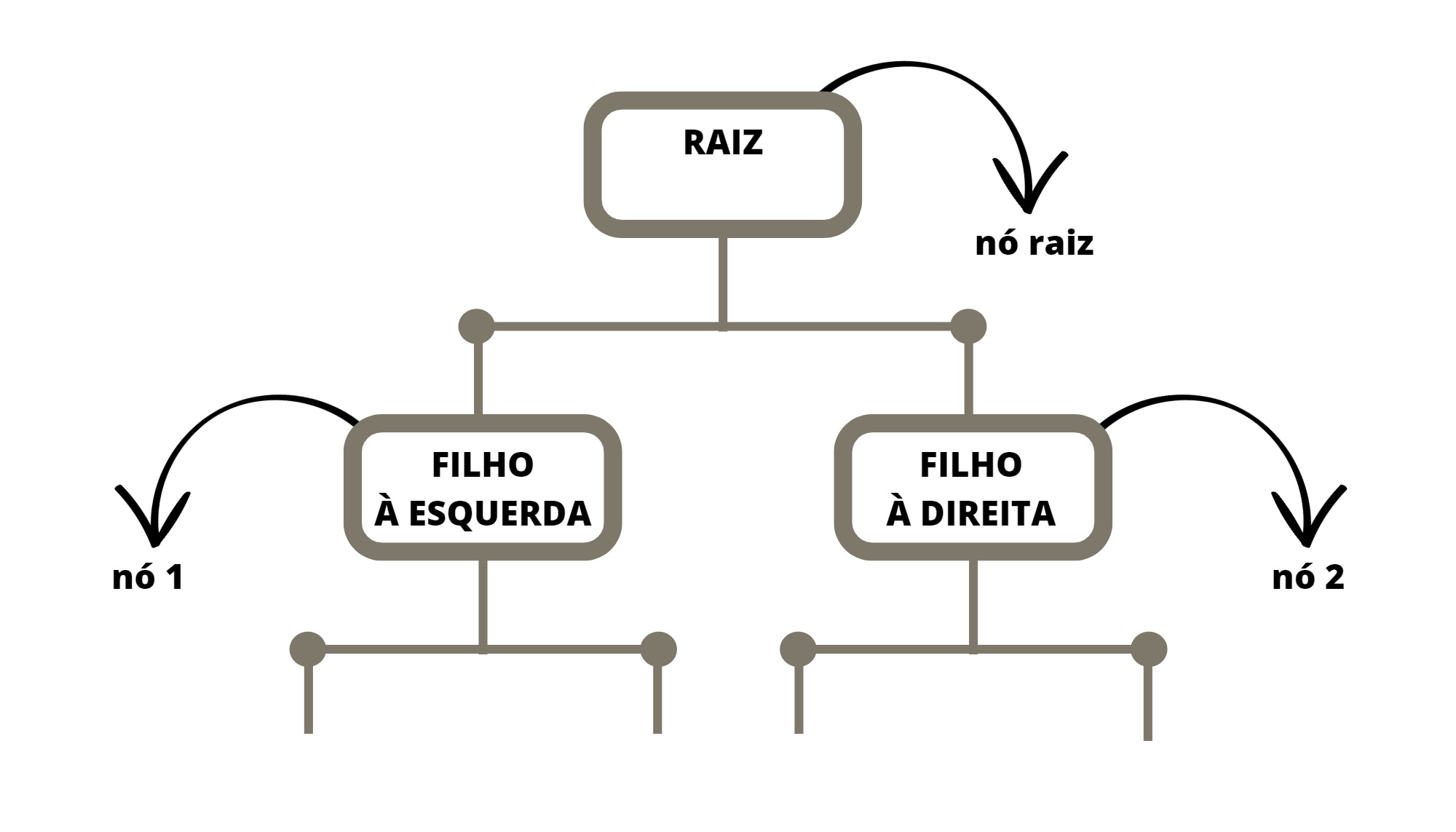
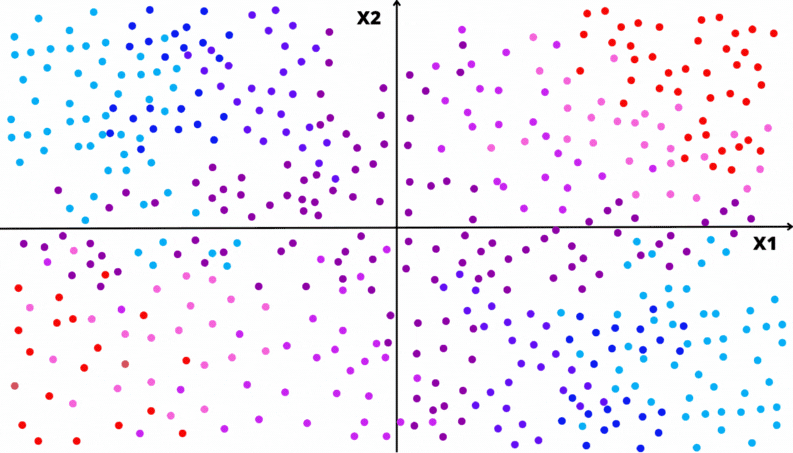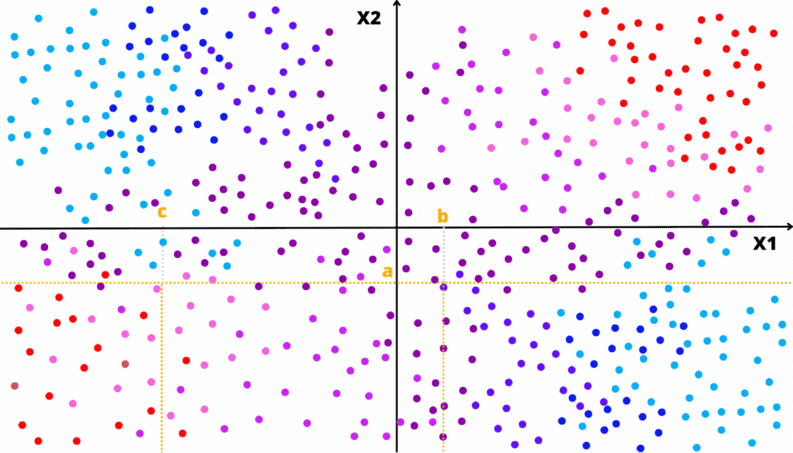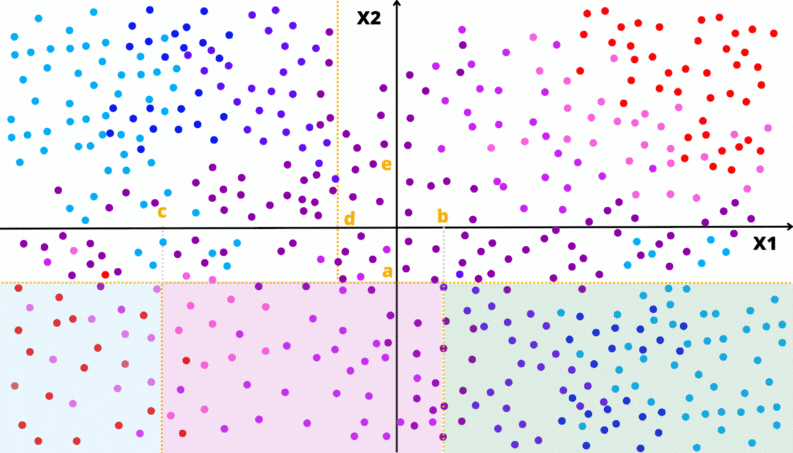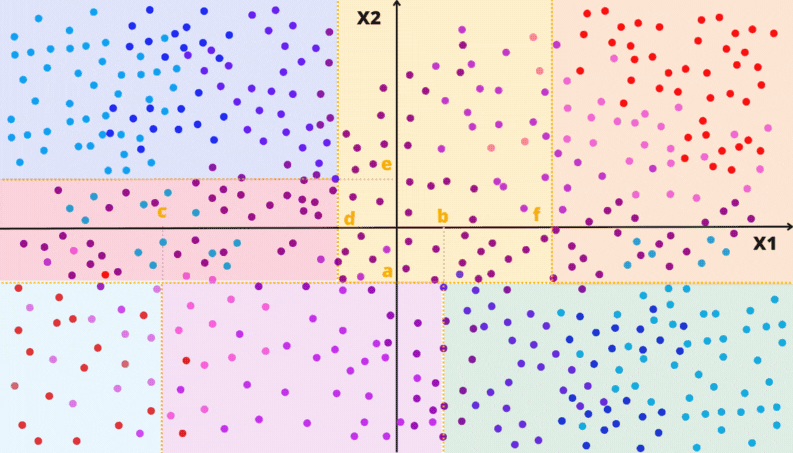
A ideia básica do modelo de Árvore de Decisão é dividir o conjunto de dados de um certo nó em subconjuntos menores, de acordo com características relevantes dos dados que chegaram no nó em questão. Estas divisões são feitas de maneira hierárquica, começando pelo nó raiz, que recebe a base de treino completa.
É chamado de raiz o primeiro nó de uma árvore de decisão. Este nó recebe todos as instâncias da base de treino e é a partir dele que começa a divisão. O nó raiz dá origem a dois filhos, o filho à direita e o filho à esquerda. Cada filho pode ser um nó, caso ele tenha dois outros filhos, ou uma folha, caso ele não tenha filhos. Cada nó define uma partição dos dados de entrada e cada folha define uma região no domínio.
Suponha uma base de dados supervisionada cuja variável alvo é \(Y\) e as covariáveis são \(X_1\), \(X_2\), \(\ldots\) \(X_p\). Suponha também a base de dados é formada por \(n\) observações. Desta forma \(Y_i\) é o valor da variável alvo para a observação \(i\) e \(X_{i,j}\) é o valor da covariável \(j\) para a observação \(i\). Posto isso, segue a idéia principal da árvore para prever o valor de \(Y\).
No nó raiz “chegam” todos as observações. Busca-se então a covariável \(X_j\) e o valor de \(cte\) tais que, a partição da base definida pelas observações \(A_1 = \{ i | X_{i,j} \le cte \}\) e \(A_2 = \{ i | X_{i,j} > cte \}\) apresente a menor “impureza” entre todos as possíveis partições formadas com diferentes valores de \(j\) e \(cte\). Essa medida de impureza depende se a árvore é de classificação ou de reggressão.
Uma das principais vantagens do modelo de árvore de decisão é sua capacidade de lidar com dados categóricos e numéricos, bem como sua interpretabilidade. As árvores de decisão podem ser facilmente visualizadas e compreendidas, o que ajuda a explicar as decisões tomadas pelo modelo.
No entanto, as árvores de decisão também têm algumas limitações. Elas podem ser sensíveis a pequenas variações nos dados de treinamento, o que pode levar a problemas de sobreajuste (overfiting). Para mitigar isso, técnicas como a poda da árvore ou o uso de conjuntos de árvores, como o algoritmo Random Forest, podem ser aplicadas.
No R o pacote para trabalhar com árvores de decisão é o rpart (Therneau and Atkinson 2022) e a função que cria as estruturas de árvore também se chama rpart.
4.1 Árvores de Regressão
As árvores de regressão são métodos baseados em árvores de decisão para o caso da variável alvo ser quantitativa.
As animações apresentadas nas Figuras @ref(fig:gifarvorereg) e @ref(fig:gifparticaoreg) ilustram um problema de regressão com duas covariáveis. A variável alvo é quantitativa e está representada pela escala de cor. Por exemplo, quanto mais perto do vermelho, maior o valor; quanto mais perto do azul, menor o valor.

4.1.1 Medida de impureza
Para um conjunto de variávels quantitativas as maneiras mais comuns de medir a impureza dos valores são o MSE (Mean Squase Erro) ou o RSS (Residual Sum of Squares), este inclusive usado no material (James et al. 2013).
Seja \(Y\) a variável alvo e \(Y_i\) a \(i\)-ésima observação dela. Considere também \(R\) uma região do \(\mathbb{R}^p\), \(I\) os índices dos dados de entrada que pertencem à \(R\) e \(n\) a quantidade de elementos em \(I\), isto é, o número de pontos da base de entrada que pertencem à \(R\). A média dos valores da base de entrada em \(R\) pode ser definida por: \[ \bar{Y} = \sum_{i \in I} \dfrac{Y_i}{n}. \] E, para o caso das árovers de regressão, os valores de \(MSE\) e do \(RSS\) na região \(R\) são:
\[ MSE_R = \dfrac{\sum_{i \in I} (Y_i - \bar{Y})^2}{n} \ \ \ \ \text{e} \ \ \ \ RSS_R = \sum_{i \in I} (Y_i - \bar{Y})^2 \]
Entendemos que um método de regressão é bom quando os valores de \(MSE\) ou \(SSE\) são baixos. Ou seja, para dois modelos de classificação pra mesma base de dados e variável alvo, aquele com menor valor de \(MSE\) e \(RSS\) será o mais adequado para o problema.
4.1.2 Algoritmo
Define-se os critérios de parada, que em geral são: um valor limite para o MSE ou RSS; a quantidade de elementos que chegaram ao nó; ou a profundidade da árvore.
Considere \(X\) o conjunto dos dados de entrada e \(X_j\) as covariáveis do problema.
Escolhe-se a variável \(j\) e o valor \(s\) tais que minimizam a soma dos MSE (ou RSS) nos conjuntos \(R_1 = \{X|X_j < s\}\) e \(R2 = \{X|X_j \ge s\}\).
Sejam \(Y_1\) os valores das variáveis alvo dos pontos de \(X\) que pertencem à \(R_1\) e \(Y_2\) os valores das variáveis alvo dos pontos de \(X\) que pertencem à \(R_2\)
Verifique se um dos critérios de parada foi atingido pelos elementos de \(Y_1\). Se sim, este nó é uma folha e FIM. Se não, faça \(X = R_1\) e volte para o passo 3.
Verifique se um dos critérios de parada foi atingido pelos elementos de \(Y_2\). Se sim, este nó é uma folha e FIM. Se não, faça \(X = X_2\) e volte para o passo 3.
4.1.3 Como realizar previsão
Uma vez que a árvore de regressão é construída, ela pode ser utilizada para fazer previsões para novos exemplos. Isso é feito percorrendo a árvore a partir da raiz até chegar a uma folha correspondente. O valor previsto é geralmente a média dos valores da variável alvo das amostras de treinamento que pertencem a essa folha.
4.1.4 Vamos praticar
Segue-se analisando a base com informações sobre as escolas. O arquivo que foi salvo depois da limpeza da base pode ser recuperado e a base de treino final obtida.
library(tidyverse)
library(rpart)
base_treino = readRDS(file="salvos//base_treino_final.rds")O problema proposto será prever a nota média de matemática de uma escola dada informações sobre a escola. O modelo é ajustado com a função rpart, do pacote rpart (Therneau and Atkinson 2022) e é informado para a função que o problema é de regressão através do argumento method = "reg".
Lembre-se de retirar da base de treino as demais variáveis alvo e também as variáveis de identificação.
TREE_REG = rpart(formula = NU_MEDIA_MT ~
SG_UF_ESCOLA +
TP_DEPENDENCIA_ADM_ESCOLA +
TP_LOCALIZACAO_ESCOLA +
NU_MATRICULAS +
INSE +
PC_FORMACAO_DOCENTE +
NU_TAXA_PERMANENCIA +
NU_TAXA_REPROVACAO +
NU_TAXA_ABANDONO +
PORTE_ESCOLA, data = base_treino)Carregar o pacote rpart.plot (Milborrow 2022) gera gráficos mais bonitos.
library("rpart.plot")
rpart.plot(TREE_REG,type=5,cex=1)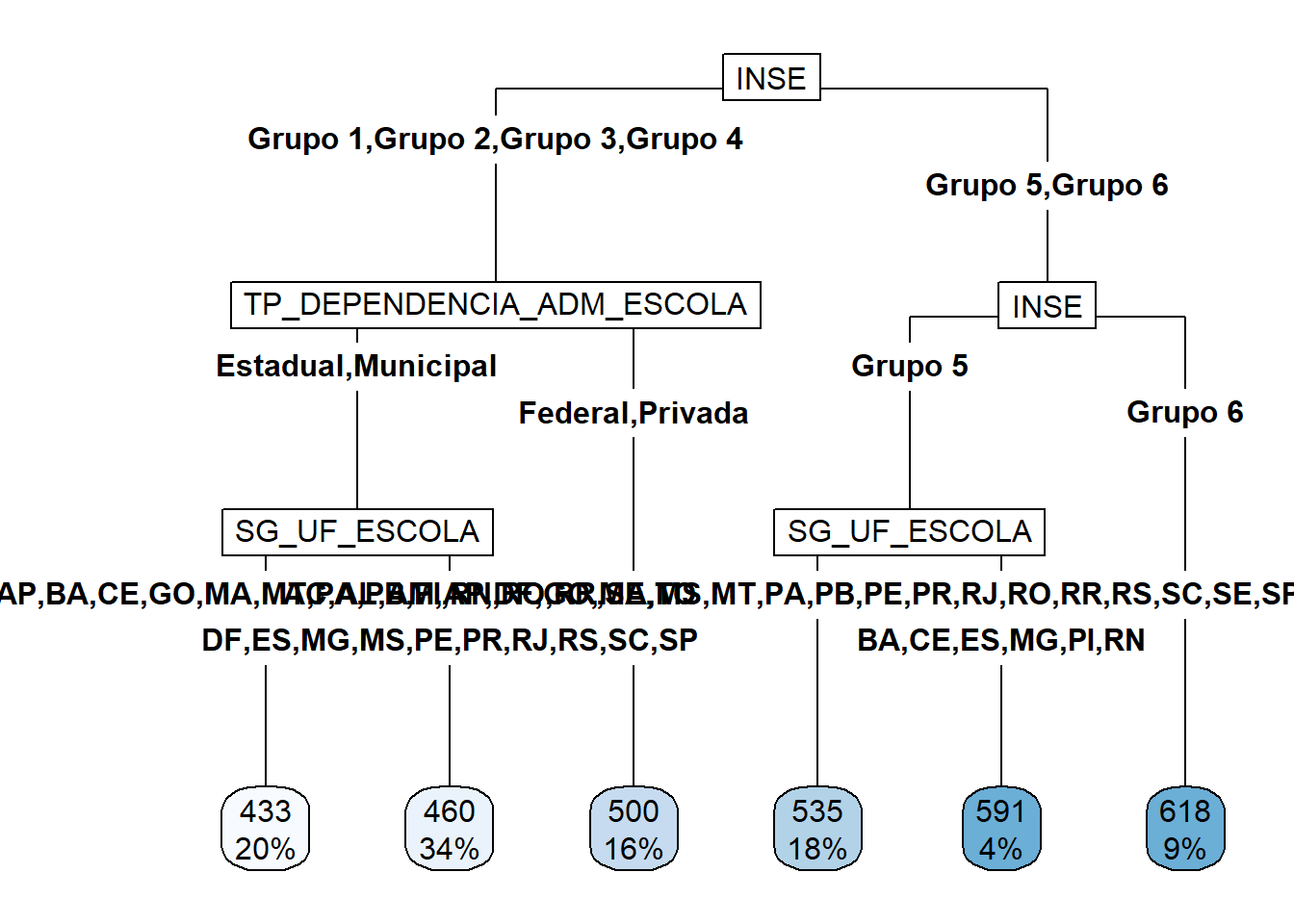
Ainda é possível obter as variáveis mais relevantes para o problema com a função varImp do pacote caret (Kuhn 2022). A importância (overall) de uma variável é calculada com base na redução da medida de impureza quando esta variável é removida da base. Para isso são feitas combinações das covariáveis e, para cada combinação, uma árvore é gerada. Então calcula-se a média dos \(MSE\) ou \(SSE\) das árvores geradas com a covariável no ajuste. Depois calcula-se a média dos \(MSE\) ou \(SSE\) das árovores geradas sem a covariável no ajuste. A diferença entre as duas médias é o valor do overall (Kuhn 2008). Quando maior este valor, maior a importância da variável para o problema.
imp <- caret::varImp(TREE_REG, scale = FALSE)
importancia = tibble(overall = imp$Overall,
var = rownames(imp))
importancia |> arrange(desc(overall))# A tibble: 10 × 2
overall var
<dbl> <chr>
1 1.06 INSE
2 0.918 TP_DEPENDENCIA_ADM_ESCOLA
3 0.623 NU_TAXA_ABANDONO
4 0.569 SG_UF_ESCOLA
5 0.0992 NU_TAXA_REPROVACAO
6 0.0990 PC_FORMACAO_DOCENTE
7 0.0529 NU_TAXA_PERMANENCIA
8 0 TP_LOCALIZACAO_ESCOLA
9 0 NU_MATRICULAS
10 0 PORTE_ESCOLA Para calcular os valores previstos das notas das escolas e então encontrar valores de medidas dos erros pode-se usar os comandos a seguir.
y_ = predict(TREE_REG)
y = base_treino$NU_MEDIA_MT
(RSS = sum((y - y_)^2))[1] 18890237(EMQ = mean((y-y_)^2))[1] 1614.55(R2 = 1 - sum((y-y_)^2)/sum((y-mean(y))^2))[1] 0.6576849Para que possamos usar este resultado no futuro e não seja preciso realizar o código para chegar nele, vamos salvar o objeto com o modelo criado.
saveRDS(TREE_REG,file = "salvos//TREE_REG.rds")4.2 Árvores de Classificação
As árvores de classificação são métodos baseados em árvores de decisão para o caso da variável alvo ser qualitativa. Neste caso a medida de impureza que define as partições e o método de prever a variável alvo precisam ser pensados para o problema de classificação.
As animações apresentadas nas Figuras @ref(fig:gifarvore) e @ref(fig:gifparticao) ilustram um problema de classificação com duas covariáveis. A variável alvo, aqui qualitativa, é representada pela cor do ponto: vermelho ou azul.

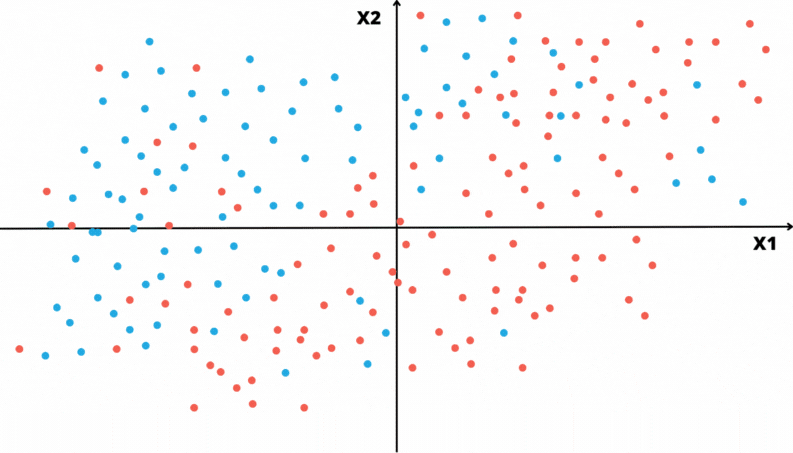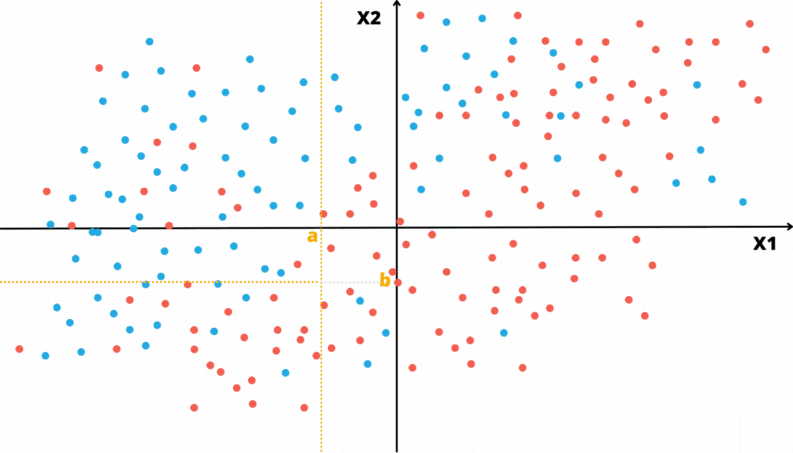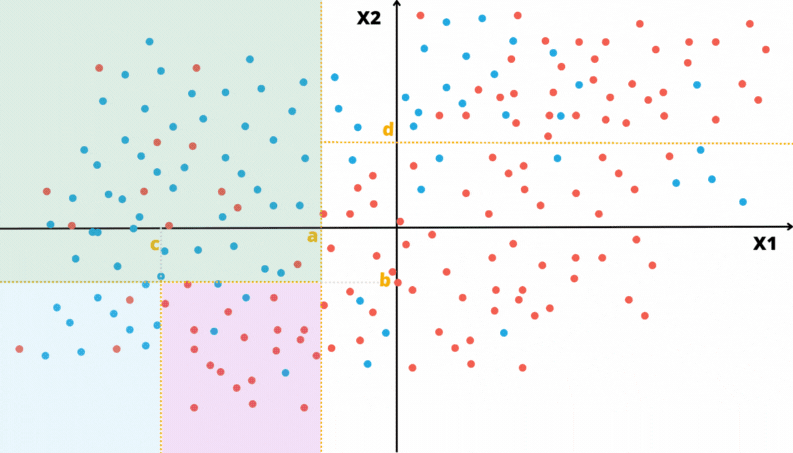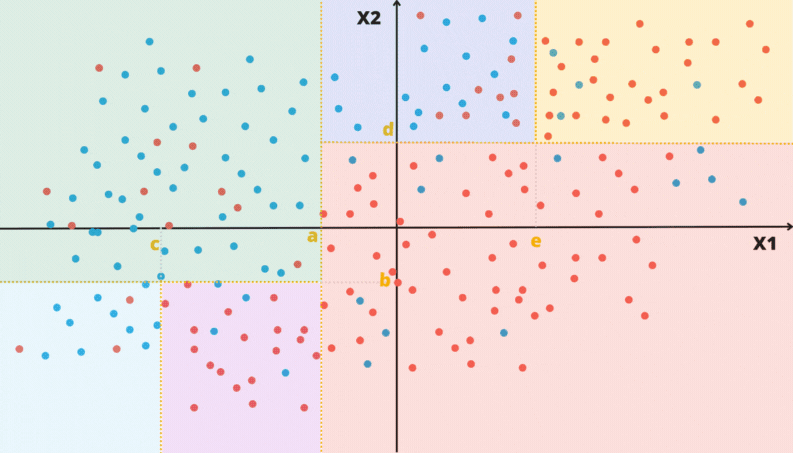
4.2.1 Medida de impureza
Índice de GINI para problemas com duas classes
No caso dos problemas de classificação a medida de impureza comumente usada é o índice de GINI. O índice de GINI fornece uma medida de impureza para um dada região. Se o problema for de duas classes, essa medida é definida por
\[ G_R = 1 - q^2 - (1-q)^2 \]
sendo \(q\) a proporção das observações da classe de referência dentro da região \(R\).
A Figura @ref(fig:exgini) apresenta diferentes regiões com diferentes proporção entre duas classes. Considere a classe vermelha como a de referência.
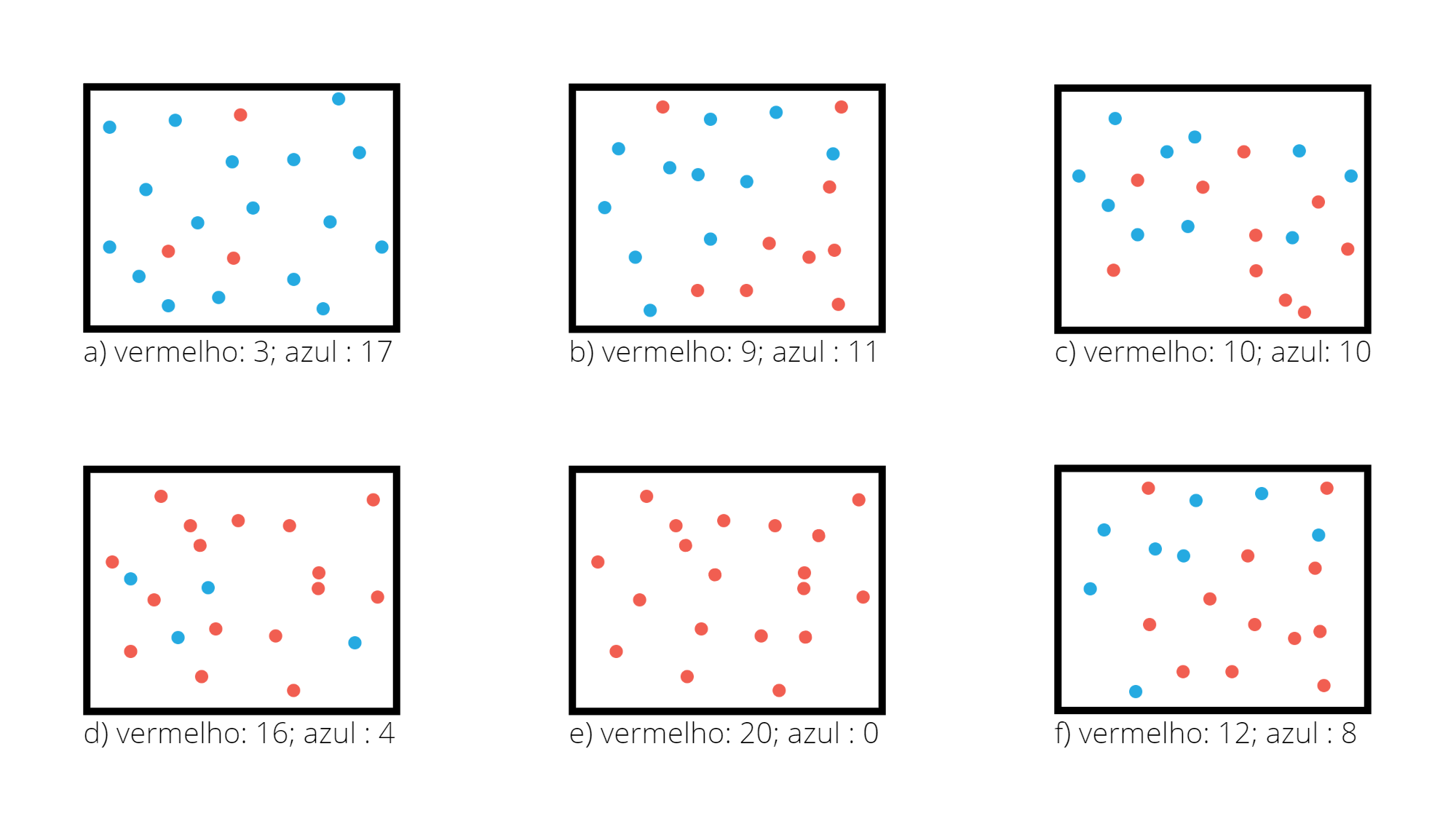
Para a região da Figura @ref(fig:exgini).a o valor do índice de Gini é \(0,255\).
q = 3/20
1 - q^2 - (1-q)^2[1] 0.255Para a região da Figura @ref(fig:exgini).b o valor do índice de Gini é \(0,495\).
q = 9/20
1 - q^2 - (1-q)^2[1] 0.495Para a região da Figura @ref(fig:exgini).c o valor do índice de Gini é \(0,5\).
q = 10/20
1 - q^2 - (1-q)^2[1] 0.5Para a região da Figura @ref(fig:exgini).d o valor do índice de Gini é \(0,32\).
q = 16/20
1 - q^2 - (1-q)^2[1] 0.32Para a região da Figura @ref(fig:exgini).e o valor do índice de Gini é \(0,0\).
q = 20/20
1 - q^2 - (1-q)^2[1] 0Para a região da Figura @ref(fig:exgini).f o valor do índice de Gini é \(0,48\).
q = 12/20
1 - q^2 - (1-q)^2[1] 0.48Se a região contiver apenas valores de uma das classes, isso seria uma região com impureza nula, \(q=1\) ou \(q=0\) e com isso \(G_R = 0\). O caso oposto, considerado com maior impureza, seria quando a região contém uma proporção igual de observações das duas classes, neste caso \(q=0,5\) e \(G_R = 1 - 0,25 - 0,25 = 0,5\). Para o caso de existirem apenas duas classes, o valor máximo do índice de Gini é \(0,5\) e ele ocorre quando \(q=0,5\).
Índice de GINI para problemas com três classes ou mais
Se o problema for multi-classes, a expressão do índice de Gini será generalizada. Suponha um problema de \(k\) classes. O índice de Gini na região \(R\) é definido por
\[ G_R = 1 - \sum_{i=1}^k q_i^2 \]
sendo \(q_i\) a proporção das observações da região \(R\) que pertencem à classe \(i\).
A Figura @ref(fig:exgini4) apresenta diferentes regiões com diferentes proporção entre quatro classes.
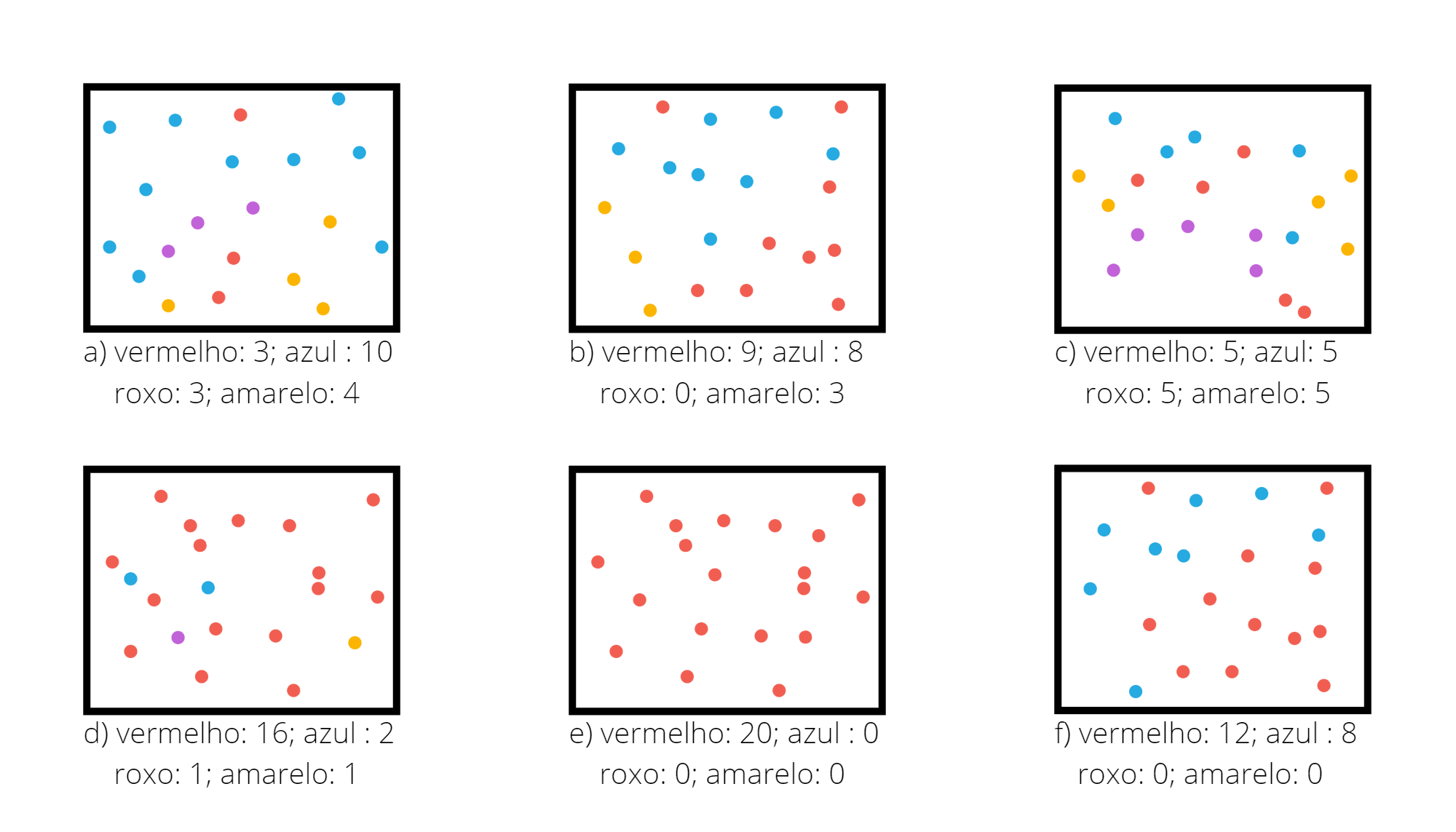
Para a região da Figura @ref(fig:exgini4).a o valor do índice de Gini é \(0,684125\).
q1 = 3/20
q2 = 10/20
q3 = 3/20
q4 = 4/20
1 - q1^2 - q2^2 - q3^3 - q4^2[1] 0.684125Para a região da Figura @ref(fig:exgini4).b o valor do índice de Gini é \(0,615\).
q1 = 9/20
q2 = 8/20
q3 = 0/20
q4 = 3/20
1 - q1^2 - q2^2 - q3^2 - q4^2[1] 0.615Para a região da Figura @ref(fig:exgini4).c o valor do índice de Gini é \(0,75\).
q1 = 5/20
q2 = 5/20
q3 = 5/20
q4 = 5/20
1 - q1^2 - q2^2 - q3^2 - q4^2[1] 0.75Para a região da Figura @ref(fig:exgini4).d o valor do índice de Gini é \(0,345\).
q1 = 16/20
q2 = 2/20
q3 = 1/20
q4 = 1/20
1 - q1^2 - q2^2 - q3^2 - q4^2[1] 0.345Para a região da Figura @ref(fig:exgini).e o valor do índice de Gini é \(0,0\).
q1 = 20/20
q2 = 0/20
q3 = 0/20
q4 = 0/20
1 - q1^2 - q2^2 - q3^2 - q4^2[1] 0Para a região da Figura @ref(fig:exgini).f o valor do índice de Gini é \(0,48\).
q1 = 12/20
q2 = 8/20
q3 = 0/20
q4 = 0/20
1 - q1^2 - q2^2 - q3^2 - q4^2[1] 0.48No método de Árvores de Classificação toda vez que uma partição é realizada e para isso são escolhidos os valores de \(X_j\) e \(cte\), estes valores são escolhidos de forma que minimizam a soma dos índices de Gini das duas partições criadas. Por exemplo, suponha que no nó em questão chegaram as observações \(A\). Quando é escolhido \(j\) e \(cte\) é definida uma partição para \(A\) de forma que \(A_1 = \{ X_i \in A \ | \ x_{i,j} \le cte \}\) e \(A_2 = \{ X_i \in A \ | \ x_{i,j} > cte \}\). São então calculados os índices de Gini em \(A_1\) e \(A_2\), denominados \(G_{A_1}\) e \(G_{A_2}\). A escolha de \(X_j\) e \(cte\) é feita de forma a minimizar a soma \(G_{A_1} + G_{A_2}\).
4.2.2 Algoritmo
Define-se os critérios de parada, que em geral são: um valor limite para o indice de Gini; a quantidade de elementos que chegaram ao nó; ou a profundidade da árvore.
Considere \(X\) o conjunto dos dados de entrada e \(X_j\) as covariáveis do problema.
Escolhe-se a variável \(j\) e o valor \(s\) tais que minimizam a soma dos índices Gini nas regiões \(R_1 = \{X|X_j < s\}\) e \(R_2 = \{X|X_j \ge s\}\).
Sejam \(Y_1\) os valores das variáveis alvo dos pontos de \(X\) que pertencem à \(R_1\) e \(Y_2\) os valores das variáveis alvo dos pontos de \(X\) que pertencem à \(R_2\).
Verifique se um dos critérios de parada foi atingido pelos elementos de \(Y_1\). Se sim, este nó é uma folha e FIM. Se não, faça \(X = R_1\) e volte para o passo 3.
Verifique se um dos critérios de parada foi atingido pelos elementos de \(Y_2\). Se sim, este nó é uma folha e FIM. Se não, faça \(X = X_2\) e volte para o passo 3.
4.2.3 Como realizar previsões
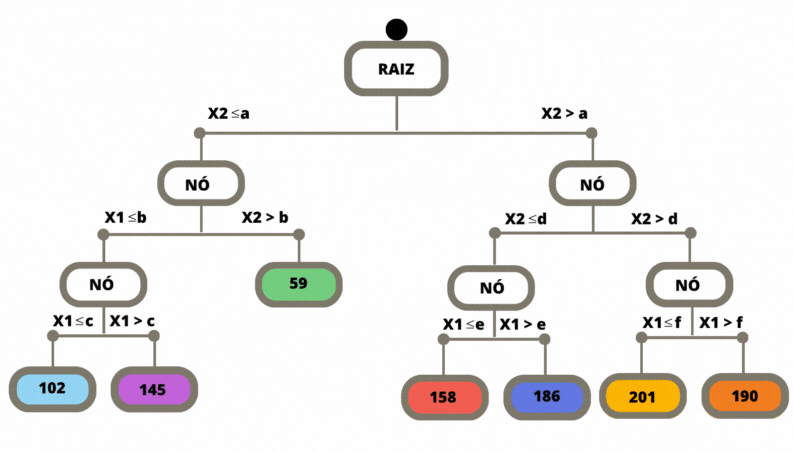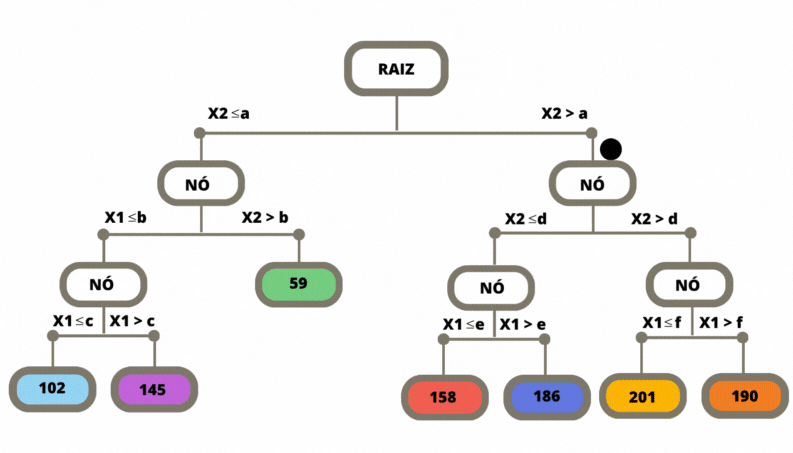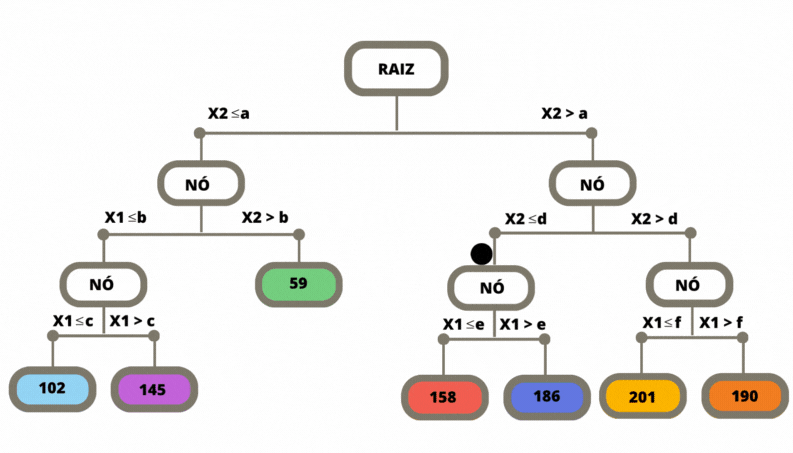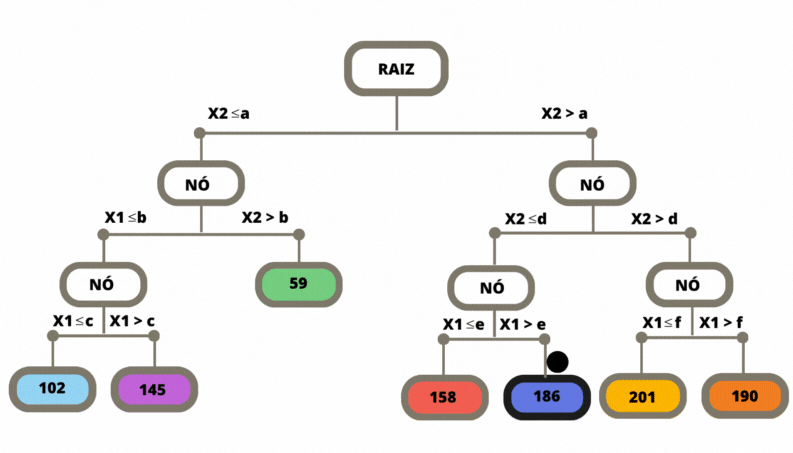
Uma vez a árvore construída, ela pode ser usada para prever a classse da variável alvo de novas observações. O dado de entrada percorre a árvore, seguindo os ramos que correspondem às características das covariáveis, até alcançar uma folha. Veja Figura @ref(fig:prevtree).
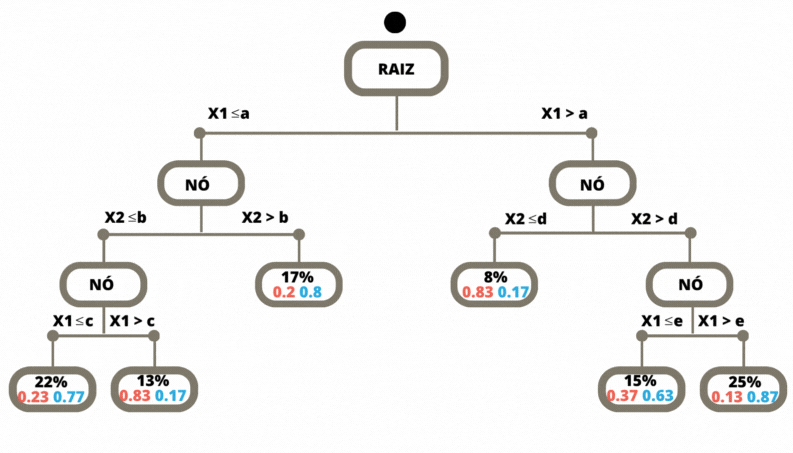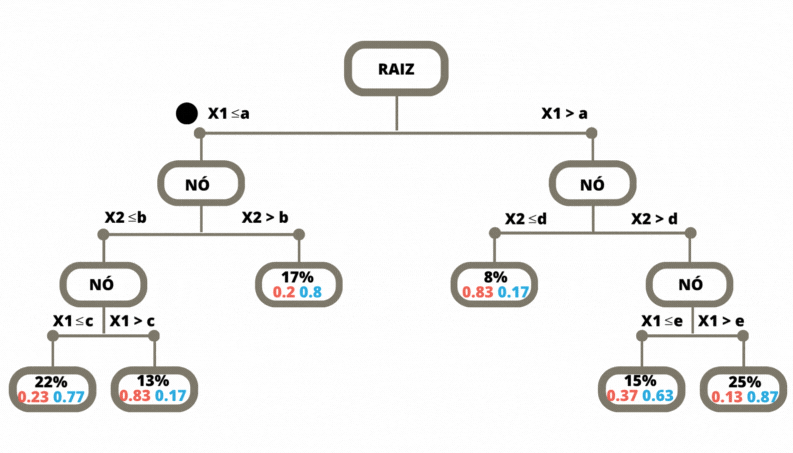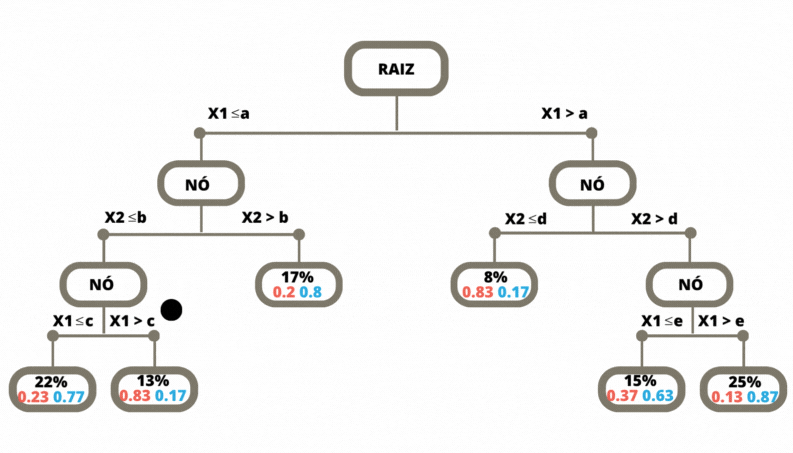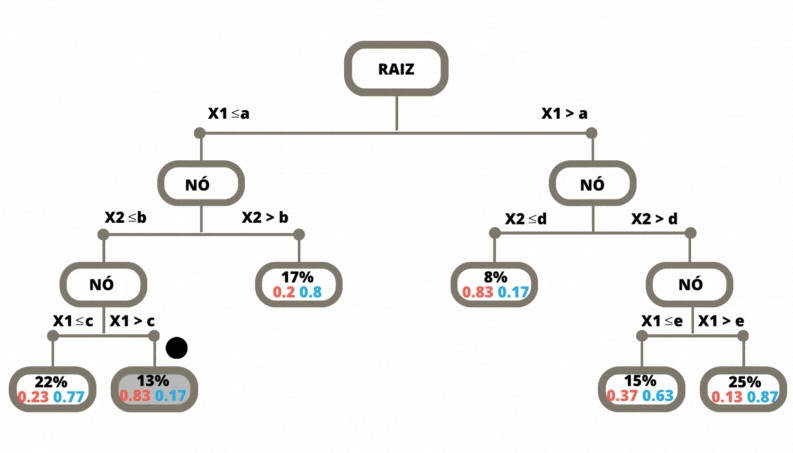
Os métodos de classificação, em geral, não retornam a classe prevista e sim um número no intervalo \([0,1]\) para cada classe, que indica a probabilidade daquela classe ser a classe correta. Para as árvores de decisão a nova observação, para a qual não conhecemos a sua classe, percorre a árvore de acordo com os valores das suas covariáveis (atributos). Ao chegar em uma folha é verificado então, considerando os dados de treinamento, a proporção de cada uma das classes que chegaram nesta mesma folha. Para este exemplo o método retorna os valores \((0.83, 0.17)\).
4.2.4 Vamos praticar
Segue-se analisando a base com informações sobre as escolas. Aquele arquivo que foi salvo depois do Capítulo 2 pode ser recuperado e a base de treino final obtida.
library(tidyverse)
library(rpart)
base_treino = readRDS(file="salvos//base_treino_final.rds")4.2.5 Classificação Binária
O problema proposto é classificar uma escola quanto a sua taxa de participação. Vamos tentar identificar as escolas com baixa participação.
base_treino = base_treino |>
mutate(TAXA_PART_BAIXA =
ifelse(base_treino$TAXA_PART_CAT == "baixa",1,0))O modelo é ajustado com a função rpart, do pacote rpart (Therneau and Atkinson 2022).
TREE_CLASS_2 <- rpart(formula = TAXA_PART_BAIXA ~
SG_UF_ESCOLA +
TP_DEPENDENCIA_ADM_ESCOLA +
TP_LOCALIZACAO_ESCOLA +
NU_MATRICULAS +
INSE +
PC_FORMACAO_DOCENTE +
NU_TAXA_PERMANENCIA +
NU_TAXA_REPROVACAO +
NU_TAXA_ABANDONO +
PORTE_ESCOLA,
data = base_treino,
method = "class"
)Use o pacote rpart.plot (Milborrow 2022) gera gráficos mais bonitos do que os básicos do pacote rpart (Therneau and Atkinson 2022).
library("rpart.plot")
rpart.plot(TREE_CLASS_2,type=5,cex=1)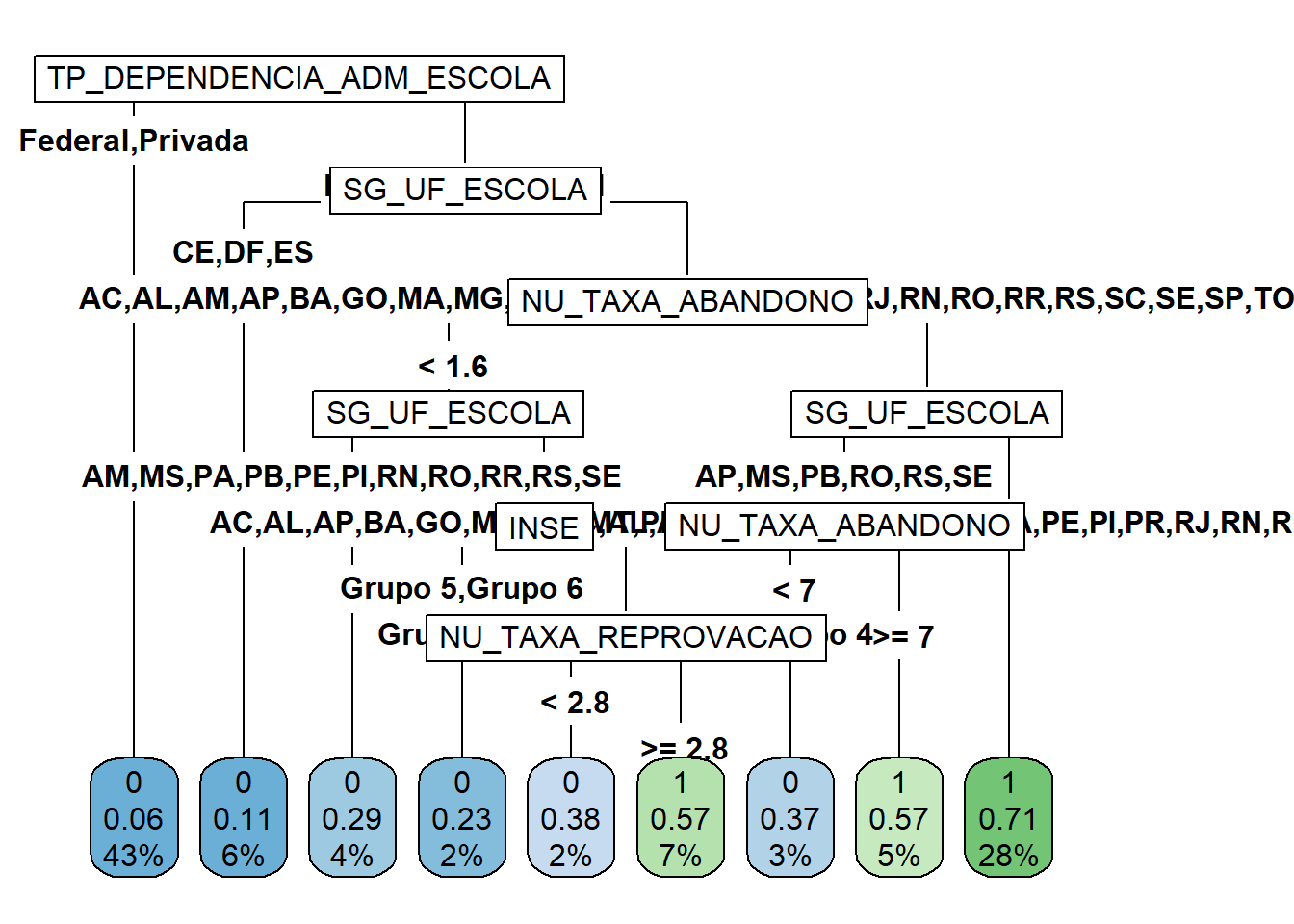
Ainda é possível obter as variáveis mais relevantes para o problema com a função varImp do pacote caret (Kuhn 2022). A importância (overall) de uma variável é calculada com base na redução do índice de Gini quando esta variável é removida da base. Para isso são feitas combinações das covariáveis e, para cada combinação, uma árvore é gerada. Então calcula-se a média do índice de Gini nas regiões definidas pelas árvores que usaram a covariável no ajuste. Depois calcula-se a média do índice de Gine das regiões definidas pelas árvores criadas sem esta covariável. A diferença entre as duas médias é o valor do overall (Kuhn 2008). Quando maior este valor, maior a importância da variável para o problema.
imp <- caret::varImp(TREE_CLASS_2, scale = FALSE)
importancia = tibble(overall = imp$Overall,
var = rownames(imp))
importancia |> arrange(desc(overall))# A tibble: 10 × 2
overall var
<dbl> <chr>
1 1327. TP_DEPENDENCIA_ADM_ESCOLA
2 1220. NU_TAXA_ABANDONO
3 771. INSE
4 487. SG_UF_ESCOLA
5 395. NU_MATRICULAS
6 331. NU_TAXA_REPROVACAO
7 48.6 PC_FORMACAO_DOCENTE
8 18.9 NU_TAXA_PERMANENCIA
9 9.84 PORTE_ESCOLA
10 0 TP_LOCALIZACAO_ESCOLA Novamente é usada a função predict para realizar previsões. No caso da árvore de classificação, a previsão será uma matriz com 2 colunas. A primeira coluna guarda a probabilidade da classe 0 e a segunda a probabilidade da classe 1.
y_ = predict(TREE_CLASS_2)
class(y_)[1] "matrix" "array" dim(y_)[1] 11700 2head(y_) 0 1
1 0.9372997 0.06270032
2 0.9372997 0.06270032
3 0.7088036 0.29119639
4 0.6322751 0.36772487
5 0.9372997 0.06270032
6 0.4346350 0.56536503Para gerar a curva ROC, o pacote pROC (Robin et al. 2011) .
y = base_treino$TAXA_PART_BAIXA
library(pROC)
ROC = roc(response = y,predictor = y_[,"1"])
plot.roc(ROC,
print.auc = TRUE,
print.thres = TRUE)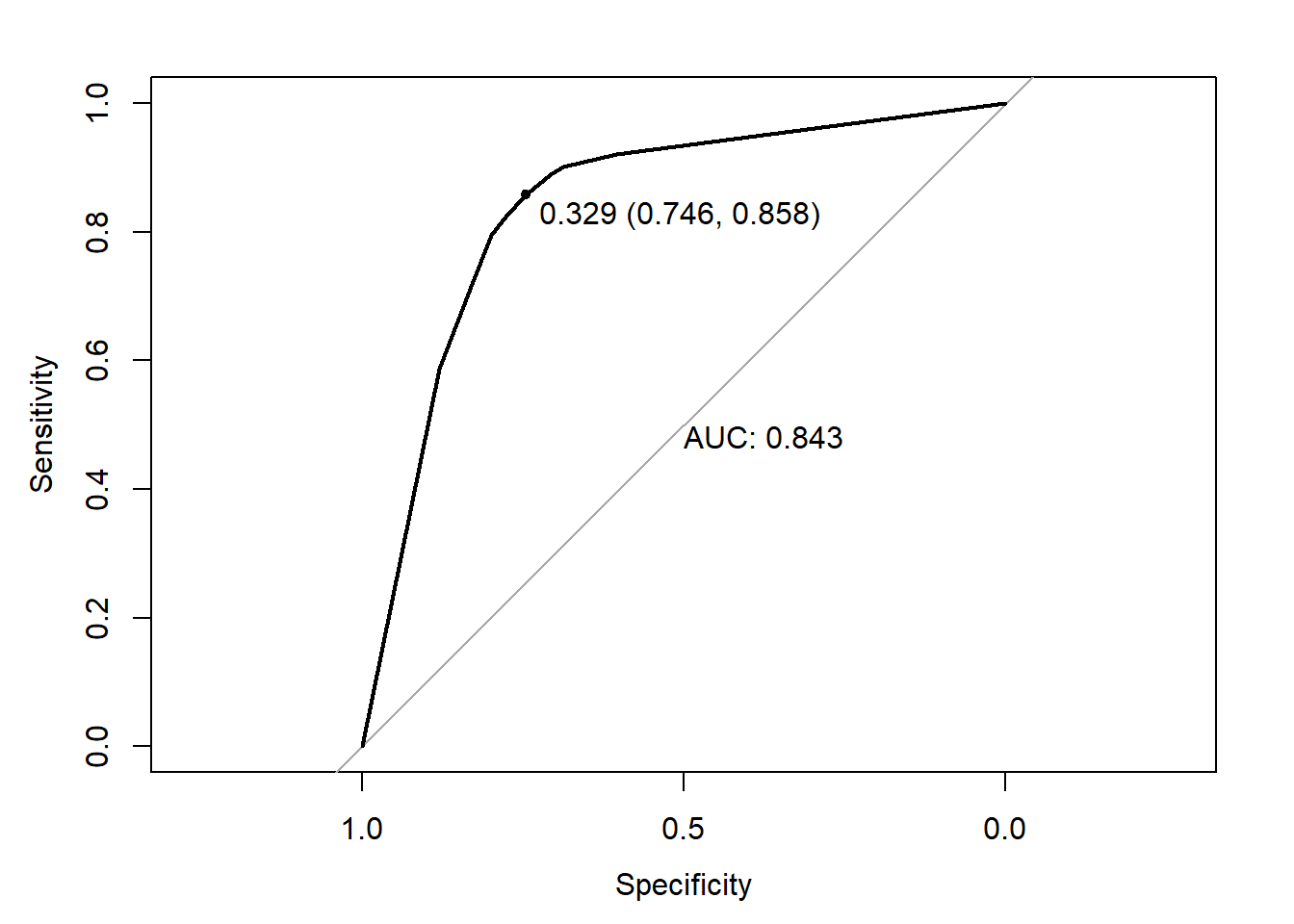
y_classe = ifelse(y_[,"1"]>0.329,1,0)
library(caret)
confusionMatrix(as.factor(y),as.factor(y_classe))Confusion Matrix and Statistics
Reference
Prediction 0 1
0 5768 1969
1 564 3399
Accuracy : 0.7835
95% CI : (0.7759, 0.7909)
No Information Rate : 0.5412
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.5552
Mcnemar's Test P-Value : < 2.2e-16
Sensitivity : 0.9109
Specificity : 0.6332
Pos Pred Value : 0.7455
Neg Pred Value : 0.8577
Prevalence : 0.5412
Detection Rate : 0.4930
Detection Prevalence : 0.6613
Balanced Accuracy : 0.7721
'Positive' Class : 0
Para que possamos usar este resultado no futuro e não seja preciso realizar o código para chegar nele, vamos salvar o objeto com o modelo criado.
saveRDS(TREE_CLASS_2,file = "salvos//TREE_CLASS_2.rds")Classificação multi-classes
Agora, em vez de identificar se uma escola tem baixa taxa de participação ou não, vamos tentar classificá-la em baixa, média ou alta taxa de participação.
TREE_CLASS_3 <- rpart(formula = TAXA_PART_CAT ~
SG_UF_ESCOLA +
TP_DEPENDENCIA_ADM_ESCOLA +
TP_LOCALIZACAO_ESCOLA +
NU_MATRICULAS +
INSE +
PC_FORMACAO_DOCENTE +
NU_TAXA_PERMANENCIA +
NU_TAXA_REPROVACAO +
NU_TAXA_ABANDONO +
PORTE_ESCOLA,
data = base_treino,
method = "class")
)Esse processo com três classe já fica bem mais custoso do que o com duas classes.
rpart.plot(TREE_CLASS_3,type=5,cex=1)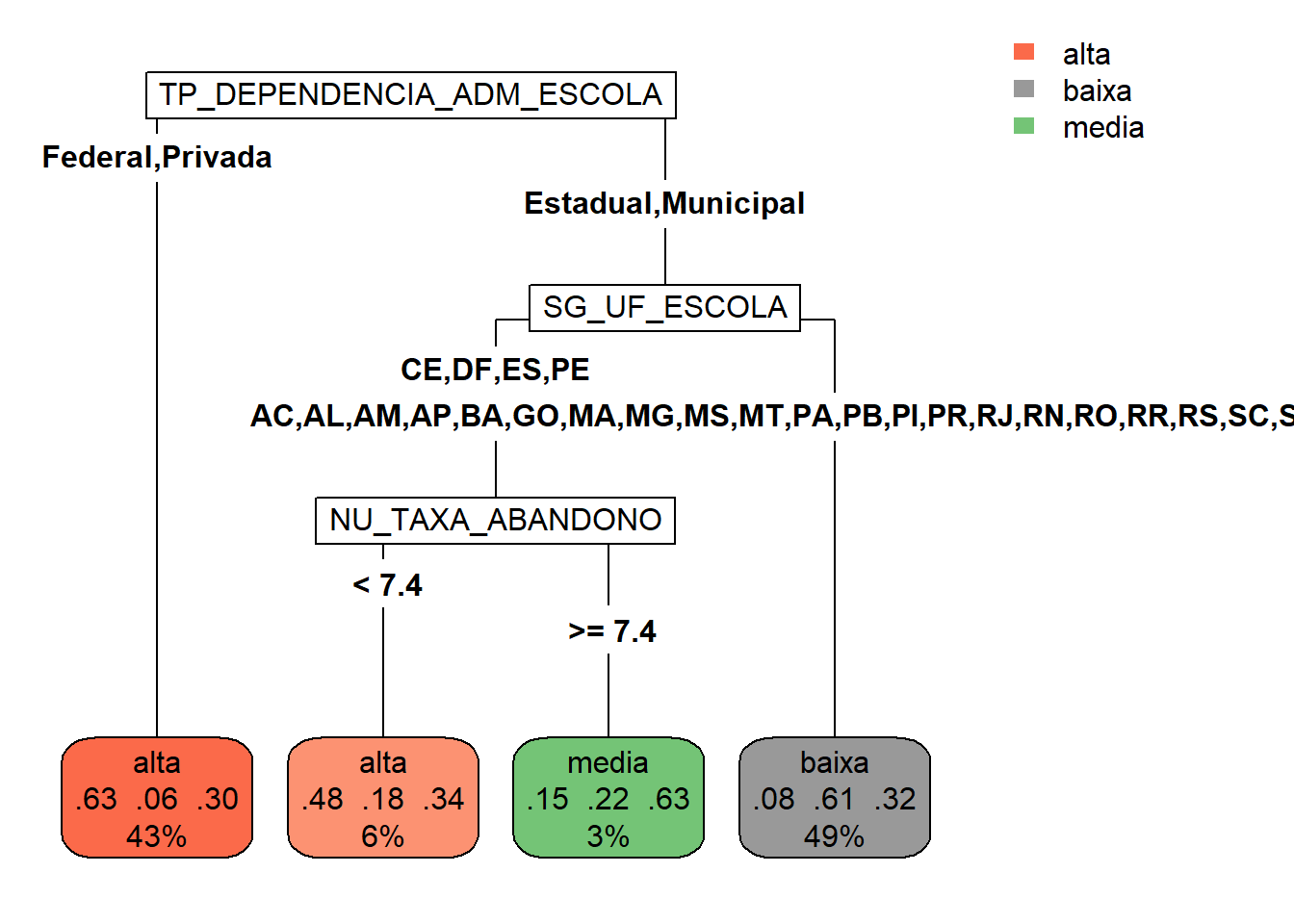
As variáveis mais relevantes para o problema são apresentadas com o código a seguir, o mesmo usado para os problemas de duas classes.
imp <- caret::varImp(TREE_CLASS_3, scale = FALSE)
importancia = tibble(overall = imp$Overall,
var = rownames(imp))
importancia |> arrange(desc(overall))# A tibble: 10 × 2
overall var
<dbl> <chr>
1 1410. TP_DEPENDENCIA_ADM_ESCOLA
2 1141. NU_TAXA_ABANDONO
3 722. INSE
4 372. NU_TAXA_REPROVACAO
5 270. NU_MATRICULAS
6 256. SG_UF_ESCOLA
7 26.5 NU_TAXA_PERMANENCIA
8 0 TP_LOCALIZACAO_ESCOLA
9 0 PC_FORMACAO_DOCENTE
10 0 PORTE_ESCOLA Usando a função predict agora temos como saída uma matriz com 3 colunas.
y_ = predict(TREE_CLASS_3)
head(y_) alta baixa media
1 0.63261218 0.06270032 0.3046875
2 0.63261218 0.06270032 0.3046875
3 0.07839355 0.60592774 0.3156787
4 0.07839355 0.60592774 0.3156787
5 0.63261218 0.06270032 0.3046875
6 0.07839355 0.60592774 0.3156787y_classe = ifelse(y_[,"alta"]>y_[,"baixa"] & y_[,"alta"]>y_[,"media"],"alta", ifelse(y_[,"baixa"]>y_[,"media"],"baixa","media"))
y_classe = factor(y_classe)
levels(y_classe)[1] "alta" "baixa" "media"head(y_classe) 1 2 3 4 5 6
alta alta baixa baixa alta baixa
Levels: alta baixa mediay = base_treino$TAXA_PART_CAT
head(y)[1] alta alta alta alta media baixa
Levels: alta baixa mediaconfusionMatrix(data = y_classe, reference = y)Confusion Matrix and Statistics
Reference
Prediction alta baixa media
alta 3487 439 1757
baixa 447 3455 1800
media 47 69 199
Overall Statistics
Accuracy : 0.6103
95% CI : (0.6014, 0.6192)
No Information Rate : 0.3403
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.4105
Mcnemar's Test P-Value : < 2.2e-16
Statistics by Class:
Class: alta Class: baixa Class: media
Sensitivity 0.8759 0.8718 0.05298
Specificity 0.7155 0.7096 0.98540
Pos Pred Value 0.6136 0.6059 0.63175
Neg Pred Value 0.9179 0.9153 0.68757
Prevalence 0.3403 0.3387 0.32103
Detection Rate 0.2980 0.2953 0.01701
Detection Prevalence 0.4857 0.4874 0.02692
Balanced Accuracy 0.7957 0.7907 0.51919Para que possamos usar este resultado no futuro e não seja preciso realizar o código para chegar nele, vamos salvar o objeto com o modelo criado.
saveRDS(TREE_CLASS_3,file = "salvos//TREE_CLASS_3.rds")