22 Assignment 3 (Guide)

For this assignment let $[a]$ be a beta distribution with $\alpha=2$ and $\beta=1$ (i.e., $a\sim\text{beta}(\alpha=2,\beta=1)$).

1. The first half involves using analytical mathematics to find the Metropolis-Hastings ratio. Realize that this problem differs in format from the applications in Ch. 4 of BBM2L. The important thing to realize is that we are sampling from $[a]$ and not from the posterior distribution of a Bayesian model. The Metropolis-Hastings ratio is

$$mh = \frac{[a^{(*)}][a^{(k-1)}|a^{(*)}]}{[a^{(k-1)}][a^{(*)}|a^{(k-1)}]},$$ where $a^{(*)}$ is the proposed value of $a$ and $a^{(k-1)}$ is the previous (or initial) value of $a$. Since we are using a uniform PDF for the proposal distribution, the Metropolis-Hastings ratio simplifies to

$$mh = \frac{[a^{(*)}]}{[a^{(k-1)}]},$$ because $[a^{(k-1)}|a^{(*)}]=1$ and $[a^{(*)}|a^{(k-1)}]=1$. Now substitute the PDF for $a$ into the Metropolis-Hastings ratio and you get

$$mh = \frac{2a^{*}}{2a^{(k-1)}}.$$ This which simplifies to

$$mh = \frac{a^{*}}{a^{(k-1)}}.$$

The R code below implements the Metropolis-Hastings algorithm.

a.init <- 0.01
K <- 5000
samples <- matrix(,K,1)
samples[1,] <- a.init

for(k in 2:K){
  a.old <- samples[k-1,]
  a.try <- runif(1)
  mh <- a.try/a.old
  keep <- ifelse(mh>1,1,rbinom(1,1,mh))
  samples[k,] <- ifelse(keep==1,a.try,a.old) 
}

2. The R code below does what is asked in question #2.

   hist(samples[-c(1:1000)],freq=FALSE,xlab=expression(italic(a)),ylab=expression("["*italic(a)*"]"),main="")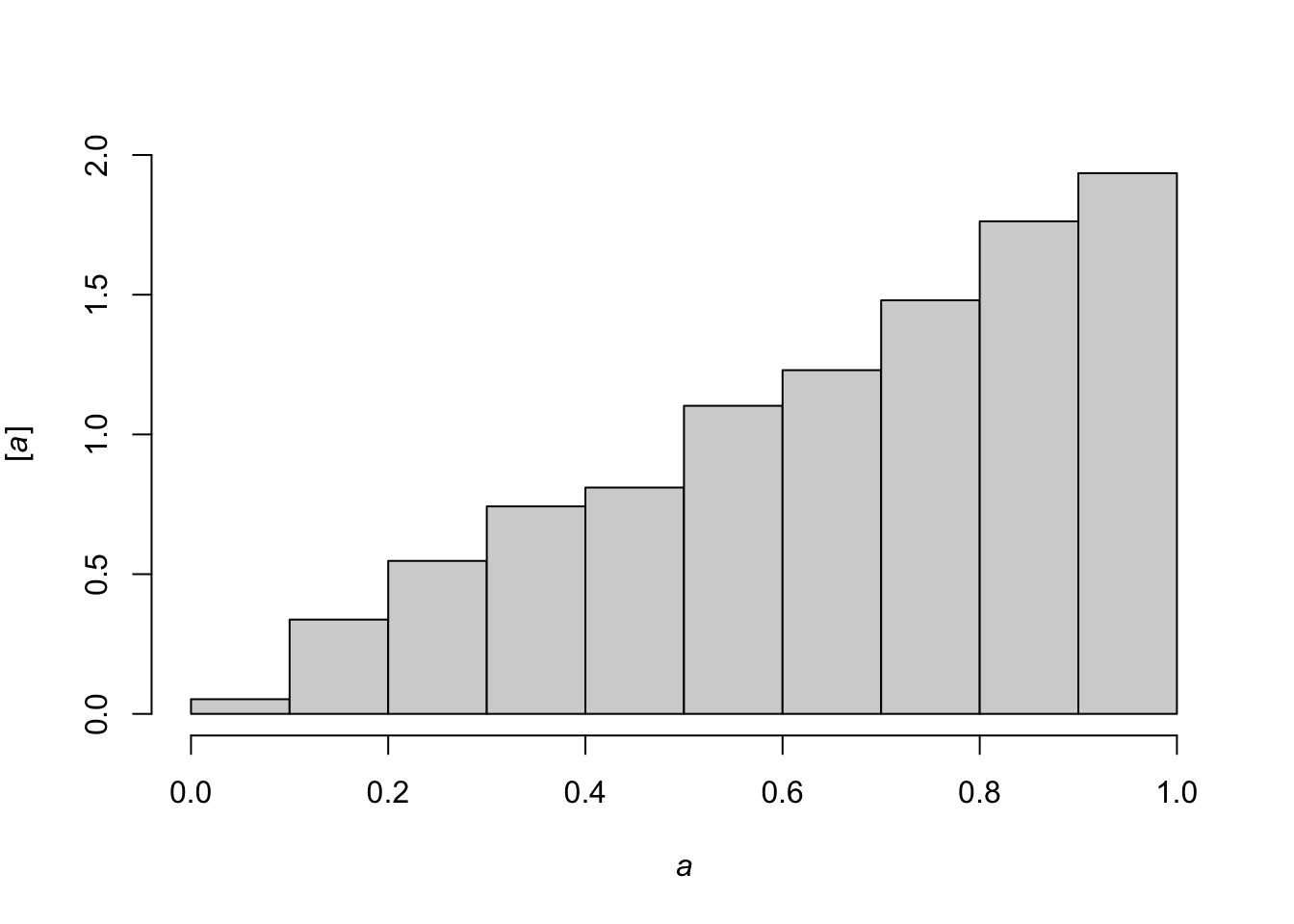

   

3. The R code below provides a Monte Carlo approximation to the integral

$$\int_{0}^{1}a[a]da$$ where [a] is a beta(2,1) distribution with probability mass function $[a]=2a$.

mean(samples[-c(1:1000)])

## [1] 0.6793755

4. Trevor needs to finish this