3 Day 3 (June 5)
3.1 Announcements
If office hours times don’t work for you let me know
Recommended reading
- Chapters 1 and 2 (pgs 1 - 28) in Linear Models with R
- Chapter 2 in Applied Regression and ANOVA Using SAS
3.2 Matrix algebra
- Column vectors
- \(\mathbf{y}\equiv(y_{1},y_{2},\ldots,y_{n})^{'}\)
- \(\mathbf{x}\equiv(x_{1},x_{2},\ldots,x_{n})^{'}\)
- \(\boldsymbol{\beta}\equiv(\beta_{1},\beta_{2},\ldots,\beta_{p})^{'}\)
- \(\boldsymbol{1}\equiv(1,1,\ldots,1)^{'}\)
- In R
## [,1] ## [1,] 1 ## [2,] 2 ## [3,] 3 - Matrices
- \(\mathbf{X}\equiv(\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{p})\)
- In R
## [,1] [,2] ## [1,] 1 4 ## [2,] 2 5 ## [3,] 3 6 - Vector multiplication
- \(\mathbf{y}^{'}\mathbf{y}\)
- \(\mathbf{1}^{'}\mathbf{1}\)
- \(\mathbf{1}\mathbf{1}^{'}\)
- In R
## [,1] ## [1,] 14 - Matrix by vector multiplication
- \(\mathbf{X}^{'}\mathbf{y}\)
- In R
## [,1] ## [1,] 14 ## [2,] 32 - Matrix by matrix multiplication
- \(\mathbf{X}^{'}\mathbf{X}\)
- In R
## [,1] [,2] ## [1,] 14 32 ## [2,] 32 77 - Matrix inversion
- \((\mathbf{X}^{'}\mathbf{X})^{-1}\)
- In R
## [,1] [,2] ## [1,] 1.4259259 -0.5925926 ## [2,] -0.5925926 0.2592593 - Determinant of a matrix
- \(|\mathbf{I}|\)
- In R
## [,1] [,2] [,3] ## [1,] 1 0 0 ## [2,] 0 1 0 ## [3,] 0 0 1## [1] 1 - \(|\mathbf{I}|\)
- Quadratic form
- \(\mathbf{y}^{'}\mathbf{S}\mathbf{y}\)
- Derivative of a quadratic form (Note \(\mathbf{S}\) is a symmetric matrix; e.g., \(\mathbf{X}^{'}\mathbf{X}\))
- \(\frac{\partial}{\partial\mathbf{y}}\mathbf{y^{'}\mathbf{S}\mathbf{y}}=2\mathbf{S}\mathbf{y}\)
- Other useful derivatives
- \(\frac{\partial}{\partial\mathbf{y}}\mathbf{\mathbf{x^{'}}\mathbf{y}}=\mathbf{x}\)
- \(\frac{\partial}{\partial\mathbf{y}}\mathbf{\mathbf{X^{'}}\mathbf{y}}=\mathbf{X}\)
3.3 Introduction to linear models
What is a model?
What is a linear model?
Most widely used model in science, engineering, and statistics
Vector form: \(\mathbf{y}=\beta_{0}+\beta_{1}\mathbf{x}_{1}+\beta_{2}\mathbf{x}_{2}+\ldots+\beta_{p}\mathbf{x}_{p}+\boldsymbol{\varepsilon}\)
Matrix form: \(\mathbf{y}=\mathbf{X}\boldsymbol{\beta}+\boldsymbol{\varepsilon}\)
Which part of the model is the mathematical model
Which part of the model makes the linear model a “statistical” model
Visual
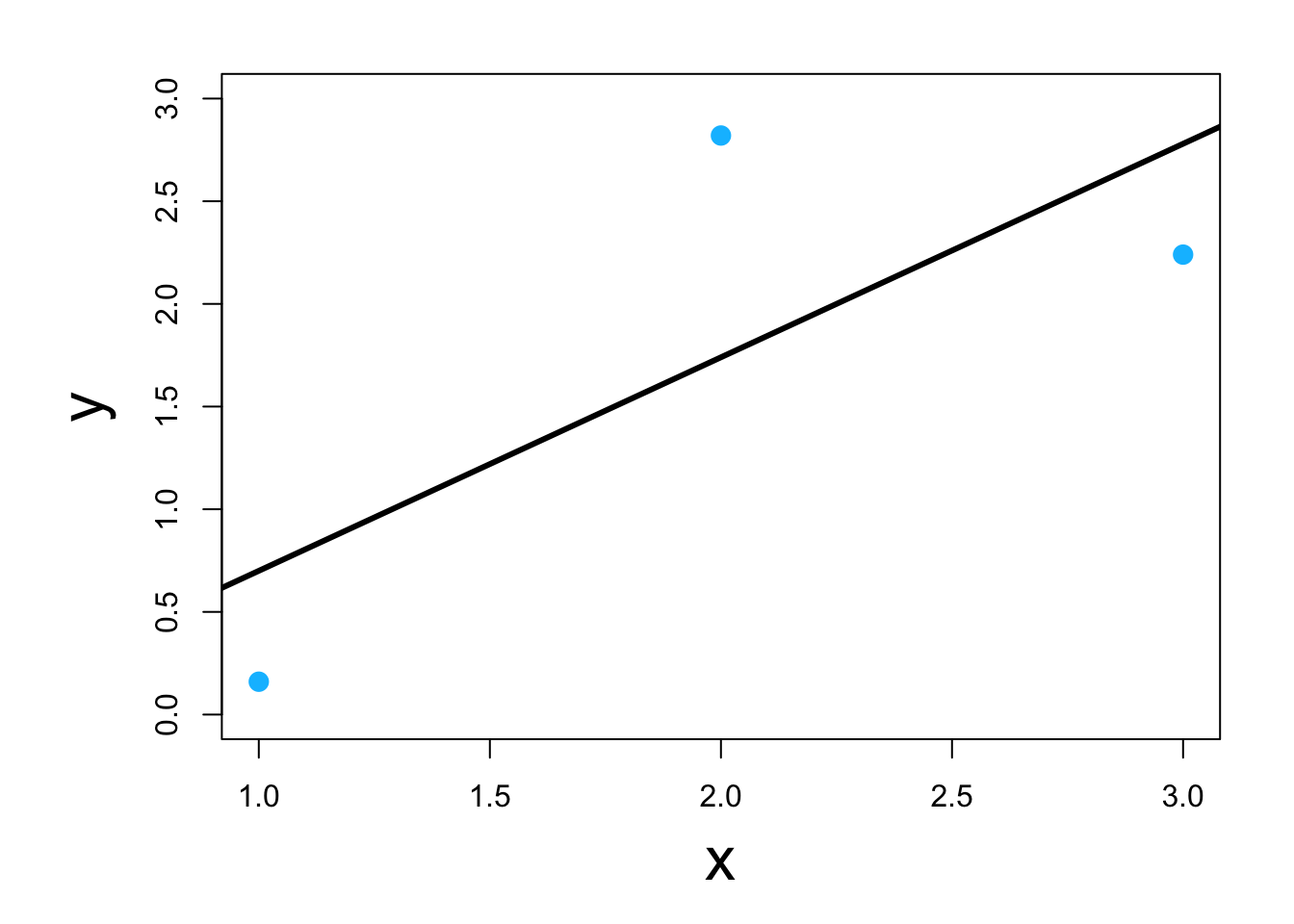
Which of the four below are a linear model \[\mathbf{y}=\beta_{0}+\beta_{1}\mathbf{x}_{1}+\beta_{2}\mathbf{x}^{2}_{1}+\boldsymbol{\varepsilon}\] \[\mathbf{y}=\beta_{0}+\beta_{1}\mathbf{x}_{1}+\beta_{2}\text{log(}\mathbf{x}_{1}\text{)}+\boldsymbol{\varepsilon}\] \[\mathbf{y}=\beta_{0}+\beta_{1}e^{\beta_{2}\mathbf{x}_{1}}+\boldsymbol{\varepsilon}\] \[\mathbf{y}=\beta_{0}+\beta_{1}\mathbf{x}_{1}+\text{log(}\beta_{2}\text{)}\mathbf{x}_{1}+\boldsymbol{\varepsilon}\]
Why study the linear model?
- Building block for more complex models (e.g., GLMs, mixed models, machine learning, etc)
- We know the most about it