23 SÍNTESIS

A manera de síntesis, se presenta una función de baja complejidad, en la que todas las instrucciones que se usan han sido cubiertas en el presente libro. Se espera que, tras un estudio juicioso, el usuario esté en capacidad de elaborar funciones similares que satisfagan sus necesidades.

Esta función construye un diagrama con la media y alguna medida de dispersión, para una variable numérica, acorde con los niveles de algún criterio de clasificación.

A continuación, se detallan sus argumentos:

`groups`	Criterio de agrupamiento (nombre o número de columna; def: 1).
`y`	Variable (nombre o número de columna; def: 2).
`data`	Data frame con la variable y el criterio de agrupamiento (def: `data`).
`type`	Tipo de barras de error: `"de"`: Desviación estándar (por defecto). `"ee"`: Error estándar. `"ic"`: Intervalo de confianza del 95 %.
`pooled`	Estimador promedio ponderado (def: `F`).
`k`	Ancho de los bigotes (def: 0.1).
`tit`	Título principal opcional.
`xlab`	Título opcional para la abscisa.
`ylab`	Título opcional para la ordenada.
`line`	Línea de tendencia que une las medias (def: `FALSE`).
`...`	Otros argumentos aplicables.

Mediante el presente ejemplo, se ilustran algunas estrategias frecuentemente utilizadas en las funciones de R y, en general, en cualquier lenguaje de programación.

Realización de tareas comunes, sin importar el valor de los parámetros. En este caso, tales tareas se realizan en la sección de definición de grupos y estadísticas por grupo.
Realización de tareas diferenciadas, acorde con el valor de algún parámetro. Esto se logra mediante el uso de condicionales. En el presente ejemplo, tales condicionales direccionan a tareas diferentes, dependiendo de los valores traspasados (escritos por el usuario) para el tipo de medida de dispersión y para la forma en que se calcula (conjunta o individual).
Verificación de situaciones contingentes. En el presente ejemplo, se utiliza este recurso en dos ocasiones. En el primer caso, para verificar que el tipo de medida de dispersión solicitada por el usuario sí sea una de las que se han programado en la función. De no ser así, se muestra un aviso en el que se indica cuáles son las medidas válidas y se detiene la función. Este recurso de verificación de situaciones contingentes también se utiliza para evaluar que todos los grupos tengan más de una lectura, en caso de que el usuario haya solicitado cálculos individuales dentro de cada grupo (pooled = F). Igualmente podría haberse programado un mensaje de error y la detención de la función. No obstante, se optó por modificar el parámetro en cuestión, para obtener las medidas de dispersión grupales a partir de la varianza promedio ponderada, presentando el correspondiente mensaje de advertencia.

Cabe destacar el uso del argumento especial ..., mediante el cual pueden incorporarse parámetros que, aunque no aparecen explícitamente en grafBar, serían aplicables en algunas de las funciones internas.

Este argumento debe aparecer tanto en la definición de la función (en la definición de grafBar, en este caso), como en las funciones internas a las que se desee traspasar el valor de tales argumentos; en este caso, se usa en las funciones points, lines y segments.

Mediante la incorporación de este argumento queda abierta la posibilidad de que el usuario personalice el gráfico. Así, si en lugar de un gráfico con las líneas que la función segments traza por defecto (líneas negras, continuas, de ancho 1), el usuario deseara líneas con otras características, bastaría con suministrar tales argumentos al invocar la función grafBar. Si quisiera, por ejemplo, líneas rojas, discontinuas, de ancho 1.5 y además quisiera que el tamaño del símbolo fuera el doble del que se usaría por defecto, incluiría los siguientes argumentos adicionales al invocar la función grafBar, aunque estos no aparezcan explícitamente en la definición de la función:

col = 'red', lty = 5, lwd = 1.5, cex = 2

Vale la pena destacar también el recurso utilizando mediante la función par, que permite definir valores por defecto para algunos parámetros gráficos, sin que estos aparezcan explícitamente como argumentos en la definición de la función principal, manteniéndola así más limpia. En el presente ejemplo, al definir par(pch = 19), se proporciona un valor por defecto para el símbolo mediante el cual se representan las medias (círculo relleno). Sin embargo, la incorporación del argumento especial triple punto en la función points deja abierta la posibilidad de cambiar cualquiera de los parámetros gráficos que no haya sido definido explícitamente.

grafBar <- function (groups = 1, y = 2, data = NULL, type = 'de', pooled = F,
                     k = 0.1, tit = NULL, xlab = NULL, ylab = NULL, line = F,
                     ...) {
  
  # Verificación del tipo de prueba -------------------------------------------
  if (!any(type == c('de', 'ee', 'ic'))) {
    cat('\n', 'Debe elegir uno de los siguientes tipos de dispersión:',
        '\n', '\n')
    cat("'de' : Desviación estándar (por defecto)", '\n')
    cat("'ee' : Error estándar", '\n')
    cat("'ic' : Intervalo de confianza del 95%", '\n', '\n')
    stop("Valor type = '", type,"' no reconocido")
  }
  
  # Lectura de base de datos por defecto --------------------------------------
  if (is.null(data))
    data <- .GlobalEnv$data

  # Definición de grupos y estadísticos por grupo -----------------------------
  y        <- substitute(y)
  groups   <- substitute(groups)
  data     <- data[!is.na(data[[y]]), ]  # Eliminación de valores perdidos
  nombre.y <- names(data[y])             # Nombre de la variable
  nombre.g <- names(data[groups])        # Nombre del grupo
  y        <- data[[y]]                  # Variable
  groups   <- factor(data[[groups]])     # Grupo (criterio de clasificación)
  n.g      <- length(levels(groups))     # Número de grupos
  med.g    <- tapply(y, groups, mean)    # Media por grupo
  v.g      <- tapply(y, groups, var)     # Varianza por grupo
  r.g      <- as.numeric(rep(NA, n.g))   # Inicialización vector de réplicas
  for (i in 1:n.g)
    r.g[i] <- sum(groups == levels(groups) [i])  # Réplicas por nivel

  # Verificación de que haya más de una réplica por grupo ---------------------
  if (sum(r.g == 1) > 0 & pooled == F) {
    r1 <- levels(groups)[which(r.g == 1)]
    cat('\n', '¡Advertencia!', '\n', '\n',
        'Se calculó la dispersión con base en la varianza promedio,', '\n',
        'porque hay niveles de', nombre.g, 'con una sola réplica:', '\n')
    print(r1)
    pooled <- TRUE
  }
  
  # Varianza promedio ---------------------------------------------------------
  if (pooled)
    v.g <- weighted.mean (v.g, r.g - 1)
  
  # Medida de dispersión por grupo (d.g) --------------------------------------
  if (type == 'de') {
    # Desviación estándar (por defecto)
    main1 <- paste('Medias y desviaciones estándar de', nombre.y)
    main2 <- paste('por nivel de', nombre.g)
    d.g  <- sqrt(v.g)
  }
  
  if (type == 'ee') {
    # Error estándar
    main1 <- paste('Medias y errores estándar de', nombre.y)
    main2 <- paste('por nivel de', nombre.g)
    
    d.g  <- sqrt(v.g)/sqrt(r.g)
  }
  
  if (type == 'ic') {
    # Intervalos de confianza del 95%
    main1 <- paste('Medias e intervalos de confianza del 95% para', nombre.y)
    main2 <- paste('por nivel de', nombre.g)
    
    if (pooled) {
      t.crit <- qt(0.025, df = length(y) - n.g, lower.tail = F)
      d.g <- t.crit * sqrt(v.g)/sqrt(length(y) - n.g)
    }
    else {
      t.crit <- qt(0.025, df = r.g - 1, lower.tail = F)
      d.g <- t.crit * sqrt(v.g)/sqrt(r.g)
    }
  }
  
  # Gráfico -------------------------------------------------------------------
  # Título principal
  if (pooled & is.null(tit))
    main <- c(main1, main2,
              'usando la varianza promedio ponderada dentro de grupos')
  else if (is.null(tit))
    main <- c(main1, main2,
              'usando la varianza individual dentro de cada grupo')
  else
    main <- tit
  
  # Marco del gráfico
  if (is.null(xlab))
    xlab <- nombre.g
  if (is.null(ylab))
    ylab <- nombre.y
  plot(groups, y, border = 'white', col = 'white',
       main = main, xlab = xlab, ylab = ylab, las = 1,
       ylim = c(min(med.g - d.g), max(med.g + d.g)))
  
  # Medias
  par(pch = 19)
  points(c(1:n.g), med.g, ...)
  
  # Líneas verticales
  segments(c(1:n.g), med.g - d.g, c(1:n.g), med.g + d.g, ...)
  
  # Líneas horizontales
  segments(c(1:n.g) - k, med.g - d.g, c(1:n.g) + k, med.g - d.g, ...)
  segments(c(1:n.g) - k, med.g + d.g, c(1:n.g) + k, med.g + d.g, ...)
  
  # Línea de tendencia, que une las medias
  if (line)
    lines(c(1:n.g), med.g, ...)
}

\[ \]

A continuación se ilustra el uso de la función grafBar para construir un diagrama con barras de dispersión, usando las desviaciones estándar individuales (valores por defecto), para la longitud del sépalo (Variable ubicada en la primera columna del data frame) de cada una de las especies contenidas en la base de datos iris, usando líneas azules, de ancho 2, y rombos, con un factor de expansión de 2, para representar las medias. Adicionalmente, se personalizan los títulos para la abscisa y la ordenada.

La primera línea del siguiente fragmento de código (source("grafBar.R)) carga la función en memoria, con lo cual queda disponible para ser invocada.

source("grafBar.R")
grafBar(group = "Species", y = 1, iris, xlab = "Especie",
        ylab = "Longitud del sépalo", lwd = 2, col = "blue", pch = 18, cex = 2)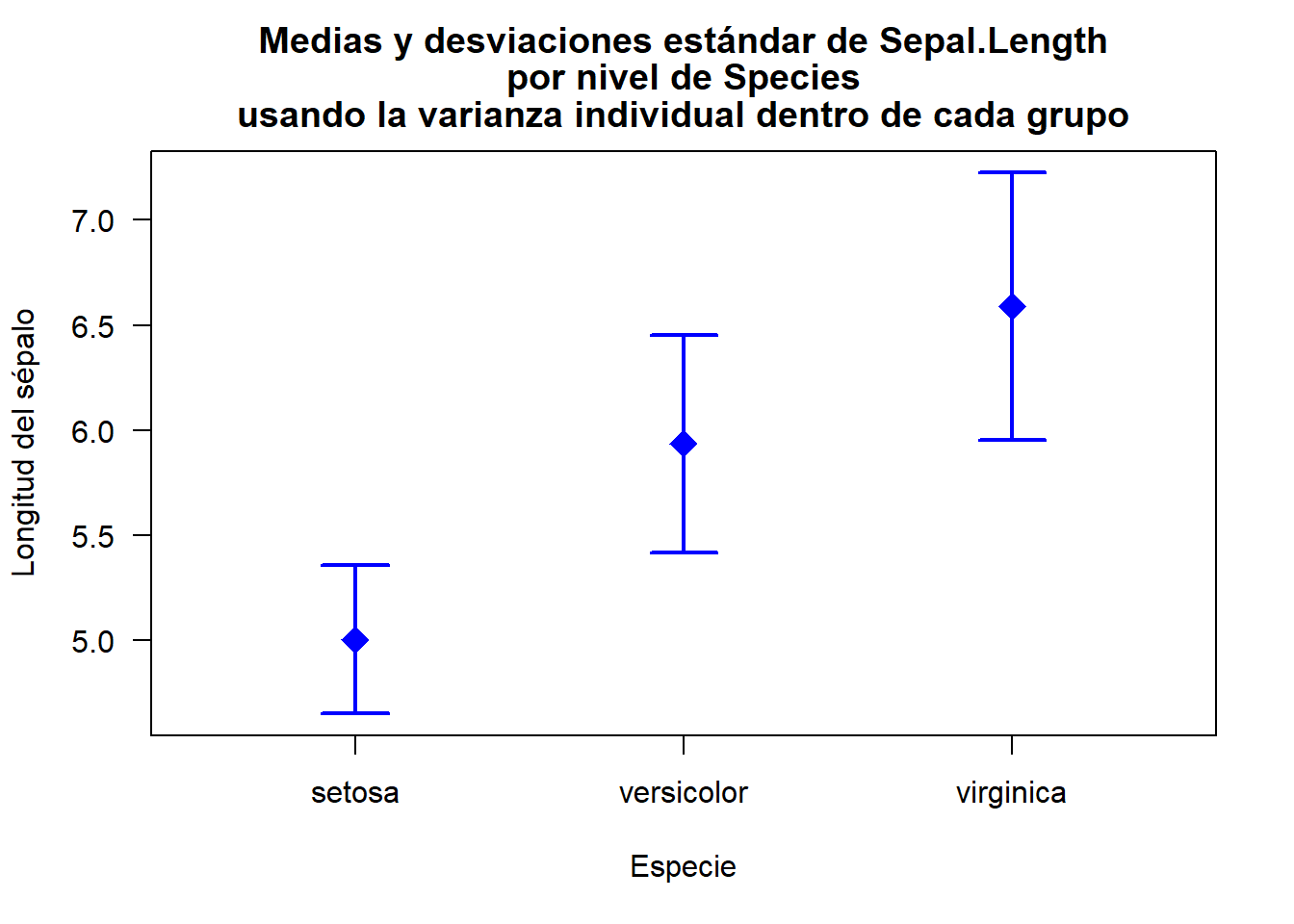

Estimado lector, si usted me ha seguido hasta este punto, no queda más que extenderle una invitación, haciendo eco del nombre de la conferencia anual patrocinada por la Fundación R, que ha llegado a convertirse en lema:

¡Use R!

22 ESTILO

Referencias bibliográficas