8 ESTRUCTURAS DE DATOS

R es un lenguaje con características compatibles con la programación orientada a objetos. Un objeto es una entidad sobre la cual puede operarse. Así, un número es un objeto, también son objetos una cadena de caracteres, una fórmula o un resultado. Aunque es evidente la posibilidad de operar sobre un número, no lo es tanto la posibilidad de operar sobre una cadena de caracteres, sobre una fórmula o sobre un resultado. No obstante, si se considera, por ejemplo, la función print, tomando tales objetos como argumento para mostrarlos en la consola, la posibilidad de operar sobre los mismos se hace clara.

Un grupo de objetos de gran interés es el de los que actúan como contenedores de información, permitiendo agruparla o estructurarla. La estructura más básica es el vector, el cual está definido como un conjunto unidimensional de elementos del mismo tipo (todos enteros, todos reales, todos complejos, todos caracteres, todos lógicos o todos en bruto). En orden de complejidad, sigue la matriz, definida como una estructura bidimensional de elementos del mismo tipo. Está también el arreglo, que constituye la generalización de la matriz, pudiendo tener más de dos dimensiones; la matriz sería un arreglo particular de dos dimensiones. El data frame, al igual que la matriz, es una estructura bidimensional, pero es más general que la matriz, por cuanto admite elementos de diferente tipo. Esta es la manera en la que suelen estructurarse datos de diferente tipo (entero, real, carácter, complejo, lógico, bruto); el data frame es la base de datos por excelencia en R. La lista es la estructura más general, teniendo la posibilidad de contener no solo vectores de diferente tipo, sino también cualquiera de las otras estructuras, incluyendo otras listas.

Los vectores, las matrices y los arreglos están restringidos a contener elementos de un único tipo; a tales estructuras se les denomina atómicas. Los data frames y las listas son estructuras que admiten elementos de diferentes tipos; a tales estructuras se les denomina recursivas.

En resumen, las estructuras contenedoras de datos en R, en orden de complejidad son: vector, matriz, arreglo, data frame y lista. Las tres primeras son estructuras atómicas; las dos últimas, recursivas.

8.1 Vectores

La manera más común de crear un vector es mediante el uso de la función de concatenación, c, y el operador de asignación (<-). Si se desea crear, por ejemplo, un vector llamado a, que contenga los elementos 3, 5 y 9, podrá usarse la siguiente instrucción:

a <- c(3, 5, 9)

Valga anotar que, en la anterior expresión, es la función c la que define el vector (nemotécnicamente, puede recordarse como combinar); el paso correspondiente al almacenamiento de dicho objeto en el ambiente de trabajo (la asignación) se requeriría únicamente si en un paso posterior fuera a usarse dicho vector. Si no se realizara el paso de asignación, se generaría un vector que a pesar de su existencia efímera (únicamente existiría en la línea en la que hubiera sido creado) podría bastar para un propósito dado, tal y como servir de argumento en una función determinada. Así, por ejemplo, la instrucción c(3, 5, 9) crearía un vector numérico con los elementos 3, 5 y 9 y lo mostrará en la consola; no obstante, dicho vector no podría recuperarse en una instrucción posterior.

La siguiente instrucción crea un vector tipo carácter. Al definir este tipo de vectores, es necesario entrecomillar cada uno de los elementos constituyentes, siendo posible usar comillas dobles o comillas sencillas.

nombres <- c("Gabriela", 'Carlina', "Luz", 'Marina')

Para verificar si un objeto es un vector se usa la función is.vector(objeto), la cual genera un resultado lógico (falso o verdadero), con ciertas salvedades que se comentan en la sección 10.4.

8.2 Matrices

Las matrices son estructuras bidimensionales (filas y columnas) que agrupan objetos del mismo tipo. La manera usual de crear una matriz es mediante la función matrix.

Supóngase que se quiere crear la siguiente matriz numérica con dos filas y tres columnas:

2	0	5
-1	9	0

Para tal efecto, se usa la siguiente instrucción.

matrix(c(2, 0, 5, -1, 9, 1), nrow = 2, ncol = 3, byrow = TRUE)

Además de la especificación del número de filas (nrow) y del número de columnas (ncol), es importante anotar que el valor por defecto del argumento byrow es FALSE, con lo cual, si dicho argumento fuera omitido, los elementos ingresados se ordenarían por columnas y, en lugar de la matriz objetivo, se obtendría la siguiente matriz:

#>      [,1] [,2] [,3]
#> [1,]    2    5    9
#> [2,]    0   -1    1

Considérense los vectores a, b y c:

a <- c(2, 0)
b <- c(5, -1)
c <- c(9, 1)

Podría pensarse en concatenar dichos vectores, así: c(a, b, c), para obtener la última matriz. No obstante, la función c siempre da lugar a vectores, con lo cual el resultado obtenido será un vector, con los valores 2, 0, 5, -1, 9 y 1.

Existen, sin embargo, un par de funciones de concatenación que dan lugar a matrices: rbind, que permite combinar vectores por filas (rows), y cbind, que permite concatenar vectores por columnas (columns).

m1 <- cbind(a, b, c)

#>      a  b c
#> [1,] 2  5 9
#> [2,] 0 -1 1

Obsérvese que, mediante el uso de la función cbind, se han combinado los vectores a, b y c, de manera que cada uno de ellos constituye una columna de la matriz m1. Para verificar si el objeto m1 es una matriz, se usa is.matrix(m1).

Las matrices en R comparten las características de las matrices como concepto matemático, siendo posible realizar operaciones matriciales con base en estas; entre las más comunes, se destacan la suma (operador +), el producto matricial (operador %*%), la trasposición (t), la inversión (solve), la obtención de la diagonal (diag), la descomposición espectral (eigen) y la descomposición en valores singulares (svd).

Asimismo, puede obtenerse la suma de productos cruzados y la suma de cuadrados, mediante las funciones crossprod y tcrossprod.

Las siguientes instrucciones son equivalentes y dan lugar al producto \(X’X\).

crossprod(X)
crossprod(X, X)
t(X) %*% X

También son equivalentes las siguientes instrucciones.

crossprod(X, y)
t(X) %*% y

Asimismo, se tienen la siguiente equivalencia.

tcrossprod(X)
tcrossprod(X, X)
(X) %*% t(X)

Y esta otra equivalencia.

tcrossprod(X, y)
(X) %*% t(y)

No está de más anotar que para obtener los productos cruzados de dos matrices o cualquier otro producto entre dos matrices, estas deben ser conformables, esto es, que el número de columnas de la primera matriz sea igual al número de filas de la segunda.

También vale la pena anotar que el operador * daría lugar al producto, elemento por elemento, de los dos objetos relacionados; no al producto matricial.

m1 * m1
#>      a  b  c
#> [1,] 4 25 81
#> [2,] 0  1  1

En adición a las funciones básicas presentadas anteriormente, que forman parte del paquete base, el paquete Matrix contiene funciones adicionales para realizar operaciones avanzadas de álgebra lineal.

Aunque los vectores en R son simples contenedores unidimensionales que no guardan correspondencia con el concepto del álgebra lineal, también admiten operaciones matriciales, adaptándose, cuando sea del caso, a matrices fila o matrices columna según corresponda.

Considérense los siguientes objetos:

a  <- c(3, 5, 9)
b  <- c(7, 2)
m2 <- matrix(c(2, 0, 5, -1, 9, 1), nrow = 2, ncol = 3, byrow = TRUE)

m2 es una matriz 2 x 3, mientras que a y b son vectores de tamaño 3 y 2, respectivamente.

Todas las siguientes operaciones están adecuadamente definidas:

b %*% m2

El vector b se adapta a una matriz fila (1 x 2). El resultado es una matriz \(1 \times 3\).

m2 %*% a

El vector a se adapta a una matriz columna (3 x 1). El resultado es una matriz \(2 \times 1\).

t(a) %*% a

La anterior operación también está adecuadamente definida, puesto que siempre que se usa el operador de trasposición (t) sobre un vector, este se convierte en una matriz fila (\(1 \times 3\), en este caso). El segundo factor se adecúa a una matriz columna (\(3 \times 1\), en este caso). El resultado es una matriz \(1 \times 1\).

a %*% a

En este caso, se obtiene el mismo resultado que en el caso anterior. El primer factor se adecúa a una matriz fila (\(1 \times 3\)). El segundo factor se adecúa a una matriz columna (\(3 \times 1\)). El resultado es una matriz \(1 \times 1\).

a %*% t(a)

Al usar el operador de trasposición (t) sobre el segundo factor, este se convierte en una matriz fila (\(1 \times 3\), en este caso). Por tanto, el primer factor se adecúa a una matriz columna (\(3 \times 1\), en este caso). El resultado es una matriz \(3 \times 3\).

t(b) %*% b

El operador de trasposición (t) convierte al primer factor en una matriz fila (\(1 \times 2\)). El segundo factor se adecúa a una matriz columna (\(2 \times 1\)). El resultado es una matriz \(1 \times 1\).

b %*% t(b)

Al usar el operador de trasposición (t) sobre el segundo factor, este se convierte en una matriz fila (\(1 \times 2\)). Por tanto, el primer factor se adecúa a una matriz columna (\(2 \times 1\)). El resultado es una matriz \(2 \times 2\).

8.3 Arreglos

Cuando se tienen más de dos dimensiones con elementos del mismo tipo, es posible estructurar la información en arreglos. Considérese una situación hipotética en la que se evalúan tres variables sobre cuatro unidades muestrales, en dos tiempos, pudiendo obtenerse como resultado cualquiera de las letras del alfabeto.

Tiempo1
	v1	v2	v3
unidad1	a	x	d
unidad2	c	m	b
unidad3	f	j	u
unidad4	d	l	y

Tiempo2
	v1	v2	v3
unidad1	b	h	r
unidad2	j	o	s
unidad3	h	w	n
unidad4	l	p	q

La anterior información podría estructurase en un arreglo de tres dimensiones, con las unidades en la primera dimensión, las variables en la segunda y el tiempo en la tercera, lo cual puede visualizarse como un cubo, en el que las tres dimensiones representan altura, ancho y profundidad, respectivamente.

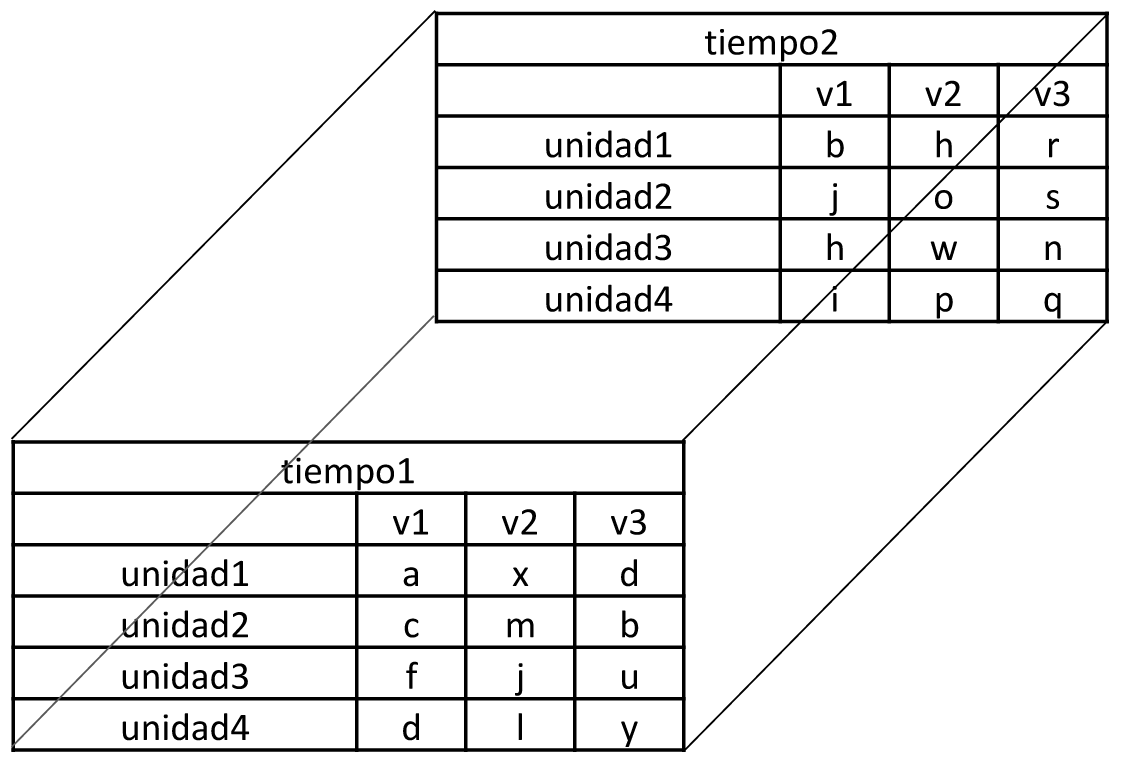
Aunque la analogía entre un cubo y un arreglo de tres dimensiones puede facilitar el entendimiento del arreglo, la inexistencia de este tipo de relaciones en arreglos con mayor número de dimensiones no impide la existencia de estos. Si se tuviera otro factor, como localidad, por ejemplo, podría incorporarse en la cuarta dimensión. De igual manera, podrían generarse dimensiones adicionales.

Aunque podría usarse una única instrucción para construir el arreglo en cuestión, a fin de hacer más claro el proceso, se ilustrará en dos pasos. Inicialmente, se construye un vector de 24 elementos con toda la información.

vector <- c('a', 'c', 'f', 'd', 'x', 'm', 'j', 'l', 'd', 'b',
            'u', 'y', 'b', 'j', 'h', 'i', 'h', 'o', 'w', 'p',
            'r', 's', 'n', 'q')

A continuación, se genera el arreglo:

letras <- array(vector, dim = c(4, 3, 2))

Obsérvese que la función array concatena los objetos contenidos en vector, por columnas (no existe la opción para concatenar por filas). En el argumento dim debe proporcionarse un vector de enteros, con la longitud de cada una de las dimensiones.

Para verificar si el objeto letras es un arreglo, se utiliza is.array(letras). Todas las matrices son a su vez arreglos; sin embargo, solo los arreglos de dos dimensiones son matrices.

En el Anexo C se presenta una ilustración práctica del arreglo como contenedor multidimensional.

8.4 Data frames

Las estructuras ilustradas anteriormente (vectores, matrices y arreglos) exigen que todos los elementos sean del mismo tipo. Por tal motivo se les denomina objetos atómicos (puede verificarse con la función is.atomic(objeto)). El data frame es una estructura rectangular (dos dimensiones), que puede estar conformada por objetos atómicos de diferente tipo en cada columna.

Considérense los siguientes vectores: id es un vector de caracteres, v1 es numérico y v2 es complejo.

id <- c("a23", "f31", "j33", "m54")
v1 <- c(2.4, 7.9, 1.1, 8.5)
v2 <- c(4+3i, 2-0.8i, 1+1.1i, 3-5i)

Una manera de generar un data frame es a través de la agregación de vectores, sin importar que estos sean de diferente tipo. La siguiente instrucción genera un data frame concatenando por columnas los vectores definidos anteriormente.

df <- data.frame(id, v1, v2)

#>    id  v1     v2
#> 1 a23 2.4 4+3.0i
#> 2 f31 7.9 2-0.8i
#> 3 j33 1.1 1+1.1i
#> 4 m54 8.5 3-5.0i

Esta capacidad de combinar objetos de diferentes tipos hace del data frame la estructura ideal para alojar bases de datos, las cuales suelen organizarse con objetos o individuos en filas, y variables en columnas.

No es necesario que los objetos que se concatenan para conformar un data frame sean vectores; también pueden concatenarse matrices, arreglos u otros data frames, exigiéndose únicamente que todos tengan el mismo número de filas.

Puesto que el data frame es una estructura bidimensional, al incluir un arreglo en la definición de un data frame, este se “aplanaría” a dos dimensiones. Si se toma el arreglo letras, generado anteriormente (ver letras en 8.3) y se escribe la instrucción: df2 <- data.frame(letras), se obtiene un arreglo rectangular de cuatro filas y seis columnas en el que los tiempos están concatenados por columnas.

Cuando se usan las funciones read.table, read.delim, read.delim2, read.csv, read.csv2 o read_excel (capítulo 6), los objetos que se generan son data frames. Para evaluar si un objeto es un data frame, se usa la función is.data.frame. Este aspecto es de particular relevancia, pues muchas funciones que trabajan sobre datos exigen que estos sean de una clase particular. Se indicaba, por ejemplo, que las operaciones matriciales exigen objetos de la clase matriz (eventualmente, también vectores; cf. sección 8.2). Si bien las matrices están conformadas por vectores del mismo tipo, esta no es una condición suficiente para tener una matriz. Así, cuando se importa, por ejemplo, un conjunto de vectores numéricos, se obtiene un data frame; no una matriz. Para llevar un objeto a la clase matriz, se utiliza la función as.matrix.

El data frame está diseñado como el contenedor ideal para bases de datos; no obstante, resulta insuficiente para otros fines, al no admitir objetos de cualquier clase, no admitiendo, por ejemplo, funciones (objetos de la clase function).

8.5 Listas

La lista constituye la estructura más flexible, pudiendo estar conformada por objetos de cualquier tipo y clase, incluso por otras listas. Dada la diversidad de objetos que pueden conformar una lista, en estas no existe el concepto de filas, columnas ni de ninguna otra dimensión. De hecho, las listas son objetos unidimensionales y a menudo se hace referencia a las mismas como ‘vectores genéricos’, esto es, vectores que pueden contener elementos de distintos tipos, a diferencia de los vectores básicos definidos anteriormente que están restringidos a contener objetos de un único tipo. A estos vectores básicos se les denomina vectores atómicos cuando se desea diferenciarlos de las listas.

La siguiente figura ilustra el concepto de las listas como vectores genéricos. En el panel de la izquierda se representan dos vectores, cada uno de los cuales está restringido a contener elementos de un mismo tipo, los cuales se ubican a lo largo de una única dimensión. En el panel de la derecha se representa una lista, la cual, a pesar de manejar también una única dimensión, puede contener elementos de cualquier tipo.

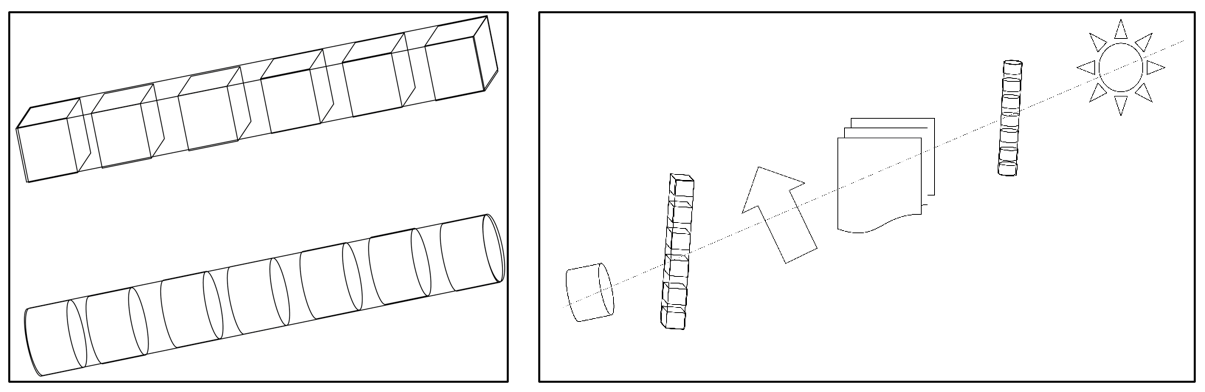
Considérense los siguientes objetos:

nombre <- c('Iván', 'Rosa', 'Diana')  # Vector tipo carácter
edad <- c(34, 43)  # Vector tipo doble precisión
aprobado <- c(TRUE, TRUE, FALSE)  # Vector tipo lógico
m1 <- matrix(c(2, 0, 5, -1, 9, 1), nrow = 2, ncol = 3)  # Matriz doble precisión

Los anteriores objetos pueden concatenarse en una lista, así:

lis1 <- list(nombre, edad, aprobado, m1)  # Lista

A partir de los anteriores objetos puede generarse una nueva lista:

lis2 <- list(nombre, edad, aprobado, m1, lis1) # Lista

Nótese que uno de los elementos de lis2 es también una lista (lis1)

Para verificar si el objeto lis2 es una lista, se utiliza is.list(lis2). Mediante la función is.vector, es posible verificar que los objetos lis1 y lis2 definidos anteriormente en adición a ser listas, también son vectores¹⁹.

En resumen, el lenguaje R proporciona una variada gama de contenedores que resulta suficiente para satisfacer las necesidades de organización de la información. El vector constituye la manera más básica de agrupar datos; es el objeto más utilizado para la definición de argumentos secundarios en las funciones de R; es la estructura que se utilizaría siempre que los datos fueran del mismo tipo y no exigieran un arreglo multidimensional. Cuando se requiera realizar operaciones matriciales, los objetos deben ser matrices (o eventualmente vectores; cf. sección 8.2). El arreglo resulta útil para organizar datos del mismo tipo en más de dos dimensiones. El data frame es la estructura en la que se organizan las bases de datos en R. La mayoría de los procedimientos estadísticos implementados en R exigen que el objeto de entrada sea un data frame. Cuando se importan datos, se genera un data frame. La lista resulta útil cuando se requiere tener información de diversa índole en un mismo contenedor. Este es el objeto que suele usarse para alojar los resultados de las funciones.