Anexo C Arreglos como contenedores multidiminsionales

---

Casi todas las estructuras contenedoras de datos tienen un nicho muy definido. Se usa el vector cuando los datos son del mismo tipo y no se requiere más de una dimensión. La matriz, por su parte, resulta adecuada cuando se realizan operaciones matriciales. El data frame es la base de datos por excelencia. La lista resulta útil cuando se desea alojar información de diversa índole (tamaño, dimensionalidad, tipo…) en un solo objeto; en particular para presentar, las salidas de las funciones. En contraste con estos usos tan claramente definidos, que cubren prácticamente todas las necesidades, los arreglos no son muy comunes.

A continuación se ejemplifica el uso de un arreglo como contenedor multidimensional de información. Aunque, desde luego, no es esta la única opción posible, sí se considera muy práctica, por permitir organizar todos los datos en un solo objeto.

Considérese el coeficiente general de similitud de Gower (Gower 1971)

\[ SG=\frac{\sum\limits_{j= 1}^{p}{W_{ii'j}S_{ii'j}}}{\sum_{j=1}^{p}{W_{ii'j}}} \]

donde:

\(SG\) : Coeficiente general de similitud de Gower.
\(W_{ii'j}\) : \(j\)-ésima ponderación para la comparación entre \(i\)-ésimo y el \(i'\)-ésimo individuo.
\(S_{ii'j}\) : Similitud parcial entre el \(i\)-ésimo y el \(i'\)-ésimo individuo, a partir de la \(j\)-ésima variable.

Este coeficiente es, en esencia, un promedio ponderado de las similitudes parciales. El aspecto que le agrega complejidad a este cálculo es el hecho de que ni las ponderaciones ni las similitudes parciales pueden definirse de manera general; cada una de ellas se determina al momento de comparar un par de observaciones. Estos cálculos deberán generar finalmente una matriz simétrica de similitudes de tamaño \(n \times n\), siendo \(n\) el número de observaciones.

Para calcular la matriz de similitudes, resulta conveniente colectar la información en un arreglo de cuatro dimensiones, en el que las dos primeras dimensiones correspondan a las observaciones que se compararan; la tercera dimensión, a las similitudes parciales, y la cuarta, a las ponderaciones. Este arreglo podría visualizarse como un cubo doble, en el que el primer cubo contiene las similitudes parciales, mientras que el segundo contiene las ponderaciones. Para ilustrarlo gráficamente, supóngase una situación sencilla en la que se tienen 3 observaciones y 5 variables. El arreglo podría representarse así:

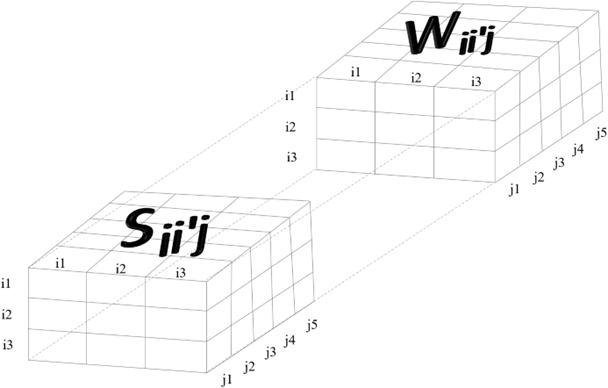
La cara frontal de cada uno de los cubos (2 primeras dimensiones del arreglo) relaciona cada observación con cada una de las demás observaciones. En este ejemplo, la cara en cuestión es 3 x 3. La tercera dimensión (profundidad del primer cubo) contiene las similitudes parciales, \(S_{ii'j}\), entre cada par de observaciones, para cada una de las variables consideradas (5 variables en este ejemplo). La cuarta dimensión (profundidad del segundo cubo) contiene las ponderaciones, \(W_{ii'j}\), para la comparación de cada par de observaciones, a través de cada una de las variables. Para acceder a cada una de las posiciones, basta con usar los correspondientes descriptores de acceso, acorde con lo ilustrado en el capítulo 13.

Puesto que el objetivo de este anexo es ilustrar la utilidad del arreglo como contenedor multidimensional, más que detallar el coeficiente general de similitud de Gower, nos limitaremos a señalar que hay una serie de reglas que determinan tanto las similitudes parciales (s en el script), como las ponderaciones (w en el script), dependiendo del tipo de variable (presencia/ausencia, categórica o numérica), de los valores observados y de que los datos estén presentes o no.

Suponiendo una situación en la que se tienen \(n\) observaciones y \(p\) variables, la parte central de una función que organice esta información en un arreglo, dejándola preparada para calcular la matriz de similitudes podría tener el siguiente aspecto:

SW <- array(0, dim = c(n, n, p, 2))
for (j in 1:p) {
  for (i1 in 1:n) {
    for (i2 in 1:n) {
      SW <-(i1, i2, j, 1) <- s
      SW <-(i1, i2, j, 2) <- w
    }
  }
}

La primera instrucción genera un arreglo tetradimensional de tamaño \(n \times n \times p \times 2\), conformado inicialmente por ceros. Seguidamente se escriben tres ciclos anidados, mediante los cuales se realizan todas los posibles comparaciones entre pares de observaciones a través de todas las variables. La primera instrucción del ciclo más interno irá llenando el primer cubo con las similitudes parciales, \(S_{ii'j}\), mientras que la segunda instrucción del mismo ciclo llenará el segundo cubo con las correspondientes ponderaciones, \(W_{ii'j}\).

El cálculo final del coeficiente de similitud general de Gower podría realizarse, utilizando las funciones para cálculos por dimensiones ilustradas en el capítulo 18:

SW[, , , 1] <- SW[, , , 1] * SW[, , , 2]
SG <- apply(SW[ , , , 1], c(1, 2), sum)/
      apply(SW[ , , , 2], c(1, 2), sum)

La primera instrucción calcula los productos entre las similitudes parciales y sus correspondientes ponderaciones, dando lugar a los diferentes sumandos del numerador del coeficiente. Esta información se sobrescribe en el primer cubo. El segundo cubo sigue conservando los ponderadores. La segunda instrucción calcula para cada una de las celdas de las dos primeras dimensiones el coeficiente general de similitud de Gower, generando una matriz simétrica \(n \times n\).