19 GRÁFICOS
La alta calidad de los gráficos generados por R y sus amplias posibilidades de personalización, lo hacen ideal para este fin. Aunque algunos de los gráficos que se generan por defecto puedan parecer un tanto simples y faltos de estética, mediante una adecuada personalización pueden lograrse verdaderas obras de arte.
Si se tiene interés en profundizar en las capacidades gráficas de R, se invita a explorar el paquete lattice, a través del libro escrito por su autor (Lattice: Multivariate data visualization with R 2008), en el que detalla cómo sacar provecho de dicho potencial, con particular énfasis en la representación de datos multivariantes y de gráficos trellis. En este texto no se exploran las funcionalidades de dicho paquete, lo cual exigiría un libro completo, excepto por la ilustración de uso de la función xyplot, en la sección 19.1.
En general, la construcción de un gráfico puede involucrar tres categorías de funciones:
Una función principal de graficación (v. gr.
plot,matplotybarplot)Funciones para incorporar características específicas en un gráfico (v. gr.
box,points,axis,text,legend,abline,lines,segments,arrowsypolygon)Una función para definir parámetros generales:
par.
Las funciones del segundo grupo, es decir, las que permiten incorporar características específicas en un gráfico, exigen la construcción previa de un gráfico, mediante alguna de las funciones principales de graficación.
El conjunto de instrucciones para construir un gráfico puede tener un aspecto similar al siguiente:
par(argumentos) # Definición de parámetros generales
plot(argumentos) # Construcción del gráfico
axis(argumentos) # Detalles del gráfico (ejes)
text(argumentos) # Detalles del gráfico (texto)
lines(argumentos) # Detalles del gráfico (líneas)
arrows(argumentos) # Detalles del gráfico (flechas)
box() # Detalles del gráfico (caja)Aunque no todos los gráficos exigen un conjunto de instrucciones como el anterior, siempre es necesario usar al menos una función principal de graficación.
A continuación, se presentan los gráficos más utilizados en la práctica estadística cotidiana, ilustrando algunos de los aspectos más relevantes de su personalización. Puesto que muchas de las estrategias de personalización son comunes a diferentes tipos de gráficos, estas se presentan con mayor detalle en los diagramas de dispersión, que son los que aparecen en primer lugar.
19.1 Diagramas de dispersión
La función plot{graphics} permite construir un diagrama de dispersión bidimensional. La manera más básica de usar esta función es con dos argumentos: el primero, un vector numérico, para las coordenadas de la abscisa (x), y el segundo, un vector numérico, para las de la ordenada (y).
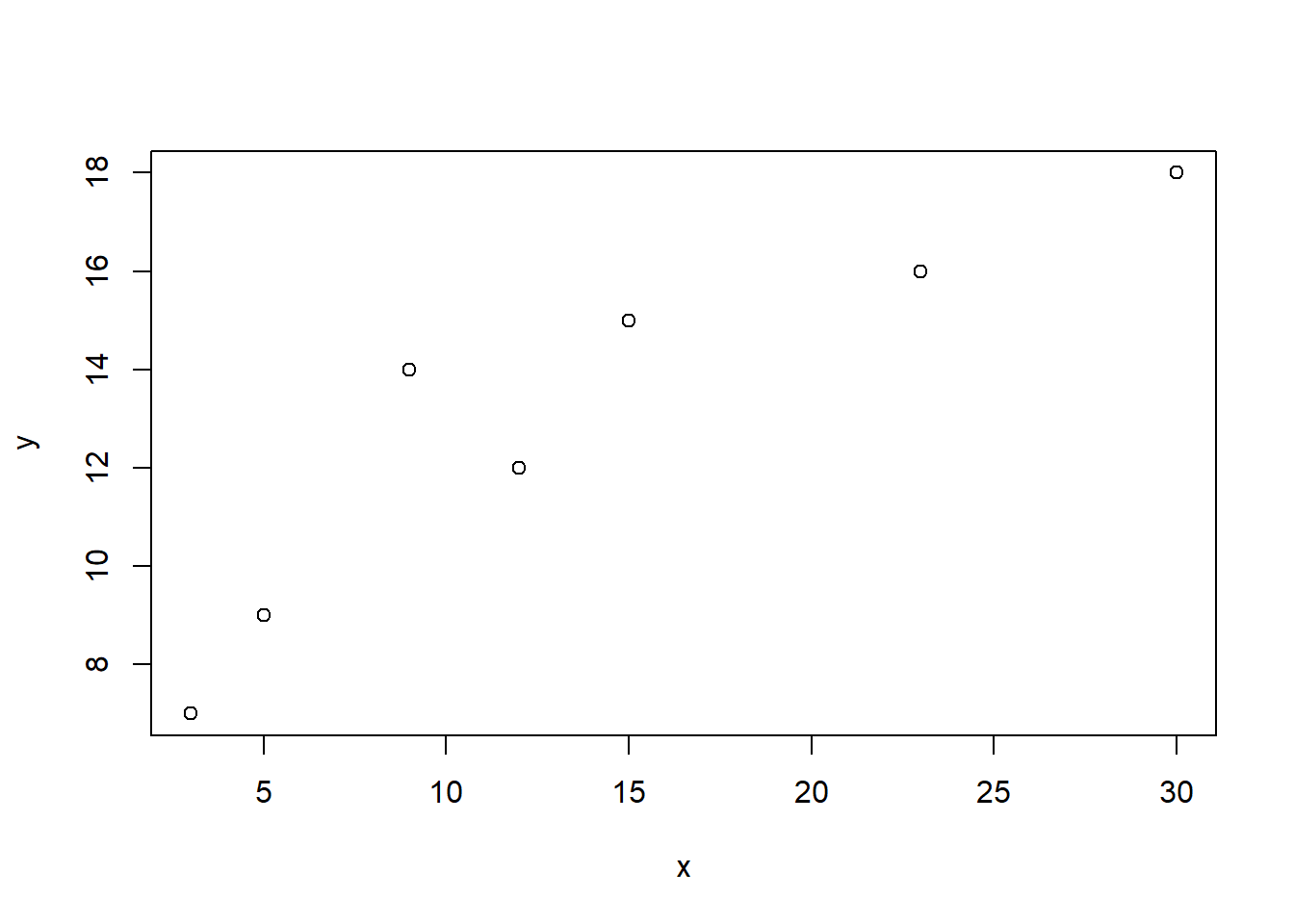
Asimismo, puede usarse como único argumento un objeto bidimensional (una matriz o un data frame) con las coordenadas de la abscisa y de la ordenada.
Cualquiera de los siguientes pares de instrucciones genera el mismo diagrama.
coor.m <- cbind(x, y) # Matriz de coordenadas
plot(coor.m)coor.df <- data.frame(x, y) # Data frame de coordenadas
plot(coor.df)También es común usar como argumento una fórmula que exprese la relación entre dos variables mediante la virgulilla (~). En las expresiones en las que se usa esta notación, la variable que aparece a la izquierda de la virgulilla actúa como respuesta, graficándose, por tanto, en la ordenada, mientras que la que aparece a la derecha actúa como predictora, graficándose en la abscisa. La siguiente instrucción genera el mismo diagrama de dispersión.
plot(y ~ x)Existen numerosos argumentos opcionales que le permiten al usuario personalizar las características del gráfico. A continuación, se presentan algunos de ellos.
El argumento pch (plotting character) permite especificar mediante un entero o un carácter individual (que debe escribirse entrecomillado) el símbolo que ha de usarse para la identificación de los puntos en el diagrama. El valor por defecto de dicho argumento es 1, que corresponde a un círculo sin relleno, como el que se muestra en la figura anterior. Los códigos numéricos de 0 a 25 corresponden a los símbolos más usados.
plot(x, y, pch = 16)Mediante el argumento cex (character expansion) es posible controlar el tamaño del símbolo usado para graficación. El valor por defecto es cex = 1; si se define un valor diferente, este actúa como factor multiplicativo del tamaño original; así, un valor de 3 da lugar a símbolos cuyo tamaño es tres veces mayor que el tamaño original (300 %), mientras que 0.5 genera símbolos de la mitad del tamaño original.
plot(x, y, cex = 1.5)Hay muchas formas en las que puede modificarse el color de los símbolos, mediante el uso del argumento col (color). Los colores básicos pueden designarse con un código numérico entre 1 y 8 o usando sus correspondientes nombres entre comillas; sus códigos hexadecimales se obtienen mediante la función palette(). Para obtener una lista más completa de colores, se usa la función colors(), siendo válido usar cualquiera de los 657 nombres de dicha lista.
El Departamento de Bioestadística de la Universidad de Columbia ofrece una bonita y funcional guía de colores en línea, la cual puede descargarse en un archivo pdf.
Las versiones más recientes de RStudio reconocen los códigos de color que aparecen en los scripts y los iluminan en consecuencia. Esto facilita visualizar la apariencia de los colores desde la escritura misma del script.
También es posible identificar un color mediante su correspondiente código RGB (red, green, blue). Si se desea, por ejemplo, usar un púrpura profundo, el cual tiene código RGB: 80 para el rojo, 32 para el verde y 117 para azul, el argumento para el color queda así: col <- rgb(80, 32, 117, max = 255). Nótese el uso del argumento max = 255 dentro de la función rgb, el cual es necesario si se desea referenciar los valores RGB en la escala usual, que va de 0 a 255 para cada componente.
Los símbolos identificados con los códigos numéricos entre 21 y 25 admiten diferentes colores para el borde y para el fondo. En tales casos, el argumento col se usa para definir el color del borde, mientras que el argumento bg (background) define el color del fondo.
plot(x, y, pch = 22, col = "black", bg = rgb(255, 102, 0, max = 255))
Cuando un gráfico genera puntos que se traslapan, puede resultar práctico incorporar cierto nivel de trasparencia. Esto se logra mediante la función adjustcolor{grDevices}, asignando un valor entre cero (trasparencia total) y 1 (color sólido) al argumento alpha.f. Así, para usar, por ejemplo, el símbolo 21 (círculo con fondo), de color rojo en el fondo, con una opacidad de 0.3, se define el color así:
rojo.tr <- adjustcolor("red", alpha.f = 0.3)
set.seed(6)
abscisa <- rnorm(1000)
ordenada <- abscisa + runif(1000, -1, 1)
plot(abscisa, ordenada, pch = 21, col = "black", bg = rojo.tr)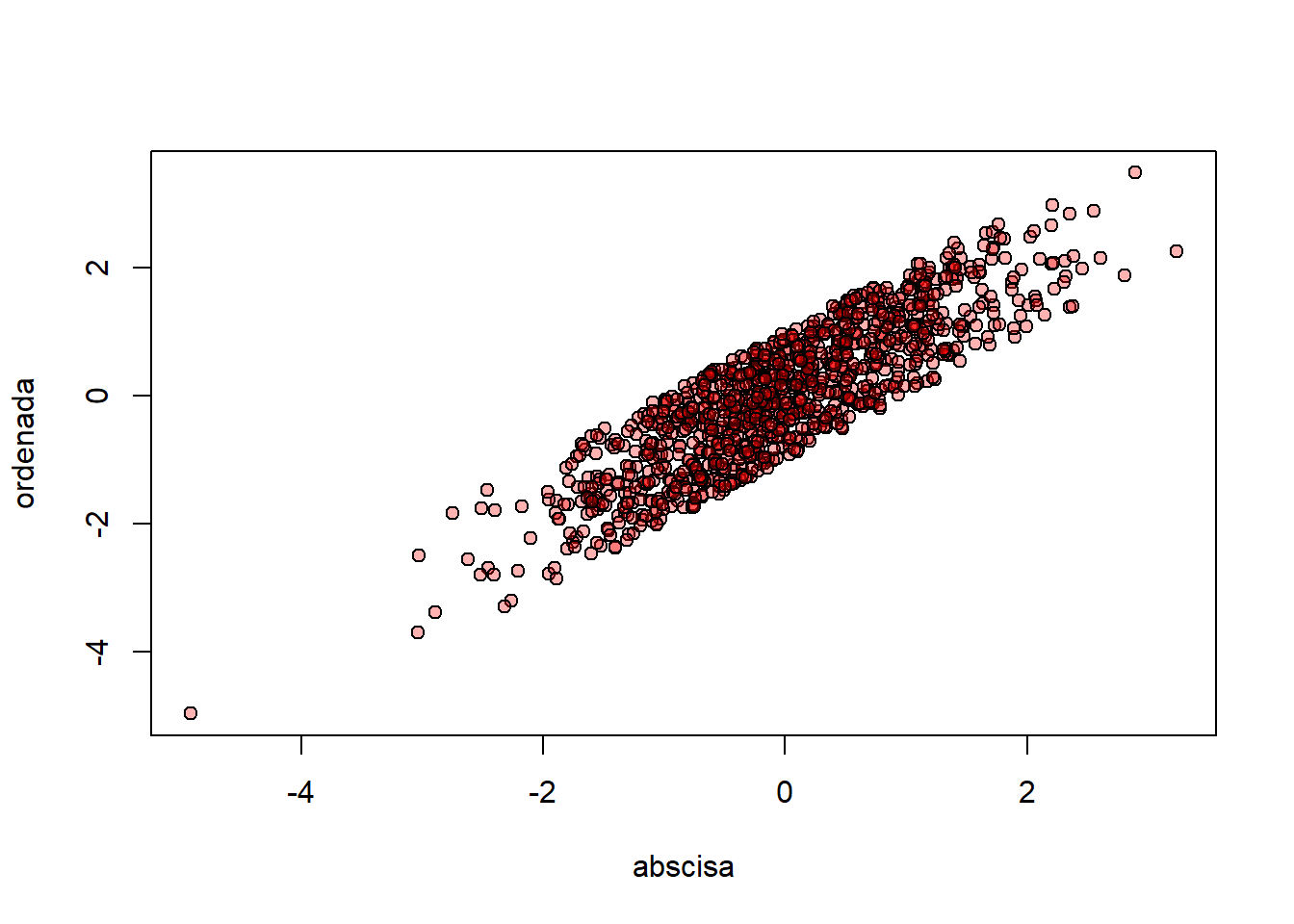
Para cambiar las etiquetas de los ejes, se usan los argumentos xlab (x label) y ylab (y label), para la abscisa y la ordenada correspondientemente. Para agregarle un título a la gráfica, se usa el argumento main (main label). El contenido de tales argumentos se escribe entre comillas.
Mediante los argumentos cex.lab (character expansion for labels) y cex.main (character expansion for main label), que actúan de igual manera que el argumento cex, es posible modificar el tamaño de las etiquetas.
plot(x, y, xlab = "Dimensión 1", ylab = "Dimensión 2", main = "ACP",
cex.lab = 1.5, cex.main = 2)Algunas técnicas dan lugar a la representación de puntos en un espacio bidimensional, en el cual la distancia entre los puntos se interpreta como disimilitud entre los mismos. En tales casos es muy importante construir los diagramas con un valor unitario para la razón entre la escala de la ordenada y la de la abscisa, de manera que las distancias en cualquier dirección sean equivalentes. Para tal efecto se usa el argumento asp = 1.
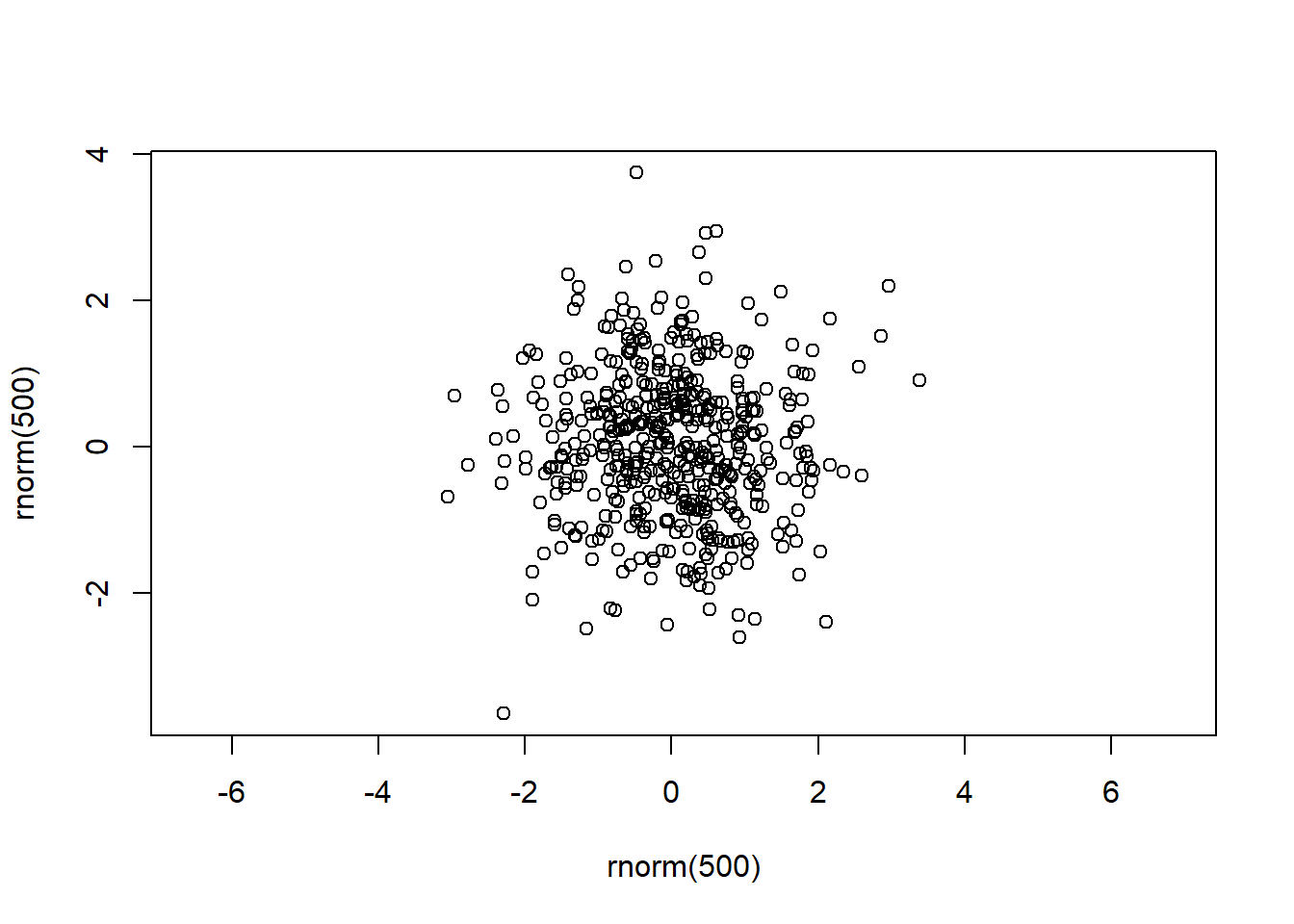
En el anterior diagrama, puede verificarse la distancia unitaria es exactamente igual en ambos ejes.
El escalamiento de los ejes se realiza de manera automática, adaptándose a los datos graficados, lo que generalmente resulta adecuado. No obstante, en ocasiones el usuario puede tener interés en realizar un escalamiento particular de los ejes. Esto puede lograrse mediante los argumentos xlim (x limits) y ylim (y limits), que permiten establecer los límites de la abscisa y la ordenada, respectivamente. Cada uno de tales argumentos se define mediante un vector de dos valores, con los correspondientes límites inferior y superior.
plot(x, y, xlim = c(0, 35), ylim = c(2, 20))
La definición de los límites es particularmente importante cuando se desea superponer varios gráficos, con lo cual se garantiza que todos estén referenciados en el mismo sistema de coordenadas.
Para cambiar el tamaño de los números (o caracteres) que definen las escalas de los ejes, se usa el argumento cex.axis (character expansion for axis). El argumento font permite definir la fuente, mediante un código numérico. El argumento las (labels style) se usa para establecer la dirección en que se grafican los valores de los ejes, así: 0: siempre paralelo a los ejes (valor por defecto), 1: siempre horizontal, 2: siempre perpendicular a los ejes, 3: siempre vertical.
plot(x, y, cex.axis = 1.8, font = 5, las = 1)Para tener mayor control en la presentación de los ejes, puede usarse el argumento axes = F, con lo cual no aparecerán los ejes que vienen por defecto. Seguidamente, cada eje se dibuja por separado, mediante la función axis. Esta función tiene como primer argumento side, mediante el cual se especifica la ubicación del eje, así: 1 para el eje inferior (abscisa), 2 para para el eje izquierdo (ordenada), 3 para el eje superior y 4 para el eje derecho. Mediante el argumento at se definen los puntos que irán con marcación. Tales puntos pueden definirse a conveniencia del usuario, sin que tengan que corresponder necesariamente a un conjunto de valores interespaciados. Para la marcación se usan, por defecto, los correspondientes valores numéricos; sin embargo, podría usarse el argumento labels, para definir cualquier otro conjunto de etiquetas.
Para llenar los espacios que quedan entre los ejes, generando el aspecto encajado de los diagramas que se construyen por defecto, se usa la función box.
plot(x, y, pch = 22, cex = 2, col = 1, bg = 'orangered1',
main = 'Diagrama de dispersión', cex.main = 2.5, xlab = 'dim 1',
ylab = 'dim 2', cex.lab = 1.5, xlim = c(0, 35), ylim = c(2, 24),
axes = F)
axis(1, at = seq(0, 35, 5), cex.axis = 1.4)
axis(2, at = seq(2, 24, 2), cex.axis = 1.4, las = 1)
box()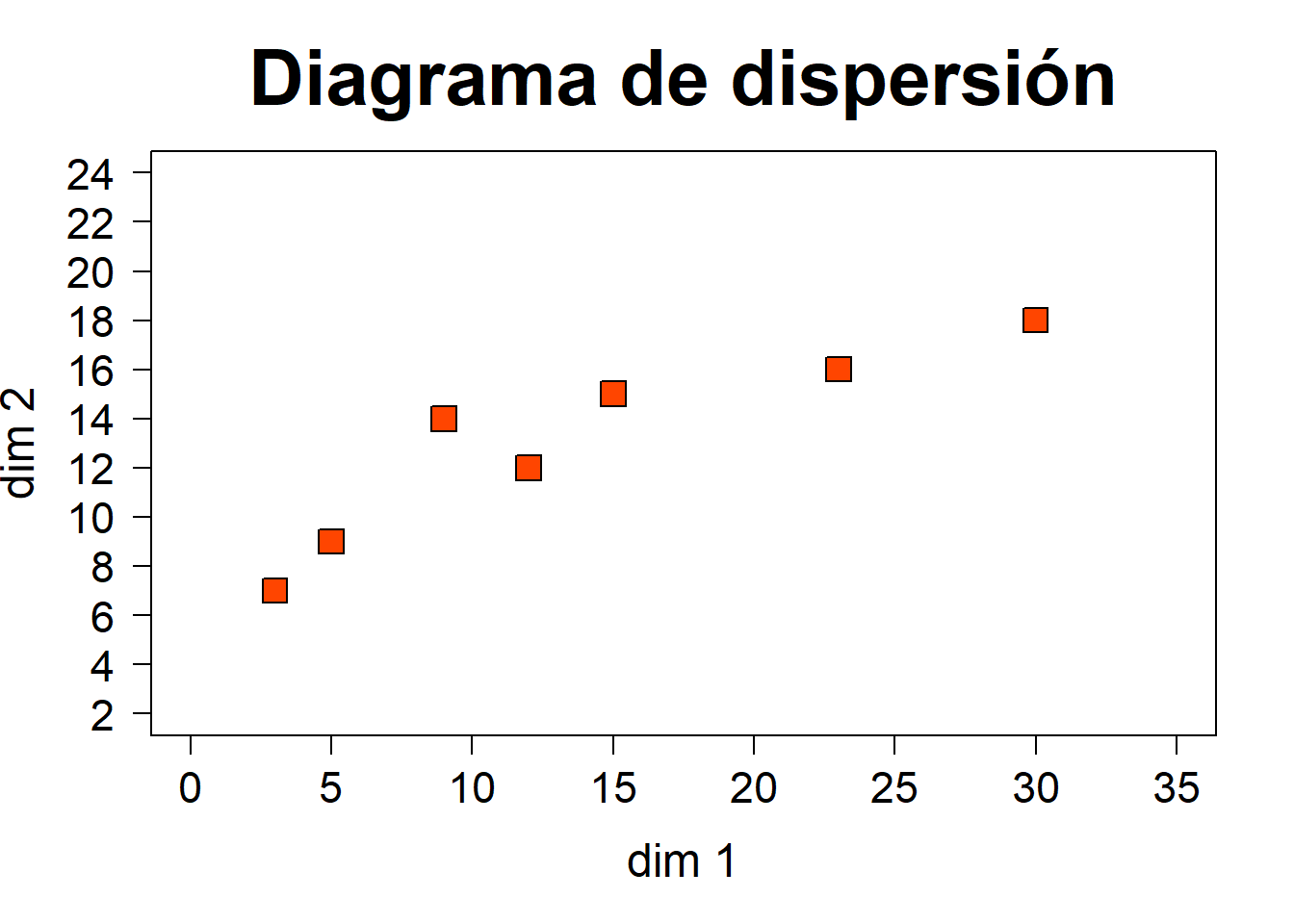
Para incluir puntos adicionales en un gráfico, se usa la función points, con las coordenadas de los puntos como primer(os) argumento(s), tal y como se indicó para la función plot.
Supóngase que, tras construir el diagrama anterior, se corre la siguiente instrucción.
points(c(10, 20, 30), c(8, 22, 14),
pch = 24, bg = "blue", cex = 2.5)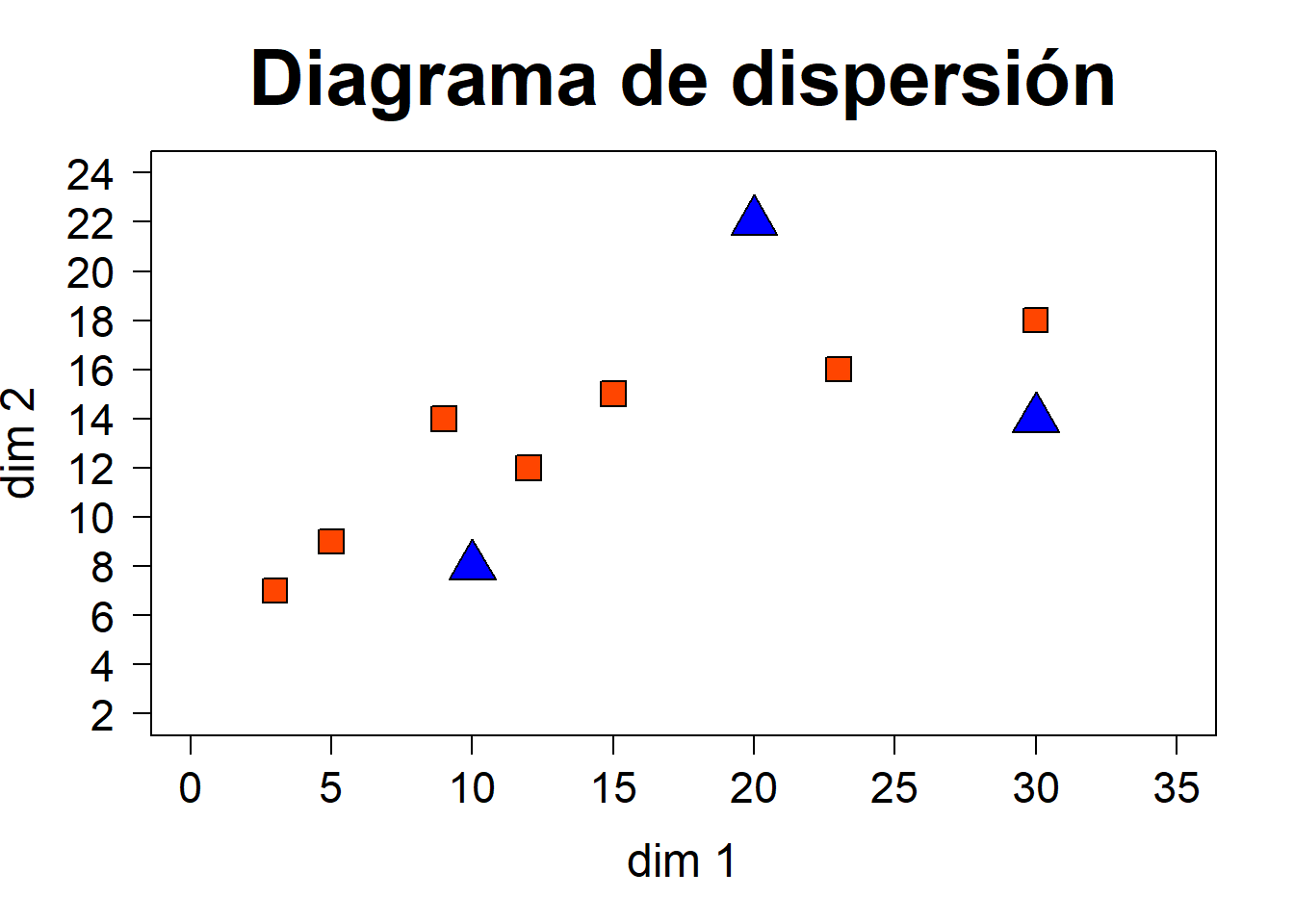
En ocasiones se requiere identificar cada punto con una etiqueta. Esto puede hacerse mediante la función text, bien sea manteniendo el punto y agregando la etiqueta o eliminando la impresión del punto y dejando únicamente la etiqueta. Para eliminar la impresión del punto, se incluye el argumento type = 'n', en la función plot. La función text tiene como primer(os) argumento(s) las coordenadas, tal y como se describió para la función plot; mediante el argumento labels, que debe estar conformado por un vector de caracteres, se especifica el texto que se desea imprimir.
etiq.puntos <- c('a12', 'd31', 'f23', 'a34', 'g18', 'b52', 'g49')
plot(x, y, type = 'n')
text(x, y, labels = etiq.puntos, cex = 0.7, col = 'blue')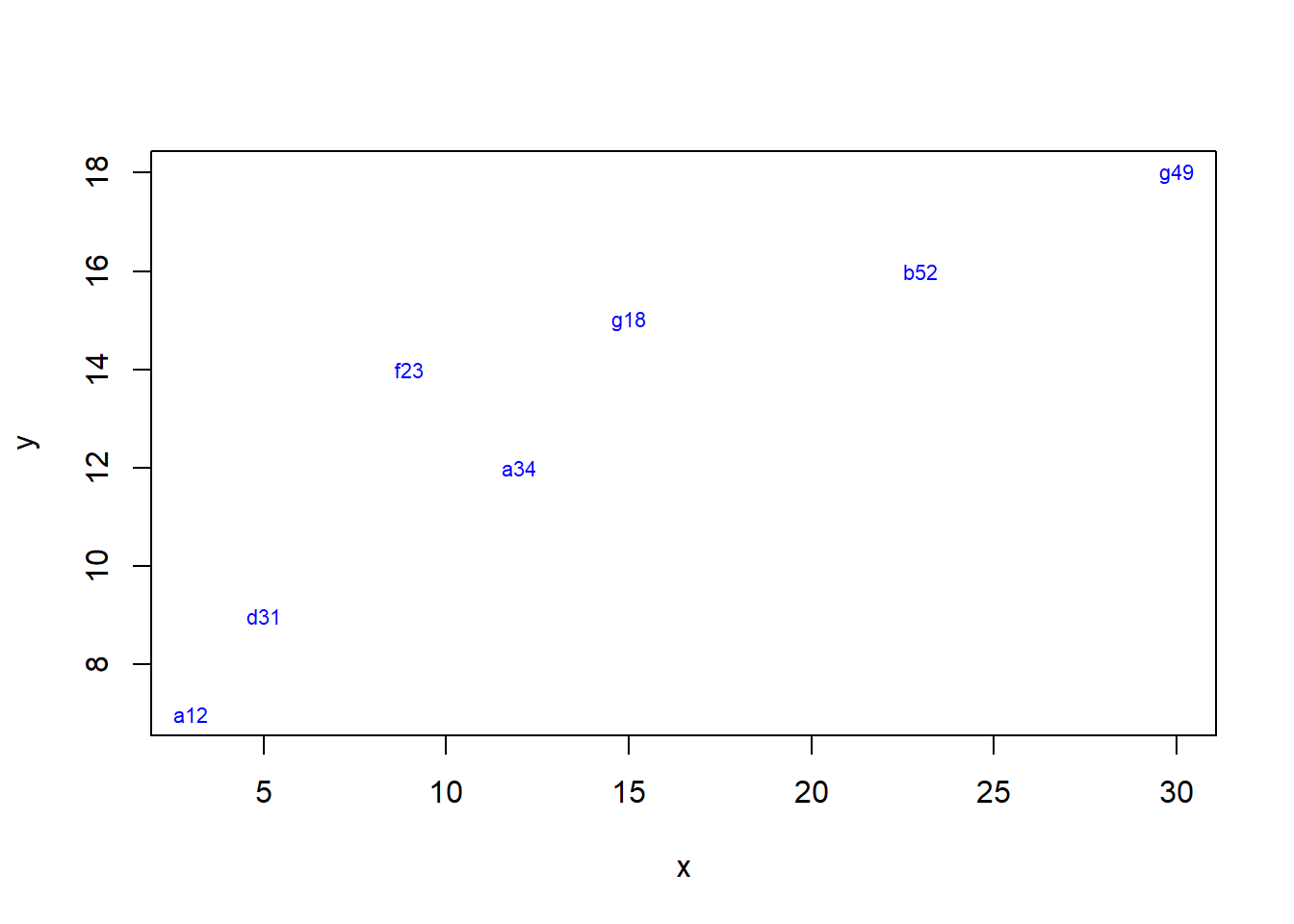
Si se ha optado por adicionar la etiqueta, manteniendo también la impresión del punto, puede resultar conveniente realizar un ajuste al sitio en el que se grafica la etiqueta, de manera que no se sobreponga con el símbolo de identificación para el punto. Para tal efecto, se utiliza el argumento pos, el cual puede tomar una de los siguientes valores numéricos: 1 (debajo de las coordenadas especificadas), 2 (a la izquierda), 3 (encima), 4 (a la derecha).
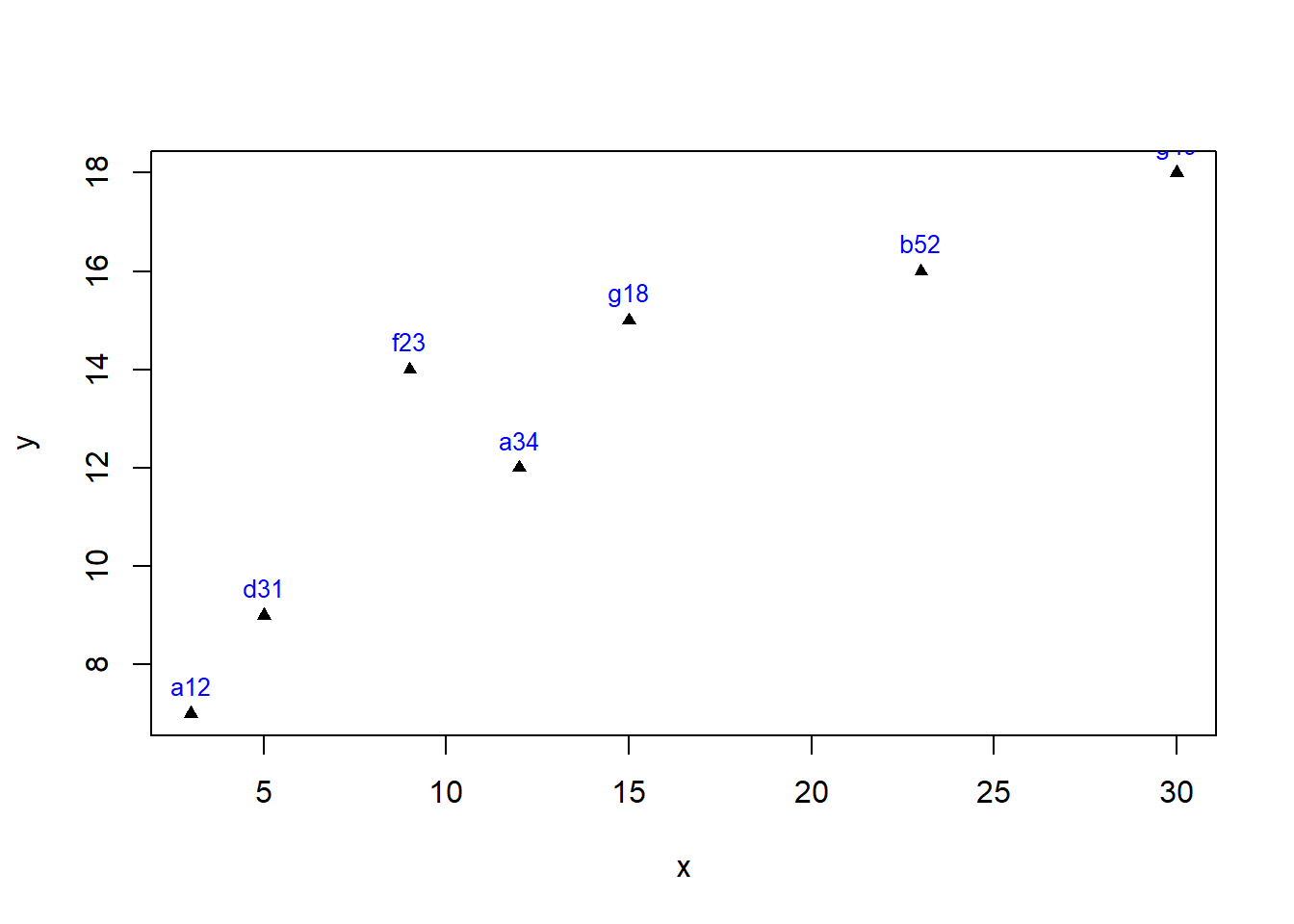
La función text es bastante versátil, pudiendo usarse para incorporar cualquier texto en cualquier lugar del gráfico. Basta con definir las coordenadas que han de servir de centro para el texto en cuestión. Mediante el argumento labels se indica la cadena de caracteres. Adicionalmente pueden incorporarse otros argumentos como font para la fuente, col para el color, cex para el tamaño (character expansion) y srt (string rotation) para rotar la cadena de caracteres en un ángulo determinado.
plot(0:5, 0:5, type = "n", xlab = "", ylab = "")
text(0, 3, "texto a 90°", srt = 90, col = "red", font = 6, cex = 1.5)
text(5, 3, "texto a 270°", srt = 270, col = "blue", font = 3)
text(2.5, 1, "texto a 180°", srt = 180, col = "orange")
text(2.5, 3, "texto a 45°", srt = 45, col = "green", cex = 2)
El siguiente conjunto de instrucciones permite generar gráficos guía para los símbolos, colores y tipos de línea más comunes, usando códigos numéricos para su elección. Todas las instrucciones utilizadas ya han sido presentadas anteriormente, excepto matplot, que aparece en la sección 19.3. Este es un recurso que vale la pena tener a la mano.
a <- matrix(rep(0:25, 10), nrow = 10, ncol = 26, byrow = T)
# Símbolos ----------------------------------------------------
matplot(a, lty = 1, pch = c(0:25), col = 1, main = "pch = c(0:25)",
axes = F, ylab = "", cex = 1.4)
axis(2, at = 0:25, cex.axis = 0.9, las = 1)
abline(h = c(0:25), lty = 3)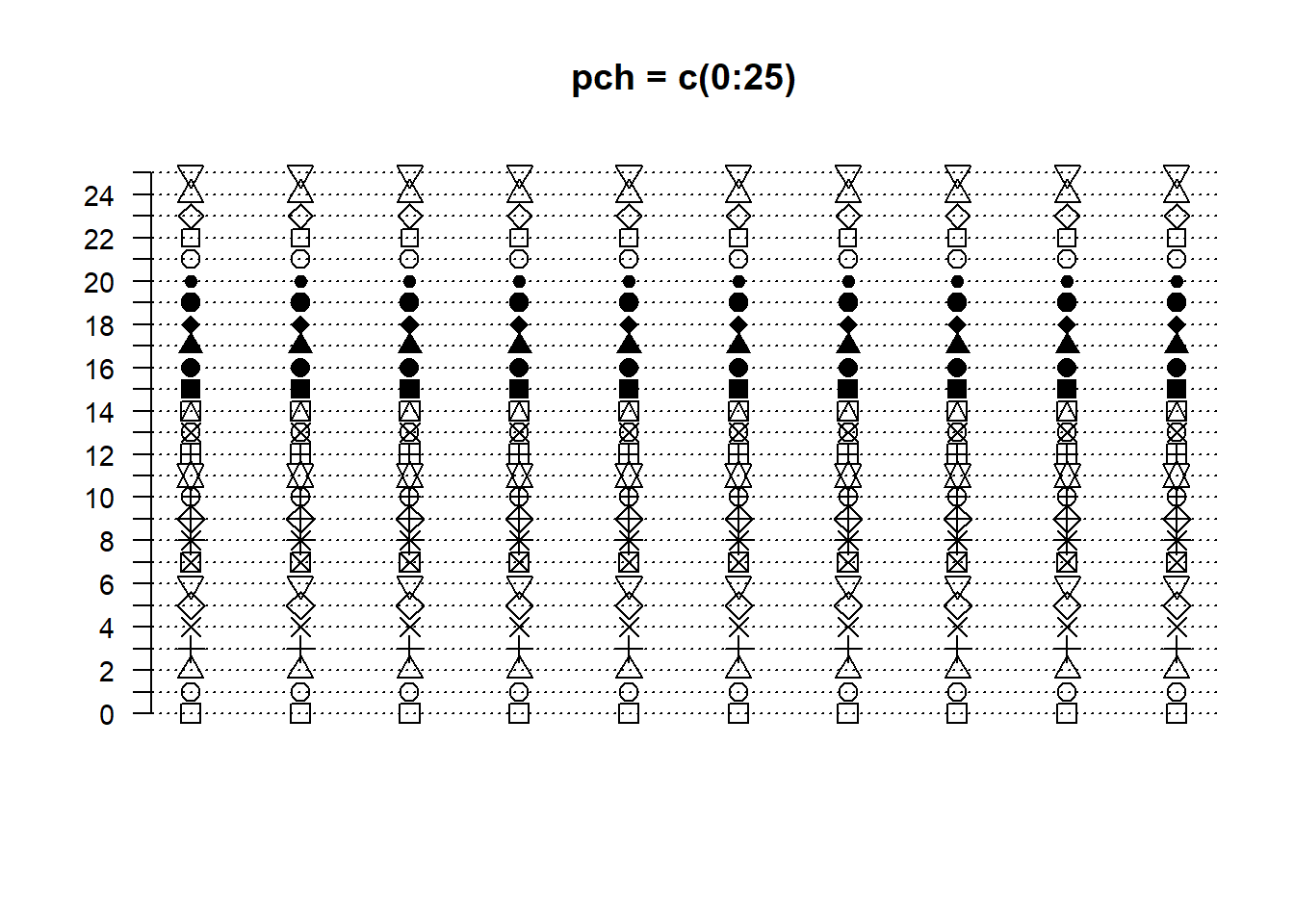
# Colores -----------------------------------------------------
matplot(a[, 1:10], lty = 1, col = 0, axes = F, ylab = "",
main = "col = c(0:8)", cex = 1.4)
axis(2, at = 0:8, cex.axis = 0.9, las = 1)
abline(h = 0:8, lty = 1, col = 0:8, lwd = 4)
# Trazados de línea -------------------------------------------
matplot(a[, 1:7], pch = (20), col = 1, main = "lty = c(0:6)",
axes = F, ylab = "", cex = 1.4)
axis(2, at = seq(0, 6), cex.axis = 0.9, las = 1)
abline(h = 0:6, lty = 0:6)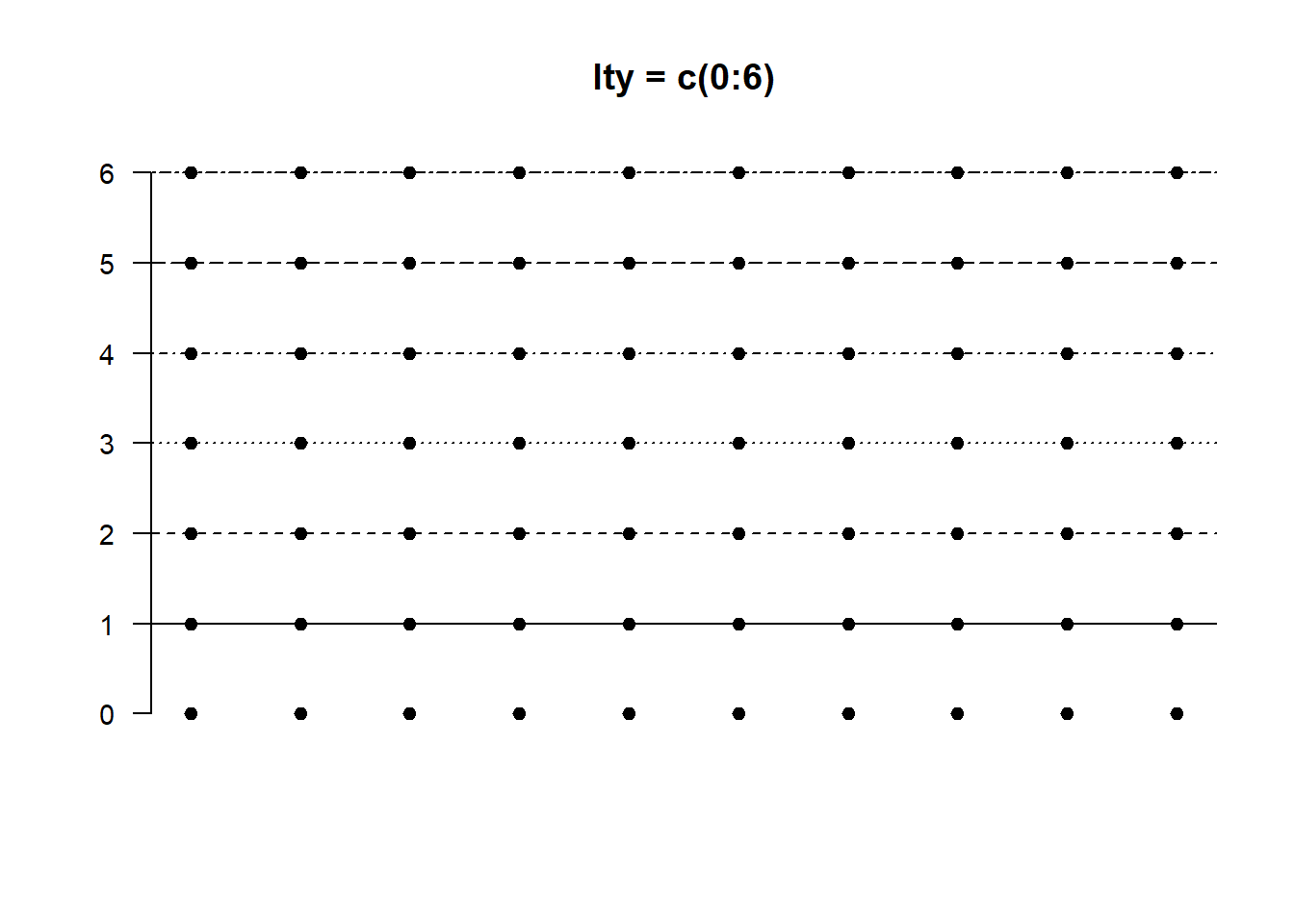
19.2 Diagramas de dispersión por grupos
La generación de un diagrama de dispersión en el que los puntos estén diferenciados por colores y/o símbolos, acorde con su membresía a un grupo determinado, podría lograrse mediante la personalización de la función plot. No obstante, su construcción puede llegar a ser bastante dispendiosa. Este tipo de diagramas puede generarse rápidamente mediante la función xyplot{lattice}.
La función xyplot requiere un primer argumento en el que las coordenadas se expresen mediante una fórmula. Para lograr la diferenciación por grupos, debe indicarse el correspondiente criterio a través del argumento groups. Si adicionalmente se desea generar una leyenda, es necesario incluir el argumento auto.key = T.
Para ilustrarlo, considérese el data frame iris, que forma parte del paquete datasets de R, el cual contiene información sobre la longitud y el ancho del sépalo y el pétalo de tres especies de flores del género Iris (I. setosa, I. versicolor e I. virginica). El diagrama de dispersión se construirá con base en las coordenadas de un Análisis de Componentes Principales, el cual se ejecuta en la primera línea y se guarda en la lista pc, diferenciando por especie.
pc <- princomp(iris[1:4]) # Análisis de Componentes Principales
library(lattice)
xyplot(pc$scores[, 2] ~ pc$scores[, 1], groups = iris$Species,
pch = 21:23, xlab = "PC 1", ylab = "PC 2", auto.key = T)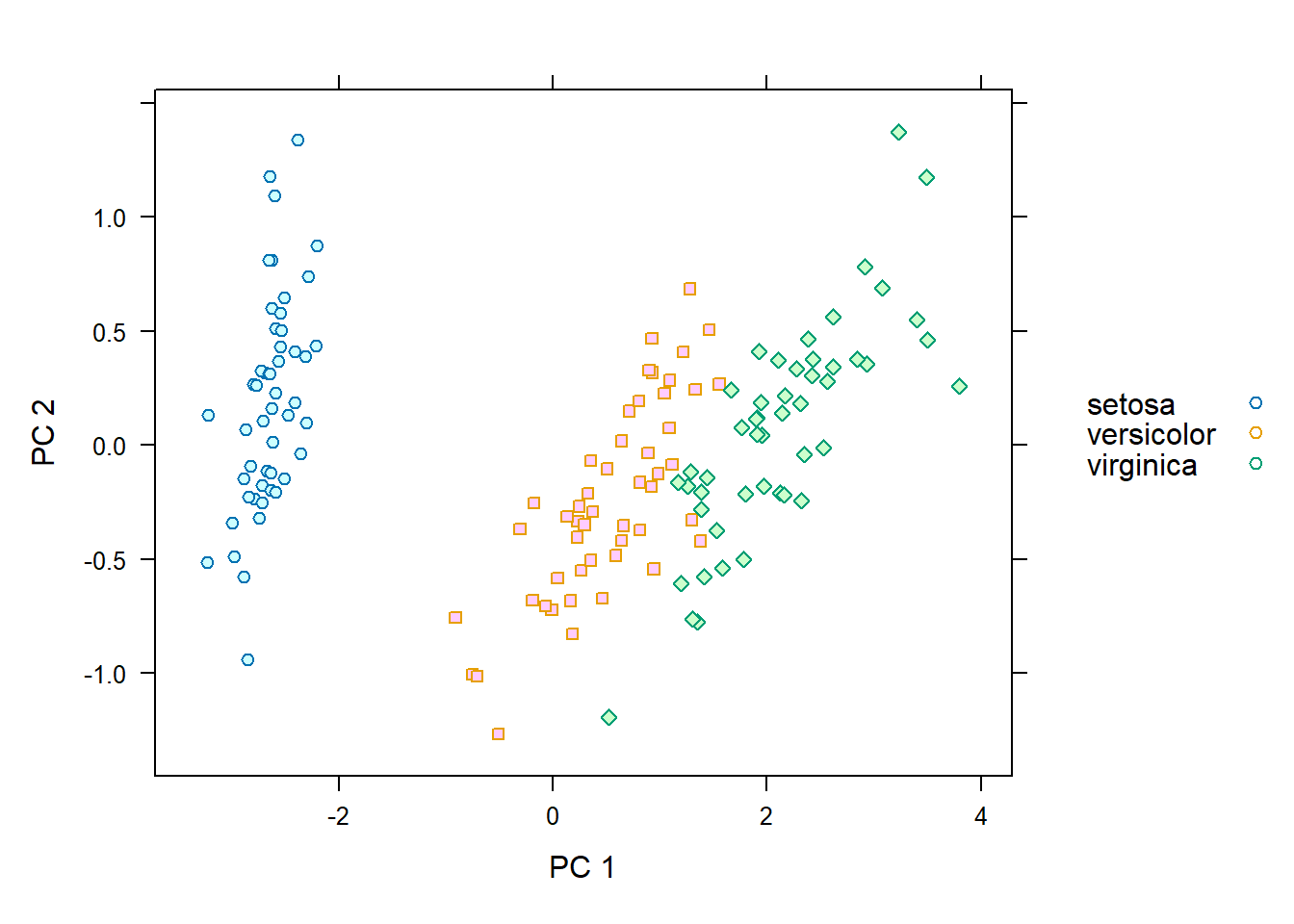
19.3 Series
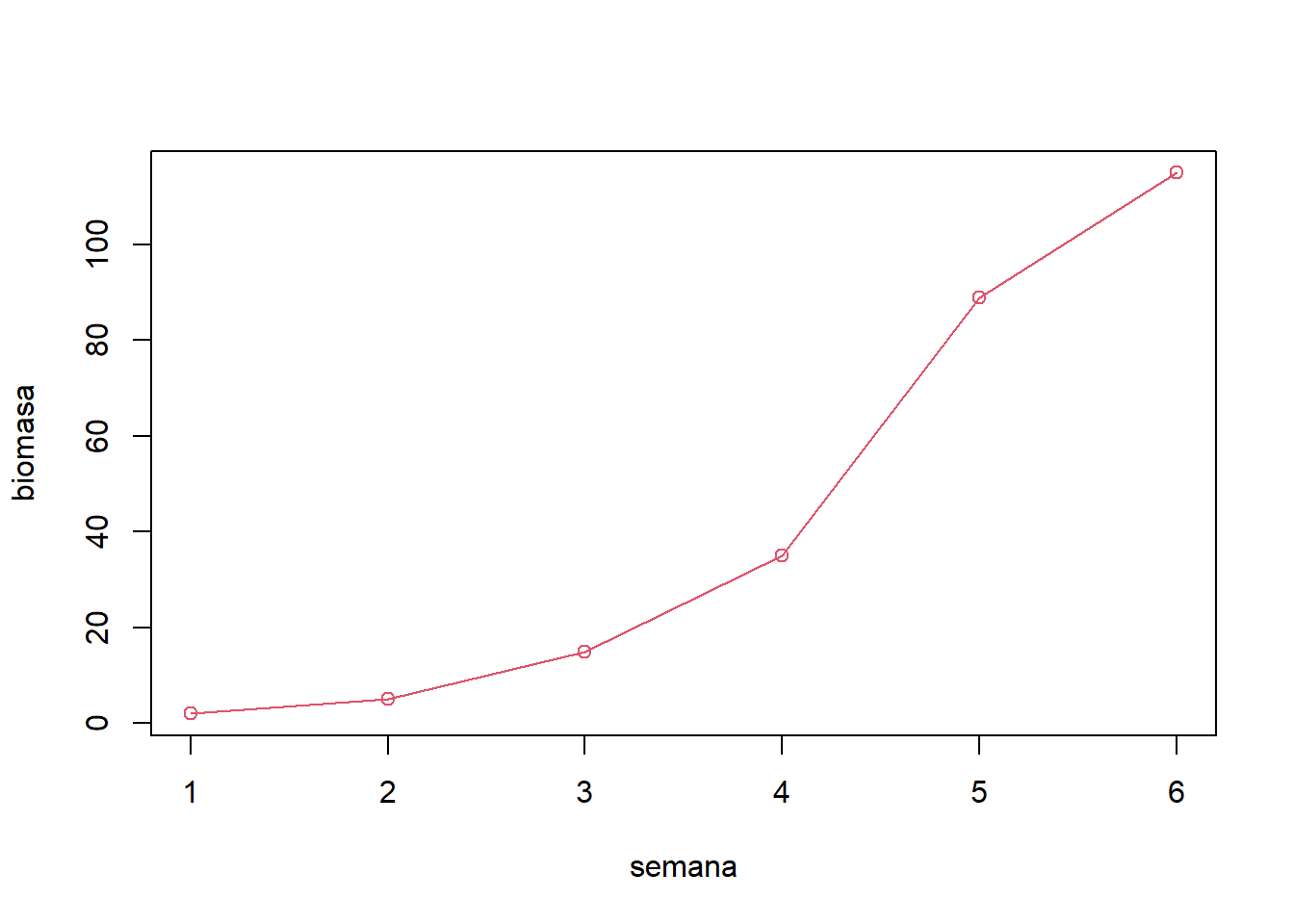
Una serie consiste en un conjunto ordenado de datos numéricos, cada uno de cuyos valores usualmente corresponde a la lectura de una variable en un tiempo dado. Así, la siguiente tabla representa una serie de datos de biomasa, evaluada a lo largo de seis semanas.
| Semana | Biomasa |
|---|---|
| 1 | 2 |
| 2 | 5 |
| 3 | 15 |
| 4 | 35 |
| 5 | 89 |
| 6 | 115 |
Son usuales las representaciones gráficas con la variable índice (usualmente el tiempo) en el eje horizontal y la variable principal en el eje vertical, uniendo cada punto de la serie mediante un segmento de línea. Para tal efecto puede usarse la función plot, con el argumento type = "b", o type = "o", en adición a cualquiera de los argumentos reseñados en la sección correspondiente a diagramas de dispersión (cf. sección 19.1). El argumento lty (line type), que puede tomar cualquier valor entre 0 y 6, define el tipo de línea, siendo 1 la línea continua (valor por defecto). El argumento lwd (line width), que puede tomar el valor de cualquier entero positivo (por defecto 1), permite definir el ancho de la línea.
Es bastante frecuente que se requiera mostrar varias series en un mismo gráfico. Aunque para ello también podría usarse la función plot con ciertas adecuaciones, resulta más práctico el uso de la función matplot{graphics}, la cual reconoce los mismos argumentos que la función plot (cf. sección 19.1).
Para el presente caso se usaría como primer argumento la variable índice (el tiempo) y como segundo argumento las diferentes series. Si se omite el argumento correspondiente a la variable índice, este se genera de manera automática con los enteros entre 1 a n, siendo n el número de observaciones.
Considérese la siguiente información.
| Mes | Serie1 | Serie2 | Serie3 |
|---|---|---|---|
| Enero | 147 | 8 | 20 |
| Febrero | 146 | 14 | 50 |
| Marzo | 144 | 26 | 114 |
| Abril | 141 | 46 | 134 |
| Mayo | 138 | 76 | 150 |
| Junio | 132 | 100 | 158 |
| Julio | 115 | 114 | 162 |
| Agosto | 89 | 126 | 165 |
| Septiembre | 35 | 134 | 167 |
| Octubre | 15 | 138 | 169 |
| Noviembre | 5 | 140 | 170 |
| Diciembre | 2 | 141 | 170 |
Supóngase que, usando cualquiera de las funciones reseñadas en el capítulo 6, se incorpora la anterior información en un data frame llamado datos. A continuación, podría usarse la siguiente línea para graficar las tres series.
matplot(datos[, 2:4], type = "b")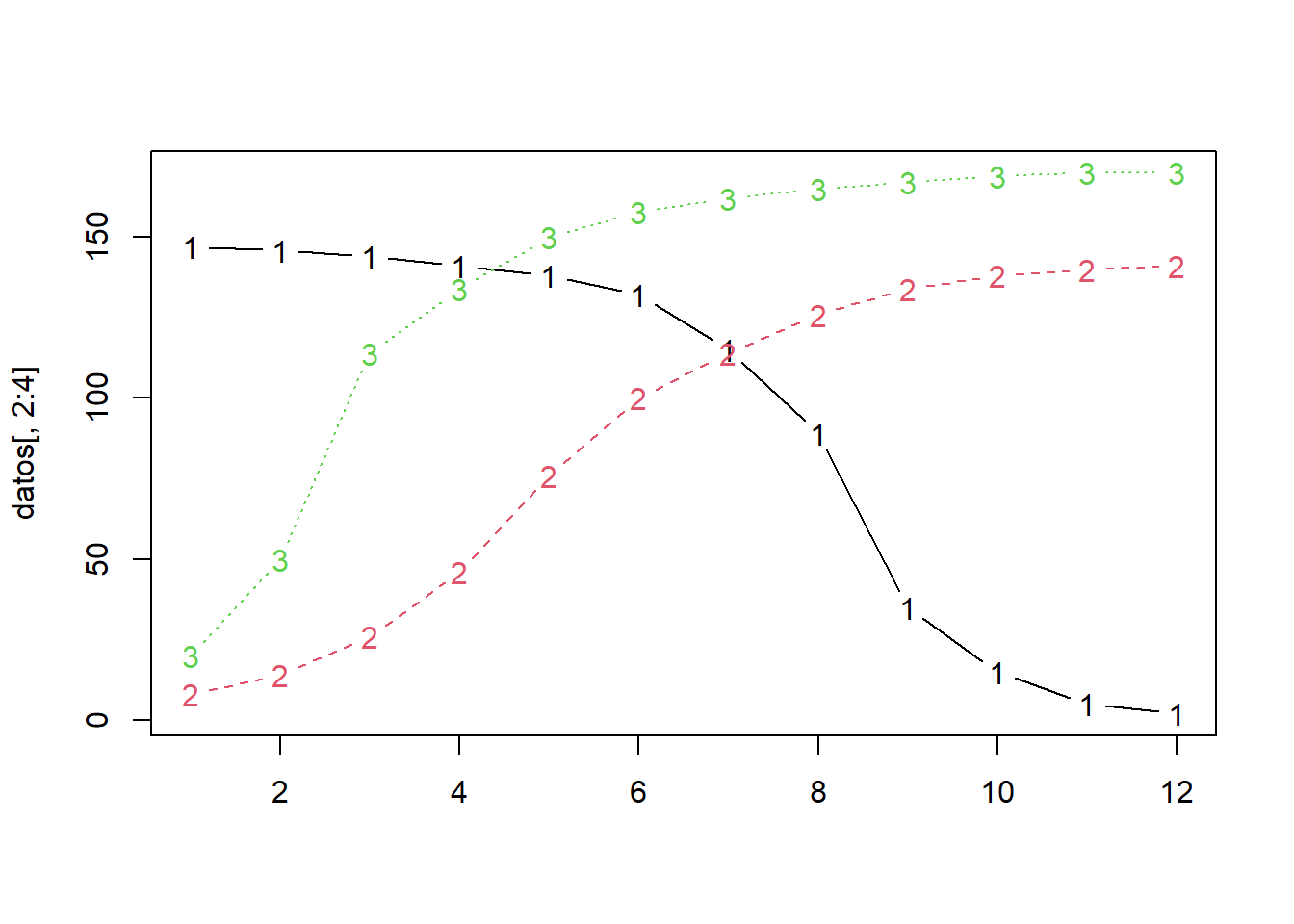
Aunque se cumple el objetivo de graficar las tres series de manera simultánea, el resultado no es muy llamativo. No obstante, usando algunas opciones de personalización, mediante los argumentos adecuados, puede lograrse un mejor resultado.
matplot(datos[, 2:4], type = "o", xlab = " ", ylab = "Biomasa",
pch = c(2, 8, 15), col = c(2,3,4), axes = F, lty = 1)
axis(1, at = seq(1, 12), labels = datos[[1]], cex.axis = 0.9, las = 2)
axis(2, at = seq(0, 190, 20), cex.axis = 0.9, las = 1)
box()
legend(6, 70, names(datos[, 2:4]), col = c(2, 3, 4), cex = 0.9,
pch = c(2, 8, 15), lty = 1)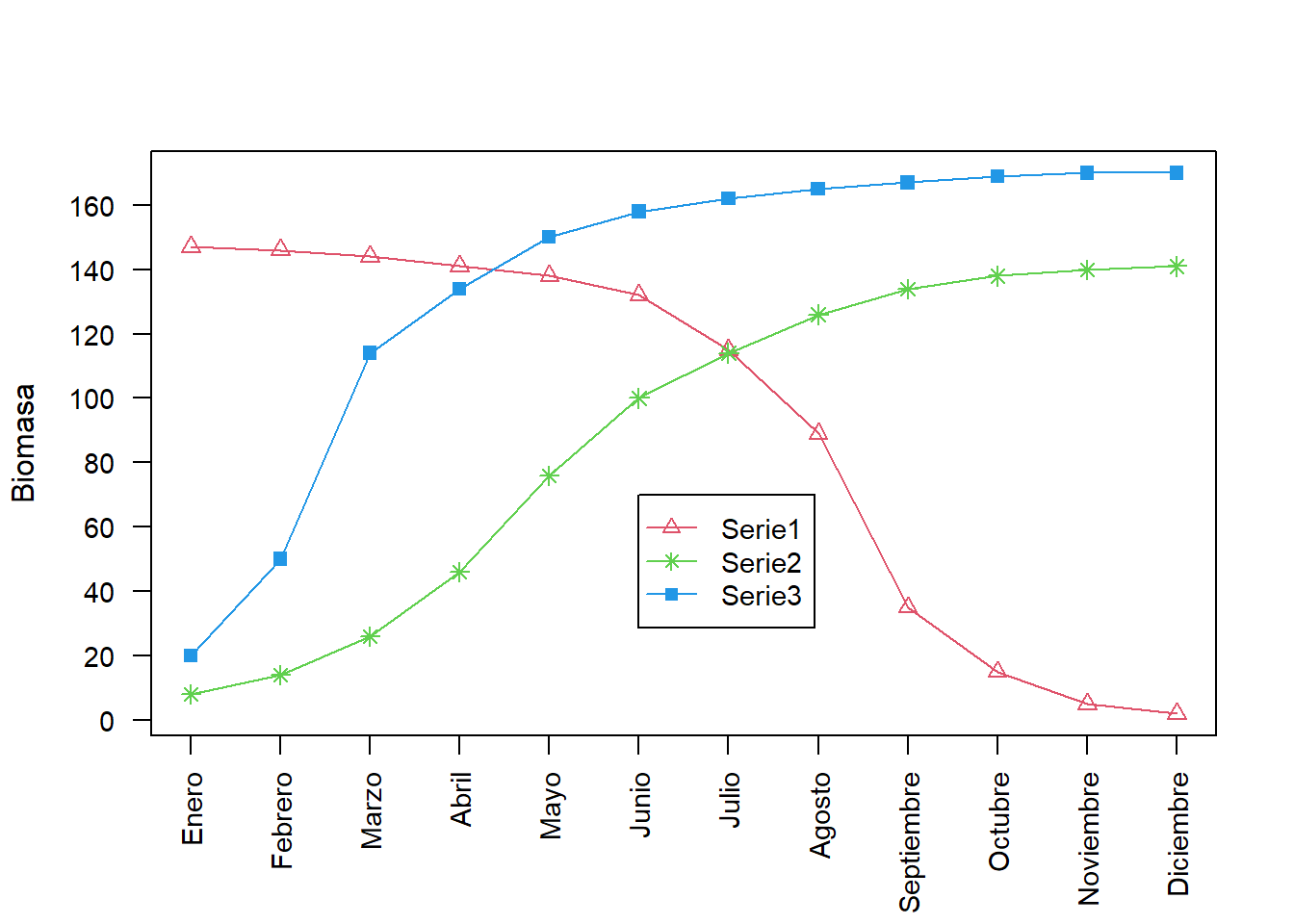
19.4 Diagramas de caja y bigotes (Box-and-whiskers plot)
Una de las características del lenguaje de programación orientado a objetos es el polimorfismo. Para el caso de las funciones, esto significa que, manteniendo el mismo nombre, estas pueden comportarse diferentemente, acorde con las características del objeto que les sirva de argumento. Ese es el caso de la función plot, que se adapta a los argumentos de entrada. Ya se ilustró cómo al usar argumentos numéricos se obtiene un diagrama de dispersión. Cuando se usa un argumento tipo factor para la abscisa y uno numérico para la ordenada se genera un diagrama de caja y bigotes.
La base de datos warpbreaks{datasets} contiene información sobre el número de rupturas (breaks) del hilo en un proceso de tejido, bajo diferentes tensiones (L: low, M: medium y H: high).
plot(breaks ~ tension, data = warpbreaks, xlab = "tension", ylab = "breaks",
col = "khaki1")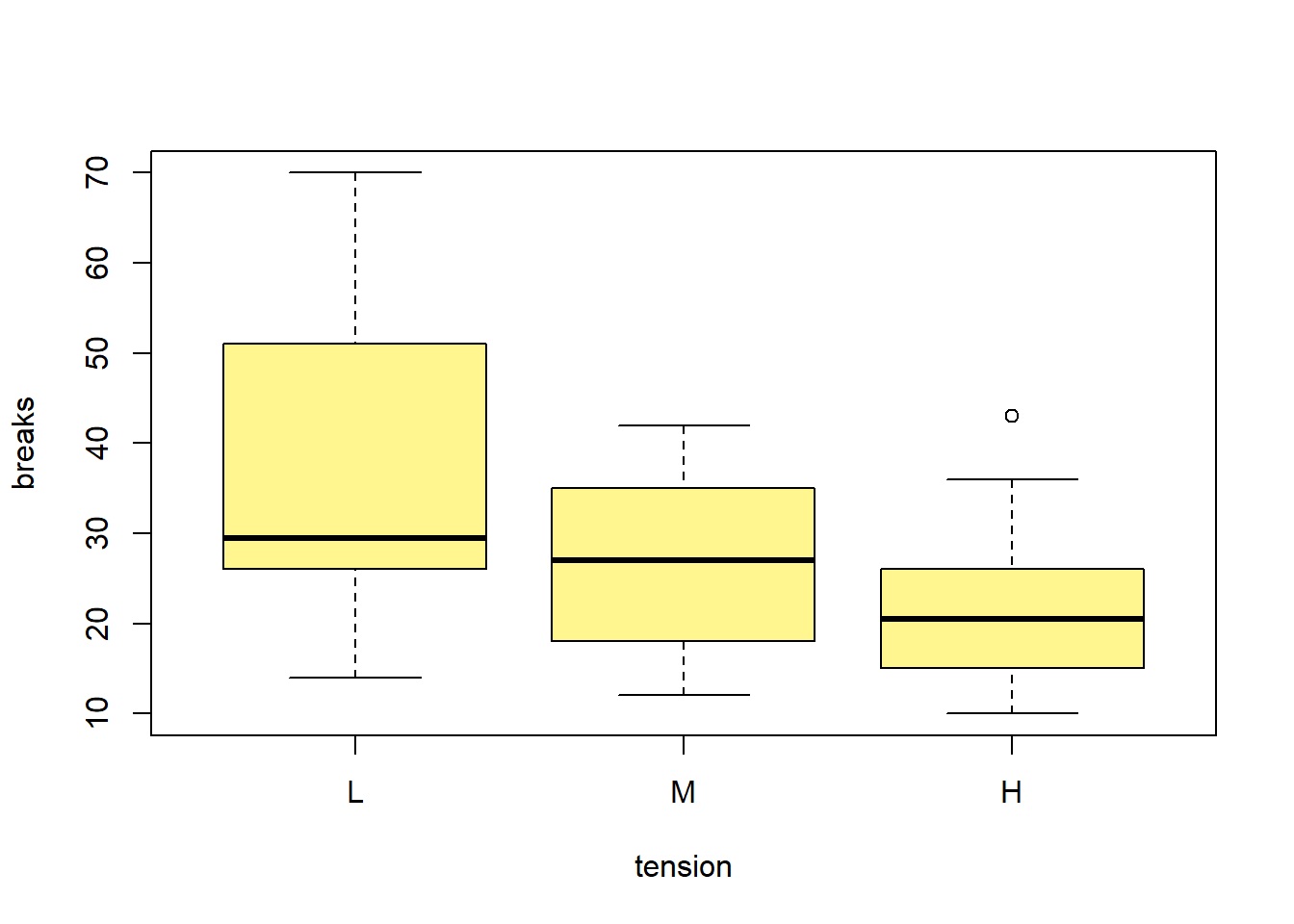
19.5 Diagramas de barras
La función barplot{graphics}, con el argumento height permite construir un diagrama de barras básico, siendo height un vector con las alturas de las barras.
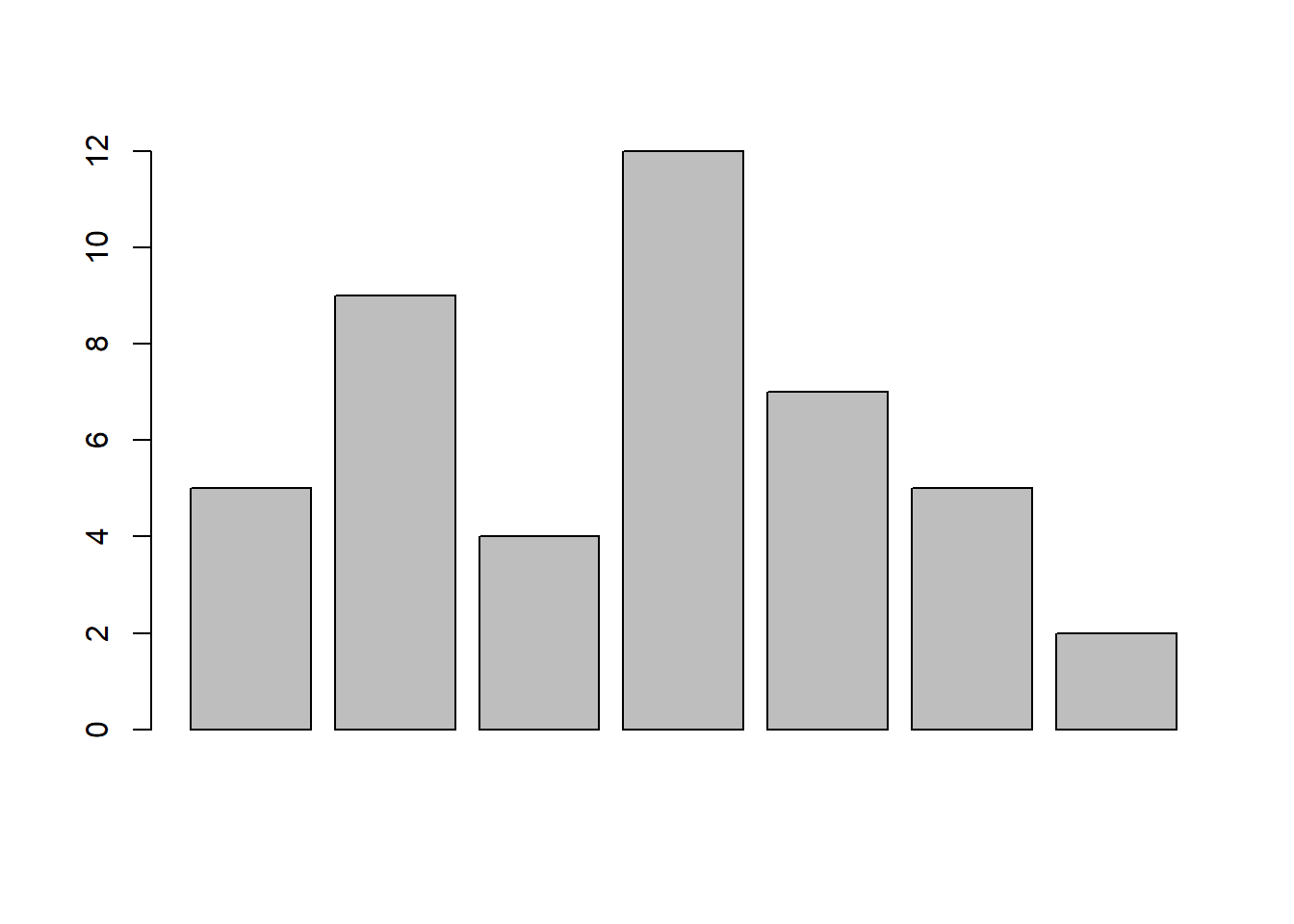
Para etiquetar cada una de las barras, se usa el argumento names.arg:
et <- c('tto5', 'tto2', 'tto1', 'tto7', 'tto6', 'tto3', 'tto4')
h <- c(5, 9, 4, 12, 7, 5, 2)
barplot(height = h, names.arg = et)Muchos de los argumentos usados en la función plot (cf. sección 19.1) funcionan de manera análoga en la función barplot. Así, col permite cambiar el color de las barras; xlab y ylab se usan para asignar etiquetas a los ejes horizontal y vertical, respectivamente, y cex.lab para modificar el tamaño de tales etiquetas; main se usa para definir el título principal y cex.main para modificar su tamaño; cex.axis permite modificar el tamaño de los valores que definen la escala del eje vertical; font se usa para cambiar las fuentes de ambas escalas; ylim y xlim permite redefinir las escalas vertical y horizontal, respectivamente; el argumento las se usa para establecer la dirección en que se grafican los valores de los ejes. Asimismo, es posible usar el argumento axes = F en conjunción con las funciones axis para definir cada uno de los ejes de manera personalizada, tal y como se ilustró para la función plot, pudiendo usarse también la función box para encerrar todo el diagrama en una caja.
En adición a los anteriores argumentos, se usa el argumento cex.names para definir un factor de expansión para el tamaño de las etiquetas de las barras. El argumento axis.lty = 1 dibuja el eje horizontal, el cual está suprimido por defecto (axis.lty = 0). El argumento border permite cambiar el color por defecto (negro) del borde. El argumento density permite definir la densidad del trazado usado para llenar las barras. Una densidad igual a cero dará lugar a una barra vacía, sin ningún trazo interior; densidades entre uno y aproximadamente 100 (dependiendo del tamaño del diagrama) darán lugar a barras con trazos oblicuos con diferentes niveles de separación, densidades por encima de 300 generan barras sólidas.
Para dibujar barras horizontales, en lugar de verticales (valor por defecto), se usa el argumento horiz = T.
Los argumentos optativos col, border y density pueden definirse con un único valor, en cuyo caso, todas las barras tendrán el mismo aspecto. También es posible definir un valor diferente para cada barra. En caso de que la longitud del vector con los valores de cualquiera de tales argumentos sea menor que el número de barras, tales valores se reciclan, es decir, que se repiten cíclicamente (cf. sección 9.4).
barplot(height = h, names.arg = et, xlab = "Grupos",
ylab = "Frecuencia", cex.lab = 1.5, cex.axis = 1.2, cex.names = 1.2,
las = 1, axis.lty = 1, col = "salmon1", density = c(0, 5, 30, 300),
border = c(1, 'blue', 'red'), ylim = c(0,15))
box()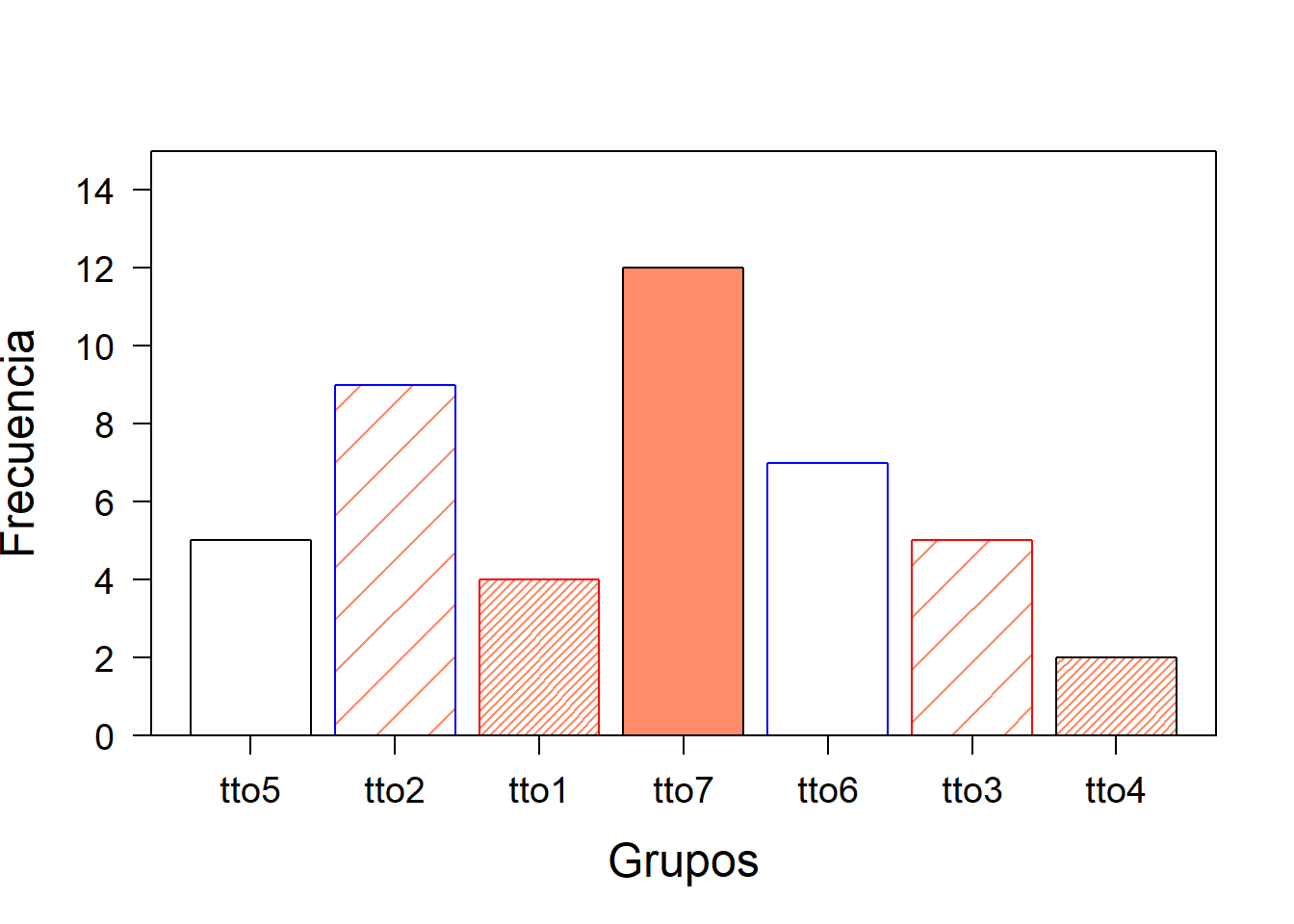
Cuando se usa una matriz numérica como argumento principal (height) de la función barplot, se genera un diagrama de barras por grupos. Por defecto, cada una de las variables se apila (beside = F); no obstante, si se usa el argumento beside = T, se generan grupos de barras por categoría.
Para ilustrarlo, considérese nuevamente el data frame iris, ya presentando en la sección 19.3.
data("iris")
L.sepalo <- with(iris, tapply(Sepal.Length, Species, mean))
A.sepalo <- with(iris, tapply(Sepal.Width, Species, mean))
L.petalo <- with(iris, tapply(Petal.Length, Species, mean))
A.petalo <- with(iris, tapply(Petal.Width, Species, mean))
(datos <- rbind(L.sepalo, A.sepalo, L.petalo, A.petalo))
#> setosa versicolor virginica
#> L.sepalo 5.006 5.936 6.588
#> A.sepalo 3.428 2.770 2.974
#> L.petalo 1.462 4.260 5.552
#> A.petalo 0.246 1.326 2.026El objeto datos es una matriz de 4 filas y 3 columnas. Las filas corresponden con cada una de las medidas tomadas en las flores y cada una de ellas tiene un nombre, el cual puede verificarse con la función rownames(datos); las columnas corresponden a cada una de las categorías de agrupación (especies, en este caso).
Al construir un diagrama de barras con un objeto como el presente, usando el argumento legend = T, se genera una leyenda con base en los nombres de las filas, la cual ubica por defecto en la esquina superior derecha.
barplot(datos, col = c("skyblue", "orchid1", "#f9d99a",
"wheat4"), beside = T, ylim = c(0, 10), legend = T,
xlab = "especie", ylab = "centímetros", cex.lab = 1.5,
cex.names = 1.5, las = 1)
box()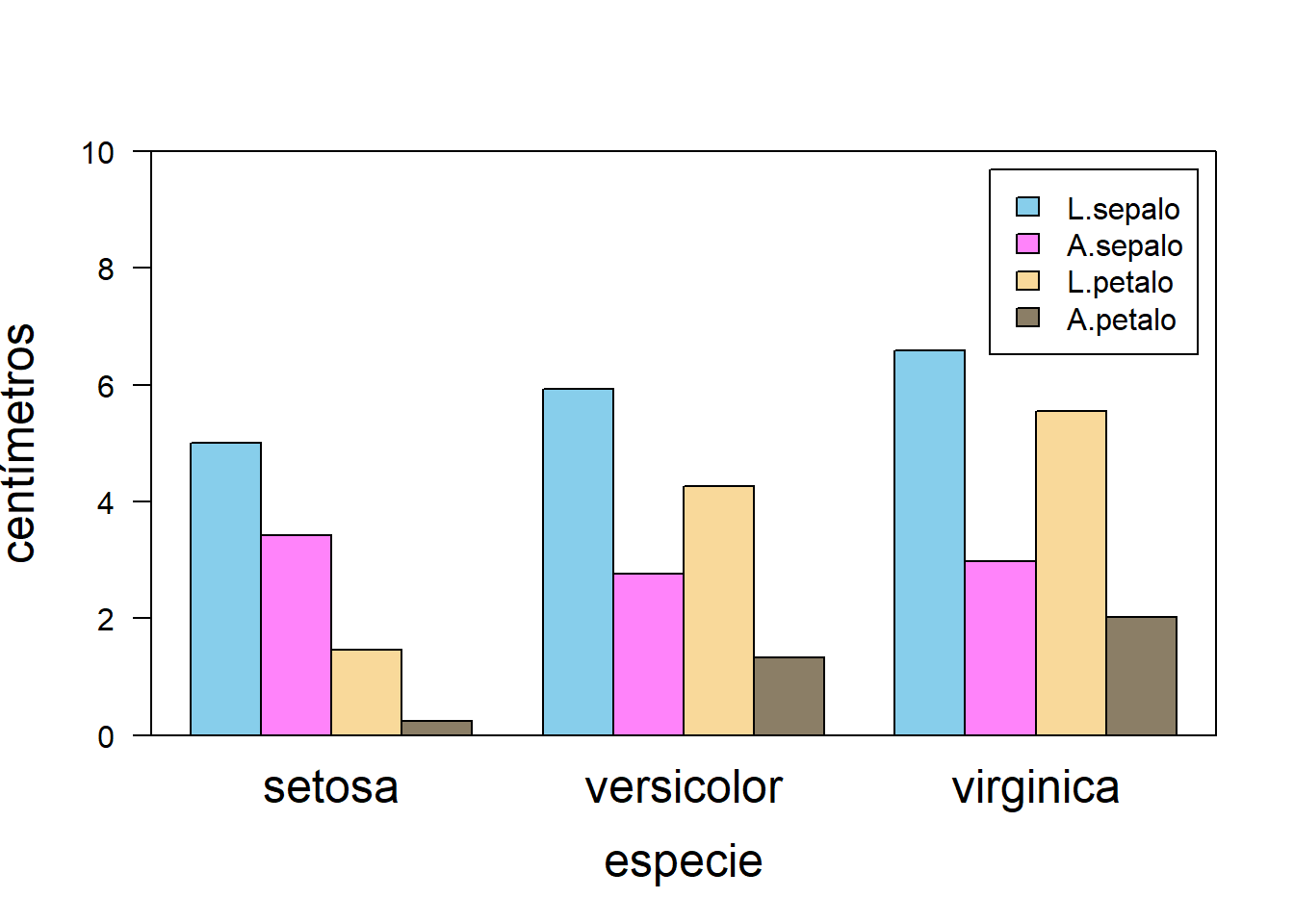
Supóngase ahora que se desea construir un diagrama de barras, agrupando las distintas especies por variable. Para el efecto, basta con trabajar sobre la transpuesta de la matriz datos, realizando las adecuaciones del caso en lo concerniente a colores.
Para personalizar la leyenda, se omite el argumento legend = T y se genera aparte, con la función legend, tal y como se ilustra a continuación.
barplot(t(datos), beside = T, col = c("blueviolet", "#fa5f49",
"cadetblue1"), ylim = c(0, 11), xlab = "medida",
ylab = "centímetros", cex.lab = 1.5, cex.names = 1.3,
las = 1)
legend(1, 10, c("I. setosa", "I. versicolor", "I. virginica"),
fill = c("blueviolet", "#fa5f49", "cadetblue1"),
cex = 0.9)
box()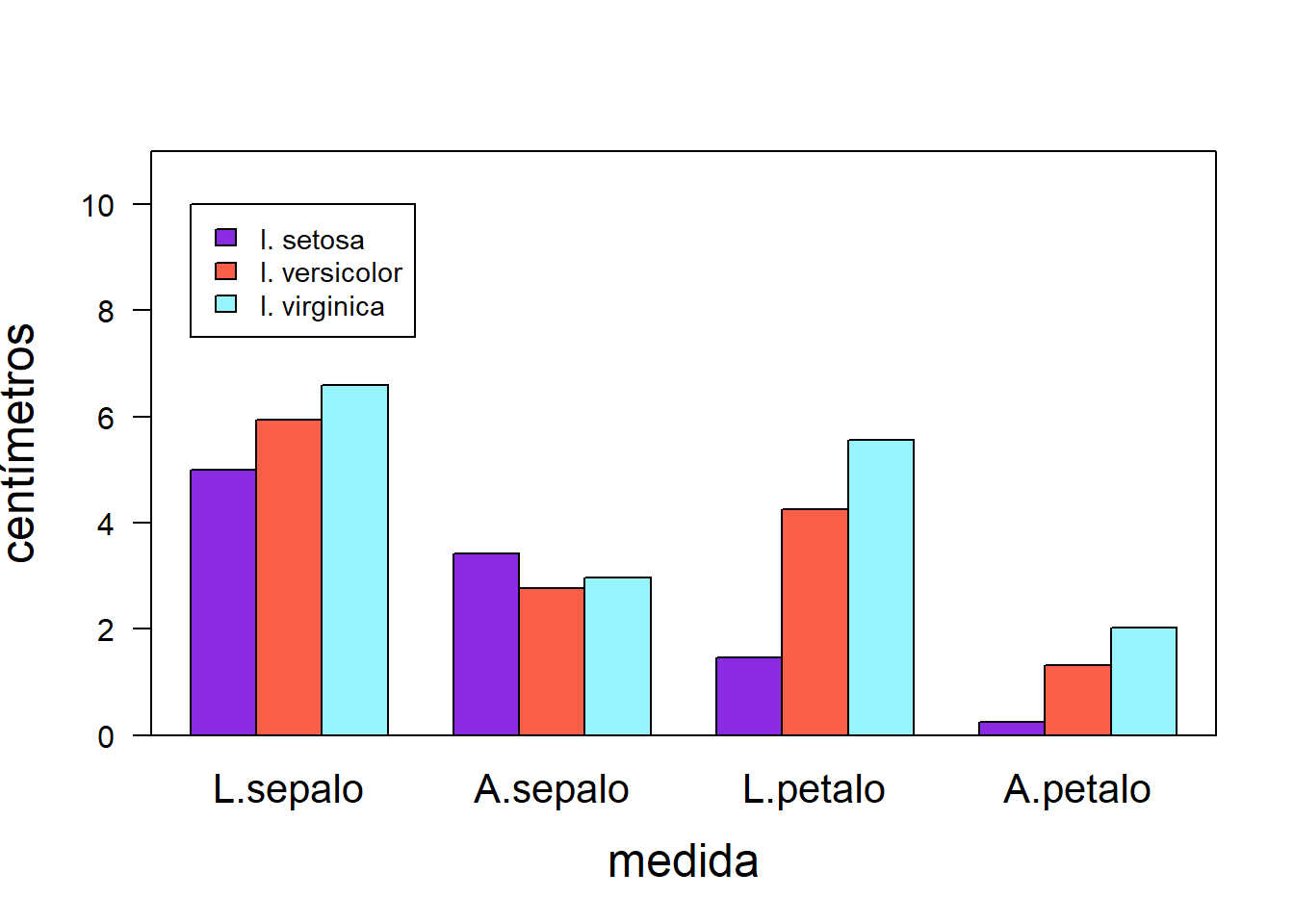
19.6 Rectas
Las funciones abline , lines, segments y arrows permiten trazar líneas o segmentos de líneas sobre un gráfico, que tiene que haber sido creado previamente.
Para trazar líneas horizontales, se usa la función abline con el argumento h; para líneas verticales, con el argumento v. En adición puede modificarse el tipo de línea, su color y su ancho, mediante los argumentos lty, col y lwd, respectivamente (cf. secciones 19.1 y 19.3).
Cuando se traza más de una línea, el uso de un único valor por argumento modificador da lugar a una serie de líneas de igual aspecto. Si se usan diferentes valores, estos se asignan a cada una de las líneas trazadas, reciclándose de ser necesario (cf. sección 9.4).
plot(NA, xlim = c(0, 20), ylim = c(0, 10), type = 'n', xlab = '',
ylab = '')
abline(v = seq(0, 20, 2), col = seq(1, 8), lty = seq(1,6),
lwd = seq(1,11))
abline(h = seq(0, 10, 2), col = c('gold4', 'maroon'),
lty = c(3, 1), lwd = 3)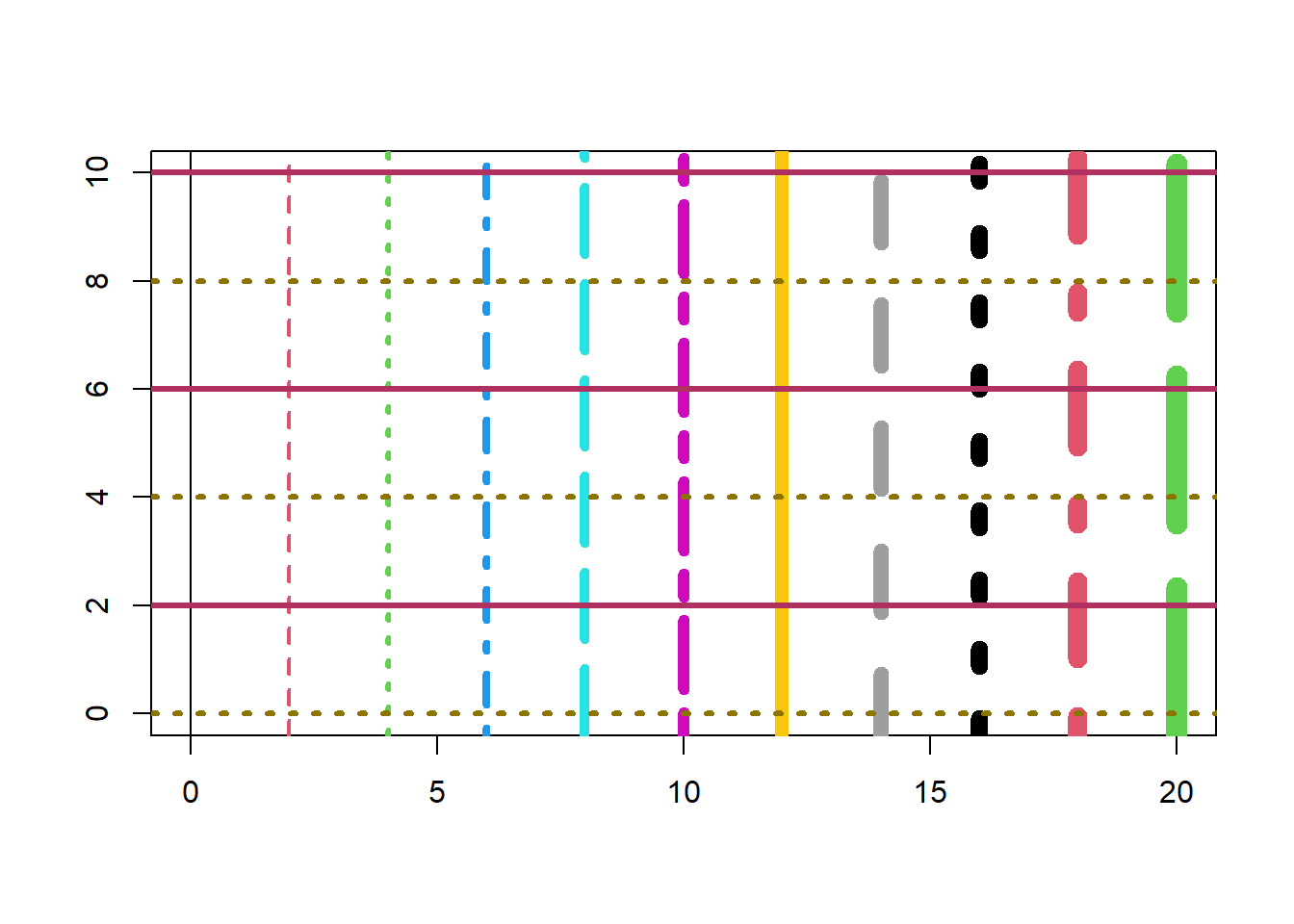
Puede usarse la función abline, especificando el intercepto (a) y la pendiente (b), para dibujar una recta cualquiera (sobre un gráfico generado previamente).
abline(2, 1, lwd = 3)
abline(10, -1, lwd = 3)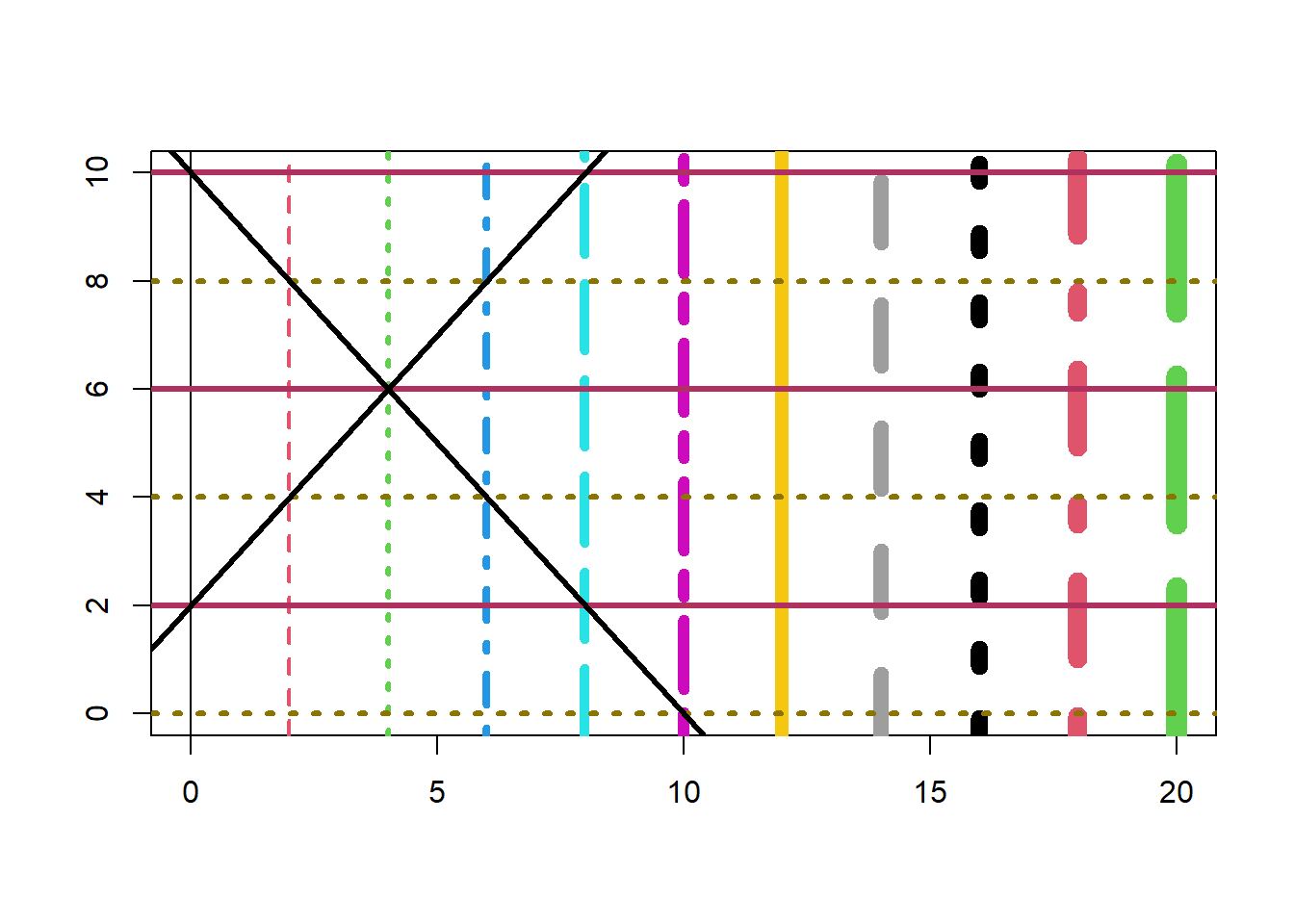
Los coeficientes a y b pueden presentarse en un vector de dos elementos. Así, las anteriores instrucciones podrían escribirse equivalentemente de la siguiente forma:abline(c(2, 1), lwd = 3)
abline(c(10, -1), lwd = 3)La función abline también admite como argumento de entrada un objeto con dos coeficientes, tal y como los objetos de la clase lm, que se generan al ajustar un modelo de regresión rectilínea simple.
Nótese que en todos los casos anteriores, la línea trazada cubre completamente el marco de graficación. Para trazar una línea que una un par de puntos cualesquiera, se usan la funciones lines, segments y arrows.
Para trazar una línea que una el punto (5, 4) con el punto (20, 6), se usa el siguiente código.
lines(c(5, 20), c(4, 6))Esta forma de definir los argumentos puede parecer un poco antiintuitiva; no obstante, cobra sentido, si se considera que el primer argumento contiene las coordenadas x, mientras que el segundo contiene las coordenadas y. En este caso, el segmento de recta va de 5 a 20 en la abscisa y de 4 a 6 en la ordenada.
Para este mismo fin puede usarse la función segments. No obstante, es necesario reescribir las coordenadas, pues el formato de entrada es diferente. La función segments maneja cuatro argumentos independientes para las coordenadas (no pueden agruparse en vectores): x0, y0, x1 y y1. Los dos primeros argumentos (x0 y y0) son obligatorios y definen las coordenadas del punto de origen. Los argumentos x1 y y1, de los cuales al menos uno de ellos es obligatorio definen las coordenadas del punto final. En caso de que no se suministre un valor para x1, este se toma igual a x0, con lo cual se traza una línea vertical; si el valor faltante fuera y1, se tomaría el mismo valor de y0, lo que produce una línea horizontal.
Para trazar la misma línea que se ilustró mediante la función lines, se usa:
segments(x0 = 5, y0 = 4, x1 = 20, y1 = 6)O simplemente:
segments(5, 4, 20, 6)Para trazar una línea horizontal pasando por y = 4, que vaya desde x = 5 hasta x = 15, se usa:
segments(x0 = 5, y0 = 4, x1 = 15)Para dibujar una flecha, se usa la función arrows, cuyas coordenadas se indican, usando el mismo formato que para la función segments. La longitud de la cabeza de la flecha puede modificarse con el argumento length; el ángulo de apertura de la cabeza de la flecha, con el argumento angle.
A continuación, se presenta un gráfico conformado por rectas, en el que se usan las funciones abline, lines, segments y arrows.
plot(NA, xlim = c(0, 20), ylim = c(0, 10), type = 'n',
xlab = '', ylab = '')
abline(h = 0, lty = 3)
abline(h = 10, lty = 3)
abline(v = 0, lty = 3)
abline(v = 20, lty = 3)
lines(c(0, 20), c(0, 10), col = "blue", lwd = 2)
lines(c(0, 20), c(10, 0), col = "blue", lwd = 2)
segments(5, 2, 5, 8, col = "red")
segments(15, 2, y1 = 8, col = "red")
segments(5, 2, 15, 2, col = "red")
segments(5, 8, 15, col = "red")
arrows(10, 5, 10, 8, col = "green")
arrows(10, 5, y1 = 2, col = "green", length = 0.1)
arrows(10, 5, y1 = 2, col = "green", length = 0.1)
arrows(10, 5, 15, col = "green", length = 0.1, angle = 60)
arrows(10, 5, 5, col = "green", length = 0.1, angle = 10)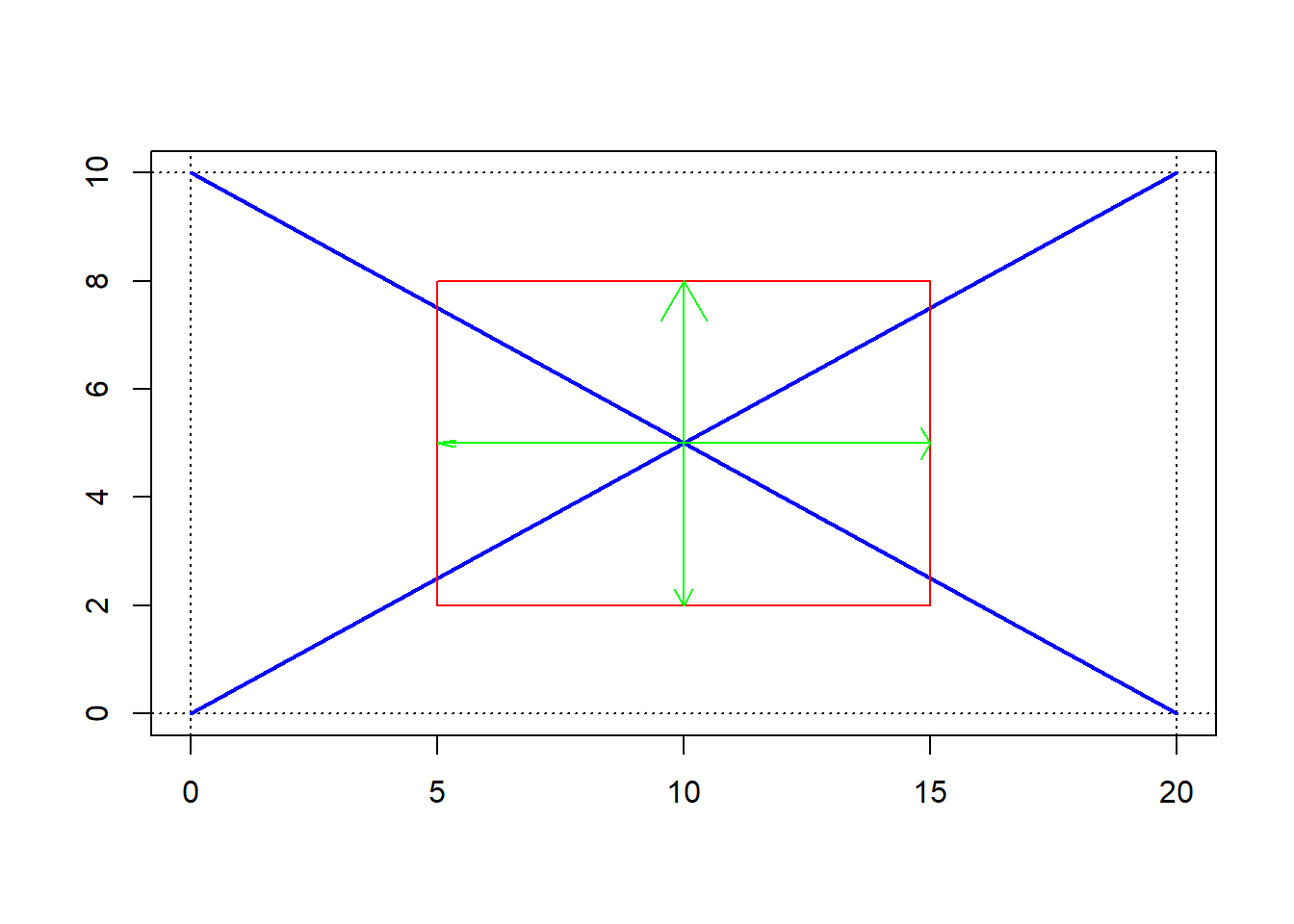
Para construir un polígono mediante la función lines, basta con usar como primer argumento un vector con todas las coordenadas de la abscisa (x) y como segundo argumento un vector con todas las coordenadas de la ordenada (y).
plot(NA, xlim = c(0, 100), ylim = c(0, 100), type = 'n',
xlab = '', ylab = '')
lines(c(20, 0, 20, 50, 80, 100, 80),
c(0, 20, 60, 90, 60, 20, 0), col = "red")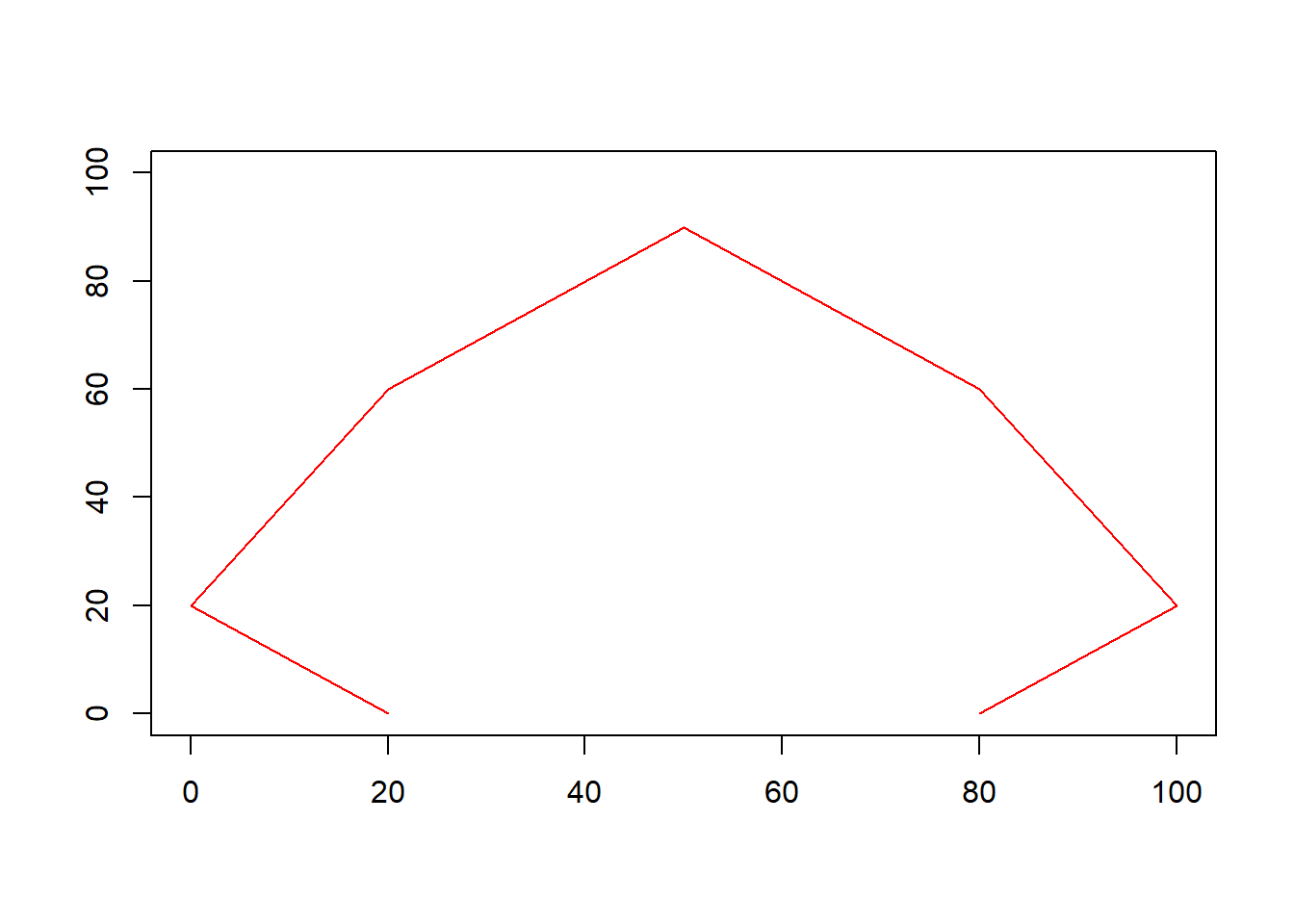
Usando un juego de coordenadas como el ilustrado anteriormente como argumentos de la función polygon, se obtienen un polígono cerrado. Adicionalmente, pueden usarse los argumentos density para definir la densidad del relleno (por defecto, relleno sólido; 0, para no usar relleno), angle para definir el ángulo de las líneas de relleno y border para definir el color del borde.
plot(NA, xlim = c(0, 100), ylim = c(0, 100), type = 'n',
xlab = '', ylab = '')
polygon(c(20, 0, 20, 50, 80, 100, 80),
c(0, 20, 60, 90, 60, 20, 0), col = "chocolate1",
density = 5, angle = 30)
polygon(c(20, 0, 20, 50, 80, 100, 80),
c(0, 20, 60, 90, 60, 20, 0), col = "red",
density = 10, angle = 45, border = "black")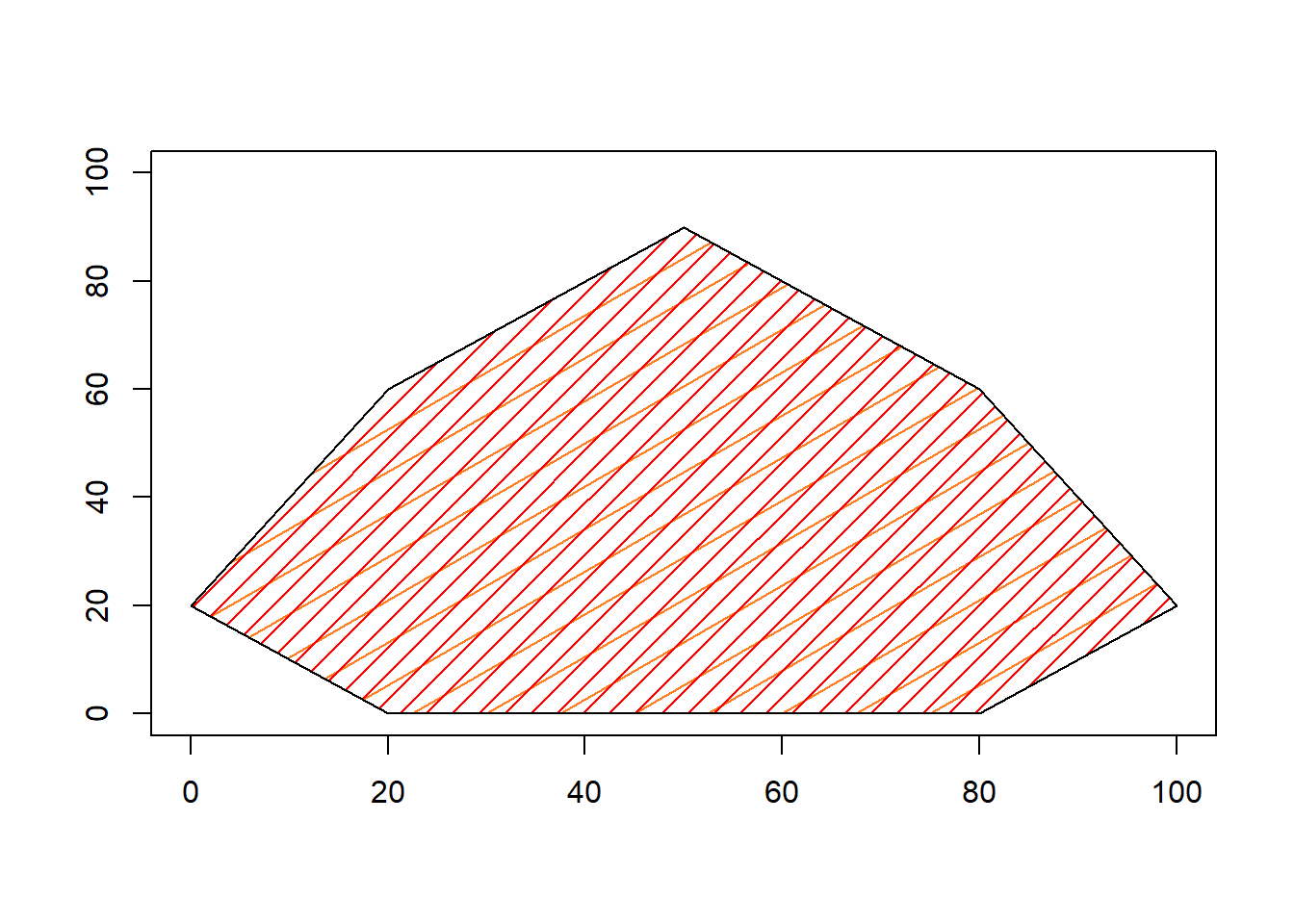
19.7 Parámetros generales
La función par{graphics} establece o muestra los valores de los parámetros que rigen el comportamiento de los gráficos creados mediante las funciones del paquete graphics. Los parámetros establecidos mediante esta función no afectan los gráficos que se generan mediante las funciones del paquete lattice (xyplot).
Al invocar par(), se obtiene una lista de tamaño 72, con dichos valores. Los valores contenidos en dicha lista actúan como valores por defecto de las funciones que contengan argumentos con el mismo nombre. Es posible verificar o modificar individualmente cualquiera de tales parámetros.
par()$lwd
#> [1] 1Esto significa que el valor por defecto del parámetro lwd (ancho de línea) es 1. Por tanto, todas las funciones gráficas que involucren ancho de línea trabajarán con dicho valor, excepto aquellas en las que dicho argumento se modifique explícitamente.
Si se desea que el valor por defecto del ancho de línea sea, por ejemplo, 3, se escribe:
par(lwd = 3)El parámetro mar está constituido por un vector de cuatro valores que representan las márgenes inferior, izquierda, superior y derecha, respectivamente. Sus valores por defecto son 5.1, 4.1, 4.1 y 2.1.
El parámetro mgp está constituido por un vector de tres valores que representan las márgenes para las etiquetas de los ejes, los marcadores de los ejes y las líneas de los ejes. Sus valores por defecto son 3, 1 y 2.
Es posible definir simultáneamente varios parámetros gráficos, mediante una sola invocación a la función par:
par(mar = c(3, 1, 1, 2), mgp = c(1, 1, 3), col = 'green')Algunos parámetros no existen como argumentos de las funciones de graficación, por lo que únicamente pueden establecerse mediante la función par. Entre estos, es de particular importancia el parámetro new, cuyo valor por defecto es falso, con lo cual se genera un nuevo gráfico cada vez que se llama una función de graficación. Si se desea superponer varias gráficas, es necesario establecer par(new = T). Este parámetro se reinicia a FALSE cada vez que se invoca una función de graficación. Luego, para superponer, por ejemplo, tres gráficas construidas mediante la función plot, se usaría el siguiente esquema.
plot(argumentos)
par(new = T)
plot(argumentos)
par(new = T)
plot(argumentos)19.8 Dispositivos gráficos
Se denomina dispositivo gráfico (graphical device) al medio hacia el cual se envía un gráfico. Puede tratarse de la pantalla o de un archivo en un formato determinado.
Cada dispositivo se identifica con un nombre. Estos son los dispositivos más comunes de salida por pantalla:
-
windows: ventana en sistema operativo Windows. -
quartz: ventana en Mac. -
x11: ventana en Unix/Linux.
Estos son los dispositivos de archivo (o formatos de archivo) más comunes:
-
pdf: archivo en formato pdf. -
svg: archivo en formato svg. -
tiff: archivo en formato tiff. -
png: archivo en formato png. -
jpeg: archivo en formato jpg. -
bmp: archivo en formato bmp.
Por defecto, los gráficos se muestran en pantalla. Los que se generan directamente en R, sin ninguna IDE, se envían a una ventana. Cuando se usa RStudio, los gráficos se envían al panel gráfico de esta interfaz.
Es común generar salidas por pantalla para los análisis exploratorios iniciales. Los archivos, por su parte, resultan más prácticos para compartir con otros usuarios, para imprimir y para incorporar en los informes.
Una vez surtido el análisis exploratorio inicial, en el que suele graficarse en pantalla, es común enviar los gráficos a algún dispositivo de archivo para uso posterior. Cada dispositivo cuenta con una función homónima.
Existe una función para cada uno de los formatos, la cual abre o activa el dispositivo en cuestión. Todo lo que se grafique a continuación —mientras el dispositivo se mantenga abierto— se envía a dicho dispositivo, es decir, se guarda en un archivo con el formato especificado. Para concluir el proceso, se requiere cerrar o desactivar el dispositivo.
Las siguientes instrucciones ilustran el proceso de graficación en un archivo pdf.
pdf()
plot(rnorm(100), rnorm(100))
dev.off()
La función dev.off se usa desactivar cualquier dispositivo de archivo, dejando activo el dispositivo de pantalla.
Vale la pena señalar que cuando se usan dispositivos de archivo, cada gráfico genera un archivo, excepto si se usa el dispositivo pdf, en cuyo caso se genera un solo archivo con un gráfico por hoja. Esto puede resultar útil para recoger de manera compacta numerosas salidas gráficas.
Los argumentos width y height permiten personalizarse el tamaño de las salidas (ver ayudas).
Los dispositivos pdf y svg generan gráficos vectoriales, mientras que los dispositivos
tiff, png, jpeg y bmp generan gráficos basados en pixeles. Los gráficos vectoriales ofrecen una apariencia impecable en gráficos basados en líneas y curvas con colores sólidos, mientras que los gráficos basados en pixeles reflejan de manera más realista objetos con bordes irregulares o indefinidos, así como diversas gamas y matices de color, lo cual puede resultar muy deseable cuando se procesan imágenes.