4 PONDERACIÓN

La ponderación que se le asigne a una variable que forme parte de la definición de una dimensión indica qué tan importante es dicha variable dentro de la dimensión considerada. En este caso, las variables que se consideren más importantes/informativas llevarán altas ponderaciones; en contraste, las variables que se consideren poco importantes/informativas irán con ponderaciones bajas.

Debe tenerse presente que algunas variables que, pudiendo ser conceptualmente importantes/informativas, no son fáciles de registrar ya sea por acceso, costo, tiempo, imprecisión o cualquier otro factor, lo que a menudo resulta en estimaciones vagas de tales variables. Consecuentemente, dichas variables deberían recibir bajas ponderaciones, de manera que el mayor peso de la información descanse en otras variables cuyo registro sea más confiable.

Es importante resaltar que la asignación de ponderaciones es un ejercicio conceptual que debe desligarse tanto de la escala de calificación definida para una variable (sección 3.1) como de las calificaciones particulares que pudiera recibir una UE (capítulo 5). Las ponderaciones deben asignarse mediante un ejercicio realizado con los desarrolladores de la herramienta, análogo al que se detalla en la sección 3.1.

Aunque los conceptos ponderación y escala de calificación de una variable son claramente diferentes, en ocasiones se hace difícil desligarlos, aun para expertos y diseñadores de la herramienta. En tal sentido, no se recomienda realizar estos dos ejercicios en simultánea para cada variable. Por el contrario, se recomienda un ejercicio en el que los participantes estén concentrados exclusivamente en el proceso de definición de la escala de calificación (sección 3.1) y otro en el que se concentren en el proceso de asignación de ponderaciones (sección 4.1).

El ejercicio de definición de ponderaciones debe estar en consonancia con los objetivos de los diseñadores de la herramienta, siendo esperable que ejercicios realizados por grupos con objetivos diferentes den lugar a distintas ponderaciones. Consecuentemente, es absolutamente necesario que todos los expertos que participen en el taller tengan presente qué es lo que se busca medir a través del ICI y los índices de condición de cada una de las dimensiones.

Debe tenerse presente que una variable podría aportar información sobre dos o más dimensiones con ponderaciones diferentes.

Aunque un ejercicio de asignación de ponderaciones puede basarse en cualquier escala, se considera cómodo tomar como guía una escala entre 1 y 5, a cuyos valores enteros podría hacérseles coincidir las siguientes etiquetas, para facilitar su visualización:

5: Máxima importancia/información
4: Alta importancia/información
3: Media Importancia/información
2: Baja importancia/información
1: Mínima importancia/información

Al asignar las ponderaciones, debe tenerse en cuenta que los niveles propuestos constituyen únicamente un guía, sin que el usuario deba restringirse a estos. La única restricción es mantenerse dentro de tales límites; no obstante, puede usarse cualquier valor intermedio de dicha escala. Asimismo, pueden repetirse ponderaciones, sin que sea necesario usar todos los niveles, ni satisfacer ninguna condición en cuanto a la suma de los ponderadores. En contraste con el ejercicio de definición de la escala de calificación, en este caso no se requiere incluir los valores extremos.

Debe tenerse presente que los ponderadores tienen un efecto multiplicativo y que la participación de las variables en el índice es relativa a la razón de sus ponderadores. Esto significa que una variable a la que se le asigne una ponderación de 4 tendrá el doble de peso sobre el cálculo del índice que una a la que se le haya asignado una ponderación de 2. Un par de ponderadores 2 y 1 tendrían exactamente el mismo efecto sobre la participación relativa de ese par de variables. El uso de los ponderadores extremos (5 y 1) tiene por efecto que la variable con máxima ponderación quede con 5 veces más peso que aquella con menor peso.

Asimismo, debe tenerse en cuenta que la participación diferenciada de las variables en una dimensión surge de los ponderadores diferenciados que se hubieran propuesto para tal dimensión. Así, si para una dimensión determinada se concluyera que todas las variables son absolutamente relevantes, asignándoles a todas ellas ponderación 5, el índice para la dimensión en cuestión se obtendría con base en un promedio aritmético (equiponderado) de las calificaciones de las diferentes variables. Esto sería equivalente a una situación en la que se considere que todas las variables son absolutamente irrelevantes, asignándoles a todas ellas ponderación de 1. En ambos casos todas las variables de la dimensión tendrían exactamente el mismo peso.

Una estrategia que facilita la asignación de ponderaciones diferenciadas —si fuera del caso— consiste en tomar como punto de partida una ponderación de 3 para todas las variables. A partir de este punto se analizaría cada variable, considerando si debería incrementársele o disminuírsele su ponderación con respecto al de una variable de importancia media, o si debería dejarse como tal.

Durante el ejercicio es necesario revisar constantemente las ponderaciones relativas de cada variable con respecto a todas las demás. Si se tiene, por ejemplo, la terna de ponderaciones 5, 2 y 1 para v1, v2 y v3 respectivamente, v2 queda con el doble de importancia con respecto a v3, pero pesa 2.5 veces menos que v1. Asimismo, v1 pesa 5 veces más que v3. Si esta situación no correspondiera con lo que se tenía en mente, habría que modificar las ponderaciones.

El ICI se calcula mediante el promedio ponderado de los índices de condición de las diferentes dimensiones consideradas, tal y como se detalla en el capítulo 6. Desde luego, la manera en que se ponderen las diferentes dimensiones, dándoles más peso a unas que a otras, deberá responder a los objetivos de quienes diseñan la herramienta. Si eventualmente se considerara que el ICI debería calcularse con igual participación de todas las dimensiones, bastaría con asignarles la misma ponderación (cualquiera que sea) a todas las dimensiones.

Cabe resaltar que la participación de las diferentes dimensiones en el cálculo del ICI depende exclusivamente de la ponderación que se les asigne, no viéndose afectada por el número de variables que se hubieran usado para calcular el índice de cada una de ellas. Luego, podría asignárseles la misma participación en el ICI a dos dimensiones, sin importar que el índice de una de ellas se hubiera calculado con base en 100 variables, mientras que el de la otra se hubiera calculado con solo 5.

Eventualmente podrían detectarse situaciones en las que un mismo aspecto se mida de muchas maneras diferentes, dando lugar a variables aparente diferentes que, sin embargo, son redundantes, y se refieren a un mismo concepto. Para evitar que la redundancia en la evaluación de tal concepto dé lugar a una sobreponderación del mismo, puede recurrirse a convertir el concepto en cuestión en un constructo intermedio, mediante la estrategia del uso de constructos de diferentes jerarquias que se exponen en el capítulo 8.

Vale la pena anotar que el ejercicio de ponderación de las dimensiones es independiente de los ejercicios de ponderación de cada una de las variables que conforman las dimensiones. Con el fin de resaltar la diferencia de tales ponderaciones, se han elegido símbolos diferentes: \(p_i\) para las ponderaciones de las variables sobre las dimensiones, y \(\pi_j\) para las ponderaciones de las dimensiones sobre el ICI (capítulo 6).

Finalmente, cabe señalar que, aunque en muchas ocasiones el usuario pude querer contar con un índice de condición integral, para fines de valoración global de las UE, en muchas otras puede considerarse carente de sentido un índice que pretenda integrar dimensiones muy disímiles. En cualquier caso —sea que se calcule el ICI o no— podrán calcularse los índices de condición para cada una de las dimensiones.

4.1 Definición de las ponderaciones

La manera en la que se asignen las ponderaciones de cada variable sobre una dimensión específica define la esencia de dicha dimensión. Su definición es un aspecto netamente conceptual que depende exclusivamente del enfoque y los objetivos de los diseñadores de la herramienta. Por ende, no se recomienda generar ponderaciones mediante ningún procedimiento estadístico (v. g., componentes principales).

Tal y como se indicó en la sección 3.1, la complejidad del proceso evaluado, así como las especificidades de sus dimensiones indicarán si puede realizarse un único taller con expertos holísticos o si, por el contrario, resulta más pertinente realizar múltiples talleres con expertos de diferentes áreas.

A continuación se presentan los pasos que podrían seguirse en la realización de un taller de ponderaciones.

1. Tras haber convocado y reunido al grupo de panelistas, el moderador expone lo concerniente a la escala de ponderación general que se utilizará, haciendo notar que las ponderaciones dan lugar a pesos relativos, con lo cual una variable que se pondere con 4 pesará el doble que una que se pondere con 2. Igualmente, en este paso puede sugerírseles la estrategia de tomar como punto de partida una ponderación de 3 para todas las variables.

   Se hace énfasis en que en esta etapa no se analizan las diferentes categorías de las variables, sino que cada variable se considera como un todo, valorando lo importante o poco importante y/o informativa que sea en la definición de una dimensión determinada.

2. A continuación, el moderador realiza una exposición sobre la primera dimensión y las variables que la conforman, destacando el peso o importancia de cada una de ellas en la conformación de dicha dimensión. Debe mencionarse en esta parte lo concerniente a la dificultad que podría subyacer en la calificación de ciertas variables o a la poca confiabilidad de tales calificaciones.

3. A continuación, puede abrirse un espacio de discusión en el que los participantes que lo deseen amplíen, puntualicen o rectifiquen lo expresado inicialmente por el moderador. También podrían proponerse otras variables que inicialmente no hubieran sido consideradas como informativas para dicha dimensión. Cuando se tenga suficiente ilustración, se pasará a proponer las ponderaciones.

4. Cada uno de los participantes propondrá ponderaciones para cada una de las variables que conformen la dimensión considerada. Es conveniente que cada panelista analice simultáneamente todas las variables de la dimensión (en lugar de ponderar independientemente cada variable), de manera que, mientras esté trabajando una dimensión específica, tenga un panorama completo de los pesos relativos de todas las variables que la conforman, reajustándolos si fuera del caso, para generar una ponderación consistente.

   En esta etapa, se les sugiere a los participantes que se abstengan de proponer ponderaciones para variables cuyo peso sobre una dimensión determinada no se tenga muy claro. Esto no afecta el proceso, sino que, por el contrario, lo hace más objetivo, dado que las ponderaciones resultantes estarán basadas en las que propongan quienes tengan un criterio más claro al respecto.

   Debe indicárseles que, aun en caso de haber atendido la recomendación de tomar ponderaciones 3 como punto de partida para todas las variables, deberían retirar aquellas de las que no se sientan muy seguros.

   Es importante aclarar que las abstenciones tienen lugar dejando el espacio vacío o borrando cualquier valor previo que pudiera haber estado en el espacio. No debe usarse 0 como indicador de abstención, pues este valor entraría en el cálculo como una ponderación nula, excluyendo la variable de la dimensión.

5. Por la complejidad de la escala multiplicativa, no sería adecuado resumir las propuestas de ponderación de los diferentes panelistas usando directamente la mediana (ni tampoco la media). Los cálculos para llegar a una propuesta consenso deben realizarse con base en la metodología que se expone en la sección 4.1.1.

6. Tras finalizar las ponderaciones de una dimensión, se pasa a la siguiente, retomando desde el segundo punto. Debe tenerse en cuenta que las nuevas dimensiones que se consideren podrían involucrar variables que ya hubieran participado en otras dimensiones. No obstante, la ponderación de tales variables debe enfocarse en la dimensión que se esté evaluando, sin importar cómo hubiera sido su ponderación para otras dimensiones.

7. Al final del ejercicio podría proponerse una ponderación de cada una de las dimensiones, para la construcción de un ICI. Para tal efecto, podría adaptarse lo expuesto en los numerales 2 a 5.

Tal y como se indicó para el ejercicio de definición de la escala de calificación (cf. sección 3.1), podría considerarse una variante de la anterior propuesta, en la que no se busque captar los criterios de los expertos de manera independiente, sino a través de un consenso. En tal caso, las diferentes exposiciones, tanto del moderador como de los expertos, irían abordando simultáneamente la importancia de las diferentes variables en cada dimensión, junto con sus ponderaciones. Se esperaría que al final del análisis de cada dimensión, las diferentes variables que la conforman quedaran asociadas con una ponderación. Los diseñadores de la herramienta deberán evaluar la pertinencia de una u otra metodología (conceptos independientes vs. consenso), pudiendo incluso adaptar alguna metodología híbrida.

4.1.1 Cálculo de las ponderaciones

Debido a la naturaleza multiplicativa de las ponderaciones, se hace necesario ‘estandarizar’¹⁰ las propuestas de los expertos antes de generar un conjunto de ponderaciones consenso.

Considérese una situación en la que un par de expertos, A y B, realizan propuestas de ponderación sobre las variables v1 y v2, acorde con la información consignada en la siguiente tabla.

Variable	Ponderación experto A	Ponderación experto B
v1	1	4
v2	2	2

En la situación ilustrada, el experto A considera que v2 debería tener el doble de peso con respecto a v1. El experto B, por su parte, considera que es v1 la que debería tener el doble de ponderación con respecto a v2. Un adecuado proceso para consensuar los criterios de los dos expertos debería conducir a iguales ponderaciones para cada una de las variables, lo que significaría aplicar un promedio aritmético a las calificaciones que estas hubieran recibido sobre una UE particular.

Para ilustrar lo indicado anteriormente, supongamos que, en adición a las ponderaciones propuestas, se tienen las siguientes calificaciones para una UE particular: v1 = 5 , v2 = 3 . Acorde con lo expuesto, un índice basado en estas dos variables sería el promedio aritmético de tales calificaciones, es decir, 4. Esto puede ilustrarse promediando los índices obtenidos a partir de las propuestas de los dos expertos¹¹.

\[\begin{align*} ind &= \frac{ind_{\text{expA}}+ind_{\text{expB}}} {2}\\\\ &= \frac{\frac{\color{blue}1(\color{gray}5)+\color{blue}2(\color{gray}3)}{3}+\frac{\color{red}4(\color{gray}5)+\color{red}2(\color{gray}3)}{6}}{2}\\\\ &=\frac{\frac{11}{3}+\frac{26}{6}}{2}= \frac{\frac{11}{3}+\frac{13}{3}}{2}\\\\ &= \frac{\frac{24}{3}}{2}= \frac{8}{2}=4\\\\ \end{align*}\]

Sin embargo, no es esto lo que se obtendría si tras un ejercicio como el que se detalla en la sección 4.1 se promediaran las propuestas de ponderación de los diferentes expertos para cada variable y se calculara posteriormente el índice. En tal caso, la ponderación promedio de v1 sería 2.5, y la de v2 quedaría en 2 , con lo cual v1 quedaría pesando 1.25 veces más que v2: el índice sería 4.11.

A fin de hacer comparables las ponderaciones propuestas por los diferentes expertos, es necesario estandarizar los valores propuestos por cada uno de los participantes, de manera que se sigan manteniendo las relaciones de razón definidas por cada uno de ellos y que las propuestas de los diferentes participantes tengan el mismo centro. Esto se logra dividiendo las ponderaciones de cada participante entre el promedio de sus ponderaciones . En el presente ejemplo, las propuestas de ponderación del experto A se dividen entre 1.5, mientras que las del experto B se dividen entre 3.

Variable	Ponderación experto A	Ponderación experto B	Pond. experto A estandarizada	Pond. experto B estandarizada	Ponderación consenso
v1	1	4	0.6666	1.3333	1
v2	2	2	1.3333	0.6666	1
v2	1.5	3	1	1

Puede observarse que, las ponderaciones estandarizadas siguen manteniendo las relaciones de razón propuestas inicialmente por los expertos (1:2 para el experto A y 2:1 para el experto B), y adicionalmente tienen el mismo centro (quedan centradas en 1). En virtud de ello, se hace posible promediar las diferentes ponderaciones, llegándose a una propuesta consensuada, que, para el presente ejemplo, es de un ponderador 1 para v1 y un ponderador 1 para v2.

Este procedimiento puede expresarse así:

\[ p_i= \frac{\sum\limits_{j=1}^{e} {\frac{p_{ij}}{\overline{p}_{\bullet j}}}} {e} \] donde:
\(p_i\) : Ponderación consenso de la \(i\)-ésima variable
\(e\) : Número de expertos
\(p_{ij}\) : Ponderación propuesta para la \(i\)-ésima variable por el \(j\)-ésimo experto
\(\overline{p}_{\bullet j}\) : Ponderación promedio del \(j\)-ésimo experto

Aunque este procedimiento resuelve el problema de centrado, permitiendo promediar las diferentes propuestas, sigue latente la falta de robustez de la media frente a la presencia de valores extremos. Consecuentemente, tras realizar el procedimiento de estandarización resulta más deseable calcular la mediana de los diferentes ponderadores estandarizados, lo cual puede expresarse así:

\[ p_i= \text{mediana}\left\{ \frac {p_{ij}} {{\overline{p}_{\bullet j}}} \right\}_{j=1}^e \] donde:
\(p_i\) : Ponderación consenso de la \(i\)-ésima variable
\(p_{ij}\) : Ponderación propuesta para la \(i\)-ésima variable por el \(j\)-ésimo experto
\(\overline{p}_{\bullet j}\) : Ponderación promedio del \(j\)-ésimo experto
\(e\) : Número de expertos

Debe tenerse presente que, sea que se calcule la media o la mediana, las ponderaciones faltantes no participan en el cálculo. Cuando se realizan los cálculos mediante una hoja de Excel o similar, debe prestarse particular atención a esta situación, asegurándose de no convertir inadvertidamente la información faltante en ceros.

Aunque el procedimiento expuesto genera las ponderaciones consenso requeridas para alimentar directamente la función ici (capítulo 7) y calcular los índices de interés, estas no son fáciles de visualizar por causa de la estandarización realizada. Luego, aunque sean completamente válidas para los cálculos, podrían desconcertar a los invitados al taller, quienes no verían allí reflejadas sus aportaciones. Incluso para los constructores de la herramienta, esta escala estandarizada resultaría incómoda y difícil de interpretar, no siendo evidentes las relaciones de razón que se dan entre las diferentes variables. En consecuencia, es recomendable aplicar un escalamiento a las ponderaciones obtenidas, para facilitar su visualización e interpretación.

Es válido usar cualquier transformación multiplicativa, es decir, multiplicar las ponderaciones obtenidas por cualquier constante. Tales transformaciones conservan las relaciones de razón. A continuación se presentan 3 opciones de escalamiento igualmente válidas, que pueden facilitar el análisis de las ponderaciones desde diferentes puntos de vista.

La primera de ellas le asigna el valor 1 a la mínima ponderación, lo que facilita visualizar cuántas veces más pesa cada variable con respecto a la de ponderación mínima. Este escalamiento se obtiene mediante la siguiente expresión:

\[ p_{Fj}=\frac {p_{Ij}}{\text{min}{\{p_{Ij}\}}} \] donde:
\(p_{Fj}\) : Ponderación final para la \(j\)-ésima variable
\(p_{Ij}\) : Ponderación inicial para la \(j\)-ésima variable por el \(j\)-ésimo experto
\(\text{min}{\{p_{Ij}\}}\) : Mínima ponderación inicial del conjunto de ponderaciones sobre las \(j\) variables

Aunque el escalamiento propuesto anteriormente facilita visualizar cuántas veces más pesa cada variable con respecto a la de mínima ponderación, el usuario podría no tener mucho interés en comparar todas las variables contra la más irrelevante. Por el contrario, el usuario podría estar más interesado en las variables de mayor relevancia. Un segundo escalamiento le asigna el valor 5 a la máxima ponderación, lo que facilita visualizar qué tan alejadas están las demás variables con respecto a la más importante. Este escalamiento se obtiene mediante la siguiente expresión:

\[ p_{Fj}=\frac {5p_{Ij}}{\text{max}{\{p_{Ij}\}}} \]

donde:
\(p_{Fj}\) : Ponderación final para la \(j\)-ésima variable
\(p_{Ij}\) : Ponderación inicial para la \(j\)-ésima variable por el \(j\)-ésimo experto
\(\text{max}{\{p_{Ij}\}}\) : Máxima ponderación inicial del conjunto de ponderaciones sobre las \(j\) variables

Un último escalamiento presenta las ponderaciones de manera porcentual, entre 0 y 100. Aunque este escalamiento pueda no ser muy intuitivo para visualizar relaciones de razón¹², brinda cierta familiaridad al presentar la repartición de las ponderaciones en la torta porcentual. Este escalamiento se obtiene mediante la siguiente expresión:

\[ p_{Fj}=\frac {100p_{Ij}}{\sum\limits_{j} {{p_{Ij}}}} \] donde:
\(p_{Fj}\) : Ponderación final para la \(j\)-ésima variable
\(p_{Ij}\) : Ponderación inicial para la \(j\)-ésima variable por el \(j\)-ésimo experto
\(\sum\limits_{j} {{p_{Ij}}}\) : Total de las ponderaciones iniciales sobre las \(j\) variables

La figura 4.1 esquematiza los procesos realizados para la obtención de las ponderaciones consenso escaladas.

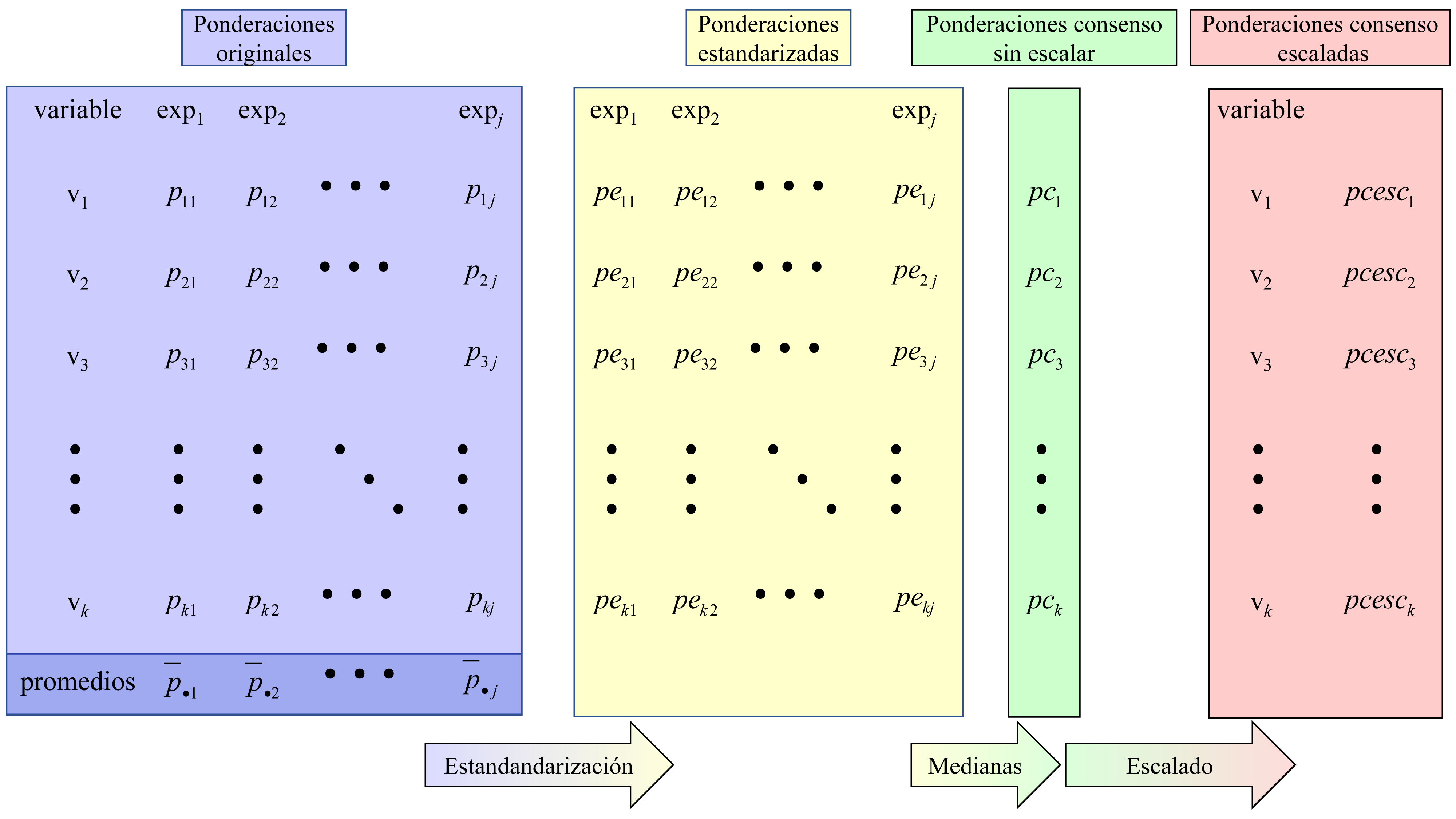
Figura 4.1: Procesos involucrados en la obtención de las ponderaciones consenso escaladas.

Para ilustrar el proceso completo, considérese la propuesta de ponderación de 10 expertos para 5 variables que se encuentra en el libro Excel ici_pond.xlsx. Los cálculos manuales se ilustran en la segunda hoja (pond.consenso manual). Nótese que algunos expertos dejaron de ponderar algunas de las variables e incluso, uno de los expertos (e4) no propuso ponderaciones para ninguna de las variables.

Variable	e1	e2	e3	e4	e5	e6	e7	e8	e9	e10
v1	2	3			1	1	3	4	1	1
v2	2	5			2	1	3	4	1
v3	2		2		3	3	5	5	1
v4	1	1	2		4	3	5	5	2
v5	5	1	2		5	3	5	5	2	2

Alternativamente, si se hubiera realizado un ejercicio en línea, podrían leerse las ponderaciones desde una hoja de cálculo de Google¹³, que estuviera conformada por una hoja (sheet) por cada uno de los expertos que hubieran participado en el ejercicio. La hoja correspondiente a cada experto estaría marcada con su nombre o algún otro identificador y constaría de dos columnas. En la primera irían los nombres de las variables consideradas; en la segunda, las ponderaciones propuestas.

La hoja correspondiente al segundo experto tendría el siguiente aspecto:

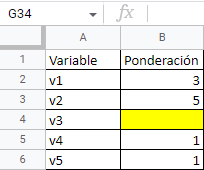
En este caso no se usaría el argumento data; en su lugar se usaría el argumentos ID, mediante el cual se incluye el identificador de la hoja, es decir, la parte larga de la dirección la dirección que aparece entre dos barras. Este identificador debe ir entrecomillado. También puede usarse la URL completa.

Si las ponderaciones se leen desde un archivo Excel, la función ici_pond{ici} se invoca usando como argumento el nombre del archivo que contiene la información:

ici_pond("ici_pond.xlsx")

Si la información se recogió en una hoja de cálculo de Google, la función se invoca usando el ID del como argumento¹⁴: :

ici_pond(ID = "1Rl1XpHYHWJWdlUalLZQYypjprt0o7RpwF1NGrufQoE4")

Se obtiene el siguiente resultado:

#>    Variable   min1 wg   max5 wg   percent wg
#>          v1      1.00      2.68         14.6
#>          v2      1.00      2.68         14.6
#>          v3      1.40      3.75         20.4
#>          v4      1.59      4.27         23.2
#>          v5      1.87      5.00         27.2

Puede verificarse que para cualquiera de los escalamientos se satisfacen las mismas relaciones de razón entre los ponderadores de diferentes variables. Luego, cualquiera de estas versiones dará lugar a los mismos índices de condición. Se insiste en que estos diferentes escalamientos se presentan únicamente para facilitar la visualización e interpretación de las ponderaciones resultantes.

Cuando se trabaja en la nube usando hojas de cálculo de Google, los resultados se copian por defecto en una hoja llamada consensus weight, la cual se agrega al final de la hoja de cálculo de Google (Google Sheets). Para evitar que se genere la hoja de ponderaciones consenso, basta con usar el argumento cons = FALSE; en tal caso, en lugar de generar la hoja adicional, los resultados se mostrarán en consola.

Si tras la realización de ejercicios piloto se hubiera creado la hoja resumen consensus weight, no sería necesario eliminarla para realizar adaptaciones posteriores; la función ici_pond reconocería la hoja en cuestión, sin incorporarla en los nuevos cálculos y sobrescribiéndola acorde con estos.