Chapter 9 Bias correction and Downscaling

9.1 Terminology

• In the scientific literature both ‘bias correction’ and ‘bias adjustment’ are used, here we use bias correction.

9.2 Why are models biased and do we need bias correction?

• Why do we need bias correction? —> direct output from Climate Data Store could be used, but: for impact studies these outputs are often not useful because of significant biases, for example:
  • Temperature can be consistently too high
  • Rainfall too high or low
  • Model does an incorrect simulation of the monsoon, the rains start too early or too late
  • Climate models tend to overestimate the number of days with rain and underestimate precipitation extremes.
• Why are the models biased?
  • Limited spatial resolution (large grid boxes)
  • Simplified physics
  • Incomplete knowledge of the earth’s climate system

9.3 Examples of model bias

9.3.1 Geographical differences

Precipitation example: for a result of model precipitation estimates (a), there is a certain bias (Multi Model Mean Bias) depending on the location (b). This can also be expressed in Multi Model Mean of Absolute Error (c) and Multi Model Mean of Relative Error (d). A similar analysis can be made for temperature.

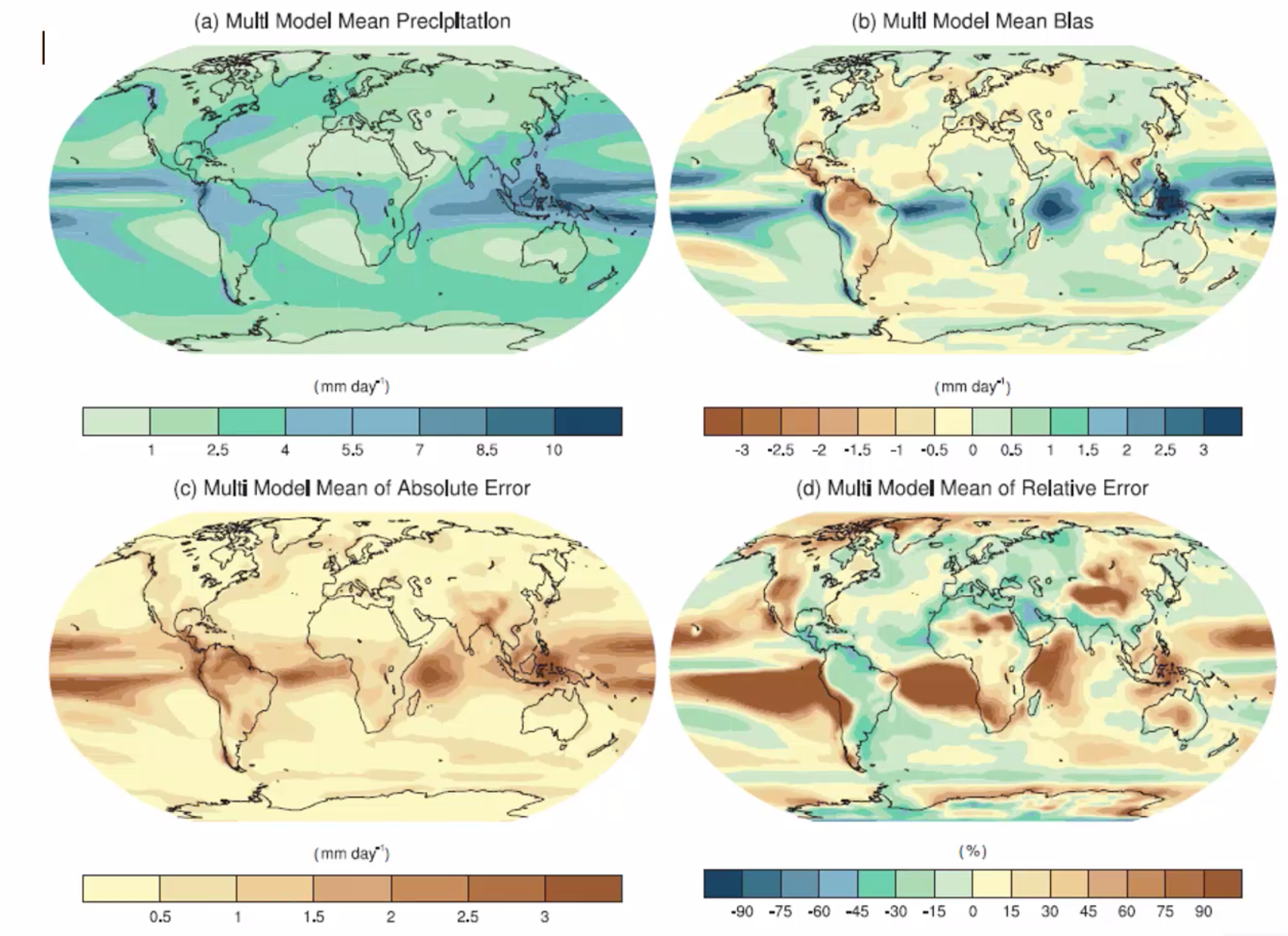
precipitation bias

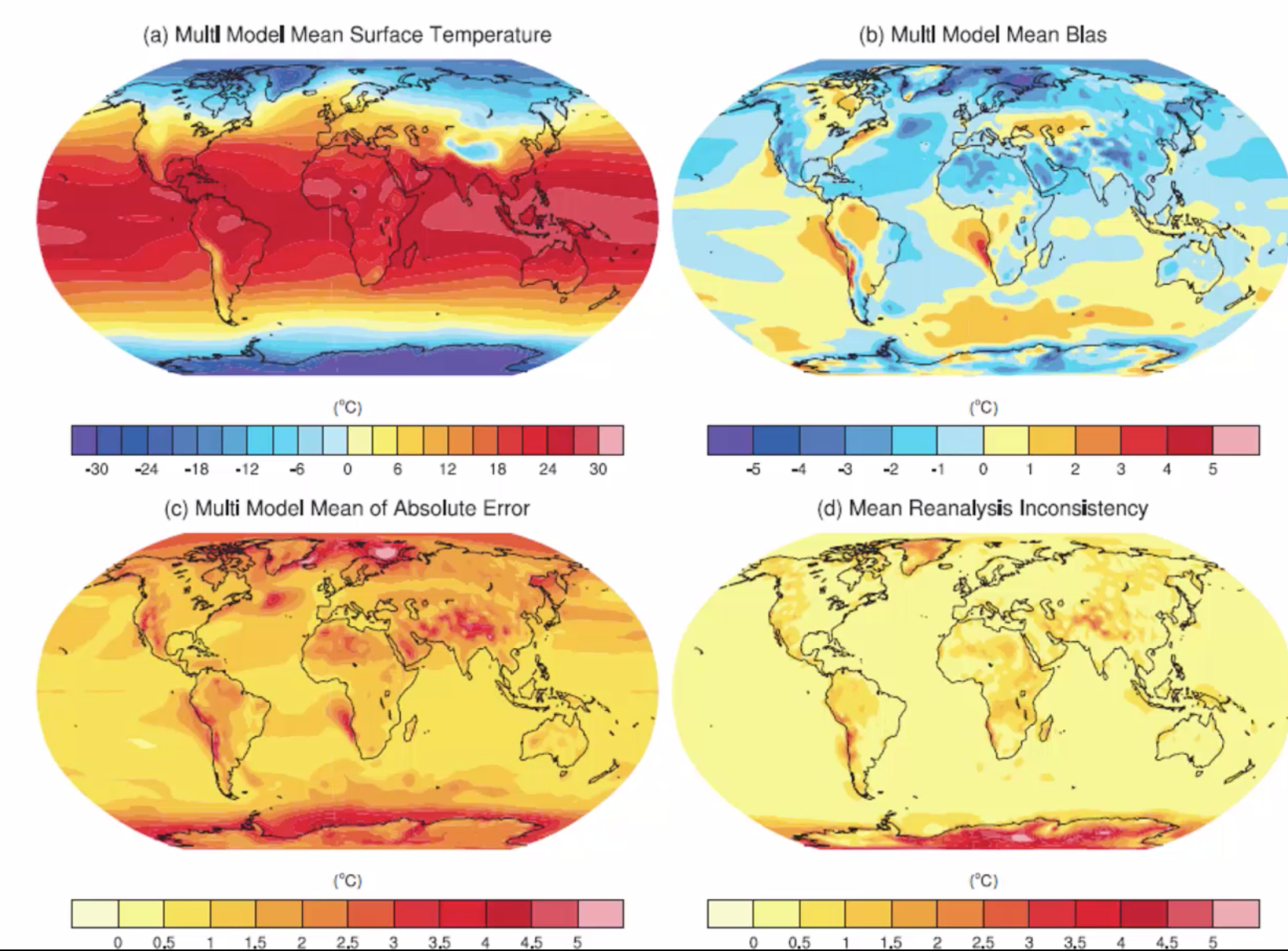
temperature-bias

9.3.2 Differences in amount of bias

When looking at model bias for temperature and precipitation for different regions (x-axis), it can be seen that the predicted change in temperature is equal to the bias in the model. For precipitation the bias is even more important. Lots of models over- or underestimate precipitation (sometimes only 50 % of what is observed on-site/in-situ)

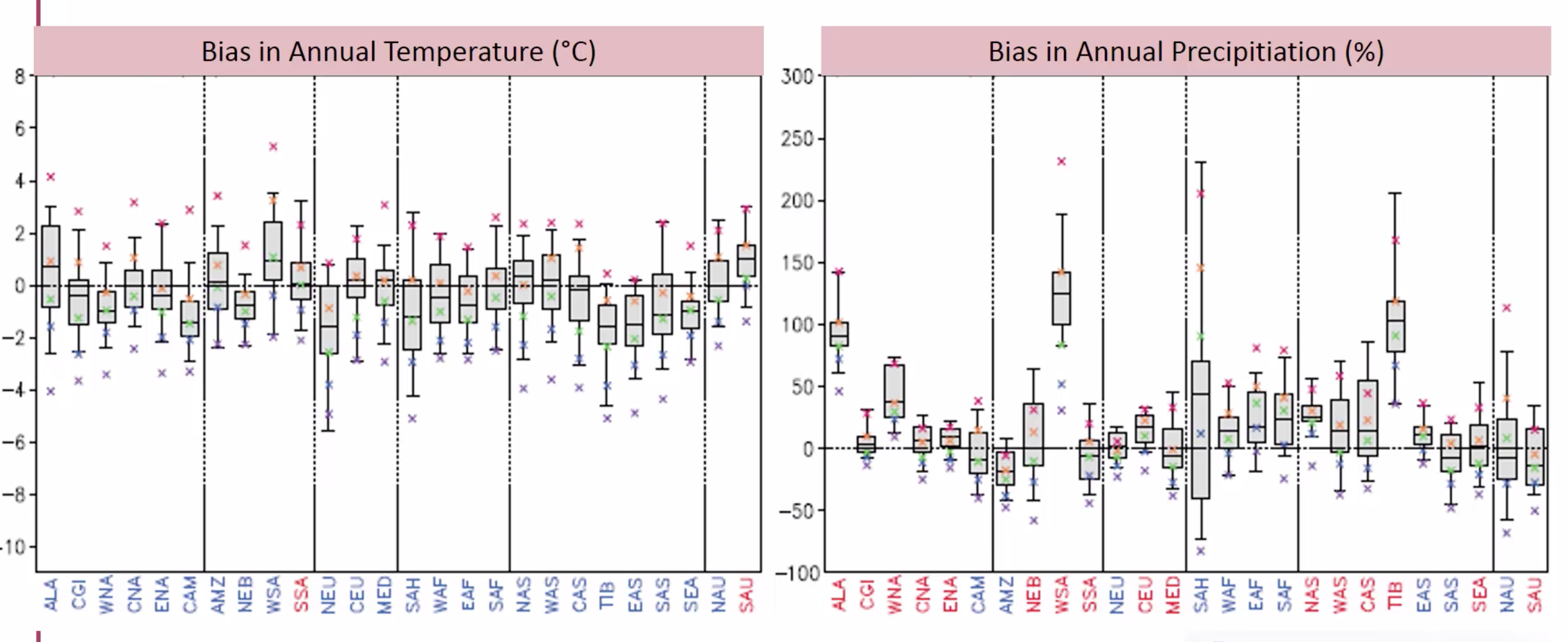
temperature-precipitation-bias

9.4 Impact of model bias on climate assessments

• If your main interest is relative change in future climate, bias is not a big problem.
• Bias is important for:
  • Threshold analysis (crop behavior at certain temperatures, …)
  • Water availability analysis: bias in rainfall can have large impact
  • Estimation of extremes: future changes in flood risk can be calculated wrong

9.5 Theory of bias correction and downscaling

For an overview of theory of dynamical and statistical downscaling, see [the dedicated chapter above][Dynamical and statistical downscaling theory]

Bias correction model: present climate as simluated by the climate model (G) or observed (O) : difference is bias B. We also have change (C) to a future climate as modeled by the model (G’) and the future observed climate (O’).

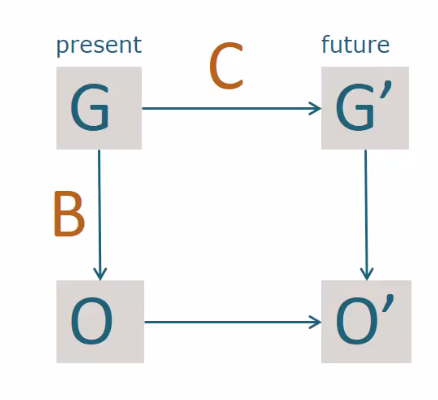
bias-correction-theory

• Assumptions applied when using this model:
  • Bias of present and future model is equal
  • The climate model results of the current climate is more or less correct
• function B can have different shapes:
  • Linear function
  • Scale transfer function with mean, variance and shape.
• B can be estimated:
  • Dynamical (using climate models)
  • Statistical, using:
    • weather typing/analogues
    • weather generator [ (non) stationary ]
    • transfer functions: (non) linear or PDF mapping functions (with distribution)

9.6 Bias correction example - tutorial

See excel files Bias correction tutorial COP10 ULS.xlsxand Bias correction tutorial COP10 ULS-solution.xlsx. Given data (for Kenya) is the historical rainfall (observations + 4 GCM model results) and 4 GCM predictions.

1. calculate average rainfall for observations + each of the GCM models —> large differences, bias needed
2. calculate absolute bias by substracting observations from global climate model results.
3. To correct future data (2070-2099) and calculate future average rainfall, we need relative bias correction factors: divide the observation output by the GCM output.
4. To correc the future data, multiply the non-bias corrected GCM output with the relative bias correction factor, and calculate the average for each GCM.