• Notes for STAT 510 ISU
  • Introduction
  • 1 Preliminaries
  • 2 Review of Linear Models
  • 3 The F test for Comparing Reduced vs. Full Models
  • 4 Analysis of Two-Factor Experiments Based on Cell Means Models
  • 5 Analysis of Two-Factor Experiments Based on Additive Models
  • 6 Analysis of Variance (ANOVA)
  • 7 ANOVA for Balanced Two-Factor Experiments
  • 8 ANOVA for Unbalanced Two-Factor Experiments
  • 9 Orthogonal Linear Combinations, Contrasts and Additional Partitioning of ANOVA Sums of Squares
  • 10 The Aitken Model
  • 11 Linear Mixed-Effects Models
  • 12 The ANOVA Approach to the Analysis of Linear Mixed-Effects Models
  • 13 The Cochran-Satterthwaite Approximation for Linear Combination of Mean Squares
  • 14 Linear Mixed-Effects Models for Data from Split-Plot Experiments
  • 15 ANOVA for Balanced Split-Plot Experiments
    • Inference for Whole-Plot
    • Inference for Split-Plot
    • Inference for Interactions
  • 16 SAS Analysis of Split-Plot Experiments
  • 17 R Analysis of Split-Plot Experiments
  • 18 More Example Split-Plot Experiments
  • 19 Maximum Likelihood Estimation for the General Linear Model
  • 20 REML Estimation of Variance Components
  • 21 BLUP of Random Effects in Normal Linear Mixed Effects Model
  • 22 Additional Topics Related to Likelihood
  • 23 Repeated Measures
  • 24 R Code for the Repeated Measures
  • 25 SAS Code for the Repeated Measures
  • 26 A Generalized Linear Model for Bernoulli Response Data
  • 27 A Generalized Linear Model for Binomial Response Data
  • 28 A Generalized Linear Model for Poison Response Data
  • 29 Generalized Linear Mixef-Effects Model
  • Go to my webpage

510 Notes

Chapter 22 Additional Topics Related to Likelihood

  • Akaike’s Information Criteria: \(AIC = -2\ell(\hat\theta) + 2k\).

  • Schwarz’s Bayesian Information Criterion: \(BIC = -2\ell(\hat\theta) + k\ln n\)

    If REML likelihoods are used, compared models must have the same model for the response mean. Different models for the mean would yield different error contrasts and different datasets for computation of maximized REML likelihoods.

  • Asymptotic normality of \(\hat\theta\): for sufficiently large \(n\), \(\hat\theta \stackrel{\cdot}{\sim} N(\theta, I^{-1}(\theta))\) where \(I(\theta) = \left[-E\{\frac{\partial^2 \ell(\theta)}{\partial \theta_i \partial \theta_j} \} \right]\) is called Fisher Information matrix.

    • This implies \((\hat\theta - \theta)'[\widehat{Var}(\hat\theta)]^{-1}(\hat\theta - \theta) \stackrel{\cdot}{\sim}(\hat\theta - \theta) \stackrel{d}{\rightarrow} z'z \sim \chi_k^2\).

  • Wald Tests: Suppose for large \(n\) that \(\hat\theta \stackrel{\cdot}{\sim} N(\theta, \widehat{Var}(\hat\theta))\), then a confidence interval for \(c'\theta\) that has confidence level approximately equal to \(1 - \alpha\) is \(c'\hat\theta \pm z_{1-\alpha/2}\sqrt{c'\widehat{Var}(\hat\theta)c}\). Likewise, if \(C\) is a \(q \times k\) matrix of rank \(q\), a test of \(H_0: C\theta = d\) can be based on the test statistic \[ (C\hat\theta - d)'[C\widehat{Var}(\hat\theta)C']^{-1}(C\hat\theta - d) \sim \chi_q^2 \]

  • Multivarite Delta Method: Suppose a \(g\) is a function from \(R^k\) to \(R^m\), i.e. \(g = [g_1(\theta), \ldots, g_m(\theta)]'\). Let \(D \equiv \frac{\partial g}{\partial \theta}\) be the derivative matrix. By Taylor’s theorem, \(g(\hat\theta) \approx g(\theta) + D'(\hat\theta - \theta)\) which implies \(E(g(\hat\theta)) \approx g(\theta) + D'E(\hat\theta - \theta) = g(\theta)\) and \(Var(g(\hat\theta)) \approx Var[g(\theta) + D'(\hat\theta - \theta)] = D'Var(\hat\theta)D\). Therefore, \(g(\hat\theta) \stackrel{\cdot}{\sim} N(g(\theta), D'Var(\hat\theta) D)\).

  • Likelihood Ratio: Define \(\Lambda\) as \(\frac{\text{Reduced Model Maximial likelihood}}{\text{Full Model Maximized Likelihood}}\). \(-2\ln(\Lambda)\) is known as the likelihood ratio test statisti and \(-2\ln(\Lambda) \sim \chi_{k_f - k_r}^2\) under the null hypothesis.

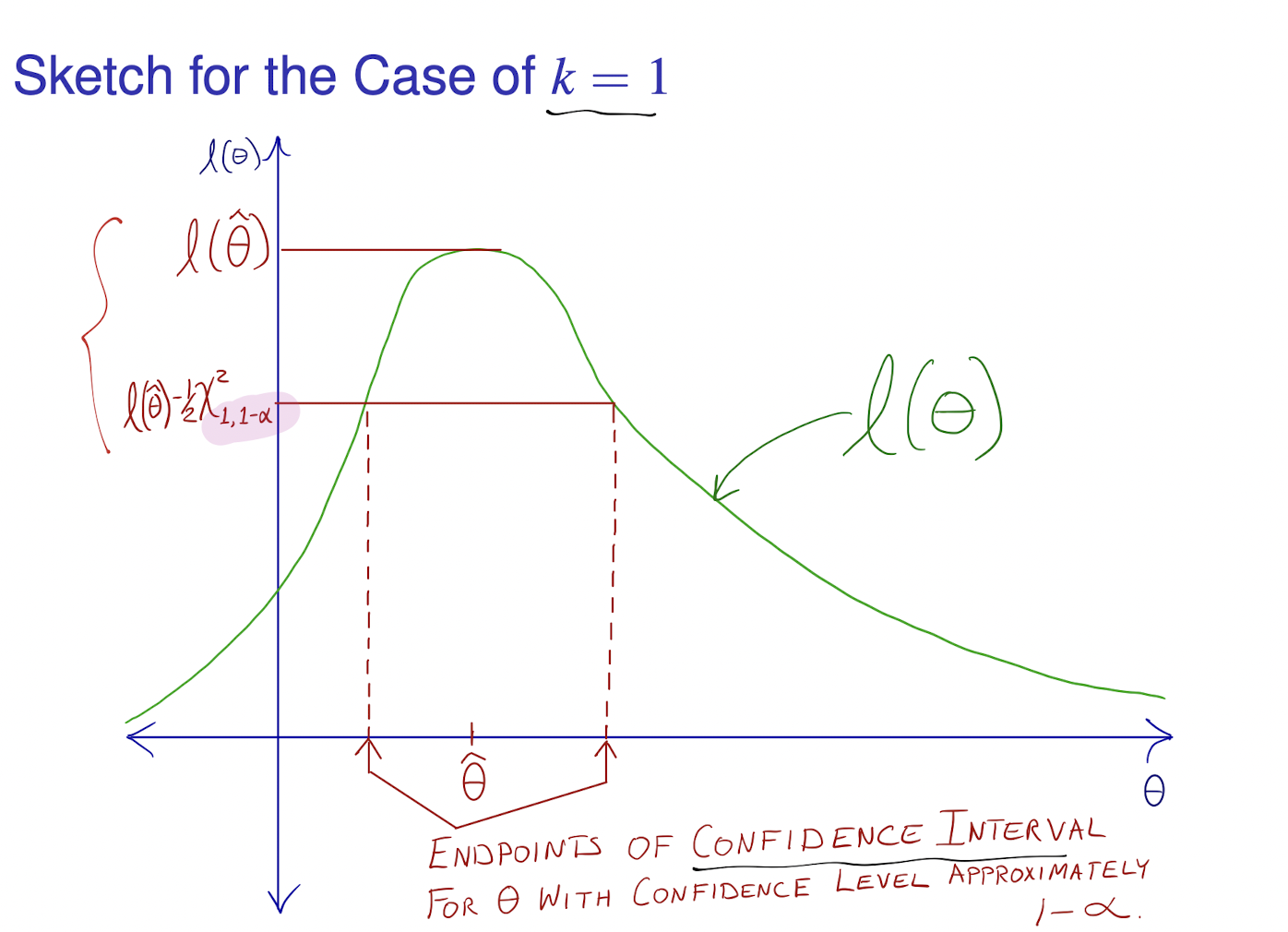
  • Profile Likelihood Confidence: \(\{\theta_1: \ell(\theta_1, \hat\theta_2(\theta_1)) \geq \ell(\hat\theta) - \frac{1}{2} \chi_{k_1, 1-\alpha}^2\}\).